Determination of Dielectric Properties of Cells using AC Electrokinetic-based Microfluidic Platform: A Review of Recent Advances
Abstract
:1. Introduction
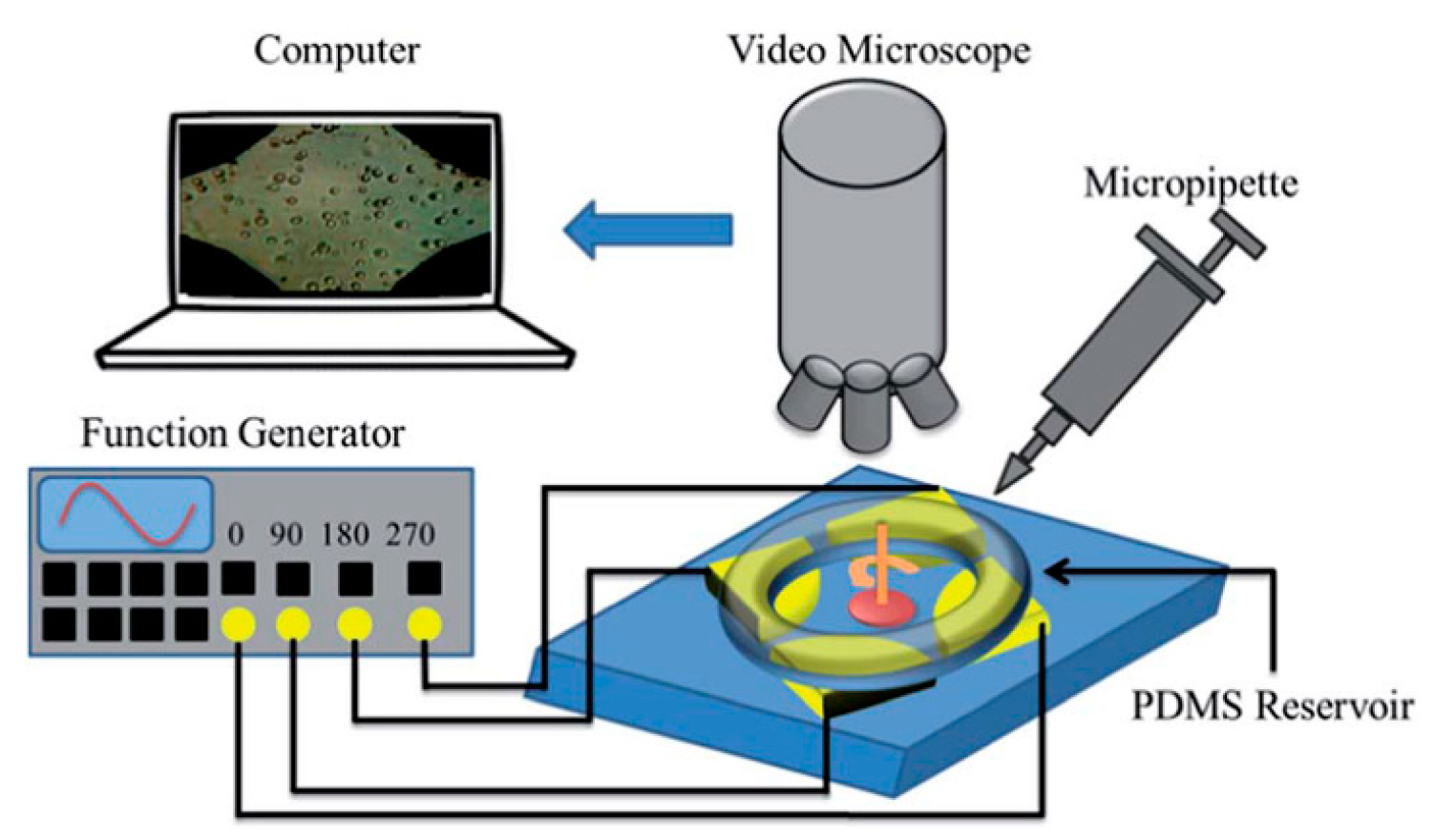
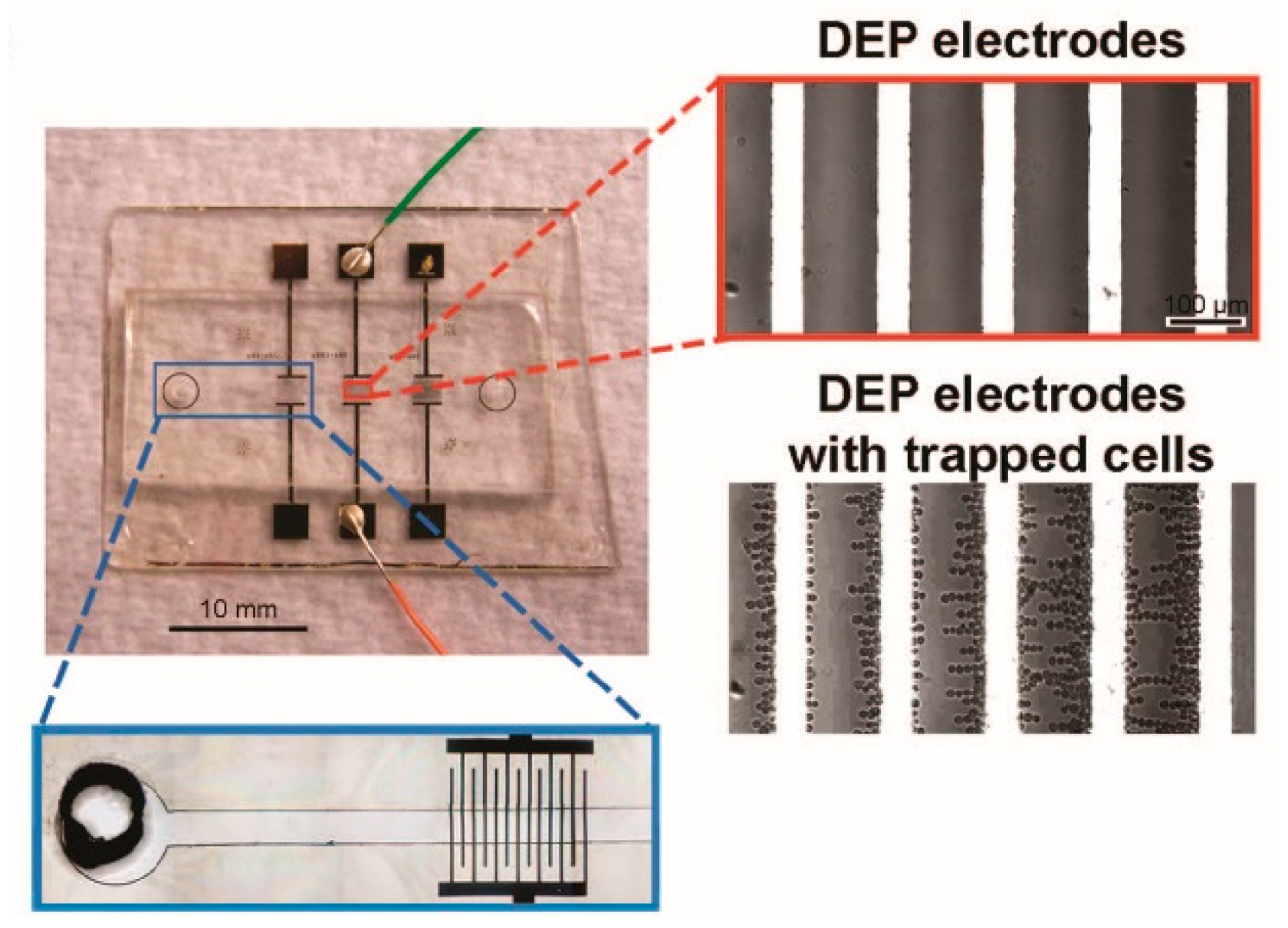
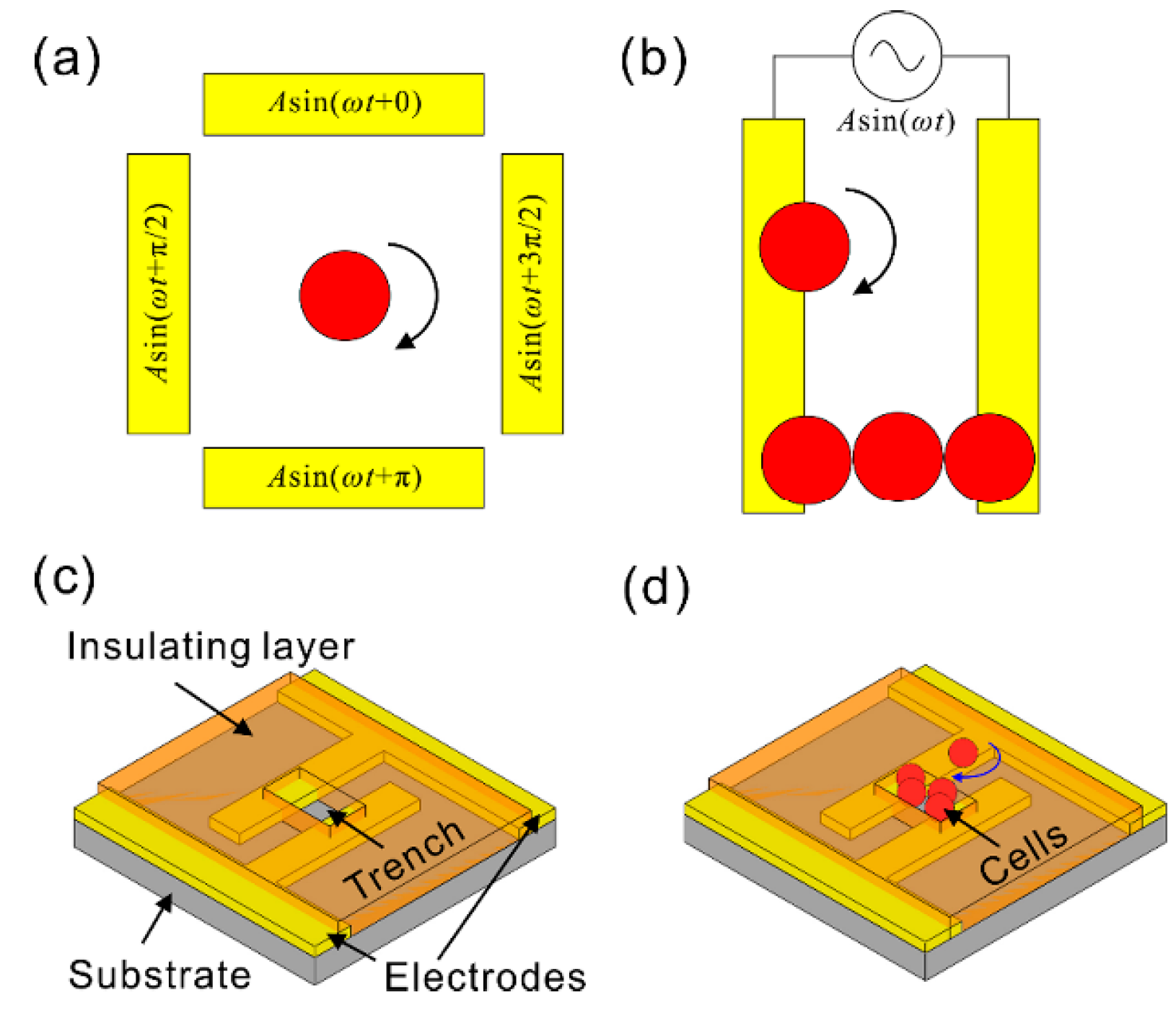
2. Chip Structure and Working Principle
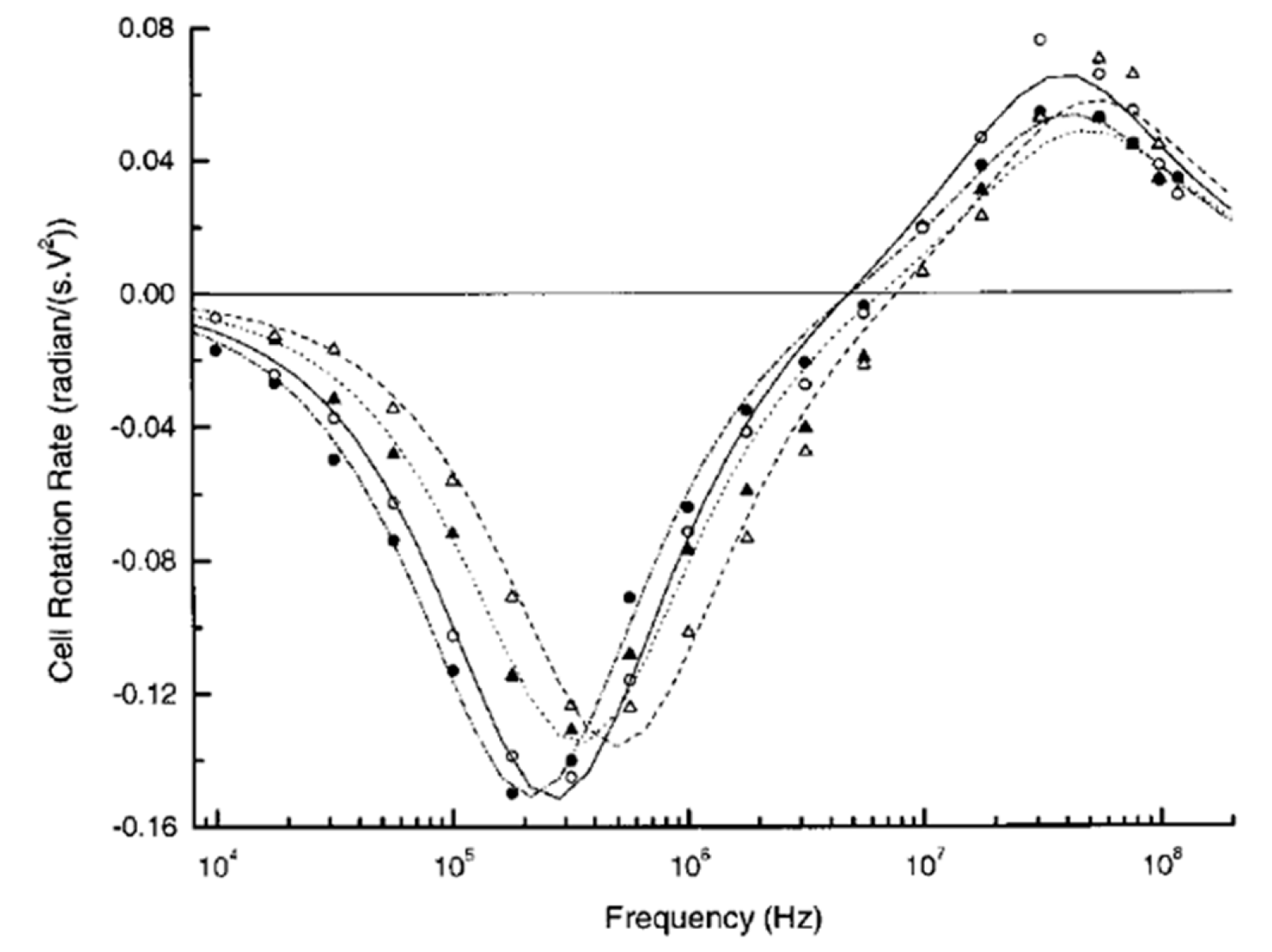
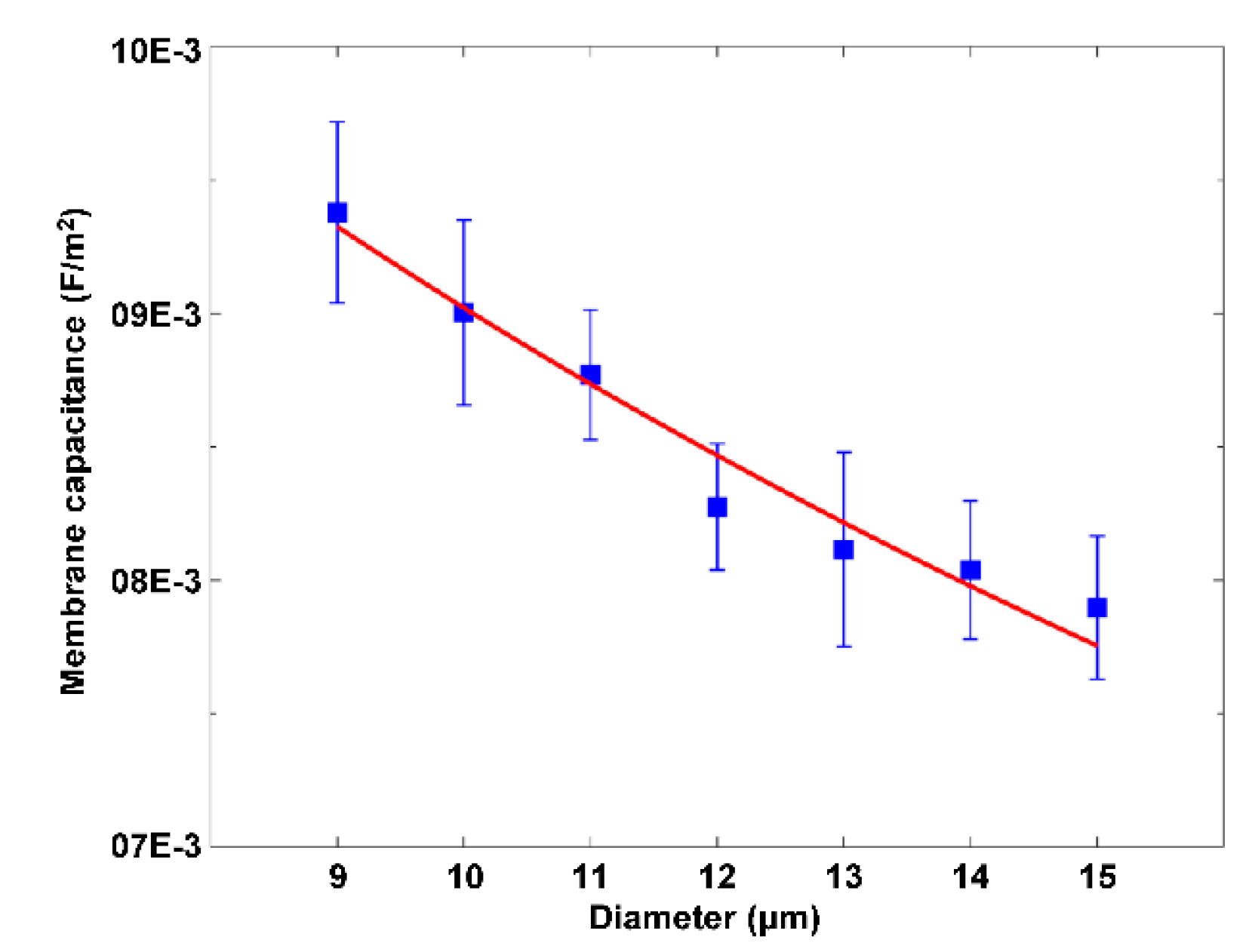
3. ROT-Based Extraction of Cell Dielectric Parameters and Its Applications
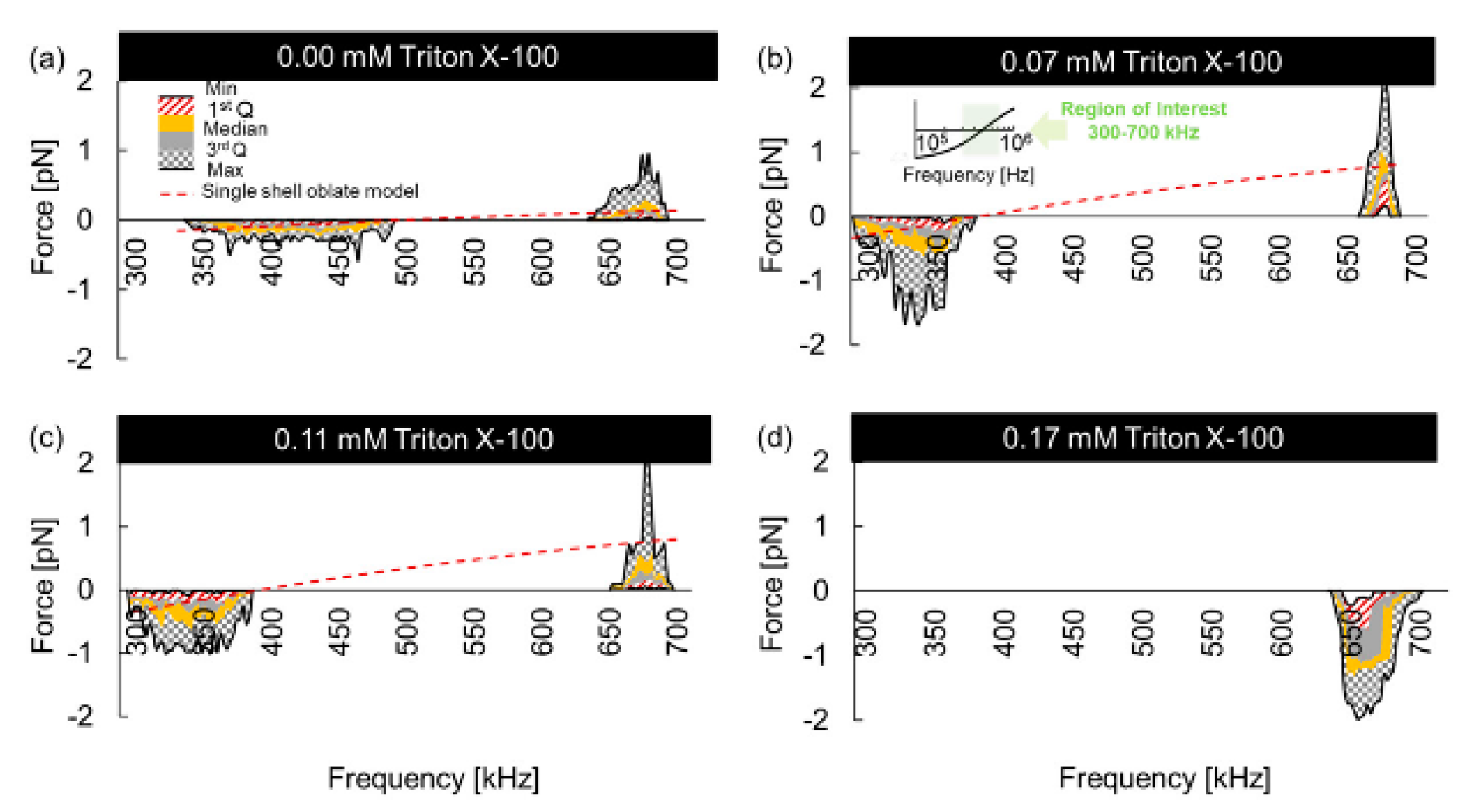
4. DEP/ODEP-Based Determination of Cell Dielectric Parameters and Its Applications
5. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- von Erlach, T.C.; Bertazzo, S.; Wozniak, M.A.; Horejs, C.-M.; Maynard, S.A.; Attwood, S.; Robinson, B.K.; Autefage, H.; Kallepitis, C.; del Río Hernández, A.; et al. Cell-geometry-dependent changes in plasma membrane order direct stem cell signalling and fate. Nat. Mater. 2018, 17, 237–242. [Google Scholar] [CrossRef] [PubMed]
- Colavin, A.; Shi, H.; Huang, K.C. RodZ modulates geometric localization of the bacterial actin MreB to regulate cell shape. Nat. Commun. 2018, 9, 1280. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wang, Y.; Zhang, H.; Min, C.; Zhang, Y.; Zhang, C.; Xin, Z.; Zhu, S.; Yang, Y.; Burge, R.E.; et al. Graphene-based confocal refractive index microscopy for label-free differentiation of living epithelial and mesenchymal cells. ACS Sensors 2020. [Google Scholar] [CrossRef] [PubMed]
- Rappaz, B.; Marquet, P.; Cuche, E.; Emery, Y.; Depeursinge, C.; Magistretti, P.J. Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy. Opt. Express 2005, 13, 9361–9373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asmani, M.; Velumani, S.; Li, Y.; Wawrzyniak, N.; Hsia, I.; Chen, Z.; Hinz, B.; Zhao, R. Fibrotic microtissue array to predict anti-fibrosis drug efficacy. Nat. Commun. 2018, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Vorselen, D.; van Dommelen, S.M.; Sorkin, R.; Piontek, M.C.; Schiller, J.; Döpp, S.T.; Kooijmans, S.A.A.; van Oirschot, B.A.; Versluijs, B.A.; Bierings, M.B.; et al. The fluid membrane determines mechanics of erythrocyte extracellular vesicles and is softened in hereditary spherocytosis. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Teng, Y.; Pang, M.; Huang, J.; Xiong, C. Mechanical characterization of cancer cells during TGF-$β$1-induced epithelial-mesenchymal transition using an electrodeformation-based microchip. Sens. Actuators B Chem. 2017, 240, 158–167. [Google Scholar] [CrossRef]
- Phillip, J.; Wu, P.-H.; Gilkes, D.; Williams, W.; McGovern, S.; Daya, J.; Chen, J.; Aifuwa, I.; Lee, J.; Fan, R.; et al. Biophysical and biomolecular determination of cellular age in humans. Nat. Biomed. Eng. 2017, 1, 93. [Google Scholar] [CrossRef]
- Cross, S.E.; Jin, Y.-S.; Rao, J.; Gimzewski, J.K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2007, 2, 780–783. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, Y.; Liu, L.; Wang, Y.; Dong, Z.; Li, W.J.; Lee, G.-B.; Xiao, X.; Zhang, W. Rapid and label-free separation of Burkitt’s lymphoma cells from red blood cells by optically-induced electrokinetics. PLoS ONE 2014, 9, e90827. [Google Scholar] [CrossRef]
- Wu, M.; Ouyang, Y.; Wang, Z.; Zhang, R.; Huang, P.-H.; Chen, C.; Li, H.; Li, P.; Quinn, D.; Dao, M.; et al. Isolation of exosomes from whole blood by integrating acoustics and microfluidics. Proc. Natl. Acad. Sci. USA 2017, 114, 10584–10589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koch, M.; Wright, K.E.; Otto, O.; Herbig, M.; Salinas, N.D.; Tolia, N.H.; Satchwell, T.J.; Guck, J.; Brooks, N.J.; Baum, J. Plasmodium falciparum erythrocyte-binding antigen 175 triggers a biophysical change in the red blood cell that facilitates invasion. Proc. Natl. Acad. Sci. USA 2017, 114, 4225–4230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bagnaninchi, P.O.; Drummond, N. Real-time label-free monitoring of adipose-derived stem cell differentiation with electric cell-substrate impedance sensing. Proc. Natl. Acad. Sci. USA 2011, 108, 6462–6467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, A.P.; Aghaamoo, M.; Adams, T.N.G.; Flanagan, L.A. It’s Electric: When Technology Gives a Boost to Stem Cell Science. Curr. Stem Cell Reports 2018, 4, 116–126. [Google Scholar] [CrossRef]
- Iliescu, F.; Sim, W.J.; Heidari, H.P.; Poenar, D.; Miao, J.; Taylor, H.K.; Iliescu, C. Highlighting the uniqueness in dielectrophoretic enrichment of circulating tumor cells. Electrophoresis 2019, 40, 1457–1477. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Zhang, Y.; Chen, D.; Tan, H.; Zheng, Y.; Wang, J.; Chen, J. Characterization of Single-Nucleus Electrical Properties by Microfluidic Constriction Channel. Micromachines 2019, 10, 740. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Huang, L.; Zhao, P.; Liang, F.; Wang, W. A microfluidic device integrating impedance flow cytometry and electric impedance spectroscopy for high-efficiency single-cell electrical property measurement. Anal. Chem. 2019, 91, 15204–15212. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Chen, D.; Wang, K.; Wei, Y.; Xu, Y.; Huang, C.; Wang, J.; Chen, J. Crossing constriction channel-based microfluidic cytometry capable of electrically phenotyping large populations of single cells. Analyst 2019, 144, 1008–1015. [Google Scholar] [CrossRef]
- Holmes, D.; Pettigrew, D.; Reccius, C.H.; Gwyer, J.D.; van Berkel, C.; Holloway, J.; Davies, D.E.; Morgan, H. Leukocyte analysis and differentiation using high speed microfluidic single cell impedance cytometry. Lab Chip 2009, 9, 2881–2889. [Google Scholar] [CrossRef]
- Ye, T.; Shi, H.; Phan-Thien, N.; Lim, C.T.; Li, Y. Relationship between transit time and mechanical properties of a cell through a stenosed microchannel. Soft Matter 2018, 14, 533–545. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, Y.; Wang, X.; Shehata, N.; Wang, C.; Sun, Y. Stiffness increase of red blood cells during storage. Microsystems Nanoeng. 2018, 4, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Davis, S.P.; Yang, F.; Paulsen, K.S.; Kumar, M.; Sinnott DeVaux, R.; Wang, X.; Conklin, D.S.; Oberai, A.; Herschkowitz, J.I.; et al. Inertial microfluidic cell stretcher (iMCS): fully automated, high-throughput, and near real-time cell mechanotyping. Small 2017, 13, 1700705. [Google Scholar] [CrossRef] [PubMed]
- Dufrêne, Y.F.; Ando, T.; Garcia, R.; Alsteens, D.; Martinez-Martin, D.; Engel, A.; Gerber, C.; Müller, D.J. Imaging modes of atomic force microscopy for application in molecular and cell biology. Nat. Nanotechnol. 2017, 12, 295. [Google Scholar] [CrossRef] [PubMed]
- Jiang, N.; You, M.; Wang, Y.; Huang, Y.; Xie, S.; Lin, Y.; Yang, H. Probing the biophysical properties of tumor cells during mitosis by atomic force microscopy. Biomech. Model. Mechanobiol. 2018, 17, 1209–1215. [Google Scholar] [CrossRef]
- Hashemzadeh, H.; Allahverdi, A.; Ghorbani, M.; Soleymani, H.; Kocsis, Á.; Fischer, M.B.; Ertl, P.; Naderi-Manesh, H. Gold Nanowires/Fibrin Nanostructure as Microfluidics Platforms for Enhancing Stem Cell Differentiation: Bio-AFM Study. Micromachines 2020, 11, 50. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Xi, N.; Wang, Y.; Liu, L. Advances in atomic force microscopy for single-cell analysis. Nano Res. 2019, 12, 703–718. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z.; Zhang, W.; Zhu, X.; Li, L.; Weng, Z. Analysis of Colchicine-Induced Effects on Hepatoma and Hepatocyte Cells by Atomic Force Microscopy. J. Nanosci. Nanotechnol. 2018, 18, 4248–4254. [Google Scholar] [CrossRef]
- Li, M.; Liu, L.; Xu, X.; Xing, X.; Dang, D.; Xi, N.; Wang, Y. Nanoscale characterization of dynamic cellular viscoelasticity by atomic force microscopy with varying measurement parameters. J. Mech. Behav. Biomed. Mater. 2018, 82, 193–201. [Google Scholar] [CrossRef]
- Liu, Y.; Song, H.; Zhu, P.; Lu, H.; Tang, Q. Experiment study and FEM simulation on erythrocytes under linear stretching of optical micromanipulation. AIP Adv. 2017, 7, 85003. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Liu, Y.; Zhang, B.; Tian, K.; Zhu, P.; Lu, H.; Tang, Q. Study of in vitro RBCs membrane elasticity with AOD scanning optical tweezers. Biomed. Opt. Express 2017, 8, 384–394. [Google Scholar] [CrossRef]
- Tan, Y.; Sun, D.; Wang, J.; Huang, W. Mechanical characterization of human red blood cells under different osmotic conditions by robotic manipulation with optical tweezers. IEEE Trans. Biomed. Eng. 2010, 57, 1816–1825. [Google Scholar] [CrossRef] [PubMed]
- Sheikh-Hasani, V.; Babaei, M.; Azadbakht, A.; Pazoki-Toroudi, H.; Mashaghi, A.; Moosavi-Movahedi, A.A.; Reihani, S.N.S. Atorvastatin treatment softens human red blood cells: an optical tweezers study. Biomed. Opt. Express 2018, 9, 1256–1261. [Google Scholar] [CrossRef] [Green Version]
- Michel, K.E.J.; Pavel, Y.; Eugene, M.; Kouacou, M.A.; Zoueu, J.T. Dynamics study of the deformation of red blood cell by optical tweezers. Open J. Biophys. 2017, 7, 59. [Google Scholar] [CrossRef] [Green Version]
- Tan, Y.; Kong, C.; Chen, S.; Cheng, S.H.; Li, R.A.; Sun, D. Probing the mechanobiological properties of human embryonic stem cells in cardiac differentiation by optical tweezers. J. Biomech. 2012, 45, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Hartono, D.; Liu, Y.; Tan, P.L.; Then, X.Y.S.; Yung, L.-Y.L.; Lim, K.-M. On-chip measurements of cell compressibility via acoustic radiation. Lab Chip 2011, 11, 4072–4080. [Google Scholar] [CrossRef]
- Augustsson, P.; Karlsen, J.T.; Su, H.-W.; Bruus, H.; Voldman, J. Iso-acoustic focusing of cells for size-insensitive acousto-mechanical phenotyping. Nat. Commun. 2016, 7, 11556. [Google Scholar] [CrossRef]
- Luo, J.; Hou, P.; Ding, J.; Qu, A. Kernel Based Non-Iterative Automatic Fast Capacitance Compensation in Patch-Clamp Experiments. Cell. Mol. Bioeng. 2012, 5, 440–449. [Google Scholar] [CrossRef]
- Zhang, H.; Xiong, J.; Luo, J.; Qu, A. Experimental determination of Cm measurement related hardware parameters of the patch-clamp amplifier. J. Neurosci. Methods 2009, 176, 246–253. [Google Scholar] [CrossRef]
- Balletta, A.; Lorenz, D.; Rummel, A.; Gerhard, R.; Bigalke, H.; Wegner, F. Human mast cell line-1 (HMC-1) cells exhibit a membrane capacitance increase when dialysed with high free-Ca2+ and GTP$γ$S containing intracellular solution. Eur. J. Pharmacol. 2013, 720, 227–236. [Google Scholar] [CrossRef]
- Gentet, L.J.; Stuart, G.J.; Clements, J.D. Direct measurement of specific membrane capacitance in neurons. Biophys. J. 2000, 79, 314–320. [Google Scholar] [CrossRef] [Green Version]
- Kodandaramaiah, S.B.; Franzesi, G.T.; Chow, B.Y.; Boyden, E.S.; Forest, C.R. Automated whole-cell patch-clamp electrophysiology of neurons in vivo. Nat. Methods 2012, 9, 585–587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Abdelgawad, M.; Yu, L.; Shakiba, N.; Chien, W.-Y.; Lu, Z.; Geddie, W.R.; Jewett, M.A.S.; Sun, Y. Electrodeformation for single cell mechanical characterization. J. Micromechanics Microengineering 2011, 21, 54012. [Google Scholar] [CrossRef]
- Doh, I.; Lee, W.C.; Cho, Y.-H.; Pisano, A.P.; Kuypers, F.A. Deformation measurement of individual cells in large populations using a single-cell microchamber array chip. Appl. Phys. Lett. 2012, 100, 173702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teng, Y.; Zhu, K.; Xiong, C.; Huang, J. Electrodeformation-based biomechanical chip for quantifying global viscoelasticity of cancer cells regulated by cell cycle. Anal. Chem. 2018, 90, 8370–8378. [Google Scholar] [CrossRef]
- Bai, G.; Li, Y.; Chu, H.K.; Wang, K.; Tan, Q.; Xiong, J.; Sun, D. Characterization of biomechanical properties of cells through dielectrophoresis-based cell stretching and actin cytoskeleton modeling. Biomed. Eng. Online 2017, 16, 41. [Google Scholar] [CrossRef] [Green Version]
- Qiang, Y.; Liu, J.; Yang, F.; Dieujuste, D.; Du, E. Modeling erythrocyte electrodeformation in response to amplitude modulated electric waveforms. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Çağlayan, Z.; Yalçın, Y.D.; Külah, H. Examination of the dielectrophoretic (DEP) spectra of MCF7 breast cancer cells and leukocytes. Electrophoresis 2020. [Google Scholar] [CrossRef]
- Lentz, C.J.; Hidalgo-Caballero, S.; Lapizco-Encinas, B.H. Low frequency cyclical potentials for fine tuning insulator-based dielectrophoretic separations. Biomicrofluidics 2019, 13, 44114. [Google Scholar] [CrossRef]
- Hanson, C.; Barney, J.T.; Bishop, M.M.; Vargis, E. Simultaneous isolation and label-free identification of bacteria using contactless dielectrophoresis and Raman spectroscopy. Electrophoresis 2019, 40, 1446–1456. [Google Scholar] [CrossRef]
- Huang, C.; Chen, A.; Wang, L.; Guo, M.; Yu, J. Electrokinetic measurements of dielectric properties of membrane for apoptotic HL-60 cells on chip-based device. Biomed. Microdevices 2007, 9, 335–343. [Google Scholar] [CrossRef]
- Liang, X.; Graham, K.A.; Johannessen, A.C.; Costea, D.E.; Labeed, F.H. Human oral cancer cells with increasing tumorigenic abilities exhibit higher effective membrane capacitance. Integr. Biol. 2014, 6, 545–554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Gaddar, A.; Frénéa-Robin, M.; Voyer, D.; Aka, H.; Haddour, N.; Krähenbühl, L. Assessment of 0.5 T static field exposure effect on yeast and HEK cells using electrorotation. Biophys. J. 2013, 104, 1805–1811. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Jiang, A.; Kim, E.; Ro, C.; Adams, T.; Flanagan, L.A.; Taylor, T.J.; Hayes, M.A. Identification of neural stem and progenitor cell subpopulations using DC insulator-based dielectrophoresis. Analyst 2019, 144, 4066–4072. [Google Scholar] [CrossRef] [PubMed]
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef]
- Jamshidi, A.; Pauzauskie, P.J.; Schuck, P.J.; Ohta, A.T.; Chiou, P.-Y.; Chou, J.; Yang, P.; Wu, M.C. Dynamic manipulation and separation of individual semiconducting and metallic nanowires. Nat. Photonics 2008, 2, 86–89. [Google Scholar] [CrossRef]
- Wu, M.C. Optoelectronic tweezers. Nat. Photonics 2011, 5, 322–324. [Google Scholar] [CrossRef]
- Zhao, Y.; Lai, H.S.S.; Zhang, G.; Lee, G.-B.; Li, W.J. Rapid determination of cell mass and density using digitally controlled electric field in a microfluidic chip. Lab Chip 2014, 14, 4426–4434. [Google Scholar] [CrossRef]
- Zhao, Y.; Lai, H.S.S.; Zhang, G.; Lee, G.-B.; Li, W.J. Measurement of single leukemia cell’s density and mass using optically induced electric field in a microfluidics chip. Biomicrofluidics 2015, 9, 22406. [Google Scholar] [CrossRef] [Green Version]
- Liang, W.; Zhang, K.; Yang, X.; Liu, L.; Yu, H.; Zhang, W. Distinctive translational and self-rotational motion of lymphoma cells in an optically induced non-rotational alternating current electric field. Biomicrofluidics 2015, 9, 014121. [Google Scholar] [CrossRef] [Green Version]
- Liang, W.; Zhao, Y.; Liu, L.; Wang, Y.; Li, W.J.; Lee, G.-B. Determination of Cell Membrane Capacitance and Conductance via Optically Induced Electrokinetics. Biophys. J. 2017, 113, 1531–1539. [Google Scholar] [CrossRef] [Green Version]
- Liang, W.; Liu, L.; Zhang, H.; Wang, Y.; Li, W.J. Optoelectrokinetics-based microfluidic platform for bioapplications: A review of recent advances. Biomicrofluidics 2019, 13, 051502. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liang, W.; Zhang, G.; Mai, J.D.; Liu, L.; Lee, G.-B.; Li, W.J. Distinguishing cells by their first-order transient motion response under an optically induced dielectrophoretic force field. Appl. Phys. Lett. 2013, 103, 183702. [Google Scholar] [CrossRef]
- Chau, L.-H.; Liang, W.; Cheung, F.W.K.; Liu, W.K.; Li, W.J.; Chen, S.-C.; Lee, G.-B. Self-rotation of cells in an irrotational AC E-field in an opto-electrokinetics chip. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neale, S.L.; Mody, N.; Selman, C.; Cooper, J.M. Optoelectronic tweezers for the measurement of the relative stiffness of erythrocytes. In Proceedings of the Optical Trapping and Optical Micromanipulation IX, International Society for Optics and Photonics, San Diego, CA, USA, 12–16 August 2012; Volume 8458, p. 845827. [Google Scholar]
- Yang, X.; Niu, X.; Liu, Z.; Zhao, Y.; Zhang, G.; Liang, W.; Li, W.J. Accurate extraction of the self-rotational speed for cells in an electrokinetics force field by an image matching algorithm. Micromachines 2017, 8, 282. [Google Scholar] [CrossRef] [Green Version]
- Bahrieh, G.; Erdem, M.; Özgür, E.; Gündüz, U.; Külah, H. Assessment of effects of multi drug resistance on dielectric properties of K562 leukemic cells using electrorotation. RSC Adv. 2014, 4, 44879–44887. [Google Scholar] [CrossRef]
- Ouyang, M.; Ki Cheung, W.; Liang, W.; Mai, J.D.; Keung Liu, W.; Jung Li, W. Inducing self-rotation of cells with natural and artificial melanin in a linearly polarized alternating current electric field. Biomicrofluidics 2013, 7, 054112. [Google Scholar] [CrossRef] [Green Version]
- Morgan, H.; Sun, T.; Holmes, D.; Gawad, S.; Green, N.G. Single cell dielectric spectroscopy. J. Phys. D. Appl. Phys. 2006, 40, 61–70. [Google Scholar] [CrossRef]
- Sun, T.; Morgan, H. Single-cell microfluidic impedance cytometry: a review. Microfluid. Nanofluidics 2010, 8, 423–443. [Google Scholar] [CrossRef]
- Trainito, C.I.; Sweeney, D.C.; Čemažar, J.; Schmelz, E.M.; Français, O.; Le Pioufle, B.; Davalos, R. V Characterization of sequentially-staged cancer cells using electrorotation. PLoS ONE 2019, 14, e0222289. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Y.; Wang, X.; Wang, X.-B.; Becker, F.F.; Gascoyne, P.R.C. Dielectric Properties of Human Leukocyte Subpopulations Determined by Electrorotation as a Cell Separation Criterion. Biophys. J. 1999, 76, 3307–3314. [Google Scholar] [CrossRef] [Green Version]
- Kiesel, M.; Reuss, R.; Endter, J.; Zimmermann, D.; Zimmermann, H.; Shirakashi, R.; Bamberg, E.; Zimmermann, U.; Sukhorukov, V.L. Swelling-Activated Pathways in Human T-Lymphocytes Studied by Cell Volumetry and Electrorotation. Biophys. J. 2006, 90, 4720–4729. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Chen, A.; Guo, M.; Yu, J. Membrane dielectric responses of bufalin-induced apoptosis in HL-60 cells detected by an electrorotation chip. Biotechnol. Lett. 2007, 29, 1307–1313. [Google Scholar] [CrossRef] [PubMed]
- De Gasperis, G.; Wang, X.; Yang, J.; Becker, F.; Gascoyne, P. Automated electrorotation: Dielectric characterization of living cells by real-time motion estimation. Meas. Sci. Technol. 1999, 9, 518. [Google Scholar] [CrossRef]
- Zhang, G.; Ouyang, M.; Mai, J.; Li, W.J.; Liu, W.K. Automated rotation rate tracking of pigmented cells by a customized block-matching algorithm. J. Lab. Autom. 2013, 18, 161–170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flanagan, L.A.; Lu, J.; Wang, L.; Marchenko, S.A.; Jeon, N.L.; Lee, A.P.; Monuki, E.S. Unique Dielectric Properties Distinguish Stem Cells and Their Differentiated Progeny. Stem Cells 2008, 26, 656–665. [Google Scholar] [CrossRef]
- Castellanos, A.; Ramos, A.; González, A.; Green, N.G.; Morgan, H. Electrohydrodynamics and dielectrophoresis in microsystems: scaling laws. J. Phys. D. Appl. Phys. 2003, 36, 2584–2597. [Google Scholar] [CrossRef]
- Ino, K.; Ishida, A.; Inoue, K.Y.; Suzuki, M.; Koide, M.; Yasukawa, T.; Shiku, H.; Matsue, T. Electrorotation chip consisting of three-dimensional interdigitated array electrodes. Sens. Actuators B Chem. 2011, 153, 468–473. [Google Scholar] [CrossRef]
- Huang, L.; Zhao, P.; Wang, W. 3D cell electrorotation and imaging for measuring multiple cellular biophysical properties. Lab Chip 2018, 18, 2359–2368. [Google Scholar] [CrossRef]
- Huang, L.; He, W.; Wang, W. A cell electro-rotation micro-device using polarized cells as electrodes. Electrophoresis 2019, 40, 784–791. [Google Scholar] [CrossRef]
- Becker, F.F.; Wang, X.B.; Huang, Y.; Pethig, R.; Vykoukal, J.; Gascoyne, P.R.C. Separation of human breast cancer cells from blood by differential dielectric affinity. Proc. Natl. Acad. Sci. USA 1995, 92, 860–864. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Wang, X.B.; Holzel, R.; Becker, F.F.; Gascoyne, P.R.C. Electrorotational studies of the cytoplasmic dielectric properties of Friend murine erythroleukaemia cells. Phys. Med. Biol. 1995, 40, 1789–1806. [Google Scholar] [CrossRef]
- Gimsa, J.; Marszalek, P.; Loewe, U.; Tsong, T.Y. Dielectrophoresis and electrorotation of neurospora slime and murine myeloma cells. Biophys. J. 1991, 60, 749–760. [Google Scholar] [CrossRef] [Green Version]
- Cristofanilli, M.; De Gasperis, G.; Zhang, L.; Hung, M.C.; Gascoyne, P.R.C.; Hortobagyi, G.N. Automated electrorotation to reveal dielectric variations related to HER-2/neu overexpression in MCF-7 sublines. Clin. Cancer Res. 2002, 8, 615–619. [Google Scholar] [PubMed]
- Chan, K.L.; Morgan, H.; Morgan, E.; Cameron, I.T.; Thomas, M.R. Measurements of the dielectric properties of peripheral blood mononuclear cells and trophoblast cells using AC electrokinetic techniques. Biochim. Biophys. Acta Mol. Basis Dis. 2000, 1500, 313–322. [Google Scholar] [CrossRef] [Green Version]
- Cen, E.G.; Dalton, C.; Li, Y.; Adamia, S.; Pilarski, L.M.; Kaler, K.V.I.S. A combined dielectrophoresis, traveling wave dielectrophoresis and electrorotation microchip for the manipulation and characterization of human malignant cells. J. Microbiol. Methods 2004, 58, 387–401. [Google Scholar] [CrossRef]
- Long, Q.; Xing, W. Detection of the apoptosis of Jurkat cell using an electrorotation chip. Front. Biol. China 2006, 1, 208–212. [Google Scholar] [CrossRef]
- Berardi, V.; Aiello, C.; Bonincontro, A.; Risuleo, G. Alterations of the Plasma Membrane Caused by Murine Polyomavirus Proliferation: An Electrorotation Study. J. Membr. Biol. 2009, 229, 19–25. [Google Scholar] [CrossRef]
- Han, S.I.; Joo, Y.D.; Han, K.H. An electrorotation technique for measuring the dielectric properties of cells with simultaneous use of negative quadrupolar dielectrophoresis and electrorotation. Analyst 2013, 138, 1529–1537. [Google Scholar] [CrossRef]
- Trainito, C.I.; Français, O.; Le Pioufle, B. Monitoring the permeabilization of a single cell in a microfluidic device, through the estimation of its dielectric properties based on combined dielectrophoresis and electrorotation in situ experiments. Electrophoresis 2015, 36, 1115–1122. [Google Scholar] [CrossRef]
- Alizadeh-Haghighi, E.; Jafarmadar, S.; Khalilarya, S. Application of genetic algorithm in extracting cell dielectric characteristics with electrorotation. J. Electr. Bioimpedance 2017, 8, 34–39. [Google Scholar] [CrossRef] [Green Version]
- Lannin, T.; Su, W.W.; Gruber, C.; Cardle, I.; Huang, C.; Thege, F.; Kirby, B. Automated electrorotation shows electrokinetic separation of pancreatic cancer cells is robust to acquired chemotherapy resistance, serum starvation, and EMT. Biomicrofluidics 2016, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keim, K.; Rashed, M.Z.; Kilchenmann, S.C.; Delattre, A.; Gonçalves, A.F.; Éry, P.; Guiducci, C. On-chip technology for single-cell arraying, electrorotation-based analysis and selective release. Electrophoresis 2019, 40, 1830–1838. [Google Scholar] [CrossRef] [PubMed]
- Sano, M.B.; Henslee, E.A.; Schmelz, E.; Davalos, R.V. Contactless dielectrophoretic spectroscopy: Examination of the dielectric properties of cells found in blood. Electrophoresis 2011, 32, 3164–3171. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Lanry Yung, L.-Y.; Lim, K.-M. Dielectrophoretic capture voltage spectrum for measurement of dielectric properties and separation of cancer cells. Biomicrofluidics 2012, 6, 014113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Narayanan Unni, H.; Hartono, D.; Yue, L.; Yung, L.; Mah-Lee Ng, M.; Pueh Lee, H.; Cheong Khoo, B.; Lim, K.-M. Characterization and separation of Cryptosporidium and Giardia cells using on-chip dielectrophoresis. Biomicrofluidics 2012, 6, 012805. [Google Scholar] [CrossRef] [Green Version]
- Salmanzadeh, A.; Sano, M.B.; Gallo-Villanueva, R.C.; Roberts, P.C.; Schmelz, E.M.; Davalos, R.V. Investigating dielectric properties of different stages of syngeneic murine ovarian cancer cells. Biomicrofluidics 2013, 7, 011809. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zheng, T.; Zhu, R. Characterization of single-cell biophysical properties and cell type classification using dielectrophoresis model reduction method. Sens. Actuators B Chem. 2020, 304, 127326. [Google Scholar] [CrossRef]
- Gascoyne, P.R.C.; Shim, S.; Noshari, J.; Becker, F.F.; Stemke-Hale, K. Correlations between the dielectric properties and exterior morphology of cells revealed by dielectrophoretic field-flow fractionation. Electrophoresis 2013, 34, 1042–1050. [Google Scholar] [CrossRef]
- Sanchis, A.; Brown, A.P.; Sancho, M.; Martínez, G.; Sebastián, J.L.; Muñoz, S.; Miranda, J.M. Dielectric characterization of bacterial cells using dielectrophoresis. Bioelectromagnetics 2007, 28, 393–401. [Google Scholar] [CrossRef]
- Gascoyne, P.; Pethig, R.; Satayavivad, J.; Becker, F.F.; Ruchirawat, M. Dielectrophoretic detection of changes in erythrocyte membranes following malarial infection. Biochim. Biophys. Acta Biomembr. 1997, 1323, 240–252. [Google Scholar] [CrossRef] [Green Version]
- Labeed, F.H.; Coley, H.M.; Hughes, M.P. Differences in the biophysical properties of membrane and cytoplasm of apoptotic cells revealed using dielectrophoresis. Biochim. Biophys. Acta Gen. Subj. 2006, 1760, 922–929. [Google Scholar] [CrossRef] [PubMed]
- Vykoukal, D.M.; Gascoyne, P.R.C.; Vykoukal, J. Dielectric characterization of complete mononuclear and polymorphonuclear blood cell subpopulations for label-free discrimination. Integr. Biol. 2009, 1, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Patel, P.M.; Bhat, A.; Markx, G.H. A comparative study of cell death using electrical capacitance measurements and dielectrophoresis. Enzyme Microb. Technol. 2008, 43, 523–530. [Google Scholar] [CrossRef]
- Salimi, E.; Braasch, K.; Fazelkhah, A.; Afshar, S.; Saboktakin Rizi, B.; Mohammad, K.; Butler, M.; Bridges, G.; Thomson, D. Single cell dielectrophoresis study of apoptosis progression induced by controlled starvation. Bioelectrochemistry 2018, 124. [Google Scholar] [CrossRef]
- Habibi, S.; Lee, H.Y.; Moncada-Hernandez, H.; Gooding, J.; Minerick, A.R. Impacts of low concentration surfactant on red blood cell dielectrophoretic responses. Biomicrofluidics 2019, 13, 054101. [Google Scholar] [CrossRef]
- Fujii, Y.; Ochi, Y.; Tuchiya, M.; Kajita, M.; Fujita, Y.; Ishimoto, Y.; Okajima, T. Spontaneous spatial correlation of elastic modulus in jammed epithelial monolayers observed by AFM. Biophys. J. 2019, 116, 1152–1158. [Google Scholar] [CrossRef] [Green Version]
- Lei, W.; Xie, C.; Wu, T.; Wu, X.; Wang, M. Transport mechanism of deformable micro-gel particle through micropores with mechanical properties characterized by AFM. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Proa-Coronado, S.; Séverac, C.; Martinez-Rivas, A.; Dague, E. Beyond the paradigm of nanomechanical measurements on cells using AFM: an automated methodology to rapidly analyse thousands of cells. Nanoscale Horizons 2020, 5, 131–138. [Google Scholar] [CrossRef]
- Li, P.; Liu, L.; Yang, Y.; Wang, Y.; Li, G. In-phase bias modulation mode of scanning ion conductance microscopy with capacitance compensation. IEEE Trans. Ind. Electron. 2015, 62, 6508–6518. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Perry, D.; Page, A.; Kang, M.; Unwin, P.R. Scanning Ion Conductance Microscopy: Quantitative Nanopipette Delivery–Substrate Electrode Collection Measurements and Mapping. Anal. Chem. 2019, 91, 2516–2524. [Google Scholar] [CrossRef]
- Rheinlaender, J.; Schäffer, T.E. Mapping the creep compliance of living cells with scanning ion conductance microscopy reveals a subcellular correlation between stiffness and fluidity. Nanoscale 2019, 11, 6982–6989. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Yang, S.; Huang, P.-H.; Wang, Z.; Zhang, P.; Gu, Y.; Bachman, H.; Chen, C.; Wu, M.; Xie, Y. Wave number–spiral acoustic tweezers for dynamic and reconfigurable manipulation of particles and cells. Sci. Adv. 2019, 5, eaau6062. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Yang, S.; Chen, C.; Hartman, J.H.; Huang, P.-H.; Wang, L.; Tian, Z.; Zhang, P.; Faulkenberry, D.; Meyer, J.N. Surface acoustic waves enable rotational manipulation of Caenorhabditis elegans. Lab Chip 2019, 19, 984–992. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Chen, C.; Guo, F.; Philippe, J.; Gu, Y.; Tian, Z.; Bachman, H.; Ren, L.; Yang, S.; Zhong, Z. Contactless, programmable acoustofluidic manipulation of objects on water. Lab Chip 2019, 19, 3397–3404. [Google Scholar] [CrossRef] [PubMed]
- Leiterer, C.; Wünsche, E.; Singh, P.; Albert, J.; Köhler, J.M.; Deckert, V.; Fritzsche, W. High precision attachment of silver nanoparticles on AFM tips by dielectrophoresis. Anal. Bioanal. Chem. 2016, 408, 3625–3631. [Google Scholar] [CrossRef]
- Leiterer, C.; Deckert-Gaudig, T.; Singh, P.; Wirth, J.; Deckert, V.; Fritzsche, W. Dielectrophoretic positioning of single nanoparticles on atomic force microscope tips for tip-enhanced Raman spectroscopy. Electrophoresis 2015, 36, 1142–1148. [Google Scholar] [CrossRef]
- Zhou, P.; Yu, H.; Yang, W.; Wen, Y.; Wang, Z.; Li, W.J.; Liu, L. Spatial manipulation and assembly of nanoparticles by atomic force microscopy tip-induced dielectrophoresis. ACS Appl. Mater. Interfaces 2017, 9, 16715–16724. [Google Scholar] [CrossRef]
- Ghayour, R.; Hojjat, Y.; Karafi, M.R.; Sadeghiyan, H. Development of a hybrid DEP-SAW device for trapping/sensing target cells. Appl. Acoust. 2018, 141, 355–361. [Google Scholar] [CrossRef]
- Ghayour, R. Design, Fabrication and performance of DEP-SAW sensor for measurement of cells aggregation on a lab on chip. Modares Mech. Eng. 2018, 18, 351–358. [Google Scholar]
- Witte, C.; Kremer, C.; Cooper, J.M.; Neale, S.L. Continuous cell lysis in microfluidics through acoustic and optoelectronic tweezers. In Proceedings of the SPIE MOEMS-MEMS 2013, International Society for Optics and Photonics, San Diego, CA, USA, 2–3 February 2013; Volume 8615, p. 86150. [Google Scholar]
- Witte, C.; Wilson, R.; Cooper, J.M.; Neale, S.L. OET meets acoustic tweezing. In Proceedings of the Optical Trapping and Optical Micromanipulation IX, International Society for Optics and Photonics; San Diego, CA, USA, 12–16 August 2012, Volume 8458, p. 84582I.
- Hsu, H.; Ohta, A.T.; Chiou, P.-Y.; Jamshidi, A.; Neale, S.L.; Wu, M.C. Phototransistor-based optoelectronic tweezers for dynamic cell manipulation in cell culture media. Lab Chip 2010, 10, 165–172. [Google Scholar] [CrossRef]
- Lee, G.-B.; Chang, C.-J.; Wang, C.-H.; Lu, M.-Y.; Luo, Y.-Y. Continuous medium exchange and optically induced electroporation of cells in an integrated microfluidic system. Microsystems Nanoeng. 2015, 1, 1–9. [Google Scholar] [CrossRef]
- Chu, P.-Y.; Liao, C.-J.; Hsieh, C.-H.; Wang, H.-M.; Chou, W.-P.; Chen, P.-H.; Wu, M.-H. Utilization of optically induced dielectrophoresis in a microfluidic system for sorting and isolation of cells with varied degree of viability: Demonstration of the sorting and isolation of drug-treated cancer cells with various degrees of anti-cancer dru. Sens. Actuators B Chem. 2019, 283, 621–631. [Google Scholar] [CrossRef]
- Elitas, M.; Yildizhan, Y.; Islam, M.; Martinez-Duarte, R.; Ozkazanc, D. Dielectrophoretic characterization and separation of monocytes and macrophages using 3D carbon-electrodes. Electrophoresis 2019, 40, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Weirauch, L.; Lorenz, M.; Hill, N.; Lapizco-Encinas, B.H.; Baune, M.; Pesch, G.R.; Thöming, J. Material-selective separation of mixed microparticles via insulator-based dielectrophoresis. Biomicrofluidics 2019, 13, 64112. [Google Scholar] [CrossRef] [PubMed]
- Jiang, A.Y.L.; Yale, A.R.; Aghaamoo, M.; Lee, D.-H.; Lee, A.P.; Adams, T.N.G.; Flanagan, L.A. High-throughput continuous dielectrophoretic separation of neural stem cells. Biomicrofluidics 2019, 13, 64111. [Google Scholar] [CrossRef] [Green Version]
- Chou, W.-P.; Wang, H.-M.; Chang, J.-H.; Chiu, T.-K.; Hsieh, C.-H.; Liao, C.-J.; Wu, M.-H. The utilization of optically-induced-dielectrophoresis (ODEP)-based virtual cell filters in a microfluidic system for continuous isolation and purification of circulating tumour cells (CTCs) based on their size characteristics. Sens. Actuators B Chem. 2017, 241, 245–254. [Google Scholar] [CrossRef]
- Liao, C.-J.; Hsieh, C.-H.; Chiu, T.-K.; Zhu, Y.-X.; Wang, H.-M.; Hung, F.-C.; Chou, W.-P.; Wu, M.-H. An Optically Induced Dielectrophoresis (ODEP)-Based Microfluidic System for the Isolation of High-Purity CD45neg/EpCAMneg Cells from the Blood Samples of Cancer Patients—Demonstration and Initial Exploration of the Clinical Significance of These Cells. Micromachines 2018, 9, 563. [Google Scholar] [CrossRef] [Green Version]
- Chiu, T.-K.; Chao, A.-C.; Chou, W.-P.; Liao, C.-J.; Wang, H.-M.; Chang, J.-H.; Chen, P.-H.; Wu, M.-H. Optically-induced-dielectrophoresis (ODEP)-based cell manipulation in a microfluidic system for high-purity isolation of integral circulating tumor cell (CTC) clusters based on their size characteristics. Sens. Actuators B Chem. 2018, 258, 1161–1173. [Google Scholar] [CrossRef]


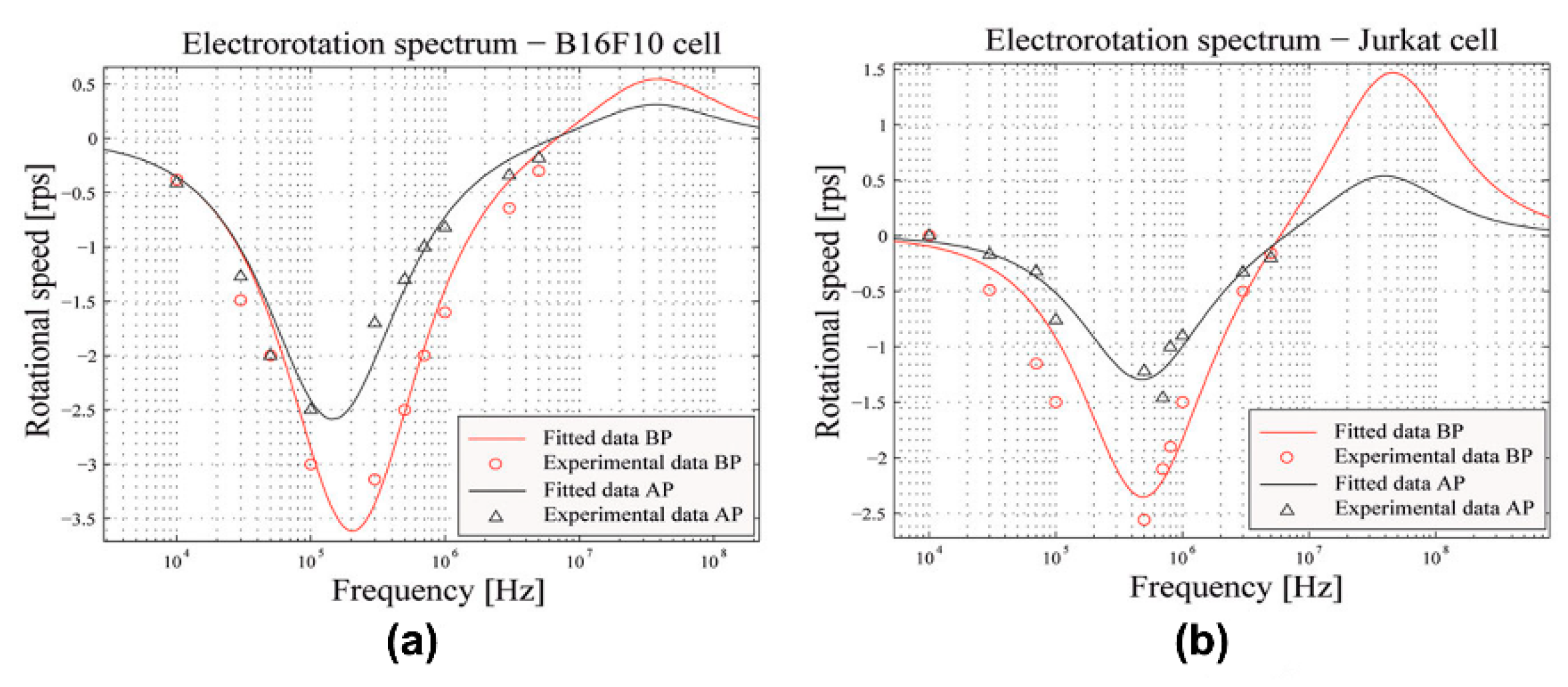
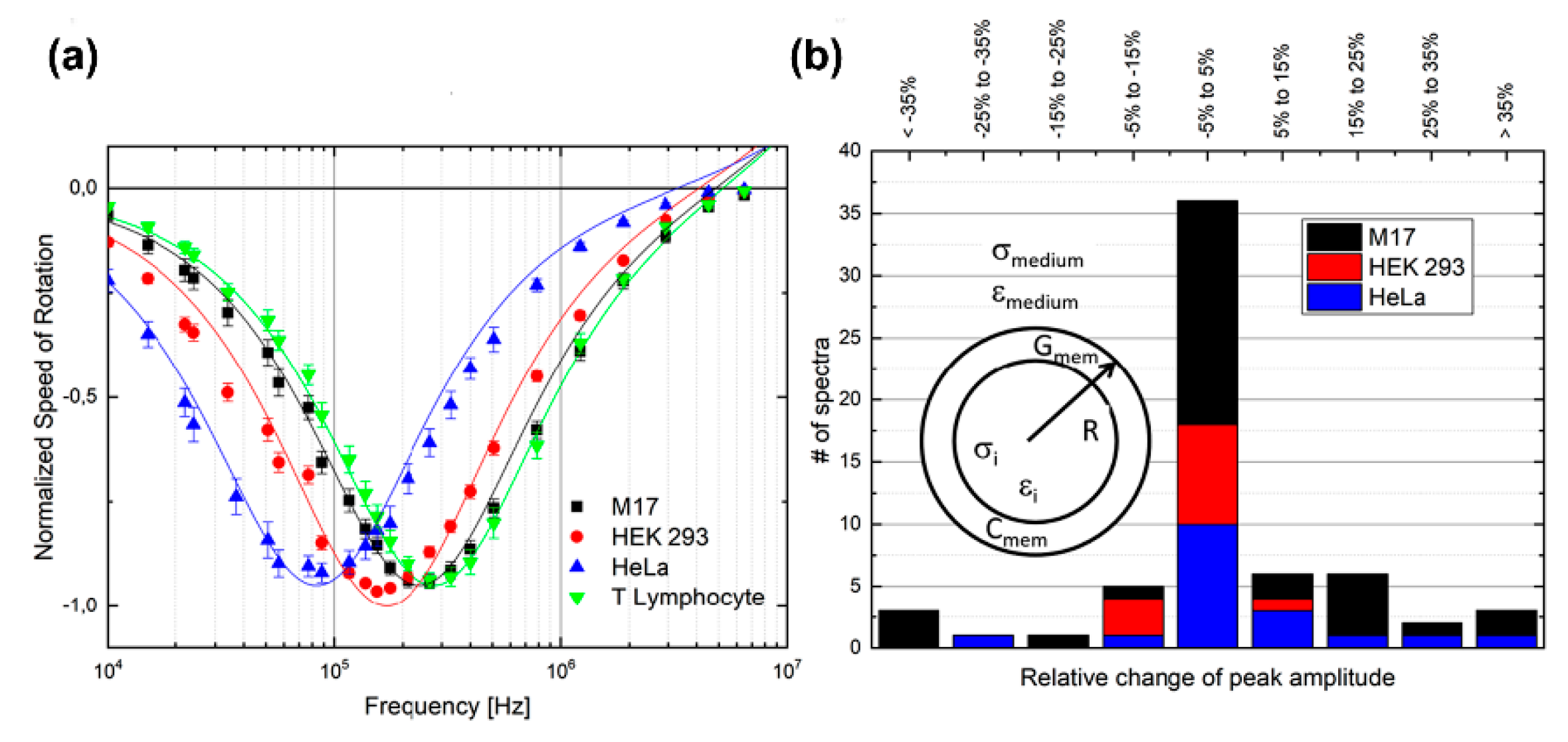
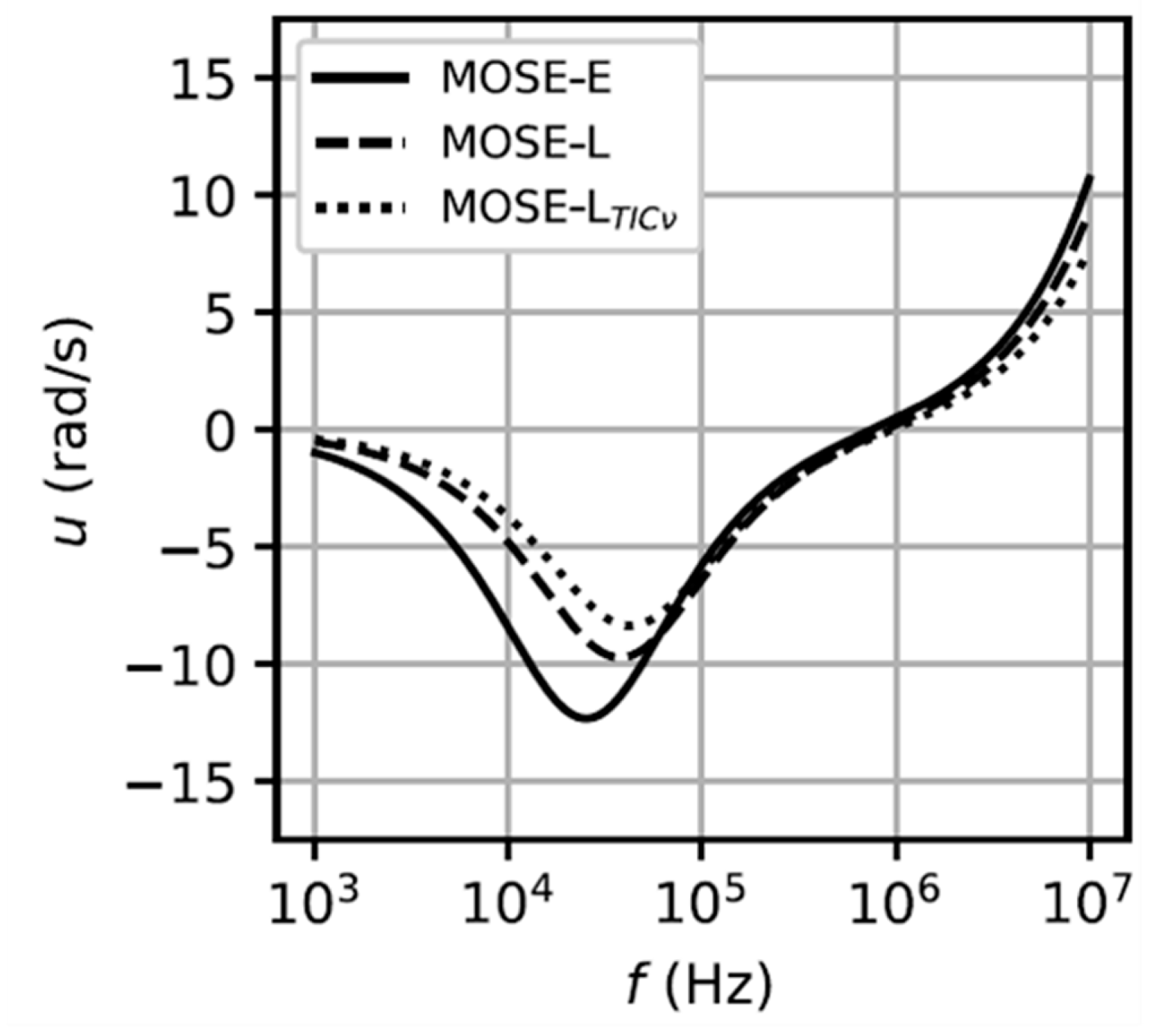
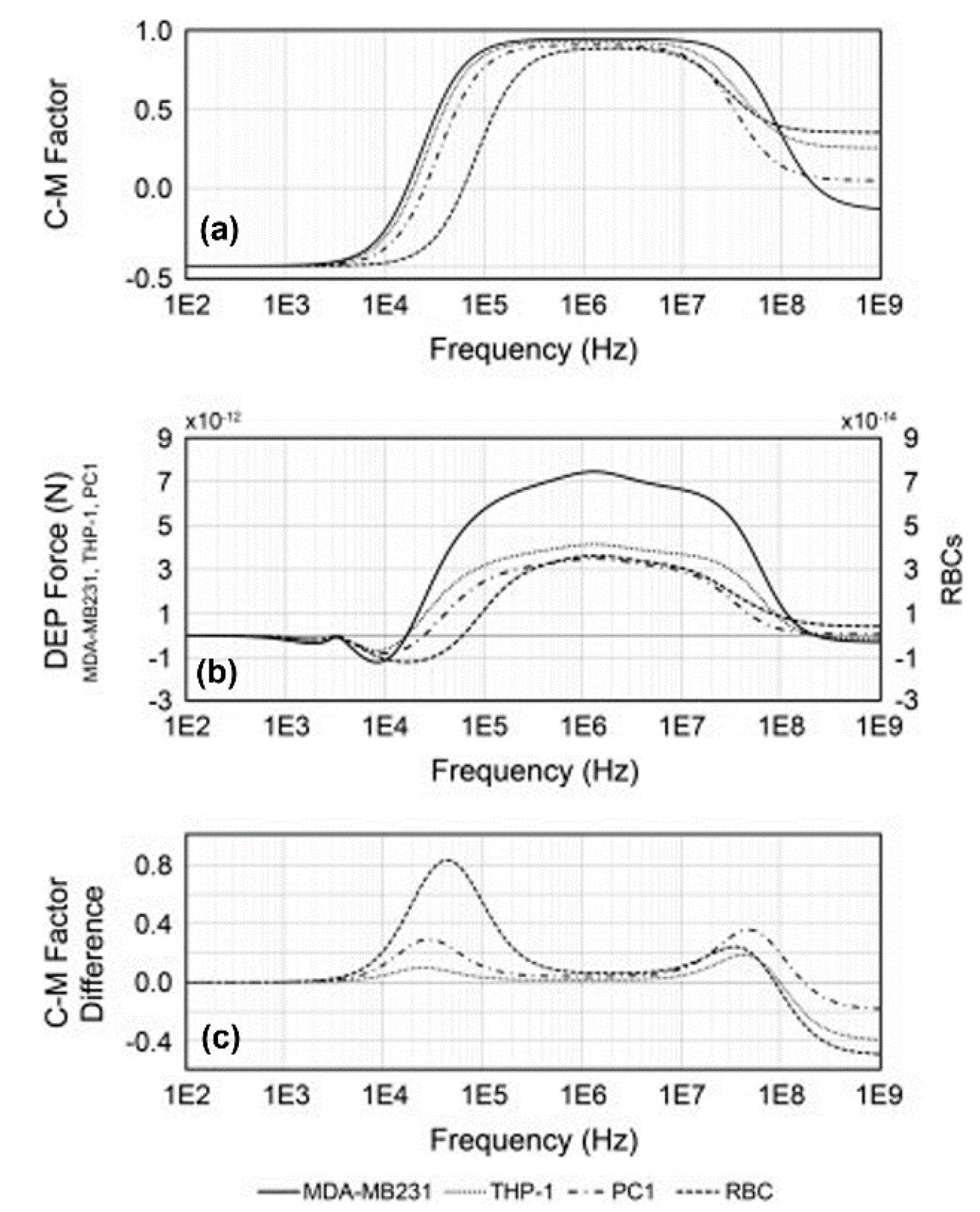
| Cell Type | Dielectric Parameters | Reference | ||||
|---|---|---|---|---|---|---|
| Cmem (mF/m2) | σmem (μS/m) | εmem/ε0 | σcyto (S/m) | εcyto/ε0 | ||
| T-lymphocytes B-lymphocytes Monocytes Granulocytes | 10.5 ± 3.1 12.6 ± 3.5 15.3 ± 4.3 11.0 ± 3.2 | - | - | 0.65 ± 0.15 0.73 ± 0.18 0.56 ± 0.10 0.60 ± 0.13 | 103.9 ± 24.5 154.4 ± 39.9 126.8 ± 35.2 150.9 ± 39.3 | [71] |
| HL-60 | 15.4 ± 0.8 | - | - | - | - | [73] |
| HeLa C3H10 B lymphocyte HepaRG | 13.11 ± 0.11 14.73 ± 0.14 10.14 ± 0.08 15.83 ± 0.12 | - | - | 0.36 ± 0.05 0.31 ± 0.04 0.55 ± 0.07 0.26 ± 0.05 | - | [79] |
| MDA231 T lymphocytes Erythrocytes | 26 ± 4.2 11 ± 1.1 9 + 0.80 | - | - | 0.62 ± 0.073 0.76 ± 0.058 0.52 ± 0.051 | 52 ± 7.3 64 ± 5.9 57 ± 5.4 | [81] |
| Friend murine erythroleukaemia cells | 18.5 | - | - | 0.77 | 92 | [82] |
| Neurospora Myeloma | 4.0 4.5 | - | - | > 1.0 0.068 | - | [83] |
| MCF/neo MCF/HER2-11 MCF/HER2-18 | 20.9 17.0 25.7 | - | - | - | - | [84] |
| Trophoblast Cytotrophoblast | 17.8 ± 9.6 26.6 ± 6.2 | - | - | - | - | [85] |
| Daudi NCI-H929 | 9.0 ± 0.4 4.2 ± 0.3 | - | - | - | - | [86] |
| Jurkat cells | 11.5 ± 1.6 | - | - | - | - | [87] |
| Murine fibroblasts | 8 ± 1 | - | - | - | - | [88] |
| T lymphocyte B lymphocyte Granulocyte Monocyte SkBr3 A549 | 7.01 ± 0.91 10.33 ± 1.6 9.14 ± 1.06 11.77 ± 2.12 14.83 ± 1.74 16.95 ± 2.93 | - | - | 0.53 ± 0.1 0.41 ± 0.1 0.31 ± 0.06 0.37 ± 0.15 0.34 ± 0.06 0.23 ± 0.05 | 100 100 100 100 100 100 | [89] |
| K562 | 8.93 ± 1.43 | - | 10.09 ± 1.61 | 0.32 ± 0.08 | - | [66] |
| HEK293 | 7.94 ± 0.4 | - | - | 0.408 ± 0.019 | 85 ± 4 | [52] |
| Jurkat E 6.1 B16F10 | - | 40 4.9 | 6.30 8.20 | 0.19 0.10 | 40.00 44.70 | [90] |
| Insulin secreting cells | - | 0.7043 | 11.3 | 1.3 | 170.3 | [91] |
| White blood cells U937 PANC1 BxPC3 | 9.8 14 20.2 22.5 | - | - | 0.721 0.750 0.476 0.453 | 111 106 90 91 | [92] |
| T-lymphocyte HEK293 Hela M17 | 8.05 ± 0.47 9.81 ± 0.39 17.51 ± 0.75 7.49 ± 0.39 | - | - | 0.5 0.5 0.84 0.5 | 78 78 60 78 | [93] |
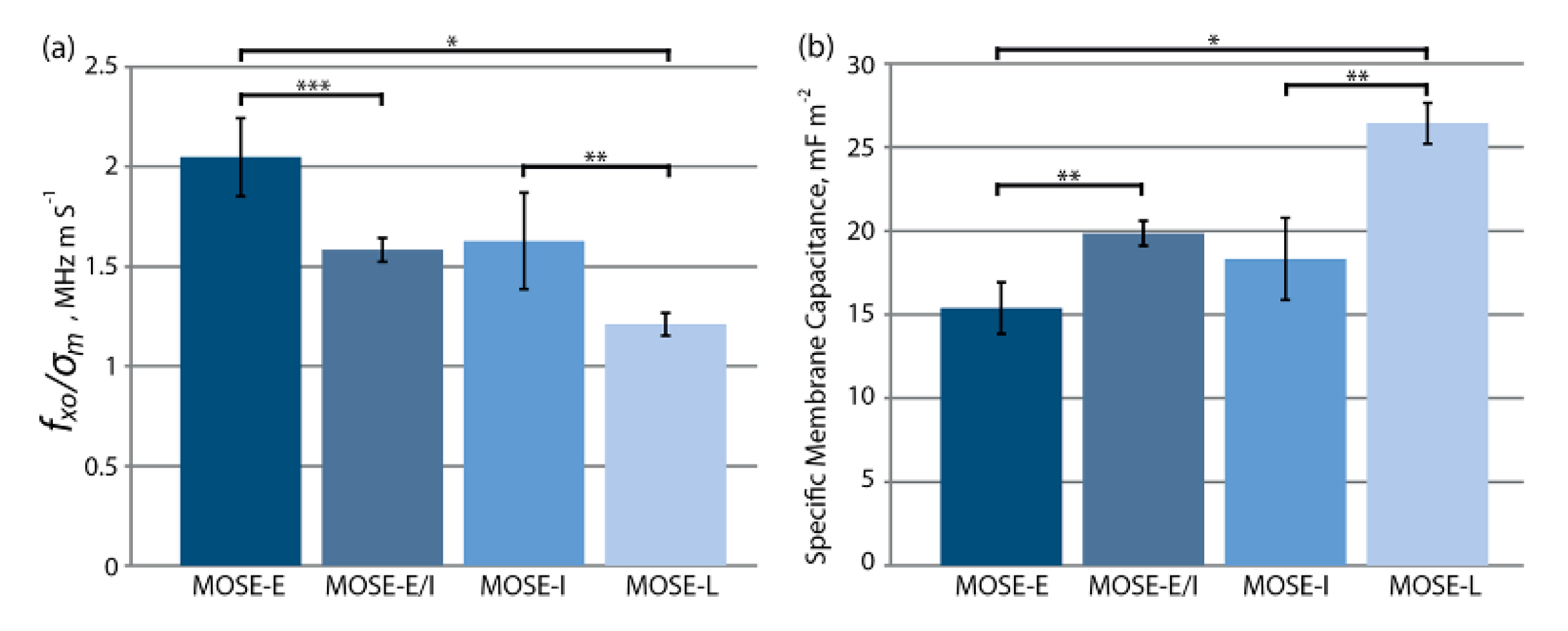
| MOSE-E MOSE-L MOSE-LTICν | - | 32 52 61 | 30 30 30 | 0.90 1.0 1.3 | 45 45 45 | [70] |
| Cell Type | Dielectric Parameters | Reference | ||||
|---|---|---|---|---|---|---|
| Cmem (mF/m2) | σmem (μS/m) | εmem/ε0 | σcyto (S/m) | εcyto/ε0 | ||
| MDA-MB231 THP-1 PC1 RBC | 15.18 ± 1.3 17.19 ± 2.0 12.75 ± 1.8 10.89 | - | - | - | - | [94] |
| HT-29 | - | 34.82 ± 1.36 | 6.01 ± 0.59 | 0.203 ± 0.017 | 61.14 ± 10.19 | [95] |
| C. parvum G. lambia C. muris | - | 0.186 2.47 0.095 | 9.84 12.11 4.39 | 0.047 0.016 0.052 | 61.35 65.58 60.46 | [96] |
| MOSE-E MOSE-E/I, MOSE-I MOSE-L | 15.39 ± 1.54 19.87 ± 0.74 18.33 ± 2.46 26.42 ± 1.22 | - | - | - | - | [97] |
| Raji MCF-7 HEK293 K562 | 11.1 ± 0.9 11.5 ± 0.8 9.0 ± 0.9 10.2 ± 0.7 | - | - | - | - | [60] |
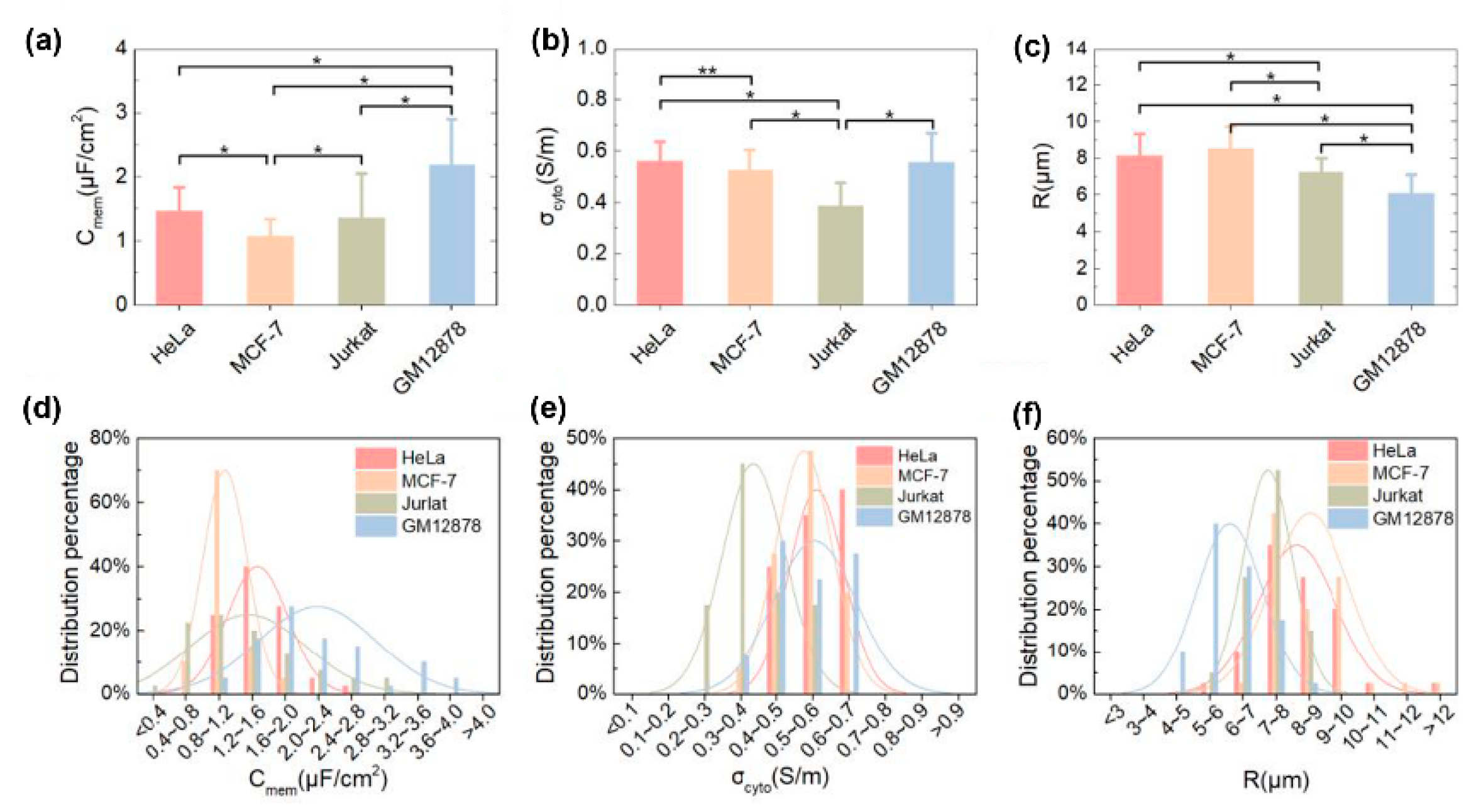
| HeLa MCF-7 Jurkat GM12878 | 14. 6 ± 3.7 10.7 ± 2.7 13.5 ± 6.9 21.9 ± 7.1 | - | - | 0.56 ± 0.07 0.53 ± 0.08 0.39 ± 0.09 0.56 ± 0.11 | - | [98] |
| BT-549 HS 578T SF-268 U251 | 14.4 ± 5.0 18.5 ± 5.6 27.5 ± 6.3 35.8 ± 6.5 | - | - | - | - | [99] |
| Normal erythrocytes Parasitized erythrocytes | - | < 1 70 ± 20 | 4.44 ± 0.45 9.03 ± 0.82 | 0.31 ± 0.03 0.052 ± 0.003 | 59 ± 6 58 ± 10 | [100] |
| Normal erythrocytes Parasitized erythrocytes | 11.8 6–9.9 | - | - | - | - | [101] |
| K562 | 9.7 (8.9–10.6) | - | - | 0.28 (0.27–0.32) | - | [102] |
| T-lymphocytes B-lymphocytes Monocytes Neutrophils Eosinophils Basophils | 13.29 ± 1.82 9.91 ± 0.80 14.23 ± 0.81 9.84 ± 0.07 9.39 ± 0.41 11.2 ± 1.25 | - | - | - | - | [103] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, W.; Yang, X.; Wang, J.; Wang, Y.; Yang, W.; Liu, L. Determination of Dielectric Properties of Cells using AC Electrokinetic-based Microfluidic Platform: A Review of Recent Advances. Micromachines 2020, 11, 513. https://doi.org/10.3390/mi11050513
Liang W, Yang X, Wang J, Wang Y, Yang W, Liu L. Determination of Dielectric Properties of Cells using AC Electrokinetic-based Microfluidic Platform: A Review of Recent Advances. Micromachines. 2020; 11(5):513. https://doi.org/10.3390/mi11050513
Chicago/Turabian StyleLiang, Wenfeng, Xieliu Yang, Junhai Wang, Yuechao Wang, Wenguang Yang, and Lianqing Liu. 2020. "Determination of Dielectric Properties of Cells using AC Electrokinetic-based Microfluidic Platform: A Review of Recent Advances" Micromachines 11, no. 5: 513. https://doi.org/10.3390/mi11050513
APA StyleLiang, W., Yang, X., Wang, J., Wang, Y., Yang, W., & Liu, L. (2020). Determination of Dielectric Properties of Cells using AC Electrokinetic-based Microfluidic Platform: A Review of Recent Advances. Micromachines, 11(5), 513. https://doi.org/10.3390/mi11050513






