Protein Dielectrophoresis: I. Status of Experiments and an Empirical Theory
Abstract
:1. Introduction
- (i)
- The internal electrical field Ei induced in an uncharged (or uniformly charged) spherical particle, of radius R, located in an electric field Em within a dielectric medium is given by:with ɛp and ɛm the relative permittivity of the particle and surrounding medium, respectively. It is assumed that ɛp and ɛm are well defined. At the molecular scale this requires certain conditions to be met regarding dipole–dipole correlations. Boundary conditions also assume that the electric potential, current density and displacement flux are continuous across an infinitesimally thin surface at the sphere’s interface with the surrounding medium. Fine details such as those that occur, for example, at the molecular interface between a protein and its hydration sheath are not considered.
- (ii)
- The induced polarization Pp per unit volume of the sphere is given by:where ɛo is the permittivity of vacuum. The macroscopic dielectric concepts involved in this equation and throughout this paper are summarized in Figure 1. It is assumed that the polarization Pm of the surrounding medium remains uniform right up to the particle–medium interface. This assumption requires examination at the molecular scale.
- (iii)
- The dipole moment m of the sphere is the value of Pp multiplied by the sphere’s volume:The term in brackets in Equations (2) and (3) is the Clausius–Mossotti (CM) function. Depending on the relative values of ɛp and ɛm, CM is limited to values between +1.0 (ɛp >> ɛm) and −0.5 (ɛp << ɛm). This represents a severe limitation, at the macroscopic scale, to the range of effective dipole moment densities that a particle can assume.
- (iv)
- For the case where Em has a gradient, the particle experiences a DEP force given by:where ∇ is the gradient (del) operator and Em is assumed irrotational (i.e., ∇×Em = 0). This assumption holds if Em is said to be a conservative field. In our particular case of DEP, this means that moving a polarized particle from location a to b, and then back again to location a, will involve no net expenditure of work by the field. The actual path taken in moving from say a to z is of no relevance. In the language of thermodynamics each infinitesimal change in location is reversible. At the molecular level, the DEP motion of a protein involves the breaking (enthalpy absorbed and entropy increased) and remaking of hydrogen-bonded water networks at the hydrodynamic plane of shear. Some interesting variations of changes in Gibbs free energy (ΔG = ΔH − T ΔS) might occur. The response of an assembly of dipoles to an external electric field is basically a thermodynamically non-equilibrium process—the thermal energy is never equally distributed among the various degrees of motional freedom of the dipoles. Perhaps, at the molecular level, each infinitesimal change in location is not reversible?
2. The Basic Problem to Be Empirically Resolved
3. The Status of Protein Dielectrophoresis (DEP) Experimentation
3.1. Summary of Protein DEP
3.2. Bovine Serum Albumin (BSA)
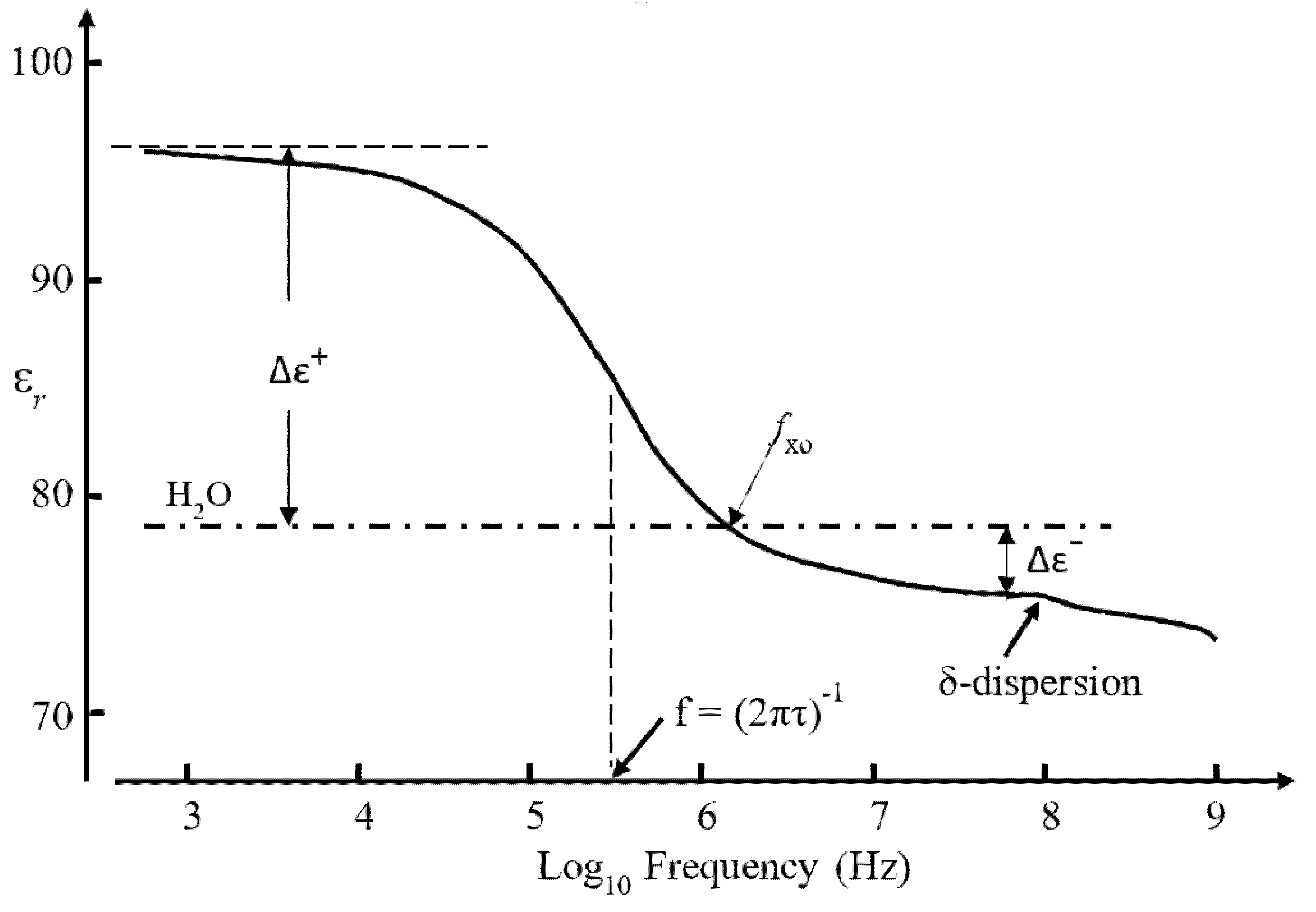
3.3. The Dielectric β-Dispersion
3.4. Empirical Relationship Connecting Clausius–Mossotti (CM) and the β-Dispersion
3.5. The β-Dispersion and Dipole Moment Density
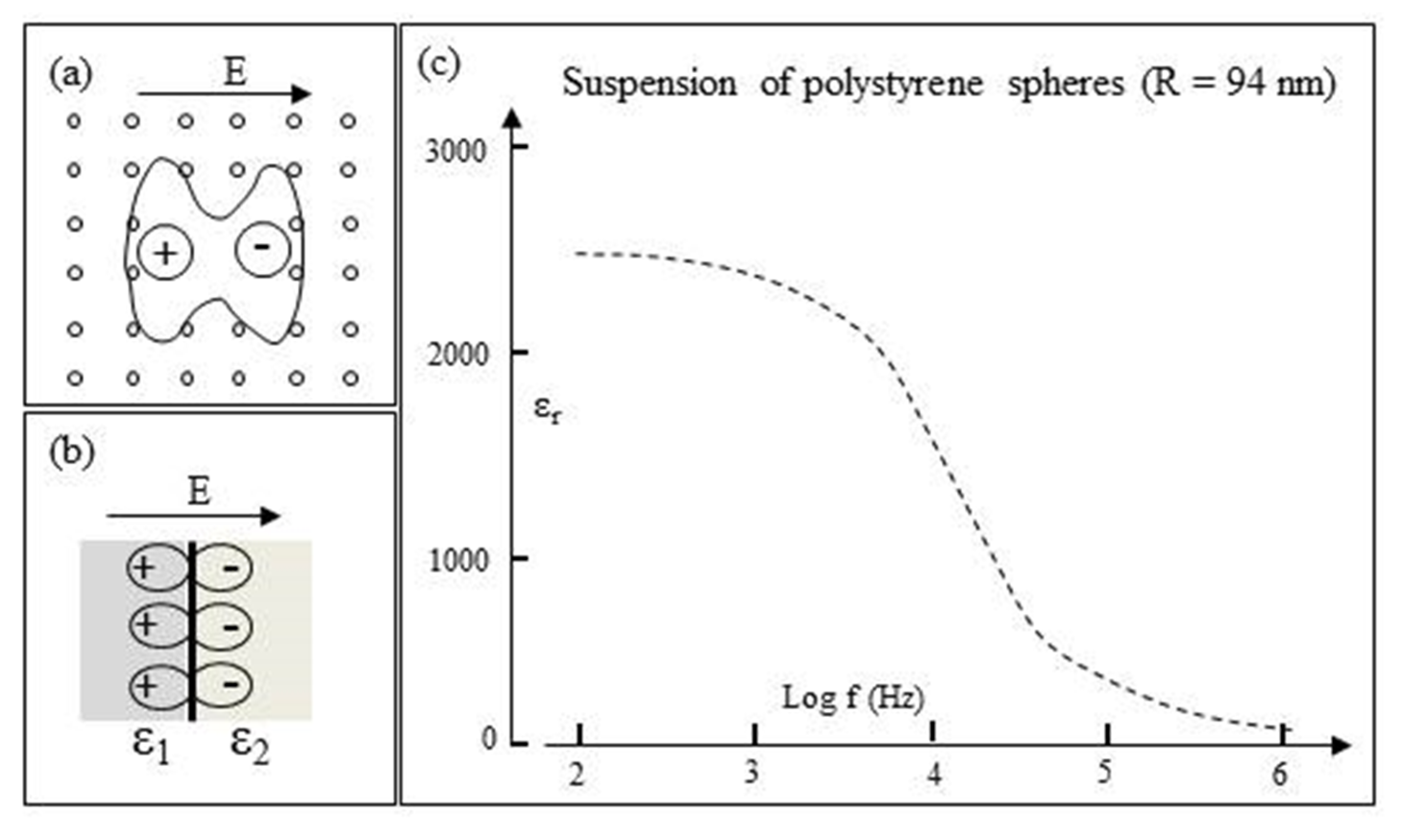
3.6. Interfacial Polarizations
3.7. Protein Dipole Polarization
3.8. Protein Stability
3.9. Other Experimental Details
4. Concluding Comments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kim, D.; Sonker, M.; Ros, A. Dielectrophoresis: From molecular to micrometer-scale analytes. Anal. Chem. 2019, 91, 277–295. [Google Scholar] [CrossRef] [PubMed]
- Washizu, M.; Suzuki, S.; Kurosawa, O.; Nishizaka, T.; Shinohara, T. Molecular dielectrophoresis of biopolymers. IEEE Trans. Ind. Appl. 1994, 30, 835–843. [Google Scholar] [CrossRef]
- Nakano, A.; Ros, A. Protein dielectrophoresis: Advances, challenges, and applications. Electrophoresis 2013, 34, 1085–1096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pethig, R. Dielectropohoresis: Theory, Methodology and Biological Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Laux, E.M.; Bier, F.F.; Hölzel, R. Electrode-based AC electrokinetics of proteins: A mini review. Bioelectrochemistry 2018, 120, 76–82. [Google Scholar] [CrossRef]
- Hayes, M.A. Dielectrophoresis of proteins: Experimental data and evolving theory. Anal. Bioanal. Chem. 2020, 115, 7144. [Google Scholar]
- Lapizco-Encinas, B.H. Microscale electrokinetic assessments of proteins employing insulating structures. Curr. Opin. Chem. Eng. 2020, 29, 9–16. [Google Scholar] [CrossRef]
- Seyedi, S.S.; Matyushov, D.V. Protein Dielectrophoresis in Solution. J. Phys. Chem. B 2018, 122, 9119–9127. [Google Scholar] [CrossRef]
- Pethig, R. Limitations of the Clausius-Mossotti function used in dielectrophoresis and electrical impedance studies of biomacromolecules. Electrophoresis 2019, 40, 2575–2583. [Google Scholar] [CrossRef]
- Matyushov, D.V. Electrostatic solvation and mobility in uniform and non-uniform electric fields: From simple ions to proteins. Biomicrofluidics 2019, 13, 064106:1–064106:15. [Google Scholar] [CrossRef]
- Hölzel, R.; Pethig, R. Protein Dielectrophoresis: II. Key dielectric parameters and evolving theory. Micromachines 2020. to be submitted. [Google Scholar]
- Debye, P. Polar Molecules; The Chemical Catalog Co.: New York, NY, USA, 1929. [Google Scholar]
- Oncley, J.L. The investigation of proteins by dielectric measurements. Chem. Rev. 1942, 30, 433–450. [Google Scholar] [CrossRef]
- Zheng, L.; Brody, J.P.; Burke, P.J. Electronic manipulation of DNA, proteins, and nanoparticles for potential circuit assembly. Biosens. Bioelectron. 2004, 20, 606–619. [Google Scholar] [CrossRef] [PubMed]
- Hübner, Y.; Hoettges, K.F.; McDonnell, M.B.; Carter, M.J.; Hughes, M.P. Applications of dielectrophoretic/electrohydrodynamic “zipper” electrodes for detection of biological nanoparticles. Int. J. Nanomed. 2007, 2, 427–431. [Google Scholar]
- Yamamoto, T.; Fujii, T. Active immobilization of biomolecules on a hybrid three-dimensional nanoelectrode by dielectrophoresis for single-biomolecule study. Nanotechnology 2007, 18, 495503:1–495503:7. [Google Scholar] [CrossRef] [PubMed]
- Lapizco-Encinas, B.H.; Ozuna-Chacón, S.; Rito-Palomares, M. Protein manipulation with insulator-based dielectrophoresis and direct current electric fields. J. Chromat. A 2008, 1206, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Agastin, S.; King, M.R.; Jones, T.B. Rapid enrichment of biomolecules using simultaneous liquid and particulate dielectrophoresis. Lab Chip 2009, 9, 2319–2325. [Google Scholar] [CrossRef] [PubMed]
- Nakano, A.; Chao, T.-C.; Camacho-Alanis, F.; Ros, A. Immunoglobulin G and bovine serum albumin streaming dielectrophoresis in a microfluidic device. Electrophoresis 2011, 32, 2314–2322. [Google Scholar] [CrossRef]
- Camacho-Alanis, F.; Gan, L.; Ros, A. Transitioning streaming to trapping in DC insulator based dielectrophoresis for biomolecules. Sens. Actuators B Chem. 2012, 173, 668–675. [Google Scholar] [CrossRef] [Green Version]
- Liao, K.-T.; Chou, C.-F. Nanoscale Molecular Traps and Dams for Ultrafast Protein Enrichment in High-Conductivity Buffers. J. Am. Chem. Soc. 2012, 134, 8742–8745. [Google Scholar] [CrossRef]
- Barik, A.; Otto, L.M.; Yoo, D.; Jose, J.; Johnson, T.W.; Oh, S.-H. Dielectrophoresis-enhanced plasmonic sensing with gold nanohole arrays. Nano Lett. 2014, 14, 2006–2012. [Google Scholar] [CrossRef]
- Laux, E.M.; Knigge, X.; Bier, F.F.; Wenger, C.; Hölzel, R. Dielectrophoretic immobilization of proteins: Quantification by atomic force microscopy. Electrophoresis 2015, 36, 2094–2101. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, C.; Kern, D.P.; Fleischer, M. Capturing molecules with plasmonic nanotips in microfluidic channels by dielectrophoresis. Lab Chip 2015, 15, 1066–1071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, P.; Liu, Y. DC biased low-frequency insulating constriction dielectrophoresis for protein biomolecules concentration. Biofabrication 2017, 9, 045003:1–045003:11. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Zhu, Y.; Liu, Y.; Dong, S.; Chen, X.; Bai, F.; Song, S.; Fu, J. Dielectrophoresis-based protein enrichment for a highly sensitive immunoassay using Ag/SiO2 nanorod arrays. Small 2018, 14, 17032265. [Google Scholar] [CrossRef]
- Bakewell, J.G.; Hughes, M.P.; Milner, J.J.; Morgan, H. Dielectrophoretic manipulation of avidin and DNA. In Proceedings of the 20th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Hong Kong, China, 1 November 1998; Volume 20, pp. 1079–1082. [Google Scholar]
- Hölzel, R.; Calander, N.; Chiragwandi, Z.; Willander, M.; Bier, F.F. Trapping single molecules by dielectrophoresis. Phys. Rev. Lett. 2005, 95, 128102:1–128102:4. [Google Scholar] [CrossRef]
- Clarke, R.W.; White, S.S.; Zhou, D.J.; Ying, L.M.; Klenerman, D. Trapping of proteins under physiological conditions in a nanopipette. Angew. Chem. Int. Ed. 2005, 44, 3747–3750. [Google Scholar] [CrossRef]
- Staton, S.J.R.; Jones, P.V.; Ku, G.; Gilman, S.D.; Kheterpal, I.; Hayes, M.A. Manipulation and capture of A beta amyloid fibrils and monomers by DC insulator gradient dielectrophoresis (DC-iGDEP). Analyst 2012, 137, 3227–3229. [Google Scholar] [CrossRef]
- Mata-Gomez, M.A.; Gallo-Villanueva, R.C.; Gonzalez-Valdez, J.; Martinez-Chapa, S.O.; Rito-Palomares, M. Dielectrophoretic behavior of PEGylated RNase A inside a microchannel with diamond-shaped insulating posts. Electrophoresis 2016, 37, 519–528. [Google Scholar] [CrossRef]
- Nakano, A.; Camacho-Alanis, F.; Ros, A. Insulator-based dielectrophoresis with β-galactosidase in nanostructured devices. Analyst 2015, 140, 860–868. [Google Scholar] [CrossRef] [Green Version]
- Liao, K.T.; Tsegaye, M.; Chaurey, V.; Chou, C.F.; Swami, N.S. Nano-constriction device for rapid protein preconcentration in physiological media through a balance of electrokinetic forces. Electrophoresis 2012, 33, 1958–1966. [Google Scholar] [CrossRef]
- Chaurey, V.; Rohani, A.; Su, Y.H.; Liao, K.T.; Chou, C.F.; Swami, N.S. Scaling down constriction-based (electrodeless) dielectrophoresis devices for trapping nanoscale bioparticles in physiological media of high-conductivity. Electrophoresis 2013, 34, 1097–1104. [Google Scholar] [CrossRef] [PubMed]
- Sanghavi, B.J.; Varhue, W.; Chavez, J.L.; Chou, C.F.; Swami, N.S. Electrokinetic Preconcentration and Detection of Neuropeptides at Patterned Graphene-Modified Electrodes in a Nanochannel. Anal. Chem. 2014, 86, 4120–4125. [Google Scholar] [CrossRef] [PubMed]
- Laux, E.-M.; Kaletta, U.C.; Bier, F.F.; Wenger, C.; Hölzel, R. Functionality of dielectrophoretically immobilized enzyme molecules. Electrophoresis 2014, 35, 459–466. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Kim, J.; Yoo, Y.K.; Lee, J.H.; Park, J.H.; Wang, K.S. Sensitivity improvement of an electrical sensor achieved by control of biomolecules based on the negative dielectrophoretic force. Biosens. Bioelectron. 2016, 85, 977–985. [Google Scholar] [CrossRef]
- Laux, E.-M.; Knigge, X.; Bier, F.F.; Wenger, C.; Hölzel, R. Aligned Immobilization of Proteins Using AC Electric Fields. Small 2015, 12, 03052:1–03052:7. [Google Scholar] [CrossRef]
- Chiou, C.-H.; Chien, L.-J.; Kuo, J.-N. Nanoconstriction-based electrodeless dielectrophoresis chip for nanoparticle and protein preconcentration. Appl. Phys. Express 2015, 8, 085201:1–085201:3. [Google Scholar] [CrossRef]
- Sharma, A.; Han, C.-H.; Jang, J. Rapid electrical immune assay of the cardiac biomarker troponin I through dielectrophoretic concentration using imbedded electrodes. Biosens. Bioelectron. 2016, 82, 78–84. [Google Scholar] [CrossRef]
- Rohani, A.; Sanghavi, B.J.; Salahi, A.; Liao, K.T.; Chou, C.F.; Swami, NS. Frequency-selective electrokinetic enrichment of biomolecules in physiological media based on electrical double-layer polarization. Nanoscale 2017, 9, 12124–12131. [Google Scholar] [CrossRef]
- Han, C.-H.; Woo, S.Y.; Bhardwaj, J.; Sharma, A.; Jang, J. Rapid and selective concentration of bacteria, viruses, and proteins using alternating current signal superimposition on two coplanar electrodes. Sci. Rep. 2018, 8, 14942:1–14942:10. [Google Scholar] [CrossRef]
- Axelsson, I. Characterization of proteins and other macromolecules by agarose gel chromatography. J. Chromatogr. A 1978, 152, 21–32. [Google Scholar] [CrossRef]
- Majorek, K.A.; Porebski, P.J.; Dayal, A.; Zimmerman, M.D.; Jablonska, K.; Stewart, A.J.; Chruszcz, M.; Minor, W. Structural and immunologic characterization of bovine, horse, and rabbit serum albumins. Mol. Immunol. 2012, 52, 174–182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Lee, J.; Lal, J.; An, L.; Huang, Q. Effects of pH on the interactions and conformation of bovine serum albumin: Comparison between chemical force microscopy and small-angle neutron scattering. J. Phys. Chem. B 2008, 112, 3797–3806. [Google Scholar] [CrossRef]
- Barbosa, L.R.S.; Ortore, M.G.; Spinozzi, F.; Mariani, P.; Bernstorff, S.; Itri, R. The importance of protein-protein interactions on the pH-induced conformational changes of bovine serum albumin: A small-angle X-Ray scattering study. Biophys. J. 2010, 98, 147–157. [Google Scholar] [CrossRef] [PubMed]
- Takeda, K.; Wada, A.; Yamamoto, K.; Moriyama, Y.; Aoki, K. Conformational change of bovine serum albumin by heat treatment. J. Protein Chem. 1989, 8, 653–659. [Google Scholar] [CrossRef] [PubMed]
- Murayama, K.; Tomida, M. Heat-induced secondary structure and conformation change of bovine serum albumin investigated by Fourier transform infrared spectroscopy. Biochemistry 2004, 43, 11526–11532. [Google Scholar] [CrossRef] [PubMed]
- Pindrus, M.A.; Cole, J.L.; Kaur, J.; Shire, S.; Yadav, S.; Kalonia, D.S. Effect of aggregation on the hydrodynamic properties of bovine serum albumin. Pharm. Res. 2017, 34, 2250–2259. [Google Scholar] [CrossRef] [PubMed]
- de Frutos, M.; Cifuentes, A.; Díez-Masa, J.C. Multiple peaks in HPLC of proteins: Bovine serum albumin eluted in a reversed-phase system. J. High Resol. Chromatogr. 1998, 21, 18–25. [Google Scholar] [CrossRef]
- Chi, E.Y.; Krishnan, S.; Randolph, T.W.; Carpenter, J.F. Physical stability of proteins in aqueous solution: Mechanism and driving forces in non-native protein aggregation. Pharm. Res. 2003, 20, 1325–1336. [Google Scholar] [CrossRef]
- Pethig, R. Dielectric properties of biological materials: Biophysical and medical applications. IEEE Trans. Electr. Insul. 1984, EI-19, 453–474. [Google Scholar] [CrossRef]
- Moser, P.; Squire, P.G.; O’Konski, C.T.O. Electric polarization in proteins—Dielectric dispersion and Kerr effect studies of isionic bovine serum albumin. J. Phys. Chem. 1966, 70, 744–756. [Google Scholar] [CrossRef]
- Grant, E.H.; Keefe, S.E.; Takashima, S. The dielectric behavior of aqueous solutions of bovine serum albumin from radiowave to microwave frequencies. J. Phys. Chem. 1968, 72, 4373–4380. [Google Scholar] [CrossRef] [PubMed]
- Fischer, H.; Polikarpov, I.; Craievich, A.F. Average protein density is a molecular-weight-dependent function. Protein Sci. 2004, 13, 2825–2827. [Google Scholar] [CrossRef] [PubMed]
- Takashima, S.; Asami, K. Calculation and measurement of the dipole moment of small proteins: Use of protein data base. Biopolymers 1993, 33, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Chari, R.; Singh, S.N.; Yadav, S.; Brems, D.N.; Kalonia, D.S. Determination of the dipole moments of RNAse SA wild type and a basic mutant. Proteins 2012, 80, 1041–1052. [Google Scholar] [CrossRef]
- Knocks, A.; Weingärtner, H. The dielectric spectrum of ubiquitin in aqueous solution. J. Phys. Chem. B 2001, 105, 3635–3638. [Google Scholar] [CrossRef]
- Keefe, S.E.; Grant, E.H. Dipole moment and relaxation time of ribonuclease. Phys. Med. Biol. 1974, 9, 701–707. [Google Scholar] [CrossRef]
- Schlecht, P. Dielectric properties of hemoglobin and myoglobin. II. Dipole moment of sperm whale myoglobin. Biopolymers 1969, 8, 757–765. [Google Scholar] [CrossRef]
- South, G.P.; Grant, E.H. Dielectric dispersion and dipole moment of myoglobin in water. Proc. R. Soc. Lond. A 1972, 328, 371–387. [Google Scholar]
- Takashima, S. Use of protein database for the computation of the dipole moments of normal and abnormal hemoglobins. Biophys. J. 1993, 64, 1550–1558. [Google Scholar] [CrossRef] [Green Version]
- Pethig, R. Protein-water interactions determined by dielectric methods. Annu. Rev. Phys. Chem. 1992, 43, 177–205. [Google Scholar] [CrossRef]
- Hedvig, P. Dielectric Spectroscopy of Polymers; Akadémiai Kiadó: Budapest, Hungary, 1977. [Google Scholar]
- Martin, D.R.; Friesen, A.D.; Matyushov, D.V. Electric field inside a “Rossky cavity” in uniformly polarized water. J. Chem. Phys. 2011, 135, 084514. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martin, D.R.; Matyushov, D.V. Dipolar nanodomains in protein hydration shells. J. Phys. Chem. Lett. 2015, 6, 407–412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Naumov, I.I.; Bellaiche, L.; Fu, H. Unusual phase transitions in ferroelectric nanodisks and nanorods. Nature 2004, 432, 737–740. [Google Scholar] [CrossRef] [PubMed]
- Seyedi, S.; Matyushov, D.V. Dipolar susceptibility of protein hydration shells. Chem. Phys. Lett. 2018, 713, 210–214. [Google Scholar] [CrossRef]
- Schwan, H.P.; Schwarz, G.; Maczuk, J.; Pauly, H. On the low-frequency dielectric dispersion of colloidal particles in electrolyte solution. J. Phys. Chem. 1962, 66, 2626–2635. [Google Scholar] [CrossRef]
- Foster, K.R.; Schwan, H.P. Dielectric properties of tissues. In Handbook of Biological Effects of Electromagnetic Fields; CRC Press Inc.: Boca Raton, FL, USA, 1996; pp. 118–122. [Google Scholar]
- Medda, L.; Monduzzi, M.; Salis, A. The molecular motion of bovine serum albumin under physiological conditions is ion specific. Chem. Commun. 2015, 51, 6663–6666. [Google Scholar] [CrossRef] [Green Version]
- Saucedo-Espinosa, M.A.; Lapizco-Encinas, B.H. Design of insulator-based dielectrophoretic devices: Effect of insulator posts characteristics. J. Chromatogr. A 2015, 1422, 325–333. [Google Scholar] [CrossRef]
- Xuan, X. Recent advances in direct current electrokinetic manipulation of particles for microfluidic applications. Electrophoresis 2019, 40, 2484–2513. [Google Scholar] [CrossRef]
- Lapizco-Encinas, B.H. On the recent development of insulator based dielectrophoresis (iDEP) by comparing the streaming and trapping regimes. Electrophoresis 2019, 40, 358–375. [Google Scholar] [CrossRef]
- Pethig, R. Review—Where is dielectrophoresis going? J. Electrochem. Soc. 2017, 164, B3049–B3055. [Google Scholar] [CrossRef]








| Protein | Mol. Wt. | Density (g/cm3) | Δɛ/cp (cp: mM) | (κ + 2)CM Equation (13) | Reference |
|---|---|---|---|---|---|
| Ubiquitin | 8600 | 1.49 | 3.82 | 4020 | [58] |
| RNAse SA | 10,500 | 1.48 | 15.00 | 15,720 | [57] |
| Phospholipase | 13,000 | 1.46 | 1.82 | 189 | [56] |
| Cytochrome-c | 13,000 | 1.46 | 5.06 | 5240 | [56] |
| Ribonuclease | 13,700 | 1.46 | 11.0 | 11,400 | [59] |
| 7.12 | 7350 | [56] | |||
| Lysozyme | 14,300 | 1.46 | 1.34 | 1390 | [56] |
| Myoglobin | 17,000 | 1.45 | 0.07 | 2090 | [60] |
| 1.79 | 1440 | [61] | |||
| Trypsin | 23,000 | 1.43 | 6.74 | 6810 | [56] |
| Carboxypeptidase | 34,000 | 1.42 | 37.24 | 37,440 | [56] |
| Hemoglobin | 64,000 | 1.41 | 1.29 | 1290 | [62] |
| BSA | 66,000 | 1.41 | 1.11 | 1110 | [53] |
| Concanavaline | 102,000 | 1.41 | 15.31 | 15,270 | [56] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hölzel, R.; Pethig, R. Protein Dielectrophoresis: I. Status of Experiments and an Empirical Theory. Micromachines 2020, 11, 533. https://doi.org/10.3390/mi11050533
Hölzel R, Pethig R. Protein Dielectrophoresis: I. Status of Experiments and an Empirical Theory. Micromachines. 2020; 11(5):533. https://doi.org/10.3390/mi11050533
Chicago/Turabian StyleHölzel, Ralph, and Ronald Pethig. 2020. "Protein Dielectrophoresis: I. Status of Experiments and an Empirical Theory" Micromachines 11, no. 5: 533. https://doi.org/10.3390/mi11050533
APA StyleHölzel, R., & Pethig, R. (2020). Protein Dielectrophoresis: I. Status of Experiments and an Empirical Theory. Micromachines, 11(5), 533. https://doi.org/10.3390/mi11050533





