Influence of Temperature Effect on the Static and Dynamic Performance of Gas-Lubricated Microbearings
Abstract
:1. Introduction
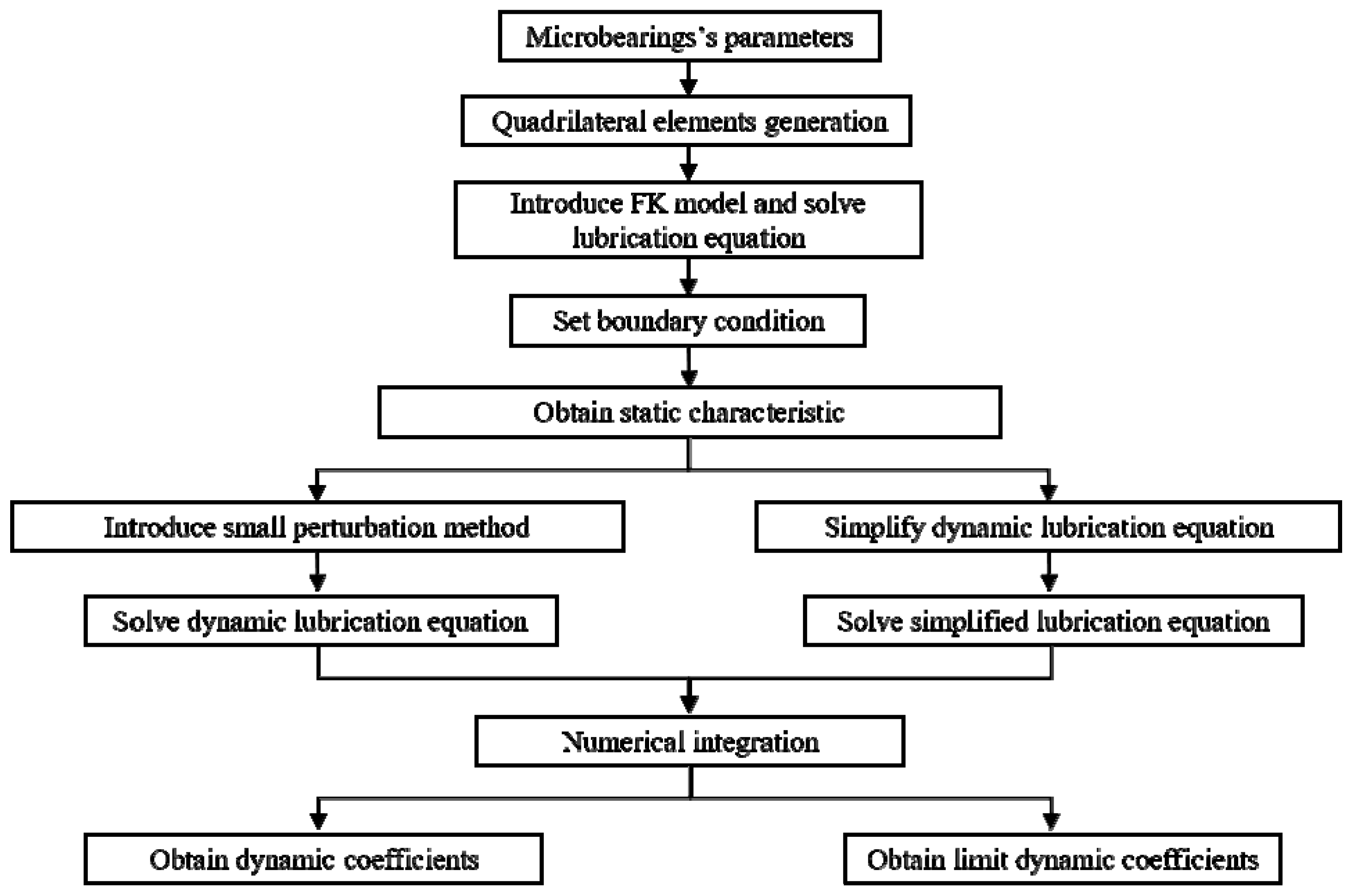
2. Numerical Method
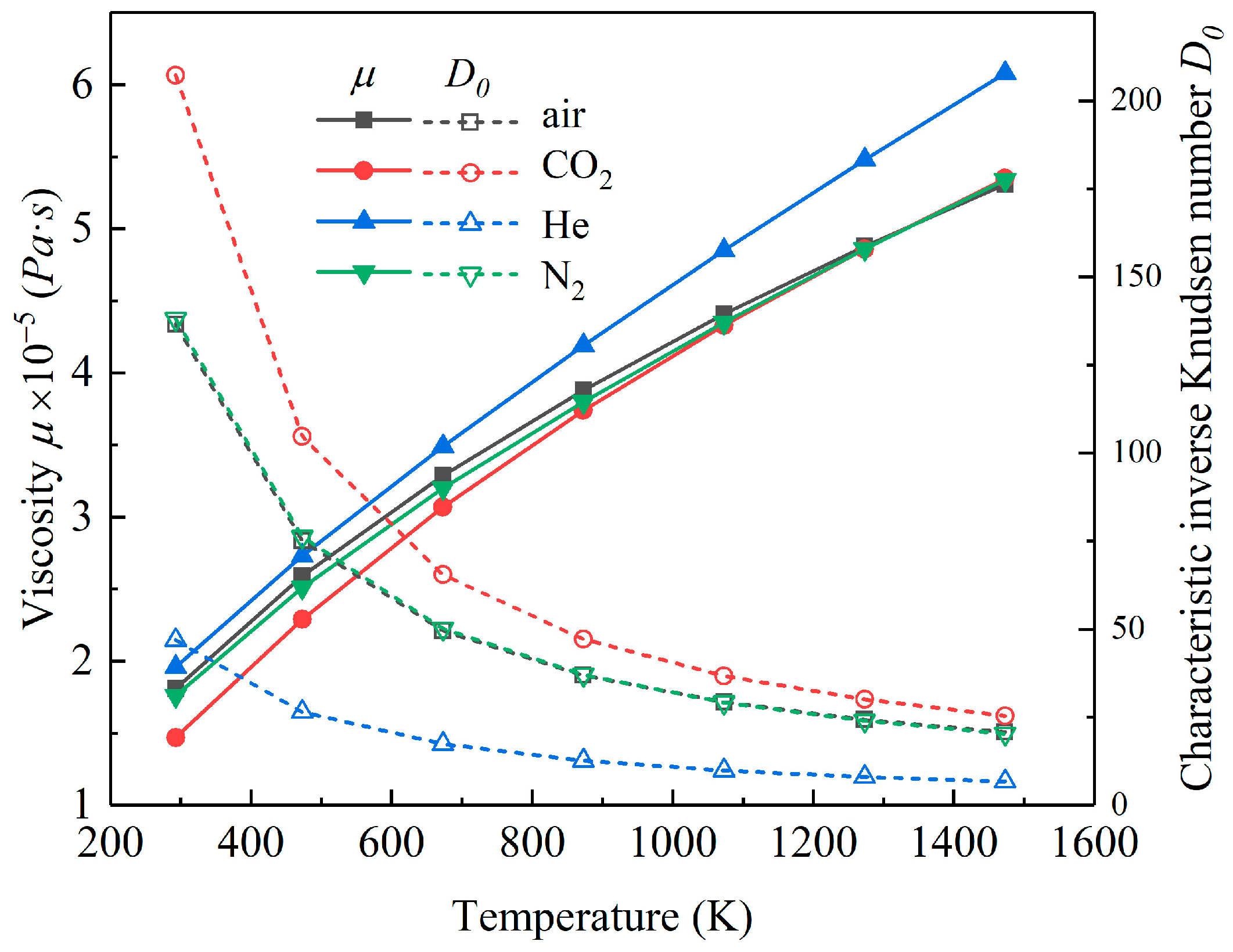
2.1. Treatment of Temperature and Rarefaction Effect
2.2. Control Equations and Solution Method
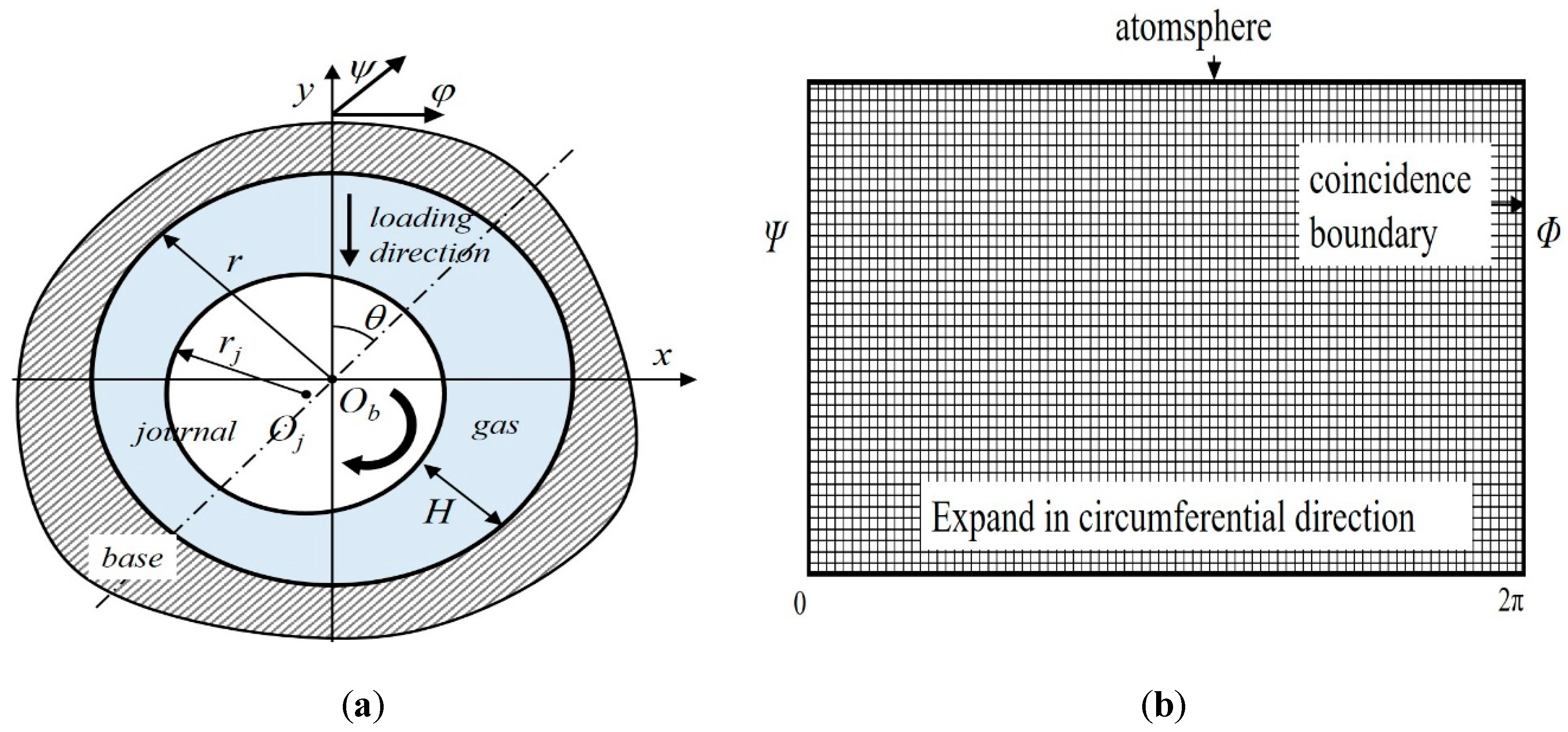
2.3. Model Parameters and Boundary Condition
2.4. Example Case
3. Results and Discussion
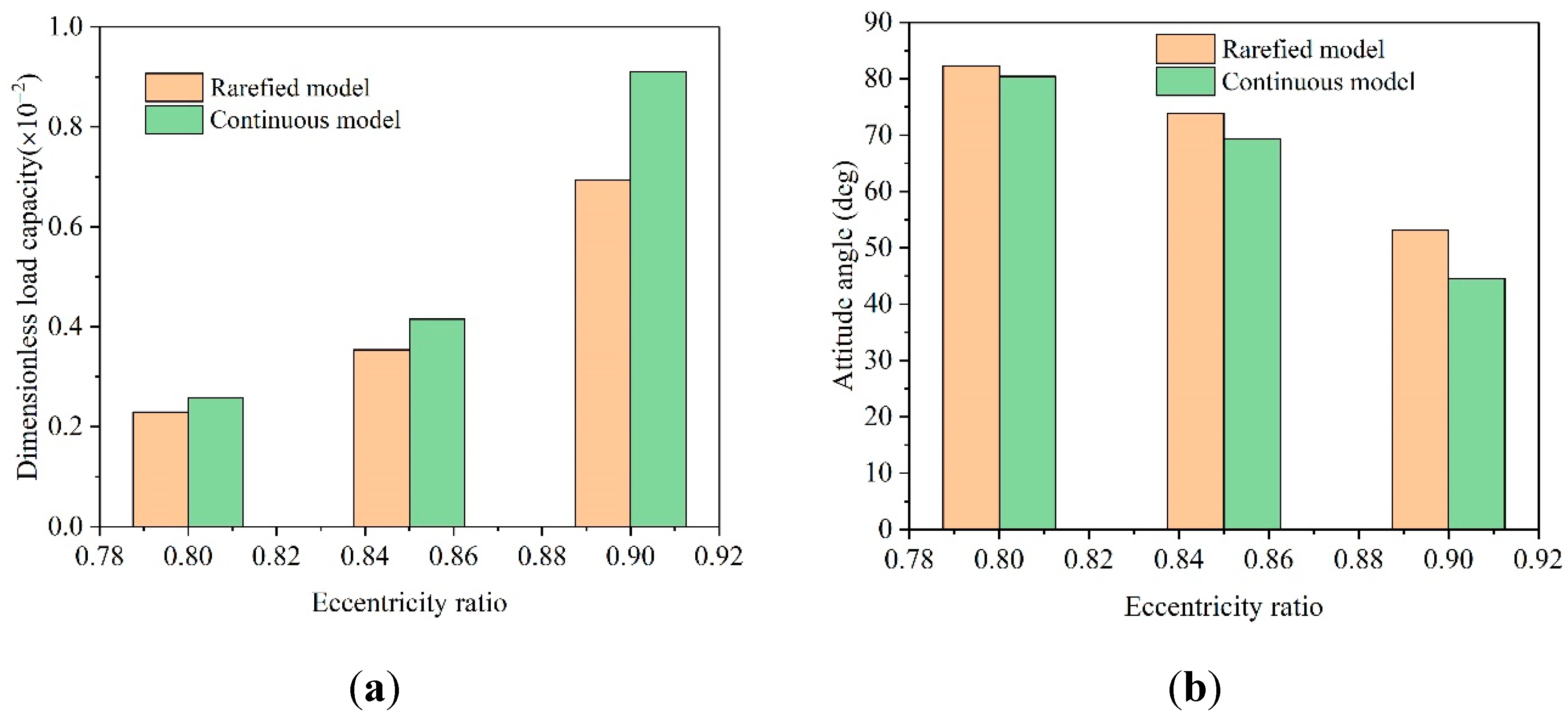
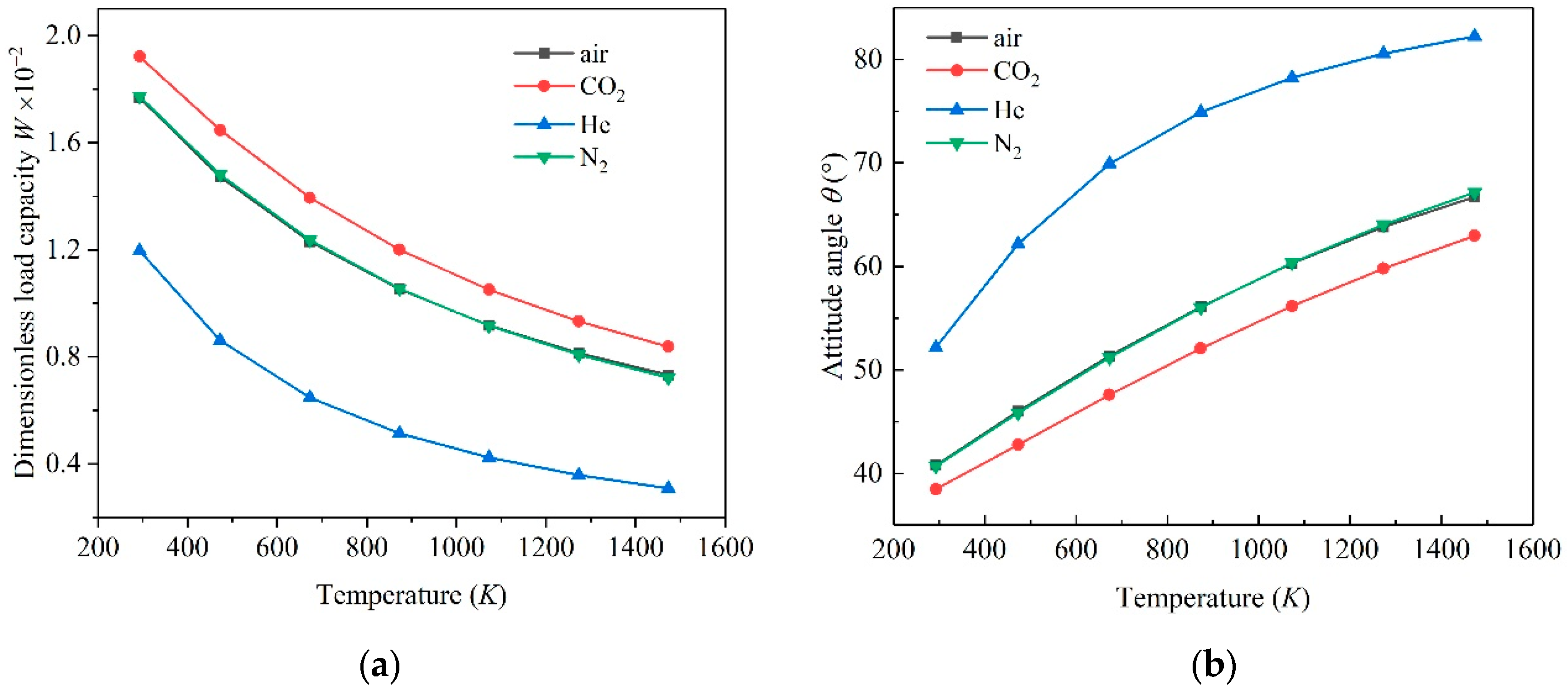
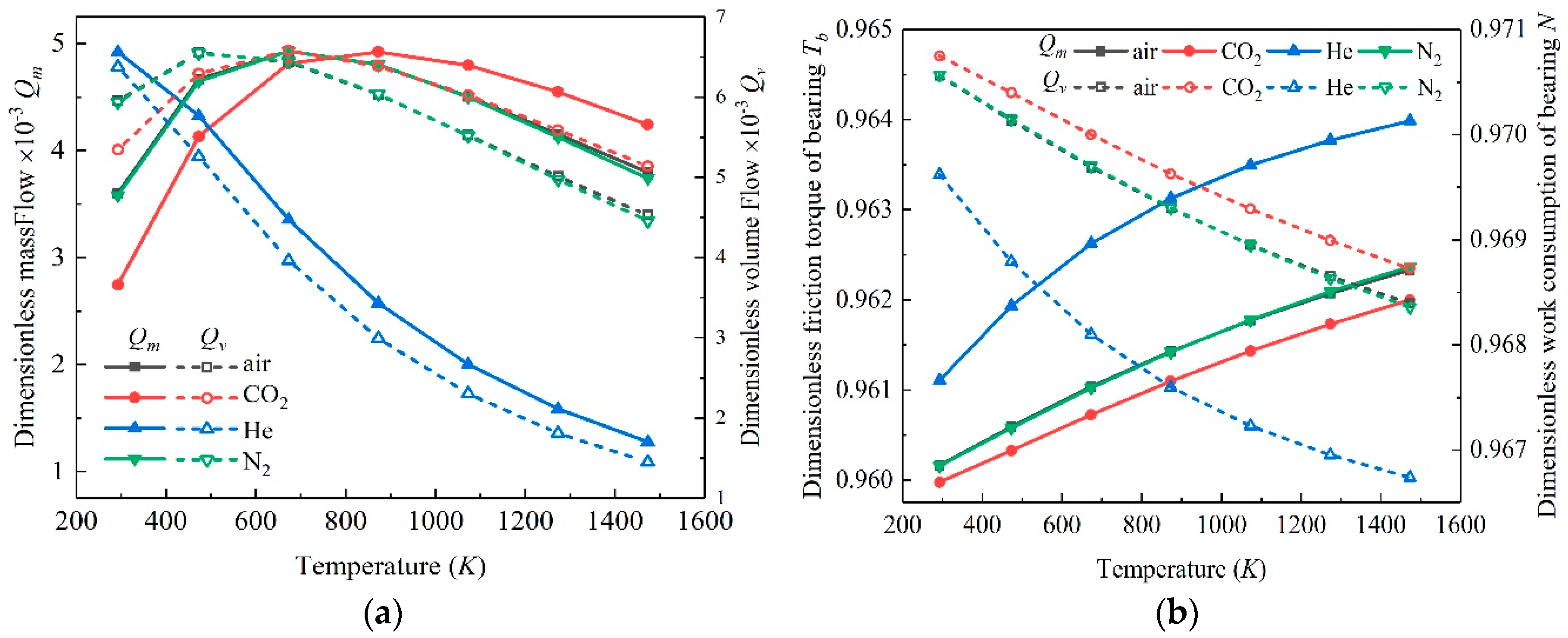
3.1. Effect of Temperature on Static Performance
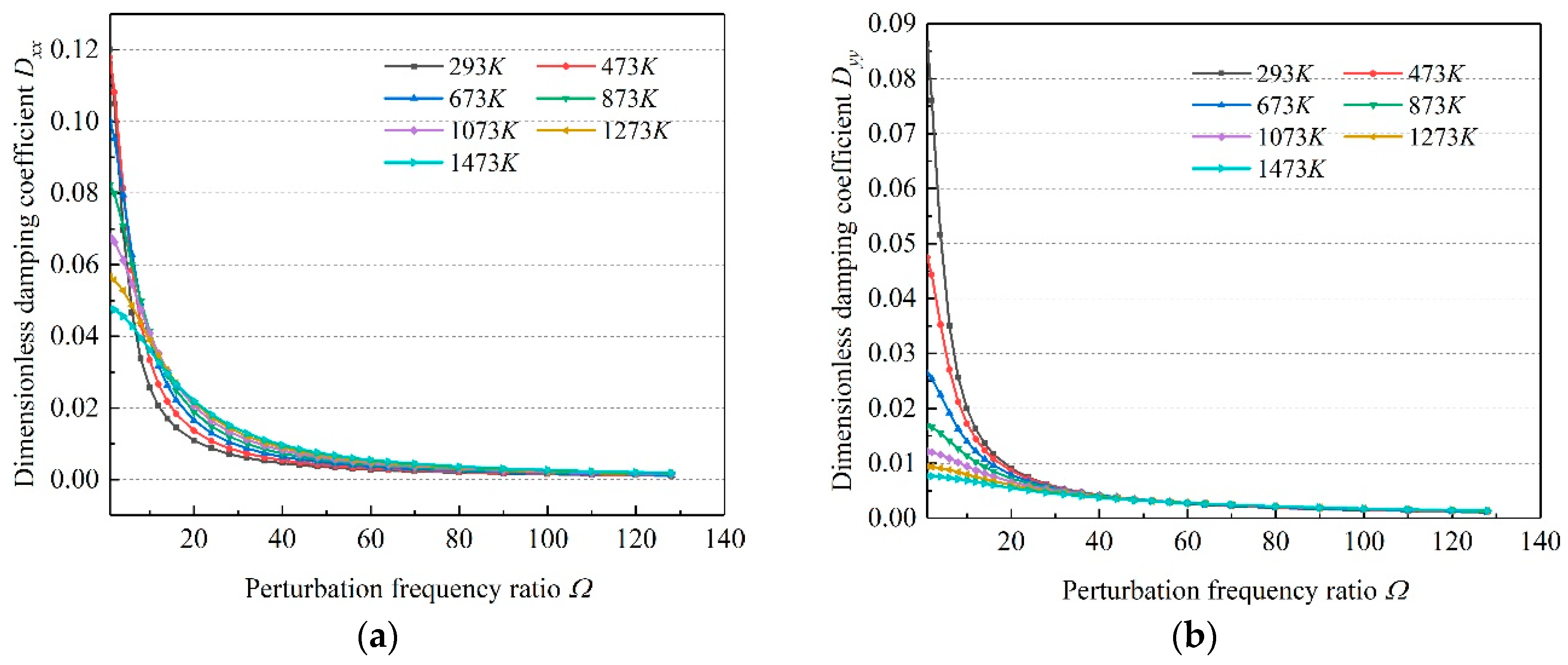
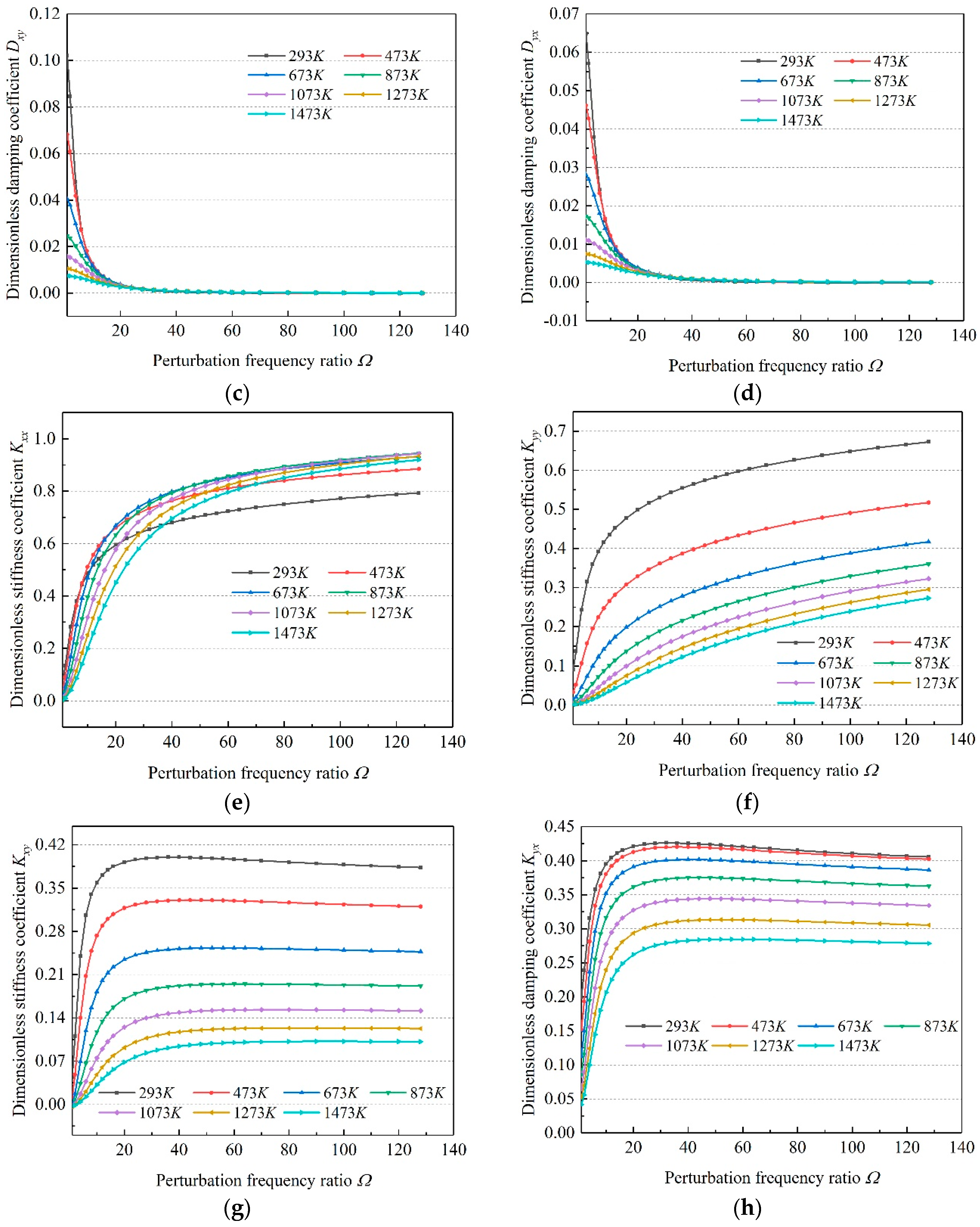
3.2. Effect of Temperature on the Dynamic Characteristics of Microbearings
3.3. Effect of Temperature on +∞ Dynamic Limit Characteristics of Microbearings
3.4. Effect of Temperature on Zero Dynamic Limit Characteristics of Microbearings
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| c | radius clearance/mm |
| d | molecular diameter of the gas |
| D | inverse Knudsen number |
| D0 | characteristic inverse Knudsen number |
| D(x,y), D(ε,θ) | Dimensionless damping coefficients |
| E0 | perturbation amplitude of eccentricity |
| H | dimensionless film thickness, H = h/c |
| H0 | Dimensionless steady film thickness |
| HE, HΘ | derivative of Hd0 to. E0 and Θ0 |
| Kn | Knudsen number |
| K(x,y), K(ε,θ) | Dimensionless stiffness coefficients |
| L | bearing length/mm |
| n | Journal rotating speed/r·min−1 |
| N | Dimensionless friction work consumption |
| m | molecular mass of the gas |
| pa | atmospheric pressure/Pa |
| P | dimensionless pressure, P = p/pa |
| P0 | Dimensionless steady film pressure |
| PE, PΘ | derivative of Pd0 to. E0 and Θ0 |
| Qcon | flow rate for continuum flow |
| Qp | flow rate coefficients for Poiseuille flows |
| dimensionless flow rate coefficients for Poiseuille flows | |
| r | bearing radius/mm |
| rj | journal radius/mm |
| R | gas constant |
| Rg | gas constant/J·mol−1·K−1·kg−1 |
| Ta | temperature/K |
| ε | eccentricity ratio |
| ε0 | eccentricity ratio in static position |
| θ | attitude angle/deg |
| θ0 | attitude angle in static position/deg |
| Θ0 | perturbation amplitude of attitude angle/deg |
| Λ | bearing number |
| μ | air viscosity/Pa·s |
| τ | dimensionless time |
| φ, ψ | cylinder coordinates |
| Ω | Perturbation frequency ratio |
References
- Feng, K.; Liu, L.-J.; Guo, Z.-Y.; Zhao, X.-Y. Parametric study on static and dynamic characteristics of bump-type gas foil thrust bearing for oil-free turbomachinery. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 944–961. [Google Scholar] [CrossRef]
- Li, L.; Zhang, D.; Xie, Y. Probabilistic Sensitivity Analysis of Wear Property for MEMS Gas Bearing. Appl. Sci. 2019, 9, 4409. [Google Scholar] [CrossRef] [Green Version]
- Epstein, A.; Senturia, S.; Al-Midani, O.; Anathasuresh, G.; Ayon, A.; Breuer, K.; Chen, K.S. Micro-heat engines, gas turbines, and rocket engines-The MIT microengine project. In Proceedings of the 28th Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997; p. 29. [Google Scholar]
- Maxwell, J. On stresses in rarefied gases arising from Inequalities of temperature (abstract) Phil. Magazine 1878, 27, 304. [Google Scholar]
- Zhang, X.-Q.; Wang, X.-L.; Liu, R.; Wang, B. Influence of temperature on nonlinear dynamic characteristics of spiral-grooved gas-lubricated thrust bearing-rotor systems for microengine. Tribol. Int. 2013, 61, 138–143. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, C.; Yang, Q. Characteristics of Micro Gas Journal Bearings Based on Effective Viscosity. J. Tribol. 2009, 131. [Google Scholar] [CrossRef]
- Liu, R.; Wang, X.-L.; Zhang, X.-Q. Effects of gas rarefaction on dynamic characteristics of micro spiral-grooved thrust bearing. J. Tribol. 2012, 134, 022201. [Google Scholar] [CrossRef]
- Park, D.-J.; Kim, C.-H.; Jang, G.-H.; Lee, Y.-B. Theoretical considerations of static and dynamic characteristics of air foil thrust bearing with tilt and slip flow. Tribol. Int. 2008, 41, 282–295. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Zhang, H. Unbalance response of micro gas bearing-rotor system considering rarefaction effect. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015. [Google Scholar] [CrossRef]
- Bird, G. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Oxford Engineering Science Series; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Liu, N.; Ng, E.Y.-K. The posture effects of a slider air bearing on its performance with a direct simulation Monte Carlo method. J. Micromech. Microeng. 2001, 11, 463. [Google Scholar] [CrossRef]
- Huang, H.; Meng, G.; Chen, J. Investigations of Slip Effect on the Performance of Micro Gas Bearings and Stability of Micro Rotor-Bearing Systems. Sensors 2007, 7, 1399–1414. [Google Scholar] [CrossRef] [Green Version]
- Fukui, S.; Kaneko, R. Analysis of ultra-thin gas film lubrication based on linearized Boltzmann equation: First report—Derivation of a generalized lubrication equation including thermal creep flow. J. Tribol. 1988, 110, 253–261. [Google Scholar] [CrossRef]
- Fukui, S.; Kaneko, R. A database for interpolation of Poiseuille flow rates for high Knudsen number lubrication problems. J. Tribol. 1990, 112, 78–83. [Google Scholar] [CrossRef]
- Fukui, S.; Yamane, K. DSMC/MGL comparisons of stresses on slider air bearing with nanometer spacings. IEEE Trans. Magn. 2002, 38, 2153–2155. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, L.; Wu, W.; Xu, T. Research on Static and Dynamic Characteristics of Gas-lubricated Microbearings for Microfluidic Devices. Appl. Sci. 2020, 10, 1634. [Google Scholar] [CrossRef] [Green Version]
- Li, L.L.; Zhang, D.; Xie, Y.H. Effect of misalignment on the dynamic characteristic of MEMS gas bearing considering rarefaction effect. Tribol. Int. 2019, 139, 22–35. [Google Scholar] [CrossRef]
- Howard, S.; Dellacorte, C.; Valco, M.J.; Prahl, J.M.; Heshmat, H. Dynamic Stiffness and Damping Characteristics of a High-Temperature Air Foil Journal Bearing. Tribol. Trans. 2001, 44, 657–663. [Google Scholar] [CrossRef]
- Sim, K.; Lee, Y.B.; Jin, W.S.; Kim, J.B.; Kim, T.H. Identification of the dynamic performance of a gas foil journal bearing operating at high temperatures. J. Mech. Sci. Technol. 2014, 28, 43–51. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Q.; Wang, B.; Zhang, L.; Yang, H.; Peng, Z. Effect of surface waviness on the static performance of aerostatic journal bearings. Tribol. Int. 2016, 103, 394–405. [Google Scholar] [CrossRef]
- San Andre’s, L.; Kim, T.H.; Ryu, K. Thermal Management and Rotordynamic Performance of a Hot Rotor-Gas Foil Bearings System: Part 2—Predictions Versus Test Data. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 263–271. [Google Scholar]
- San Andre’s, L.; Kim, T.H.; Ryu, K. Thermal Management and Rotordynamic Performance of a Hot Rotor-Gas Foil Bearings System: Part 1—Measurements. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 253–262. [Google Scholar]
- Ryu, K.; San Andrés, L. On the Failure of a Gas Foil Bearing: High Temperature Operation Without Cooling Flow. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and ExpositioN2013, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Martowicz, A.; Roemer, J.; Lubieniecki, M.; Żywica, G.; Bagiński, P. Experimental and numerical study on the thermal control strategy for a gas foil bearing enhanced with thermoelectric modules. Mech. Syst. Signal Process. 2020, 138, 106581. [Google Scholar] [CrossRef]
- Zhou, W.D.; Liu, B.; Yu, S.K.; Hua, W.; Wong, C.H. A generalized heat transfer model for thin film bearings at head-disk interface. Appl. Phys. Lett. 2008, 92, 043109. [Google Scholar] [CrossRef]
- Shrestha, S.K.; Kim, D.; Cheol Kim, Y. Experimental Feasibility Study of Radial Injection Cooling of Three-Pad Air Foil Bearings. J. Tribol. 2013, 135. [Google Scholar] [CrossRef]
- Sim, K.; Song, J.W.; Lee, Y.-B.; Kim, T.H. Thermal Performance of a Bump Type Gas Foil Bearing Floating on a Hollow Shaft for Increasing Rotating Speed and Static Load. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and ExpositioN2011, Vancouver, BC, Canada, 6–10 June 2011; pp. 651–662. [Google Scholar]
- Zhang, X.; Chen, Q.; Liu, J. Steady Characteristics of High-Speed Micro-Gas Journal Bearings with Different Gaseous Lubricants and Extreme Temperature Difference. J. Tribol. 2016, 139. [Google Scholar] [CrossRef]
- Talmage, G.; Carpino, M. Thermal Structural Effects in a Gas-Lubricated Foil Journal Bearing. Tribol. Trans. 2011, 54, 701–713. [Google Scholar] [CrossRef]
- Yang, L.; Qi, S.; Yu, L. Limits of Dynamic Coefficients of Self-Acting Tilting-Pad Gas Bearings. Tribol. Trans. 2009, 52, 323–330. [Google Scholar]
- Tang, S.; Haipeng, G.; Hao, L.; Lei, Q. The FEM Model Driven Method of the Static Performance Calculation for Gas Joumal Bearing by Python. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 18–22. [Google Scholar]


| Parameters of Microbearings | Values |
|---|---|
| Length/radius (L/r) | 0.125 |
| Clearance (c), μm | 10 |
| Rotating speed (n), r/min | 500,000 |
| Gas type | Air, He, CO2, N2 |
| Gas temperature (Ta), K | 293, 473, 673, 873, 1073, 1273,1473 |
| Viscosity (η), Pa·s | correspond to temperature and gas type |
| Eccentricity ratio (ε) | 0.9 |
| Gas Type | Temperature | Kxx|Ω→∞ | Kyy|Ω→∞ | Kxy|Ω→∞ | Kyx|Ω→∞ | Dxx|Ω→∞ | Dyy|Ω→∞ | Dxy|Ω→∞ | Dyx|Ω→∞ |
|---|---|---|---|---|---|---|---|---|---|
| He | 293 K | 0.9769 | 0.8575 | 0.3783 | 0.3783 | 0 | 0 | 0 | 0 |
| 473 K | 1.0844 | 0.7183 | 0.3181 | 0.3181 | 0 | 0 | 0 | 0 | |
| 673 K | 1.1514 | 0.6337 | 0.2474 | 0.2474 | 0 | 0 | 0 | 0 | |
| 873 K | 1.1847 | 0.5916 | 0.1928 | 0.1928 | 0 | 0 | 0 | 0 | |
| 1073 K | 1.2019 | 0.5695 | 0.1532 | 0.1532 | 0 | 0 | 0 | 0 | |
| 1273 K | 1.2114 | 0.5571 | 0.1244 | 0.1244 | 0 | 0 | 0 | 0 | |
| 1473 K | 1.2168 | 0.5497 | 0.1032 | 0.1032 | 0 | 0 | 0 | 0 | |
| CO2 | 293 K | 0.8152 | 1.0912 | 0.3949 | 0.3949 | 0 | 0 | 0 | 0 |
| 473 K | 0.8656 | 1.0135 | 0.3983 | 0.3983 | 0 | 0 | 0 | 0 | |
| 673 K | 0.9234 | 0.9305 | 0.3927 | 0.3927 | 0 | 0 | 0 | 0 | |
| 873 K | 0.9758 | 0.8591 | 0.3787 | 0.3787 | 0 | 0 | 0 | 0 | |
| 1073 K | 1.0218 | 0.7985 | 0.3589 | 0.3589 | 0 | 0 | 0 | 0 | |
| 1273 K | 1.0605 | 0.7486 | 0.3358 | 0.3358 | 0 | 0 | 0 | 0 | |
| 1473 K | 1.0920 | 0.7086 | 0.3117 | 0.3117 | 0 | 0 | 0 | 0 | |
| N2 | 293 K | 0.8411 | 1.0505 | 0.3976 | 0.3976 | 0 | 0 | 0 | 0 |
| 473 K | 0.9024 | 0.9602 | 0.3959 | 0.3959 | 0 | 0 | 0 | 0 | |
| 673 K | 0.9656 | 0.8728 | 0.3821 | 0.3821 | 0 | 0 | 0 | 0 | |
| 873 K | 1.0203 | 0.8005 | 0.3597 | 0.3597 | 0 | 0 | 0 | 0 | |
| 1073 K | 1.0662 | 0.7414 | 0.3319 | 0.3319 | 0 | 0 | 0 | 0 | |
| 1273 K | 1.1020 | 0.6959 | 0.3028 | 0.3028 | 0 | 0 | 0 | 0 | |
| 1473 K | 1.1294 | 0.6614 | 0.2749 | 0.2749 | 0 | 0 | 0 | 0 |
| Temperature | Kxx|Ω→0 | Kyy|Ω→0 | Kxy|Ω→0 | Kyx|Ω→0 | Dxx|Ω→0 | Dyy|Ω→0 | Dxy|Ω→0 | Dyx|Ω→0 | |
|---|---|---|---|---|---|---|---|---|---|
| He | 293 K | 0.0416 | 0.0718 | 0.0157 | 0.0931 | 0.1262 | 0.0904 | 0.1092 | 0.0678 |
| 473 K | 0.0154 | 0.0261 | −0.0026 | 0.0500 | 0.1216 | 0.0486 | 0.0710 | 0.0475 | |
| 673 K | 0.0041 | 0.0104 | −0.0061 | 0.0288 | 0.1022 | 0.0266 | 0.0414 | 0.0285 | |
| 873 K | 0.0006 | 0.0050 | −0.0058 | 0.0188 | 0.0833 | 0.0169 | 0.0250 | 0.0174 | |
| 1073 K | −0.0005 | 0.0027 | −0.0049 | 0.0133 | 0.0683 | 0.0122 | 0.0160 | 0.0112 | |
| 1273 K | −0.0007 | 0.0016 | −0.0042 | 0.0100 | 0.0568 | 0.0094 | 0.0107 | 0.0075 | |
| 1473 K | −0.0007 | 0.0010 | −0.0036 | 0.0078 | 0.0481 | 0.0077 | 0.0075 | 0.0053 | |
| CO2 | 293 K | 0.1043 | 0.2603 | 0.0970 | 0.2073 | 0.0873 | 0.1524 | 0.1299 | 0.0600 |
| 473 K | 0.0814 | 0.1754 | 0.0612 | 0.1628 | 0.1055 | 0.1363 | 0.1311 | 0.0697 | |
| 673 K | 0.0591 | 0.1115 | 0.0333 | 0.1228 | 0.1194 | 0.1131 | 0.1228 | 0.0718 | |
| 873 K | 0.0420 | 0.0726 | 0.0160 | 0.0937 | 0.1261 | 0.0909 | 0.1096 | 0.0679 | |
| 1073 K | 0.0296 | 0.0486 | 0.0059 | 0.0732 | 0.1274 | 0.0722 | 0.0949 | 0.0610 | |
| 1273 K | 0.0205 | 0.0336 | 0.0000 | 0.0583 | 0.1249 | 0.0573 | 0.0806 | 0.0531 | |
| 1473 K | 0.0139 | 0.0239 | −0.0033 | 0.0474 | 0.1202 | 0.0460 | 0.0679 | 0.0455 | |
| N2 | 293 K | 0.0920 | 0.2123 | 0.0770 | 0.1831 | 0.0974 | 0.1449 | 0.1317 | 0.0660 |
| 473 K | 0.0668 | 0.1317 | 0.0422 | 0.1363 | 0.1151 | 0.1218 | 0.1267 | 0.0719 | |
| 673 K | 0.0451 | 0.0791 | 0.0189 | 0.0989 | 0.1252 | 0.0952 | 0.1125 | 0.0690 | |
| 873 K | 0.0300 | 0.0493 | 0.0062 | 0.0738 | 0.1275 | 0.0728 | 0.0954 | 0.0613 | |
| 1073 K | 0.0193 | 0.0317 | −0.0007 | 0.0563 | 0.1243 | 0.0552 | 0.0783 | 0.0518 | |
| 1273 K | 0.0120 | 0.0212 | −0.0040 | 0.0441 | 0.1181 | 0.0425 | 0.0636 | 0.0429 | |
| 1473 K | 0.0073 | 0.0147 | −0.0056 | 0.0354 | 0.1106 | 0.0334 | 0.0516 | 0.0352 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Liu, Z.; Wang, C.; Xie, Y. Influence of Temperature Effect on the Static and Dynamic Performance of Gas-Lubricated Microbearings. Micromachines 2020, 11, 716. https://doi.org/10.3390/mi11080716
Li L, Liu Z, Wang C, Xie Y. Influence of Temperature Effect on the Static and Dynamic Performance of Gas-Lubricated Microbearings. Micromachines. 2020; 11(8):716. https://doi.org/10.3390/mi11080716
Chicago/Turabian StyleLi, Liangliang, Zhufeng Liu, Chongyu Wang, and Yonghui Xie. 2020. "Influence of Temperature Effect on the Static and Dynamic Performance of Gas-Lubricated Microbearings" Micromachines 11, no. 8: 716. https://doi.org/10.3390/mi11080716




