A Novel High Q Lamé-Mode Bulk Resonator with Low Bias Voltage
Abstract
1. Introduction
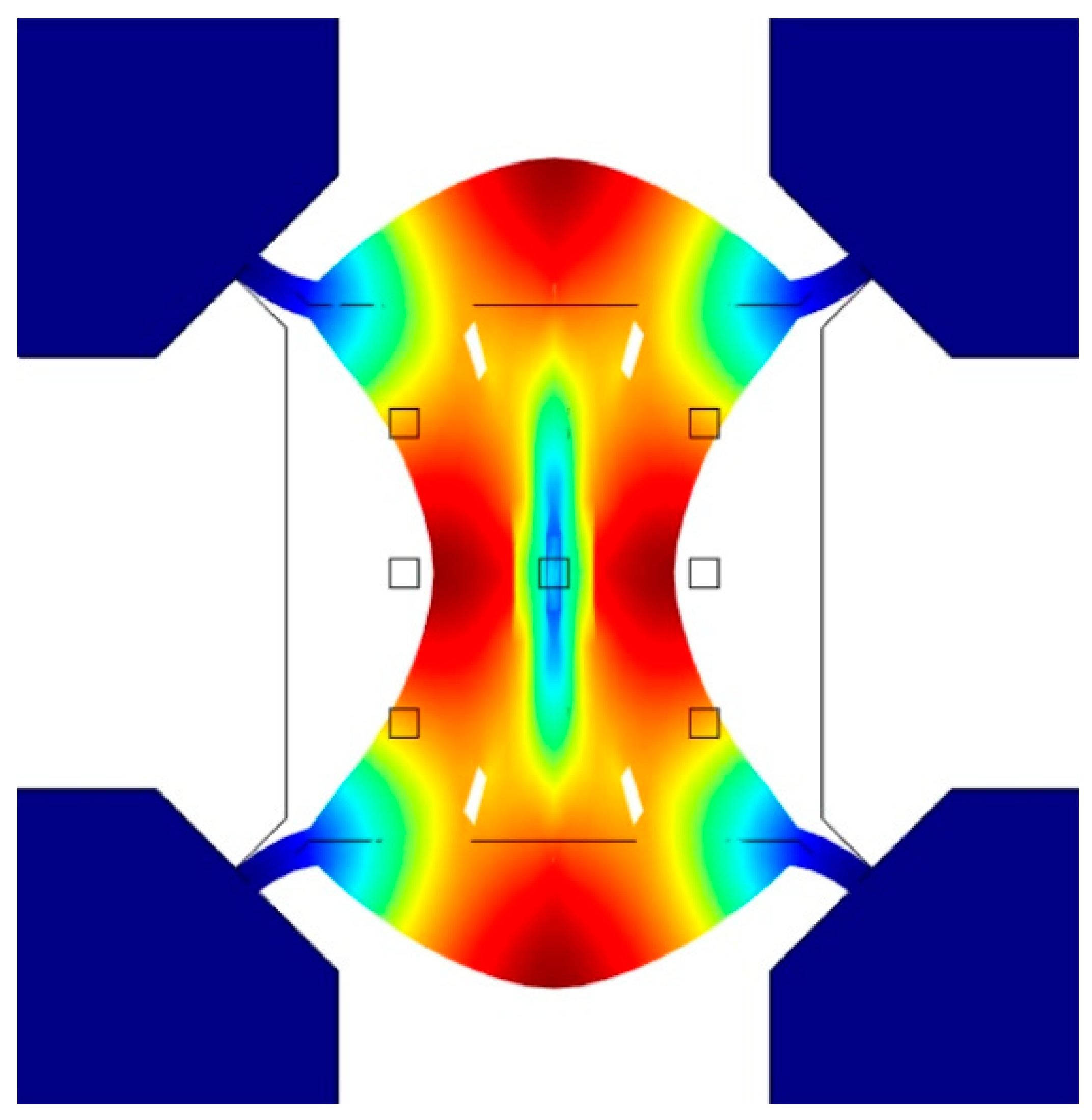
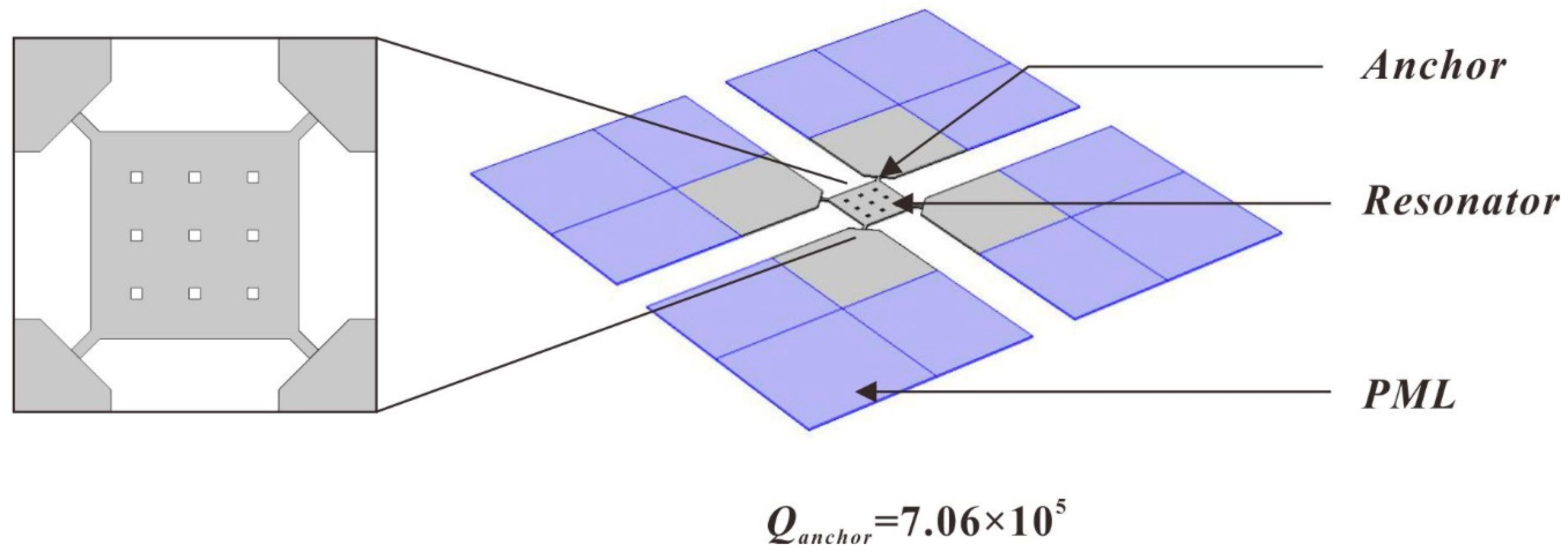
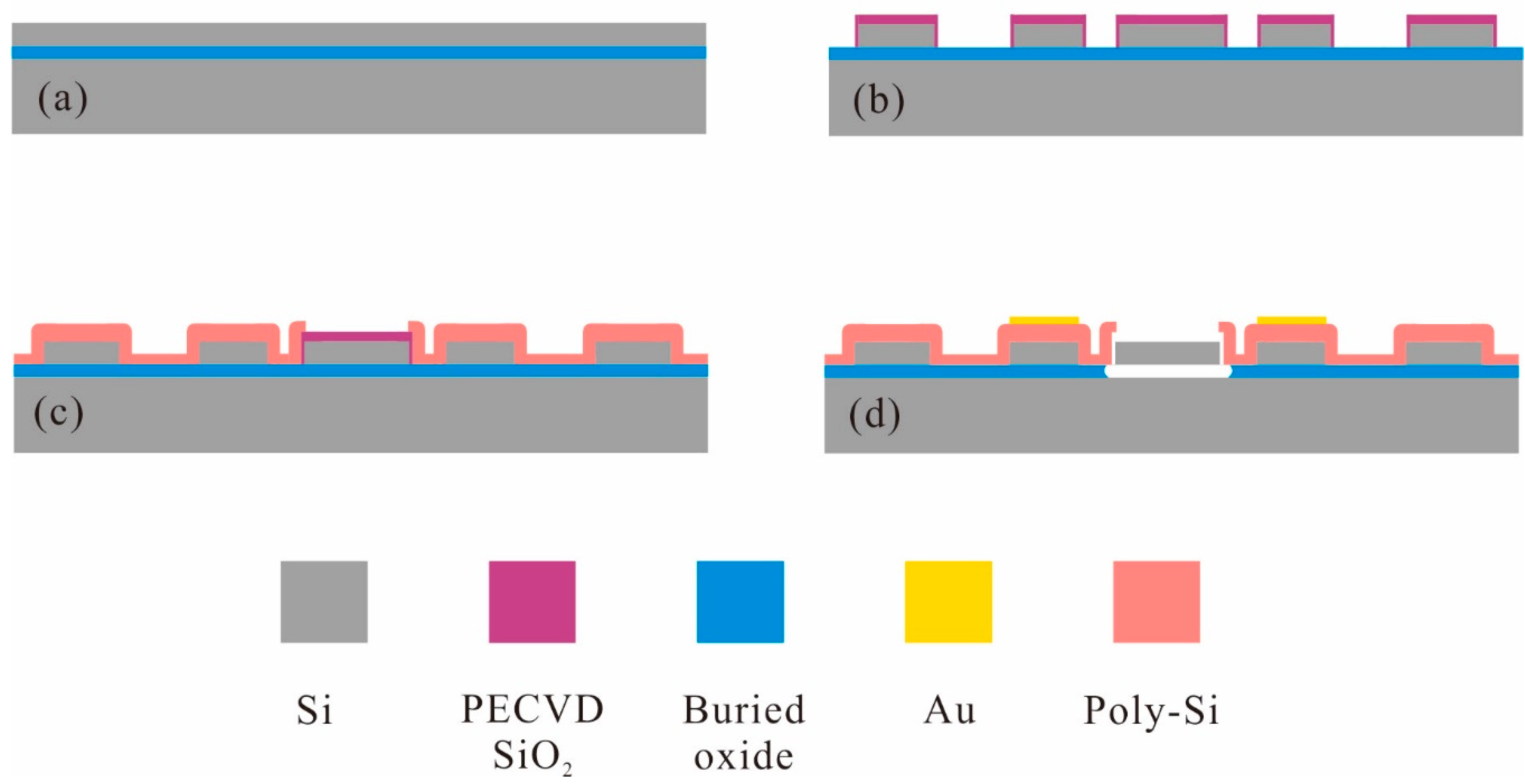
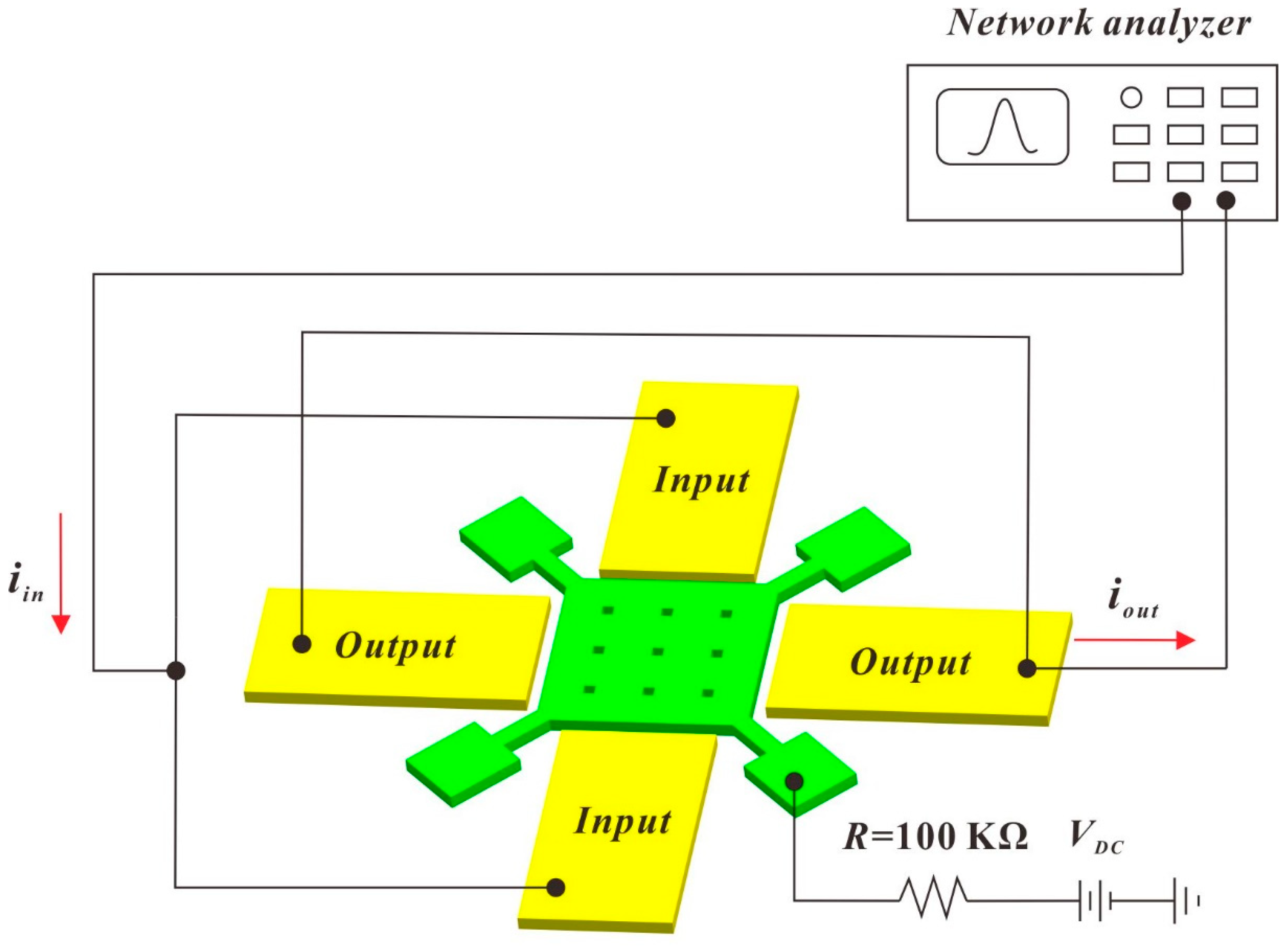
2. Design and Fabrication
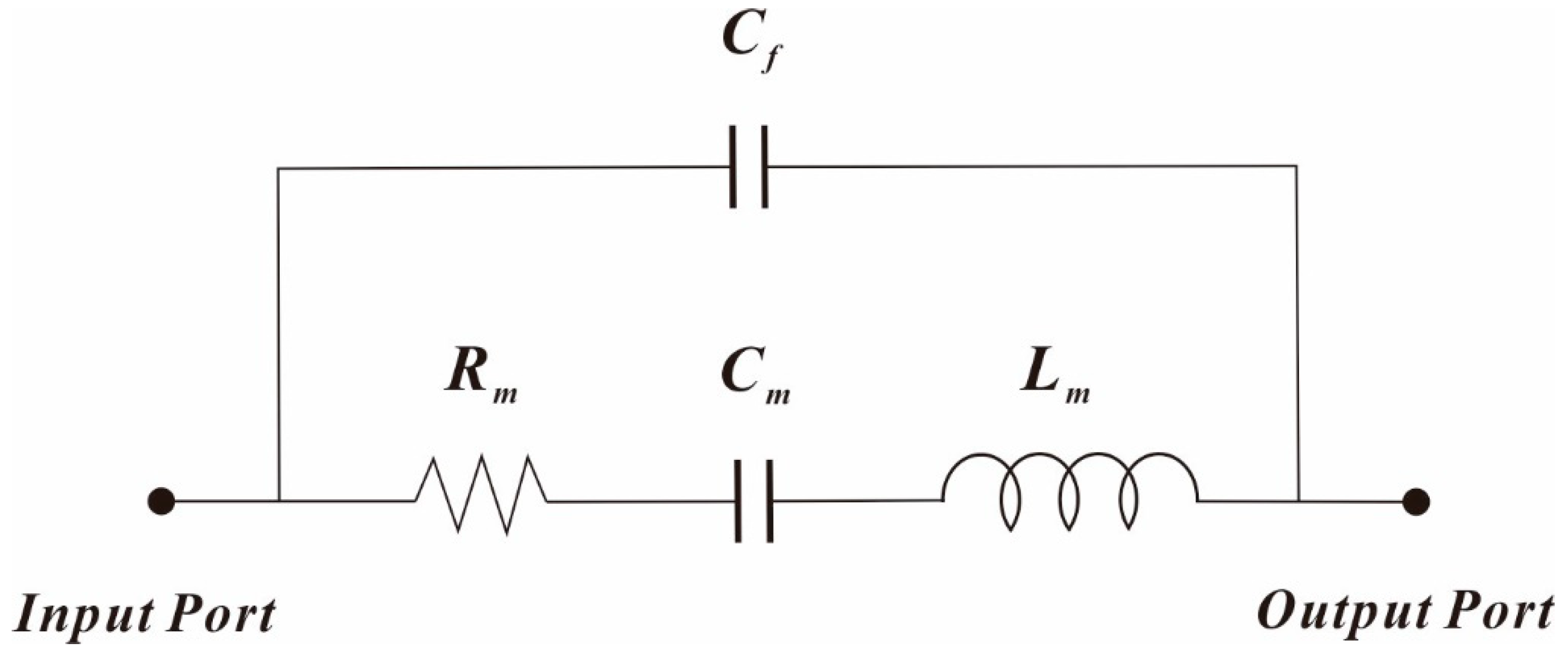
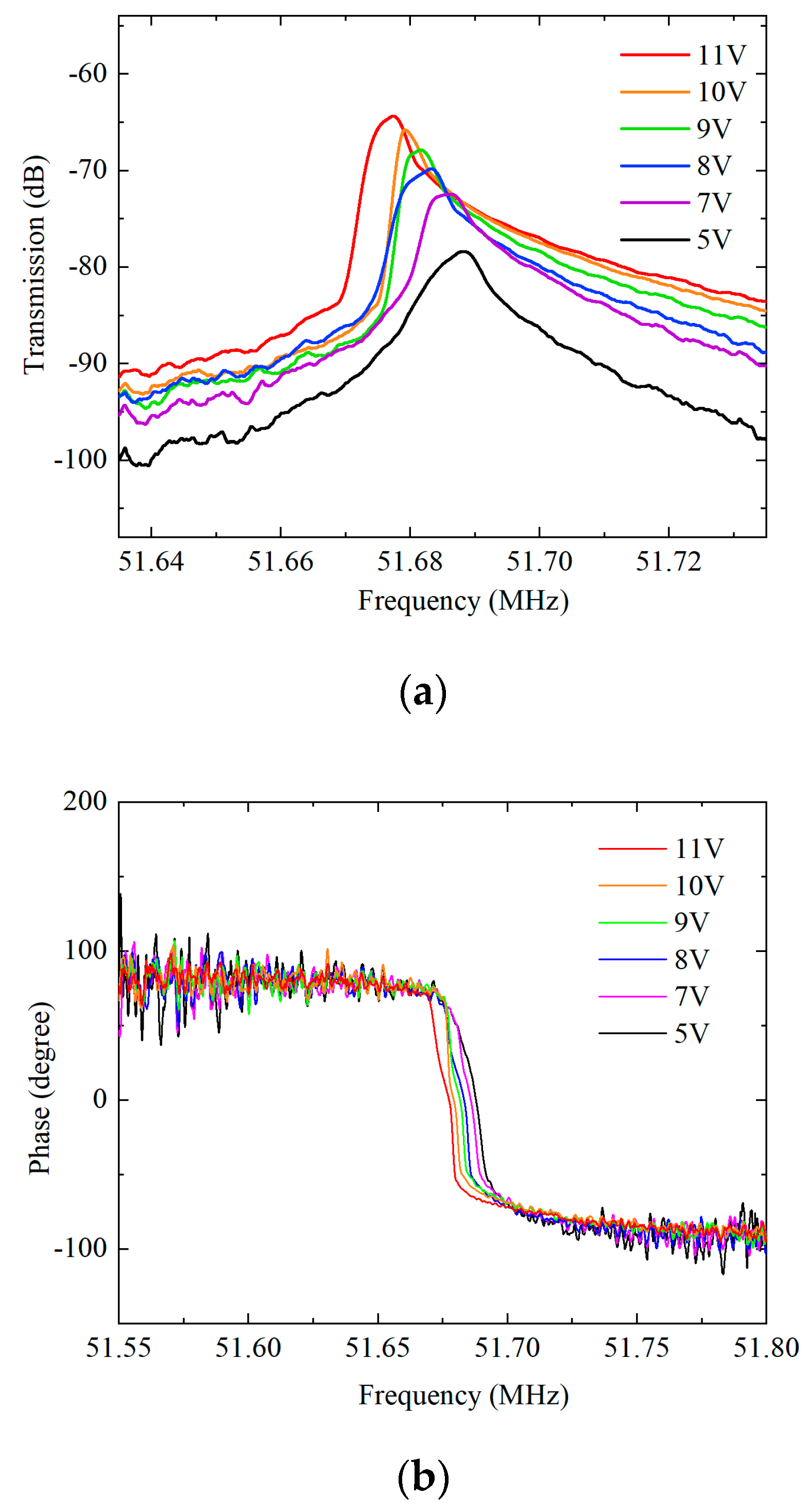
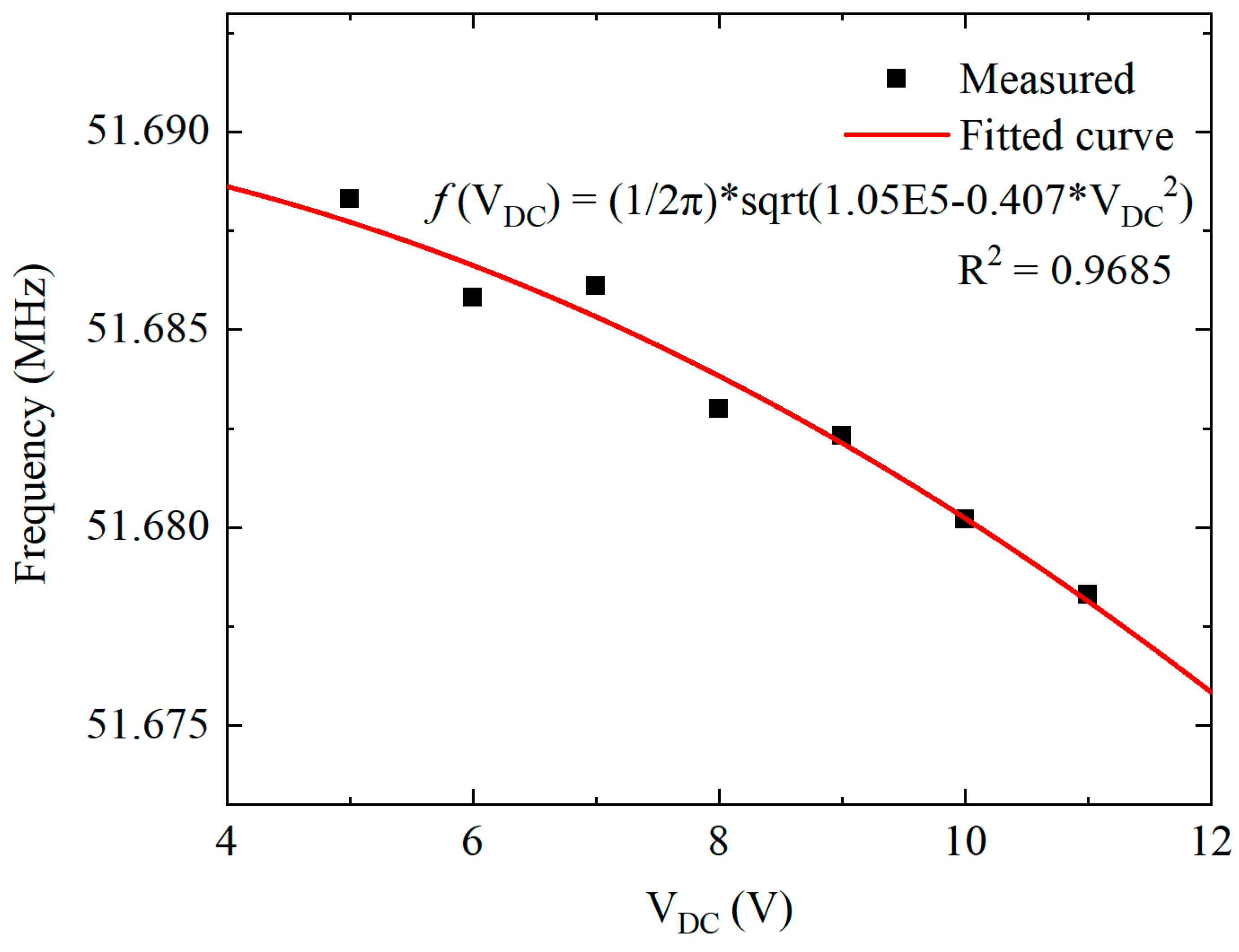
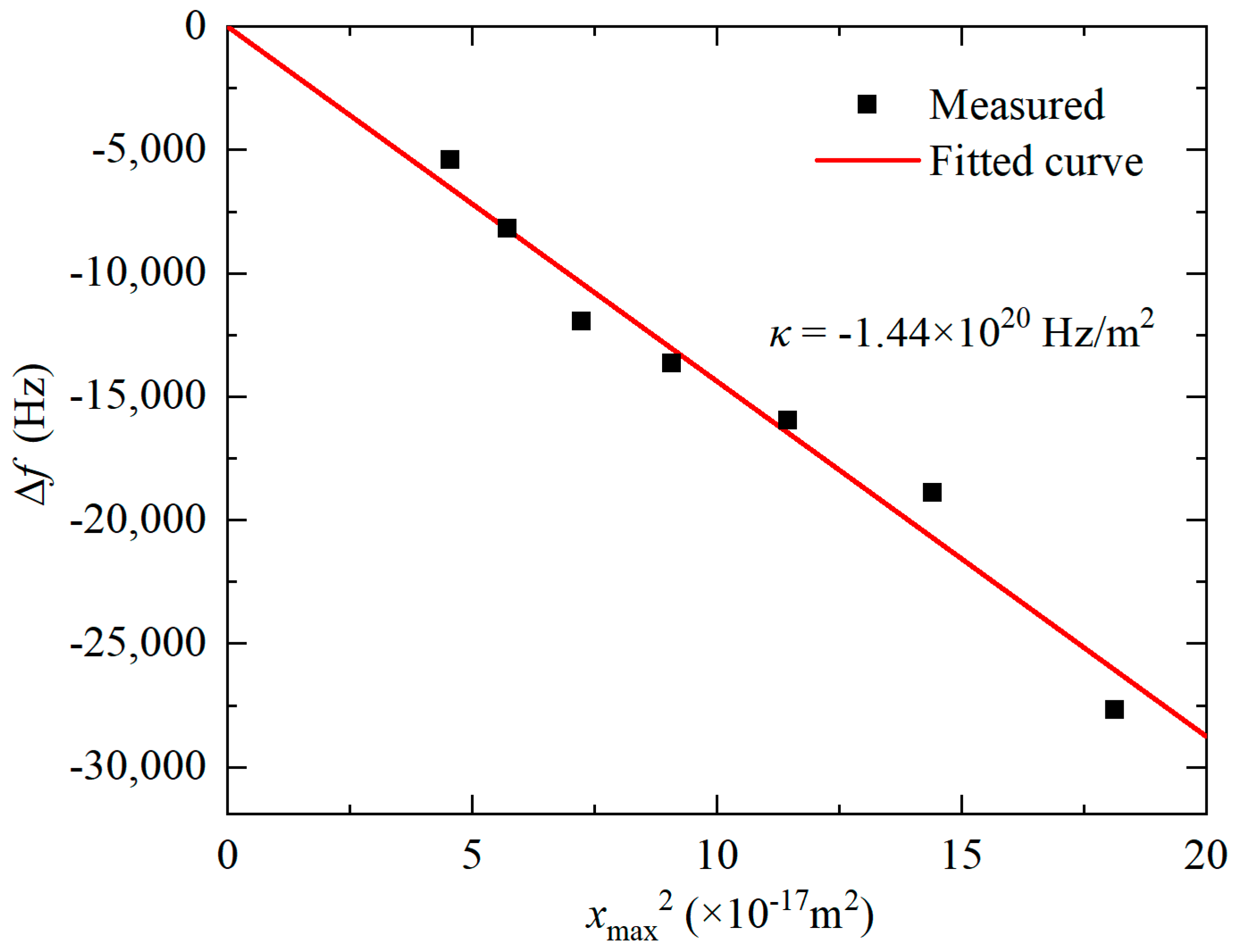
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, J.; Yang, L.; Pietrangelo, S.; Ren, Z.; Nguyen, C.T.C. RF MEMS resonators: Getting the right frequency and Q. In Proceedings of the 2007 IEEE Compound Semiconductor Integrated Circuits Symposium, Portland, OR, USA, 14–17 October 2007; pp. 1–4. [Google Scholar]
- Iannacci, J. RF-MEMS technology: An enabling solution in the transition from 4G-LTE to 5G mobile applications. In Proceedings of the 2017 IEEE SENSORS, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Bahreyni, B. Fabrication & Design of Resonant Microdevices; William Andrew: Norwich, NY, USA, 2008. [Google Scholar]
- Ng, E.; Yang, Y.; Hong, V.A.; Ahn, C.H.; Heinz, D.B.; Flader, I.; Chen, Y.; Everhart, C.L.M.; Kim, B.; Melamud, R.; et al. The long path from MEMS resonators to timing products. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems, Estoril, Portugal, 18–22 January 2015; pp. 1–2. [Google Scholar]
- Nguyen, C.T.C. MEMS technology for timing and frequency control. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007, 54, 251–270. [Google Scholar] [CrossRef] [PubMed]
- Kan, X.; Chen, Z.; Yuan, Q.; Wang, F.; Yang, J.; Yang, F. A Novel Multiple-Frequency RF-MEMS Resonator Based on the Whispering Gallery Modes. IEEE Trans. Electron. Devices 2019, 66, 3683–3685. [Google Scholar] [CrossRef]
- Yuan, Q.; Luo, W.; Zhao, H.; Peng, B.; Yang, J.; Yang, F. Frequency stability of RF-MEMS disk resonators. IEEE Trans. Electron. Devices 2015, 62, 1603–1608. [Google Scholar] [CrossRef]
- Nguyen, C.T.C. MEMS-based RF channel selection for true software-defined cognitive radio and low-power sensor communications. IEEE Commun. Mag. 2013, 51, 110–119. [Google Scholar] [CrossRef]
- Lin, Y.W.; Lee, S.; Li, S.S.; Xie, Y.; Ren, Z.; Nguyen, C.C. Series-resonant VHF micromechanical resonator reference oscillators. IEEE J. Solid -State Circuits 2004, 39, 2477–2491. [Google Scholar] [CrossRef]
- Khine, L.; Palaniapan, M.; Wong, W.K. 12.9 MHz Lamé-mode differential SOI bulk resonators. In Proceedings of the TRANSDUCERS 2007-2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 1753–1756. [Google Scholar]
- Khine, L.; Palaniapan, M.; Wong, W.K. 6MHz bulk-mode resonator with Q values exceeding one million. In Proceedings of the TRANSDUCERS 2007-2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007; pp. 2445–2448. [Google Scholar]
- Pourkamali, S.; Hao, Z.; Ayazi, F. VHF single crystal silicon capacitive elliptic bulk-mode disk resonators-part II: Implementation and characterization. J. Microelectromechanical Syst. 2004, 13, 1054–1062. [Google Scholar] [CrossRef]
- Xereas, G.; Chodavarapu, V.P. Wafer-Level Vacuum-Encapsulated Lamé Mode Resonator With fQ Product of 2.23 × 1013 Hz. IEEE Electron. Device Lett. 2015, 36, 1079–1081. [Google Scholar] [CrossRef]
- Hamelin, B.; Yang, J.; Daruwalla, A.; Wen, H.; Ayazi, F. Monocrystalline Silicon Carbide Disk Resonators on Phononic Crystals with Ultra-Low Dissipation Bulk Acoustic Wave Modes. Sci. Rep. 2019, 9, 1–8. [Google Scholar]
- Yang, J.; Hamelin, B.; Ayazi, F. Capacitive Lamé Mode Resonators in 65 μm-Thick Monocrystalline Silicon Carbide with Q-Factors Exceeding 20 Million. In Proceedings of the 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS), Vancouver, BC, Canada, 18–22 January 2020; pp. 226–229. [Google Scholar]
- Rodriguez, J.; Chandorkar, S.A.; Watson, C.A.; Glaze, G.M.; Ahn, C.H.; Ng, E.J.; Yang, Y.; Kenny, T.W. Direct detection of Akhiezer damping in a silicon MEMS resonator. Sci. Rep. 2019, 9, 1–10. [Google Scholar]
- Daruwalla, A.; Wen, H.; Liu, C.S.; Ayazi, F. Low motional impedance distributed lamé mode resonators for high frequency timing applications. Microsyst. Nanoeng. 2020, 6, 1–11. [Google Scholar] [CrossRef]
- Abele, N.; Segueni, K.; Boucart, K.; Casset, F.; Legrand, B.; Buchaillot, L.; Ancey, P.; Ionescu, A.M. Ultra-low voltage MEMS resonator based on RSG-MOSFET. In Proceedings of the 19th IEEE International Conference on Micro Electro Mechanical Systems, Istanbul, Turkey, 22–26 January 2006; pp. 882–885. [Google Scholar]
- Chen, T.T.; Huang, J.C.; Peng, Y.C.; Chu, C.-H.; Lin, C.-H.; Cheng, C.-W.; Li, C.-S.; Li, S.S. A 17.6-MHz 2.5 V ultra-low polarization voltage MEMS oscillator using an innovative high gain-bandwidth fully differential trans-impedance voltage amplifier. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013; pp. 741–744. [Google Scholar]
- Lin, A.T.; Lee, J.E.; Yan, J.; Seshia, A.A. Enhanced transduction methods for electrostatically driven MEMS resonators. In Proceedings of the TRANSDUCERS 2009-2009 International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 21–25 June 2009; pp. 561–564. [Google Scholar]
- Li, S.S.; Lin, Y.W.; Xie, Y.; Ren, Z.; Nguyen, C.C. Micromechanical “hollow-disk” ring resonators. In Proceedings of the 17th IEEE International Conference on Micro Electro Mechanical Systems, Maastricht, The Netherlands, 25–29 January 2004; pp. 821–824. [Google Scholar]
- Abdelmoneum, M.A.; Demirci, M.U.; Nguyen, C.C. Stemless wine-glass-mode disk micromechanical resonators. In Proceedings of the Sixteenth Annual International Conference on Micro Electro Mechanical Systems, Kyoto, Japan, 23 January 2003; pp. 698–701. [Google Scholar]
- Hao, Z.; Ayazi, F. Support loss in micromechanical disk resonators. In Proceedings of the 18th IEEE International Conference on Micro Electro Mechanical Systems, Miami Beach, FL, USA, 30 January–3 February 2005; pp. 137–141. [Google Scholar]
- Abdolvand, R.; Bahreyni, B.; Lee, J.E.Y.; Nabki, F. Micromachined resonators: A review. Micromachines 2016, 7, 160. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.E.; Yan, J.; Seshia, A.A. Low loss HF band SOI wine glass bulk mode capacitive square-plate resonator. J. Micromechanics Microengineering 2009, 19, 074003. [Google Scholar] [CrossRef]
- Lee, J.E.; Zhu, Y.; Seshia, A.A. A bulk acoustic mode single-crystal silicon microresonator with a high-quality factor. J. Micromechanics Microengineering 2008, 18, 064001. [Google Scholar] [CrossRef]
- Yasumura, K.Y.; Stowe, T.D.; Chow, E.M.; Pfafman, T.; Kenny, T.W.; Stipe, B.C.; Rugar, D. Quality factors in micron-and submicron-thick cantilevers. J. Microelectromechanical Syst. 2000, 9, 117–125. [Google Scholar] [CrossRef]
- Basu, J.; Bhattacharyya, T.K. Microelectromechanical resonators for radio frequency communication applications. Microsyst. Technol. 2011, 17, 1557. [Google Scholar] [CrossRef]
- Darvishian, A.; Shiari, B.; Cho, J.Y.; Nagourney, T.; Najafi, K. Anchor loss in hemispherical shell resonators. J. Microelectromechanical Syst. 2017, 26, 51–66. [Google Scholar] [CrossRef]
- Hao, Z.; Erbil, A.; Ayazi, F. An analytical model for support loss in micromachined beam resonators with in-plane flexural vibrations. Sens. Actuators A Phys. 2003, 109, 156–164. [Google Scholar] [CrossRef]
- Koyama, T.; Bindel, D.S.; He, W.; Quévy, E.P.; Govindjee, S.; Demmel, J.W.; Howe, R.T. Simulation tools for damping in high frequency resonators. In Proceedings of the SENSORS, Irvine, CA, USA, 30 October–3 November 2005; p. 4. [Google Scholar]
- Colinet, E.; Arcamone, J.; Niel, A.; Lorent, E.; Hentz, S.; Ollier, E. 100 MHz oscillator based on a low polarization voltage capacitive Lamé-mode MEMS resonator. In Proceedings of the 2010 IEEE International Frequency Control Symposium, Newport Beach, CA, USA, 1–4 June 2010; pp. 174–178. [Google Scholar]
- Pourkamali, S.; Ayazi, F. SOI-based HF and VHF single-crystal silicon resonators with sub-100 nanometer vertical capacitive gaps. In Proceedings of the TRANSDUCERS’03. 12th International Conference on Solid-State Sensors, Actuators and Microsystems, Boston, MA, USA, 8–12 June 2003; pp. 837–840. [Google Scholar]
- Hajhashemi, M.S.; Rasouli, A.; Bahreyni, B. Performance optimization of high order RF microresonators in the presence of squeezed film damping. Sens. Actuators A: Phys. 2014, 216, 266–276. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Younis, M.I. A new approach to the modeling and simulation of flexible microstructures under the effect of squeeze-film damping. J. Micromechanics Microengineering 2003, 14, 170. [Google Scholar] [CrossRef]
- Wang, J.; Ren, Z.; Nguyen, C.C. 1.156-GHz self-aligned vibrating micromechanical disk resonator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004, 51, 1607–1628. [Google Scholar] [CrossRef]
- Shao, L.C.; Niu, T.; Palaniapan, M. Nonlinearities in a high-Q SOI Lamé-mode bulk resonator. J. Micromechanics Microengineering 2009, 19, 075002. [Google Scholar] [CrossRef]
- Luo, W.; Zhao, H.; Peng, B.H.; Zhao, J.C.; Yuan, Q.; Yang, J.L.; Yang, F.H. Nonlinearity characteristic of disk resonator. In Proceedings of the SENSORS, Valencia, Spain, 2–5 November 2014; pp. 918–921. [Google Scholar]
- Lee, H.K.; Melamud, R.; Chandorkar, S.; Salvia, J.; Yoneoka, S.; Kenny, T.W. Stable operation of MEMS oscillators far above the critical vibration amplitude in the nonlinear regime. J. Microelectromechanical Syst. 2011, 20, 1228–1230. [Google Scholar] [CrossRef]
- Rajai, P.; Khan, N.; Ahamed, M.J. Modeling of nonlinear oscillations of doped Lamé-mode MEMS silicon resonator. In Proceedings of the 2019 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Naples, FL, USA, 1–5 April 2019; pp. 1–3. [Google Scholar]
- Veijola, T.; Mattila, T. Modeling of nonlinear micromechanical resonators and their simulation with the harmonic-balance method. Int. J. Rf Microw. Comput. -Aided Eng. 2001, 11, 310–321. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mecahnis: Volume 1 of Course of Theoretical Physics, 3rd ed.; Butterworth-Heinemann: Boston, MA, USA, 1982; pp. 87–92. [Google Scholar]
- Kaajakari, V.; Mattila, T.; Oja, A.; Seppa, H.A.S.H. Nonlinear limits for single-crystal silicon microresonators. J. Microelectromechanical Syst. 2004, 13, 715–724. [Google Scholar] [CrossRef]
- Zhu, H.; Tu, C.; Lee, J.E.Y. (2012, March). Material nonlinearity limits on a Lamé-mode single crystal bulk resonator. In Proceedings of the 2012 7th IEEE International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Kyoto, Japan, 5–8 March 2012; pp. 457–462. [Google Scholar]
- Yang, Y.; Ng, E.J.; Hong, V.; Ahn, C.; Chen, Y.; Ahadi, E.; Dykman, M.; Kenny, T.W. Measurement of the nonlinear elasticity of doped bulk-mode MEMS resonators. In Proceedings of the Solid-State Sensors, Actuators, Microsystems Workshop, Hilton Head Island, SC, USA, 8–12 June 2014; pp. 8–12. [Google Scholar]
- Kaajakari, V.; Koskinen, J.K.; Mattila, T. Phase noise in capacitively coupled micromechanical oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 2322–2331. [Google Scholar] [CrossRef]



| Reference | Resonator | f0 | Q | VDC | F × Q | Gap |
|---|---|---|---|---|---|---|
| Khine, L. [10] | Lamé-mode | 12.9 MHz | 7.6 × 105 | 100 V | 9.80 × 1012 | 2 μm |
| Xereas, G. [13] | Lamé-mode | 6.89 MHz | 3.24 × 106 | 40 V | 2.23 × 1013 | 1.5 μm |
| Rodriguez, J. [16] | Lamé-mode | 10 MHz | 2.65 × 106 | 30 V | 2.69 × 1013 | 700 nm |
| Hamelin, B. [14] | gyroscopic mode SiC disk | 5.3 MHz | 1.8 × 107 | 25 V | 9 × 1013 | 4.2 μm |
| Pourkamali, S. [12] | Wine-glass mode disk | 149.3 MHz | 45.700 | 17 V | 6.82 × 1012 | 100 nm |
| Yang, J. [15] | SiC Lamé-mode | 6.27 MHz | 2.0 × 107 | 15 V | 1.25 × 1014 | 5 μm |
| Daruwalla, A. [17] | Distributed Lamé-mode | 50.7 MHz | 2.5 × 105 | 5 V | 1.29 × 1013 | 270 nm |
| Lin, A.T. [20] | Lamé-mode | 2.2 MHz | 6771 | 3 V | 1.49 × 1010 | 2 μm |
| Chen, T.T. [19] | Lamé-mode | 17.6 MHz | 8000 | 2.5 V | 1.41 × 1011 | 50 nm |
| Our work | Lamé-mode | 51.3 MHz | 34,200 | 3 V | 1.75 × 1012 | 70 nm |
| Items | Rm | Lm | Cm |
|---|---|---|---|
| Measured | 293.8 kΩ | 31.2 H | 3.09 × 10−19 C |
| Calculated | 320.5 kΩ | 33.8 H | 2.81 × 10−19 C |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Chen, Z.; Jia, Q.; Yuan, Q.; Yang, J.; Yang, F. A Novel High Q Lamé-Mode Bulk Resonator with Low Bias Voltage. Micromachines 2020, 11, 737. https://doi.org/10.3390/mi11080737
Wang T, Chen Z, Jia Q, Yuan Q, Yang J, Yang F. A Novel High Q Lamé-Mode Bulk Resonator with Low Bias Voltage. Micromachines. 2020; 11(8):737. https://doi.org/10.3390/mi11080737
Chicago/Turabian StyleWang, Tianyun, Zeji Chen, Qianqian Jia, Quan Yuan, Jinling Yang, and Fuhua Yang. 2020. "A Novel High Q Lamé-Mode Bulk Resonator with Low Bias Voltage" Micromachines 11, no. 8: 737. https://doi.org/10.3390/mi11080737
APA StyleWang, T., Chen, Z., Jia, Q., Yuan, Q., Yang, J., & Yang, F. (2020). A Novel High Q Lamé-Mode Bulk Resonator with Low Bias Voltage. Micromachines, 11(8), 737. https://doi.org/10.3390/mi11080737




