A Numerical Investigation of Enhancing Microfluidic Heterogeneous Immunoassay on Bipolar Electrodes Driven by Induced-Charge Electroosmosis in Rotating Electric Fields
Abstract
:1. Introduction
2. Theory and Methods
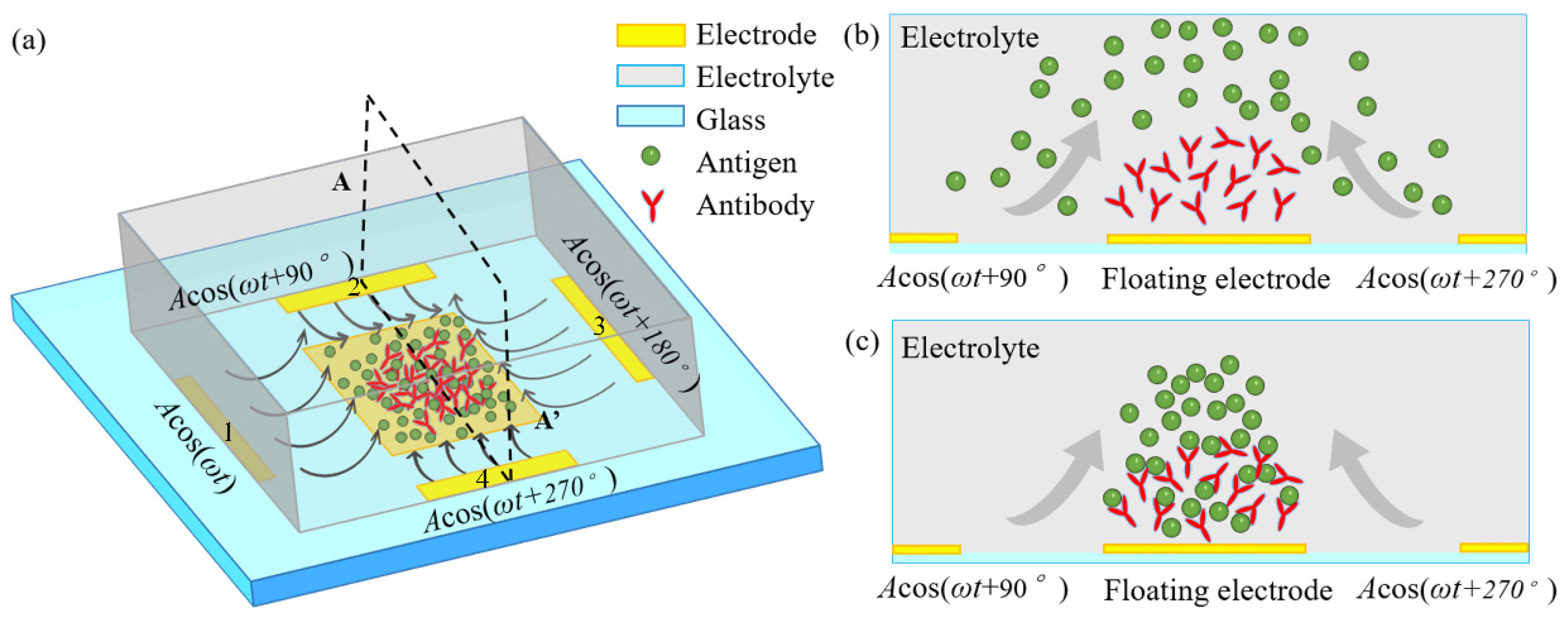
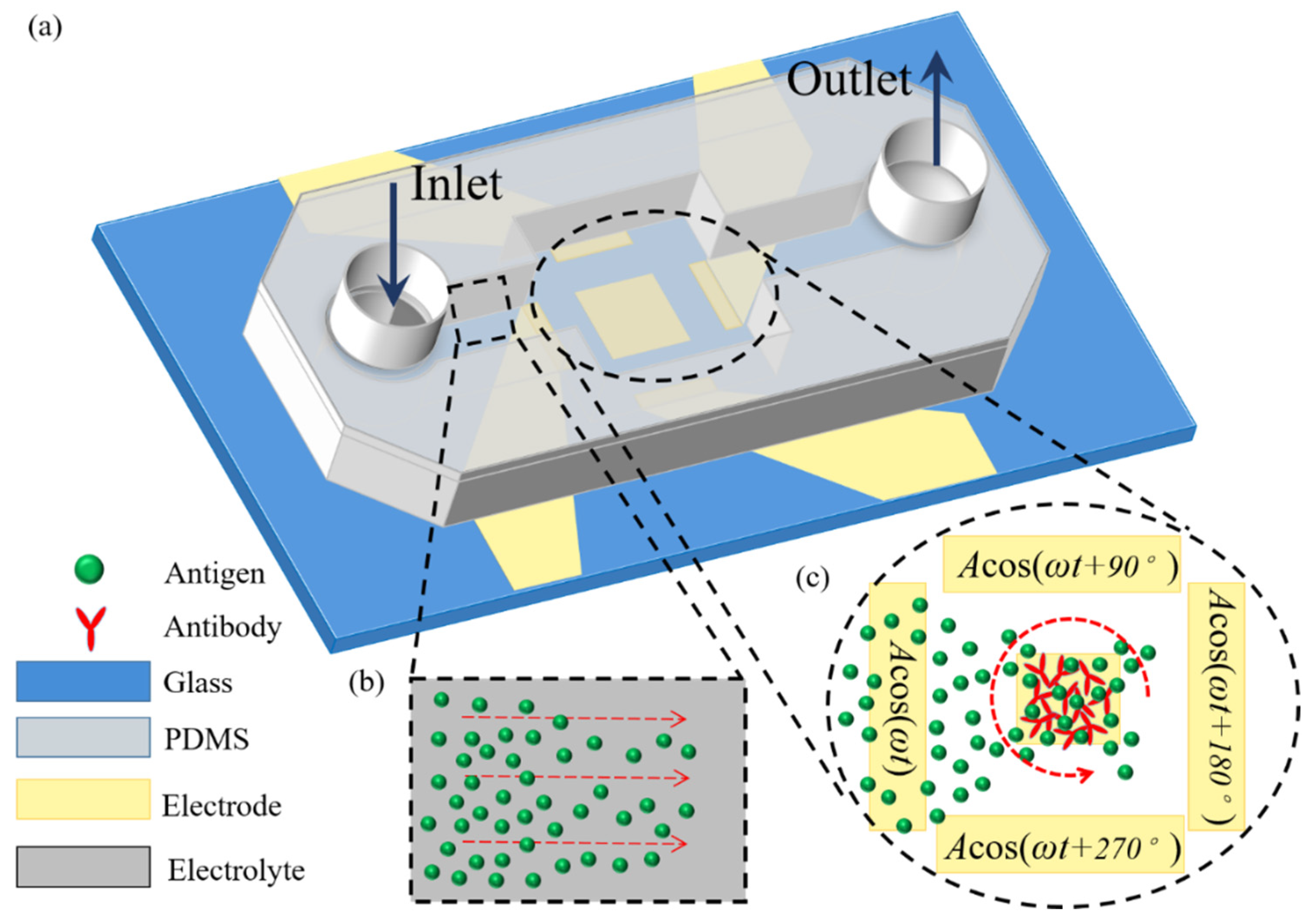
2.1. Device Geometry
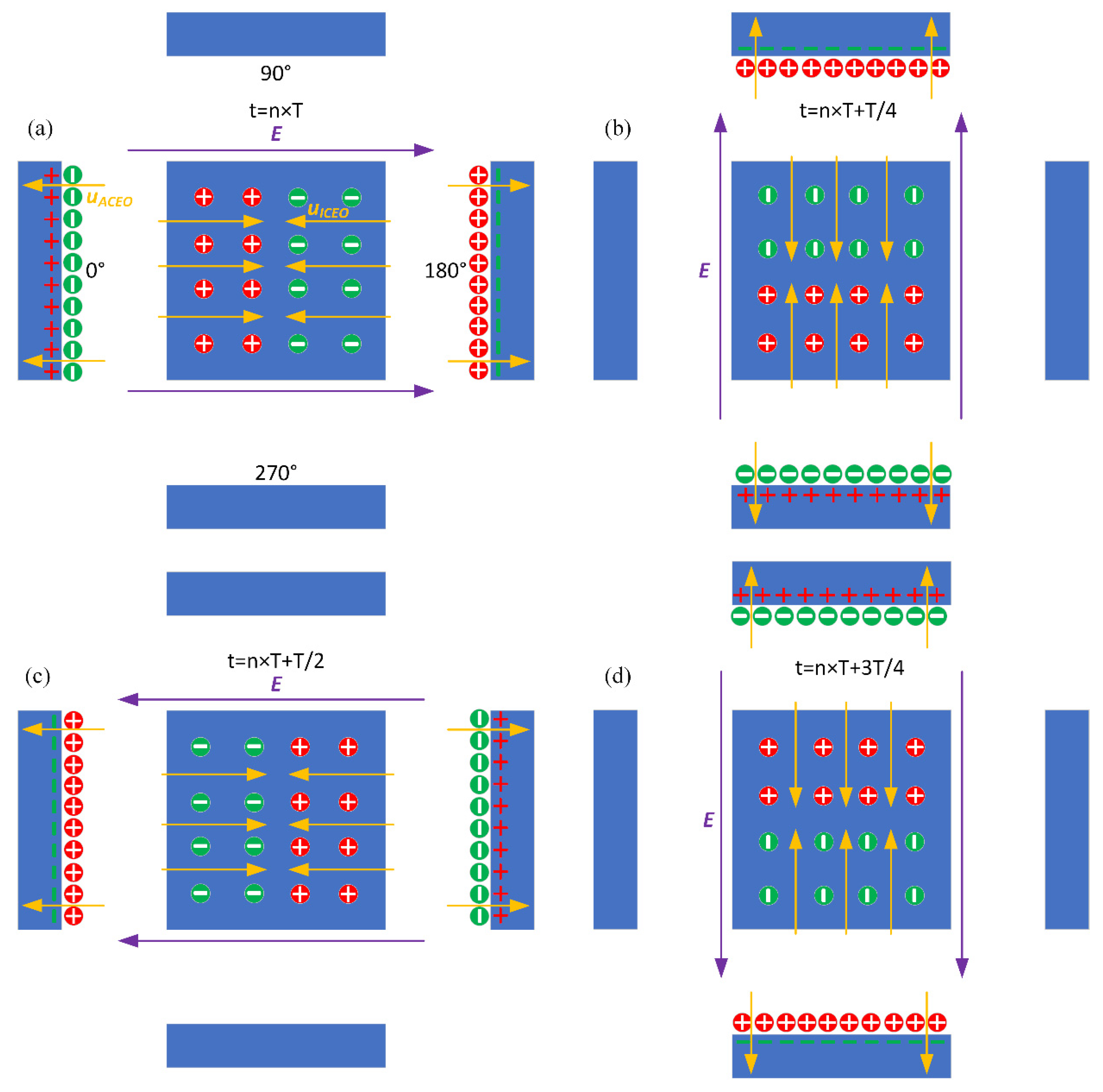
2.2. Basic Theory of ICEO Electroconvection at the Metal/Electrolyte Interface
2.3. Mass Transfer of Antigen and Binding Reaction Enhancement
3. Results and Discussion
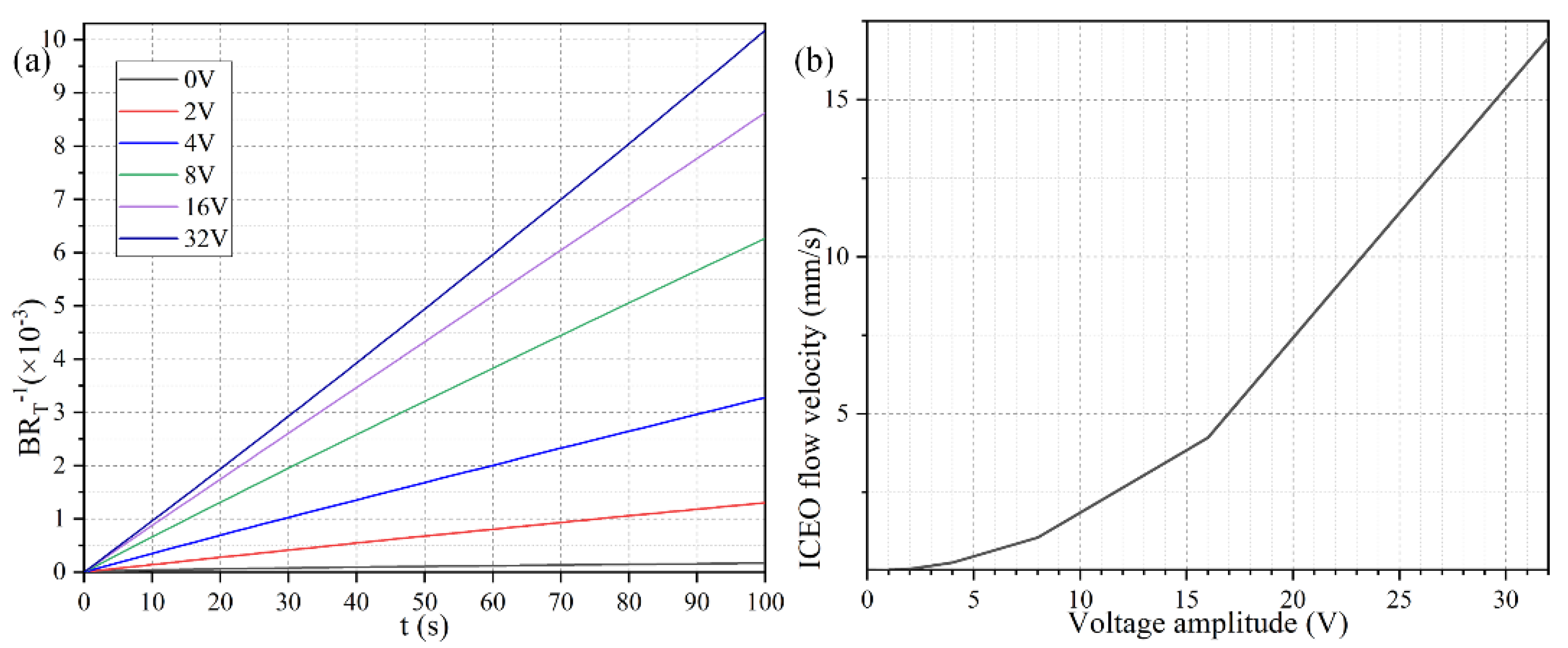
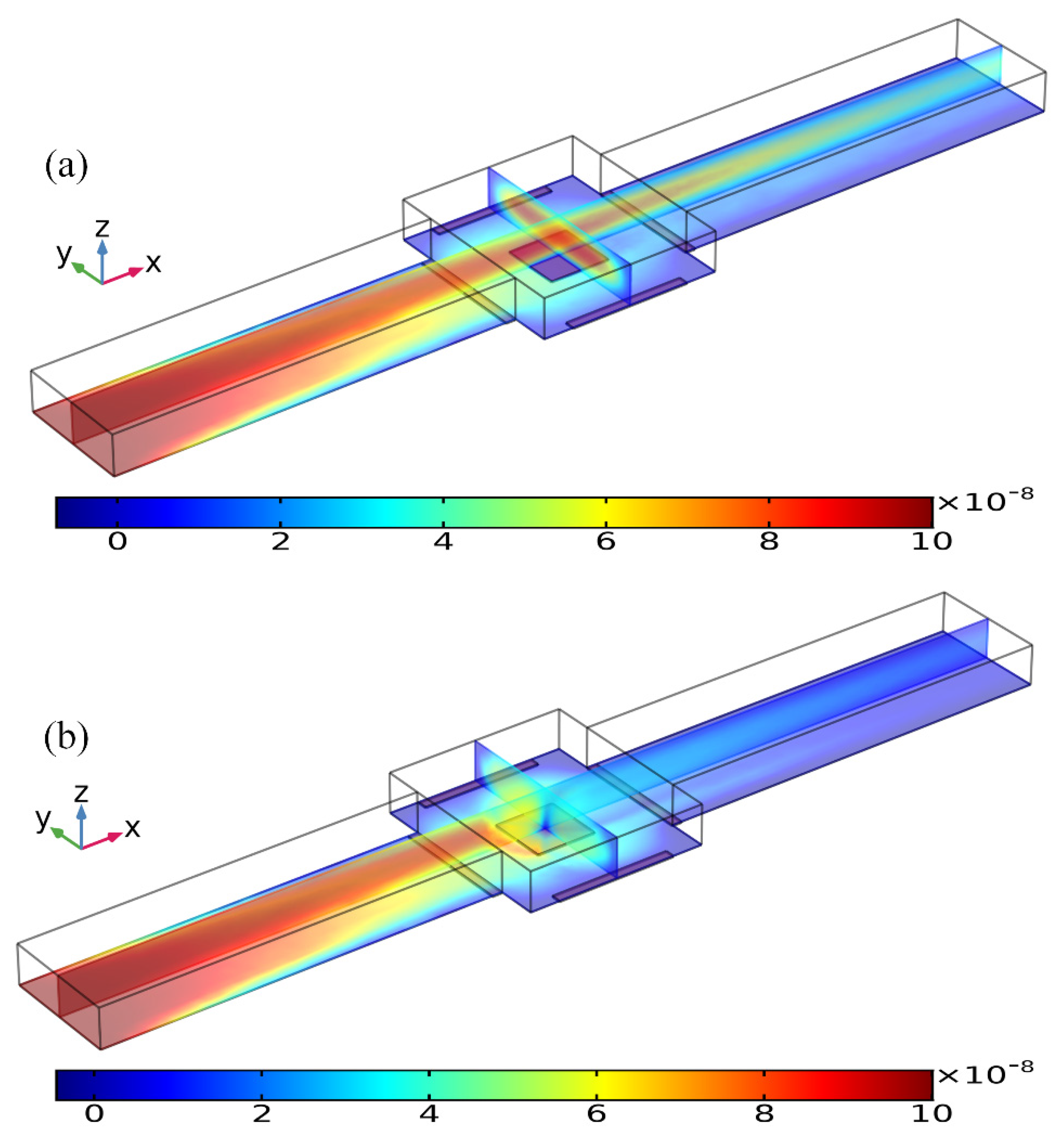
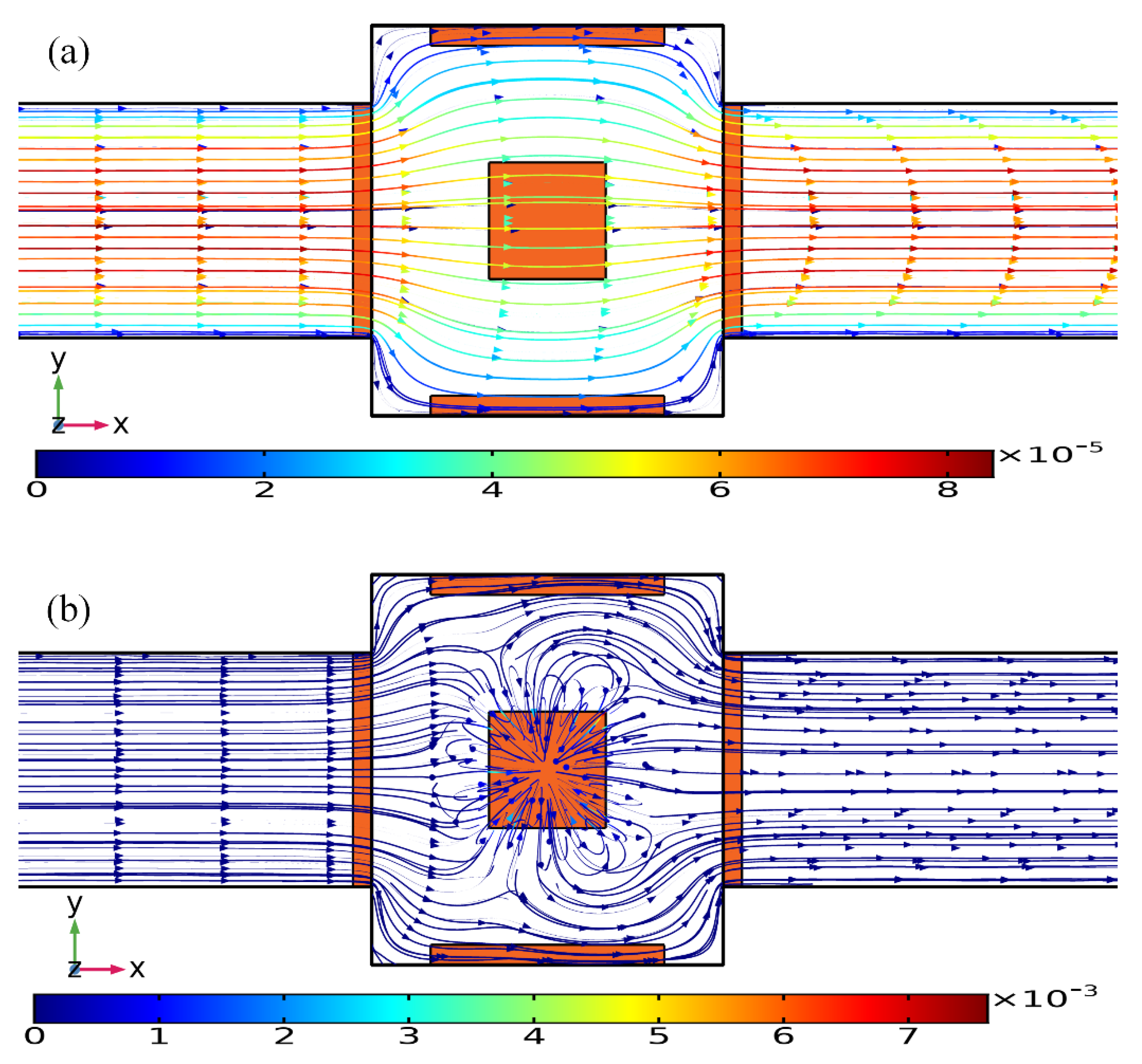
3.1. Binding Reaction Enhancement by ROT-ICEO Micro-Stirring
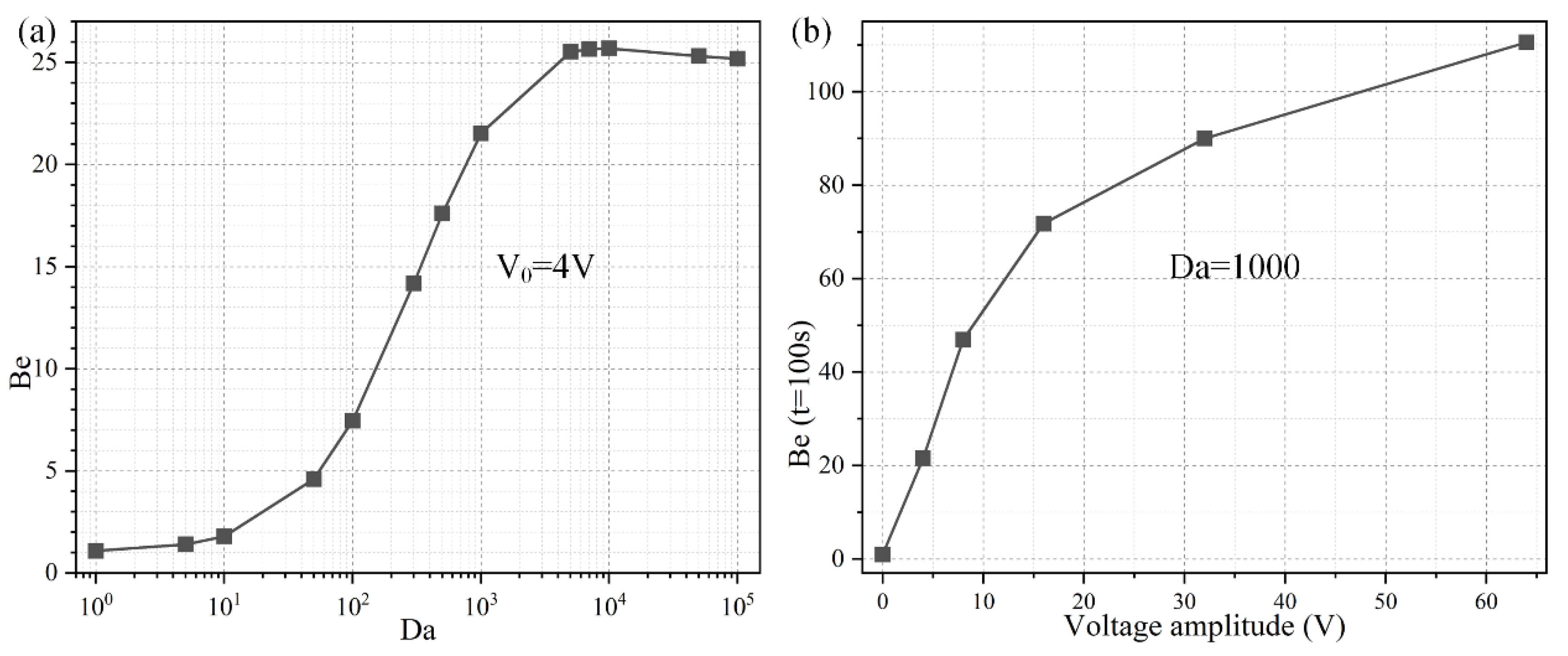
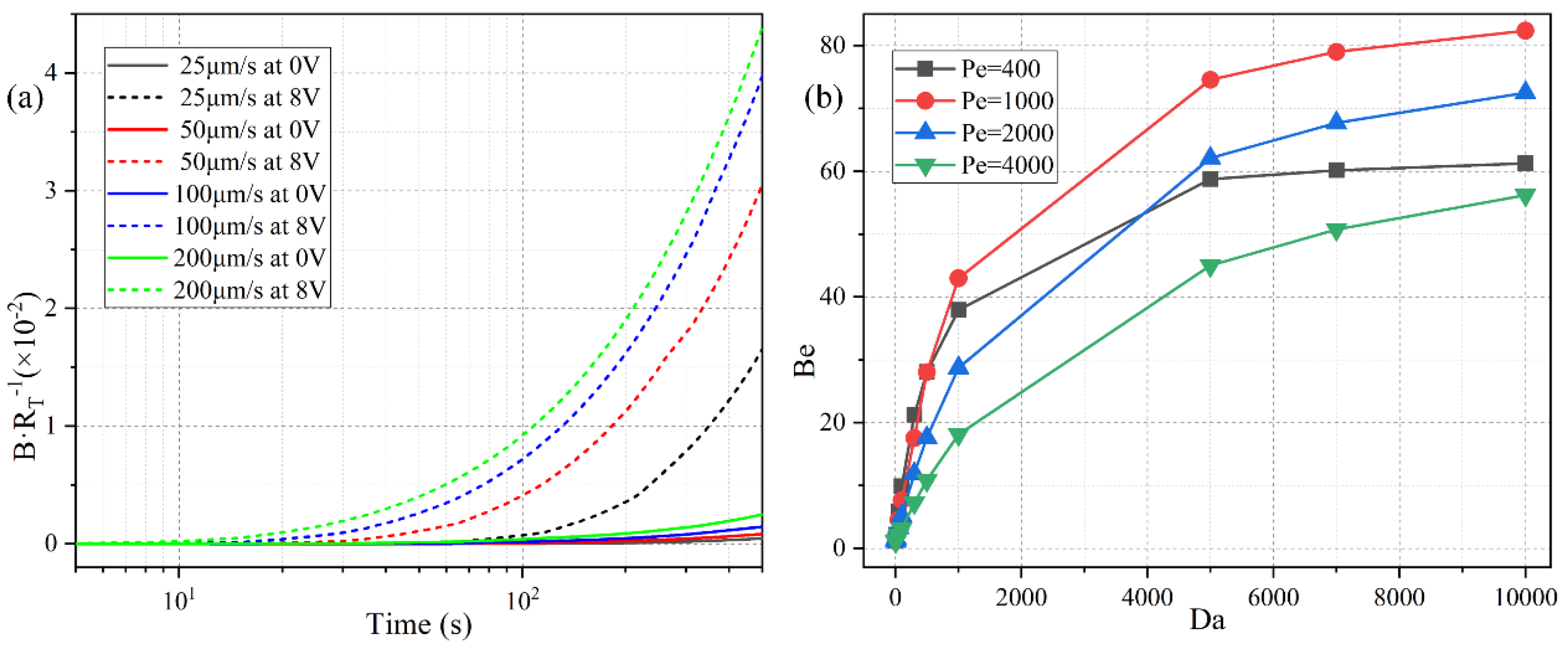
3.2. Effect of the Damkohler Number
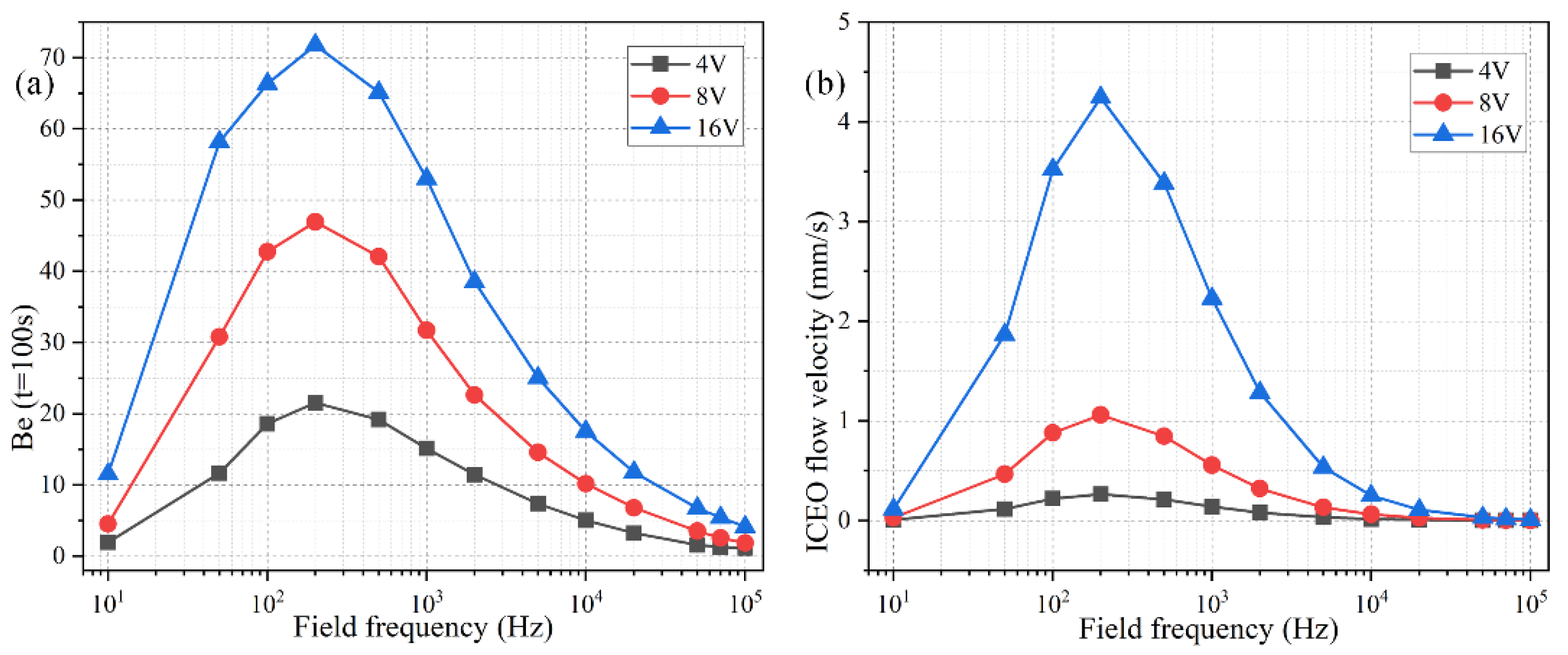
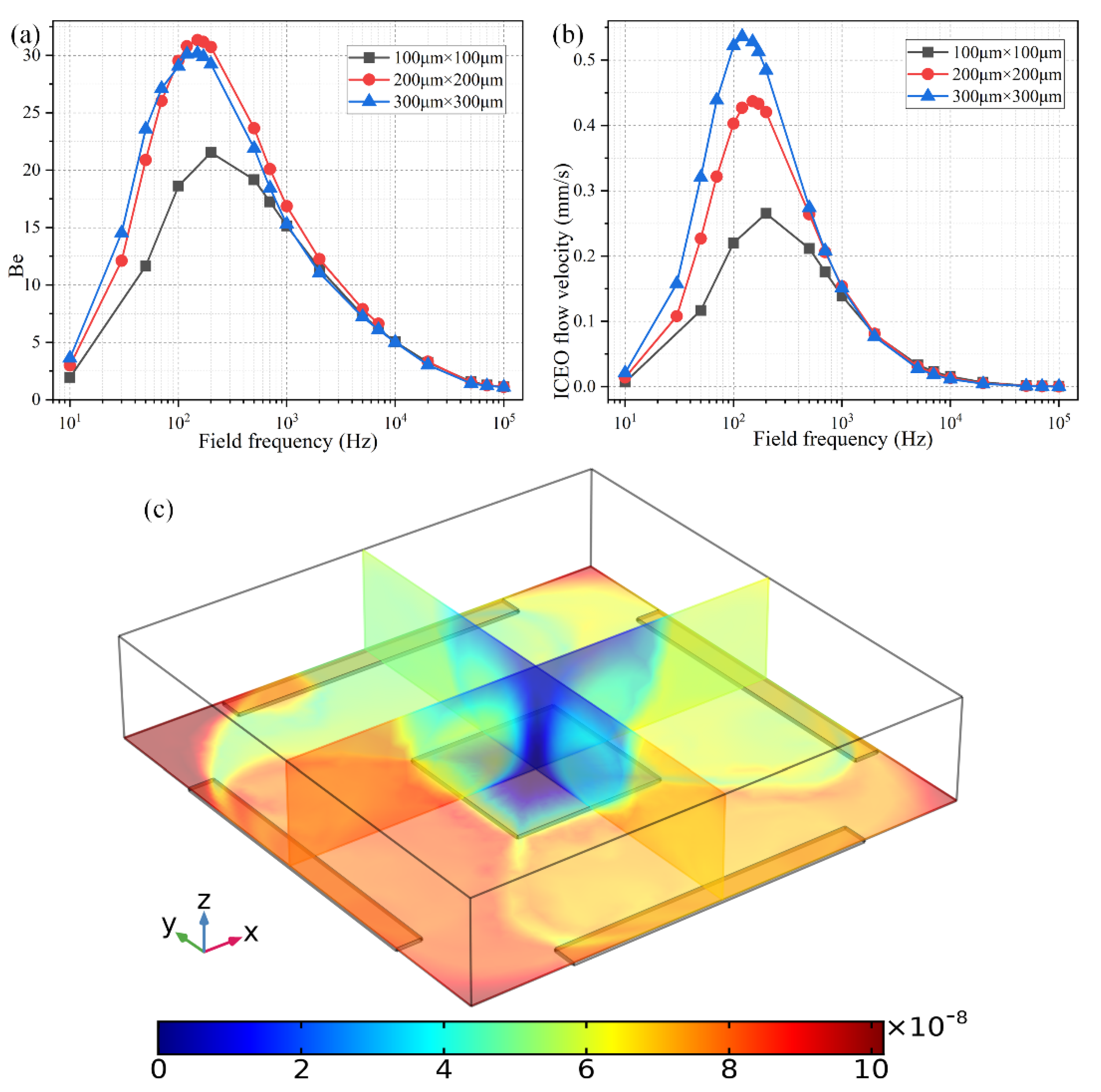
3.3. Frequency-Dependent Binding Reaction
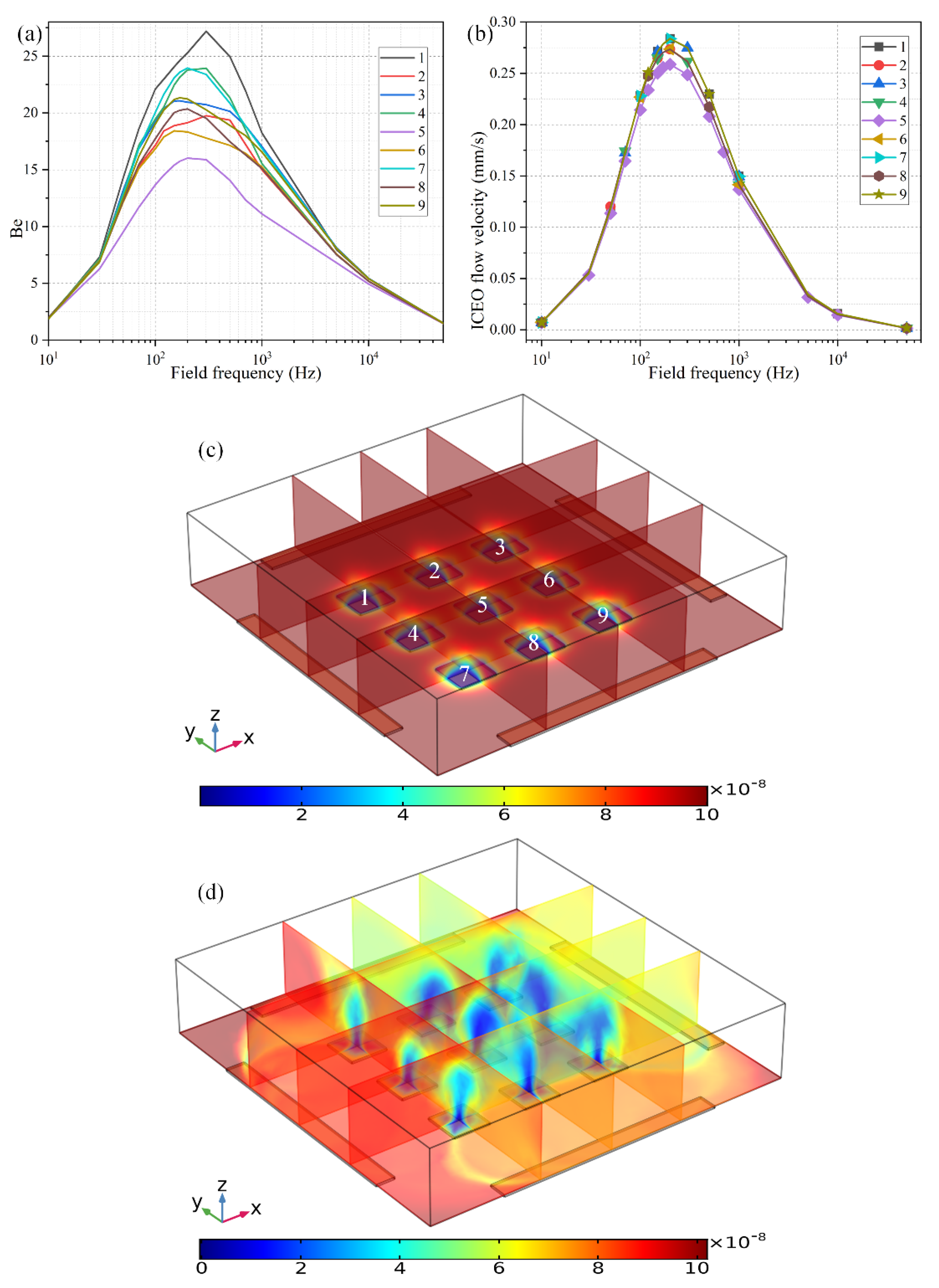
3.4. Effect of Geometric Arrangement of the Floating Electrodes
3.5. Binding Reaction Enhancement in a Pressure-Driven Flow
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nemeth, E.; Girelli, D.; Olbina, G.; Ganz, T.; Westerman, M. Immunoassay for human serum hepcidin. Blood 2008, 112, 4292–4297. [Google Scholar]
- Hales, C.N.; Randle, P.J. Immunoassay of insulin with insulin-antibody precipitate. Biochem. J. 1963, 282, 414. [Google Scholar]
- Kusnezow, W.; Hoheisel, J.R.D. Solid supports for microarray immunoassays. J. Mol. Recognit. 2003, 16, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Delehanty, J.B.; Ligler, F.S. A microarray immunoassay for simultaneous detection of proteins and bacteria. Anal. Chem. 2002, 74, 5681–5687. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.M.; Martinez, A.W.; Gong, J.; Mace, C.R.; Phillips, S.T.; Carrilho, E.; Mirica, K.A.; Whitesides, G.M. Paper-based elisa. Angew. Chem. Int. Ed. 2010, 49, 4771–4774. [Google Scholar] [CrossRef] [PubMed]
- Pullen, G.R.; Fitzgerald, M.G.; Hosking, C.S. Antibody avidity determination by elisa using thiocyanate elution. J. Immunol. Methods 1986, 86, 83–87. [Google Scholar] [CrossRef]
- OEzkumur, E.; Needham, J.W.; Bergstein, D.A.; Gonzalez, R.; Cabodi, M.; Gershoni, J.M.; Goldberg, B.B.; UEnlue, M.S. Label-free and dynamic detection of biomolecular interactions for high-throughput microarray applications. Proc. Natl. Acad. Sci. USA 2008, 105, 7988–7992. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Xu, D.; Cheng, Q. Label-free detection methods for protein microarrays. Proteomics 2006, 6, 5493–5503. [Google Scholar] [CrossRef]
- Nygren, H.K.; Werthen, M.; Stenberg, M. Kinetics of antibody binding to solid-phase-immobilised antigen: Effect of diffusion rate limitation and steric interaction. J. Immunol. Methods 1987, 101, 63–71. [Google Scholar] [CrossRef]
- Yang, C.K.; Chang, J.S.; Chao, S.D.; Wu, K.C. Effects of diffusion boundary layer on reaction kinetics of immunoassay in a biosensor. J. Appl. Phys. 2008, 103, 1160–1169. [Google Scholar] [CrossRef]
- Luppa, P.B.; Müller, C.; Schlichtiger, A.; Schlebusch, H. Point-of-care testing (poct): Current techniques and future perspectives. Trends Anal. Chem. 2011, 30, 887–898. [Google Scholar] [CrossRef] [PubMed]
- Min, J.H.; Baeumner, A. The micro- total analytical system for the detection of bacteria/viruses. J. Ind. Eng. Chem. 2003, 9, 1–8. [Google Scholar]
- Choi, S.; Chae, J. Methods of reducing non-specific adsorption in microfluidic biosensors. J. Micromech. Microeng. 2010, 20, 075015. [Google Scholar] [CrossRef]
- Wang, J.; Aki, M.; Onoshima, D.; Arinaga, K.; Kaji, N.; Tokeshi, M.; Fujita, S.; Yokoyama, N.; Baba, Y. Microfluidic biosensor for the detection of DNA by fluorescence enhancement and the following streptavidin detection by fluorescence quenching. Biosens. Bioelectron. 2014, 51, 280–285. [Google Scholar] [CrossRef] [PubMed]
- Chiu, Y.J.; Cho, S.H.; Mei, Z.; Lien, V.; Wu, T.F.; Lo, Y.H. Universally applicable three-dimensional hydrodynamic microfluidic flow focusing. Lab Chip 2013, 13, 1803. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Islam, N.; Eda, S.; Wu, J. Optimization of an ac electrokinetics immunoassay lab-chip for biomedical diagnostics. Microfluid. Nanofluid. 2017, 21, 35. [Google Scholar] [CrossRef]
- Chen, L.; Lee, S.; Choo, J.; Lee, E.K. Continuous dynamic flow micropumps for microfluid manipulation. J. Micromech. Microeng. 2007, 18, 013001. [Google Scholar] [CrossRef]
- Chen, L.; Ma, J.; Guan, Y. Study of an electroosmotic pump for liquid delivery and its application in capillary column liquid chromatography. J. Chromatogr. A 2004, 1028, 219–226. [Google Scholar] [CrossRef]
- Turek, M.; Bandura, B. Renewable energy by reverse electrodialysis. Desalination 2007, 205, 67–74. [Google Scholar] [CrossRef]
- Lin, Y.-Y.; Liu, G.; Wai, C.M.; Lin, Y. Magnetic beads-based bioelectrochemical immunoassay of polycyclic aromatic hydrocarbons. Electrochem. Commun. 2007, 9, 1547–1552. [Google Scholar] [CrossRef]
- Lee, G.U.; Metzger, S.; Natesan, M.; Yanavich, C.; Dufrêne, Y.F. Implementation of force differentiation in the immunoassay. Anal. Biochem. 2000, 287, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Selmi, M.; Echouchene, F.; Gazzah, M.H.; Belmabrouk, H. Flow confinement enhancement of heterogeneous immunoassays in microfluidics. IEEE Sens. J. 2015, 15, 7321–7328. [Google Scholar] [CrossRef]
- Park, S.; Koklu, M.; BeskoK, A. Particle trapping in high-conductivity media with electrothermally enhanced negative dielectrophoresis. Anal. Chem. 2009, 81, 2303–2310. [Google Scholar] [CrossRef] [PubMed]
- Salari, A.; Dalton, C. Simultaneous pumping and mixing of biological fluids in a double-array electrothermal microfluidic device. Micromachines 2019, 10, 92. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Green, N.G.; Ramos, A.; González, A.; Castellanos, A.; Morgan, H. Electric field induced fluid flow on microelectrodes: The effect of illumination. J. Phys. D Appl. Phys. 2000, 33, L13. [Google Scholar] [CrossRef] [Green Version]
- Salemmilani, R.; Piorek, B.D.; Mirsafavi, R.Y.; Fountain III, A.W.; Moskovits, M.; Meinhart, C.D. Dielectrophoretic nanoparticle aggregation for on-demand surface enhanced raman spectroscopy analysis. Anal. Chem. 2018, 90, 7930–7936. [Google Scholar] [CrossRef]
- Gimsa, J. A comprehensive approach to electro-orientation, electrodeformation, dielectrophoresis, and electrorotation of ellipsoidal particles and biological cells. Bioelectrochemistry 2001, 54, 23–31. [Google Scholar] [CrossRef]
- Gimsa, J.; Stubbe, M.; Gimsa, U. A short tutorial contribution to impedance and ac-electrokinetic characterization and manipulation of cells and media: Are electric methods more versatile than acoustic and laser methods? J. Electr. Bioimpedance 2014, 5, 74–91. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Yang, K.; Wadhwa, A.; Eda, S.; Li, S.; Wu, J. Development of an ac electrokinetics-based immunoassay system for on-site serodiagnosis of infectious diseases. Sens. Actuators A Phys. 2011, 171, 406–413. [Google Scholar] [CrossRef]
- Du, E.; Manoochehri, S. Enhanced ac electrothermal fluidic pumping in microgrooved channels. J. Appl. Phys. 2008, 104, 2584. [Google Scholar] [CrossRef] [Green Version]
- Green, N.G.; Ramos, A.; Gonzalez, A.; Morgan, H.; Castellanos, A. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. Iii. Observation of streamlines and numerical simulation. Phys. Rev. E 2002, 66, 026305. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. Ac electric-field-induced fluid flow in microelectrodes. J. Colloid Interface Sci. 1999, 217, 420–422. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Ben, Y.; Chang, H.-C. Particle detection by electrical impedance spectroscopy with asymmetric-polarization ac electroosmotic trapping. Microfluid. Nanofluid. 2005, 1, 161–167. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena: Theory and microfluidic applications. Phys. Rev. Lett. 2004, 92, 066101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Squires, T.M.; Bazant, M.Z. Induced-charge electro-osmosis. J. Fluid Mech. 2004, 509, 217–252. [Google Scholar] [CrossRef] [Green Version]
- Yossifon, G.; Frankel, I.; Miloh, T. Symmetry breaking in induced-charge electro-osmosis over polarizable spheroids. Phys. Fluids 2007, 19, 217. [Google Scholar] [CrossRef]
- Hart, R.; Lec, R.; Noh, H.M. Enhancement of heterogeneous immunoassays using ac electroosmosis. Sens. Actuators B Chem. 2010, 147, 366–375. [Google Scholar] [CrossRef]
- Sigurdson, M.; Wang, D.; Meinhart, C.D. Electrothermal stirring for heterogeneous immunoassays. Lab Chip 2005, 5, 1366–1373. [Google Scholar] [CrossRef]
- Feng, H.; Chang, H.; Zhong, X.; Wong, T. Recent advancement in induced-charge electrokinetic phenomena and their micro-and nano-fluidic applications. Adv. Colloid Interface Sci. 2020, 280, 102159. [Google Scholar] [CrossRef]
- Paustian, J.S.; Pascall, A.J.; Wilson, N.M.; Squires, T.M. Induced charge electroosmosis micropumps using arrays of janus micropillars. Lab Chip 2014, 14, 3300–3312. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Li, D. Micromixing using induced-charge electrokinetic flow. Electrochim. Acta 2008, 53, 5827–5835. [Google Scholar] [CrossRef]
- Harnett, C.K.; Templeton, J.; Dunphy-Guzman, K.A.; Senousy, Y.M.; Kanouff, M.P. Model based design of a microfluidic mixer driven by induced charge electroosmosis. Lab Chip 2008, 8, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.; Yeung, A.; Nandakumar, K. Efficient micromixing using induced-charge electroosmosis. J. Microelectromech. Syst. 2009, 18, 376–384. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, W.; Jia, Y.; Tao, Y.; Shao, J.; Ding, Y.; Jiang, H. Induced-charge electroosmotic trapping of particles. Lab Chip 2015, 15, 2181–2191. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, K.H.; Grego, S.; Velev, O.D. An ac electrokinetic technique for collection and concentration of particles and cells on patterned electrodes. Langmuir 2005, 21, 6603–6612. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Shao, J.; Jia, Y.; Tao, Y.; Ding, Y.; Jiang, H.; Ren, Y. Trapping and chaining self-assembly of colloidal polystyrene particles over a floating electrode by using combined induced-charge electroosmosis and attractive dipole–dipole interactions. Soft Matter 2015, 11, 8105–8112. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Liu, W.; Liu, J.; Tao, Y.; Guo, Y.; Jiang, H. Particle rotational trapping on a floating electrode by rotating induced-charge electroosmosis. Biomicrofluidics 2016, 10, 054103. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Shao, J.; Ren, Y.; Liu, J.; Tao, Y.; Jiang, H.; Ding, Y. On utilizing alternating current-flow field effect transistor for flexibly manipulating particles in microfluidics and nanofluidics. Biomicrofluidics 2016, 10, 034105. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Ren, Y.; Tao, Y.; Li, Y.; Wu, Q. On traveling-wave field-effect flow control for simultaneous induced-charge electroosmotic pumping and mixing in microfluidics: Physical perspectives and theoretical analysis. J. Micromech. Microeng. 2018, 28, 055004. [Google Scholar] [CrossRef]
- Pascall, A.J.; Squires, T.M. Induced charge electro-osmosis over controllably contaminated electrodes. Phys. Rev. Lett. 2010, 104, 088301. [Google Scholar] [CrossRef]
- Nguyen, T.; Der Meer, D.V.; Den Berg, A.V.; Eijkel, J.C.T. Investigation of the effects of time periodic pressure and potential gradients on viscoelastic fluid flow in circular narrow confinements. Microfluid. Nanofluid. 2017, 21, 37. [Google Scholar] [CrossRef] [Green Version]
- Andersson, H.; Den Berg, A.V. Microfabrication and microfluidics for tissue engineering: State of the art and future opportunities. Lab Chip 2004, 4, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Ngo, T.A.; Bang, D.D.; Wolff, A. Optimising the supercritical angle fluorescence structures in polymer microfluidic biochips for highly sensitive pathogen detection: A case study on escherichia coli. Lab Chip 2019, 19, 3825–3833. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Power Supply Modes | 1st Terminal | 2nd Terminal | 3rd Terminal | 4th Terminal |
|---|---|---|---|---|
| (i) | V1 = V0cos(ωt) | V2 = V0cos(ωt + 90°) | V3 = V0cos(ωt + 180°) | V4 = V0cos(ωt + 270°) |
| (ii) | V1 = V0cos(ωt) | V2 = V0cos(ωt) | V3 = V0cos(ωt + 180°) | V4 = V0cos(ωt + 180°) |
| (iii) | V1 = V0cos(ωt) | V2 = V0cos(ωt + 180°) | V3 = V0cos(ωt) | V4 = V0cos(ωt + 180°) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Z.; Yan, H.; Liu, W.; Song, C.; Xue, R.; Ren, Y. A Numerical Investigation of Enhancing Microfluidic Heterogeneous Immunoassay on Bipolar Electrodes Driven by Induced-Charge Electroosmosis in Rotating Electric Fields. Micromachines 2020, 11, 739. https://doi.org/10.3390/mi11080739
Ge Z, Yan H, Liu W, Song C, Xue R, Ren Y. A Numerical Investigation of Enhancing Microfluidic Heterogeneous Immunoassay on Bipolar Electrodes Driven by Induced-Charge Electroosmosis in Rotating Electric Fields. Micromachines. 2020; 11(8):739. https://doi.org/10.3390/mi11080739
Chicago/Turabian StyleGe, Zhenyou, Hui Yan, Weiyu Liu, Chunlei Song, Rui Xue, and Yukun Ren. 2020. "A Numerical Investigation of Enhancing Microfluidic Heterogeneous Immunoassay on Bipolar Electrodes Driven by Induced-Charge Electroosmosis in Rotating Electric Fields" Micromachines 11, no. 8: 739. https://doi.org/10.3390/mi11080739
APA StyleGe, Z., Yan, H., Liu, W., Song, C., Xue, R., & Ren, Y. (2020). A Numerical Investigation of Enhancing Microfluidic Heterogeneous Immunoassay on Bipolar Electrodes Driven by Induced-Charge Electroosmosis in Rotating Electric Fields. Micromachines, 11(8), 739. https://doi.org/10.3390/mi11080739







