Generating Convergent Laguerre-Gaussian Beams Based on an Arrayed Convex Spiral Phaser Fabricated by 3D Printing
Abstract
1. Introduction
2. Structure Design, Fabrication and Topography Measurement
2.1. Design and Fabrication
2.2. Topography Measurement
3. Experimental Measurement
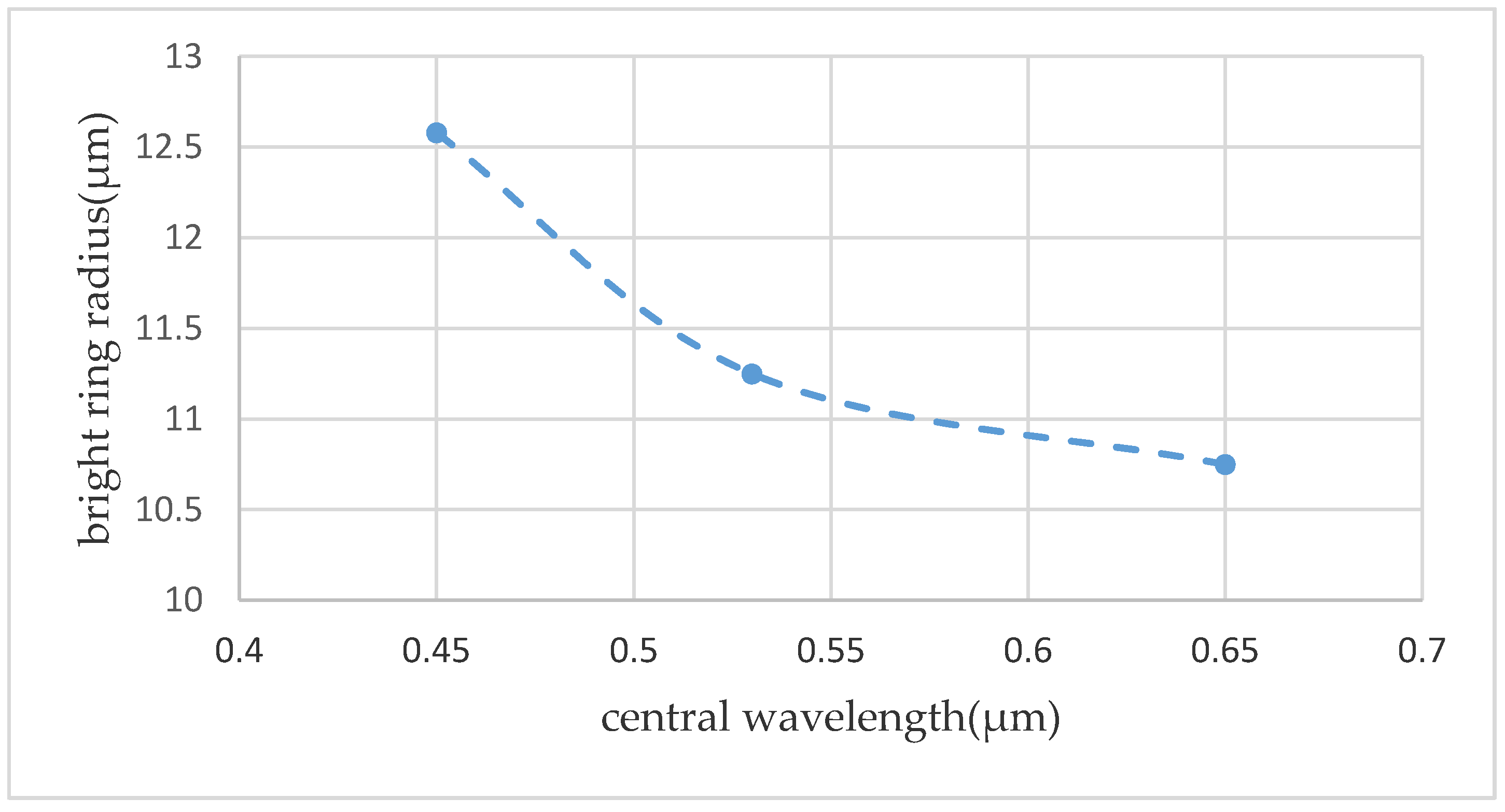
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, D.; Zhao, S.H.; Shi, L.; Liu, Y. Measurement-device-independent quantum key distribution with pairs of vector vortex beams. Phys. Rev. A 2016, 93, 032320. [Google Scholar] [CrossRef]
- Nauerth, S.; Moll, F.; Rau, M.; Fuchs, C.; Horwath, J.; Frick, S.; Weinfurter, H. Air-to-ground quantum communication. Nat. Photonics 2013, 7, 382–386. [Google Scholar] [CrossRef]
- Hsieh, M.H.; Wilde, M.M. Trading classical communication, quantum communication, and entanglement in quantum Shannon theory. IEEE Trans. Inf. Theory 2010, 56, 4705–4730. [Google Scholar] [CrossRef]
- Wengerowsky, S.; Joshi, S.K.; Steinlechner, F.; Hübel, H.; Ursin, R. Entanglement-based wavelength multiplexed quantum communication network. Nature 2018, 564, 225–228. [Google Scholar] [CrossRef]
- Liao, S.K.; Yong, H.L.; Liu, C.; Shentu, G.L.; Li, D.D.; Lin, J.; Dai, H.; Zhao, S.Q.; Li, B.; Guan, J.Y.; et al. Long-distance free-space quantum key distribution in daylight towards inter-satellite communication. Nat. Photonics 2017, 11, 509–513. [Google Scholar] [CrossRef]
- Chen, M.; Huang, S.; Shao, W.; Liu, X. Optical force and torque on a dielectric Rayleigh particle by a circular Airy vortex beam. J. Quant. Spectrosc. Radiat. Transfer. 2018, 208, 101–107. [Google Scholar] [CrossRef]
- Li, R.; Yang, R.; Ding, C.; Mitri, F.G. Optical torque on a magneto-dielectric Rayleigh absorptive sphere by a vector Bessel (vortex) beam. J. Quant. Spectrosc. Radiat. Transfer. 2017, 191, 96–115. [Google Scholar] [CrossRef]
- Gu, B.; Xu, D.; Rui, G.; Lian, M.; Cui, Y.; Zhan, Q. Manipulation of dielectric rayleigh particles using highly focused elliptically polarized vector fields. Appl. Opt. 2015, 54, 8123–8129. [Google Scholar] [CrossRef]
- Shu, J.; Chen, Z.; Pu, J. Radiation forces on a Rayleigh particle by highly focused partially coherent and radially polarized vortex beams. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2013, 30, 916–922. [Google Scholar] [CrossRef]
- Peele, A.G.; Nugent, K.A. X-ray vortex beams: A theoretical analysis. Opt. Express 2003, 11, 2315–2322. [Google Scholar] [CrossRef][Green Version]
- Shi, L.; Lindwasser, L.; Wang, W.; Alfano, R.; Adrián, R.C. Propagation of gaussian and laguerre-gaussian vortex beams through mouse brain tissue. J. Biophotonics 2017, 10, 1756–1760. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, A.D.; Bailey, M.; Cunitz, B.W.; Terzi, M.; Sapozhnikov, O.A. Vortex beams and radiation torque for kidney stone management. J. Acoust. Soc. Am. 2016, 139, 2040. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Xie, G.; Lavery, M.P.J.; Huang, H.; Ahmed, N.; Bao, C.; Ren, Y.; Cao, Y.; Li, L.; Zhao, Z. High-capacity millimetre-wave communications with orbital angular momentum multiplexing. Nat. Commun. 2014, 5, 487. [Google Scholar] [CrossRef]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padgett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Liu, S.L.; Li, Y.; Ding, D.S.; Zhang, W.; Shi, S.; Dong, M.X.; Shi, B.S.; Guo, G.C. Orbital angular momentum-entanglement frequency transducer. Phys. Rev. Lett. 2016, 117, 103601. [Google Scholar] [CrossRef]
- Vovk, I.A.; Tepliakov, N.V.; Leonov, M.Y.; Baranov, A.V.; Rukhlenko, I.D. Analytical theory of real-argument Laguerre-Gaussian beams beyond the paraxial approximation. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2017, 34, 1940–1944. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X.; Tang, H.; Zhu, K. Propagation of multi-cosine-Laguerre-Gaussian correlated Schell-model beams in free space and atmospheric turbulence. Opt. Express 2017, 25, 20071–20086. [Google Scholar] [CrossRef]
- Dasgupta, R.; Verma, R.S.; Ahlawat, S.; Chaturvedi, D.; Gupta, P.K. Long-distance axial trapping with Laguerre–Gaussian beams. Appl. Opt. 2011, 50, 1469–1476. [Google Scholar] [CrossRef]
- Parisi, G.; Mari, E.; Spinello, F.; Romanato, F.; Tamburini, F. Manipulating intensity and phase distribution of composite Laguerre-Gaussian beams. Opt. Express 2014, 22, 17135–17146. [Google Scholar] [CrossRef] [PubMed]
- Frenzen, C.L.; Wong, R. Uniform asymptotic expansions of Laguerre Polynomials. SIAM J. Math. Anal. 2015, 19, 1232–1248. [Google Scholar] [CrossRef]
- Gómez-Ullate, D.; Kamran, N.; Milson, R. Two-step Darboux transformations and exceptional Laguerre polynomials. J. Math. Anal. Appl. 2012, 387, 410–418. [Google Scholar] [CrossRef]
- Loureiro, A.F.; Maroni, P. Quadratic decomposition of Laguerre polynomials via lowering operators. J. Approx. Theory 2012, 163, 888–903. [Google Scholar] [CrossRef][Green Version]
- Boelen, L.; Assche, W.V. Variations of Stieltjes–Wigert and -Laguerre polynomials and their recurrence coefficients. J. Approx.Theory 2015, 193, 56–73. [Google Scholar] [CrossRef]
- Miyamoto, K.; Suizu, K.; Akiba, T.; Omatsu, T. Direct observation of the topological charge of a terahertz vortex beam generated by a Tsurupica spiral phase plate. Appl. Phys. Lett. 2014, 104, 537–540. [Google Scholar] [CrossRef]
- Blackburn, A.M.; Loudon, J.C. Vortex beam production and contrast enhancement from a magnetic spiral phase plate. Ultramicroscopy 2014, 136, 127–143. [Google Scholar] [CrossRef]
- Rumala, Y.S. Propagation of structured light beams after multiple reflections in a spiral phase plate. Opt. Eng. 2015, 54, 131–143. [Google Scholar] [CrossRef]
- Cottrell, D.M.; Davis, J.A.; Hernandez, T.J. Fraunhofer diffraction of a partially blocked spiral phase plate. Optics Express 2011, 19, 12873–12878. [Google Scholar] [CrossRef]
- Sun, K.; Wei, T.S.; Ahn, B.Y.; Seo, J.Y.; Dillon, S.J.; Lewis, J.A. 3D Printing of Interdigitated Li-Ion Microbattery Architectures. Adv. Mater. 2013, 25, 4539–4543. [Google Scholar] [CrossRef]
- Visser, C.W.; Pohl, R.; Sun, C.; Richardus, G.; Bernardus; Römer, E. Toward 3D printing of pure metals by laser-induced forward transfer. Adv. Mater. 2015, 27, 4087–4092. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; Abert, C.; Bruckner, F.; Groenefeld, M.; Muthsam, O.; Schuschnigg, S.; Sirak, K.; Thanhoffer, R.; Teliban, I.; Windl, R. 3D print of polymer bonded rare-earth magnets, and 3d magnetic field scanning with an end-user 3D printer. Appl. Phys. Lett. 2016, 109, 162401. [Google Scholar] [CrossRef]
- Ladd, C.; So, J.H.; Muth, J.; Dickey, M.D. 3D Printing of free standing liquid metal microstructures. Adv. Mater. 2013, 25, 5081–5085. [Google Scholar] [CrossRef] [PubMed]
- Saber, S.M.A.H.; Akhlaghi, E.A.; Saber, A. Diffractometry based vortex beams fractional topological charge measurement. Opt. Lett. 2020, 45, 3478–3481. [Google Scholar] [CrossRef]
- Luo, M.; Zhao, D. Determining the topological charge of stochastic electromagnetic vortex beams with the degree of cross-polarization. Opt. Lett. 2014, 39, 5070–5073. [Google Scholar] [CrossRef]
- Yavorsky, M.; Brasselet, E. Polarization and topological charge conversion of exact optical vortex beams at normal incidence on planar dielectric interfaces. Opt. Lett. 2012, 37, 3810–3812. [Google Scholar] [CrossRef]
- Khajavi, B.; Galvez, E.J. Determining topological charge of an optical beam using a wedged optical flat. Opt. Lett. 2017, 42, 1516–1519. [Google Scholar] [CrossRef]
- Zhao, C.L.; Wang, F.; Dong, Y.; Han, Y.; Cai, Y. Effect of spatial coherence on determining the topological charge of a vortex beam. Appl. Phys. Lett. 2012, 101, 261104. [Google Scholar] [CrossRef]
- Garcia-Gracia, H.; Gutiérrez-Vega, J.C. Diffraction of plane waves by finite-radius spiral phase plates of integer and fractional topological charge. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2009, 26, 794–803. [Google Scholar] [CrossRef]
- Li, X.Z.; Tai, Y.P.; Lv, F.J.; Nie, Z. Measuring the fractional topological charge of LG beams by using interference intensity analysis. Opt. Commun. 2015, 334, 235–239. [Google Scholar] [CrossRef]
- Marra, P.; Citro, R.; Ortix, C. Fractional quantization of the topological charge pumping in a one-dimensional superlattice. Phys. Rev. B 2015, 91, 125411. [Google Scholar] [CrossRef]
- Höllwieser, R.; Faber, M.; Heller, U.M. Intersections of thick center vortices, Dirac Eigenmodes and fractional topological charge in SU(2) Lattice Gauge Theory. J. High Energy Phys. 2011, 52, 1–20. [Google Scholar]
- Cottrell, D.M.; Moreno, I.; Davis, J.A. Analysis of multilevel spiral phase plates using a Dammann vortex sensing grating. Opt. Express 2010, 18, 25987–25992. [Google Scholar]
- Guo, C.S.; Xue, D.M.; Han, Y.J.; Ding, J. Optimal phase steps of multi-level spiral phase plates. Opt. Commun. 2006, 268, 235–239. [Google Scholar] [CrossRef]
- Ruffato, G.; Massari, M.; Carli, M.; Romanato, F. Spiral phase plates with radial discontinuities for the generation of multiring orbital angular momentum beams: Fabrication, characterization, and application. Opt. Eng. 2015, 54, 111307. [Google Scholar] [CrossRef]
- Dennis, M.R.; O’Holleran, K.; Padgett, M.J. Chapter 5 singular optics: Optical vortices and polarization singularities. Prog. Opt. 2009, 53, 293–363. [Google Scholar]

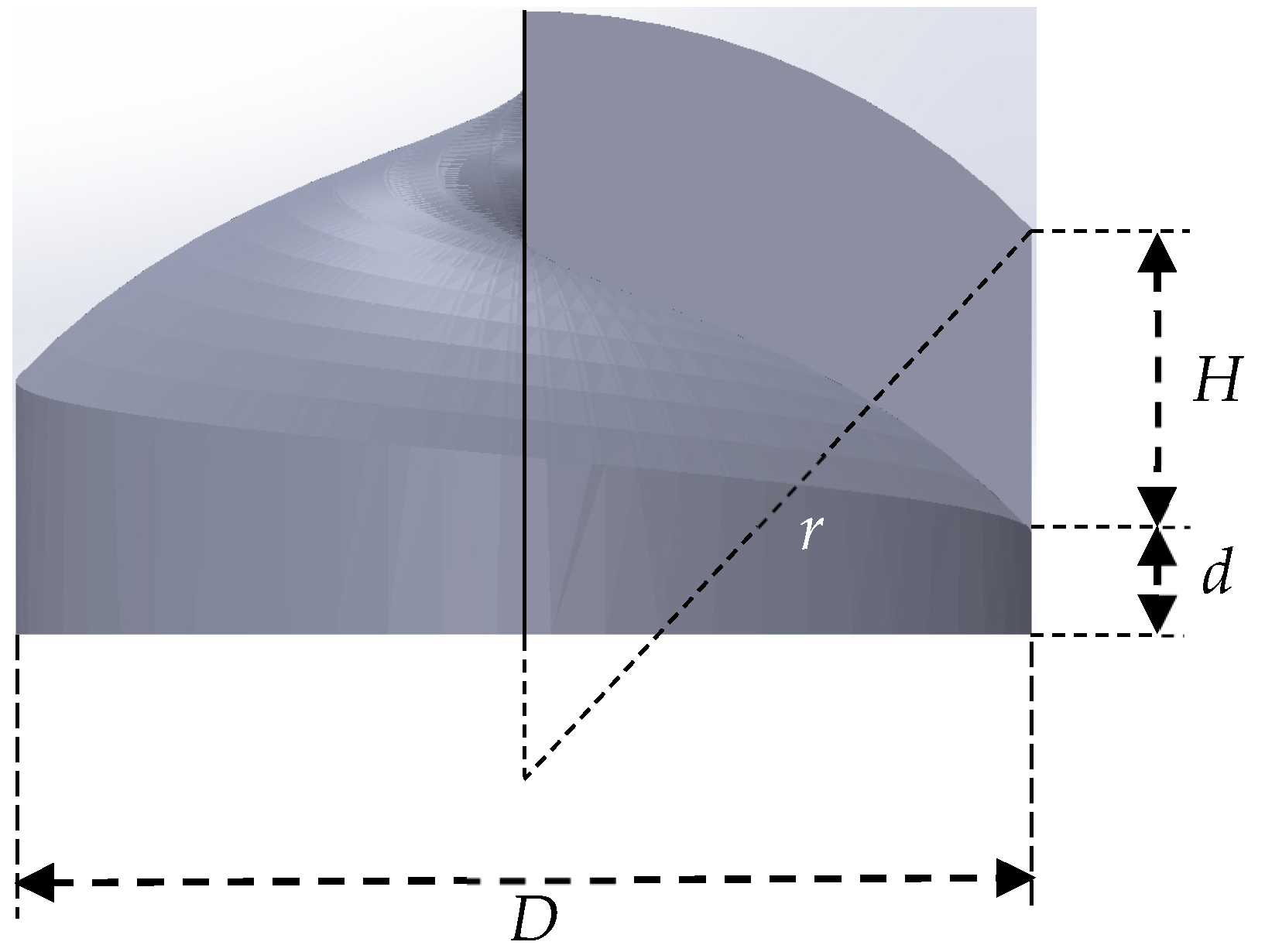

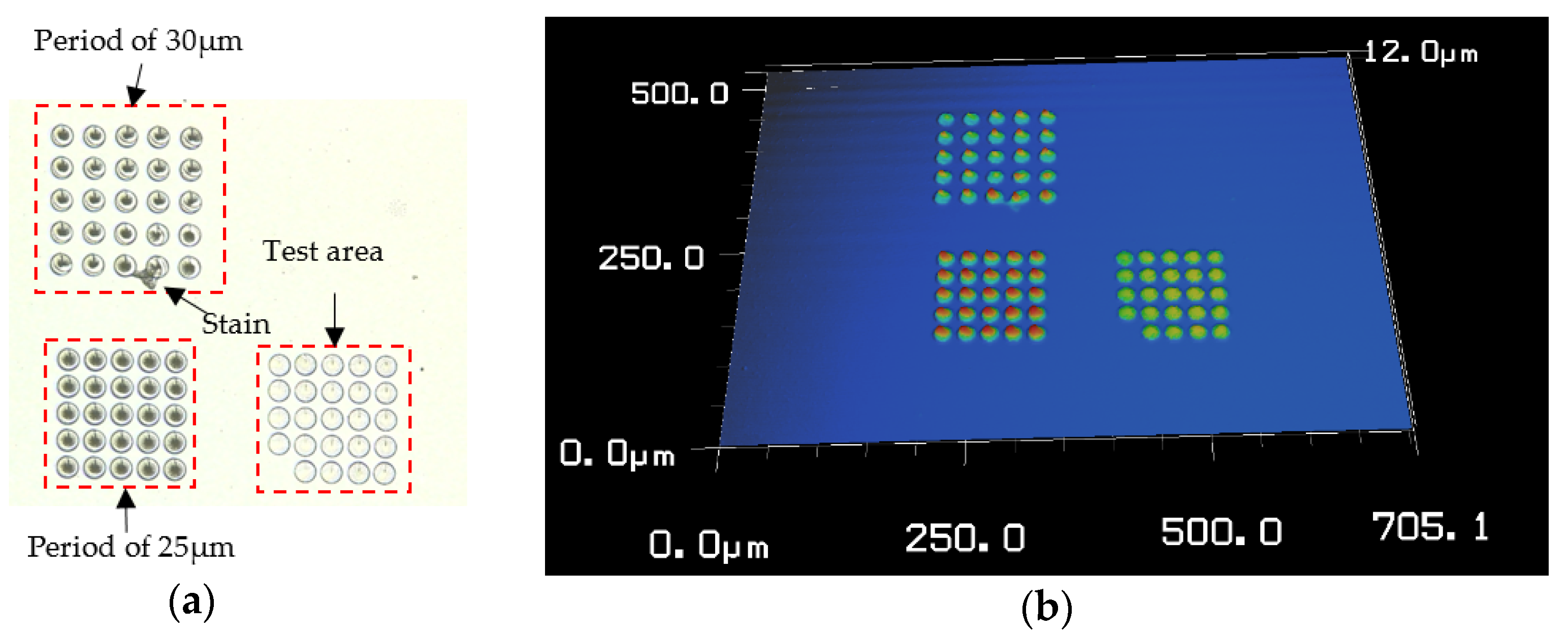

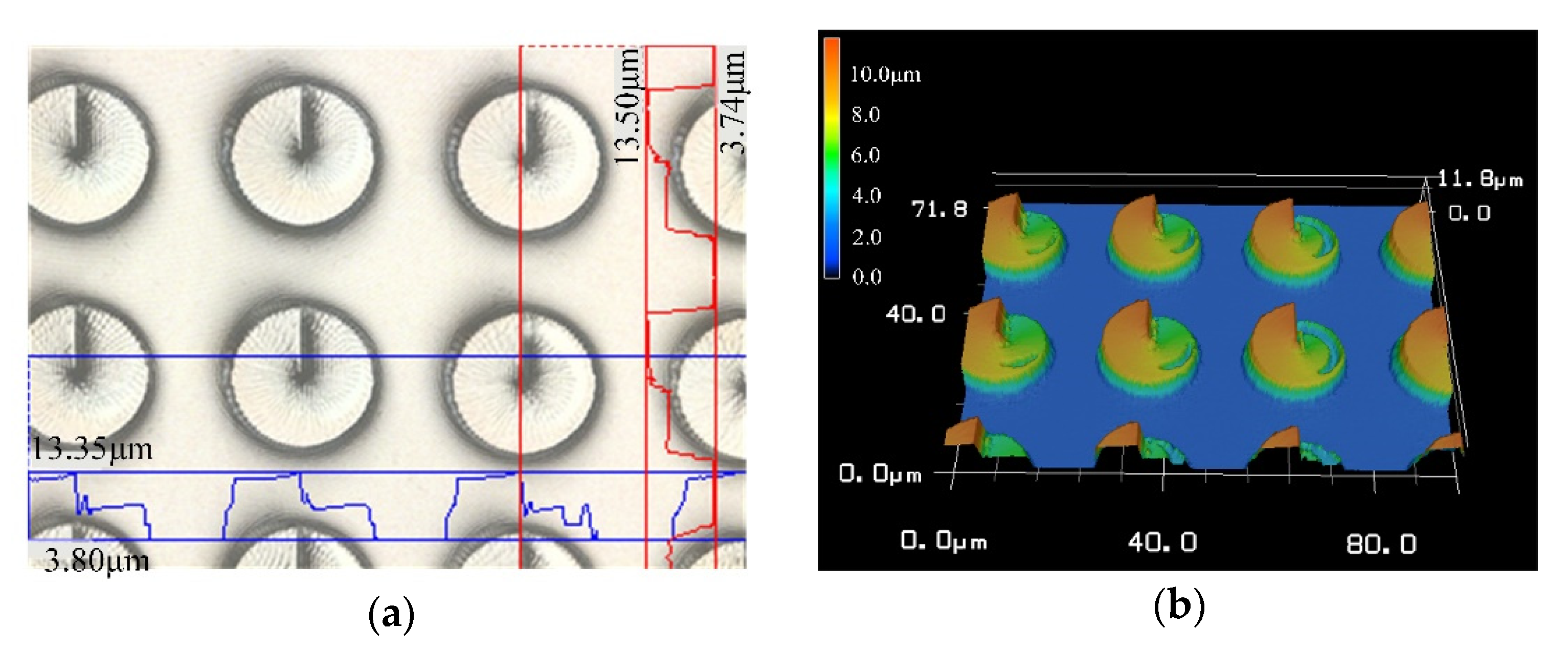

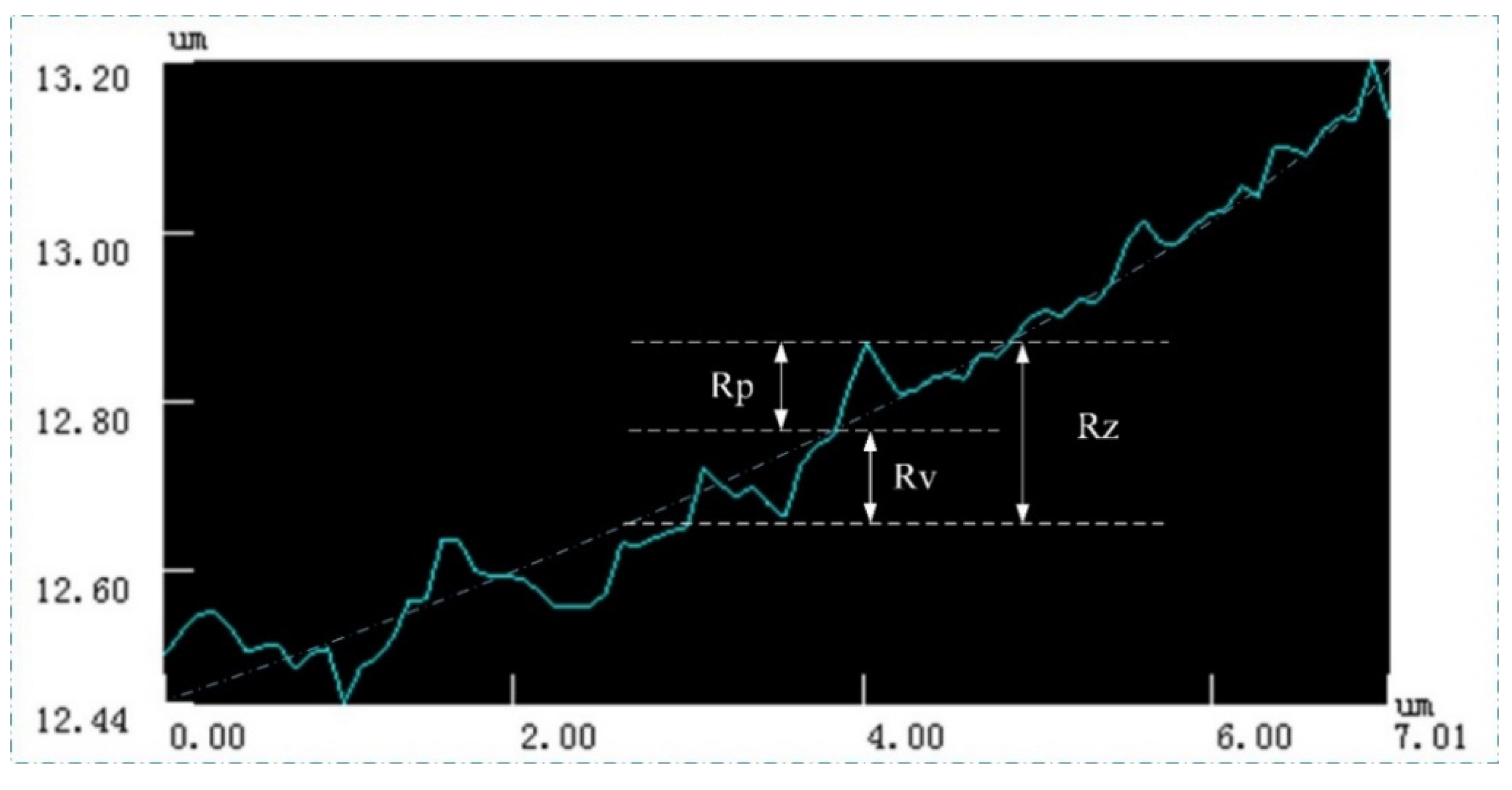
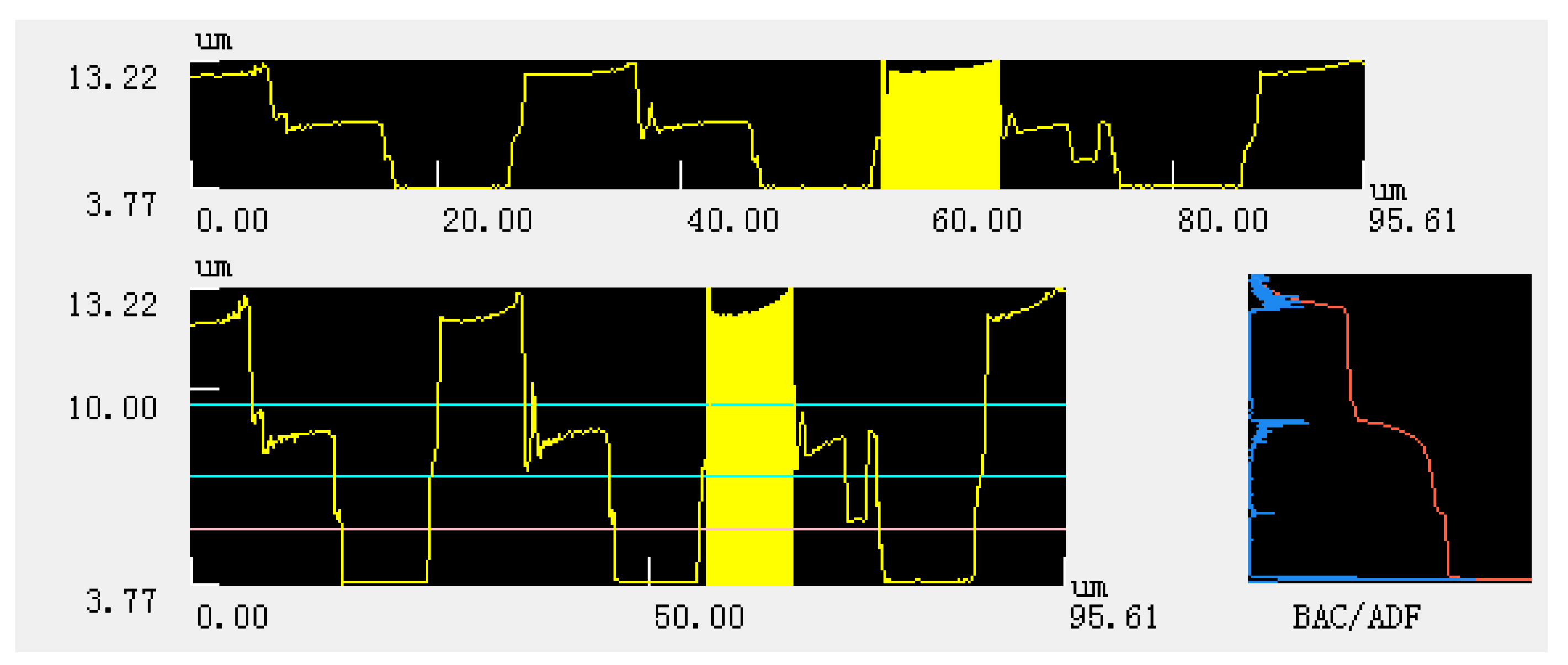

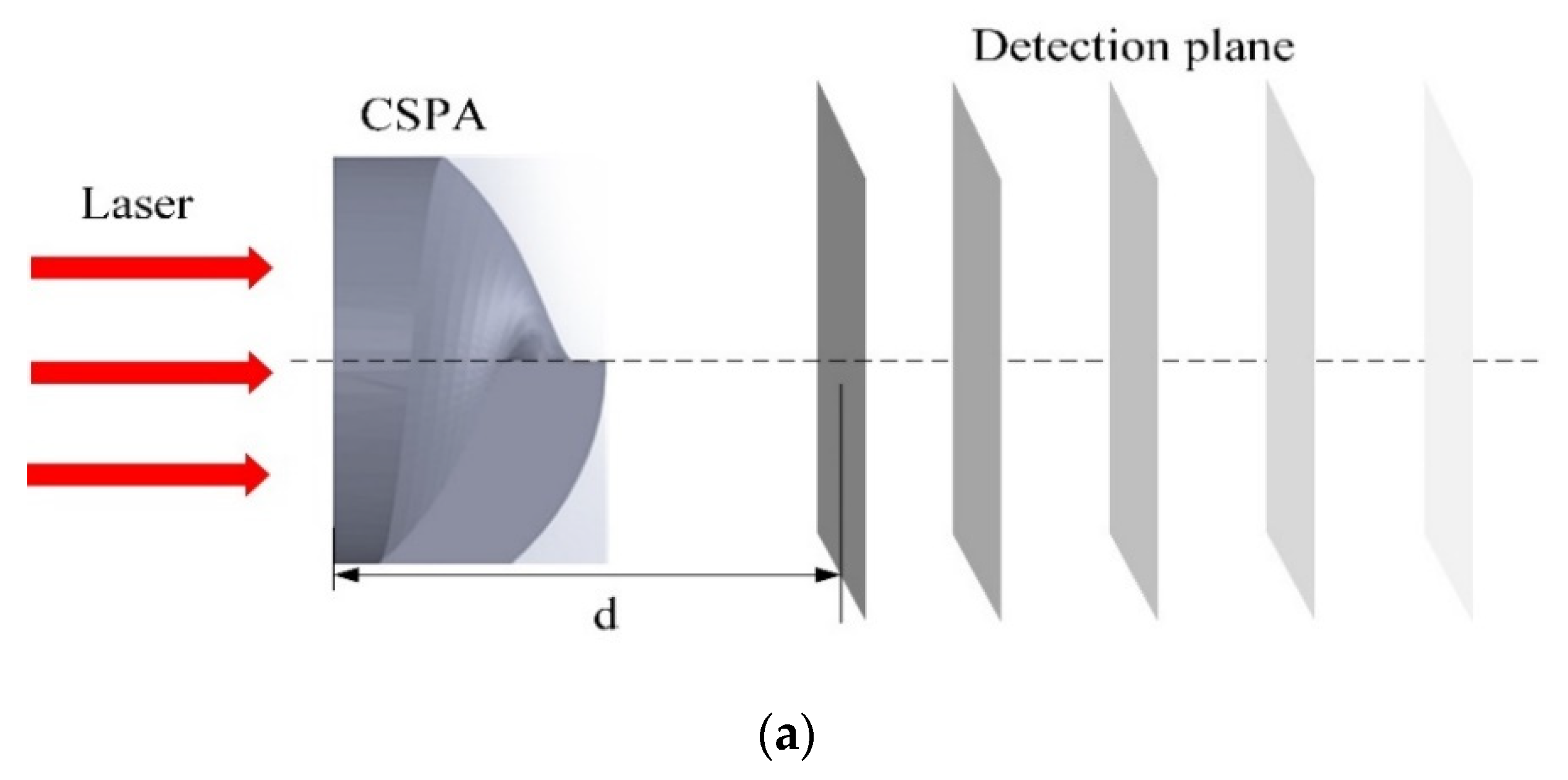


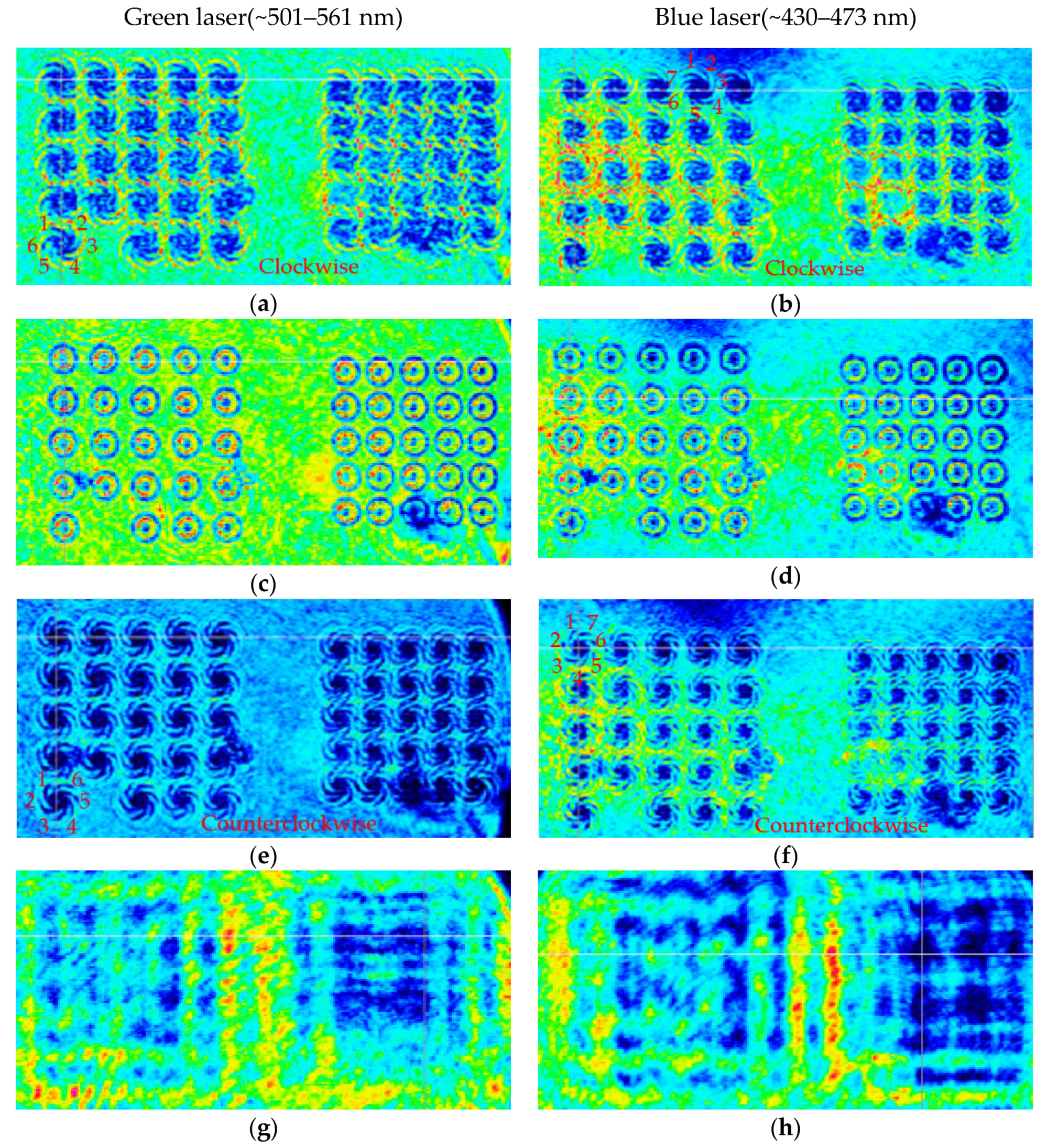

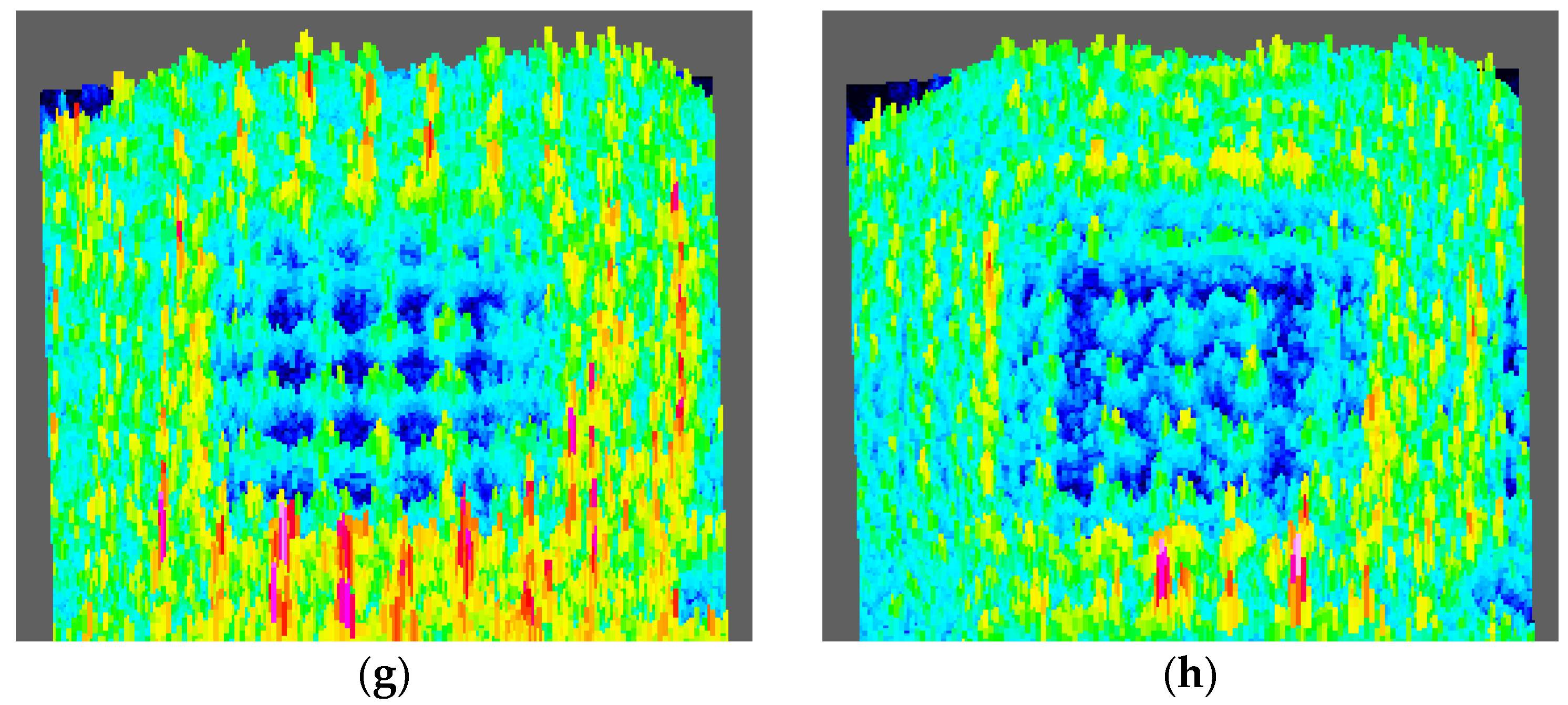
| Parameter | Value (μm) |
|---|---|
| r | 200 |
| R | 20 |
| d | 2 |
| H | 5.963 |
| Rp | Rv | Rz | Ra | Rq | Rsk | Rku | RΔq | RSm | |
|---|---|---|---|---|---|---|---|---|---|
| Seg.1 | 0.09 μm | 0.10 μm | 0.19 μm | 4.17 μm | 4.17 μm | 1.0002 | 1.0005 | 0.1922 | 0.00 μm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Hu, C.; Wei, D.; Chen, M.; Shi, J.; Wang, H.; Xie, C.; Zhang, X. Generating Convergent Laguerre-Gaussian Beams Based on an Arrayed Convex Spiral Phaser Fabricated by 3D Printing. Micromachines 2020, 11, 771. https://doi.org/10.3390/mi11080771
Liu C, Hu C, Wei D, Chen M, Shi J, Wang H, Xie C, Zhang X. Generating Convergent Laguerre-Gaussian Beams Based on an Arrayed Convex Spiral Phaser Fabricated by 3D Printing. Micromachines. 2020; 11(8):771. https://doi.org/10.3390/mi11080771
Chicago/Turabian StyleLiu, Chang, Chai Hu, Dong Wei, Mingce Chen, Jiashuo Shi, Haiwei Wang, Changsheng Xie, and Xinyu Zhang. 2020. "Generating Convergent Laguerre-Gaussian Beams Based on an Arrayed Convex Spiral Phaser Fabricated by 3D Printing" Micromachines 11, no. 8: 771. https://doi.org/10.3390/mi11080771
APA StyleLiu, C., Hu, C., Wei, D., Chen, M., Shi, J., Wang, H., Xie, C., & Zhang, X. (2020). Generating Convergent Laguerre-Gaussian Beams Based on an Arrayed Convex Spiral Phaser Fabricated by 3D Printing. Micromachines, 11(8), 771. https://doi.org/10.3390/mi11080771





