Effect of Blade Outlet Angle on the Flow Field and Preventing Overload in a Centrifugal Pump
Abstract
:1. Introduction
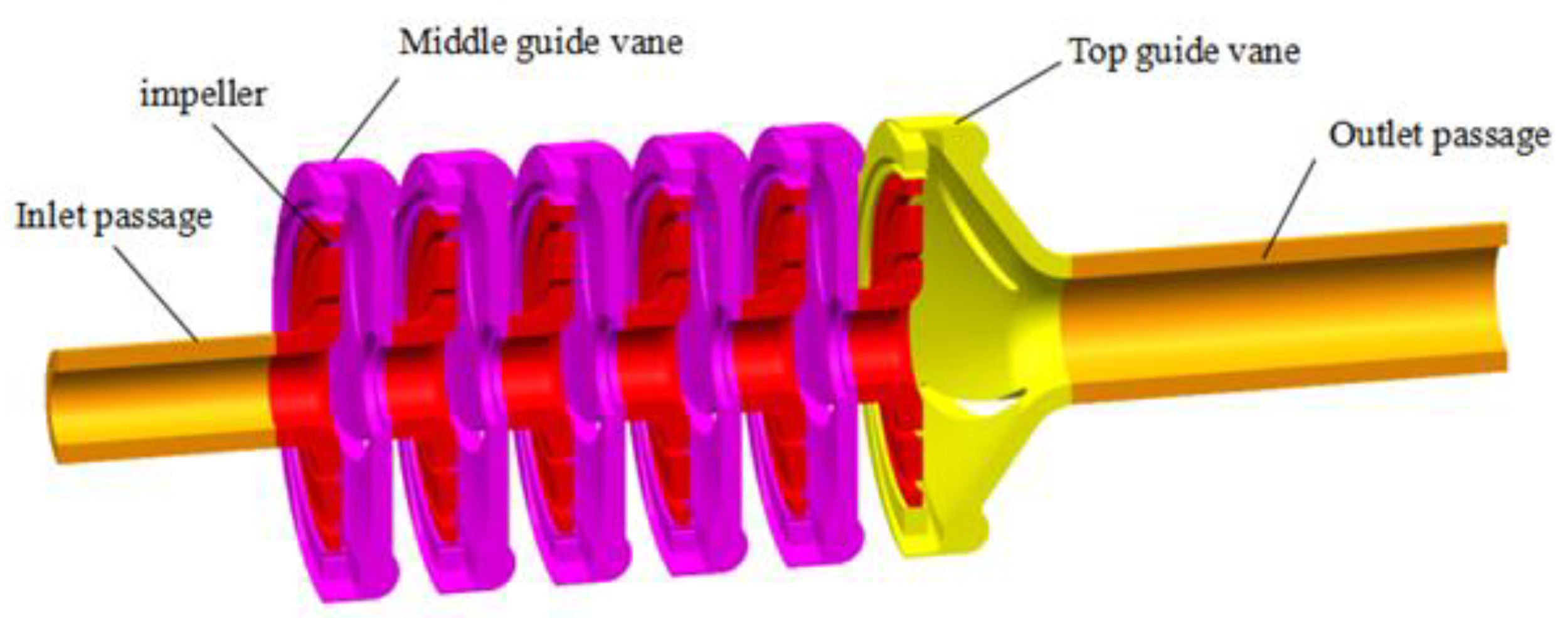
2. Geometry and Numerical Methods
2.1. Impeller Design
2.2. Modeling and Numerical Setting
3. Comparison of the Predicted and Experimental Results
4. Pump Flow Fields with Various Blade Outlet Angles
4.1. Effect of Blade Outlet Angle on the Pump Performance
4.2. Effect of Blade Angle on Preventing Overload in a Centrifugal Pump
4.3. Flow Field Analysis for Various Blade Outlet Angles
4.3.1. Pressure Distribution Characteristics
4.3.2. Velocity Distribution Characteristics
4.3.3. Turbulent Kinetic Energy and Velocity Vector Distributions
5. Conclusions
- (1)
- The head gradually increases as the blade outlet angle increases. A smaller blade outlet angle gives a steeper head curve, which indicates more severe flow conditions. Proper reduction of the blade outlet angle can make the power decrease at higher flow rates so that overloading cannot occur.
- (2)
- The pressure is low at the first-stage impeller inlet. Increasing the blade outlet angle significantly increases the low-pressure area of the impeller inlet, which increases the chance of cavitation, so the β2 = 16° design has the lowest cavitation rate.
- (3)
- Increasing the blade outlet angle increases the flow separation along the blade working face and increases the axial vortex along the blade working surface; the vortex rotates in the direction opposite to the impeller rotating direction, with the vortex extending to the inlet of the impeller.
Author Contributions
Funding
Conflicts of Interest
References
- Pottebaum, J.R. Optimal Characteristics of a Variable-Frequency Centrifugal Pump Motor Drive. IEEE Trans. Ind. Appl. 1984, IA-20, 23–31. [Google Scholar] [CrossRef]
- Peng, G.; Huang, X.; Zhou, L.; Zhou, G.; Zhou, H. Solid-liquid two-phase flow and wear analysis in a large-scale centrifugal slurry pump. Eng. Fail. Anal. 2020, 114, 104602. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Han, C.; Zhu, Y.; Shi, W. Numerical study of pressure fluctuation and unsteady flow in a centrifugal pump. Processes 2019, 7, 354. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, J.; Lin, X.; Wang, R.; Zhang, C.; Zhao, J. Experimental investigation into downstream field of a horizontal axis tidal stream turbine supported by a mono pile. Appl. Ocean Res. 2020, 101, 102257. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, W.; Hang, J.; Shi, W.; Yan, H.; Zhu, Y. Numerical investigation of a high-speed electrical submersible pump with different end clearances. Water 2020, 12, 1116. [Google Scholar] [CrossRef] [Green Version]
- Shigemitsu, T.; Fukutomi, J.; Kaji, K. Influence of Blade Outlet Angle and Blade Thickness on Performance and Internal Flow Conditions of Mini Centrifugal Pump. Turbomachinery Society of Japan, Korean Society for Fluid Machinery, Chinese Society of Engineering Thermophysics, IAHR. Int. J. Fluid Mach. Sys. 2011, 4, 179–185. [Google Scholar]
- Bacharoudis, E.C.; Filios, A.E.; Mentzos, M.D.; Margaris, D.P. Parametric study of a centrifugal pump impeller by varying the outlet blade angle. Open Mech. Eng. J. 2008, 2, 75–83. [Google Scholar] [CrossRef]
- Nishi, Y.; Fukutomi, J.; Fujiwara, R. Effect of Blade Outlet Angle on Radial Thrust of Single-blade Centrifugal Pump. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 2039. [Google Scholar] [CrossRef]
- Shigemitsu, T.; Fukutomi, J.; Nasada, R.; Kaji, K. The Effect of Blade Outlet Angle on Performance and Internal Flow Condition of Mini Turbo-Pump. J. Therm. Sci. 2011, 20, 32–38. [Google Scholar] [CrossRef]
- Gölcü, M.; Pancar, Y.; Sekmen, Y. Energy saving in a deep well pump with splitter blade. Energy Convers. Manag. 2006, 47, 638–651. [Google Scholar] [CrossRef]
- Djebedjian, B. Theoretical model to predict the performance of centrifugal pump equipped with splitter blade. Mansoura Eng. J. 2009, 34, 50–70. [Google Scholar]
- Pedersen, N.; Larsen, P.; Jacobsen, C.B. Flow in a centrifugal pump impeller at design and off-design conditions—Part I: Particle image velocimetry (PIV) and laser Doppler velocimetry (LDV) measurements. J. Fluids Eng. 2003, 125, 61–72. [Google Scholar] [CrossRef]
- Byskov, R.; Jacobsen, C.; Pedersen, N. Flow in a centrifugal pump impeller at design and off-design conditions part II: Large eddy simulations. J. Fluids Eng. 2003, 125, 73–83. [Google Scholar] [CrossRef]
- Barrios, L.; Prado, M.G. Experimental Visualization of Two-Phase Flow inside an Electrical Submersible Pump Stage. J. Energy Resour. Technol. 2011, 133, 453–467. [Google Scholar] [CrossRef]
- Shojaeefard, M.; Tahani, M.; Ehghaghi, M. Numerical study of the effects of some geometric characteristics of a centrifugal pump impeller that pumps a viscous fluid. Comput. Fluids 2012, 60, 61–70. [Google Scholar] [CrossRef]
- Yuan, S.; Huang, Q.; Zhang, J.; Zhang, X. The effect of blade outlet angle on the performance of chemical centrifugal pumps. J. Drain. Irrig. Mach. Eng. 2019, 37, 185–191. [Google Scholar]
- Cao, W.; Zhang, Y.; Yao, L. Influence of blade outlet angle on performance of centrifugal pump and correction of slip coefficient. J. Drain. Irrig. Mach. Eng. 2017, 35, 755–760; 773. [Google Scholar]
- Zhou, L.; Shi, W.; Li, W.; Agarwal, R. Numerical and experimental study of axial force and hydraulic performance in a deep-well centrifugal pump with different impeller rear shroud radius. ASME J. Fluids Eng. 2013, 135, 104501–104508. [Google Scholar] [CrossRef]
- Chakraborty, S.; Pandey, K.M.; Roya, B. Numerical analysis on effects of blade number variations on performance of centrifugal pumps with various rotational speeds. Int. J. Curr. Eng. Technol. 2012, 2, 143–152. [Google Scholar]
- Elsheshtawy, H.A. Numerical Study of Slip Factor in Centrifugal Pumps and Study Factors Affecting its Performance. In Proceedings of the 1st International Conference on Mechanical Engineering and Material Science; Atlantis Press: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef] [Green Version]
- Fard, M.; Boyaghchi, F. Studies on the Influence of Various Blade Outlet Angles in a Centrifugal Pump when Handling Viscous Fluids. J. Appl. Sci. 2007, 4, 718. [Google Scholar] [CrossRef]
- Mohammadi, N.; Fakharzadeh, M. Analysis of effect of impeller geometry including blade outlet angle on the performance of multi-pressure pumps: Simulation and experiment. Mechanika 2017, 23, 107–119. [Google Scholar] [CrossRef]
- Shi, W.; Zhou, L.; Lu, W.; Pei, P.; Lang, T. Numerical prediction and performance experiment in a deep-well centrifugal pump with different impeller outlet width. Chin. J. Mech. Eng. 2013, 26, 46–52. [Google Scholar] [CrossRef]
- Shi, W.; Li, H.; Wang, C.; Xu, Y. Numerical calculation of inlet pre-rotation of low specific speed centrifugal pump. J. Drain. Irrig. Mach. Eng. 2014, 32, 652–657. [Google Scholar]
- Yang, Y.; Zhou, L.; Shi, W.; He, Z.; Han, Y.; Xiao, Y. Interstage difference of pressure pulsation in a three-stage electrical submersible pump. J. Pet. Sci. Eng. 2020, 196, 107653. [Google Scholar] [CrossRef]
- Zhou, L.; Shi, W.; Lu, W.; Hu, B.; Wu, S. Numerical investigations and performance experiments of a deep-well centrifugal pump with different diffusers. ASME J. Fluids Eng. 2012, 134, 071102. [Google Scholar] [CrossRef]
- Yang, A.; Lang, D.; Li, G.; Chen, E.; Dai, R. Numerical Research about Influence of Blade Outlet Angle on Flow-Induced Noise and Vibration for Centrifugal Pump. Adv. Mech. Eng. 2014, 6, 583482. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, L.; Li, W.; Shi, W.; Wang, C. PIV validation of different turbulence models used for numerical simulation of a centrifugal pump diffuser. Eng. Comput. 2018, 35, 2–17. [Google Scholar] [CrossRef]
- Jin, Z.; Qiu, C.; Jiang, C.; Wu, J.; Qian, J. Effect of valve core shapes on cavitation flow through a sleeve regulating valve. J. Zhejiang Univ. Sci. A 2020, 21, 1–14. [Google Scholar] [CrossRef]
- Qian, J.; Li, X.; Wu, Z.; Jin, Z.; Sunden, B. A comprehensive review on liquid-liquid two-phase flow in microchannel: Flow pattern and mass transfer. Microfluid. Nanofluid. 2019, 23, 116. [Google Scholar] [CrossRef]
- Zhou, L.; Deshpande, K.; Zhang, X.; Agarwal, R. Process simulation of Chemical Looping Combustion using ASPEN Plus for a mixture of biomass and coal with various oxygen carriers. Energy 2020, 195, 116955. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Jiang, X.; Pang, Q.; Ye, D. Vibration in a Multistage Centrifugal Pump under Varied Conditions. Shock Vib. 2019, 3, 2057031. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, L.; Shi, W.; Li, W.; Wang, C.; Ye, D. Numerical analysis and performance experiment of electric submersible pump with different diffuser vanes number. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 89. [Google Scholar] [CrossRef]
- Qian, J.; Li, X.; Wu, Z.; Jin, Z.; Zhang, J.; Sunden, B. Slug formation analysis of liquid-liquid two-phase flow in T-junction microchannels. J. Sci. Eng. Appl. 2019, 11, 051017. [Google Scholar] [CrossRef]
- Zhou, L.; Han, C.; Bai, L.; Li, W.; El-Emam, M.; Shi, W. CFD-DEM Bidirectional Coupling Simulation and Experimental Investigation of Particle Ejections and Energy Conversion in a Spouted Bed. Energy 2020, 118672, in press. [Google Scholar] [CrossRef]
- Qian, J.; Hou, C.; Li, X.; Jin, Z. Actuation Mechanism of Microvalves: A Review. Micromachines 2020, 11, 172. [Google Scholar] [CrossRef] [Green Version]



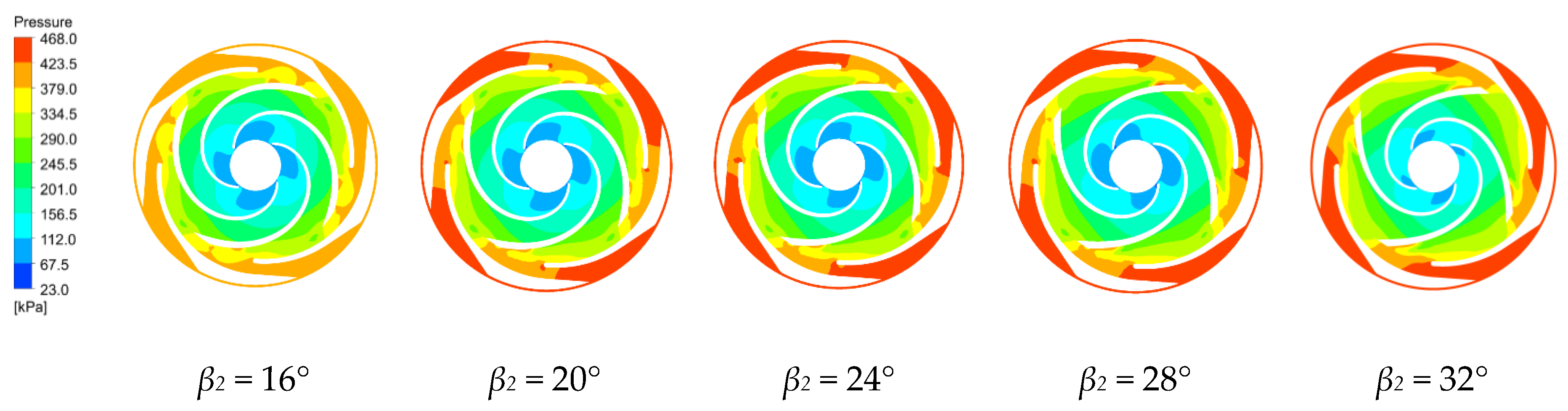


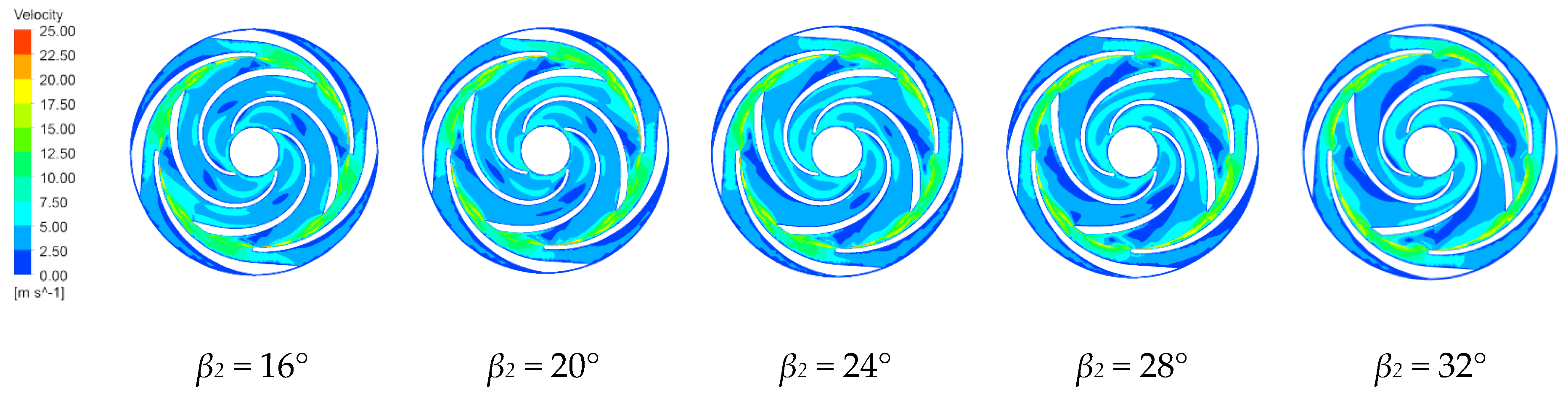
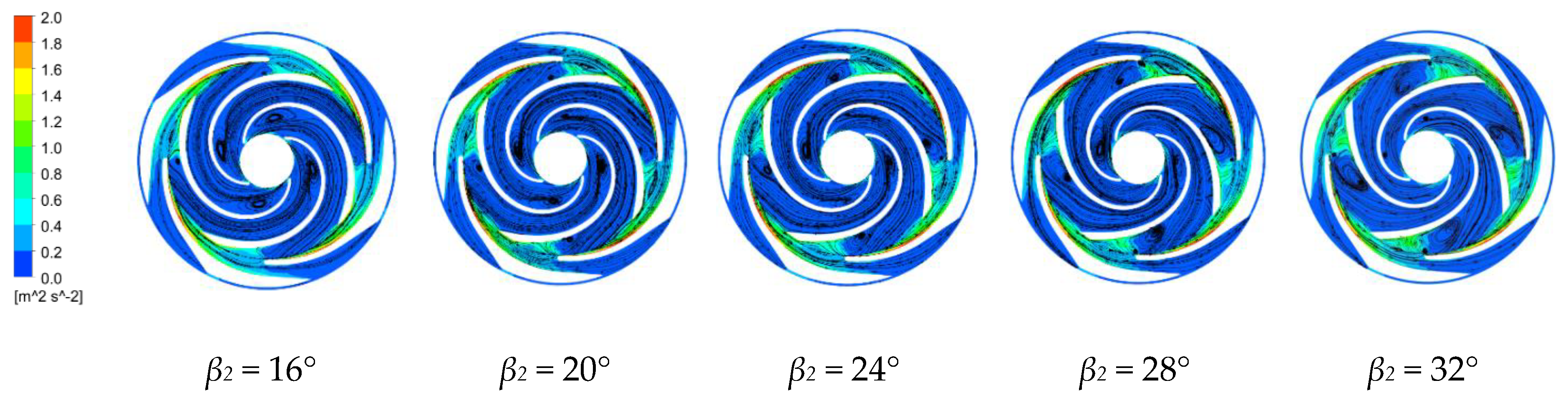

| Design Parameters | Value |
|---|---|
| Rotating speed | 2900 r/min |
| Design flow rate | 10 m3/h |
| Head | 165 m |
| Inlet diameter | 54 mm |
| Outlet width | 6.5 mm |
| Number of blades | 4 |
| Impeller outer diameter | 152 mn |
| Blade wrapping angle | 180° |
| Stages number | 6 |
| Number of Elements | Head (m) | Efficiency (%) | Power (kW) |
|---|---|---|---|
| 1,546,562 | 166.36 | 58.62 | 8.3 |
| 2,412,168 | 166.21 | 58.41 | 8.2 |
| 3,451,566 | 165.52 | 57.85 | 8.4 |
| 4,313,151 | 165.43 | 57.75 | 8.7 |
| 5,255,682 | 165.46 | 57.78 | 8.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, G.; Chen, Q.; Zhou, L.; Pan, B.; Zhu, Y. Effect of Blade Outlet Angle on the Flow Field and Preventing Overload in a Centrifugal Pump. Micromachines 2020, 11, 811. https://doi.org/10.3390/mi11090811
Peng G, Chen Q, Zhou L, Pan B, Zhu Y. Effect of Blade Outlet Angle on the Flow Field and Preventing Overload in a Centrifugal Pump. Micromachines. 2020; 11(9):811. https://doi.org/10.3390/mi11090811
Chicago/Turabian StylePeng, Guangjie, Qiang Chen, Ling Zhou, Bo Pan, and Yong Zhu. 2020. "Effect of Blade Outlet Angle on the Flow Field and Preventing Overload in a Centrifugal Pump" Micromachines 11, no. 9: 811. https://doi.org/10.3390/mi11090811






