Electric Field Induced Electrorotation of 2D Perovskite Microplates
Abstract
:1. Introduction
2. Materials and Methods
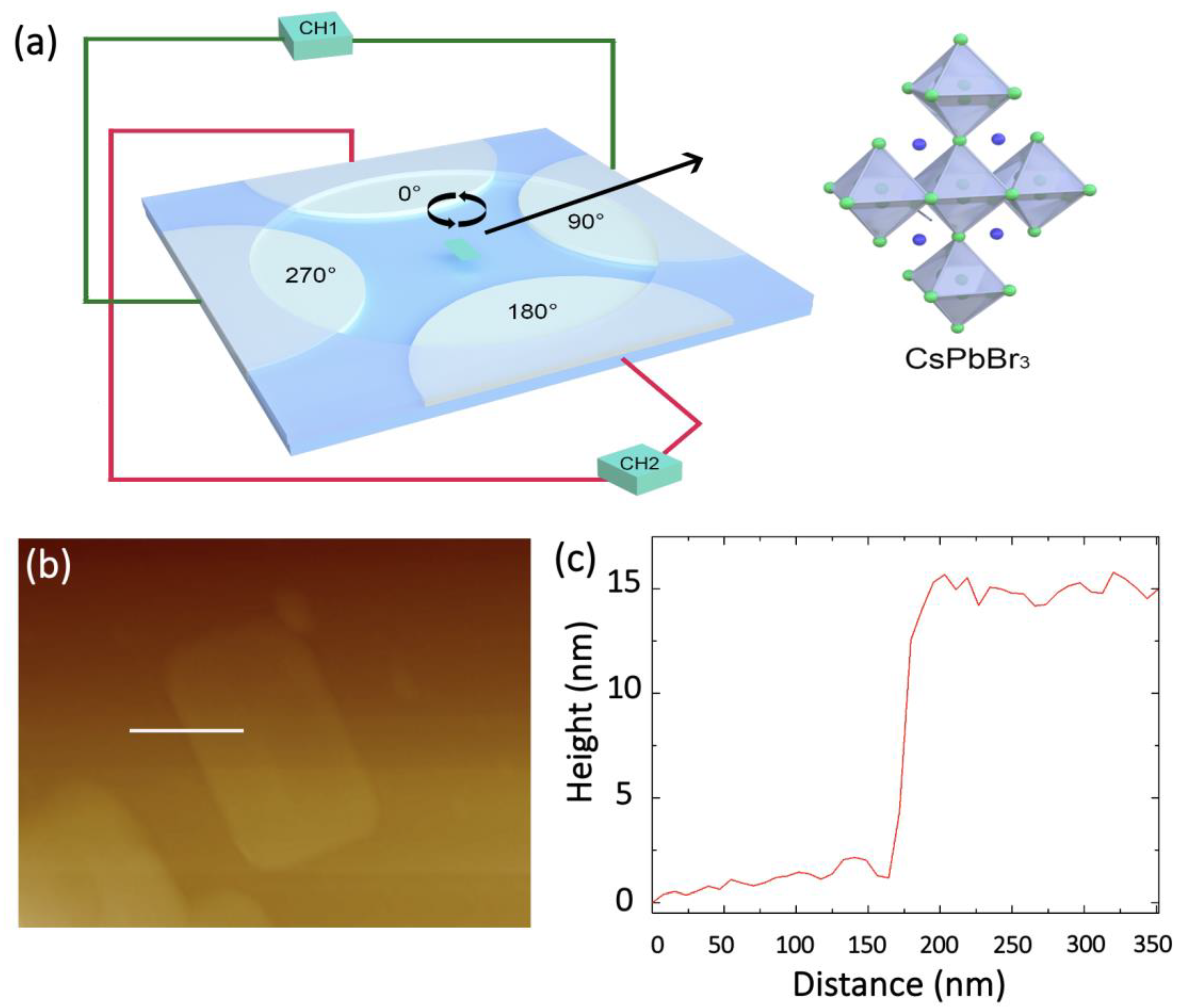
2.1. Synthesis of CsPbBr3 Microplates
2.2. Device Characterization
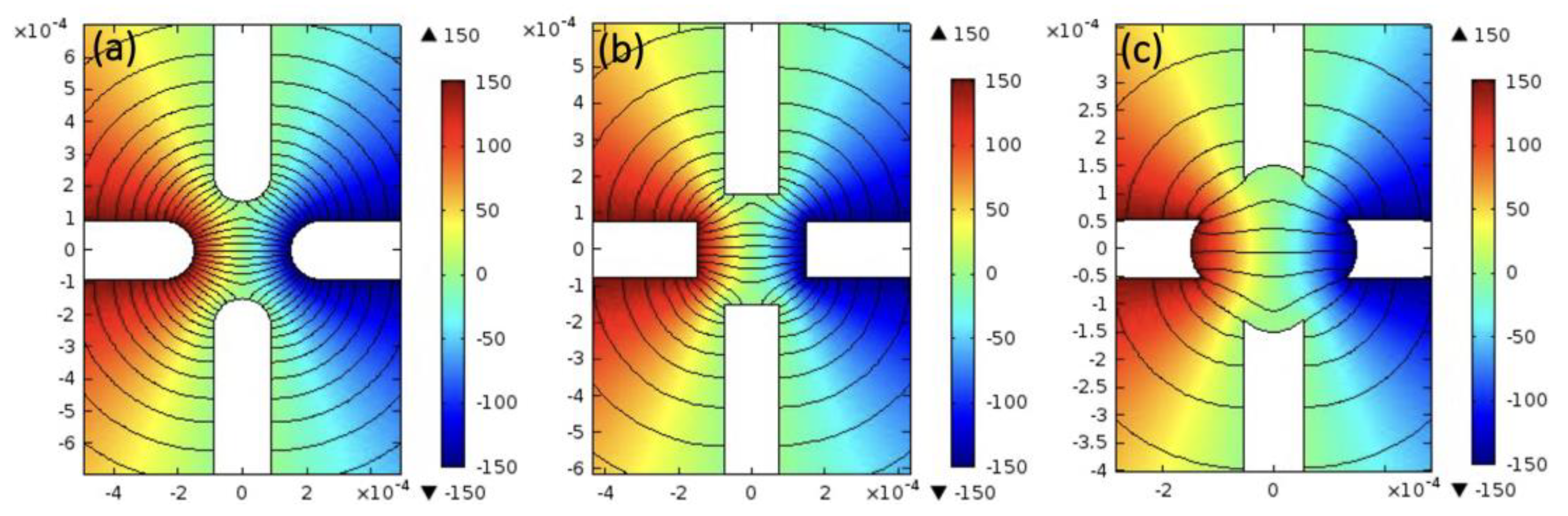
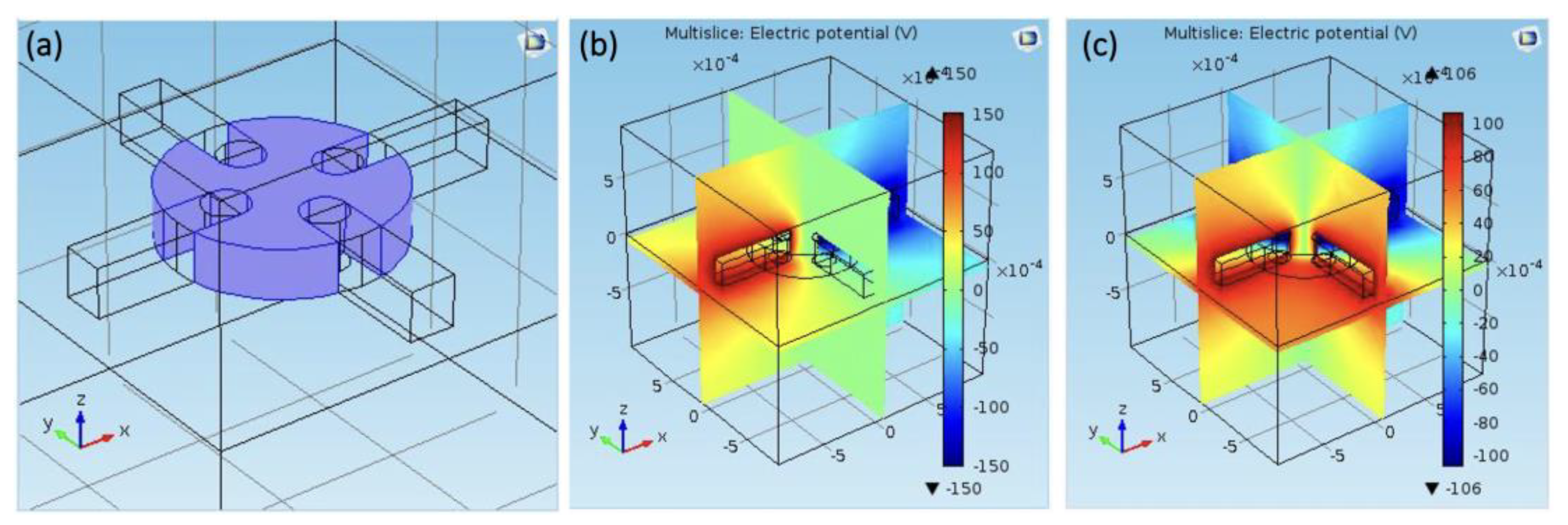
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Tu, Y.F.; Peng, F.; Wilson, D.A. Motion manipulation of micro- and nanomotors. Adv. Mater. 2017, 29, 1701970. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Zhang, B.; Wang, L.; Huang, G.; Mei, Y. Tubular micro/nanomachines: From the basics to recent advances. Adv. Funct. Mater. 2018, 28, 1705872. [Google Scholar] [CrossRef]
- Sipova-Jungova, H.; Andren, D.; Jones, S.; Kall, M. Nanoscale inorganic motors driven by light: Principles, realizations, and opportunities. Chem. Rev. 2020, 120, 269–287. [Google Scholar] [CrossRef] [PubMed]
- De Ávila, B.E.F.; Angsantikul, P.; Li, J.; Lopez-Ramirez, M.A.; Ramirez-Herrera, D.E.; Thamphiwatana, S.; Chen, C.; Delezuk, J.; Samakapiruk, R.; Ramez, V.; et al. Micromotor-enabled active drug delivery for in vivo treatment of stomach infection. Nat. Commun. 2017, 8, 272. [Google Scholar] [CrossRef] [Green Version]
- De Avila, B.E.F.; Angsantikul, P.; Li, J.; Gao, W.; Zhang, L.; Wang, J. Micromotors go in vivo: From test tubes to live animals. Adv. Funct. Mater. 2018, 28, 1705640. [Google Scholar] [CrossRef]
- Jurado-Sanchez, B.; Wang, J. Micromotors for environmental applications: A review. Environ. Sci. Nano 2018, 5, 1530–1544. [Google Scholar] [CrossRef]
- Dong, R.F.; Cai, Y.P.; Yang, Y.R.; Gao, W.; Ren, B.Y. Photocatalytic micro/nanomotors: From construction to applications. Acc. Chem. Res. 2018, 51, 1940–1947. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guix, M.; Mayorga-Martinez, C.C.; Merkoci, A. Nano/micromotors in (bio) chemical science applications. Chem. Rev. 2014, 114, 6285–6322. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, X.; Xu, X.; Xin, H.; Zhang, Y.; Li, B. Red-blood-cell waveguide as a living biosensor and micromotor. Adv. Funct. Mater. 2019, 29, 1905568. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, C.; Wu, J.; Ju, H. Bubble-propelled jellyfish-like micromotors for DNA sensing. ACS Appl. Mater. Interfaces 2019, 11, 13581–13588. [Google Scholar] [CrossRef] [PubMed]
- Fan, D.L.; Zhu, F.Q.; Cammarata, R.C.; Chien, C.L. Controllable high-speed rotation of nanowires. Phys. Rev. Lett. 2005, 94, 247208. [Google Scholar] [CrossRef]
- Li, T.; Li, J.; Morozov, K.I.; Wu, Z.; Xu, T.; Rozen, I.; Leshansky, A.M.; Li, L.; Wang, J. Highly efficient freestyle magnetic nanoswimmer. Nano Lett. 2017, 17, 5092–5098. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, S.; Soler, L.; Katuri, J. Chemically powered micro- and nanomotors. Angew. Chem. Int. Edit. 2015, 54, 1414–1444. [Google Scholar] [CrossRef] [PubMed]
- Sahore, V.; Kreidermacher, A.; Khan, F.Z.; Fritsch, I. Visualization and measurement of natural convection from electrochemically-generated density gradients at concentric microdisk and ring electrodes in a microfluidic system. J. Electrochem. Soc. 2016, 163, H3135–H3144. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, W.; Bai, L.; Gentekos, D.T.; Hoyos, M.; Mallouk, T.E. Density and shape effects in the acoustic propulsion of bimetallic nanorod motors. ACS Nano 2016, 10, 4763–4769. [Google Scholar] [CrossRef]
- Cao, Q.L.; Fan, Q.; Chen, Q.; Liu, C.T.; Han, X.T.; Li, L. Recent advances in manipulation of micro- and nano-objects with magnetic fields at small scales. Mater. Horiz. 2020, 7, 638–666. [Google Scholar] [CrossRef]
- Gu, Y.; Kornev, K.G. Ferromagnetic nanorods in applications to control of the in-plane anisotropy of composite films and for in situ characterization of the film rheology. Adv. Funct. Mater. 2016, 26, 3796–3808. [Google Scholar] [CrossRef]
- Villa, K.; Pumera, M. Fuel-free light-driven micro/nanomachines: Artificial active matter mimicking nature. Chem. Soc. Rev. 2019, 48, 4966–4978. [Google Scholar] [CrossRef] [PubMed]
- Cao, F.; Yu, D.; Gu, Y.; Chen, J.; Zeng, H. Novel optoelectronic rotors based on orthorhombic CsPb (Br/I) 3 nanorods. Nanoscale 2019, 11, 3117–3122. [Google Scholar] [CrossRef] [PubMed]
- Chen, H. Controllable fast and slow light in photonic-molecule optomechanics with phonon pump. Micromachines 2021, 12, 1074. [Google Scholar] [CrossRef] [PubMed]
- Roche, J.; Carrara, S.; Sanchez, J.; Lannelongue, J.; Loget, G.; Bouffier, L.; Fischer, P.; Kuhn, A. Wireless powering of e-swimmers. Sci. Rep. 2014, 4, 6705. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farain, K.; Esfandiar, A.; Moshfegh, A.Z. Universal rotation of nanowires in static uniform electric fields in viscous dielectric liquids. Appl. Phys. Lett. 2018, 113, 063101. [Google Scholar] [CrossRef]
- Farain, K.; Esfandiar, A.; Moshfegh, A.Z. Shooting at the nanoscale: Collection and acceleration of nanowires with an external electric field. Appl. Phys. Lett. 2019, 114, 013102. [Google Scholar] [CrossRef]
- Fan, D.; Yin, Z.; Cheong, R.; Zhu, F.Q.; Cammarata, R.C.; Chien, C.L.; Levchenko, A. Subcellular-resolution delivery of a cytokine through precisely manipulated nanowires. Nat. Nanotechnol. 2010, 5, 545–551. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Fan, D. Visible light-gated reconfigurable rotary actuation of electric nanomotors. Sci. Adv. 2018, 4, eaau0981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liang, Z.X.; Teal, D.; Fan, D.L. Light programmable micro/nanomotors with optically tunable in-phase electric polarization. Nat. Commun. 2019, 10, 5275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akin, C.; Yi, J.; Feldman, L.C.; Durand, C.; Hus, S.M.; Li, A.-P.; Filler, M.A.; Shan, J.W. Contactless determination of electrical conductivity of one-dimensional nanomaterials by solution-based electro-orientation spectroscopy. ACS Nano 2015, 9, 5405–5412. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Tutuncuoglu, G.; Mohabir, A.; Liu, L.; Feldman, L.C.; Filler, M.A.; Shan, J.W. Contactless electrical and structural characterization of semiconductor nanowires with axially modulated doping profiles. Small 2019, 15, 1805140. [Google Scholar] [CrossRef] [PubMed]
- Li, L.Q.; Wang, J.Y.; Li, T.L.; Song, W.P.; Zhang, G.Y. A unified model of drag force for bubble-propelled catalytic micro/nano-motors with different geometries in low reynolds number flows. J. Appl. Phys. 2015, 117, 104308. [Google Scholar] [CrossRef]
- Novotny, F.; Wang, H.; Pumera, M. Nanorobots: Machines squeezed between molecular motors and micromotors. Chem 2020, 6, 867–884. [Google Scholar] [CrossRef]
- Beladi-Mousavi, S.M.; Khezri, B.; Matejkova, S.; Sofer, Z.; Pumera, M. Supercapacitors in motion: Autonomous microswimmers for natural-resource recovery. Angew. Chem. Int. Ed. 2019, 58, 13340–13344. [Google Scholar] [CrossRef] [PubMed]
- Kummer, M.P.; Abbott, J.J.; Kratochvil, B.E.; Borer, R.; Sengul, A.; Nelson, B.J. Octomag: An electromagnetic system for 5-dof wireless micromanipulation. IEEE Trans. Robot. 2010, 26, 1006–1017. [Google Scholar] [CrossRef]
- Enachi, M.; Guix, M.; Postolache, V.; Ciobanu, V.; Fomin, V.M.; Schmidt, O.G.; Tiginyanu, I. Light-induced motion of microengines based on microarrays of TiO2 nanotubes. Small 2016, 12, 5497–5505. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Su, Y.; Zhang, H.; Dong, B. Light-powered direction-controlled micropump. Nano Res. 2018, 11, 1810–1821. [Google Scholar] [CrossRef]
- Gai, M.; Frueh, J.; Hu, N.; Si, T.; Sukhorukov, G.B.; He, Q. Self-propelled two dimensional polymer multilayer plate micromotors. Phys. Chem. Chem. Phys. 2016, 18, 3397–3401. [Google Scholar] [CrossRef] [PubMed]
- Hu, N.; Zhang, B.; Gai, M.; Zheng, C.; Frueh, J.; He, Q. Forecastable and guidable bubble-propelled microplate motors for cell transport. Macromol. Rapid Commun. 2017, 38, 1600795. [Google Scholar] [CrossRef] [PubMed]
- Cohen, K.J.; Rubinstein, B.Y.; Kenneth, O.; Leshansky, A.M. Unidirectional propulsion of planar magnetic nanomachines. Phys. Rev. Appl. 2019, 12, 014025. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.F.; Shinde, A.; Wang, L.; Ye, C.; Zeng, M.X.; Yan, Q.; Lin, P.C.; Chen, Y.; Cheng, Z.D. Rainbows in a vial: Controlled assembly of 2D colloids in two perpendicular external fields. 2D Mater. 2019, 6, 025031. [Google Scholar] [CrossRef]
- Piazza, R. Thermophoresis: Moving particles with thermal gradients. Soft Matter 2008, 4, 1740–1744. [Google Scholar] [CrossRef]
- Shinde, A.; Huang, D.L.; Saldivar, M.; Xu, H.F.; Zeng, M.X.; Okeibunor, U.; Wang, L.; Mejia, C.; Tin, P.; George, S.; et al. Growth of colloidal nanoplate liquid crystals using temperature gradients. ACS Nano 2019, 13, 12461–12469. [Google Scholar] [CrossRef] [PubMed]
- Son, C.H.; Ji, B.Q.; Park, J.Y.; Feng, J.; Kim, S. A magnetically actuated superhydrophobic ratchet surface for droplet manipulation. Micromachines 2021, 12, 325. [Google Scholar] [CrossRef] [PubMed]
- Zeng, M.X.; Huang, D.L.; Wang, P.M.; King, D.; Peng, B.L.; Luo, J.H.; Lei, Q.; Zhang, L.C.; Wang, L.; Shinde, A.; et al. Autonomous catalytic nanomotors based on 2D magnetic nanoplates. ACS Appl. Nano Mater. 2019, 2, 1267–1273. [Google Scholar] [CrossRef]
- Huo, C.; Liu, X.; Wang, Z.; Song, X.; Zeng, H. High-Performance low-voltage-driven phototransistors through CsPbBr3–2D crystal van der Waals heterojunctions. Adv. Opt. Mater. 2018, 6, 1800152. [Google Scholar] [CrossRef]
- Liu, X.; Yu, D.; Huo, C.; Song, X.; Gao, Y.; Zhang, S.; Zeng, H. A perovskite light-emitting device driven by low-frequency alternating current voltage. Adv. Opt. Mater. 2018, 6, 1800206. [Google Scholar] [CrossRef]
- Liu, X.; Yu, D.; Song, X.; Zeng, H. Metal halide perovskites: Synthesis, ion migration, and application in field-effect transistors. Small 2018, 14, 1801460. [Google Scholar] [CrossRef] [PubMed]
- Gu, Z.K.; Zhou, Z.H.; Huang, Z.D.; Wang, K.; Cai, Z.R.; Hu, X.T.; Li, L.H.; Li, M.Z.; Zhao, Y.S.; Song, Y.L. Controllable growth of high-quality inorganic perovskite microplate arrays for functional optoelectronics. Adv. Mater. 2020, 32, 1908006. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tan, X.; Liu, Z.; Ye, H.; Sun, B.; Shi, T.; Tang, Z.; Liao, G. Boosting the efficiency of carbon-based planar CsPbBr3 perovskite solar cells by a modified multistep spin-coating technique and interface engineering. Nano Energy 2019, 56, 184–195. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Wu, Q.; Cao, F.; Yang, D.; Shang, Y.; Ning, Z.; Zhang, W.; Zheng, W.; Yan, Y.; et al. Trifluoroacetate induced small-grained CsPbBr3 perovskite films result in efficient and stable light-emitting devices. Nat. Commun. 2019, 10, 665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Yu, D.; Cao, F.; Li, X.; Ji, J.; Chen, J.; Song, X.; Zeng, H. Low-voltage photodetectors with high responsivity based on solution-processed micrometer-scale all-inorganic perovskite nanoplatelets. Small 2017, 13, 1700364. [Google Scholar] [CrossRef]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Dusenbery, D.B. Living at Micro Scale: The Unexpected Physics of Being Small; Harvard University Press: Cambridge, UK, 2009. [Google Scholar]
- Gu, Y.; Zeng, H. Optically tunable quincke rotation of a nanometer-thin oblate spheroid. Phys. Rev. Fluids 2017, 2, 083701. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Hong, D.; Gao, S.; Gu, Y.; Liu, X. Electric Field Induced Electrorotation of 2D Perovskite Microplates. Micromachines 2021, 12, 1228. https://doi.org/10.3390/mi12101228
Zhou R, Hong D, Gao S, Gu Y, Liu X. Electric Field Induced Electrorotation of 2D Perovskite Microplates. Micromachines. 2021; 12(10):1228. https://doi.org/10.3390/mi12101228
Chicago/Turabian StyleZhou, Ruifu, Daobiao Hong, Siyu Gao, Yu Gu, and Xuhai Liu. 2021. "Electric Field Induced Electrorotation of 2D Perovskite Microplates" Micromachines 12, no. 10: 1228. https://doi.org/10.3390/mi12101228
APA StyleZhou, R., Hong, D., Gao, S., Gu, Y., & Liu, X. (2021). Electric Field Induced Electrorotation of 2D Perovskite Microplates. Micromachines, 12(10), 1228. https://doi.org/10.3390/mi12101228





