Effects of Microscopic Properties on Macroscopic Thermal Conductivity for Convective Heat Transfer in Porous Materials
Abstract
:1. Introduction
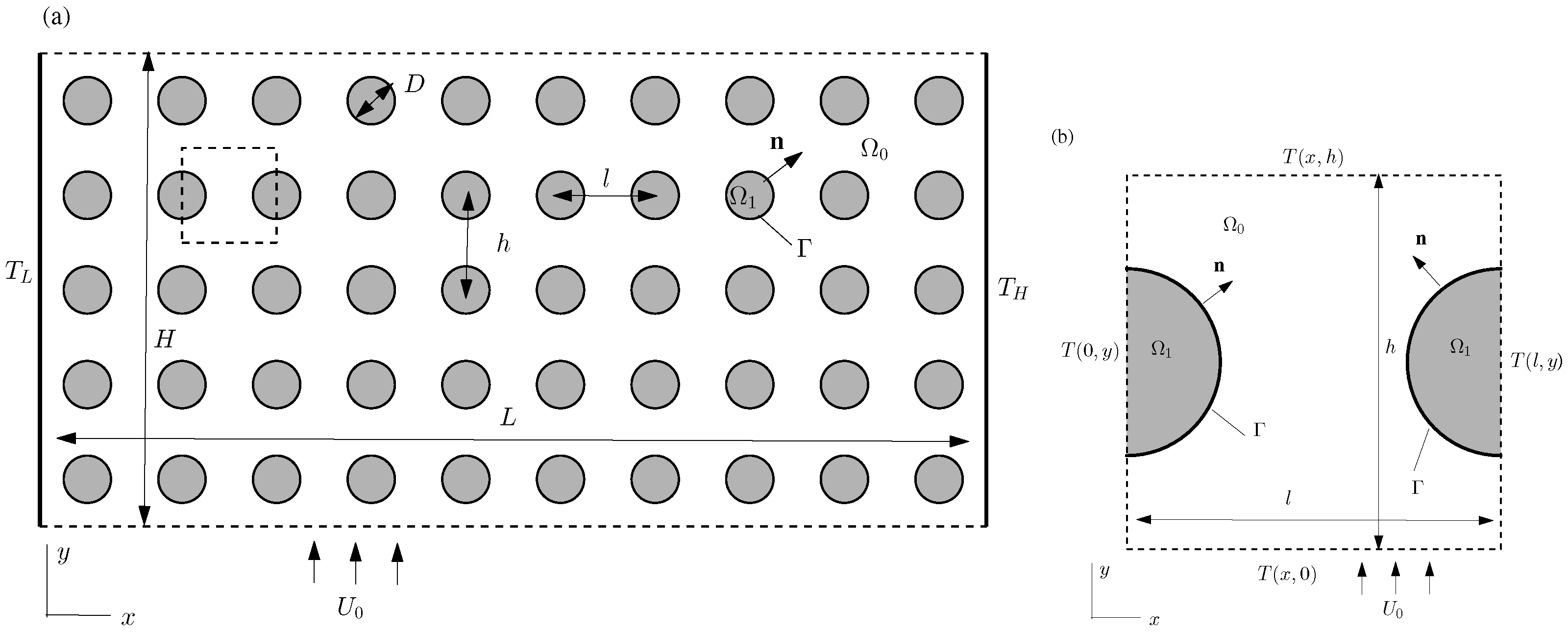
2. Governing Equations and Boundary Conditions for Periodic Unit
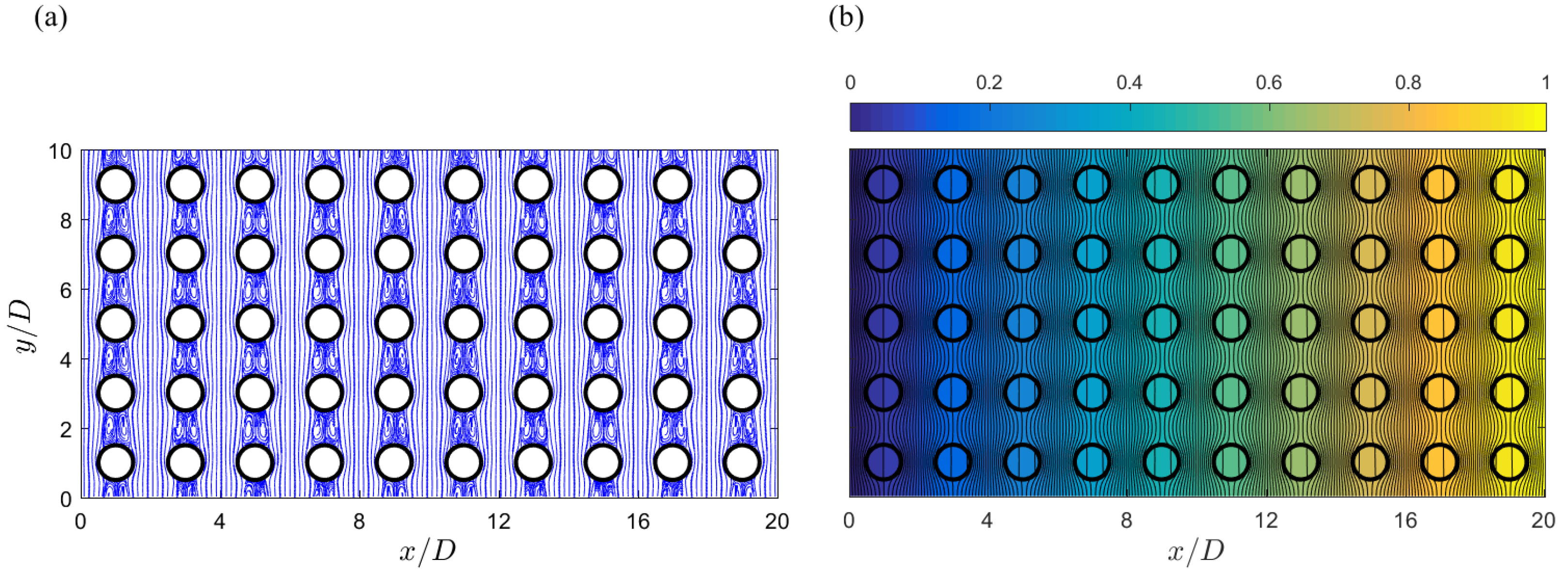
3. Numerical Validation of the Periodic Relations among Units
4. Simulation Results and Discussion
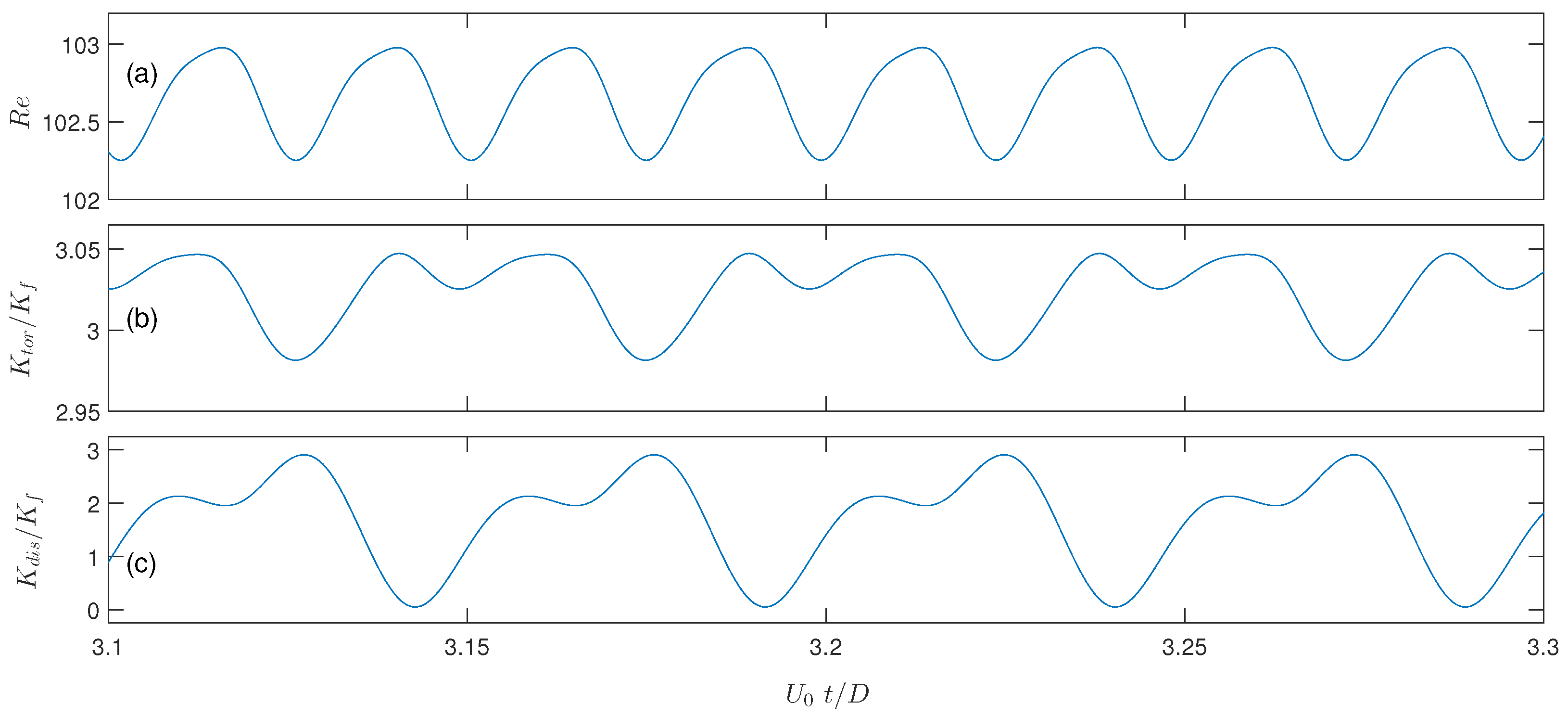
4.1. Effects of the Aspect Ratio and Reynolds Number
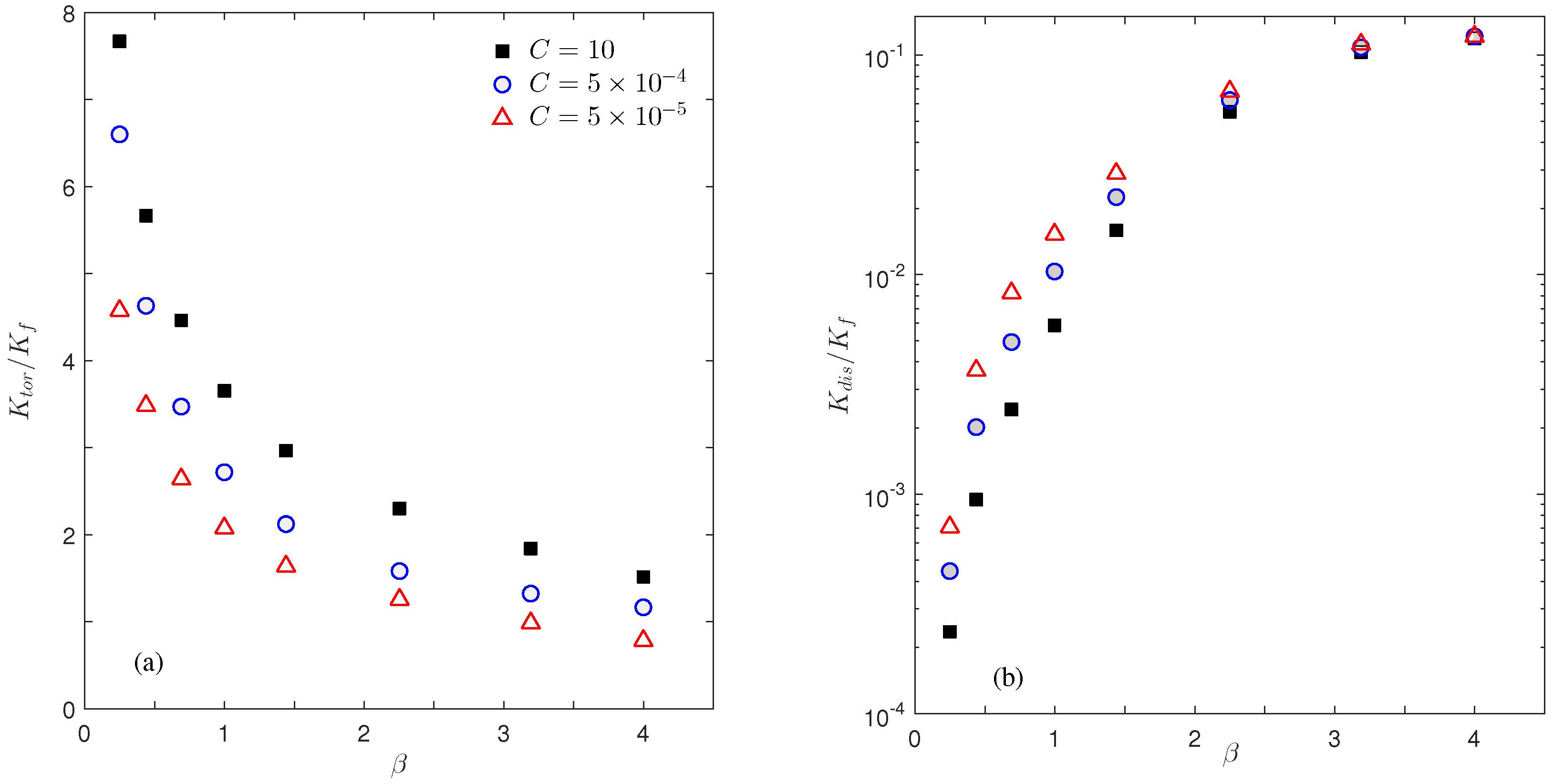
4.2. Effect of the Interfacial Conductance C
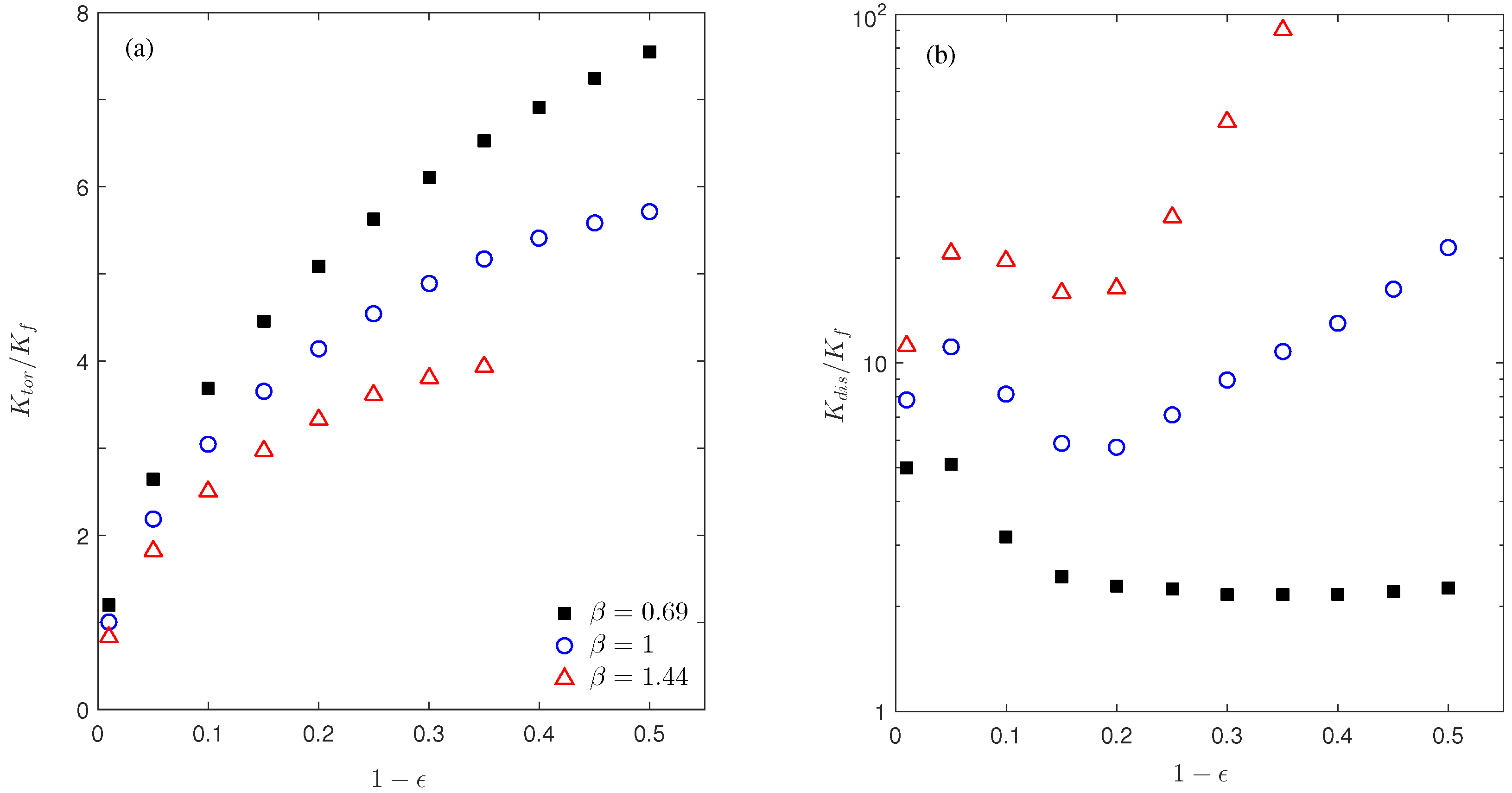
4.3. Effect of the Porosity
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Ingham, D.B.; Pop, I. Transport Phenomena in Porous Media III; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Ottenhall, A.; Illergard, J.; Ek, M. Water Purification Using Functionalized Cellulosic Fibers with Nonleaching Bacteria Adsorbing Properties. Environ. Sci. Technol. 2017, 51, 7616–7623. [Google Scholar] [CrossRef]
- Boules, D.; Sharqawy, M.H.; Ahmed, W.H. Enhancement of heat transfer from a horizontal cylinder wrapped with whole and segmented layers of metal foam. Int. J. Heat Mass Transf. 2021, 165, 120675. [Google Scholar] [CrossRef]
- Bianco, N.; Busiello, S.; Iasiello, M.; Mauro, G.M. Finned heat sinks with phase change materials and metal foams: Pareto optimization to address cost and operation time. Appl. Therm. Eng. 2021, 197, 117436. [Google Scholar] [CrossRef]
- Li, Y.; Gong, L.; Ding, B.; Xu, M.; Joshi, Y. Thermal management of power electronics with liquid cooled metal foam heat sink. Int. J. Therm. Sci. 2021, 163, 106796. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, S. Simulations of paraffine melting inside metal foams at different gravity levels with preliminary experimental validation. J. Phys. Conf. Ser. 2020, 1599, 012008. [Google Scholar] [CrossRef]
- Fu, X.; Viskanta, R.; Gore, J. Measurement and correlation of volumetric heat transfer coeffcients of cellular ceramics. Exp. Therm. Fluid Sci. 1998, 17, 285–293. [Google Scholar]
- Wang, G.; Zhang, Z.; Wang, R.; Zhu, Z. A Review on Heat Transfer of Nanofluids by Applied Electric Field or Magnetic Field. Nanomaterials 2020, 10, 2386. [Google Scholar] [CrossRef]
- Chuan, L.; Wang, X.D.; Wang, T.H.; Yan, W.M. Fluid flow and heat transfer in microchannel heat sink based on porous fin design concept. Int. Commun. Heat Mass Transf. 2015, 65, 52–57. [Google Scholar] [CrossRef]
- Behrang, A.; Taheri, S.; Kantzas, A. A hybrid approach on predicting the effective thermal conductivity of porous and nanoporous media. Int. J. Heat Mass Transf. 2016, 98, 52–59. [Google Scholar] [CrossRef]
- Gong, L.; Wang, Y.; Cheng, X.; Zhang, R.; Zhang, H. A novel effective medium theory for modelling the thermal conductivity of porous materials. Int. J. Heat Mass Transf. 2014, 68, 295–298. [Google Scholar] [CrossRef]
- Song, Y.S.; Youn, J.R. Evaluation of effective thermal conductivity for carbon nanotube/polymer composites using control volume finite element method. Carbon 2006, 44, 710–717. [Google Scholar] [CrossRef]
- Ye, C.; Huang, H.; Fan, J.; Sum, W. Numerical Study of Heat and Moisture Transfer in Textile Materials by a Finite Volume Method. Commun. Comput. Phys. 2008, 4, 929–948. [Google Scholar]
- Chiappini, D.; Festuccia, A.; Bella, G. Coupled lattice Boltzmann finite volume method for conjugate heat transfer in porous media. Numer. Heat Transf. Part A Appl. 2018, 73, 291–306. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T.S. A lattice Boltzmann model for convection heat transfer in porous media. Numer. Heat Transf. Part B Fundam. 2005, 47, 157–177. [Google Scholar] [CrossRef]
- Liu, Q.; He, Y.L. Lattice Boltzmann simulations of convection heat transfer in porous media. Phys. A Stat. Mech. Its Appl. 2017, 465, 742–753. [Google Scholar] [CrossRef]
- Azadi, P.; Farnood, R.; Yan, N. FEM-CDEM modeling of thermal conductivity of porous pigmented coatings. Comput. Mater. Sci. 2010, 49, 392–399. [Google Scholar] [CrossRef]
- Duan, Y.; He, S.; Ganesan, P.; Gotts, J. Analysis of the horizontal flow in the advanced gas-cooled reactor. Nucl. Eng. Des. 2014, 272, 53–64. [Google Scholar] [CrossRef]
- Zhou, Y.; Yan, C.; Tang, A.M.; Duan, C.; Shengshi, D. Mesoscopic prediction on the effective thermal conductivity of unsaturated clayey soils with double porosity system. Int. J. Heat Mass Transf. 2019, 130, 747–756. [Google Scholar] [CrossRef]
- Huang, P.; Zhao, Y.; Niu, Y.; Ren, X.; Chang, M.; Sun, Y. Mesoscopic Finite Element Method of the Effective Thermal Conductivity of Concrete with Arbitrary Gradation. Adv. Mater. Sci. Eng. 2018, 2018, 2352864. [Google Scholar] [CrossRef] [Green Version]
- Kuwahara, F.; Nakayama, A.; Koyama, H. A Numerical Study of Thermal Dispersion in Porous Media. J. Heat Transf. 1996, 118, 756–761. [Google Scholar] [CrossRef]
- Yang, P.; Wen, Z.; Dou, R.; Liu, X. Effect of random structure on permeability and heat transfer characteristics for flow in 2D porous medium based on MRT lattice Boltzmann method. Phys. Lett. A 2016, 380, 2902–2911. [Google Scholar] [CrossRef]
- Jeong, N.; Choi, D.H. Estimation of the thermal dispersion in a porous medium of complex structures using a lattice Boltzmann method. Int. J. Heat Mass Transf. 2011, 54, 4389–4399. [Google Scholar] [CrossRef]
- Zhao, C.; Dai, L.; Tang, G.; Qu, Z.; Li, Z. Numerical study of natural convection in porous media (metals) using Lattice Boltzmann Methods (LBM). Int. J. Heat Fluid Flow 2010, 31, 925–1934. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, H. Pore-scale study on flow and heat transfer in 3D reconstructed porous media using micro-tomography images. Appl. Therm. Eng. 2016, 100, 602–610. [Google Scholar] [CrossRef]
- Liu, Q.; He, Y.L.; Li, Q.; Tao, W.Q. A multiple-relaxation-time lattice Boltzmann model for convection heat transfer in porous media. Int. J. Heat Mass Transf. 2014, 73, 761–775. [Google Scholar] [CrossRef] [Green Version]
- Ren, Q.; Chan, C.L. Natural convection with an array of solid obstacles in an enclosure by lattice Boltzmann method on a CUDA computation platform. Int. J. Heat Mass Transf. 2016, 93, 273–285. [Google Scholar] [CrossRef]
- Jbeili, M.; Zhang, J. The Generalized Periodic Boundary Conditions for Microscopic Simulations of Heat Transfer in Heterogeneous Materials. Int. J. Heat Mass Transf. 2021, 173, 121200. [Google Scholar] [CrossRef]
- Ozgumus, T.; Mobedi, M. Effect of Pore to Throat Size Ratio on Interfacial Heat Transfer Coefficient of Porous Media. J. Heat Transf. 2015, 137, 012602. [Google Scholar] [CrossRef] [Green Version]
- Yang, P.; Wen, Z.; Dou, R.; Liu, X. Heat transfer characteristics in random porous media based on the 3D lattice Boltzmann method. Int. J. Heat Mass Transf. 2017, 109, 647–656. [Google Scholar] [CrossRef]
- Grucelski, A.; Pozorski, J. Lattice Boltzmann simulations of heat transfer in flow past a cylinder and in simple porous media. Int. J. Heat Mass Transf. 2015, 86, 139–148. [Google Scholar] [CrossRef]
- Smith, D.S.; Alzina, A.; Bourret, J.; Nait-Ali, B. Thermal conductivity of porous materials. J. Mater. Res. 2013, 28, 2260–2272. [Google Scholar] [CrossRef] [Green Version]
- Fang, W.Z.; Gou, J.; Zhang, H.; Kang, Q.; Tao, W.Q. Numerical predictions of the effective thermal conductivity for needled C/C-SiC composite materials. Numer. Heat Transf. Part A Appl. 2016, 70, 1101–1117. [Google Scholar] [CrossRef]
- Jiang, P.X.; Li, M.; Lu, T.J.; Yu, L.; Ren, Z.P. Experimental research on convection heat transfer in sintered porous plate channels. Int. J. Heat Mass Transf. 2004, 47, 2085–2096. [Google Scholar] [CrossRef]
- Wang, S.L.; Li, X.Y.; Wang, X.D.; Lu, G. Flow and heat transfer characteristics in double-layered microchannel heat sinks with porous fins. Int. Commun. Heat Mass Transf. 2018, 93, 41–47. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, Y. Effect of flow regime on convective heat transfer in porous copper manufactured by lost carbonate sintering. Int. J. Heat Fluid Flow 2019, 80, 108482. [Google Scholar] [CrossRef]
- Cengel, Y. Heat and Mass Transfer: Fundamentals and Applications; McGraw-Hill: Hoboken, NJ, USA, 2019. [Google Scholar]
- Le, G.; Oulaid, O.; Zhang, J. Counter-extrapolation method for conjugate interfaces in computational heat and mass transfer. Phys. Rev. E 2015, 91, 033306. [Google Scholar] [CrossRef]
- Jbeili, M.; Zhang, J. The Temperature Decomposition Method for Periodic Thermal Flows with Conjugate Heat Transfer. Int. J. Heat Mass Transf. 2020, 150, 119288. [Google Scholar] [CrossRef]
- Guo, K.; L, L.; Xao, G.; AuYeung, N.; Mei, R. Lattice Boltzmann method for conjugate heat and mass transfer with interfacial jump conditions. Int. J. Heat Mass Transf. 2015, 88, 306–322. [Google Scholar] [CrossRef] [Green Version]
- Patankar, S.V.; Liu, C.H.; Sparrow, E.M. Fully Developed Flow and Heat Transfer in Ducts Having Streamwise-Periodic Variations of Cross-Sectional Area. ASME J. Heat Transf. 1977, 99, 180–186. [Google Scholar] [CrossRef]
- Stalio, E.; Piller, M. Direct Numerical Simulation of Heat Transfer in Converging-Diverging Wavy Channels. J. Heat Transf. 2007, 129, 769. [Google Scholar] [CrossRef]
- Harikrishnan, S.; Tiwari, S. Unsteady Flow and Heat Transfer Characteristics of Primary and Secondary Corrugated Channels. J. Heat Transf. 2020, 142, 031803. [Google Scholar] [CrossRef]
- Wang, Z.; Shang, H.; Zhang, J. Lattice Boltzmann simulations of heat transfer in fully developed periodic incompressible flows. Phys. Rev. E 2017, 95, 063309. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J. Simulating Heat Transfer through Periodic Structures with Different Wall Temperatures: A Temperature Decomposition Method. ASME J. Heat Transf. 2018, 140, 112002. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Doolen, G.D. A Novel Thermal Model for the Lattice Boltzmann Method in Incompressible Limit. J. Comput. Phys. 1998, 146, 282–300. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific Publishing: Singapore, 2013. [Google Scholar]
- Zhang, J. Lattice Boltzmann method for microfluidics: Models and applications. Microfluid. Nanofluid. 2010, 10, 1–28. [Google Scholar] [CrossRef]
- Wang, Z.; Colin, F.; Le, G.; Zhang, J. Counter-Extrapolation Method for Conjugate Heat and Mass Transfer with Interfacial Discontinuity. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2231–2258. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Whitaker, S. Diffusion and dispersion in porous media. AIChE J. 1967, 13, 420–427. [Google Scholar] [CrossRef]
- Whitaker, S. Advances in theory of fluid motion in porous media. Ind. Eng. Chem. 1969, 61, 14–28. [Google Scholar] [CrossRef]
- d’Hueppe, A. Heat Transfer Modeling at an Interface between a Porous Medium and a Free Region. Ph.D. Thesis, Ecole Centrale Paris, Paris, France, 2011. [Google Scholar]
- de Lemos, M.J.S. Turbulence in Porous Media: Modeling and Applications; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Yin, X.; Zhang, J. An Improved Bounce-Back Scheme for Complex Boundary Conditions in Lattice Boltzmann Method. J. Comput. Phys. 2012, 231, 4295–4303. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, X.; Zhang, J. Effects of Reynolds and Prandtl Numbers on Heat Transfer Around a Circular Cylinder by the Simplified Thermal Lattice Boltzmann Model. Commun. Comput. Phys. 2015, 17, 937–959. [Google Scholar] [CrossRef]
- Dyga, R.; Placzek, M. Efficiency of heat transfer in heat exchangers with wire mesh packing. Int. J. Heat Mass Transf. 2010, 53, 5499–5508. [Google Scholar] [CrossRef]
- Alshare, A.A.; Strykowski, P.J.; Simon, T.W. Modeling of unsteady and steady fluid flow, heat transfer and dispersion in porous media using unit cell scale. Int. J. Heat Mass Transf. 2010, 53, 2294–2310. [Google Scholar] [CrossRef]
- He, J.; Zhang, J.; Shang, H. Two-Phase Dynamic Modelling and Simulation of Transport and Reaction in Catalytic Sulfur Dioxide Converters. Ind. Eng. Chem. Res. 2019, 58, 10963–10974. [Google Scholar] [CrossRef]
- Bonnet, J.P.; Topin, F.; Tadrist, L. Flow Laws in Metal Foams: Compressibility and Pore Size Effects. Transp. Porous Media 2008, 73, 233–254. [Google Scholar] [CrossRef]
- Sumirat, I.; Ando, Y.; Shimamura, S. Theoretical consideration of the effect of porosity on thermal conductivity of porous materials. J. Porous Mater. 2006, 13, 439–443. [Google Scholar] [CrossRef]
- Zhao, C.Y. Review on thermal transport in high porosity cellular metal foams with open cells. Int. J. Heat Mass Transf. 2012, 55, 3618–3632. [Google Scholar] [CrossRef]
- Iasiello, M.; Cunsolo, S.; Bianco, N.; Chiu, W.K.S.; Naso, V. Developing thermal flow in open-cell foams. Int. J. Therm. Sci. 2017, 111, 129–137. [Google Scholar] [CrossRef]
- Suleiman, A.S.; Dukhan, N. Forced convection inside metal foam: Simulation over a long domain and analytical validation. Int. J. Therm. Sci. 2014, 86, 104–114. [Google Scholar] [CrossRef]
- Matias, A.F.V.; Coelho, R.C.V.; Andrade, J.S., Jr.; Araujo, N.A.M. Flow through time–evolving porous media: Swelling and erosion. J. Comput. Sci. 2021, 53, 101360. [Google Scholar] [CrossRef]
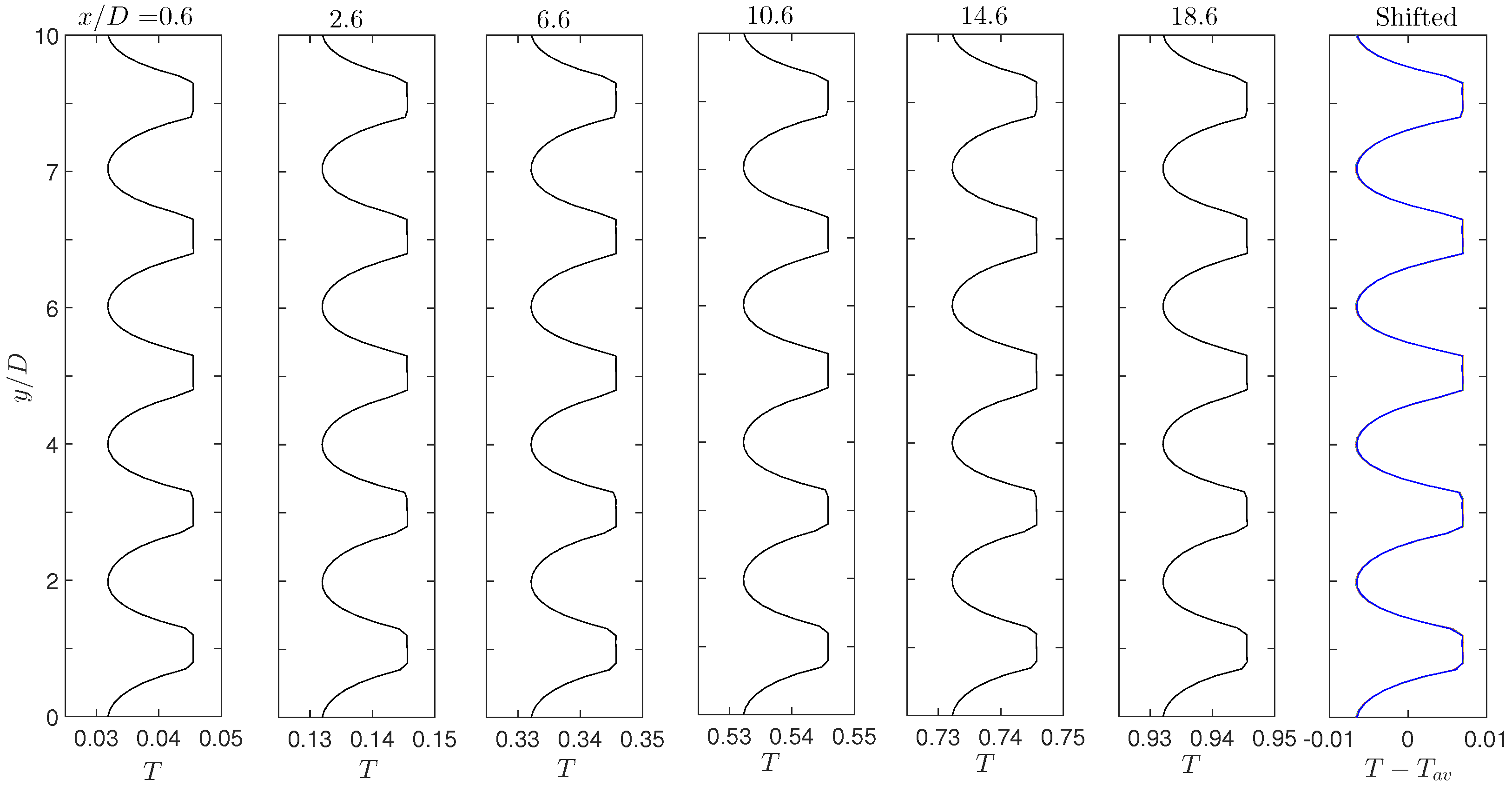




| Calculated from Simulation Results | Predicted from Equation (11) | |
|---|---|---|
| 0.6 | 0.03847 | - |
| 2.6 | 0.13857 | 0.13847 |
| 6.6 | 0.33872 | 0.33847 |
| 10.6 | 0.53881 | 0.53847 |
| 14.6 | 0.73878 | 0.73847 |
| 18.6 | 0.93860 | 0.93847 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jbeili, M.; Zhang, J. Effects of Microscopic Properties on Macroscopic Thermal Conductivity for Convective Heat Transfer in Porous Materials. Micromachines 2021, 12, 1369. https://doi.org/10.3390/mi12111369
Jbeili M, Zhang J. Effects of Microscopic Properties on Macroscopic Thermal Conductivity for Convective Heat Transfer in Porous Materials. Micromachines. 2021; 12(11):1369. https://doi.org/10.3390/mi12111369
Chicago/Turabian StyleJbeili, Mayssaa, and Junfeng Zhang. 2021. "Effects of Microscopic Properties on Macroscopic Thermal Conductivity for Convective Heat Transfer in Porous Materials" Micromachines 12, no. 11: 1369. https://doi.org/10.3390/mi12111369
APA StyleJbeili, M., & Zhang, J. (2021). Effects of Microscopic Properties on Macroscopic Thermal Conductivity for Convective Heat Transfer in Porous Materials. Micromachines, 12(11), 1369. https://doi.org/10.3390/mi12111369






