Acoustic Bessel Vortex Beam by Quasi-Three-Dimensional Reflected Metasurfaces
Abstract
:1. Introduction
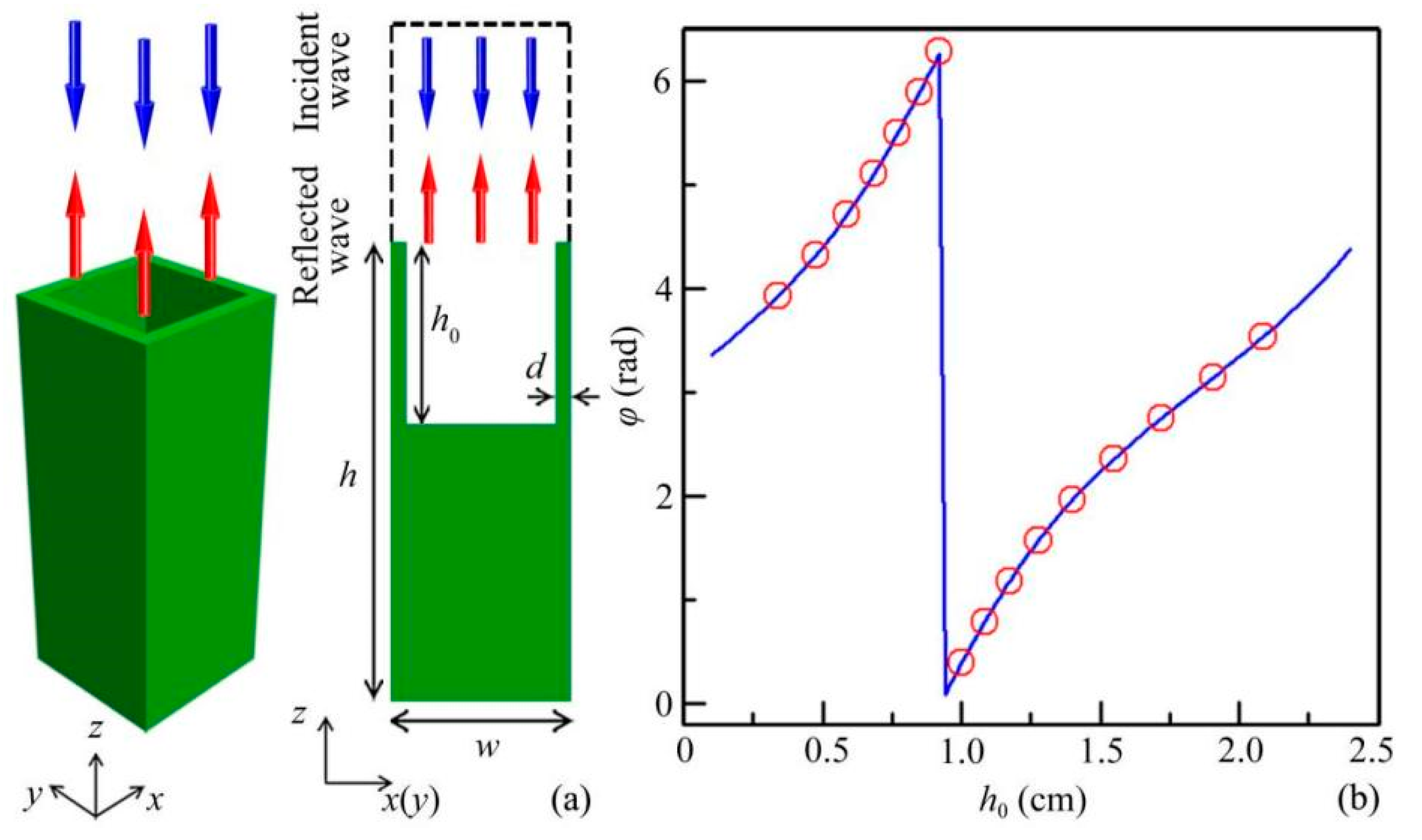
2. Design and Methods
3. Results and Discussion
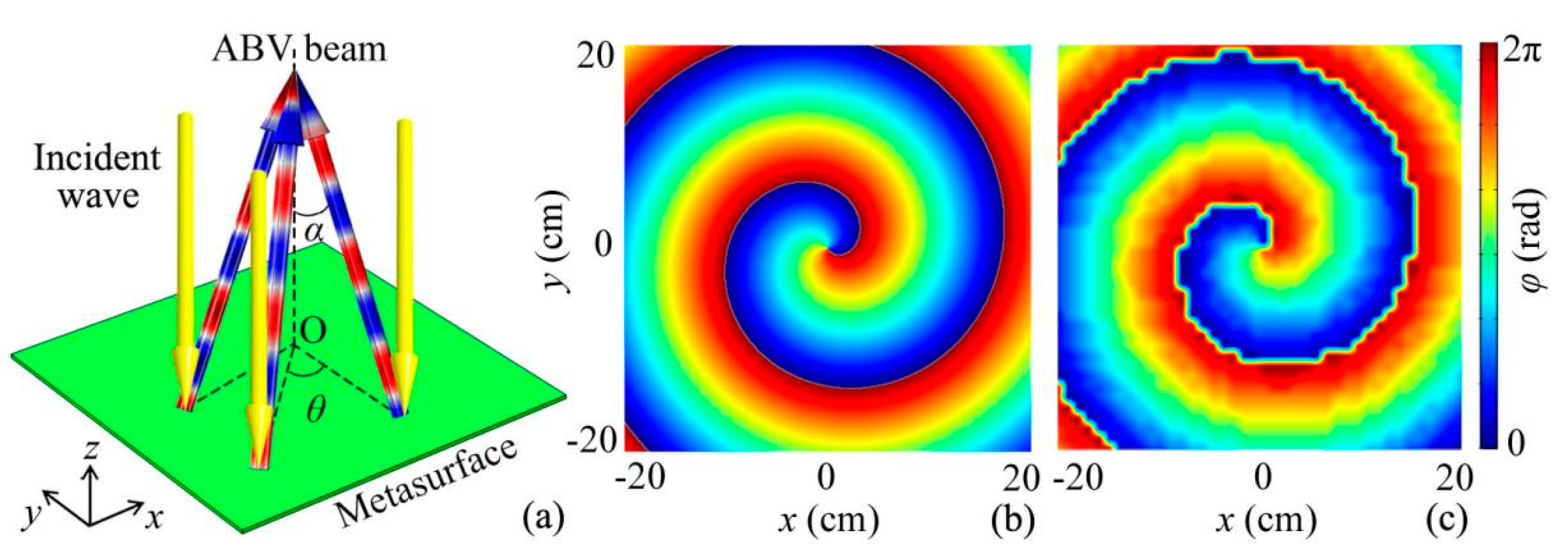
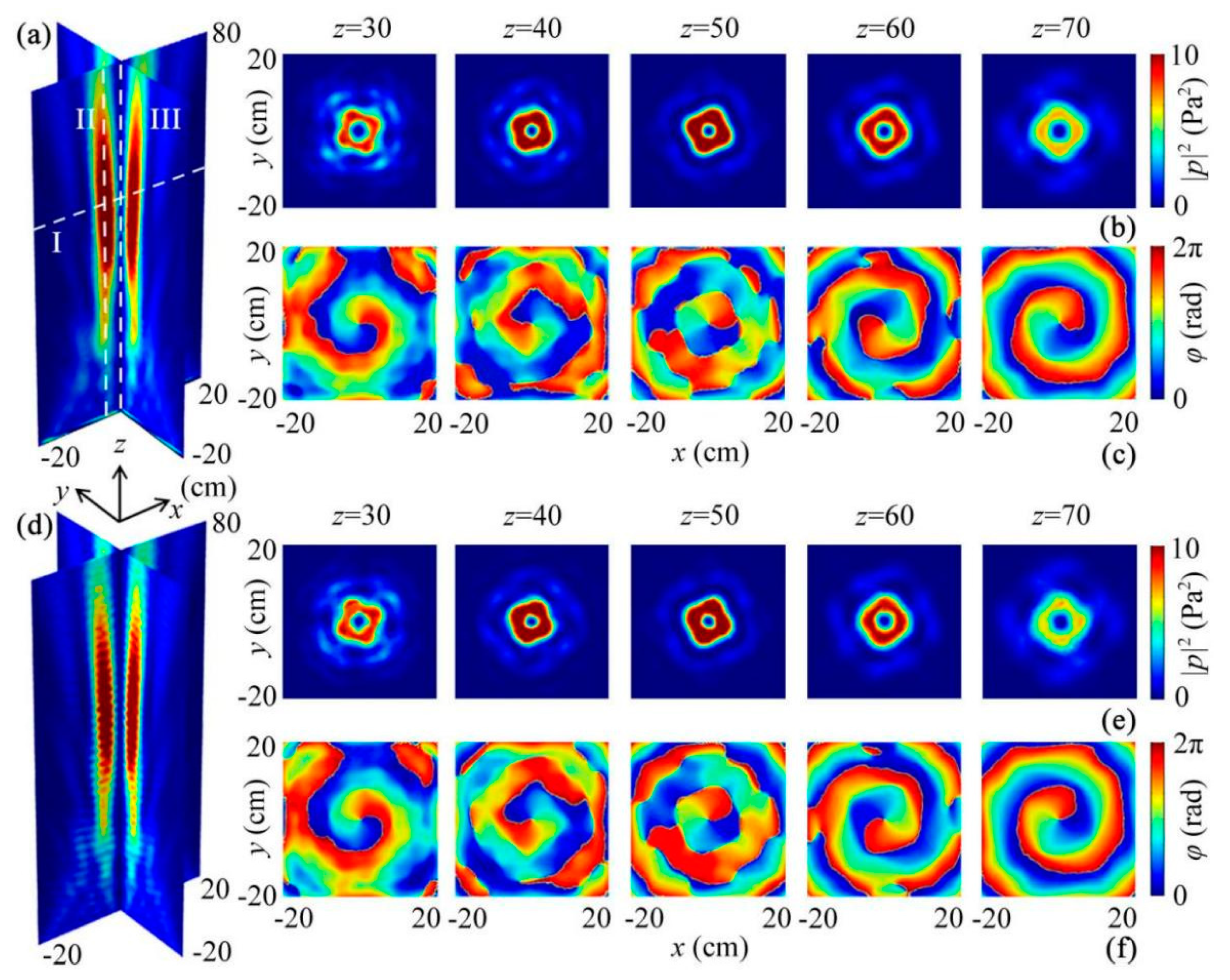
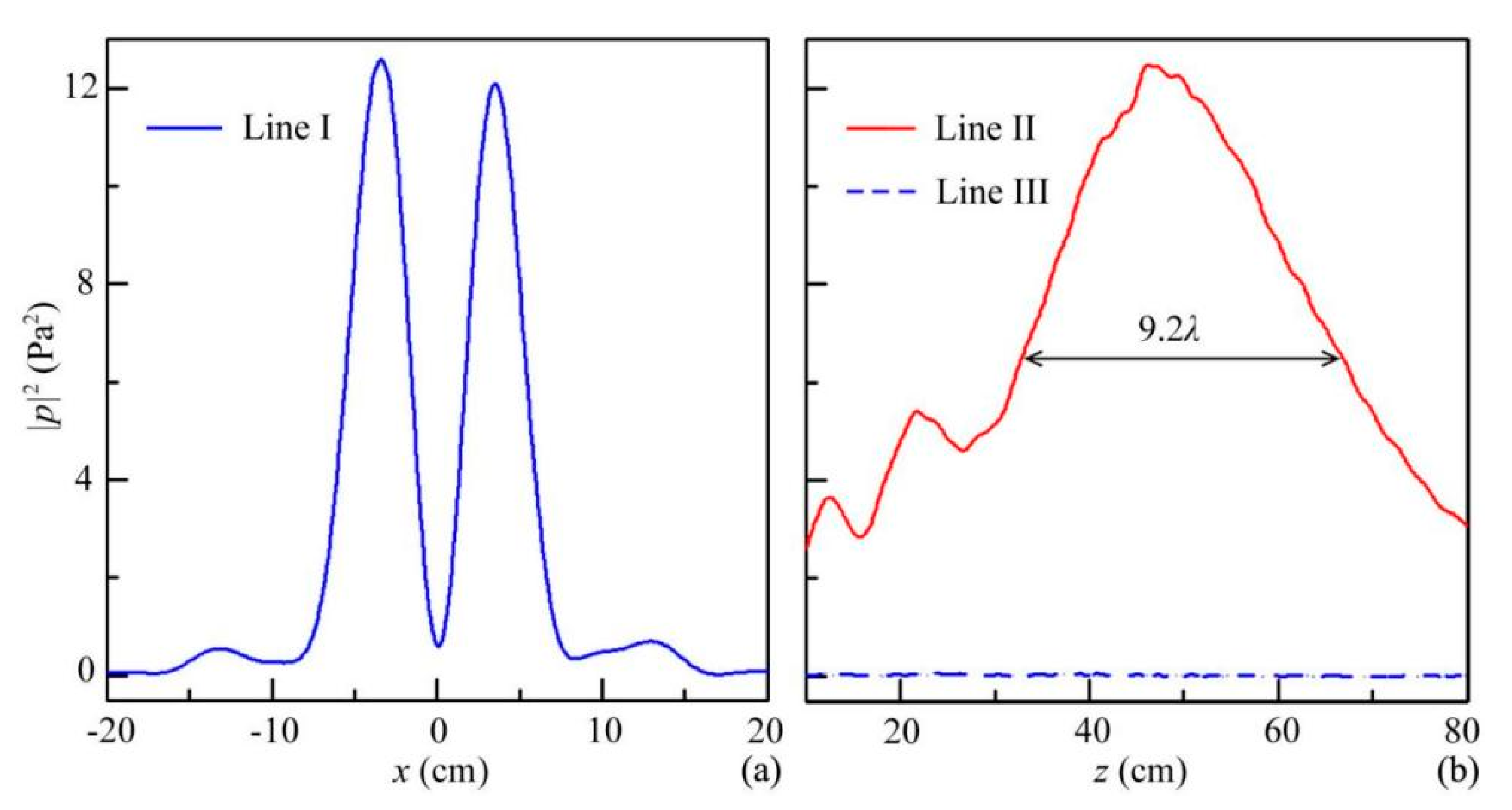
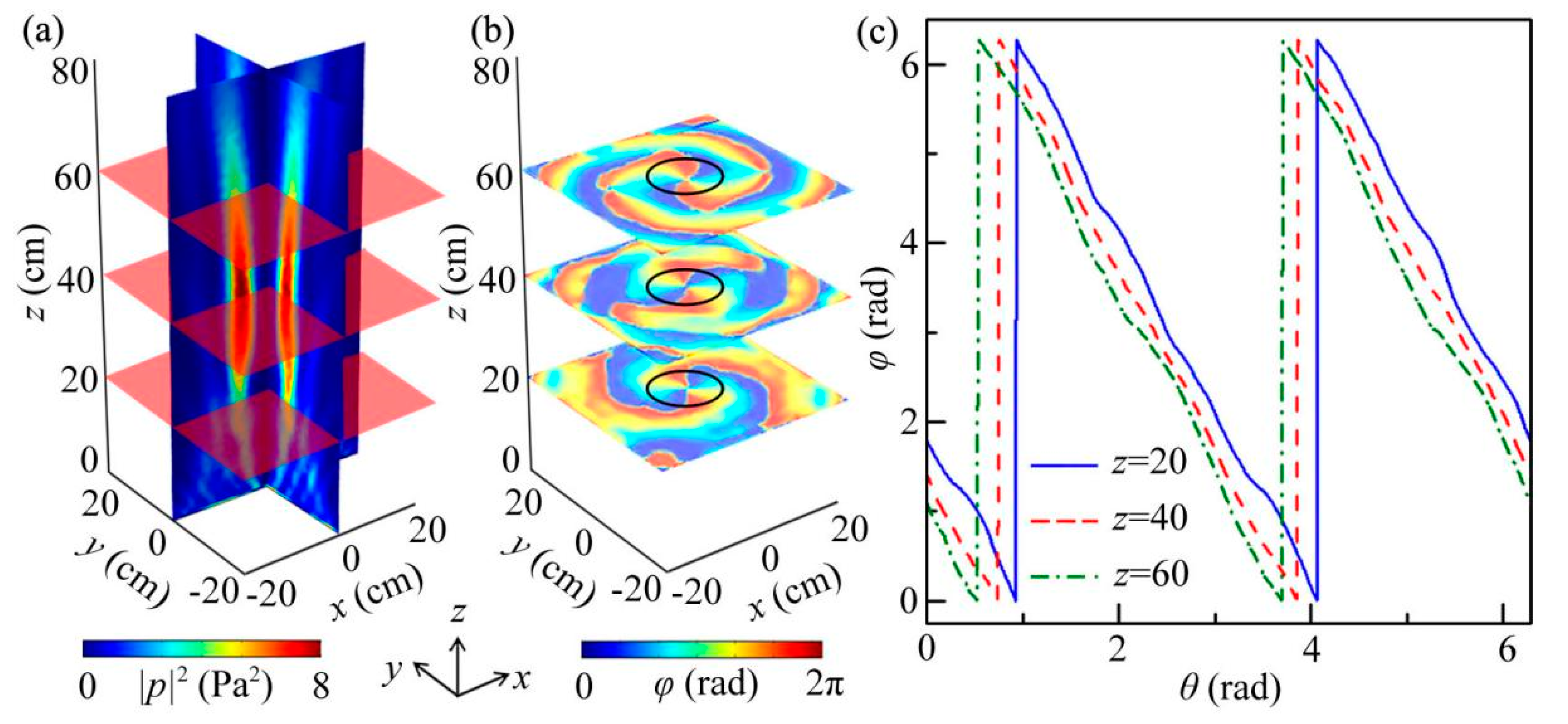
3.1. Performance of ABV Beam
3.2. Bandwidth of ABV Beam
3.3. Design of ABV Beam with Different Values of n
3.4. Design of Underwater ABV Beam
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Brunet, T.; Thomas, J.L.; Marchiano, R. Transverse shift of helical beams and subdiffraction imaging. Phys. Rev. Lett. 2010, 105, 034301. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Dubois, M.; Wang, Y.; Zhang, X. High-speed acoustic communication by multiplexing orbital angular momentum. Proc. Natl. Acad. Sci. USA 2017, 114, 7250–7253. [Google Scholar] [CrossRef] [Green Version]
- Baresch, D.; Thomas, J.L.; Marchiano, R. Observation of a single-beam gradient force acoustical trap for elastic particles: Acoustical tweezers. Phys. Rev. Lett. 2016, 116, 024301. [Google Scholar] [CrossRef] [Green Version]
- Marzo, A.; Ghobrial, A.; Cox, L.; Caleap, M.; Croxford, A.; Drinkwater, B.W. Realization of compact tractor beams using acoustic delay-lines. Appl. Phys. Lett. 2017, 110, 014102. [Google Scholar] [CrossRef]
- Ren, X.; Zhou, Q.; Xu, Z.; Liu, X. Particle trapping in arbitrary trajectories using first-order bessel-Like acoustic beams. Phys. Rev. Appl. 2021, 15, 054041. [Google Scholar] [CrossRef]
- Strahan, S.E.; Oman, L.D.; Douglass, A.R.; Coy, L. Modulation of antarctic vortex composition by the quasi-biennial oscillation. Geophys. Res. Lett. 2015, 42, 4216–4223. [Google Scholar] [CrossRef]
- Gong, Z.; Baudoin, M. Particle assembly with synchronized acoustic tweezers. Phys. Rev. Appl. 2019, 12, 024045. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhang, X.; Guo, J.; Yang, H.; Han, L.; Yao, Y.; Wu, F. Tailoring of diversified sound vortices using curved impedance-matched acoustic metasurfaces. Mod. Phys. Lett. B 2020, 34, 2050121. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Liao, Y.; Zhou, X.; Li, J.; Hu, G.; Zhang, X. Creation of acoustic vortex knots. Nat. Commun. 2020, 11, 1–6. [Google Scholar] [CrossRef]
- Wang, Q.; Ge, Y.; Sun, H.X.; Xue, H.R.; Jia, D.; Guan, Y.J.; Yuan, S.Q.; Zhang, B.L.; Chong, Y.D. Vortex states in an acoustic Weyl crystal with a topological lattice defect. Nat. Commun. 2021, 12, 1–8. [Google Scholar] [CrossRef]
- Marchiano, R.; Thomas, J.-L. Synthesis and analysis of linear and nonlinear acoustical vortices. Phys. Rev. E 2005, 71, 066616. [Google Scholar] [CrossRef] [PubMed]
- DeMore, C.E.M.; Yang, Z.; Volovick, A.; Cochran, S.; MacDonald, M.; Spalding, G. Mechanical evidence of the orbital angular momentum to energy ratio of vortex beams. Phys. Rev. Lett. 2012, 108, 194301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Riaud, A.; Thomas, J.L.; Charron, E.; Bussonnière, A.; Matar, O.B.; Baudoin, M. Anisotropic swirling surface acoustic waves from inverse filtering for on-chip generation of acoustic vortices. Phys. Rev. Appl. 2015, 4, 034004. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Li, J. Extreme acoustic metamaterial by coiling up space. Phys. Rev. Lett. 2012, 108, 114301. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Yang, M.; Sheng, P. Perspective: Acoustic metamaterials in transition. J. Appl. Phys. 2018, 123, 090901. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.D.; Zou, Z.; Zhang, L. Acoustic vortices in inhomogeneous media. Phys. Rev. Res. 2019, 1, 032014. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Díaz-Rubio, A.; Shen, C.; Jia, Z.; Tretyakov, S.; Cummer, S. Highly efficient generation of angular momentum with cylindrical bianisotropic metasurfaces. Phys. Rev. Appl. 2019, 11, 024016. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Y.Z.; Li, W.Y.; Mao, X.S. Triple-band polarization angle independent 90° polarization rotator based on fermat’s spiral structure planar chiral metamaterial. Prog. Electromagn. Res. 2019, 165, 35. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.; Chen, J.; Wu, J.H. Experimental study on performance of time reversal focusing. J. Phys. D Appl. Phys. 2019, 53, 055302. [Google Scholar] [CrossRef]
- Li, Y.; Liang, B.; Gu, Z.M.; Zou, X.Y.; Cheng, J.C. Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces. Sci. Rep. 2013, 3, srep02546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mei, J.; Wu, Y. Controllable transmission and total reflection through an impedance-matched acoustic metasurface. New J. Phys. 2014, 16, 123007. [Google Scholar] [CrossRef]
- Xia, J.P.; Zhang, X.T.; Sun, H.X.; Yuan, S.Q.; Qian, J.; Ge, Y. Broadband tunable acoustic asymmetric focusing lens from dual-layer metasurfaces. Phys. Rev. Appl. 2018, 10, 014016. [Google Scholar] [CrossRef]
- Gao, N.; Lu, K. An underwater metamaterial for broadband acoustic absorption at low frequency. Appl. Acoust. 2020, 169, 107500. [Google Scholar] [CrossRef]
- Zhou, H.T.; Fan, S.W.; Li, X.S.; Fu, W.X.; Wang, Y.F.; Wang, Y.S. Tunable arc-shaped acoustic metasurface carpet cloak. Smart Mater. Struct. 2020, 29, 065016. [Google Scholar] [CrossRef]
- Allen, K.W.; Dykes, D.J.P.; Reid, D.R.; Lee, R.T. Multi-objective genetic algorithm optimization of frequency selective metasurfaces to engineer Ku-passband filter responses. Prog. Electromagn. Res. 2020, 167, 19–30. [Google Scholar] [CrossRef]
- Jiménez, N.; Groby, J.P.; Romero-García, V. Spiral sound-diffusing metasurfaces based on holographic vortices. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wunenburger, R.; Lozano, J.I.V.; Brasselet, E. Acoustic orbital angular momentum transfer to matter by chiral scattering. New J. Phys. 2015, 17, 103022. [Google Scholar] [CrossRef]
- Jiang, X.; Shi, C.; Wang, Y.; Smalley, J.; Cheng, J.; Zhang, X. Nonresonant metasurface for fast decoding in acoustic communications. Phys. Rev. Appl. 2020, 13, 014014. [Google Scholar] [CrossRef]
- Wang, T.; Ke, M.; Li, W.; Yang, Q.; Qiu, C.; Liu, Z. Particle manipulation with acoustic vortex beam induced by a brass plate with spiral shape structure. Appl. Phys. Lett. 2016, 109, 123506. [Google Scholar] [CrossRef]
- Jia, Y.R.; Wei, Q.; Wu, D.J.; Xu, Z.; Liu, X.J. Generation of fractional acoustic vortex with a discrete archimedean spiral structure plate. Appl. Phys. Lett. 2018, 112, 173501. [Google Scholar] [CrossRef]
- Jiménez, N.; Romero-García, V.; García-Raffi, L.M.; Camarena, F.; Staliunas, K. Sharp acoustic vortex focusing by Fresnel-spiral zone plates. Appl. Phys. Lett. 2018, 112, 204101. [Google Scholar] [CrossRef]
- Ye, L.; Qiu, C.; Lu, J.; Tang, K.; Jia, H.; Ke, M.; Peng, S.; Liu, Z. Making sound vortices by metasurfaces. AIP Adv. 2016, 6, 085007. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Li, Y.; Liang, B.; Cheng, J.C.; Zhang, L. Convert acoustic resonances to orbital angular momentum. Phys. Rev. Lett. 2016, 117, 034301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xie, B.; Liu, W.; Cheng, H.; Chen, S.; Tian, J. Anomalous reflection and vortex beam generation by multi-bit coding acoustic metasurfaces. Appl. Phys. Lett. 2019, 114, 091905. [Google Scholar] [CrossRef]
- Luo, Y.; Jia, Y.; Yao, J.; Wu, D.; Liu, X. Enhanced fractional acoustic vortices by an annulus acoustic metasurface with multi-layered rings. Adv. Mater. Technol. 2020, 5, 2000356. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, D.; Yang, C.; Ge, J.; Chen, H.; Ren, J. Realization of acoustic spin transport in metasurface waveguides. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef]
- Chen, D.-C.; Zhou, Q.X.; Zhu, X.-F.; Xu, Z.; Wu, D.-J. Focused acoustic vortex by an artificial structure with two sets of discrete Archimedean spiral slits. Appl. Phys. Lett. 2019, 115, 083501. [Google Scholar] [CrossRef]
- Guo, S.; Guo, X.; Wang, X.; Du, X.; Wu, P.; Bouakaz, A.; Wan, M. Manipulation of nanodroplets via a nonuniform focused acoustic vortex. Phys. Rev. Appl. 2020, 13, 034009. [Google Scholar] [CrossRef]
- Fu, Y.; Shen, C.; Zhu, X.; Li, J.; Liu, Y.; Cummer, S.A.; Xu, Y. Sound vortex diffraction via topological charge in phase gradient metagratings. Sci. Adv. 2020, 6, 9876. [Google Scholar] [CrossRef]
- Qian, J.; Wang, Y.; Yuan, S.Q.; Sun, H.X.; Liu, X.J. Reflected acoustic wavefront manipulation by an ultrathin metasurface based on three-dimensional generalized Snell’s law. Appl. Phys. Express 2019, 12, 094001. [Google Scholar] [CrossRef]
- Liu, D.L.; Waag, R. Propagation and backpropagation for ultrasonic wavefront design. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1997, 44, 1–13. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Qian, J.; Xia, J.-P.; Ge, Y.; Yuan, S.-Q.; Sun, H.-X.; Liu, X.-J. Acoustic Bessel Vortex Beam by Quasi-Three-Dimensional Reflected Metasurfaces. Micromachines 2021, 12, 1388. https://doi.org/10.3390/mi12111388
Wang Y, Qian J, Xia J-P, Ge Y, Yuan S-Q, Sun H-X, Liu X-J. Acoustic Bessel Vortex Beam by Quasi-Three-Dimensional Reflected Metasurfaces. Micromachines. 2021; 12(11):1388. https://doi.org/10.3390/mi12111388
Chicago/Turabian StyleWang, Yin, Jiao Qian, Jian-Ping Xia, Yong Ge, Shou-Qi Yuan, Hong-Xiang Sun, and Xiao-Jun Liu. 2021. "Acoustic Bessel Vortex Beam by Quasi-Three-Dimensional Reflected Metasurfaces" Micromachines 12, no. 11: 1388. https://doi.org/10.3390/mi12111388
APA StyleWang, Y., Qian, J., Xia, J.-P., Ge, Y., Yuan, S.-Q., Sun, H.-X., & Liu, X.-J. (2021). Acoustic Bessel Vortex Beam by Quasi-Three-Dimensional Reflected Metasurfaces. Micromachines, 12(11), 1388. https://doi.org/10.3390/mi12111388






