Optimum Design of a Composite Optical Receiver by Taguchi and Fuzzy Logic Methods
Abstract
:1. Introduction
2. Design of the Composite Optical Receiver
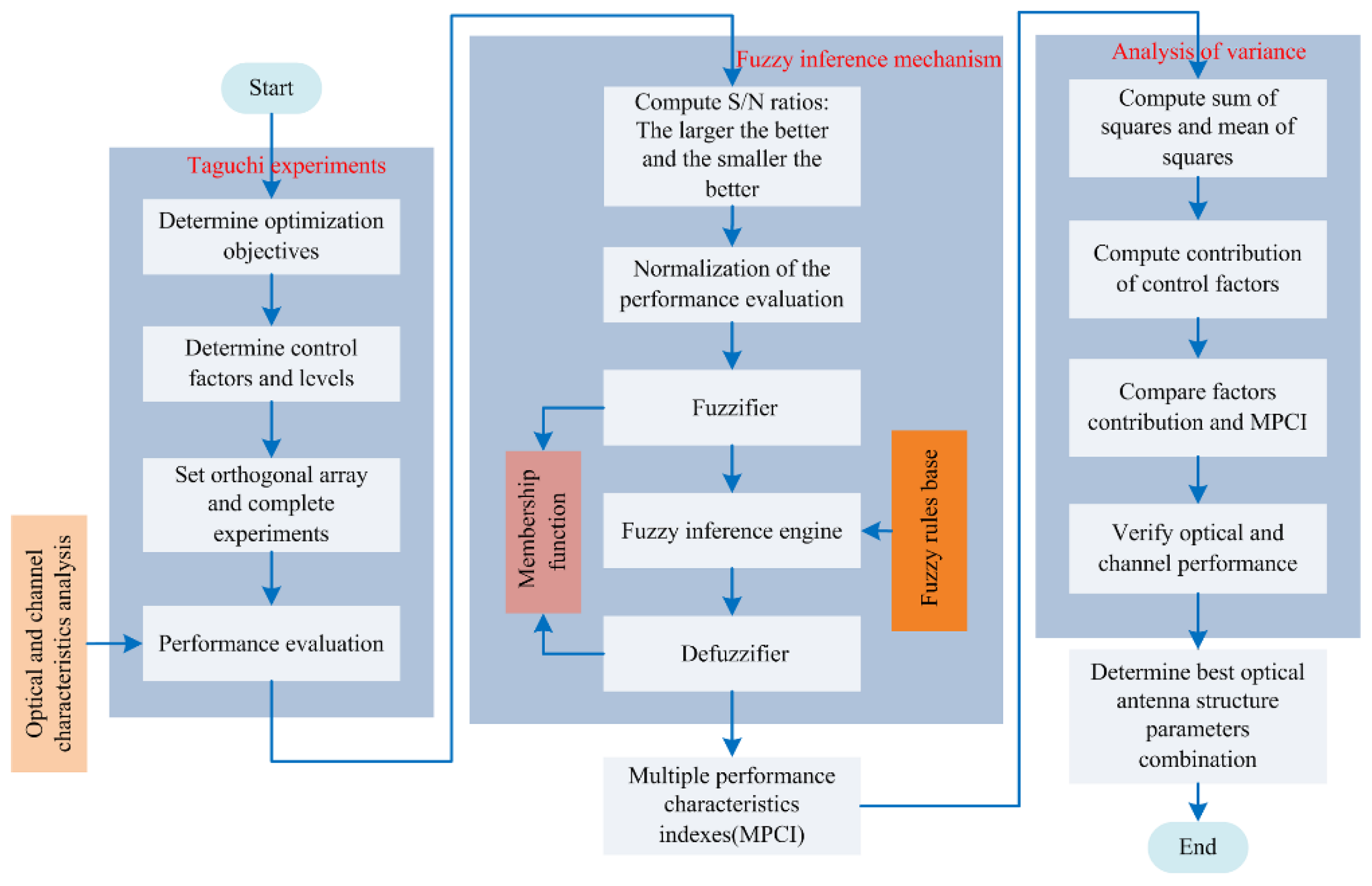
3. Optimization of the Composite Optical Receiver
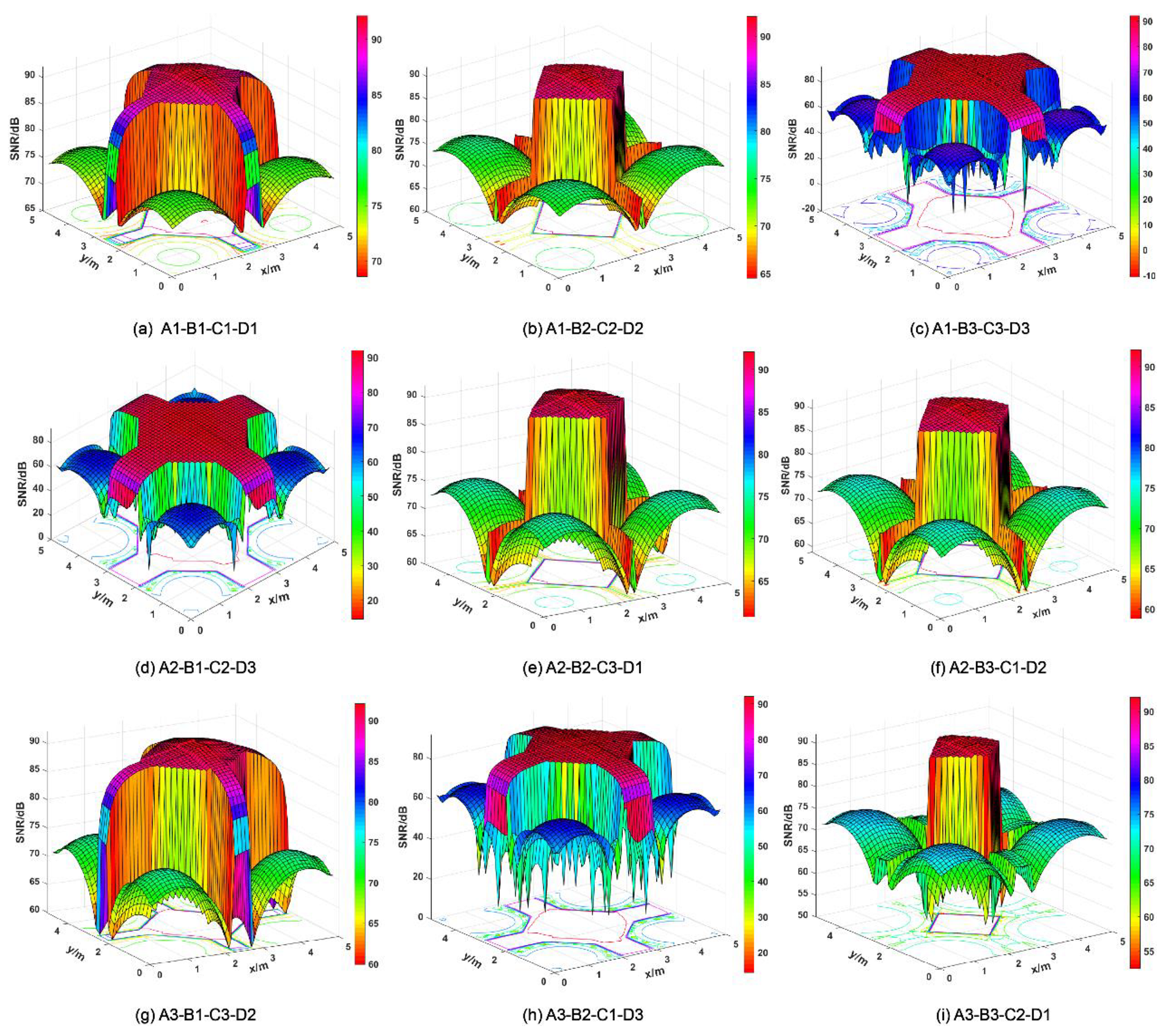
3.1. Taguchi Experimentation
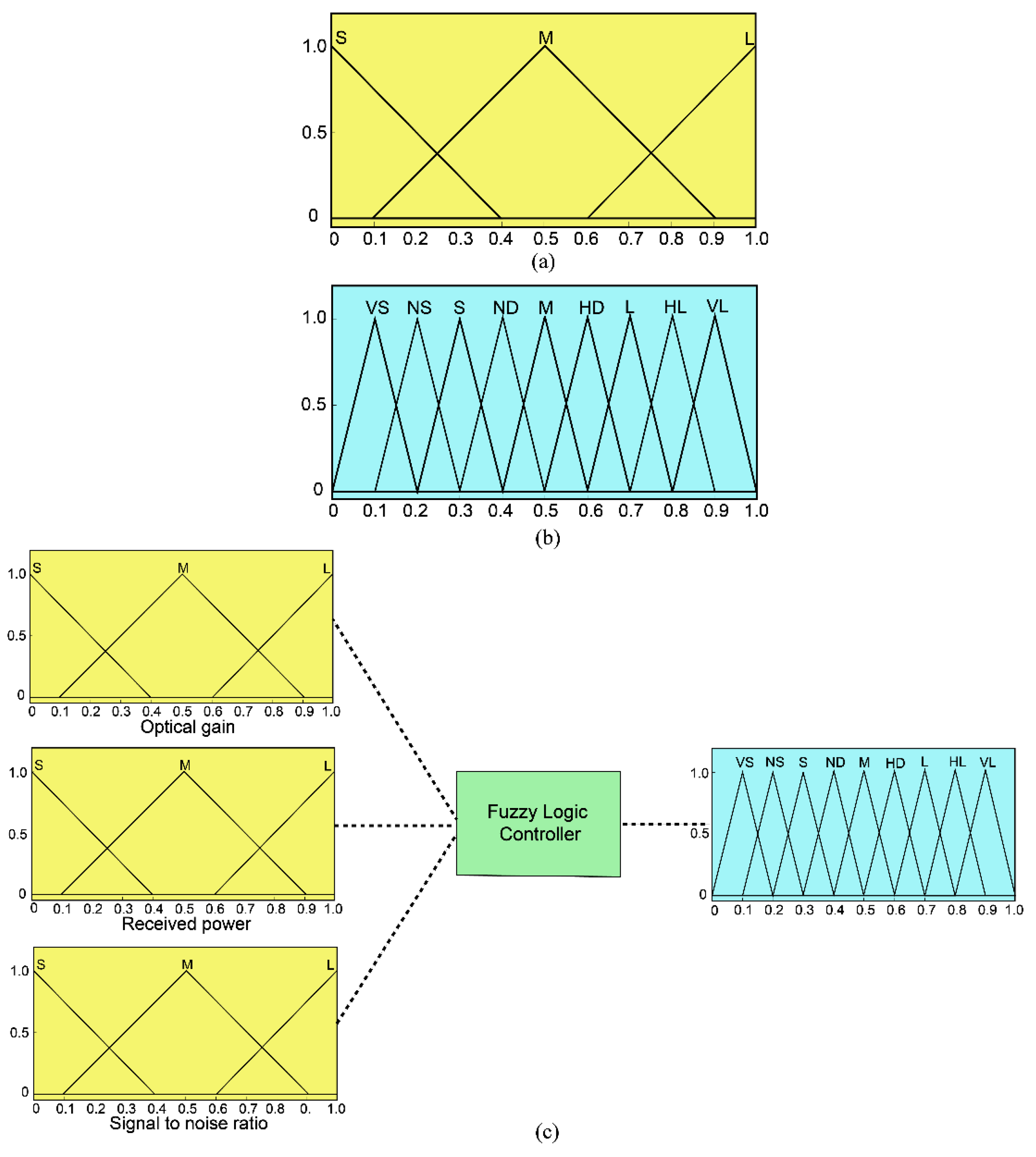
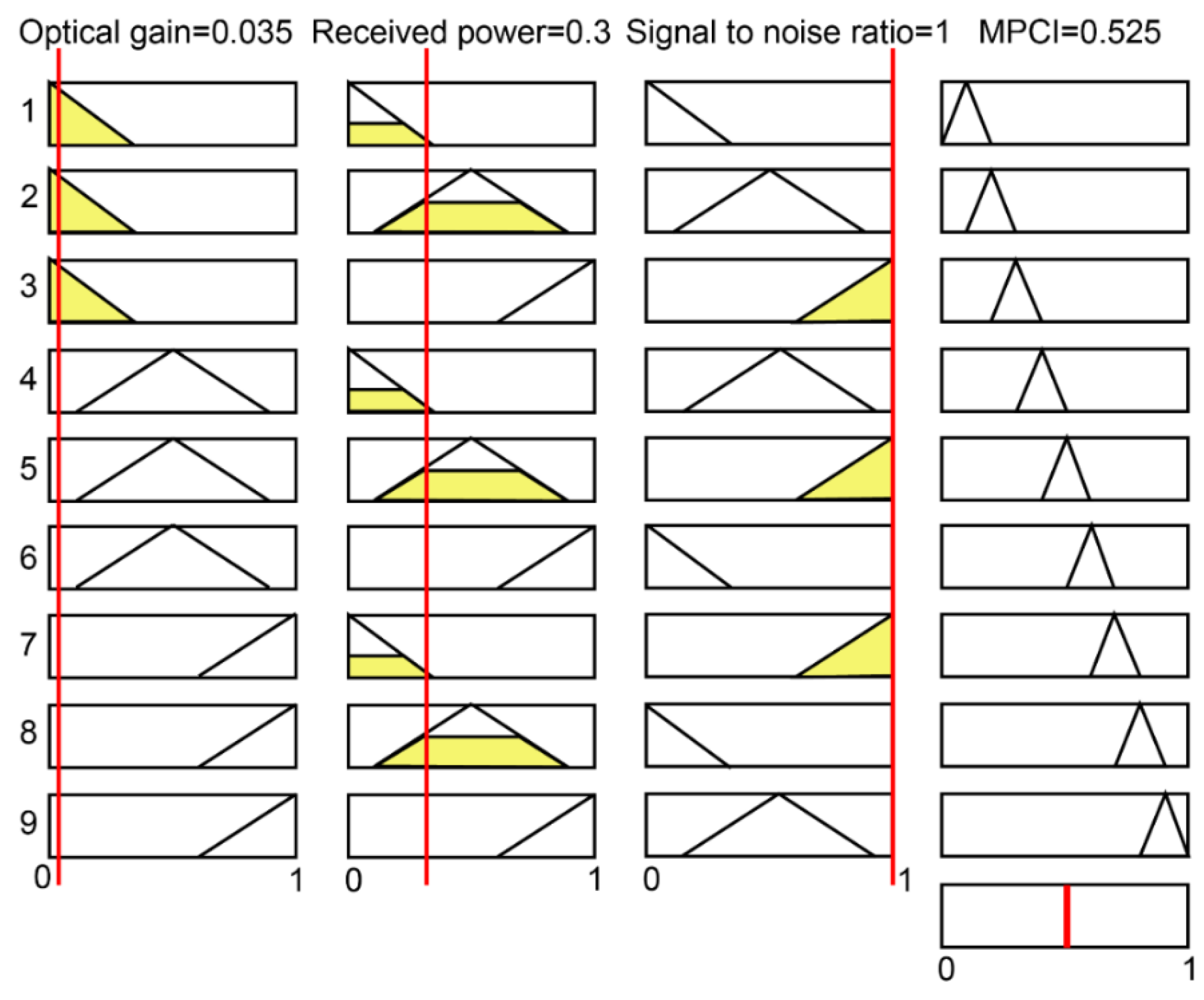
3.2. Fuzzy Logic Method
- (a)
- Choose the orthogonal array L9(34) as the starting point of the Taguchi experiments.
- (b)
- (c)
- Set the input and output membership functions and fuzzy rules (Table 5).
- (d)
- Start to calculate the fuzzy controller (fuzzy reference, defuzzification interface).
- (e)
- Calculate the values of MPCI (Table 6).
- (f)
- Perform an analysis of variance (ANOVA) on the main component points.
- (g)
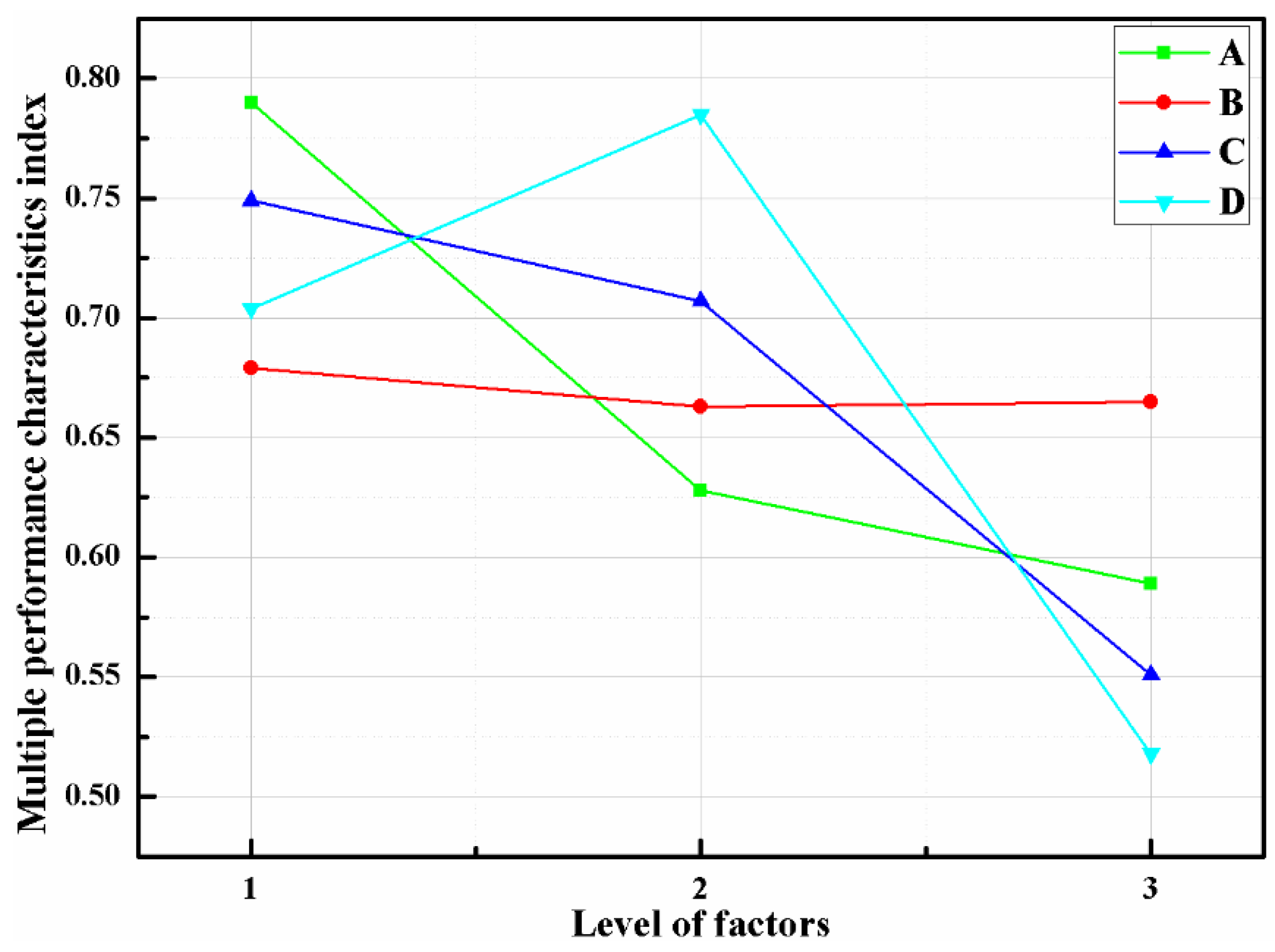
- Draw MPCI response tables and charts to determine the best combination of parameters.
- (h)
- Perform confirmation tests.
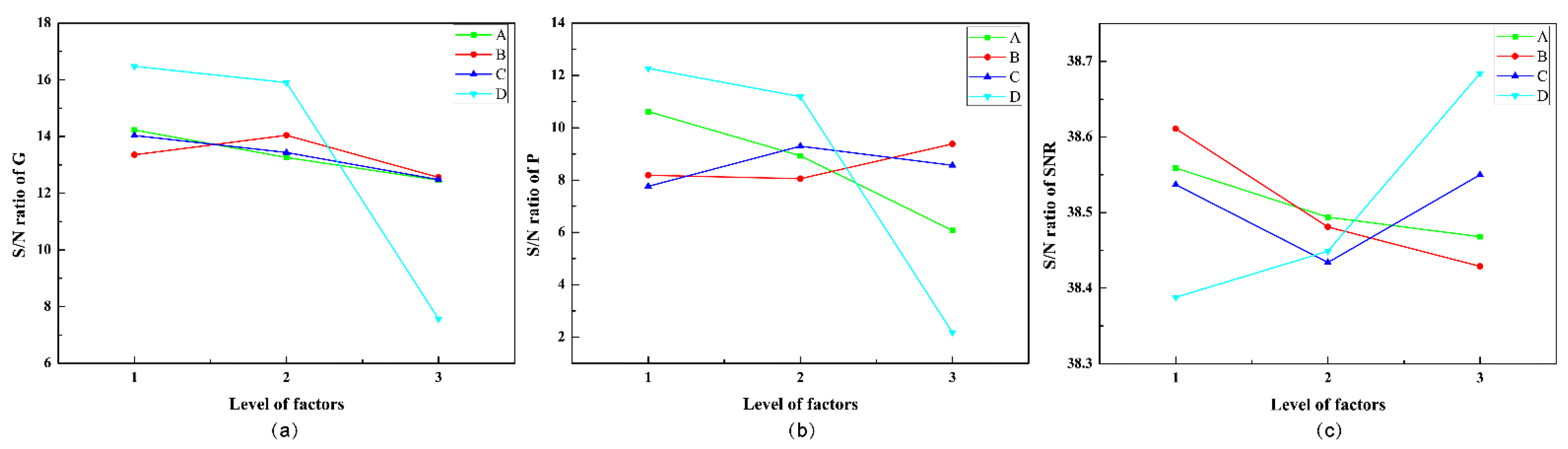
3.3. Variance Analysis
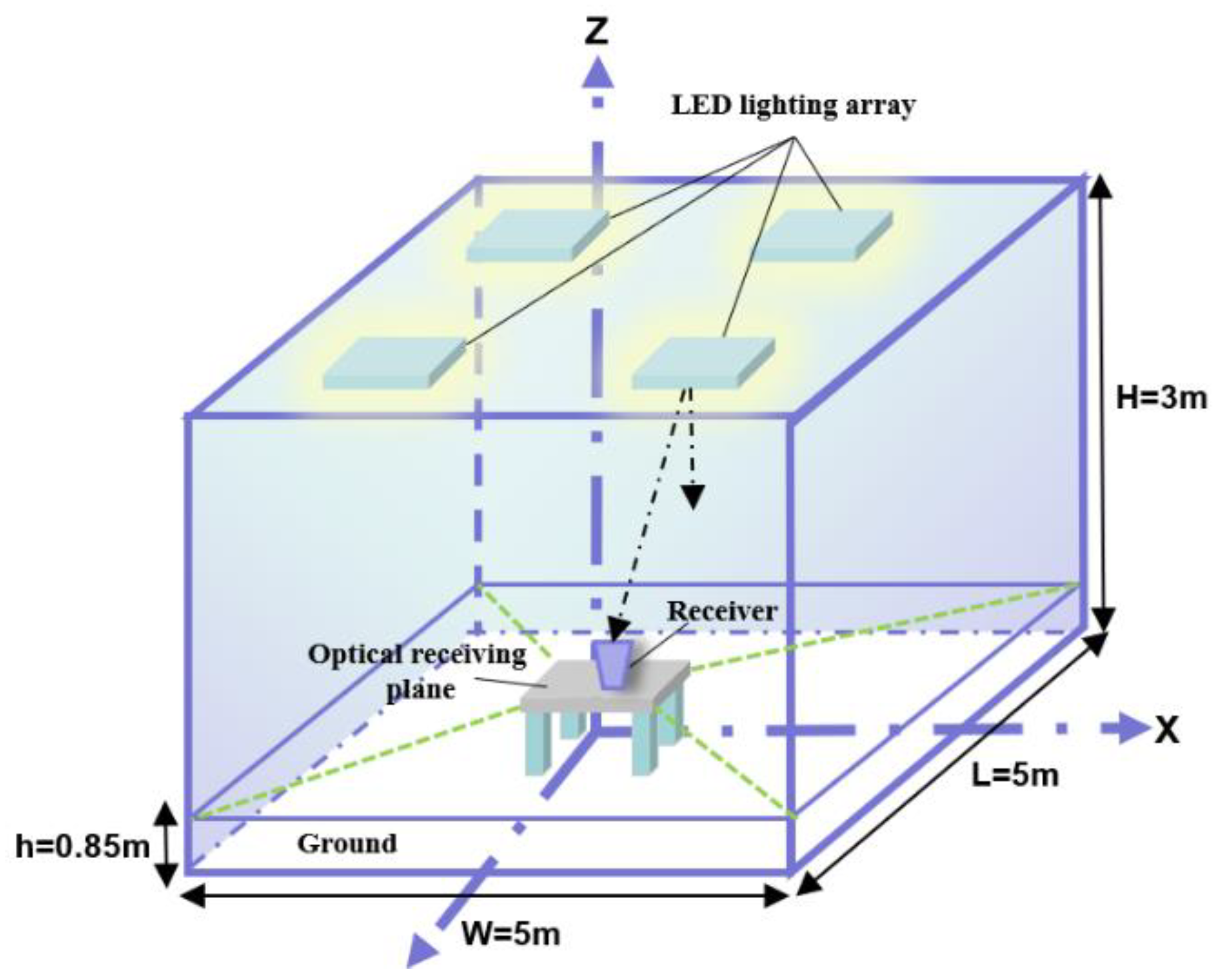
4. Channel Simulation and Analysis with the Optical Receiver
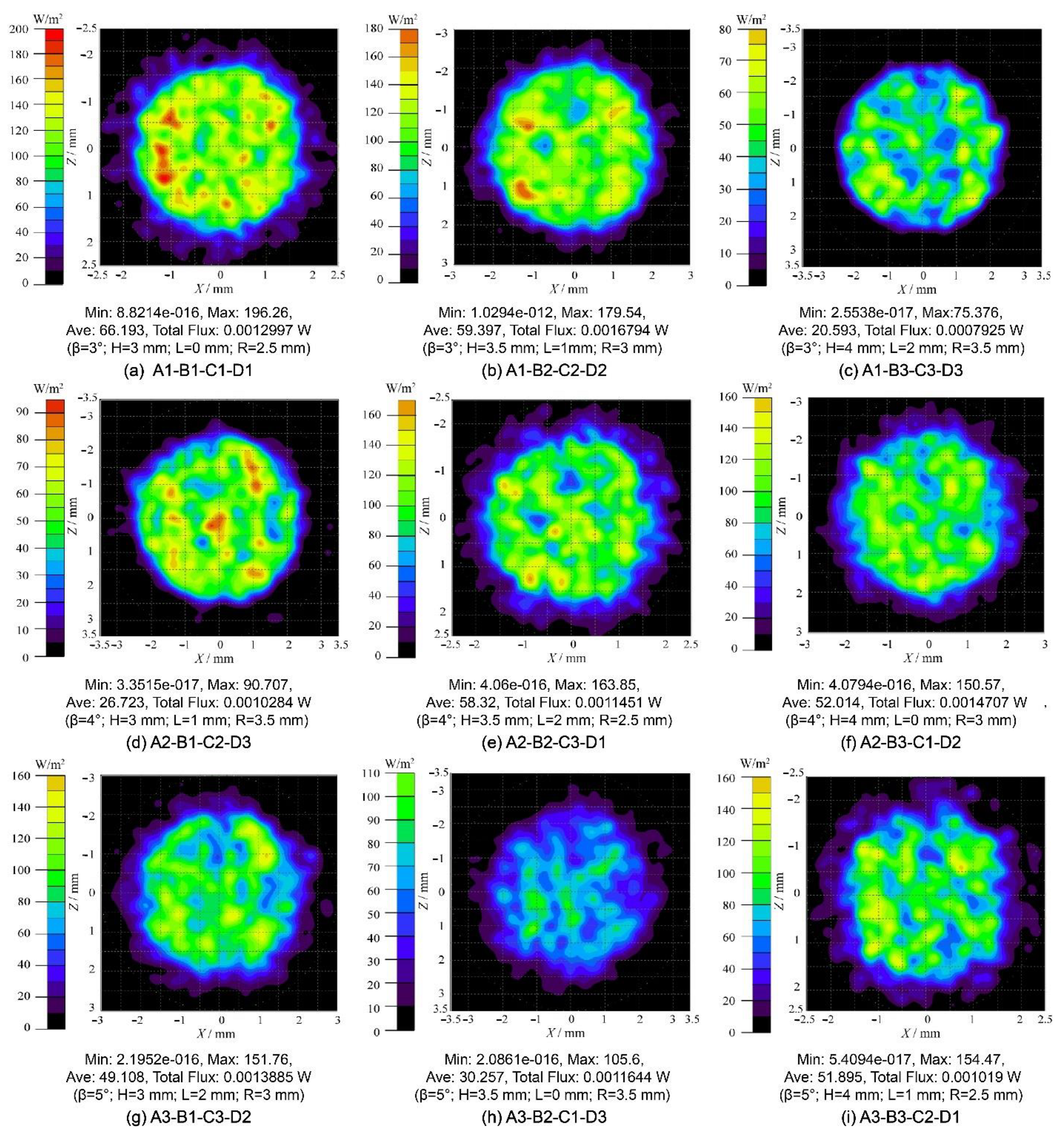
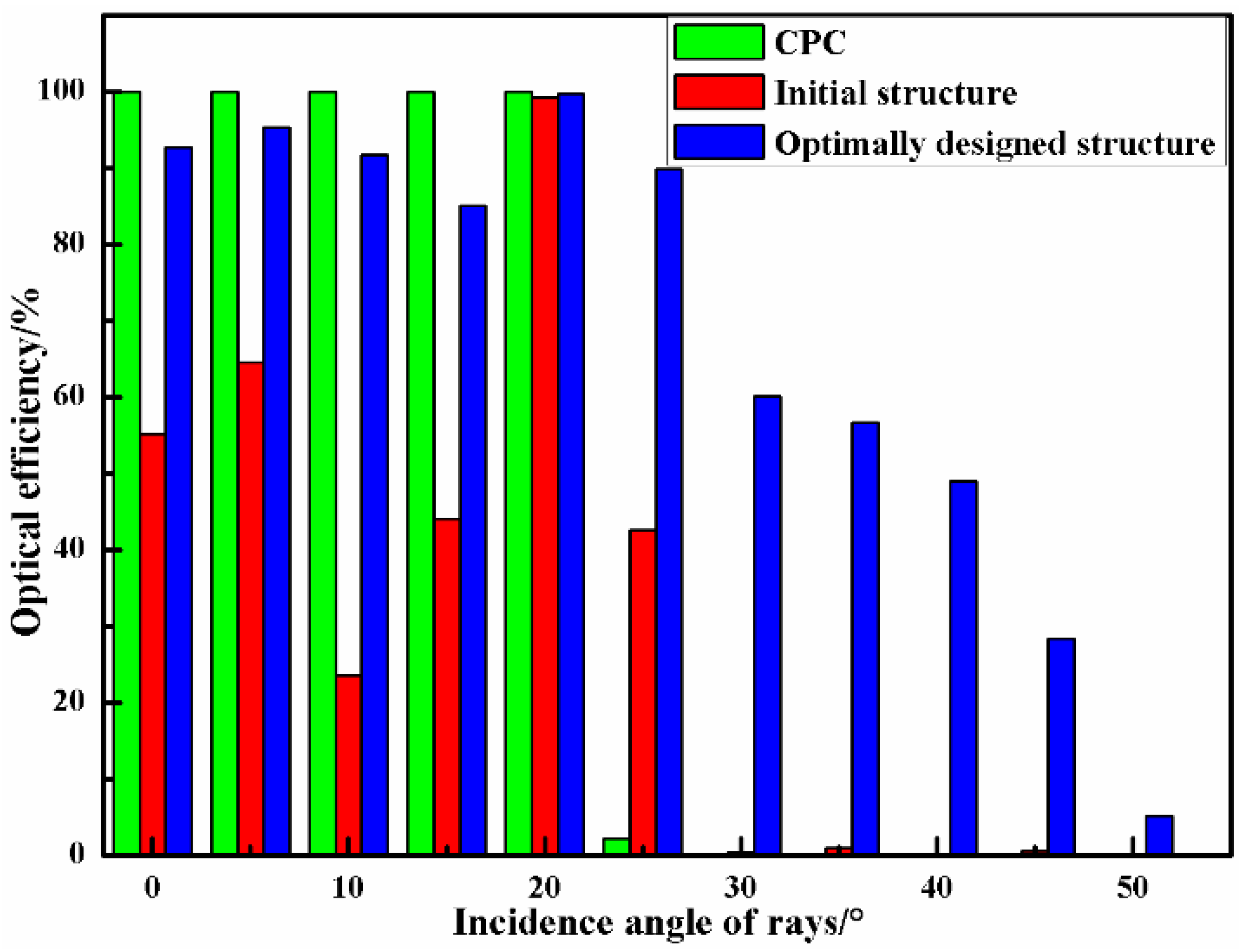
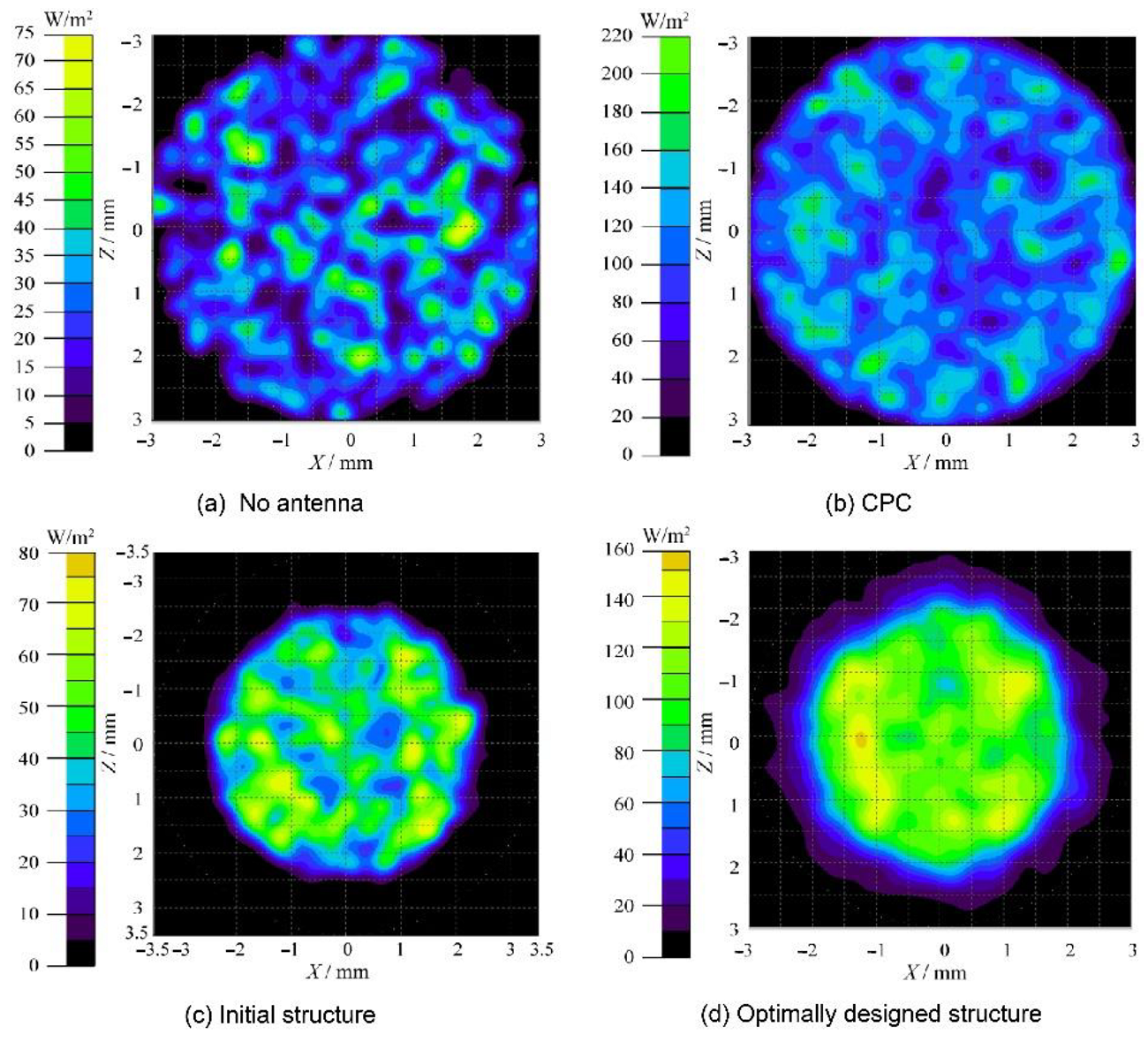
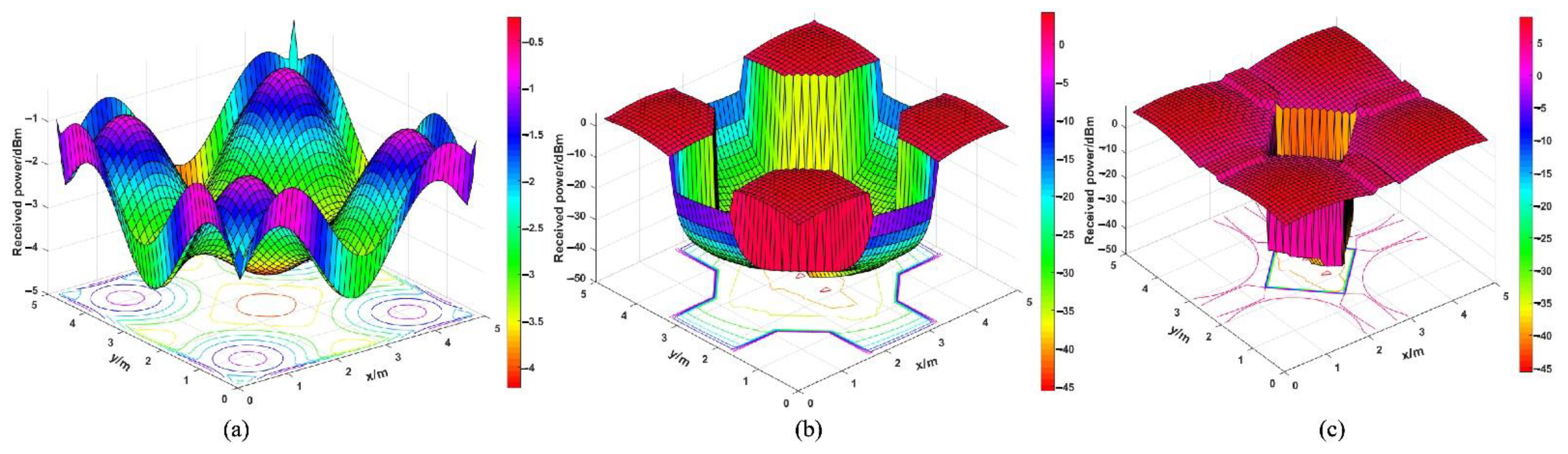
4.1. Analysis of the Optical Received Power
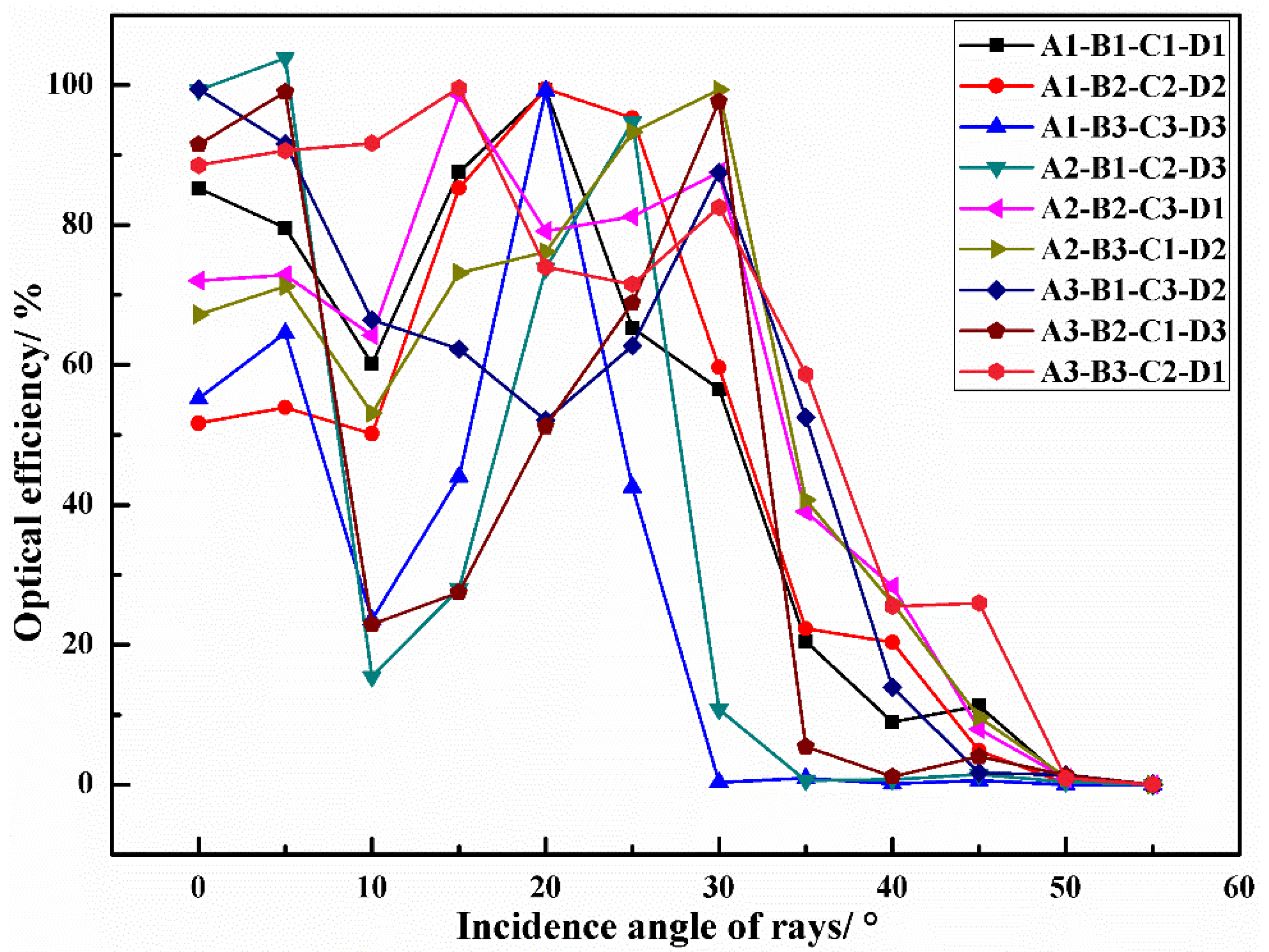
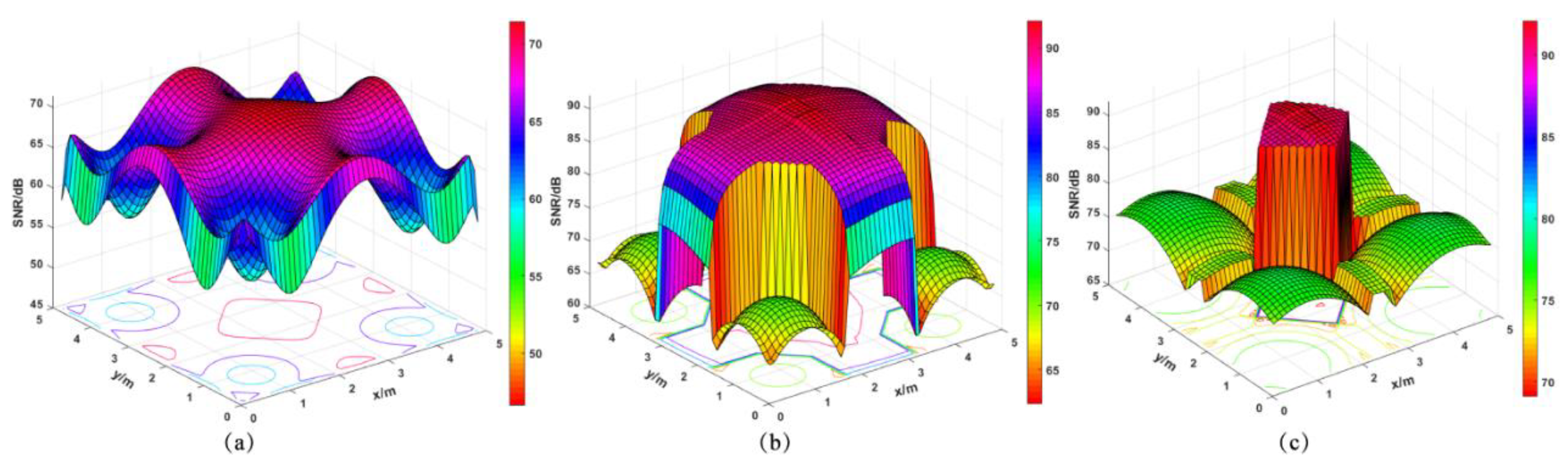
4.2. Analysis of the SNR Distribution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Kong, L.; Xu, M. Uniform Illumination for Nonplanar Surface Based on Freeform Surfaces. IEEE Photonics J. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Sun, X.; Kong, L.; Zhou, P.; Xu, M. A design of compound tailored illumination by a total-internal-reflection lens for machine vision. Light. Res. Technol. 2021, 0, 1–17. [Google Scholar] [CrossRef]
- Liu, X. Gbps Long-Distance Real-Time Visible Light Communications Using a High-Bandwidth GaN-Based Micro-LED. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Gao, Q.; Gong, C.; Xu, Z.Y. Joint transceiver and offset design for visible light communications with input-dependent shot noise. IEEE Trans. Wirel. Commun. 2017, 16, 2736–2747. [Google Scholar] [CrossRef] [Green Version]
- Barolet, D. Light-emitting diodes (LEDs) in dermatology. Semin. Cutan. Med. Surg. 2008, 27, 227–238. [Google Scholar] [CrossRef]
- Li, X.; Hussain, B.; Wang, L.; Jiang, J.; Yue, C.P. Design of a 2.2-mW 24-Mb/s CMOS VLC Receiver SoC with Ambient Light Rejection and Post-Equalization for Li-Fi Applications. J. Lightwave Technol. 2018, 36, 2366–2375. [Google Scholar] [CrossRef]
- Yang, J. Highly Uniform White Light-Based Visible Light Communication Using Red, Green, and Blue Laser Diodes. IEEE Photonics J. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Arnon, S. Optimised optical wireless car-to-traffic-light communication. Trans. Emerg. Telecommun. Technol. 2014, 25, 660–665. [Google Scholar] [CrossRef]
- Hou, Y.A.; Xiao, S.L.; Zheng, H.F.; Hu, W.S. Multiple Access Scheme Based on Block Encoding Time Division Multiplexing in an Indoor Positioning System Using Visible Light. J. Opt. Commun. Netw. 2015, 7, 489–495. [Google Scholar] [CrossRef]
- Gismalla1, M.S.M.; Abdullah, M.F.L.; Ahmed, M.S.; Mabrouk, W.A.; AL-Fadhali, N.; Saeid, E.; Supa’at, A.S.M.; Das, B. Design and Analysis of Different Optical Attocells Deployment Models for Indoor Visible Light Communication System. Int. J. Integr. Eng. 2021, 13, 253–264. [Google Scholar] [CrossRef]
- Gismalla, M.S.M.; Abdullah, M.F.L.; Das, B.; Mabrouk, W.A.; Mahfouz, N.E. Design of an optical attocells configuration for an indoor visible light communications system. Int. J. Electron. Commun. 2019, 112, 152946. [Google Scholar] [CrossRef]
- Yaqoob, I.; Hashem, I.A.T.; Mehmood, Y. Enabling communication technologies for smart cities. IEEE Commun. Mag. 2017, 55, 112–120. [Google Scholar] [CrossRef]
- Li, T.; An, C.; Tian, Z. Human sensing using visible light communication. In Proceedings of the ACM 21st Annual International Conference on Mobile Computing and Networking, Paris, France, 7–11 September 2015; pp. 331–344. [Google Scholar]
- Tang, X.; Le, M.H.; Viriyasitavat, W. Car-to-Car Visible Light Communications. In Visible Light Communications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Luo, J.; Fan, L.; Li, H. Indoor positioning systems based on visible light communication: State of the art. IEEE Commun. Surv. Tutor. 2017, 19, 2871–2893. [Google Scholar] [CrossRef]
- Huang, N.; Wang, X.D.; Chen, M. Transceiver Design for MIMO VLC Systems with Integer-Forcing Receivers. IEEE J. Sel. Areas Commun. 2017, 36, 66–77. [Google Scholar] [CrossRef]
- Wang, D.; Lan, T. Design of a gradient-index lens with a compound parabolic concentrator shape as a visible light communication receiving antenna. Appl. Opt. 2018, 57, 1510–1517. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.B.; Tang, Y.; Cui, L. Continuous zoom antenna for mobile visible light communication. Appl. Opt. 2015, 54, 9606–9612. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lan, T.; Ni, G.Q. Optical receiving system based on a compound parabolic concentrator and a hemispherical lens for visible light communication. Appl. Opt. 2016, 55, 10229–10238. [Google Scholar] [CrossRef]
- Wang, Y.; Lan, T.; Li, X. Design research and performance analysis of compound parabolic concentrators as optical antennas in visible light communication. Acta Phys. Sin. 2015, 64, 124212. [Google Scholar] [CrossRef]
- Wang, Y.; Lan, T.; Ni, G.Q. Design and analysis of composite optical receiver for indoor visible light communication. Acta Phys. Sin. 2017, 66, 084207. [Google Scholar] [CrossRef]
- Peng, X.; Kong, L. Design and optimization of optical receiving antenna based on compound parabolic concentrator for indoor visible light communication. Opt. Commun. 2020, 44, 125447. [Google Scholar] [CrossRef]
- Yu, M.Y.; Yang, H.J.; Jiang, P. On-axial defocused characteristic analysis for Cassegrain antenna in optical communication. Optik 2016, 127, 1734–1737. [Google Scholar] [CrossRef]
- Li, X.; Lan, T.; Wang, Y.; Wang, L.H. Design and study of Fresnel lens for an antenna in indoor visible light communication system. Acta Phys. Sin. 2015, 64, 024201. [Google Scholar]
- Wei, X.H.; He, Y.H.; Liu, Z.K. Fizeau interferometer with binary phase Fresnel-zone plate reference for precision measurement of large convex lens. Opt. Lasers Eng. 2018, 110, 348–355. [Google Scholar] [CrossRef]
- Yin, P.; Xu, X.P.; Jiang, Z.G. Design and Performance Analysis of Planar Concentrators as Optical Antennas in Visible Light Communication. Acta Opt. Sin. 2018, 38, 0406004. [Google Scholar]
- Li, L.F.; Wang, B.; Pottas, J. Design of a compound parabolic concentrator for a multi-source high-flux solar simulator. Sol. Energy 2019, 183, 805–811. [Google Scholar] [CrossRef]
- Winston, R. Principles of solar concentrators of a novel design. Sol. Energy 1974, 16, 89–95. [Google Scholar] [CrossRef]
- Ni, X.S.; Zhou, Z.G.; Wen, X.W. The use of Taguchi method to optimize the laser welding of sealing neuro-stimulator. Opt. Lasers Eng. 2011, 49, 297–304. [Google Scholar]
- Hernandez, B.A.; Gill, H.S.; Gheduzzi, S. Laser parameters optimization of surface treating of Al 6082-T6 with Taguchi method. Opt. Laser Technol. 2019, 120, 105714. [Google Scholar]
- Parinam, S.; Kumar, M.; Kumari, N. An improved optical parameter optimisation approach using Taguchi and genetic algorithm for high transmission optical filter design. Optik 2019, 182, 382–392. [Google Scholar] [CrossRef]
- Xie, H.L.; Wei, J.J.; Wang, Z.X. Design and performance research on eliminating multiple reflections of solar radiation within compound parabolic concentrator (CPC) in hybrid CPV/T system. Sol. Energy 2016, 129, 126–146. [Google Scholar] [CrossRef]
- Jean, M.D.; Lin, B.T.; Chou, J.H. Design of a fuzzy logic approach for optimization reinforced zirconia depositions using plasma sprayings. Surf. Coat. Technol. 2006, 201, 3129–3138. [Google Scholar] [CrossRef]
- Sun, J.H.; Fang, Y.C.; Hsueh, B.R. Combining Taguchi with fuzzy method on extended optimal design of miniature zoom optics with liquid lens. Optik 2012, 123, 1768–1774. [Google Scholar] [CrossRef]
- Ergun, B.; Sahin, C.; Ustuntas, T. Segmentation and determination of grid points of curve points in terrestrial laser scanning data for regular curve surfaces via C-means integrated fuzzy logic approach. Opt. Lasers Eng. 2014, 52, 261–268. [Google Scholar] [CrossRef]
- Tarng, Y.S.; Yang, W.H.; Juang, S.C. The Use of Fuzzy Logic in the Taguchi Method for the Optimisation of the Submerged Arc Welding Process. Int. J. Adv. Manuf. Technol. 2000, 16, 688–694. [Google Scholar] [CrossRef]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
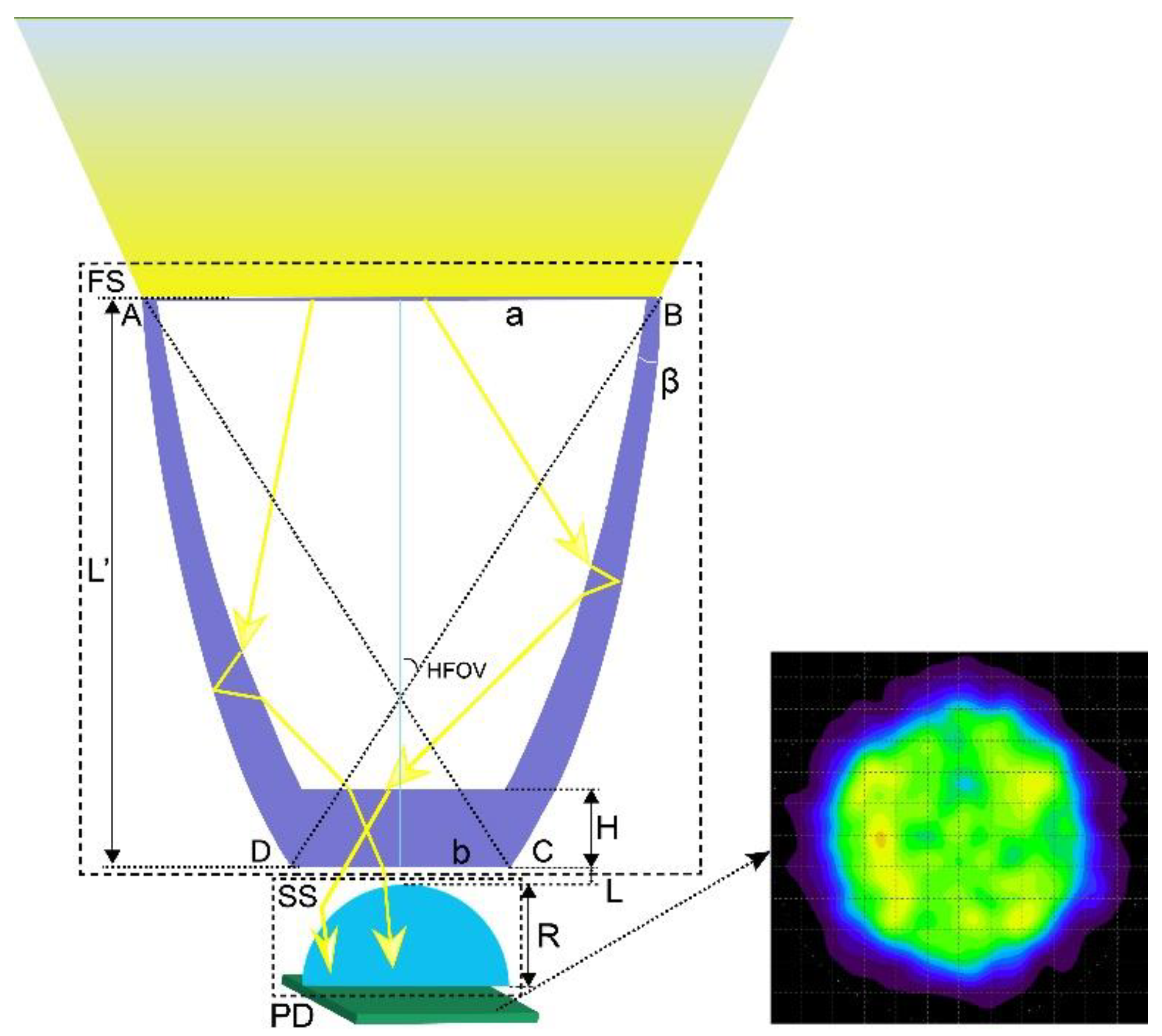
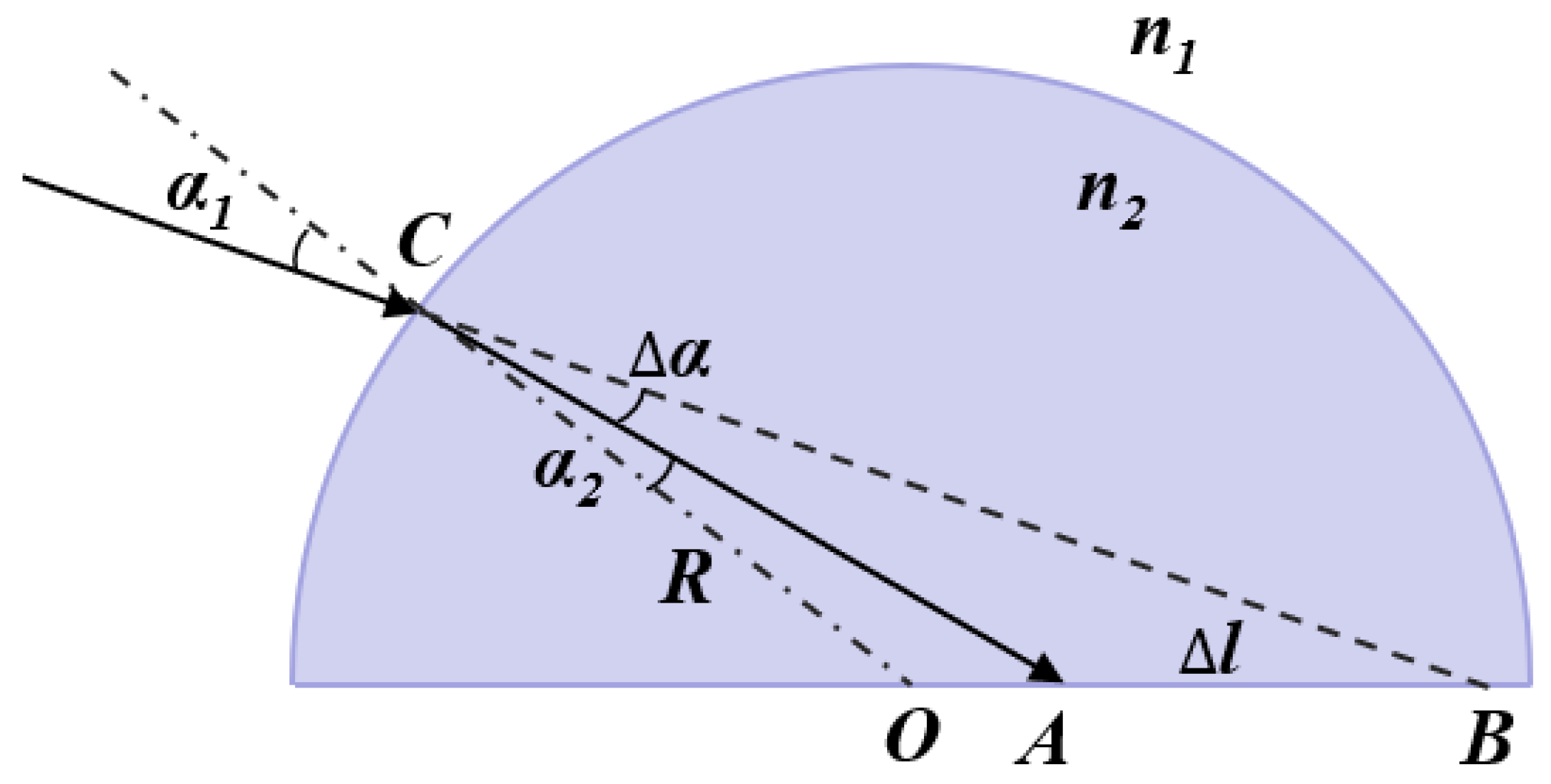


| Outlet Radius b/mm | Inlet Radius a/mm | HFOV/° | Length L’/mm | Focal Length f/mm |
|---|---|---|---|---|
| 3 | 8.8 | 20 | 22 | 4 |
| Control Factors | Levels | |||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| A | Rotation degree β (°) | 3.0 | 4.0 | 5.0 |
| B | Bottom wall’s height H (mm) | 3.0 | 3.5 | 4.0 |
| C | Spacing distance L (mm) | 0.0 | 1.0 | 2.0 |
| D | Hemispherical radius R (mm) | 2.5 | 3.0 | 3.5 |
| Exp. No. | Control Factors | Performance Evaluation of Different Characteristics | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | G | S/N of G | P /dBm | S/N of P | SNR/ dB | S/N of SNR | |
| 1 | 3.0 | 3.0 | 0.0 | 2.5 | 8.08 | 18.153 | 4.5754 | 13.209 | 84.8514 | 38.573 |
| 2 | 3.0 | 3.5 | 1.0 | 3.0 | 7.64 | 17.661 | 4.7475 | 13.529 | 83.1898 | 38.401 |
| 3 | 3.0 | 4.0 | 2.0 | 3.5 | 2.21 | 6.880 | −1.8014 | 5.112 | 86.1109 | 38.701 |
| 4 | 4.0 | 3.0 | 1.0 | 3.5 | 2.42 | 7.670 | −1.4072 | 2.967 | 86.1146 | 38.702 |
| 5 | 4.0 | 3.5 | 2.0 | 2.5 | 6.54 | 16.307 | 4.0724 | 12.197 | 83.0983 | 38.392 |
| 6 | 4.0 | 4.0 | 0.0 | 3.0 | 6.17 | 15.812 | 3.8195 | 11.640 | 83.0668 | 38.389 |
| 7 | 5.0 | 3.0 | 2.0 | 3.0 | 5.16 | 14.245 | 2.6278 | 8.392 | 84.6981 | 38.557 |
| 8 | 5.0 | 3.5 | 0.0 | 3.5 | 2.56 | 8.152 | −0.8355 | −1.561 | 85.5931 | 38.649 |
| 9 | 5.0 | 4.0 | 1.0 | 2.5 | 5.61 | 14.978 | 3.7123 | 11.393 | 81.2661 | 38.198 |
| Exp. No. | Control Factors | Quality Characteristics | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | G | P | SNR | |
| 1 | 3.0 | 3.0 | 0.0 | 2.5 | 1 | 0.979 | 0.744 |
| 2 | 3.0 | 3.5 | 1.0 | 3.0 | 0.925 | 1 | 0.404 |
| 3 | 3.0 | 4.0 | 2.0 | 3.5 | 0 | 0.442 | 0.998 |
| 4 | 4.0 | 3.0 | 1.0 | 3.5 | 0.035 | 0.300 | 1 |
| 5 | 4.0 | 3.5 | 2.0 | 2.5 | 0.737 | 0.912 | 0.385 |
| 6 | 4.0 | 4.0 | 0.0 | 3.0 | 0.675 | 0.875 | 0.378 |
| 7 | 5.0 | 3.0 | 2.0 | 3.0 | 0.502 | 0.659 | 0.713 |
| 8 | 5.0 | 3.5 | 0.0 | 3.5 | 0.059 | 0 | 0.894 |
| 9 | 5.0 | 4.0 | 1.0 | 2.5 | 0.579 | 0.858 | 0 |
| Test No. | PC1 | PC2 | PC3 | MPCI |
|---|---|---|---|---|
| 1 | S | S | S | VS |
| 2 | S | M | M | NS |
| 3 | S | L | L | S |
| 4 | M | S | M | ND |
| 5 | M | M | L | M |
| 6 | M | L | S | HD |
| 7 | L | S | L | L |
| 8 | L | M | S | HL |
| 9 | L | L | M | VL |
| Exp. No. | PC1 | PC2 | PC3 | MPCI |
|---|---|---|---|---|
| 1 | 1.000 | 0.979 | 0.744 | 0.914 |
| 2 | 0.925 | 1.000 | 0.404 | 0.938 |
| 3 | 0.000 | 0.442 | 0.998 | 0.517 |
| 4 | 0.035 | 0.300 | 1.000 | 0.525 |
| 5 | 0.737 | 0.912 | 0.385 | 0.539 |
| 6 | 0.675 | 0.875 | 0.378 | 0.821 |
| 7 | 0.502 | 0.659 | 0.713 | 0.597 |
| 8 | 0.059 | 0.000 | 0.894 | 0.511 |
| 9 | 0.579 | 0.858 | 0.000 | 0.658 |
| A | B | C | D | |
|---|---|---|---|---|
| Level 1 | 0.790 | 0.679 | 0.749 | 0.704 |
| Level 2 | 0.628 | 0.663 | 0.707 | 0.785 |
| Level 3 | 0.589 | 0.665 | 0.551 | 0.518 |
| max-min | 0.201 | 0.016 | 0.198 | 0.268 |
| Rank | 2 | 4 | 3 | 1 |
| Factors | Sum of Squares | Degree of Freedom | Mean of Squares | Contributions (%) |
|---|---|---|---|---|
| A | 8.837 | 2 | 4.419 | 29.46% |
| B | 0.703 | 2 | 0.352 | 2.34% |
| C | 8.691 | 2 | 4.346 | 28.97% |
| D | 11.768 | 2 | 5.884 | 39.23% |
| Characteristics | Initial Structure A1-B3-C3-D3 | Optimally Designed Structure A1-B1-C1-D2 | Gain |
|---|---|---|---|
| G | 6.880 | 20.481 | 13.601 |
| P | 5.112 | 16.209 | 11.097 |
| SNR | 38.701 | 39.074 | 0.373 |
| Systems | PRmax [dBm] | PRmin [dBm] | PRave [dBm] |
|---|---|---|---|
| No-antenna | −0.2428 | −4.2258 | −2.5052 |
| CPC | 4.1929 | −45.6190 | 0.3267 |
| Initial structure | 2.1986 | −45.6190 | −1.8014 |
| Optimally designed structure | 8.9900 | −45.6190 | 6.4635 |
| Parameter Types | Parameter Values |
|---|---|
| FET channel noise factor Γ | 1.5 |
| Background current Ibg | 5.1 mA |
| Fixed capacitance of photodetector per unit area η | 112 pF/cm2 |
| Noise bandwidth factors I2 | 0.562 |
| FET transconductance gm | 30 Ma |
| Noise bandwidth factors I3 [35] | 0.0868 |
| Open-loop voltage gain G | 10.0 |
| Equivalent noise bandwidth B | 100 Mbit/s |
| Absolute temperature TK | 298 K |
| Systems | SNRRmax [dB] | SNRRmin [dB] | SNRRave [dB] |
|---|---|---|---|
| No-antenna | 71.4401 | 46.6286 | 67.3383 |
| CPC | 92.1048 | 62.3373 | 86.7153 |
| Initial structure | 92.1048 | 14.4722 | 86.1109 |
| Optimally designed structure | 92.1048 | 69.0869 | 89.8874 |
| Optical Receiver | FOV [°] | Optical Gain | Spot Size [mm] | Received Power [dBm] | SNR [dB] |
|---|---|---|---|---|---|
| CPC | 40 | 3.85 | 3 | 0.3267 | 68.5486 |
| Lens-walled structure | 80 | 8.62 | 4 | 5.9484 | 82.8563 |
| Proposed optical receiver | 90 | 10.57 | 2 | 6.4635 | 89.8874 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Peng, X.; Kong, L. Optimum Design of a Composite Optical Receiver by Taguchi and Fuzzy Logic Methods. Micromachines 2021, 12, 1434. https://doi.org/10.3390/mi12121434
Wang N, Peng X, Kong L. Optimum Design of a Composite Optical Receiver by Taguchi and Fuzzy Logic Methods. Micromachines. 2021; 12(12):1434. https://doi.org/10.3390/mi12121434
Chicago/Turabian StyleWang, Ning, Xing Peng, and Lingbao Kong. 2021. "Optimum Design of a Composite Optical Receiver by Taguchi and Fuzzy Logic Methods" Micromachines 12, no. 12: 1434. https://doi.org/10.3390/mi12121434
APA StyleWang, N., Peng, X., & Kong, L. (2021). Optimum Design of a Composite Optical Receiver by Taguchi and Fuzzy Logic Methods. Micromachines, 12(12), 1434. https://doi.org/10.3390/mi12121434








