Laser Actuated Microgripper Using Optimized Chevron-Shaped Actuator
Abstract
:1. Introduction
2. Microgripper Design, Optimization, and Fabrication
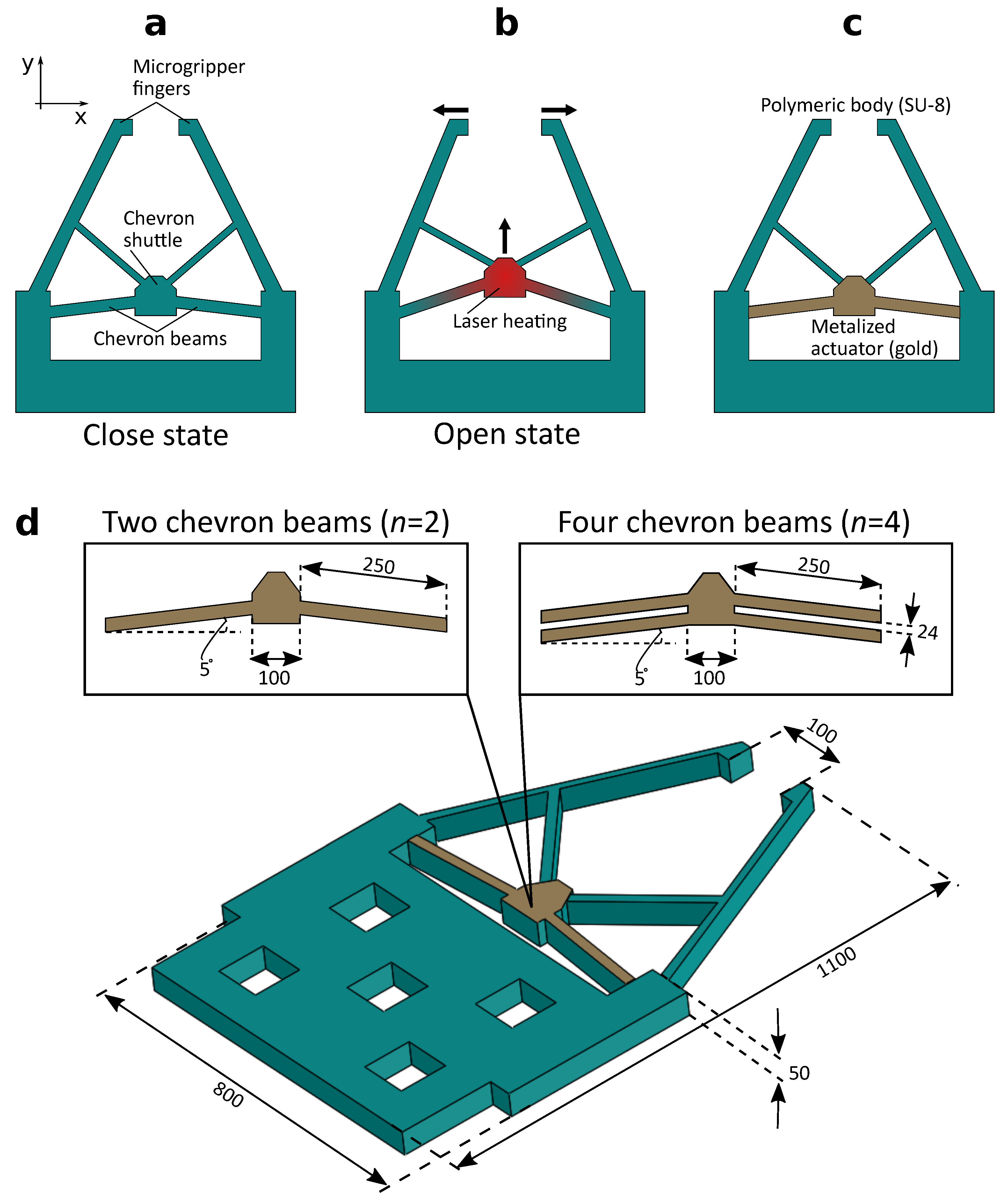
2.1. Design of Microgripper
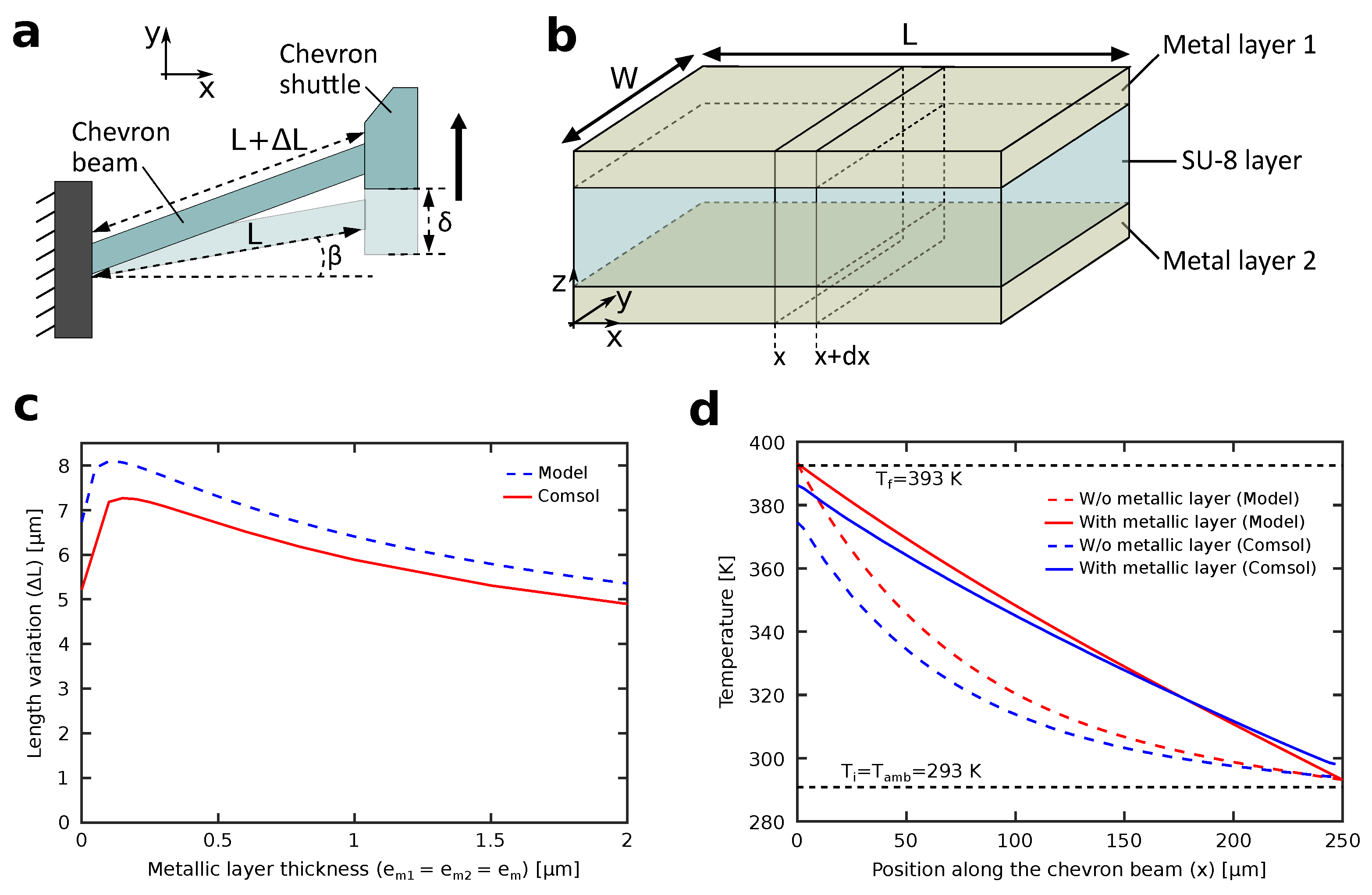
2.2. Modeling and Optimization of Metal-Coated Chevron-Shaped Actuator
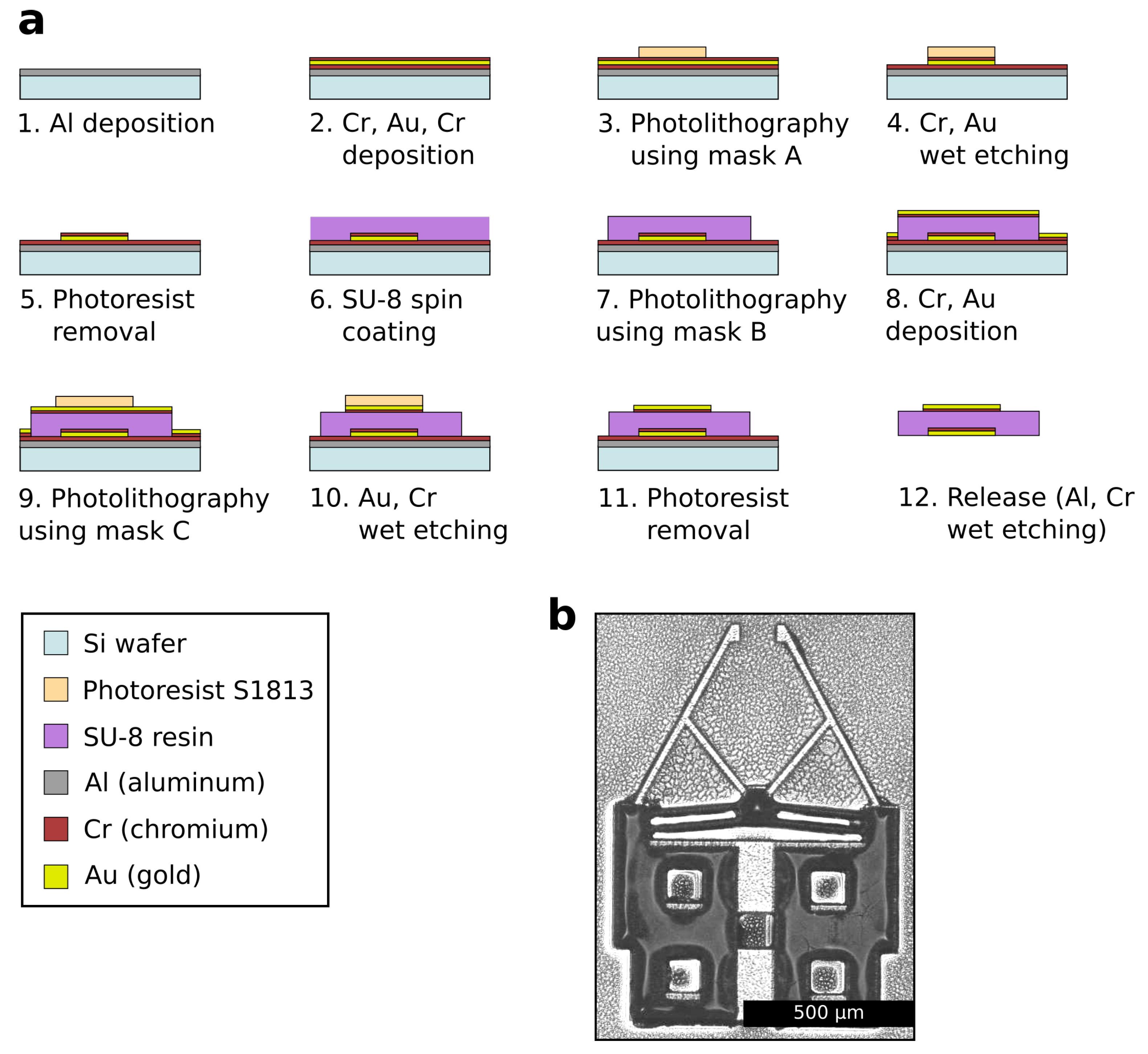
2.3. Fabrication of Microgripper
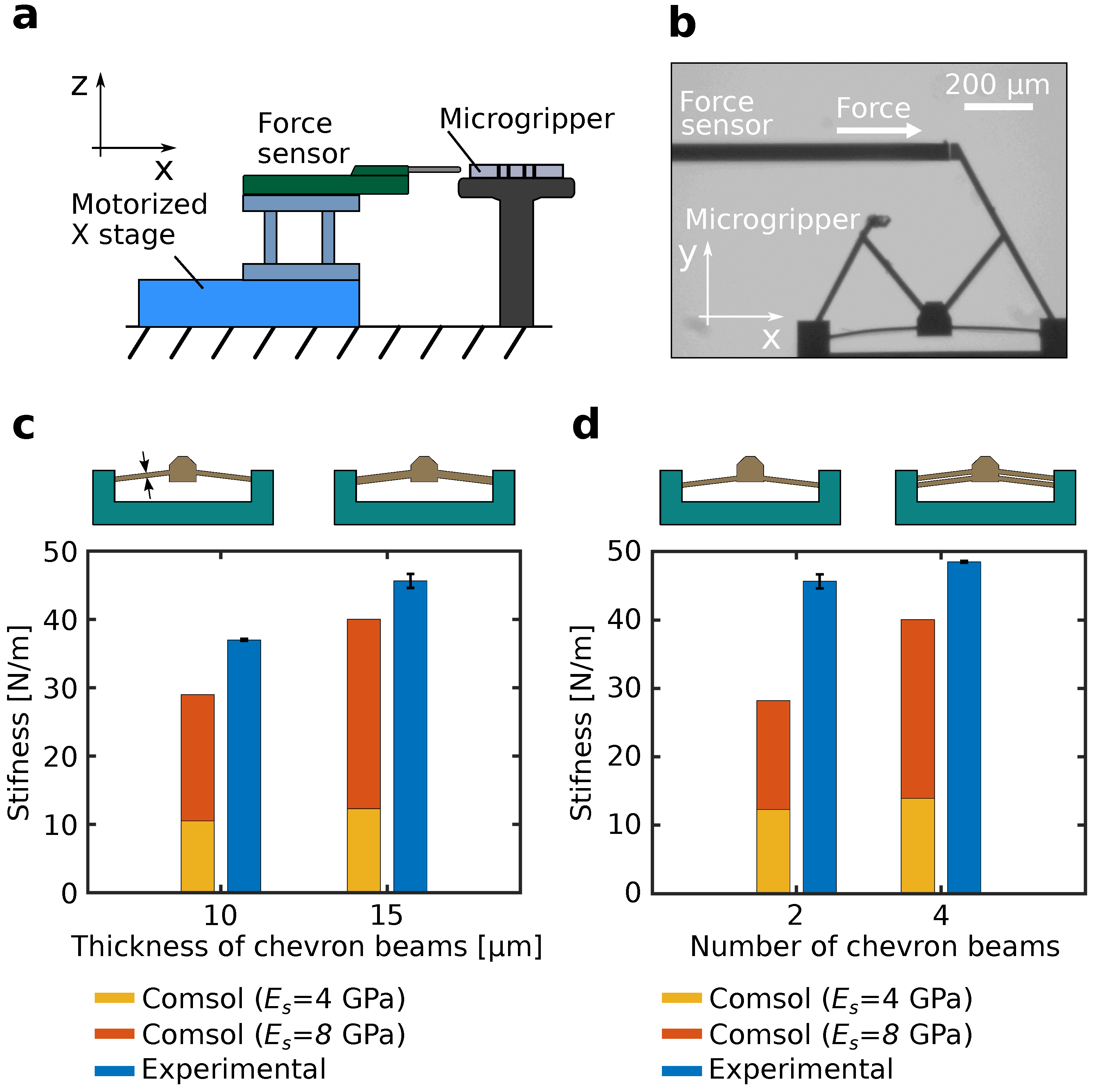
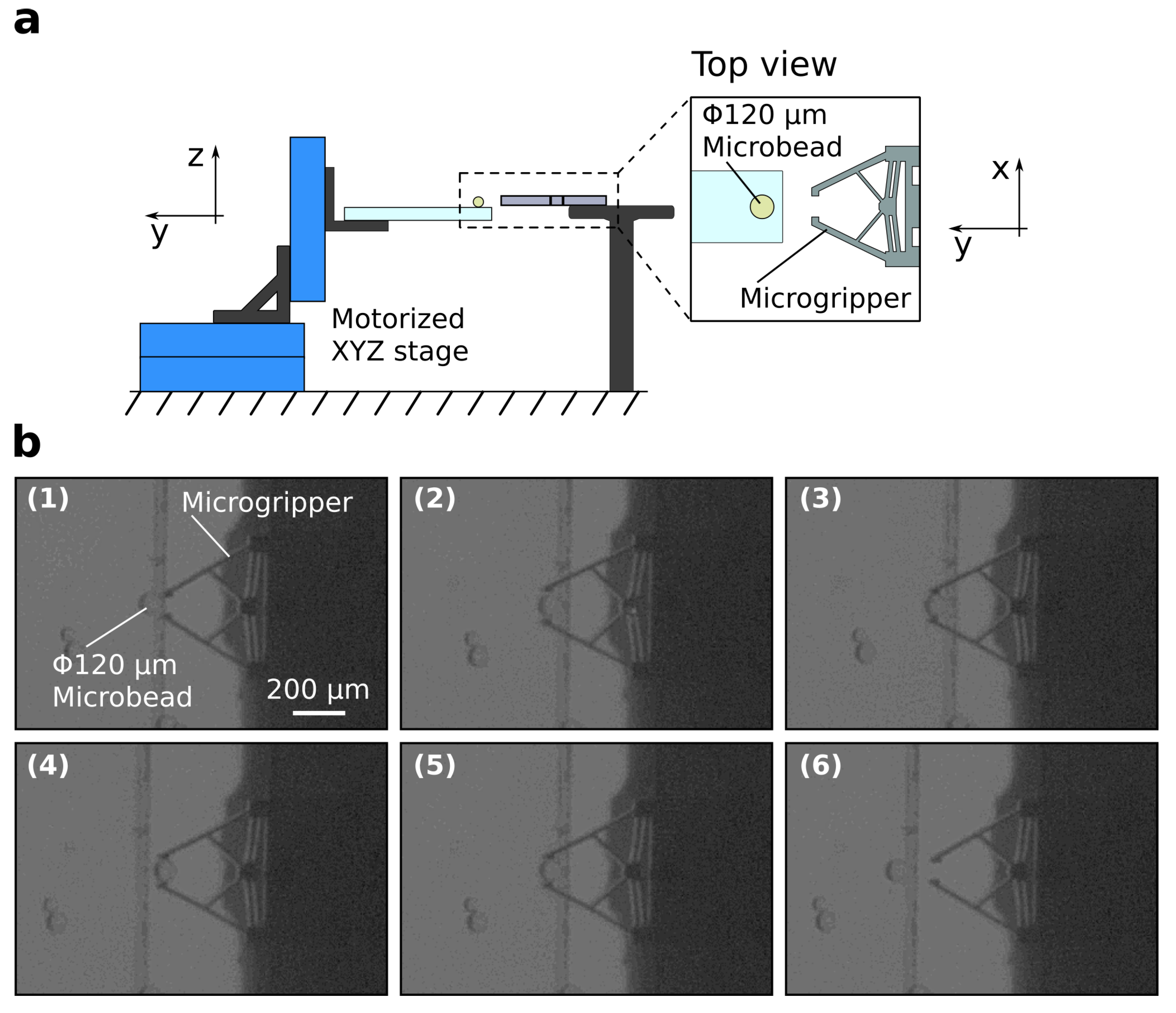
3. Experiments
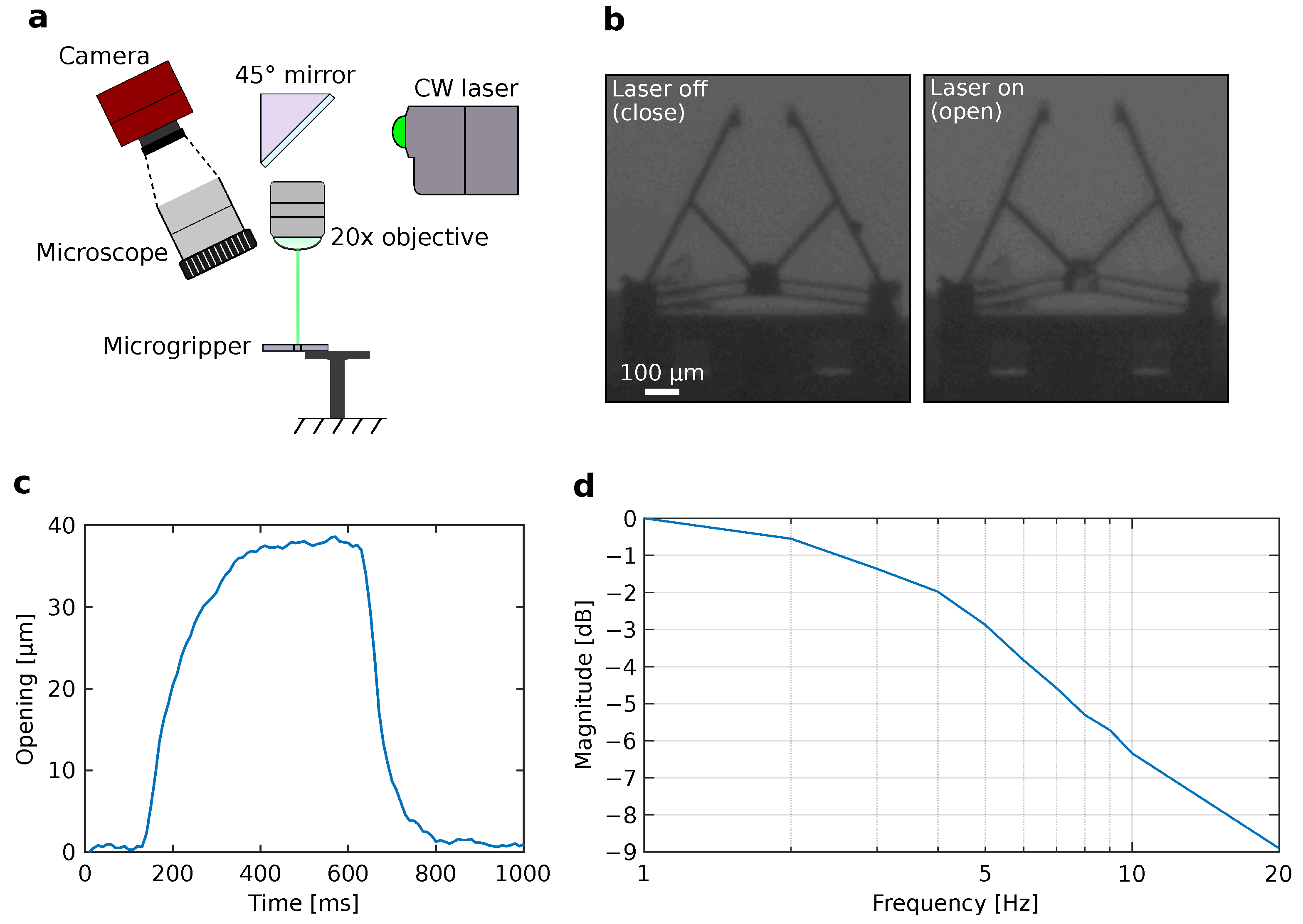
3.1. Microgripper Actuation and Response
3.2. Generated Force
3.3. Application to Micromanipulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Z.; Wang, X.; Liu, J.; Dai, C.; Sun, Y. Robotic micromanipulation: Fundamentals and applications. Annu. Rev. Control. Robot. Auton. Syst. 2019, 2, 181–203. [Google Scholar] [CrossRef]
- Li, X.; Fukuda, T. Magnetically guided micromanipulation of magnetic microrobots for accurate creation of artistic patterns in liquid environment. Micromachines 2020, 11, 697. [Google Scholar] [CrossRef] [PubMed]
- Jing, W.; Chowdhury, S.; Guix, M.; Wang, J.; An, Z.; Johnson, B.V.; Cappelleri, D.J. A microforce-sensing mobile microrobot for automated micromanipulation tasks. IEEE Trans. Autom. Sci. Eng. 2018, 16, 518–530. [Google Scholar] [CrossRef]
- Gursky, B.; Bütefisch, S.; Leester-Schädel, M.; Li, K.; Matheis, B.; Dietzel, A. A disposable pneumatic microgripper for cell manipulation with image-based force sensing. Micromachines 2019, 10, 707. [Google Scholar] [CrossRef] [Green Version]
- Power, M.; Thompson, A.J.; Anastasova, S.; Yang, G.Z. A monolithic force-sensitive 3D microgripper fabricated on the tip of an optical fiber using 2-photon polymerization. Small 2018, 14, 1703964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yin, C.; Wei, F.; Zhan, Z.; Zheng, J.; Yao, L.; Yang, W.; Li, M. Untethered microgripper-the dexterous hand at microscale. Biomed. Microdevices 2019, 21, 82. [Google Scholar] [CrossRef]
- Velosa-Moncada, L.A.; Aguilera-Cortés, L.A.; González-Palacios, M.A.; Raskin, J.P.; Herrera-May, A.L. Design of a novel MEMS microgripper with rotatory electrostatic comb-drive actuators for biomedical applications. Sensors 2018, 18, 1664. [Google Scholar] [CrossRef] [Green Version]
- Lyu, Z.; Xu, Q. Recent design and development of piezoelectric-actuated compliant microgrippers: A review. Sens. Actuators A Phys. 2021, 331, 113002. [Google Scholar] [CrossRef]
- Cauchi, M.; Grech, I.; Mallia, B.; Mollicone, P.; Sammut, N. The effects of cold arm width and metal deposition on the performance of a U-beam electrothermal MEMS microgripper for biomedical applications. Micromachines 2019, 10, 167. [Google Scholar] [CrossRef] [Green Version]
- Kuo, J.C.; Huang, H.W.; Tung, S.W.; Yang, Y.J. A hydrogel-based intravascular microgripper manipulated using magnetic fields. Sens. Actuators A Phys. 2014, 211, 121–130. [Google Scholar] [CrossRef]
- Pevec, S.; Donlagic, D. Optically controlled fiber-optic micro-gripper for sub-millimeter objects. Opt. Lett. 2019, 44, 2177–2180. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, B.; Gauthier, M.; Laurent, G.J.; Bolopion, A. Mobile Microrobots for In Vitro Biomedical Applications: A Survey. IEEE Trans. Robot. 2021, 2021. [Google Scholar] [CrossRef]
- Feng, L.; Hagiwara, M.; Ichikawa, A.; Arai, F. On-chip enucleation of bovine oocytes using microrobot-assisted flow-speed control. Micromachines 2013, 4, 272–285. [Google Scholar] [CrossRef]
- Ahmad, B.; Kawahara, T.; Yasuda, T.; Arai, F. Microrobotic platform for mechanical stimulation of swimming microorganism on a chip. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4680–4685. [Google Scholar]
- Villangca, M.J.; Palima, D.; Banas, A.R.; Glückstad, J. Light-driven micro-tool equipped with a syringe function. Light. Sci. Appl. 2016, 5, e16148. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Lv, J.A.; Tian, X.; Wang, Y.; Liu, J.; Yu, Y. A remotely driven and controlled micro-gripper fabricated from light-induced deformation smart material. Smart Mater. Struct. 2016, 25, 095009. [Google Scholar] [CrossRef]
- Elbuken, C.; Khamesee, M.B.; Yavuz, M. Design and implementation of a micromanipulation system using a magnetically levitated MEMS robot. IEEE/ASME Trans. Mechatronics 2009, 14, 434–445. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, H.; Fei, G.; Yu, B.; Tong, X.; Xia, H.; Zhao, Y. Liquid-crystalline dynamic networks doped with gold nanorods showing enhanced photocontrol of actuation. Adv. Mater. 2018, 30, 1706597. [Google Scholar] [CrossRef] [PubMed]
- Lahikainen, M.; Zeng, H.; Priimagi, A. Reconfigurable photoactuator through synergistic use of photochemical and photothermal effects. Nat. Commun. 2018, 9, 4148. [Google Scholar] [CrossRef] [Green Version]
- Shivhare, P.; Uma, G.; Umapathy, M. Design enhancement of a chevron electrothermally actuated microgripper for improved gripping performance. Microsyst. Technol. 2016, 22, 2623–2631. [Google Scholar] [CrossRef]
- Sharif, M.; Pourabbas, B.; Sangermano, M.; Sadeghi Moghadam, F.; Mohammadi, M.; Roppolo, I.; Fazli, A. The effect of graphene oxide on UV curing kinetics and properties of SU8 nanocomposites. Polym. Int. 2017, 66, 405–417. [Google Scholar] [CrossRef]
- Ge, F.; Lu, X.; Xiang, J.; Tong, X.; Zhao, Y. An optical actuator based on gold-nanoparticle-containing temperature-memory semicrystalline polymers. Angew. Chem. 2017, 129, 6222–6226. [Google Scholar] [CrossRef]
- Bagheri, M.; Chae, I.; Lee, D.; Kim, S.; Thundat, T. Selective detection of physisorbed hydrocarbons using photothermal cantilever deflection spectroscopy. Sens. Actuators B Chem. 2014, 191, 765–769. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Chang, J.K.; Aurelio, D.; Li, W.; Kim, B.J.; Kim, J.H.; Liscidini, M.; Rogers, J.A.; Omenetto, F.G. Light-activated shape morphing and light-tracking materials using biopolymer-based programmable photonic nanostructures. Nat. Commun. 2021, 12, 1651. [Google Scholar] [CrossRef] [PubMed]
- Sangermano, M.; Calvara, L.; Chiavazzo, E.; Ventola, L.; Asinari, P.; Mittal, V.; Rizzoli, R.; Ortolani, L.; Morandi, V. Enhancement of electrical and thermal conductivity of Su-8 photocrosslinked coatings containing graphene. Prog. Org. Coatings 2015, 86, 143–146. [Google Scholar] [CrossRef]
- Xu, T.; Yoo, J.H.; Babu, S.; Roy, S.; Lee, J.B.; Lu, H. Characterization of the mechanical behavior of SU-8 at microscale by viscoelastic analysis. J. Micromechanics Microengineering 2016, 26, 105001. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Liu, X.; Zhang, Y.; Sun, Y. Micronewton force-controlled manipulation of biomaterials using a monolithic MEMS microgripper with two-axis force feedback. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 3100–3105. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, B.; Chambon, H.; Tissier, P.; Bolopion, A. Laser Actuated Microgripper Using Optimized Chevron-Shaped Actuator. Micromachines 2021, 12, 1487. https://doi.org/10.3390/mi12121487
Ahmad B, Chambon H, Tissier P, Bolopion A. Laser Actuated Microgripper Using Optimized Chevron-Shaped Actuator. Micromachines. 2021; 12(12):1487. https://doi.org/10.3390/mi12121487
Chicago/Turabian StyleAhmad, Belal, Hugo Chambon, Pierre Tissier, and Aude Bolopion. 2021. "Laser Actuated Microgripper Using Optimized Chevron-Shaped Actuator" Micromachines 12, no. 12: 1487. https://doi.org/10.3390/mi12121487
APA StyleAhmad, B., Chambon, H., Tissier, P., & Bolopion, A. (2021). Laser Actuated Microgripper Using Optimized Chevron-Shaped Actuator. Micromachines, 12(12), 1487. https://doi.org/10.3390/mi12121487





