A Multi-Mode Broadband Vibration Energy Harvester Composed of Symmetrically Distributed U-Shaped Cantilever Beams
Abstract
:1. Introduction
2. Structural Design and Fabrication
2.1. Structural Design
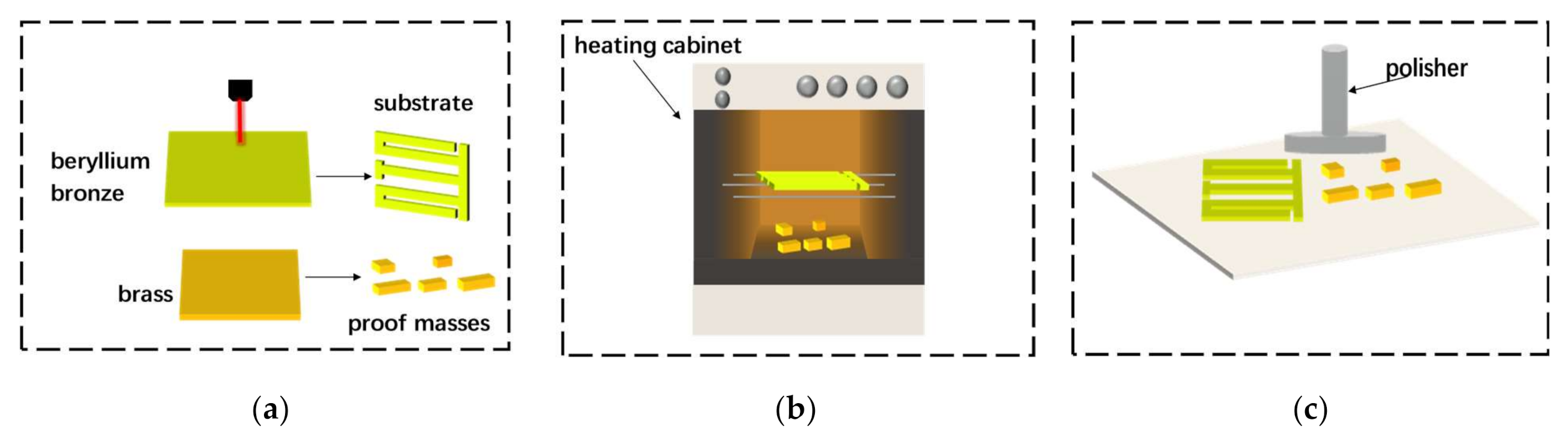
2.2. Fabrication
- (a)
- Laser cutting. A laser cutting machine is used to cut the substrate and five tip masses according to the designed geometric dimensions.
- (b)
- Surface heating. In order to make the surface of the metal substrate smooth, it needs to be placed in a heating box, heated at 300℃ for two hours and then taken out and cooled to room temperature.
- (c)
- Surface polishing. Place the cooled metal substrate and tip masses on a polishing machine and use the polishing machine to remove impurities and oxide layers on the surface of the substrate and five tip masses to ensure a clean and flat surface.
- (d)
- Surface cleaning. Put the polished metal substrate and tip masses into an ultrasonic cleaning machine to clean the surface of impurities to facilitate subsequent bonding work. Put the cleaned parts on a clean glass plate and let them dry.
- (e)
- Bonding piezoelectric ceramics and proof masses. The piezoelectric ceramic sheet and the metal substrate need to be connected with conductive silver glue to meet the requirements of mechanical connection and electrical connection. Place the piezoelectric ceramic sheet and the metal substrate on a flat operating table, use a small brush to evenly spread the conductive silver glue on the surfaces of both and then place the piezoelectric ceramic on the metal substrate and press it gently. Wipe gently with a cotton ball dipped in acetone solution to remove excess glue. Similarly, the masses are bonded. After the piezoelectric ceramics and the mass block are bonded, place the bonded structure for more than 24 h to ensure a stable bonding.
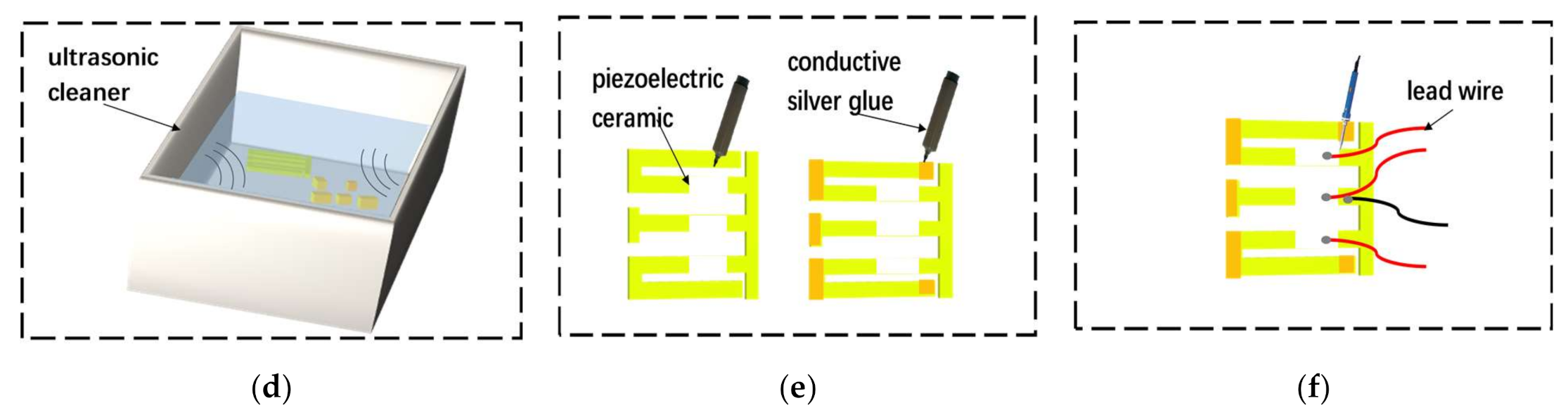
- (f)
- Wire bonding. Place the energy harvester on the operating table, and use an electric soldering iron to weld the thin wires on the three electrodes and the upper surface of the metal substrate, respectively, as the positive and negative electrodes of the energy harvester. Then, use conductive silver glue to bond the three electrodes on the surface of the piezoelectric ceramic; the three wires on the three electrodes are connected in parallel.
3. Simulation and Experimental Study
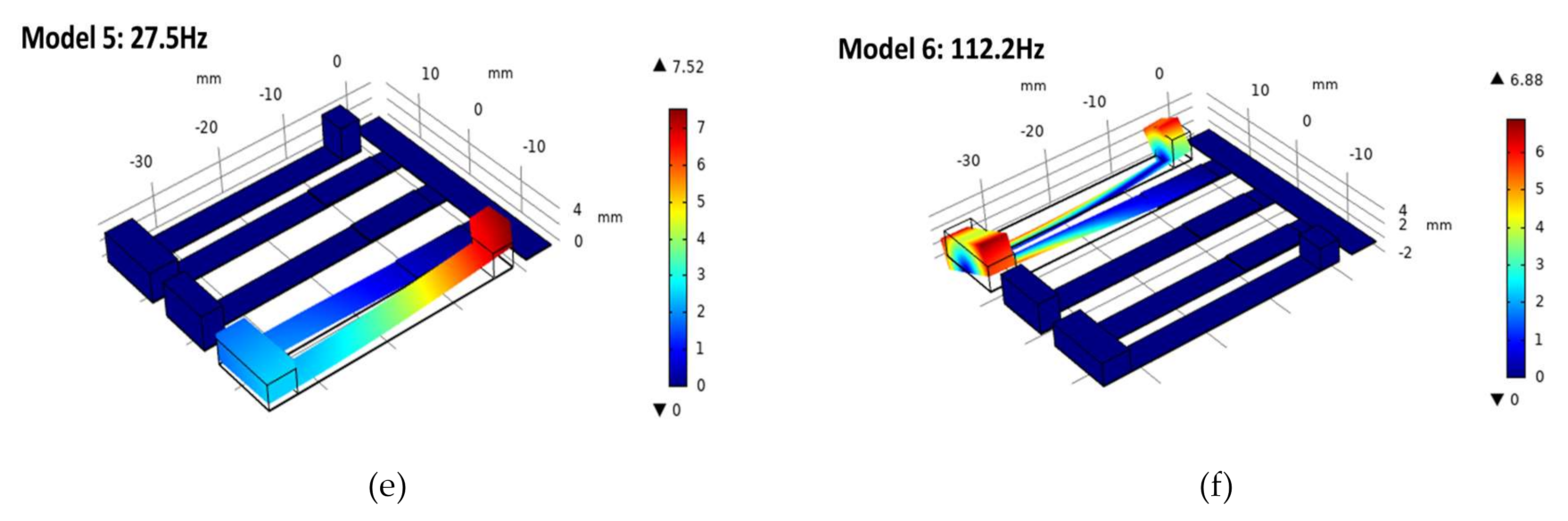
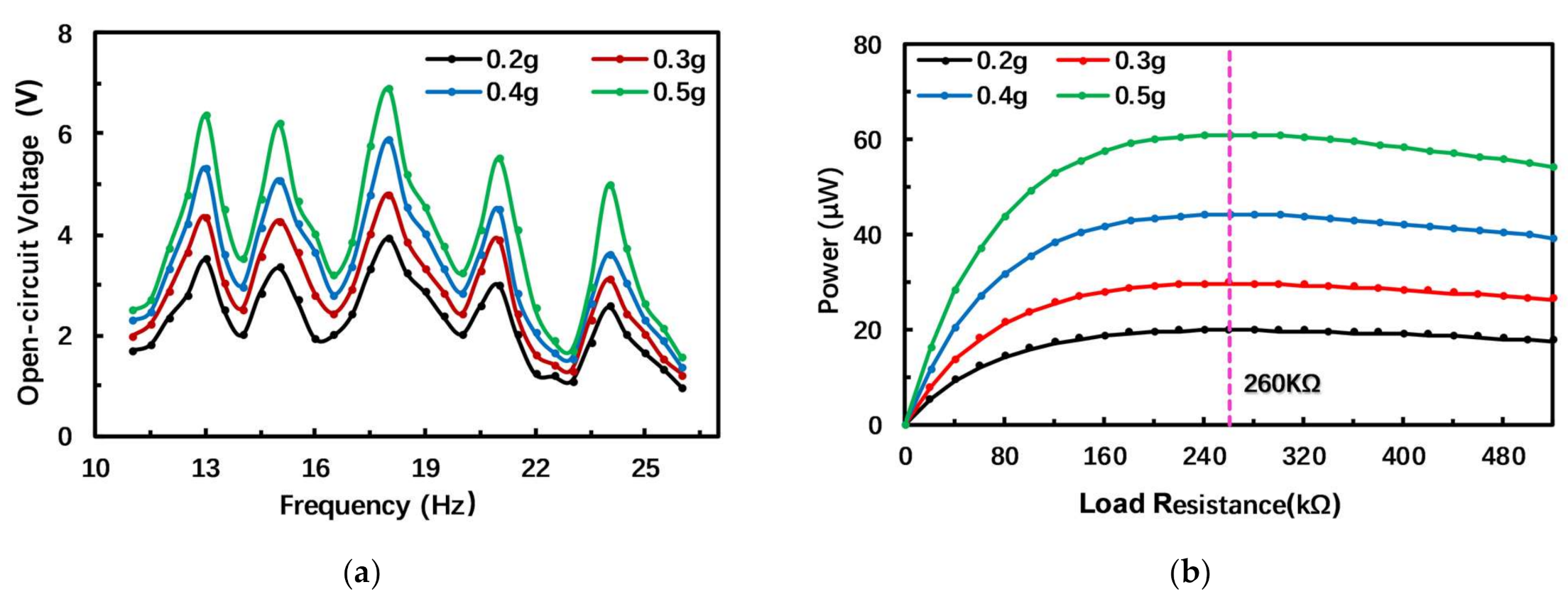
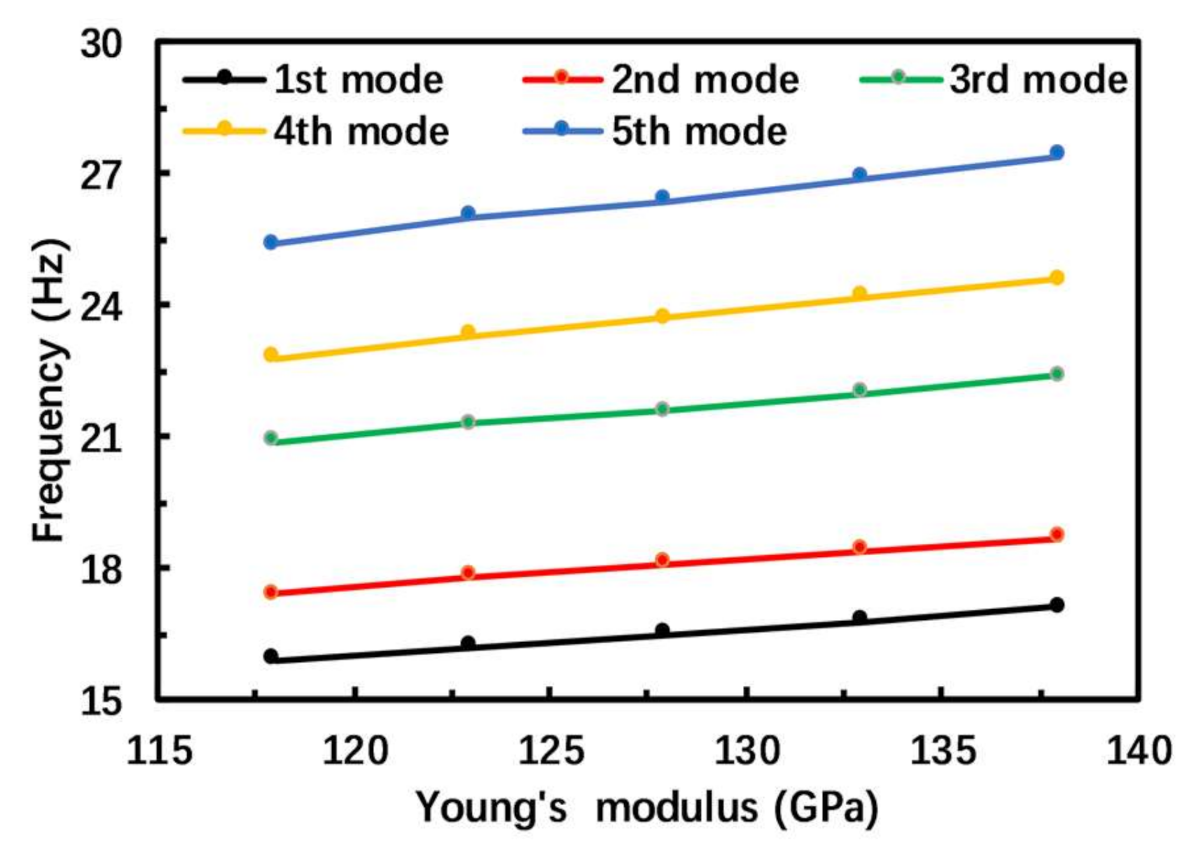
3.1. Simulation Study
3.2. Experimental Study
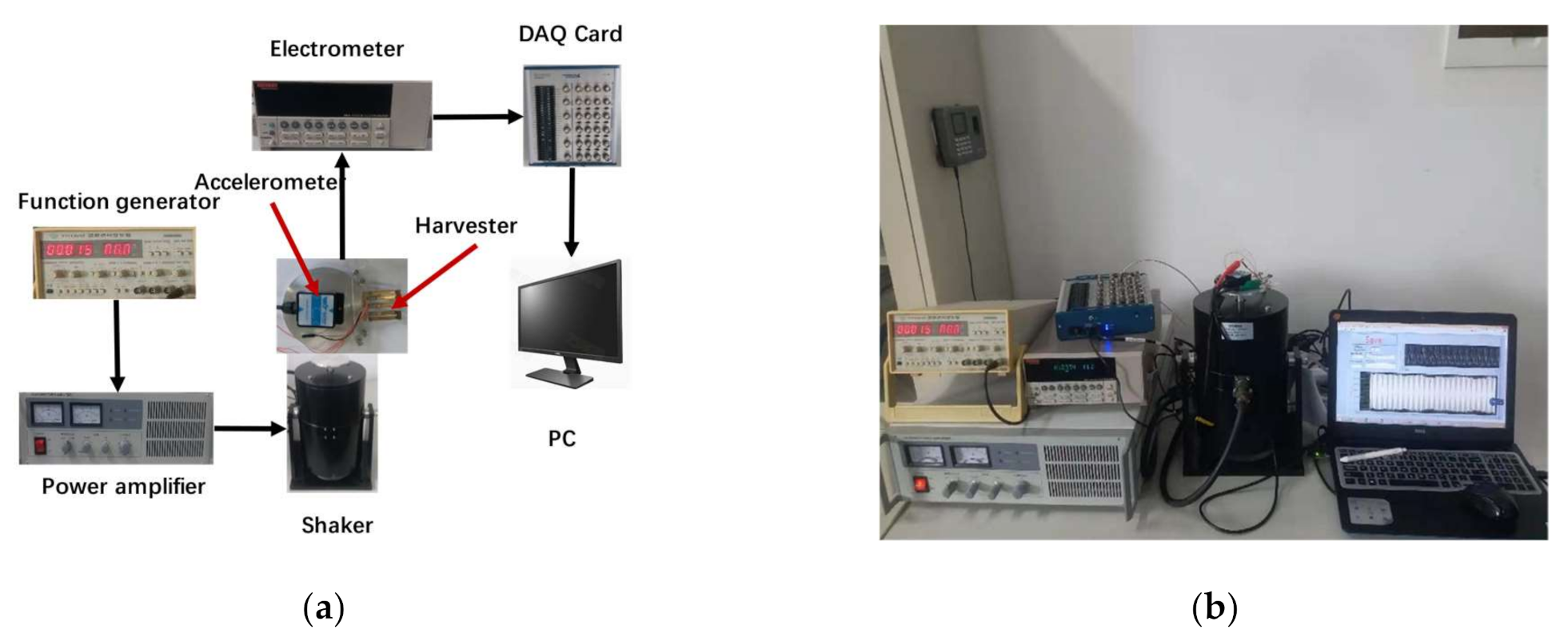
3.2.1. Experimental Setup
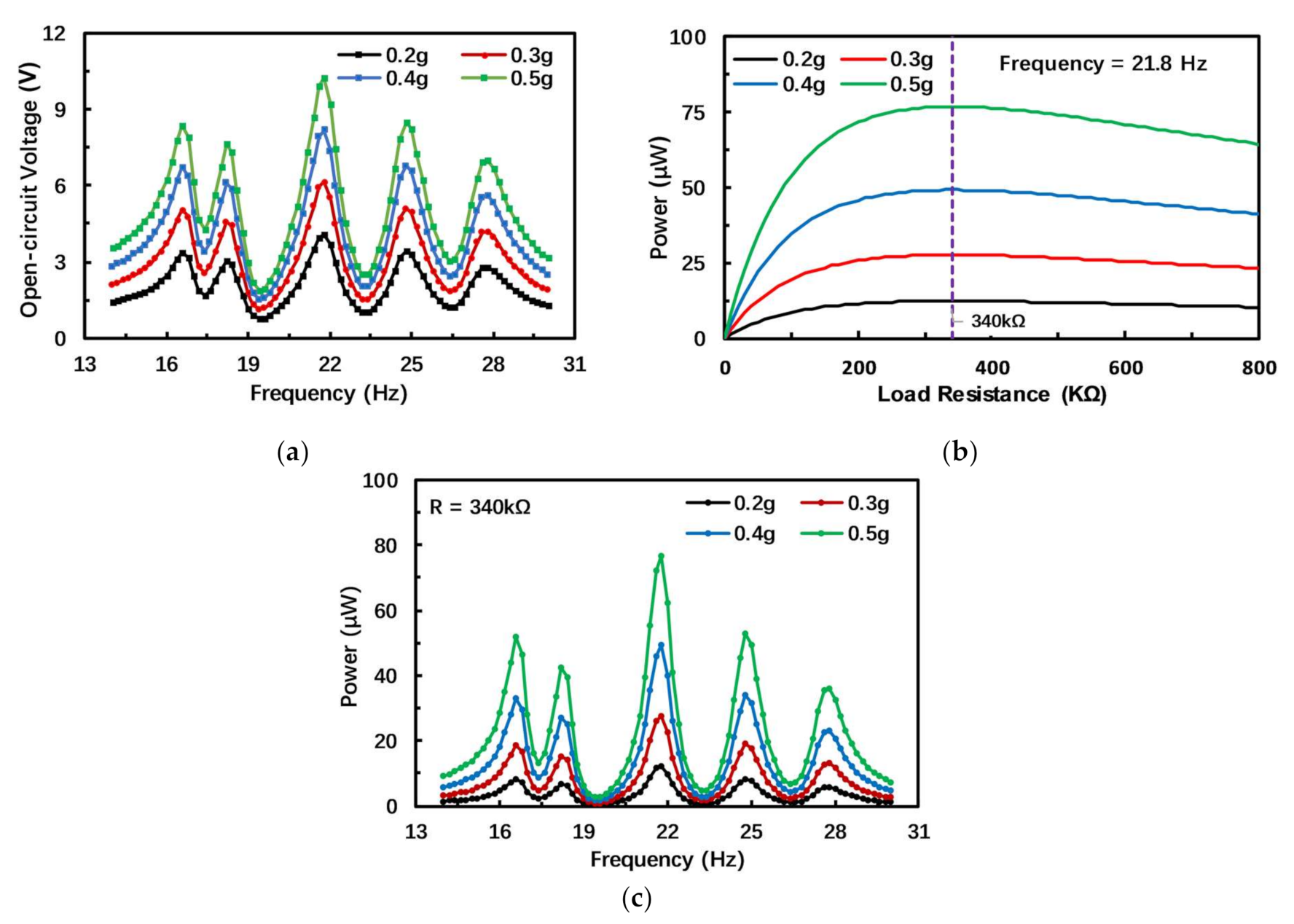
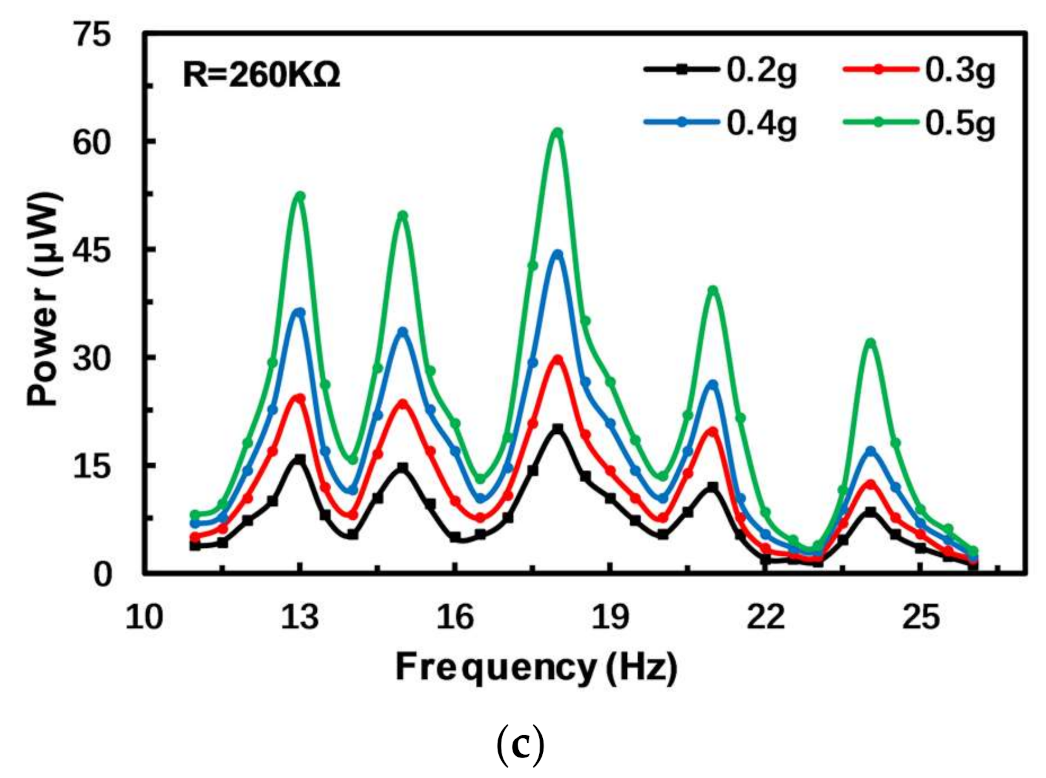
3.2.2. Experimental Results
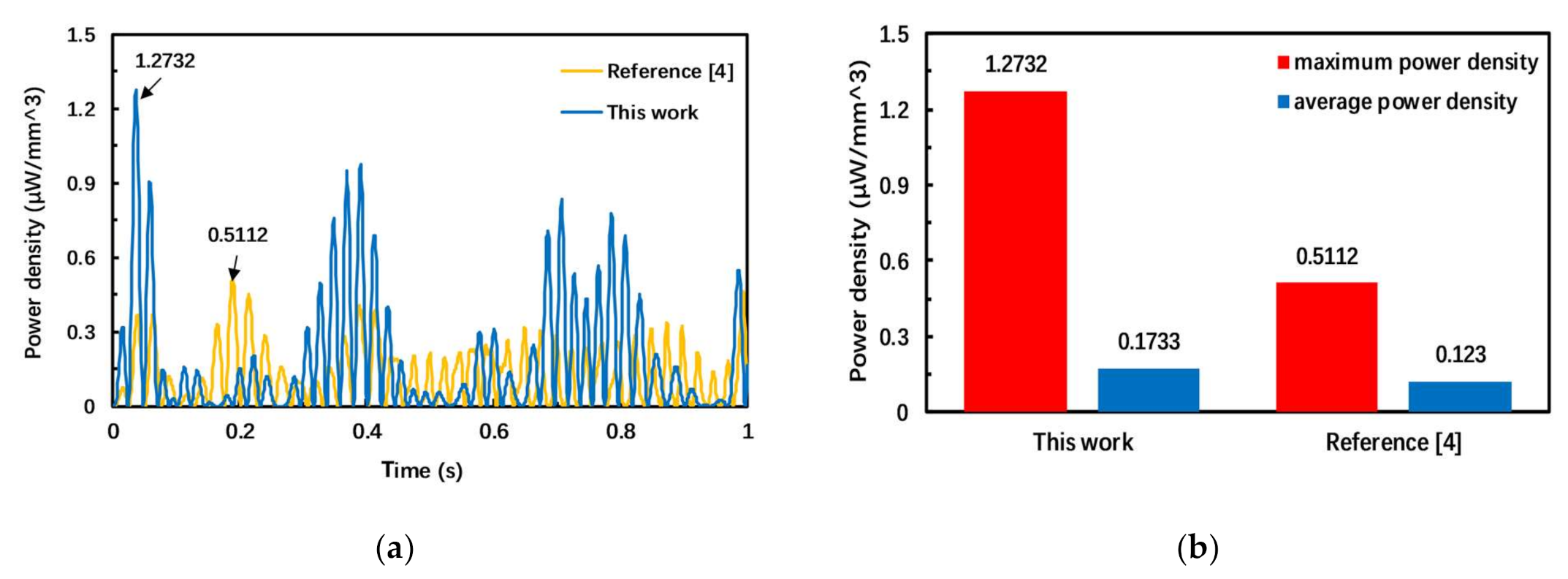
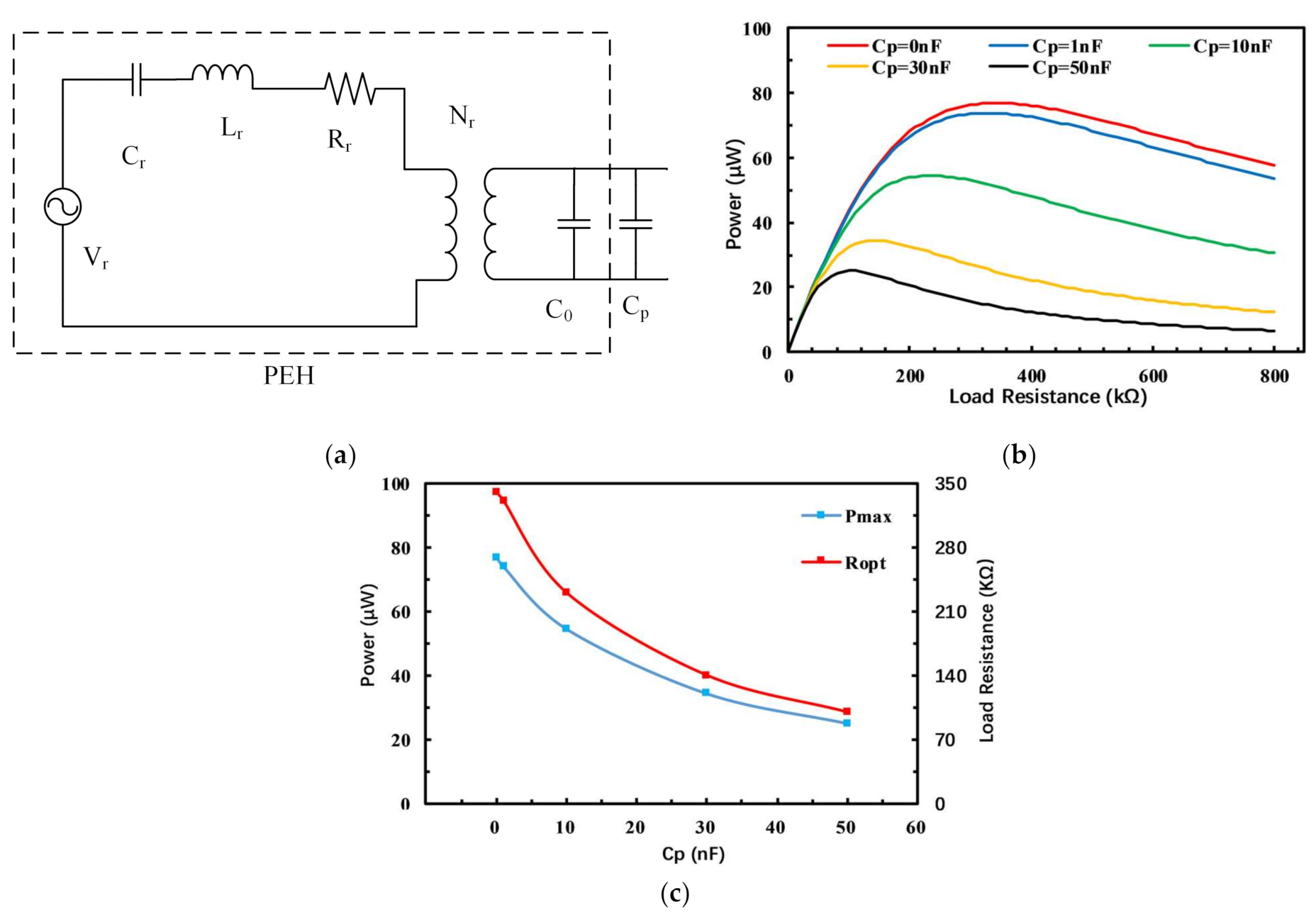
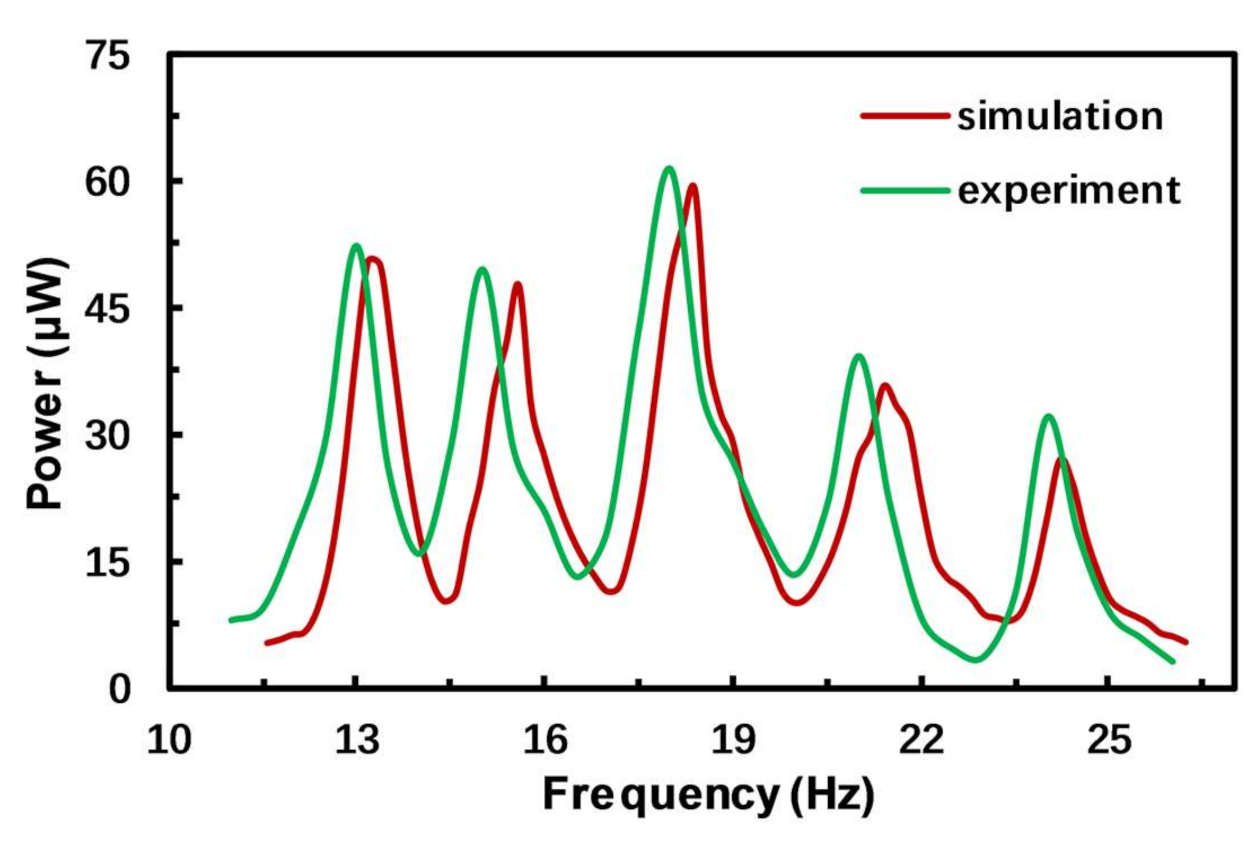
4. Error Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, H.X.; Zhao, L.C.; Gao, Q.H.; Zuo, L.; Liu, F.R.; Tan, T.; Zhang, W.M. Mechanical modulations for enhancing energy harvesting: Principles, methods and applications. Appl. Energy 2019, 255, 113871. [Google Scholar] [CrossRef]
- Dong, L.; Closson, A.B.; Jin, C.; Trase, I.; Chen, Z.; Zhang, J.X. Vibration-Energy-Harvesting System: Transduction Mechanisms, Frequency Tuning Techniques, and Biomechanical Applications. Adv. Mater. Technol. 2019, 4, 1900177. [Google Scholar] [CrossRef]
- Oh, Y.; Kwon, D.S.; Eun, Y.; Kim, W.; Kim, M.O.; Ko, H.J.; Kim, J. Flexible energy harvester with piezoelectric and thermoelectric hybrid mechanisms for sustainable harvesting. Int. J. Precis. Eng. Manuf. -Green Technol. 2019, 6, 691–698. [Google Scholar] [CrossRef]
- Wu, M.; Ou, Y.; Mao, H.; Li, Z.; Liu, R.; Ming, A.; Ou, W. Multi-resonant wideband energy harvester based on a folded asymmetric M-shaped cantilever. AIP Adv. 2015, 5, 077149. [Google Scholar] [CrossRef]
- Zhang, C.; Dai, K.; Liu, D.; Yi, F.; Wang, X.; Zhu, L.; You, Z. Ultralow Quiescent Power-Consumption Wake-Up Technology Based on the Bionic Triboelectric Nanogenerator. Adv. Sci. 2020, 7, 2000254. [Google Scholar] [CrossRef]
- Qi, N.; Dai, K.; Yi, F.; Wang, X.; You, Z.; Zhao, J. An adaptive energy management strategy to extend battery lifetime of solar powered wireless sensor nodes. IEEE Access 2019, 7, 88289–88300. [Google Scholar] [CrossRef]
- Zhou, G.; Huang, L.; Li, W.; Zhu, Z. Harvesting ambient environmental energy for wireless sensor networks: A survey. J. Sens. 2014, 2014, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Hwang, W.; Kim, K.B.; Cho, J.Y.; Yang, C.H.; Kim, J.H.; Song, G.J.; Sung, T.H. Watts-level road-compatible piezoelectric energy harvester for a self-powered temperature monitoring system on an actual roadway. Appl. Energy 2019, 243, 313–320. [Google Scholar] [CrossRef]
- Nguyen, M.S.; Yoon, Y.J.; Kim, P. Enhanced broadband performance of magnetically coupled 2-DOF bistable energy harvester with secondary intrawell resonances. Int. J. Precis. Eng. Manuf. -Green Technol. 2019, 6, 521–530. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhao, H.; Guo, Y.; Rui, P.; Shi, S.; Zhang, W.; Wang, Z.L. An Easily Assembled Electromagnetic-Triboelectric Hybrid Nanogenerator Driven by Magnetic Coupling for Fluid Energy Harvesting and Self-Powered Flow Monitoring in a Smart Home/City. Adv. Mater. Technol. 2019, 4, 1900741. [Google Scholar] [CrossRef]
- Yang, Z.; Zu, J. Toward harvesting vibration energy from multiple directions by a nonlinear compressive-mode piezoelectric transducer. IEEE ASME Trans Mechatron 2015, 21, 1787–1791. [Google Scholar] [CrossRef]
- Zhao, H.; Wei, X.; Zhong, Y.; Wang, P. A Direction Self-Tuning Two-Dimensional Piezoelectric Vibration Energy Harvester. Sensors 2020, 20, 77. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Hou, C.; Lin, J.; Li, Y.; Shi, Q.; Chen, T.; Lee, C. A non-resonant rotational electromagnetic energy harvester for low-frequency and irregular human motion. Appl. Phys. Lett. 2018, 113, 203901. [Google Scholar] [CrossRef] [Green Version]
- Fan, K.; Cai, M.; Liu, H.; Zhang, Y. Capturing energy from ultra-low frequency vibrations and human motion through a monostable electromagnetic energy harvester. Energy 2019, 169, 356–368. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y. A dual electromagnetic array with intrinsic frequency up-conversion for broadband vibrational energy harvesting. Appl. Phys. Lett. 2019, 114, 053902. [Google Scholar] [CrossRef]
- Gao, C.; Gao, S.; Liu, H.; Jin, L.; Lu, J.; Li, P. Optimization for output power and band width in out-of-plane vibration energy harvesters employing electrets theoretically, numerically and experimentally. Microsyst. Technol. 2017, 23, 5759–5769. [Google Scholar] [CrossRef]
- Xu, M.; Zhao, T.; Wang, C.; Zhang, S.L.; Li, Z.; Pan, X.; Wang, Z.L. High power density tower-like triboelectric nanogenerator for harvesting arbitrary directional water wave energy. ACS Nano 2019, 13, 1932–1939. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Pan, L.; Wang, J.; Xu, M.; Dai, G.; Zou, H.; Wang, Z.L. An ultra-low-friction triboelectric–electromagnetic hybrid nanogenerator for rotation energy harvesting and self-powered wind speed sensor. ACS Nano 2018, 12, 9433–9440. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.E.; Lee, S.; Kim, Y.Y. Mathematical model development, experimental validation and design parameter study of a folded two-degree-of-freedom piezoelectric vibration energy harvester. Int. J. Precis. Eng. Manuf. Technol. 2019, 6, 893–906. [Google Scholar] [CrossRef]
- Wang, P.; Liu, R.; Ding, W.; Zhang, P.; Pan, L.; Dai, G.; Wang, Z.L. Complementary Electromagnetic-Triboelectric Active Sensor for Detecting Multiple Mechanical Triggering. Adv. Funct. Mater. 2018, 28, 1705808. [Google Scholar] [CrossRef]
- Yang, J.; Yue, X.; Wen, Y.; Li, P.; Yu, Q.; Bai, X. Design and analysis of a 2D broadband vibration energy harvester for wireless sensors. Sens. Actuators A 2014, 205, 47–52. [Google Scholar] [CrossRef]
- Mažeika, D.; Čeponis, A.; Yang, Y. Multifrequency piezoelectric energy harvester based on polygon-shaped cantilever array. Noise Control 2018, 2018, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Priya, S. Criterion for material selection in design of bulk piezoelectric energy harvesters. IEEE Trans. Sonics Ultrason. 2010, 57, 2610–2612. [Google Scholar] [CrossRef] [PubMed]
- Somkuwar, R.; Chandwani, J.; Deshmukh, R. Wideband auto-tunable vibration energy harvester using change in centre of gravity. Microsyst. Technol. 2018, 24, 3033–3044. [Google Scholar] [CrossRef]
- Chandwani, J.; Somkuwar, R.; Deshmukh, R. Multi-band piezoelectric vibration energy harvester for low-frequency applications. Microsyst. Technol. 2019, 25, 3867–3877. [Google Scholar] [CrossRef]
- Chandwani, J.; Somkuwar, R.; Deshmukh, R. Experimental study on band merging of non-linear multi-band piezoelectric energy harvester into single broadband using magnetic coupling. Microsyst. Technol. 2020, 26, 657–671. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Huang, H.; Wu, Z.; Huang, Z.; Mao, H.; Cao, Y. Broadband spring-connected bi-stable piezoelectric vibration energy harvester with variable potential barrier. Results Phys. 2020, 18, 103173. [Google Scholar] [CrossRef]
- Yang, W.; Towfighian, S. A hybrid nonlinear vibration energy harvester. Mech. Syst. Signal Process. 2017, 90, 317–333. [Google Scholar] [CrossRef] [Green Version]
- Hajati, A.; Kim, S.G. Ultra-wide bandwidth piezoelectric energy harvesting. Appl. Phys. Lett. 2011, 99, 083105. [Google Scholar] [CrossRef] [Green Version]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Hajati, A.; Bathurst, S.P.; Lee, H.J.; Kim, S.G. Design and fabrication of a nonlinear resonator for ultra wide-bandwidth energy harvesting applications. In 2011 IEEE 24th International Conference on Micro Electro Mechanical Systems; IEEE: New York, NY, USA, 2011. [Google Scholar]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A compact 2 degree-of-freedom energy harvester with cut-out cantilever beam. Jpn. J. Appl. Phys. 2012, 51, 040211. [Google Scholar] [CrossRef]
- Sun, S.; Peter, W.T. Modeling of a horizontal asymmetric U-shaped vibration-based piezoelectric energy harvester (U-VPEH). Mech. Syst. Signal Process. 2019, 114, 467–485. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, J. A branched beam-based vibration energy harvester. J. Electron. Mater. 2014, 43, 3912–3921. [Google Scholar] [CrossRef]
- Lee, Y. A review of recent research on mm-scale sensor systems. In 2015 International SoC Design Conference (ISOCC); IEEE: New York, NY, USA, 2015; pp. 87–88. [Google Scholar]
- Ziaie, B.; Najafi, K. An implantable microsystem for tonometric blood pressure measurement. Biomed. Microdevices 2001, 3, 285–292. [Google Scholar] [CrossRef]
- Dai, K.; Wang, X.; Niu, S.; Yi, F.; Yin, Y.; Chen, L.; You, Z. Simulation and structure optimization of triboelectric nanogenerators considering the effects of parasitic capacitance. Nano Res. 2017, 10, 157–171. [Google Scholar] [CrossRef]
- Kanda, K.; Saito, T.; Iga, Y.; Higuchi, K.; Maenaka, K. Influence of parasitic capacitance on output voltage for series-connected thin-film piezoelectric devices. Sensors 2012, 12, 16673–16684. [Google Scholar] [CrossRef]
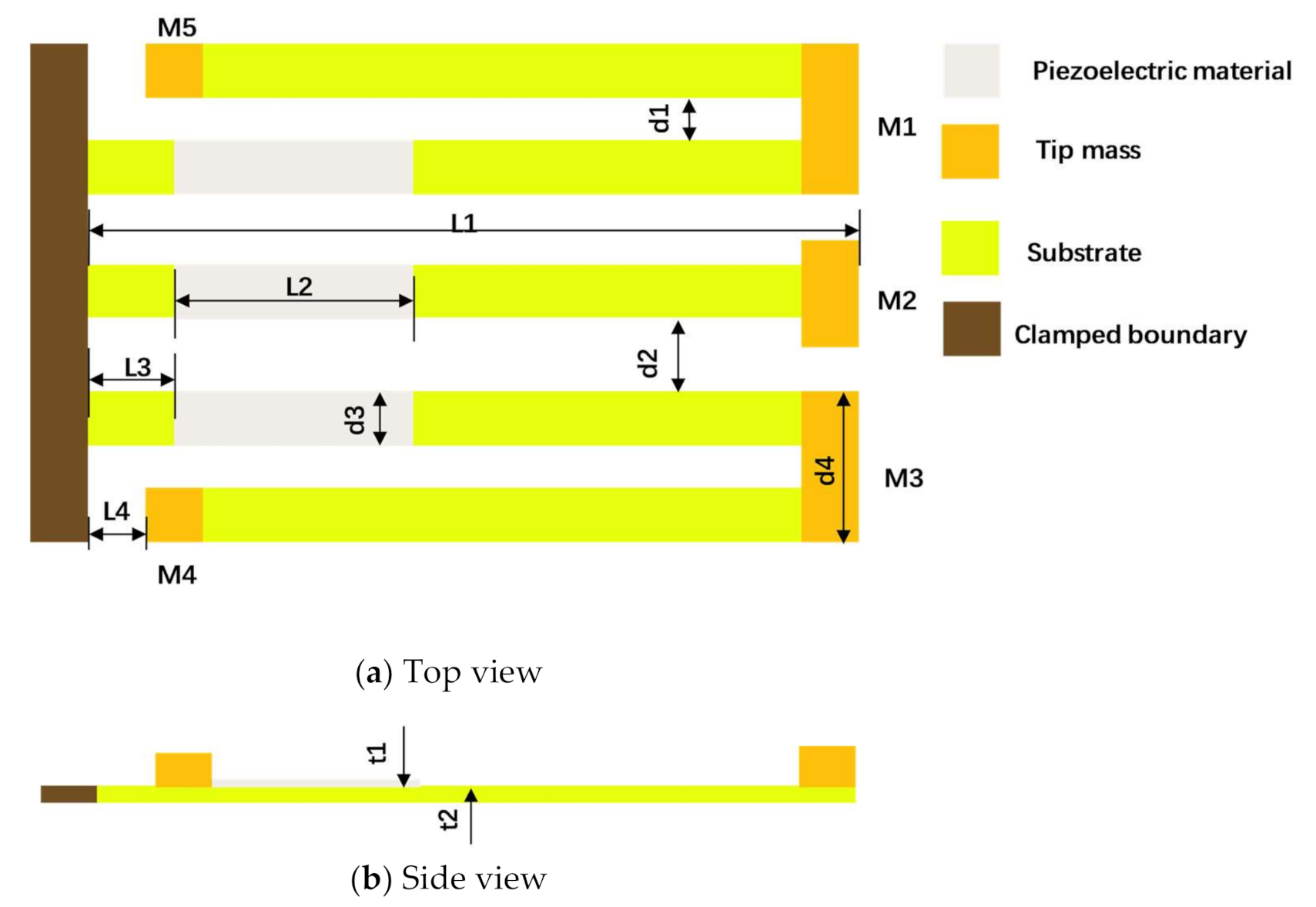

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| L1 | 38 mm | t1 | 0.15 mm |
| L2 | 10 mm | t2 | 0.15 mm |
| L3 | 4 mm | M1 | 10 4 3 |
| L4 | 2 mm | M2 | 8 3 4 |
| d1 | 2 mm | M3 | 10 4 3.5 |
| d2 | 5 mm | M4 | 4 3 4 |
| d3 | 4 mm | M5 | 4 3 3 |
| d4 | 10 mm |
| Property | Substrate | Piezoelectric | Tip Mass |
|---|---|---|---|
| Material | Beryllium Bronze | PZT-5H | Brass |
| Young’s modulus | 128 GPa | 60.6 GPa | 110 GPa |
| Density | 8300 kg/ | 7500 kg/ | 8500 kg/ |
| Piezoelectric constant (d31) | - | −2.74 ×C/N | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Zhang, C.; Dai, K. A Multi-Mode Broadband Vibration Energy Harvester Composed of Symmetrically Distributed U-Shaped Cantilever Beams. Micromachines 2021, 12, 203. https://doi.org/10.3390/mi12020203
Huang X, Zhang C, Dai K. A Multi-Mode Broadband Vibration Energy Harvester Composed of Symmetrically Distributed U-Shaped Cantilever Beams. Micromachines. 2021; 12(2):203. https://doi.org/10.3390/mi12020203
Chicago/Turabian StyleHuang, Xiaohua, Cheng Zhang, and Keren Dai. 2021. "A Multi-Mode Broadband Vibration Energy Harvester Composed of Symmetrically Distributed U-Shaped Cantilever Beams" Micromachines 12, no. 2: 203. https://doi.org/10.3390/mi12020203
APA StyleHuang, X., Zhang, C., & Dai, K. (2021). A Multi-Mode Broadband Vibration Energy Harvester Composed of Symmetrically Distributed U-Shaped Cantilever Beams. Micromachines, 12(2), 203. https://doi.org/10.3390/mi12020203







