Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner
Abstract
:1. Introduction
2. Motivation
3. Materials and Methods
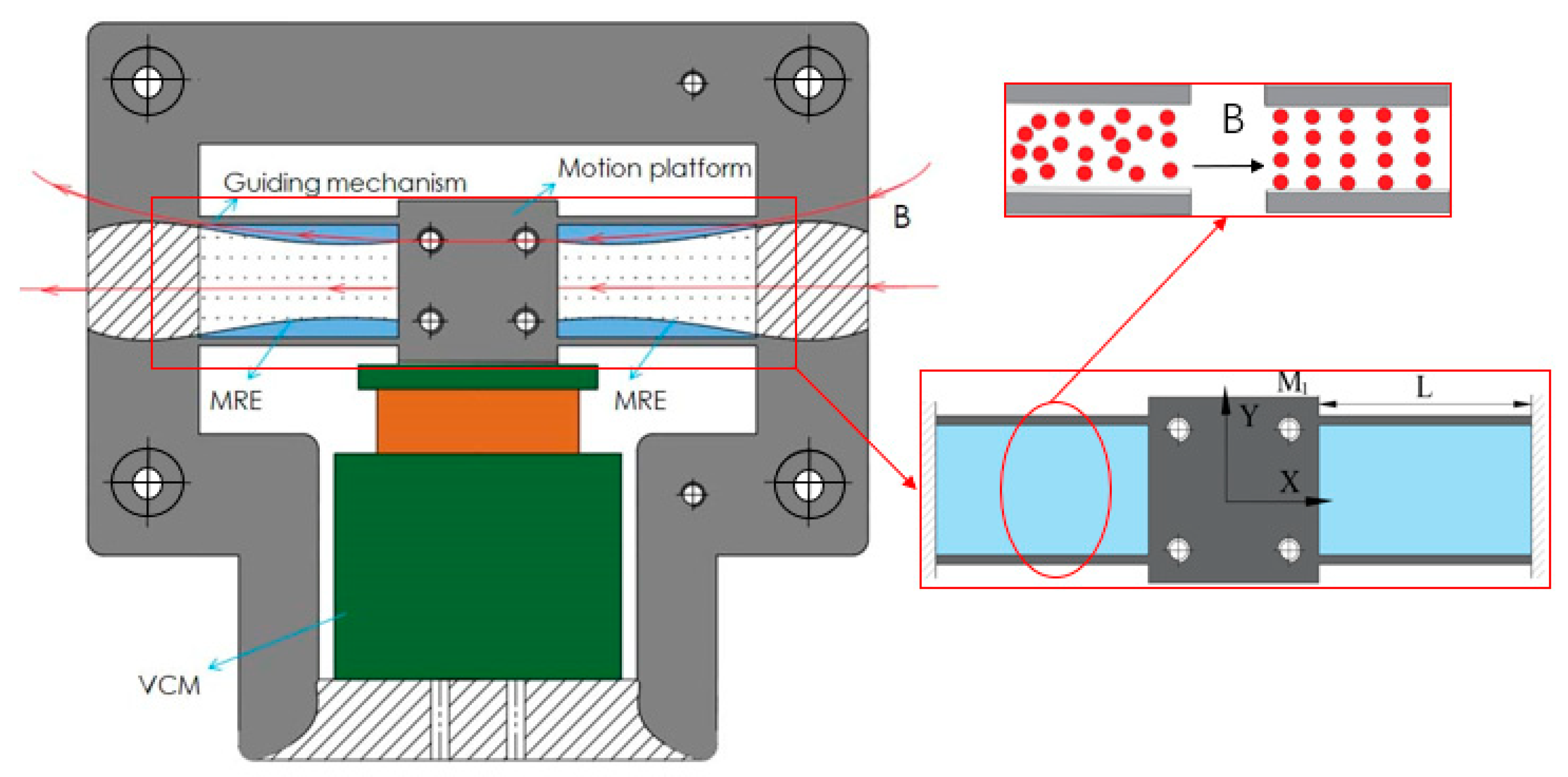
3.1. Design Overview
3.2. Kinetostatic Model of Guiding Mechanism
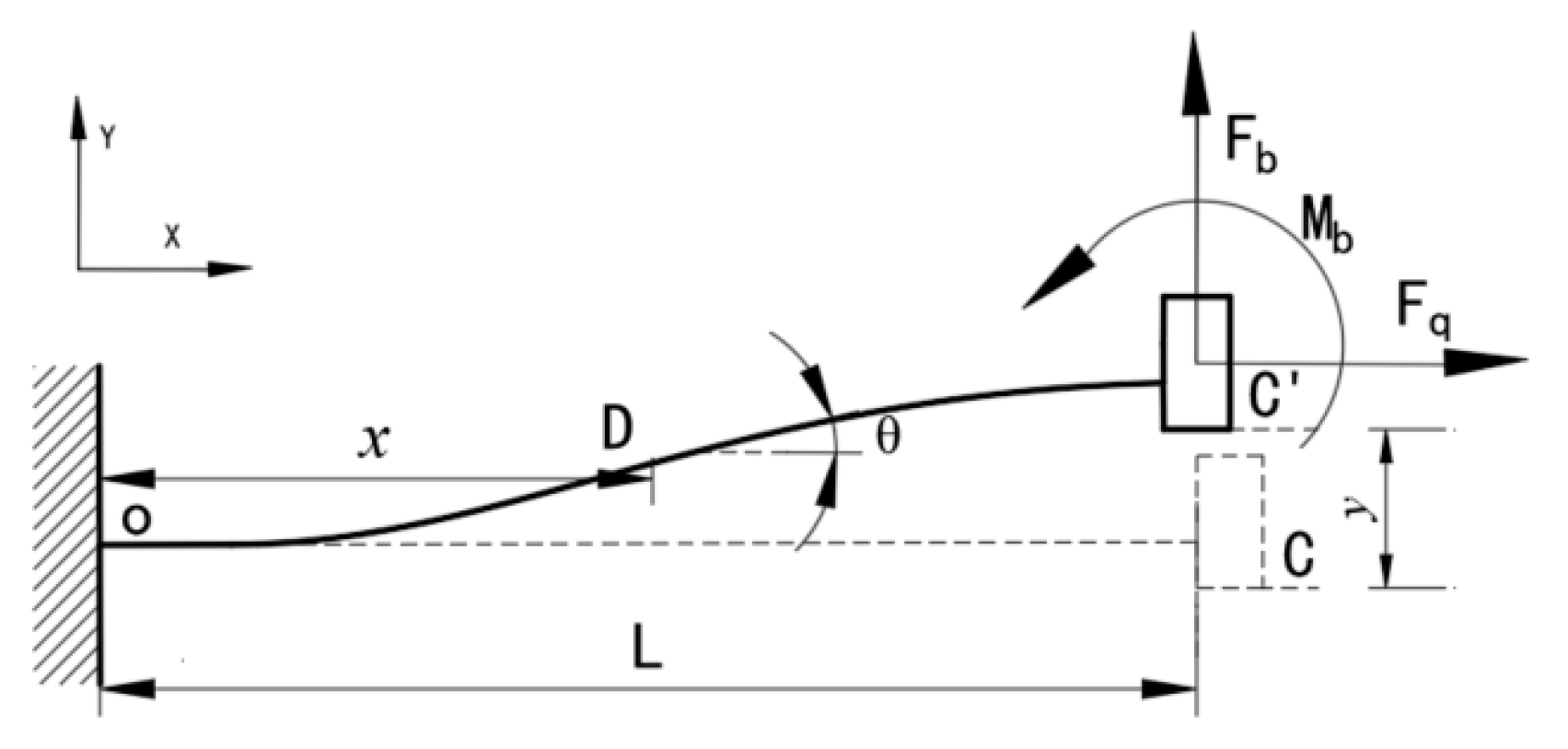
3.2.1. Deformation of the Flexure Beam
3.2.2. Analytical Model of MREs
3.2.3. Modeling of the Sandwiched Guiding Mechanism
3.3. Dynamic Analysis of Compliant Mechanisms
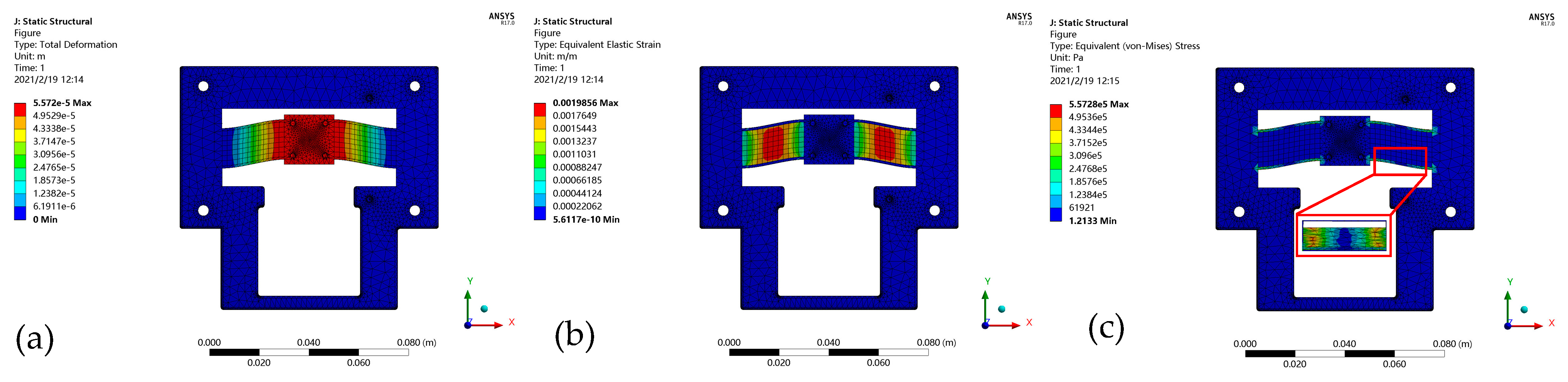
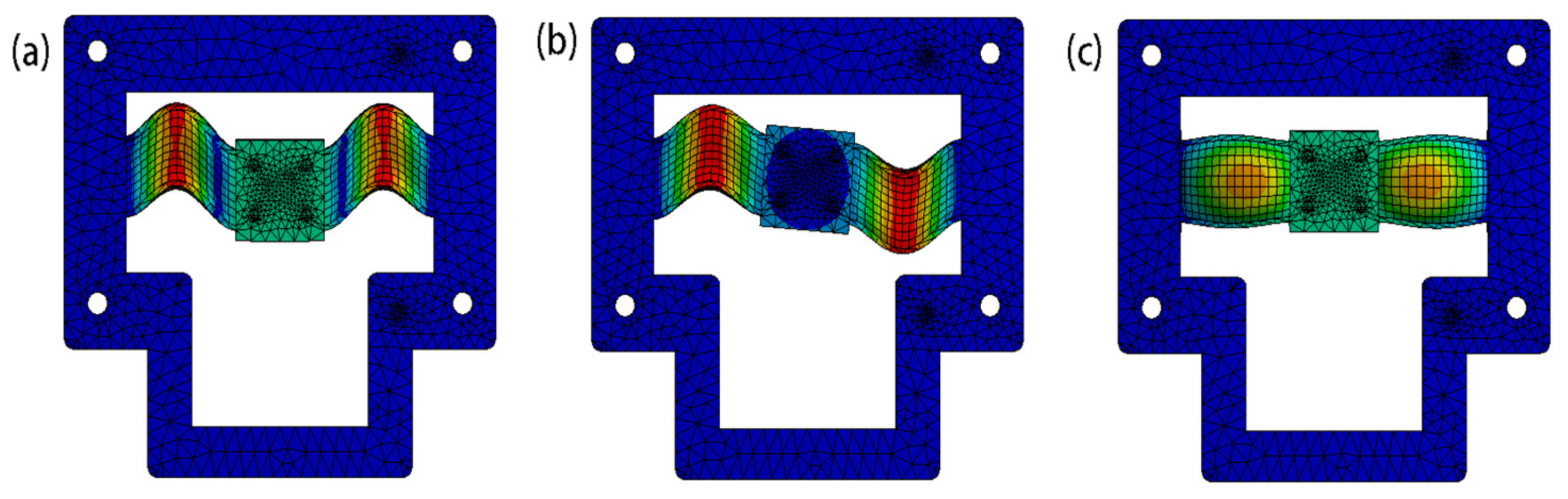
3.4. Validation via Finite Element Simulations
4. Results and Discussion
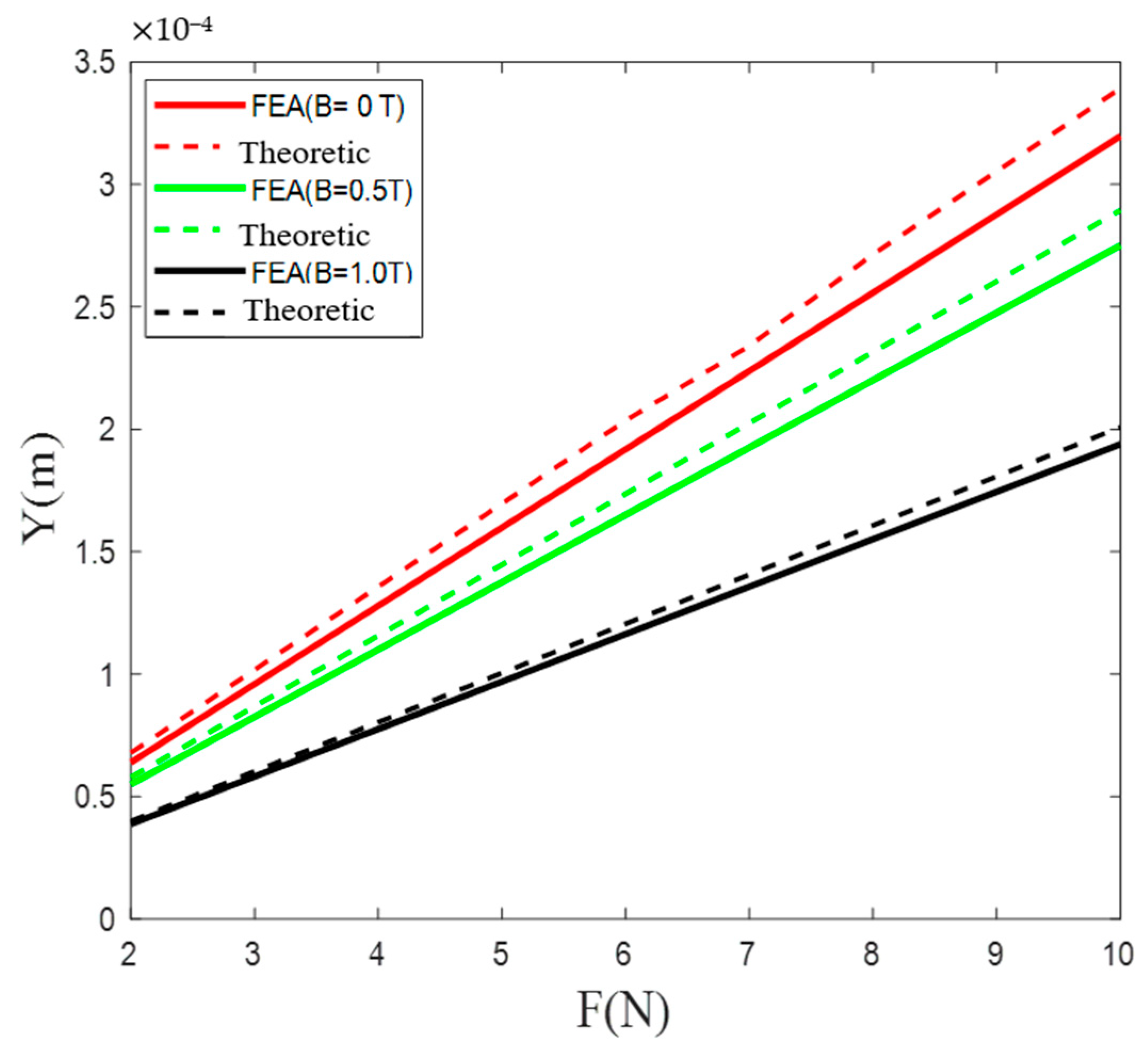
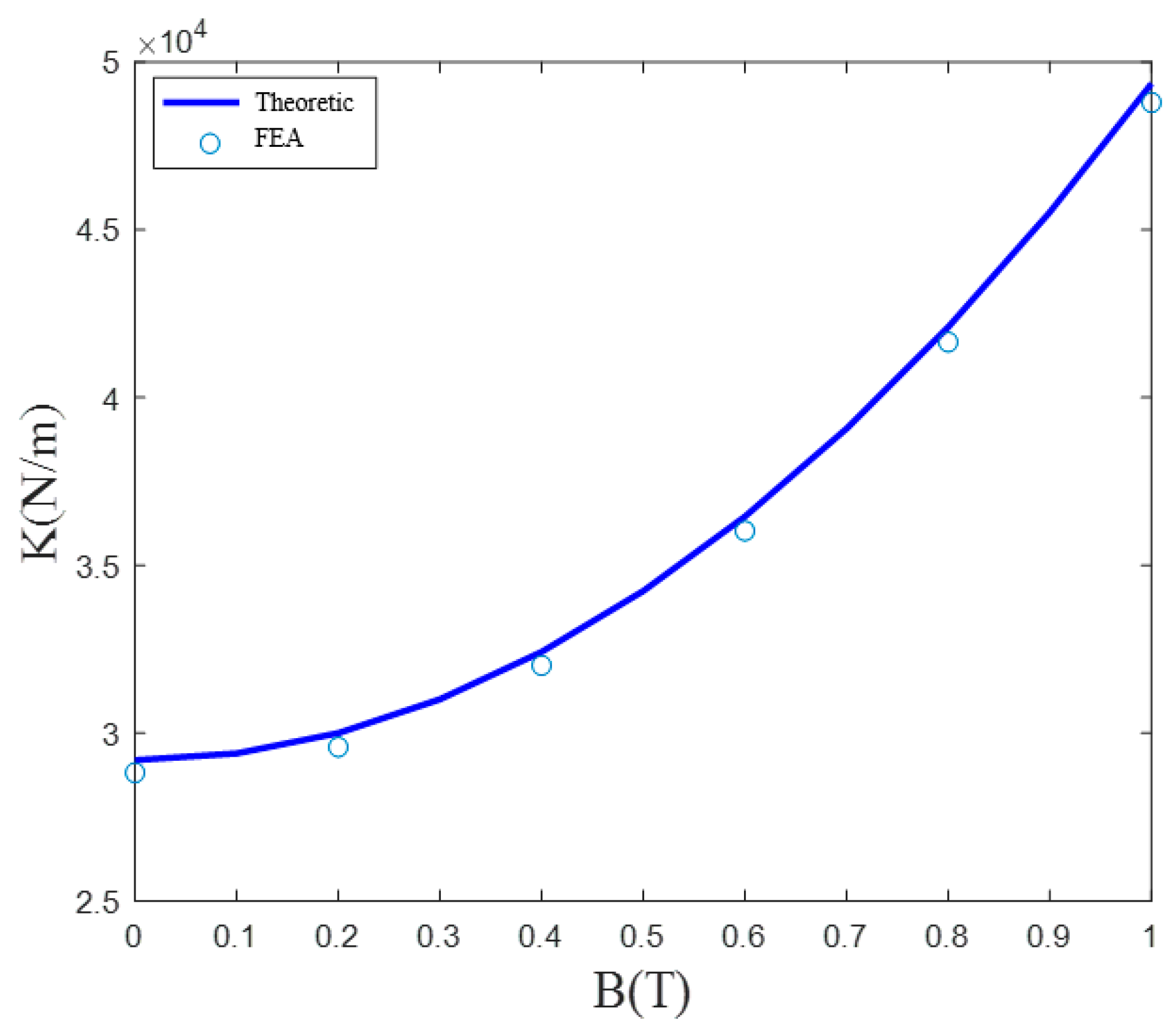
4.1. Stiffness Validation
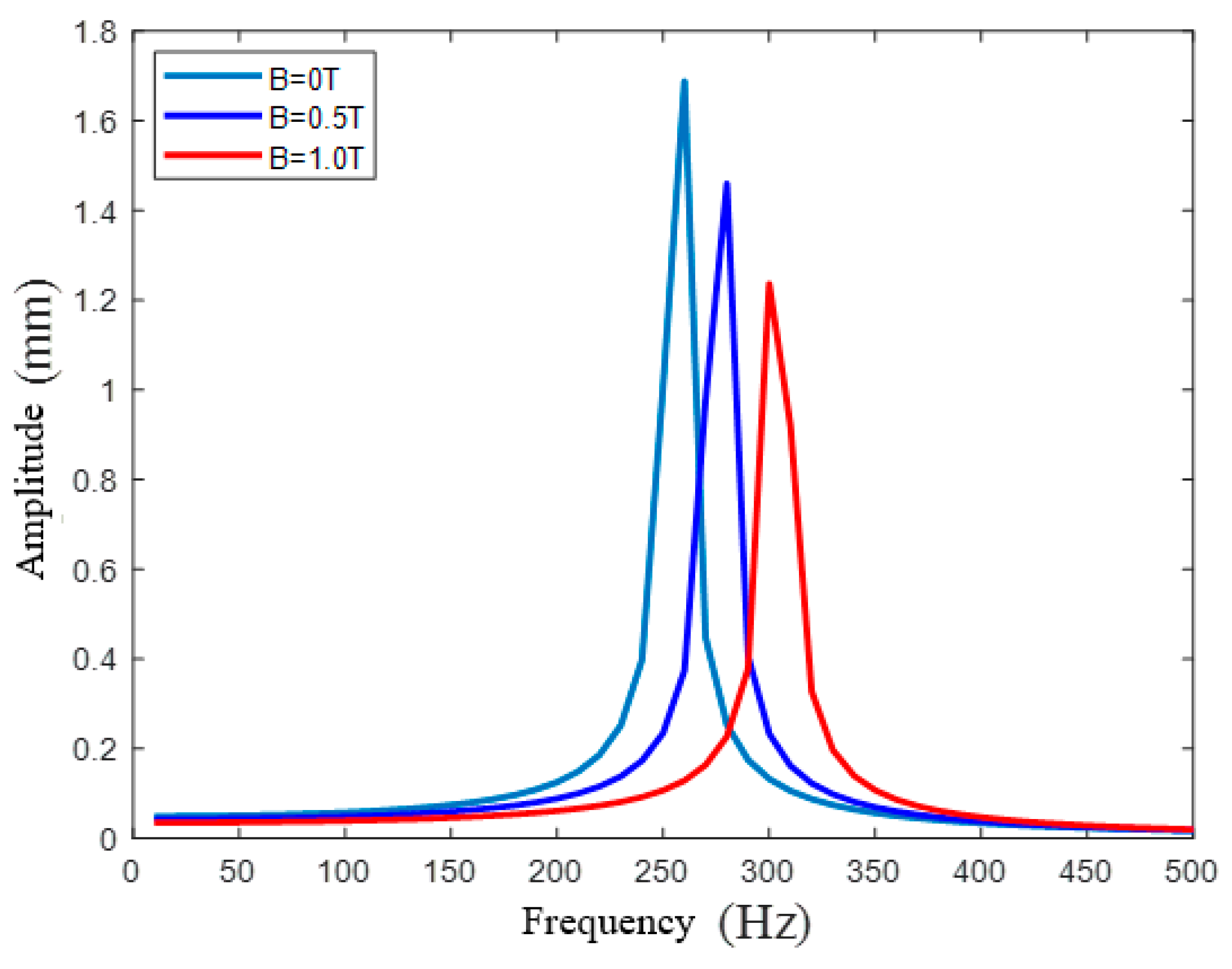
4.2. Dynamic Analysis
4.3. Experiemental Validations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lin, R.; Li, Y.; Zhang, Y.; Wang, T.; Wang, Z.; Song, Z.; Dou, Z.; Qian, J. Design of A Flexure-Based Mixed-Kinematic XY High-Precision Positioning Platform with Large Range. Mech. Mach. Theor. 2019, 142, 103609. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, Q. Design, Optimization and Testing of a Compact XY Parallel Nanopositioning Stage with Stacked Structure. Mech. Mach. Theor. 2018, 126, 171–188. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, X.; Huo, Z.; Shi, B.; Liang, C.; Tian, Y.; Zhang, D. A 2-DOF Nano-Positioning Scanner with Novel Compound Decoupling-Guiding Mechanism. Mech. Mach. Theor. 2021, 155, 104066. [Google Scholar] [CrossRef]
- Ling, M.; Cao, J.; Jiang, Z.; Zeng, M.; Li, Q. Optimal Design of a Piezo-Actuated 2-DOF Millimeter-Range Monolithic Flexure Mechanism with a Pseudo-Static Model. Mech. Syst. Signal Process. 2019, 115, 120–131. [Google Scholar] [CrossRef]
- Zhao, D.; Zhu, Z.; Huang, P.; Guo, P.; Zhu, L.; Zhu, Z. Development of a Piezoelectrically Actuated Dual-Stage Fast Tool Servo. Mech. Syst. Signal Process. 2020, 144, 106873. [Google Scholar] [CrossRef]
- Tian, Y.; Cai, K.; Zhang, D.; Liu, X.; Wang, F.; Shirinzadeh, B. Development of a XYZ Scanner for Home-Made Atomic Force Microscope Based on FPAA Control. Mech. Syst. Signal Process. 2019, 131, 222–242. [Google Scholar] [CrossRef]
- Díaz-Pérez, L.C.; Torralba, M.; Albajez, J.A.; Yagüe-Fabra, J.A. Implementation of the Control Strategy for a 2D Nanopositioning Long Range Stage. Procedia Manuf. 2017, 13, 458–465. [Google Scholar] [CrossRef]
- Safa, A.; Abdolmalaki, R.Y.; Shafiee, S.; Sadeghi, B. Adaptive Nonsingular Terminal Sliding Mode Controller for Micro/Nanopositioning Systems Driven by Linear Piezoelectric Ceramic Motors. ISA Trans. 2018, 77, 122–132. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, Q. Neural Networks-Based Model Predictive Control for Precision Motion Tracking of a Micropositioning System. Int. J. Intell. Robot. Appl. 2020, 4, 164–176. [Google Scholar] [CrossRef]
- Qian, J.; Li, Y.; Zhuge, L. An Investigation on a Novel 3-RCU Flexible Micromanipulator. Micromachines 2020, 11, 423. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Morita, T. Stepping Piezoelectric Actuators with Large Working Stroke for Nano-Positioning Systems: A Review. Sens. Actuators A Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, X. A Planar 3-DOF Nanopositioning Platform with Large Magnification. Precis. Eng. 2016, 46, 221–231. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Li, Y. Design and Analysis of a New High Precision Decoupled XY Compact Parallel Micromanipulator. Micromachines 2017, 8, 82. [Google Scholar] [CrossRef]
- Lu, S.; Yan, P.; Zhang, B. Long Stroke Displacement Measurement with Reduced Coupling Error Supporting High Precision Control of a Beam Flexure-Based Micro-Stage. Rev. Sci. Instrum. 2020, 91, 073701. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q. Design, Fabrication and Testing of a Novel Symmetrical 3-DOF Large-Stroke Parallel Micro/Nano-Positioning Stage. Robot. Comput. Integr. Manuf. 2018, 54, 162–172. [Google Scholar] [CrossRef]
- Das, T.K.; Shirinzadeh, B.; Ghafarian, M.; Al-Jodah, A.; Zhong, Y.; Smith, J. Design, Analysis and Experimental Investigations of a High Precision Flexure-Based Microgripper for Micro/Nano Manipulation. Mechatronics 2020, 69, 102396. [Google Scholar] [CrossRef]
- Blanc, L.; Delchambre, A.; Lambert, P. Flexible Medical Devices: Review of Controllable Stiffness Solutions. Actuators 2017, 6, 23. [Google Scholar] [CrossRef] [Green Version]
- Henke, M.; Gerlach, G. A Multi-Layered Variable Stiffness Device Based on Smart Form Closure Actuators. J. Intell. Mater. Syst. Struct. 2016, 27, 375–383. [Google Scholar] [CrossRef] [Green Version]
- Xie, Z.; Qiu, L.; Yang, D. Analysis of a Novel Variable Stiffness Filleted Leaf Hinge. Mech. Mach. Theor. 2020, 144, 103673. [Google Scholar] [CrossRef]
- Zeng, X.; Hurd, C.; Su, H.J.; Song, S.; Wang, J. A Parallel-Guided Compliant Mechanism with Variable Stiffness Based on Layer Jamming. Mech. Mach. Theor. 2020, 148, 103791. [Google Scholar] [CrossRef]
- Chun, H.; Han, J.M.; Wright, L.; Elwany, A.; Villarraga-Gómez, H.; Lee, C. Pressure-Fed Mechanism to Compensate for Motions and Dynamic Characteristics of Compliant Nanopositioning Stages. Precis. Eng. 2020, 63, 33–40. [Google Scholar] [CrossRef]
- Choi, D.S.; Kim, T.H.; Lee, S.H.; Pang, C.; Bae, J.W.; Kim, S.Y. Beyond Human Hand: Shape-Adaptive and Reversible Magnetorheological Elastomer-Based Robot Gripper Skin. ACS Appl. Mater. Interfaces 2020, 12, 44147–44155. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.S.; Chen, Y.; Yang, J.; Tian, T.F.; Deng, H.X.; Li, W.H.; Du, H.; Alici, G. The Development of an Adaptive Tuned Magnetorheological Elastomer Absorber Working in Squeeze Mode. Smart Mater. Struct. 2014, 23, 075009. [Google Scholar] [CrossRef]
- Lerner, A.A.; Cunefare, K.A. Performance of MRE-Based Vibration Absorbers. J. Intell. Mater. Syst. Struct. 2008, 19, 551–563. [Google Scholar] [CrossRef]
- Shen, Y.; Golnaraghi, M.F.; Heppler, G.R. Experimental Research and Modeling of Magnetorheological Elastomers. J. Intell. Mater. Syst. Struct. 2004, 15, 27–35. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value |
|---|---|---|
| Young’s modulus of flexure beams | E (GPa) | 2.2 |
| Poisson’s ratio of flexure beams | μ | 0.39 |
| Density of flexure beams | ρm (kg/m3) | 1190 |
| Initial shear modulus of magnetorheological elastomers (MREs) | G0 (MPa) | 0.8 |
| Permeability of MREs | μ1 (H/m) | 3.5 |
| Density of MREs | ρb (kg/m3) | 1100 |
| Parameter | Symbol | Value |
|---|---|---|
| Length of flexure beams | L (mm) | 25 |
| Width of flexure beams | bb (mm) | 20 |
| Thickness of flexure beams | tb (mm) | 1 |
| Width of MREs | bm (mm) | 14 |
| Thickness of MREs | tm (mm) | 20 |
| Cross-sectional area of the MREs | Am (mm2) | 280 |
| Length of central motion platform | lc (mm) | 20 |
| Width of central motion platform | wc (mm) | 20 |
| Height of central motion platform | hc (mm) | 20 |
| Modes | 1st | 2nd | 3rd |
|---|---|---|---|
| Frequency (Hz) | 247.58 | 909.31 | 958.87 |
| Magnetic Field Intensity | B = 0 T | B = 0.5 T | B = 1.0 T |
|---|---|---|---|
| Theoretical | 236.46 | 259.89 | 315.73 |
| FEA | 247.58 | 262.95 | 316.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Liu, P.; Yan, P. Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner. Micromachines 2021, 12, 212. https://doi.org/10.3390/mi12020212
Li Z, Liu P, Yan P. Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner. Micromachines. 2021; 12(2):212. https://doi.org/10.3390/mi12020212
Chicago/Turabian StyleLi, Zeying, Pengbo Liu, and Peng Yan. 2021. "Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner" Micromachines 12, no. 2: 212. https://doi.org/10.3390/mi12020212
APA StyleLi, Z., Liu, P., & Yan, P. (2021). Design and Analysis of a Novel Flexure-Based Dynamically Tunable Nanopositioner. Micromachines, 12(2), 212. https://doi.org/10.3390/mi12020212







