Multi-Field Coupling Dynamics Modeling of Aerostatic Spindle
Abstract
:1. Introduction
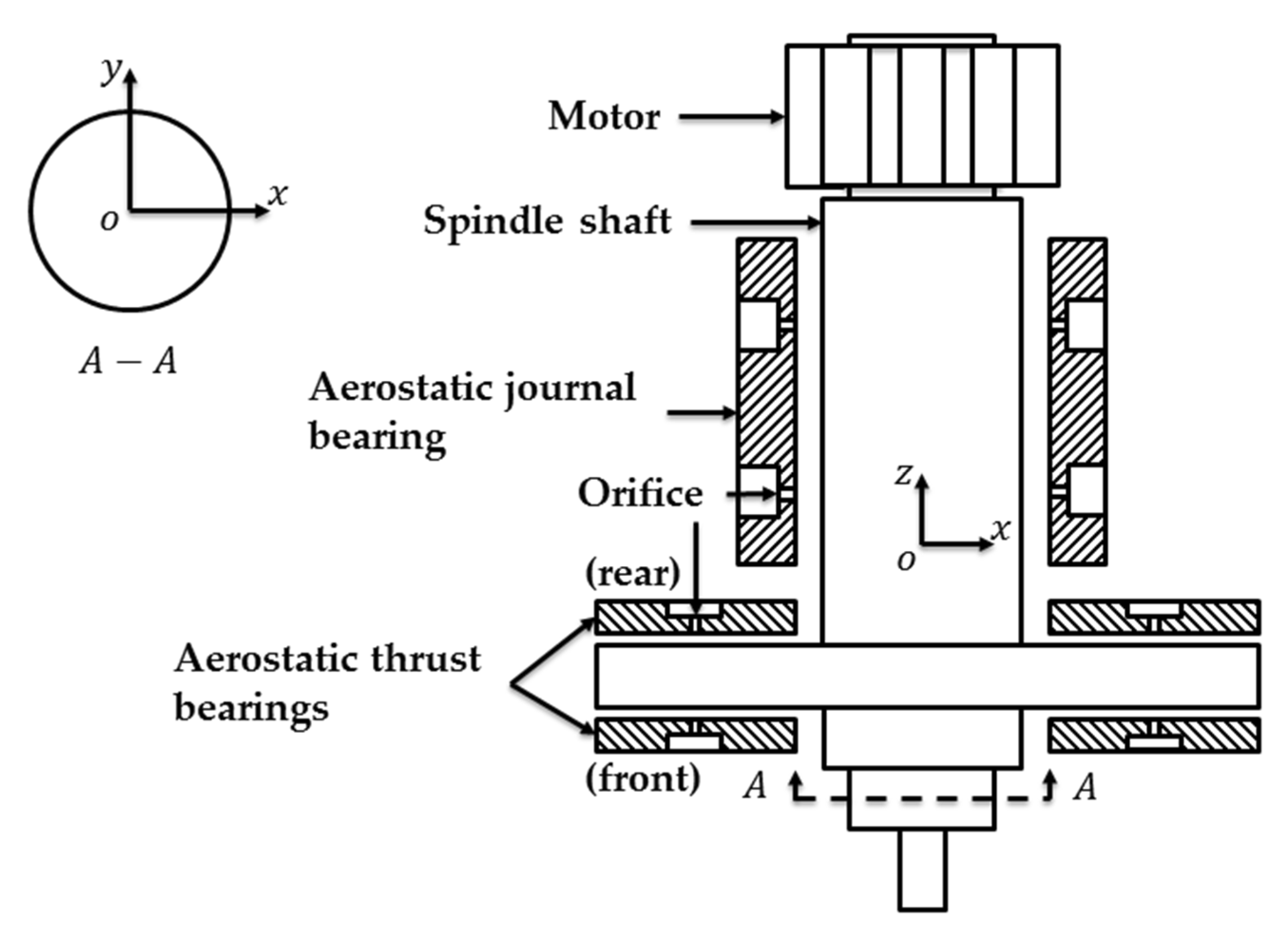
2. Mathematical Modeling of Aerostatic Spindle
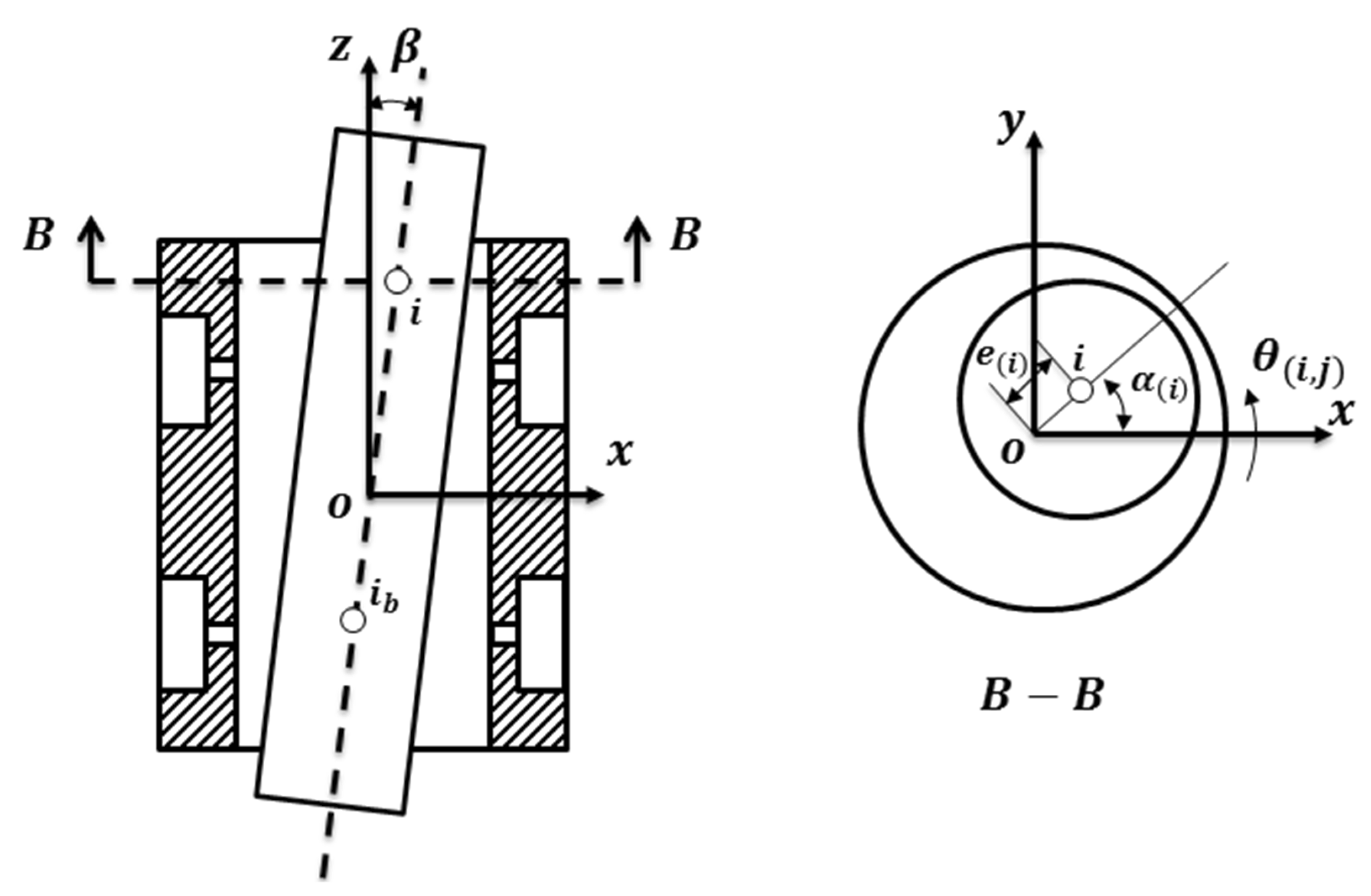
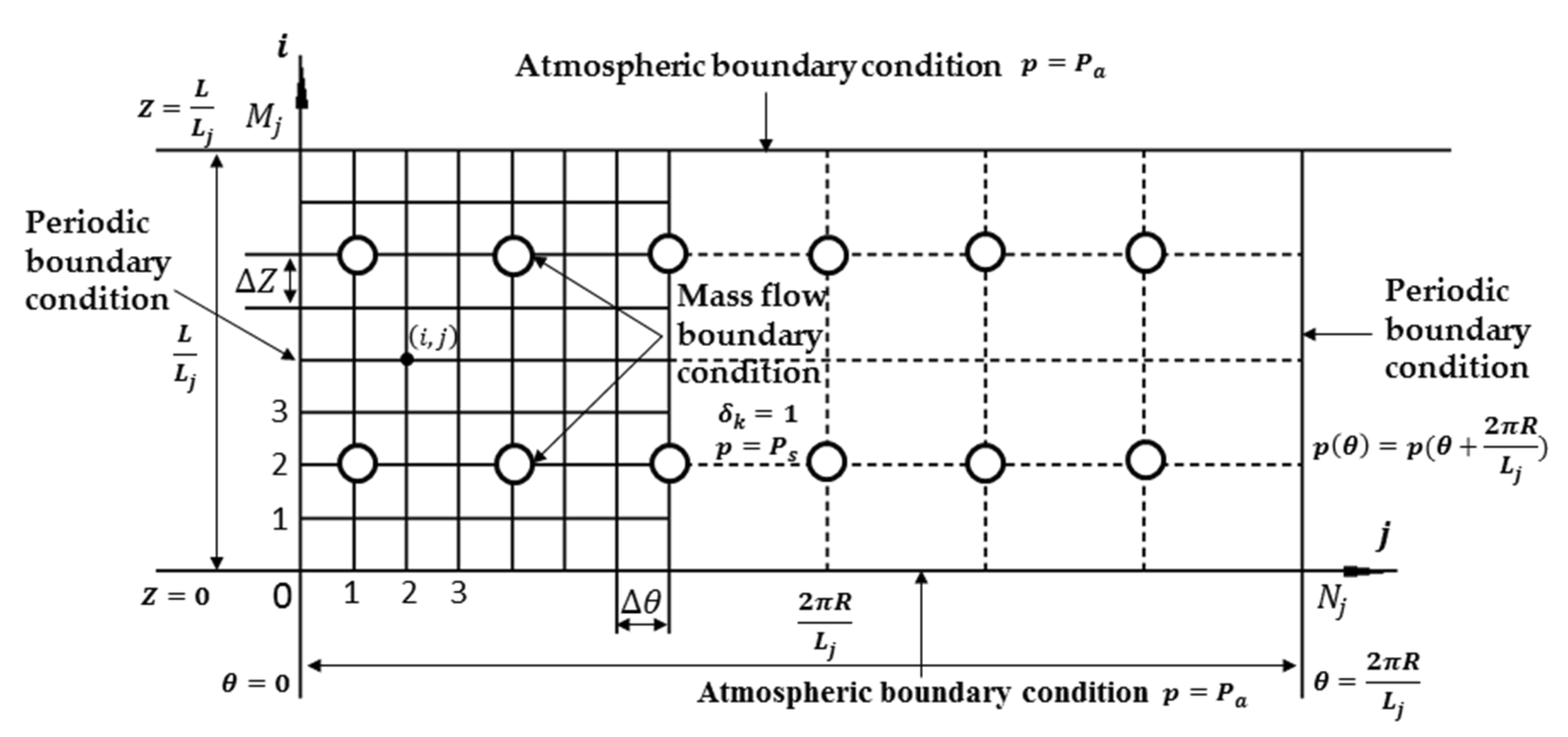
2.1. Modeling of Aerostatic Journal Bearing
2.2. Modeling of Aerostatic Thrust Bearing
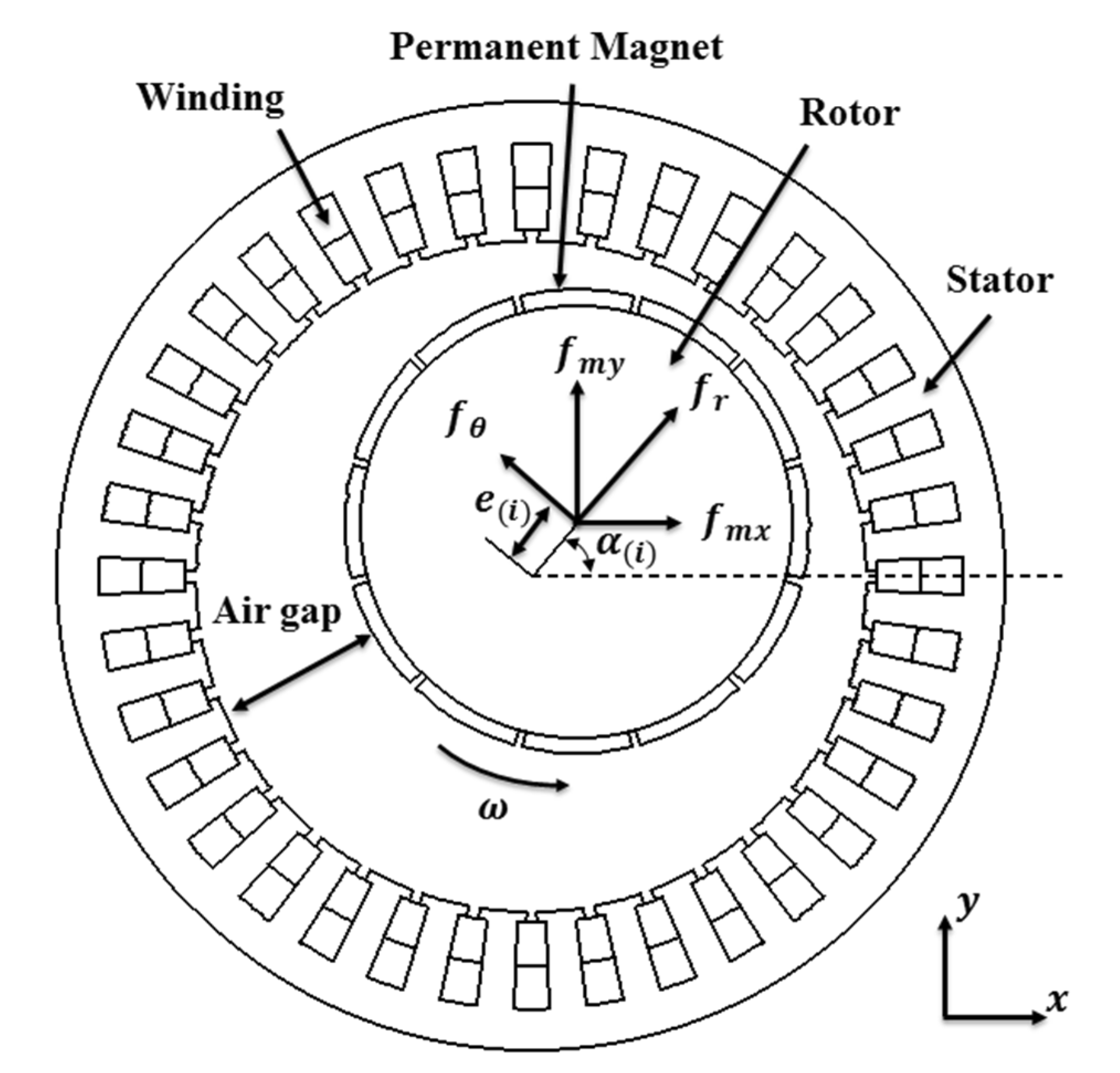
2.3. Modeling of PMSM
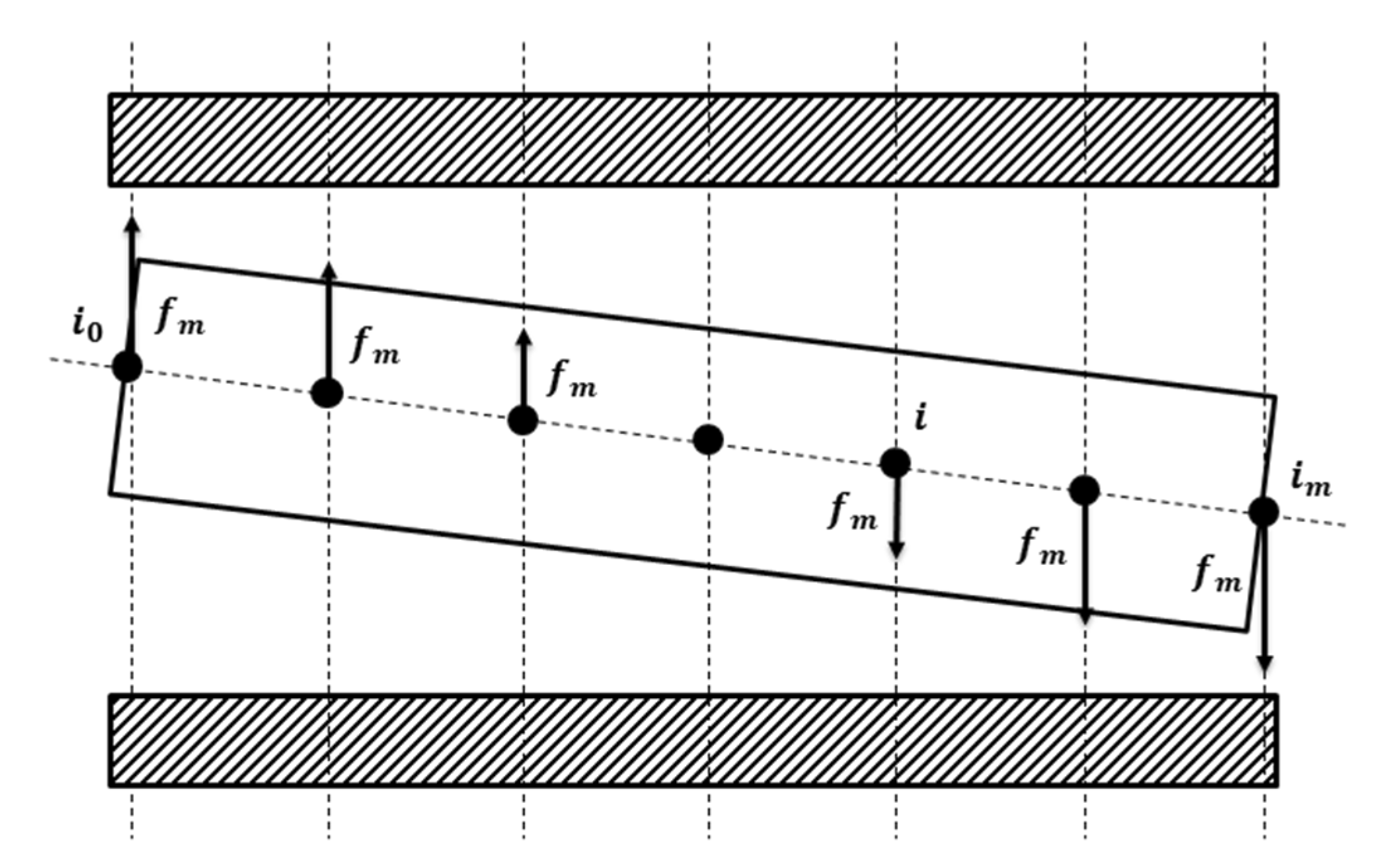
2.4. Dynamics Modeling of ABMS
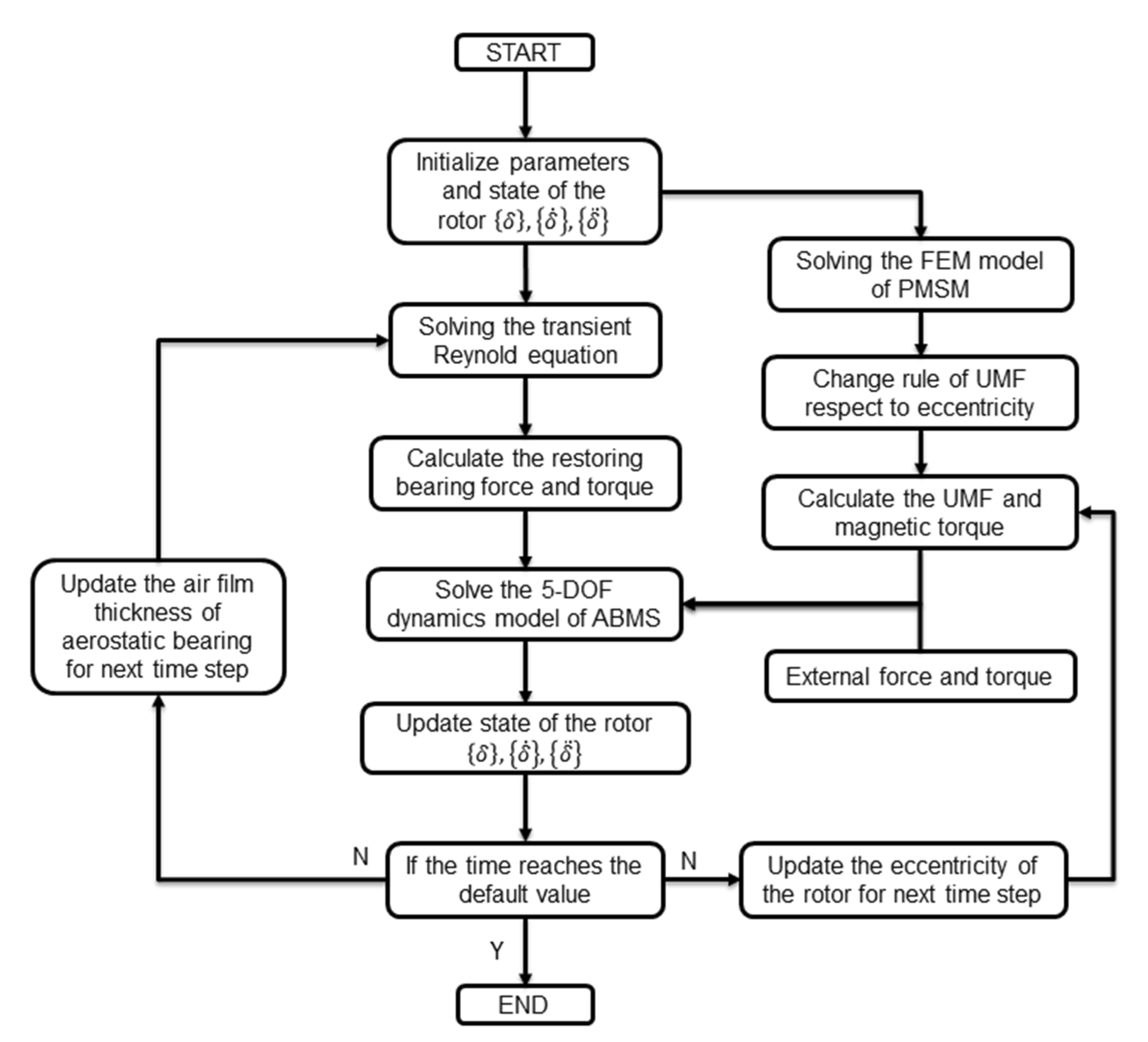
3. Numerical Simulation
3.1. Detailed Parameter
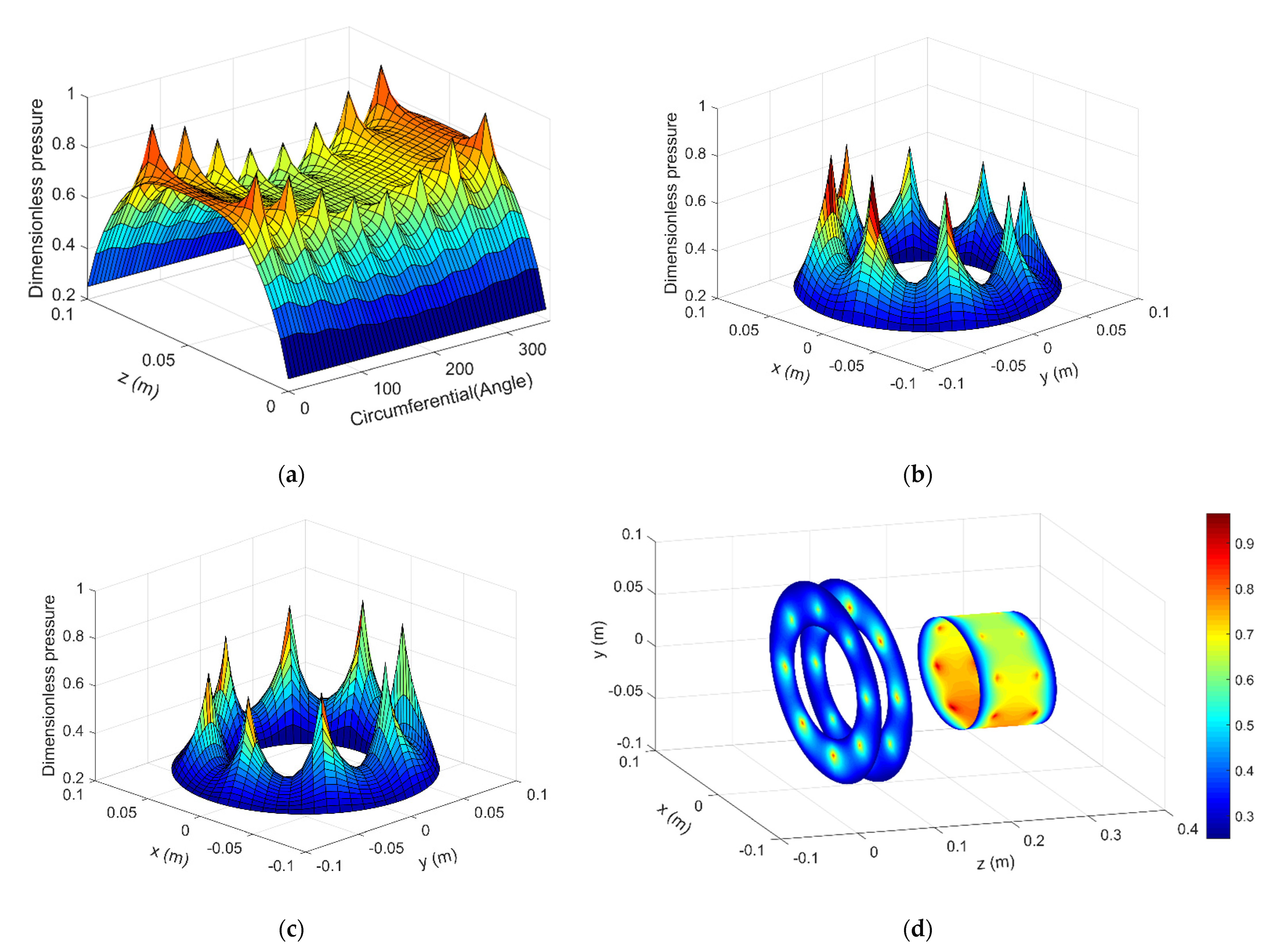
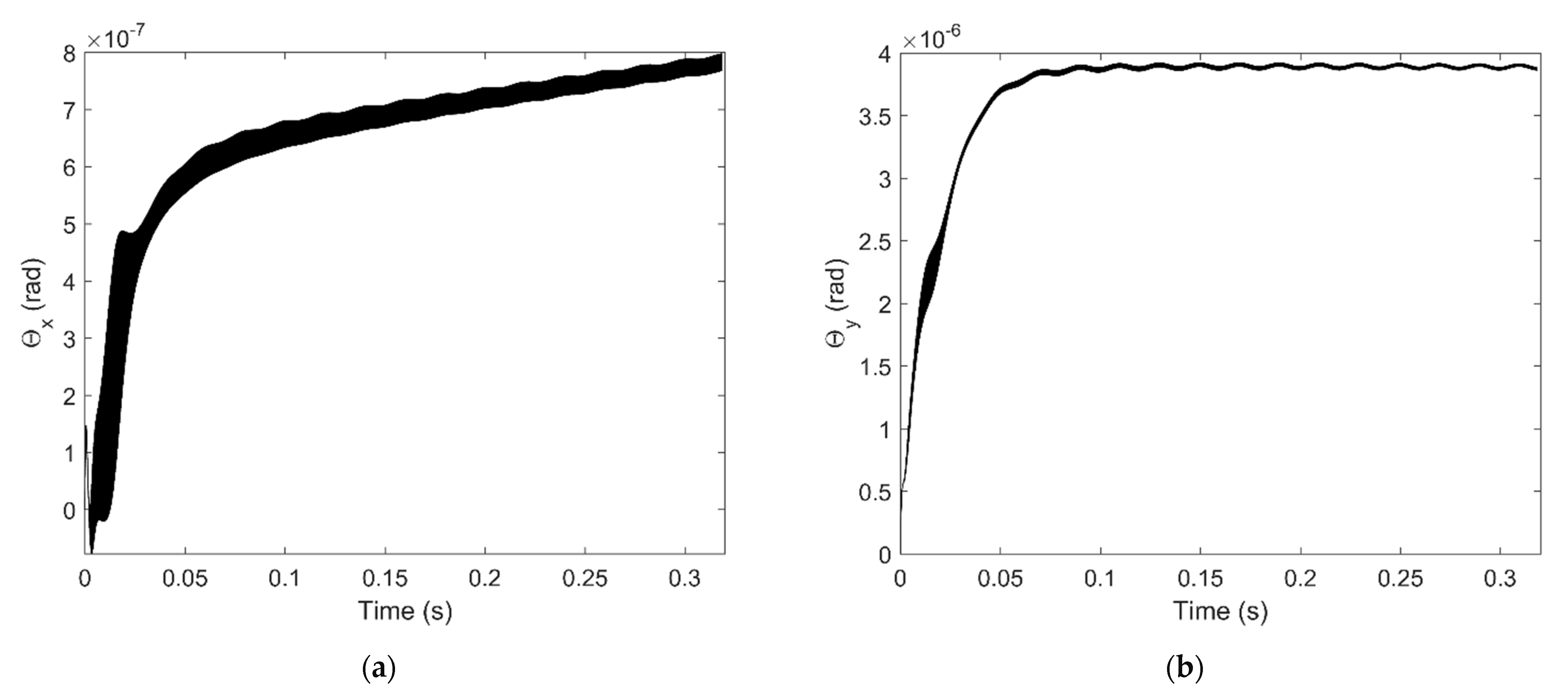
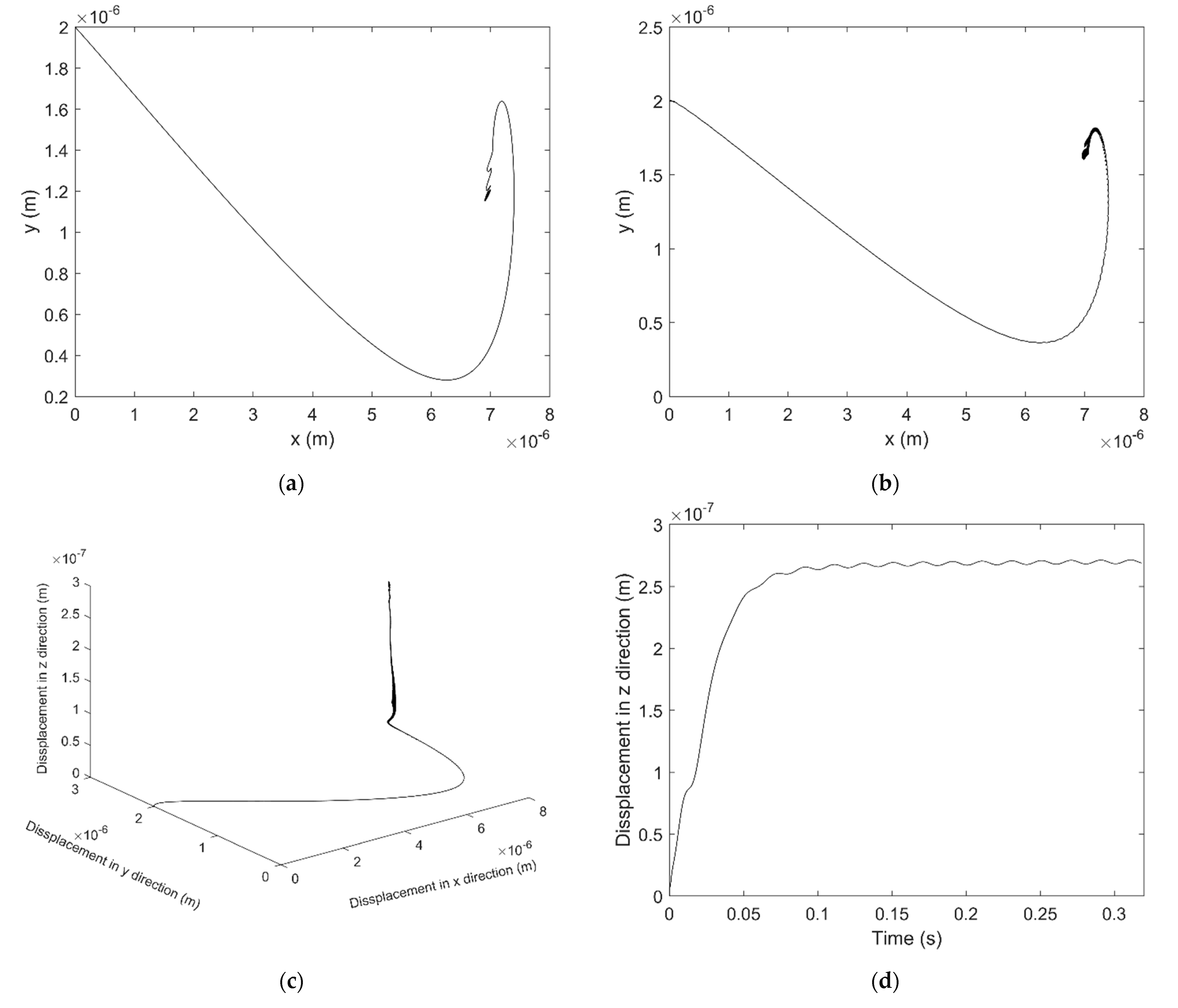
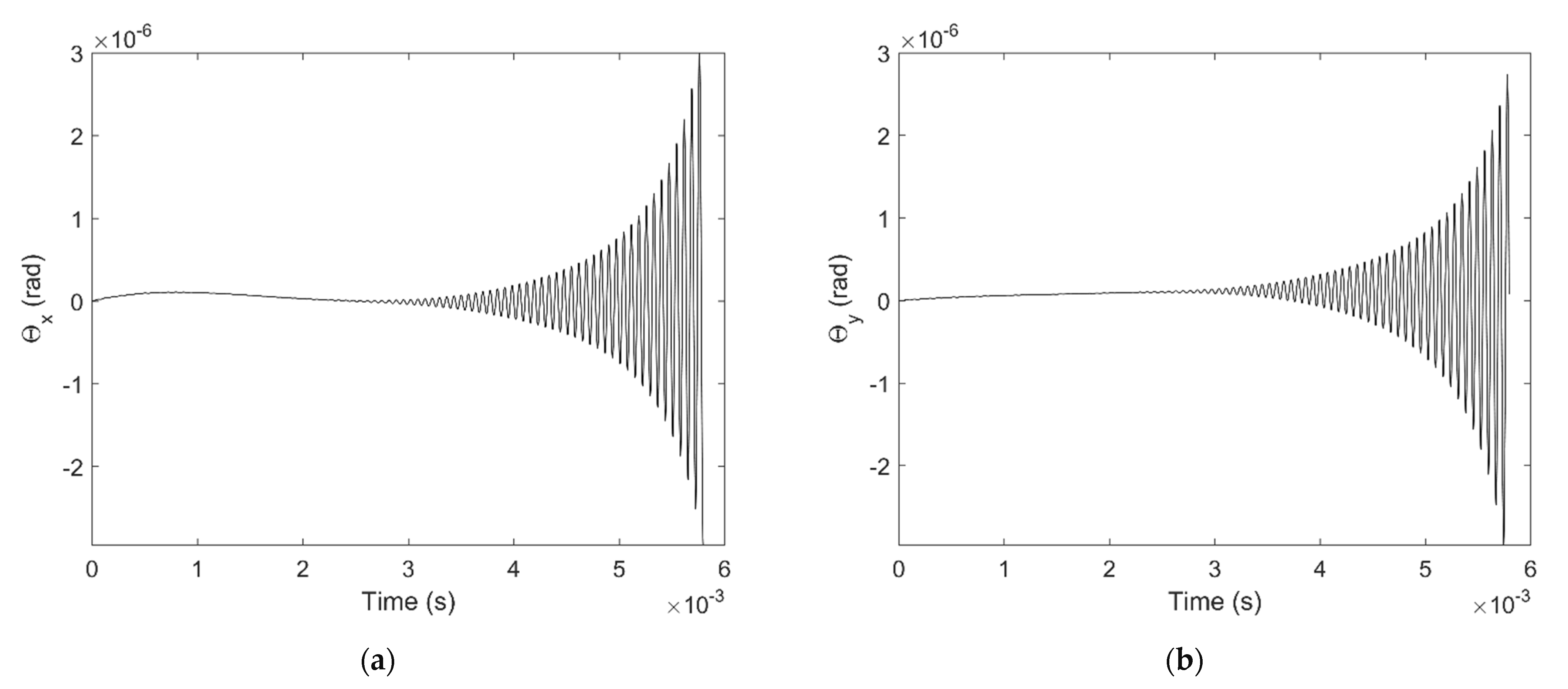
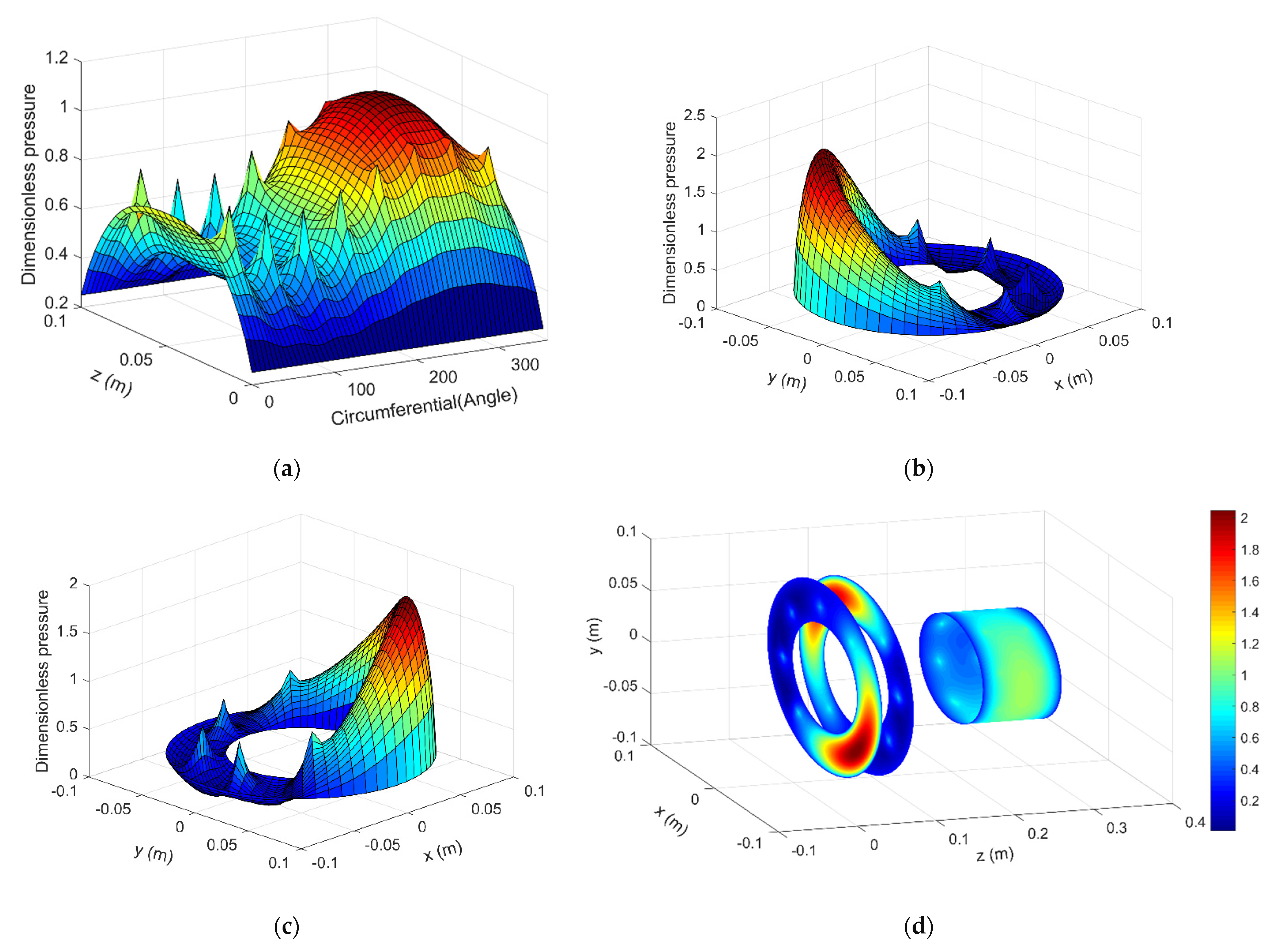
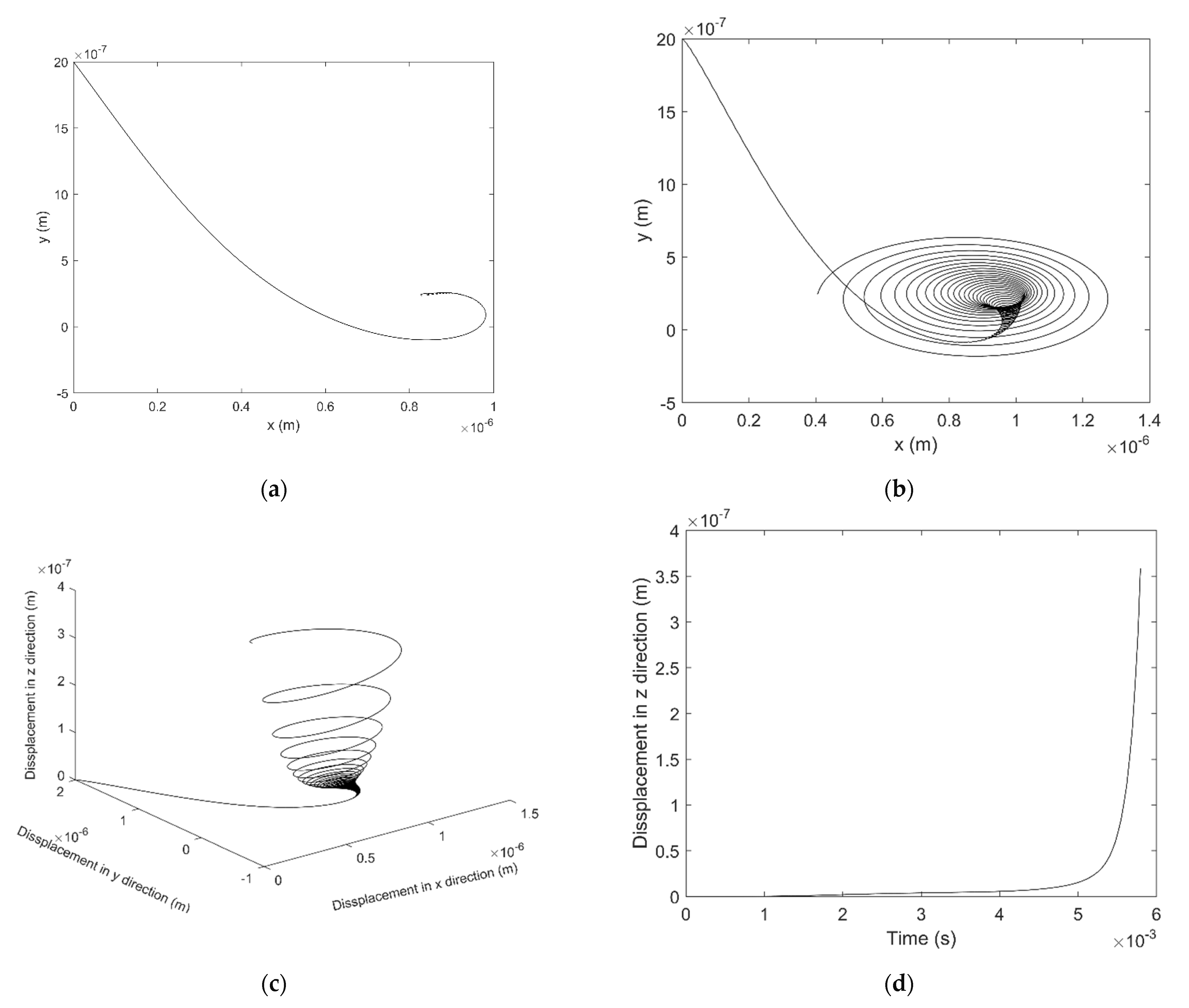
3.2. Numerical Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, G.; Ju, B.; Fang, H.; Chen, Y.; Yu, N.; Wan, Y. Air bearing: Academic insights and trend analysis. Int. J. Adv. Manuf. Technol. 2019, 106, 1191–1202. [Google Scholar] [CrossRef]
- Chen, G.; Sun, Y.; Zhang, F.; An, C.; Chen, W.; Su, H. Influence of ultra-precision flycutting spindle error on surface frequency domain error formation. Int. J. Adv. Manuf. Technol. 2017, 88, 3233–3241. [Google Scholar] [CrossRef]
- Gao, Q.; Chen, W.; Lu, L.; Huo, D.; Cheng, K. Aerostatic bearings design and analysis with the application to precision engineering: State-of-the-art and future perspectives. Tribol. Int. 2019, 135, 1–17. [Google Scholar] [CrossRef]
- Chen, G.; Chen, Y.; Lu, Q.; Wu, Q.; Wang, M. Multi-physics fields based nonlinear dynamic behavior analysis of air bearing motorized spindle. Micromachines 2020, 11, 723. [Google Scholar] [CrossRef]
- Chen, Y.; Chiu, C.; Cheng, Y. Influences of operational conditions and geometric parameters on the stiffness of aerostatic journal bearings. Precis. Eng. J. Int. Soc. Precis. Eng. Nanotechnol. 2010, 34, 722–734. [Google Scholar] [CrossRef]
- Miyatake, M.; Yoshimoto, S. Numerical investigation of static and dynamic characteristics of aerostatic thrust bearings with small feed holes. Tribol. Int. 2010, 43, 1353–1359. [Google Scholar] [CrossRef]
- Yang, D.-W.; Chen, C.-H.; Kang, Y.; Hwang, R.-M.; Shyr, S.-S. Influence of orifices on stability of rotor-aerostatic bearing system. Tribol. Int. 2009, 42, 1206–1219. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, Q.; Chen, W.; Luo, X.; Chen, G. Influence of unbalanced electromagnetic force and air supply pressure fluctuation in air bearing spindles on machining surface topography. Int. J. Precis. Eng. Manuf. 2021, 22, 1–12. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, J.; To, S.; Xiong, Z. A theoretical and experimental study of spindle imbalance induced forced vibration and its effect on surface generation in diamond turning. Int. J. Mach. Tools Manuf. 2018, 133, 61–71. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, Y.; Chen, W.; Chen, G.; Bai, Q.; Zhang, Q. Effect of motor rotor eccentricity on aerostatic spindle vibration in machining processes. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1331–1342. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, Y.; Chen, W.; Wang, Q.; Chen, G. Theoretical prediction and experimental verification of the unbalanced magnetic force in air bearing motor spindles. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 2330–2344. [Google Scholar] [CrossRef]
- Zhang, J. Analysis on motion stability of a high-speed rotor-bearing system. Chin. J. Mech. Eng. 2005, 18, 220–223. [Google Scholar] [CrossRef]
- Wang, C.-C.; Lee, T.-E. Nonlinear dynamic analysis of bi-directional porous aero-thrust bearing systems. Adv. Mech. Eng. 2017, 9, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-C. Application of a hybrid numerical method to the nonlinear dynamic analysis of a micro gas bearing system. Nonlinear Dyn. 2009, 59, 695–710. [Google Scholar] [CrossRef]
- Wang, C.-C. Theoretical and nonlinear behavior analysis of a flexible rotor supported by a relative short herringbone-grooved gas journal-bearing system. Phys. D Nonlinear Phenom. 2008, 237, 2282–2295. [Google Scholar] [CrossRef]
- Hei, D.; Lu, Y.; Zhang, Y.; Liu, F.; Zhou, C.; Müller, N. Nonlinear dynamic behaviors of rod fastening rotor-hydrodynamic journal bearing system. Arch. Appl. Mech. 2015, 85, 855–875. [Google Scholar] [CrossRef]
- Wang, C.-C. Application of a hybrid method to the nonlinear dynamic analysis of a flexible rotor supported by a spherical gas-lubricated bearing system. Nonlinear Anal. Theory, Methods Appl. 2009, 70, 2035–2053. [Google Scholar] [CrossRef]
- Zhang, G.-H.; Sun, Y.; Liu, Z.-S.; Zhang, M.; Yan, J.-J. Dynamic characteristics of self-acting gas bearing–flexible rotor coupling system based on the forecasting orbit method. Nonlinear Dyn. 2011, 69, 341–355. [Google Scholar] [CrossRef]
- Zhang, S.; To, S.; Wang, H. A theoretical and experimental investigation into five-DOF dynamic characteristics of an aerostatic bearing spindle in ultra-precision diamond turning. Int. J. Mach. Tools Manuf. 2013, 71, 1–10. [Google Scholar] [CrossRef]
- Li, J.; Liu, P. Dynamic analysis of 5-DOFs aerostatic spindles considering tilting motion with varying stiffness and damping of thrust bearings. J. Mech. Sci. Technol. 2019, 33, 5199–5207. [Google Scholar] [CrossRef]
- Li, J.; Huang, M.; Liu, P. Analysis and experimental verification of dynamic characteristics of air spindle considering varying stiffness and damping of radial bearings. Int. J. Adv. Manuf. Technol. 2019, 104, 2939–2950. [Google Scholar] [CrossRef]
- Jiang, S.; Xu, C. Dynamics characteristics of a rotary table motorized spindle with externally pressurized air bearings. J. Vibroengineering 2017, 19, 801–811. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Jiang, S. Dynamic analysis of a motorized spindle with externally pressurized air bearings. J. Vib. Acoust. 2015, 137, 041001. [Google Scholar] [CrossRef]
- Yang, P.; Zhu, K.-Q.; Wang, X.-L. On the non-linear stability of self-acting gas journal bearings. Tribol. Int. 2009, 42, 71–76. [Google Scholar] [CrossRef]
- Wu, Y.; Feng, K.; Zhang, Y.; Liu, W.; Li, W. Nonlinear dynamic analysis of a rotor-bearing system with porous tilting pad bearing support. Nonlinear Dyn. 2018, 94, 1391–1408. [Google Scholar] [CrossRef]
- Al-Bender, F. On the modelling of the dynamic characteristics of aerostatic bearing films: From stability analysis to active compensation. Precis. Eng. J. Int. Soc. Precis. Eng. Nanotechnol. 2009, 33, 117–126. [Google Scholar] [CrossRef]
- Franssen, R.; Potze, W.; De Jong, P.; Fey, R.; Nijmeijer, H. Large amplitude dynamic behavior of thrust air bearings: Modeling and experiments. Tribol. Int. 2017, 109, 460–466. [Google Scholar] [CrossRef] [Green Version]
- Lo, C.-Y.; Wang, C.-C.; Lee, Y.-H. Performance analysis of high-speed spindle aerostatic bearings. Tribol. Int. 2005, 38, 5–14. [Google Scholar] [CrossRef]
- Powell, J.W. Theory of aerostatic lubrication. In Design of Aerostatic Bearings; The Machinery Publishing Co., Ltd.: Brighton, UK, 1970; pp. 35–66. [Google Scholar]
- Rowe, W.B. Basic flow theory. In Hydrostatic, Aerostatic and Hybrid Bearing Design; Elsevier: Amsterdam, The Netherlands, 2012; pp. 25–48. [Google Scholar]
- Kawase, Y.; Mimura, N.; Ida, K. 3-D electromagnetic force analysis of effects of off-center of rotor in interior permanent magnet synchronous motor. IEEE Trans. Magn. 2000, 36, 1858–1862. [Google Scholar] [CrossRef]
- Meessen, K.K.; Paulides, J.J.; Lomonova, E.E. Force calculations in 3-D cylindrical structures using fourier analysis and the Maxwell Stress Tensor. IEEE Trans. Magn. 2012, 49, 536–545. [Google Scholar] [CrossRef]
- Shi, J.; Cao, H.; Maroju, N.K.; Jin, X. Dynamic modeling of aerostatic spindle with shaft tilt deformation. J. Manuf. Sci. Eng. Trans. ASME 2019, 142, 1–43. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Chang, Y.J. Stability boundary of non-linear orbits within clearance circle of journal bearings. J. Vib. Acoust. 1993, 115, 303–307. [Google Scholar] [CrossRef]
- Laha, S.K.; Banjare, H.; Kakoty, S.K. Stability analysis of a flexible rotor supported on finite hydrodynamic porous journal bearing using a non-linear transient method. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2008, 222, 963–973. [Google Scholar] [CrossRef]


| Parameter (Unit) | Data |
|---|---|
| Length of shaft (m) | 0.4 |
| Diameter of journal bearing (m) | 0.1 |
| Length of journal bearing (m) | 0.1 |
| Inner diameter of thrust bearing (m) | 0.1 |
| Outer diameter of thrust bearing (m) | 0.18 |
| Bearing clearance (m) | 1 × 10−5 |
| Diameter of orifice (m) | 0.0002 |
| Row number of Orifice on journal bearing | 2 |
| Row number of Orifice on thrust bearing | 1 |
| Orifice number of each row | 8 |
| Ambient pressure (Pa) | 101325 |
| Supply pressure (Pa) | 405300 |
| Density of air (kg/m3) | 1.204 |
| Kinetic viscosity of air (Pa·s) | 1.82 × 10−5 |
| Specific heat ratio of air | 1.401 |
| Flow coefficient | 0.8 |
| Outer Rotor diameter (m) | 0.1 |
| Outer stator diameter (m) | 0.15 |
| Inner rotor diameter (m) | 0.106 |
| Number of slots | 36 |
| Number of poles | 12 |
| Motor effective length (m) | 0.08 |
| Rotational speed (r/min) | 3000 |
| Winding form of motor | Three-phase of double layer winding |
| External force (N) | 50 |
| 400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Chen, Y. Multi-Field Coupling Dynamics Modeling of Aerostatic Spindle. Micromachines 2021, 12, 251. https://doi.org/10.3390/mi12030251
Chen G, Chen Y. Multi-Field Coupling Dynamics Modeling of Aerostatic Spindle. Micromachines. 2021; 12(3):251. https://doi.org/10.3390/mi12030251
Chicago/Turabian StyleChen, Guoda, and Yijie Chen. 2021. "Multi-Field Coupling Dynamics Modeling of Aerostatic Spindle" Micromachines 12, no. 3: 251. https://doi.org/10.3390/mi12030251
APA StyleChen, G., & Chen, Y. (2021). Multi-Field Coupling Dynamics Modeling of Aerostatic Spindle. Micromachines, 12(3), 251. https://doi.org/10.3390/mi12030251







