Development of a Wearable Glove System with Multiple Sensors for Hand Kinematics Assessment
Abstract
1. Introduction
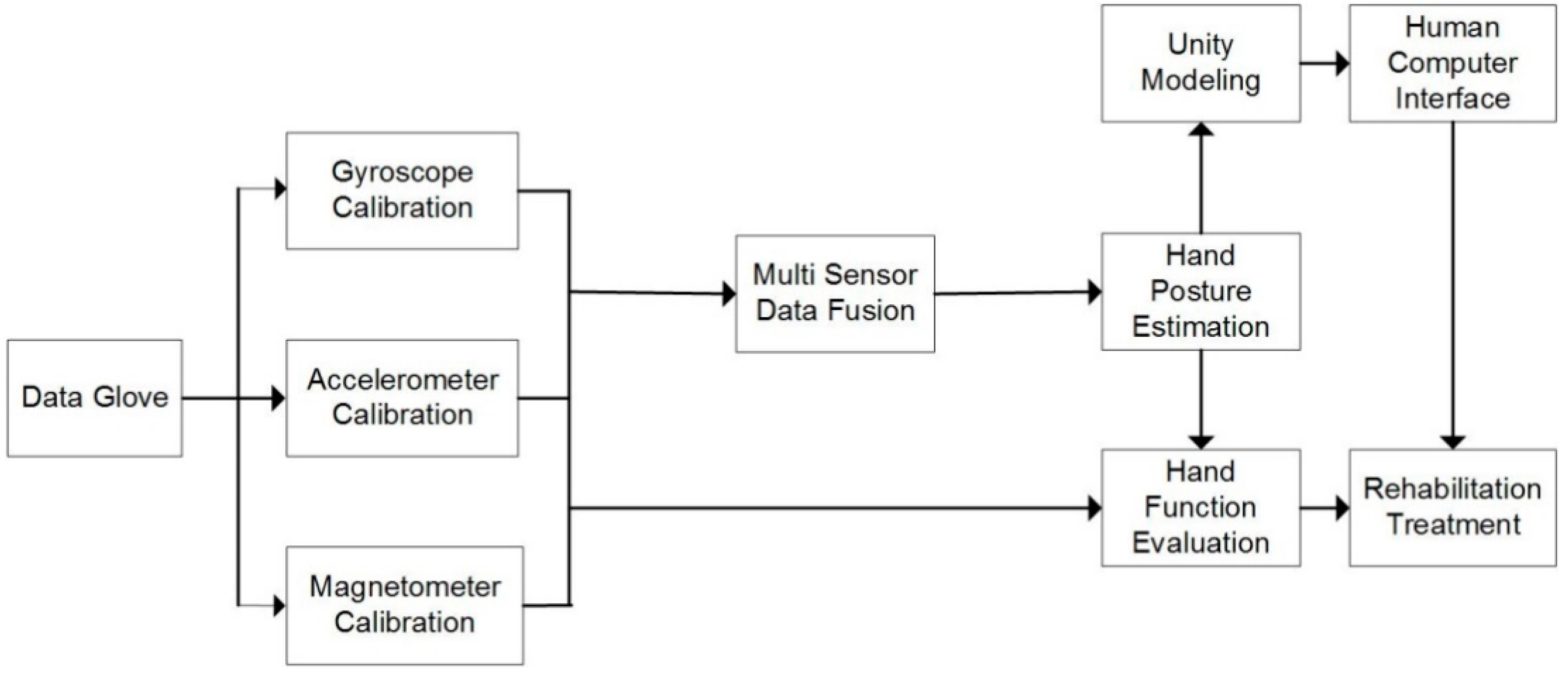
2. System Architecture
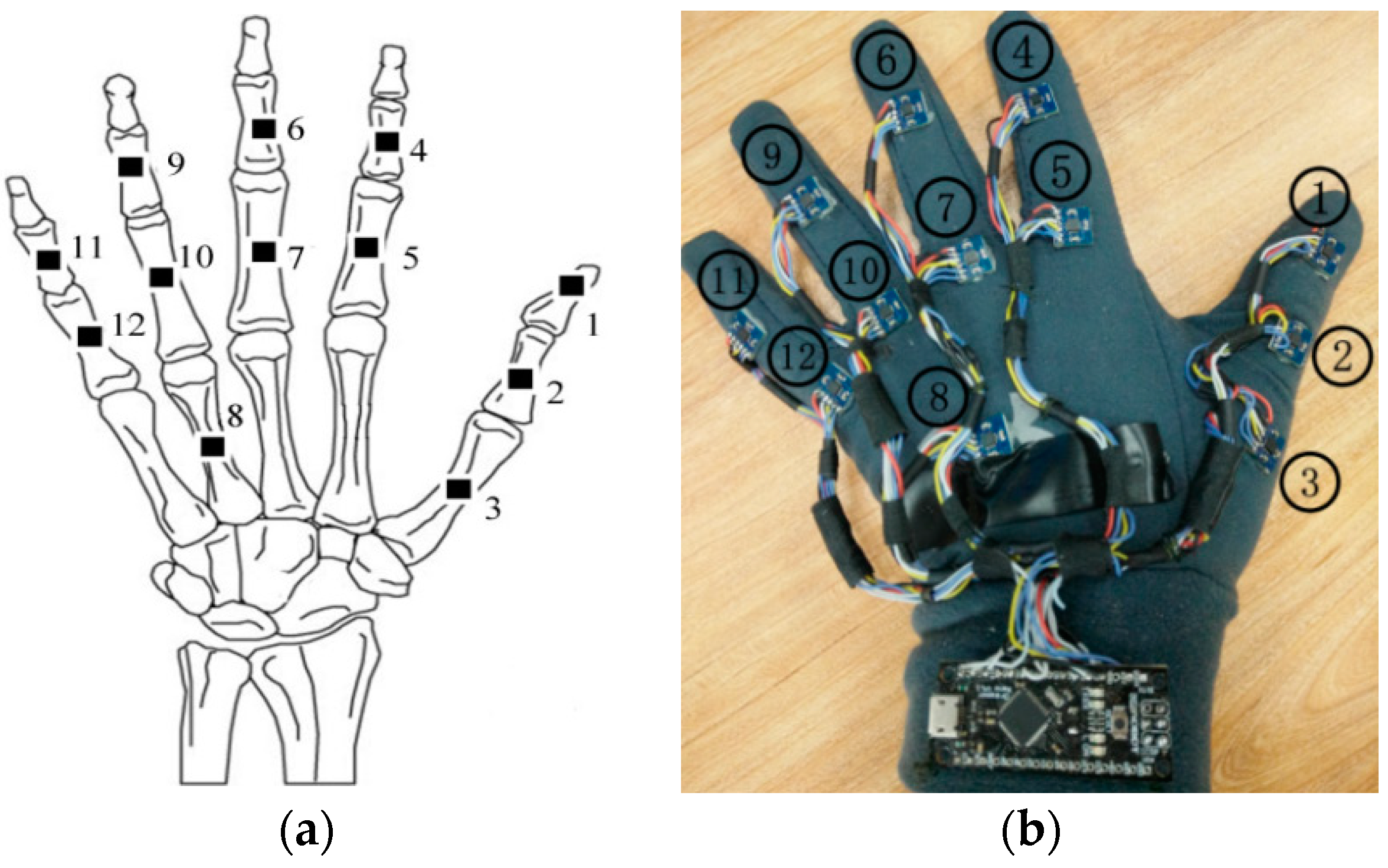
2.1. Hardware Design
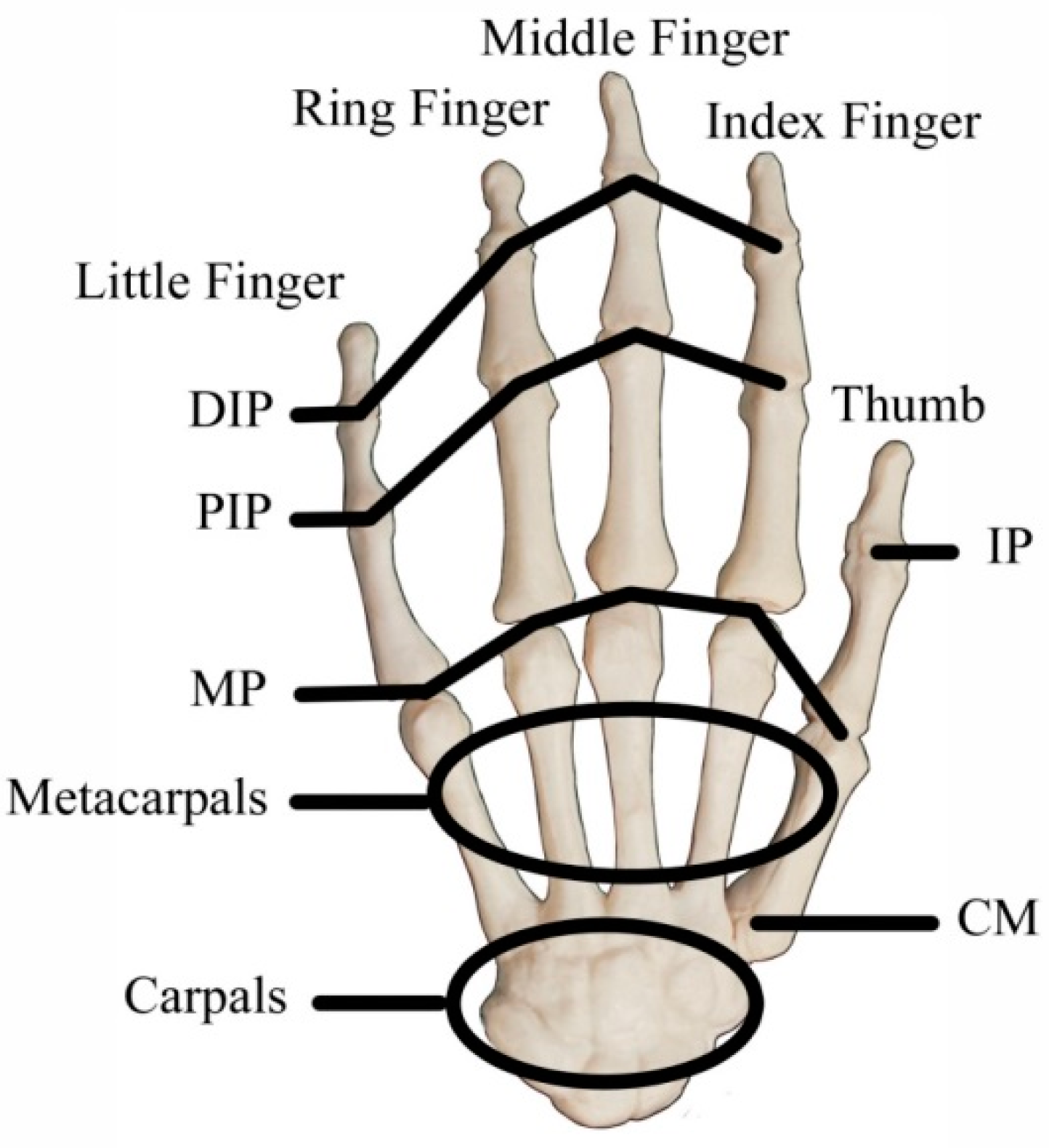
2.2. Analysis of Hand Joints and Layout of Sensors
3. Sensor Data Processing
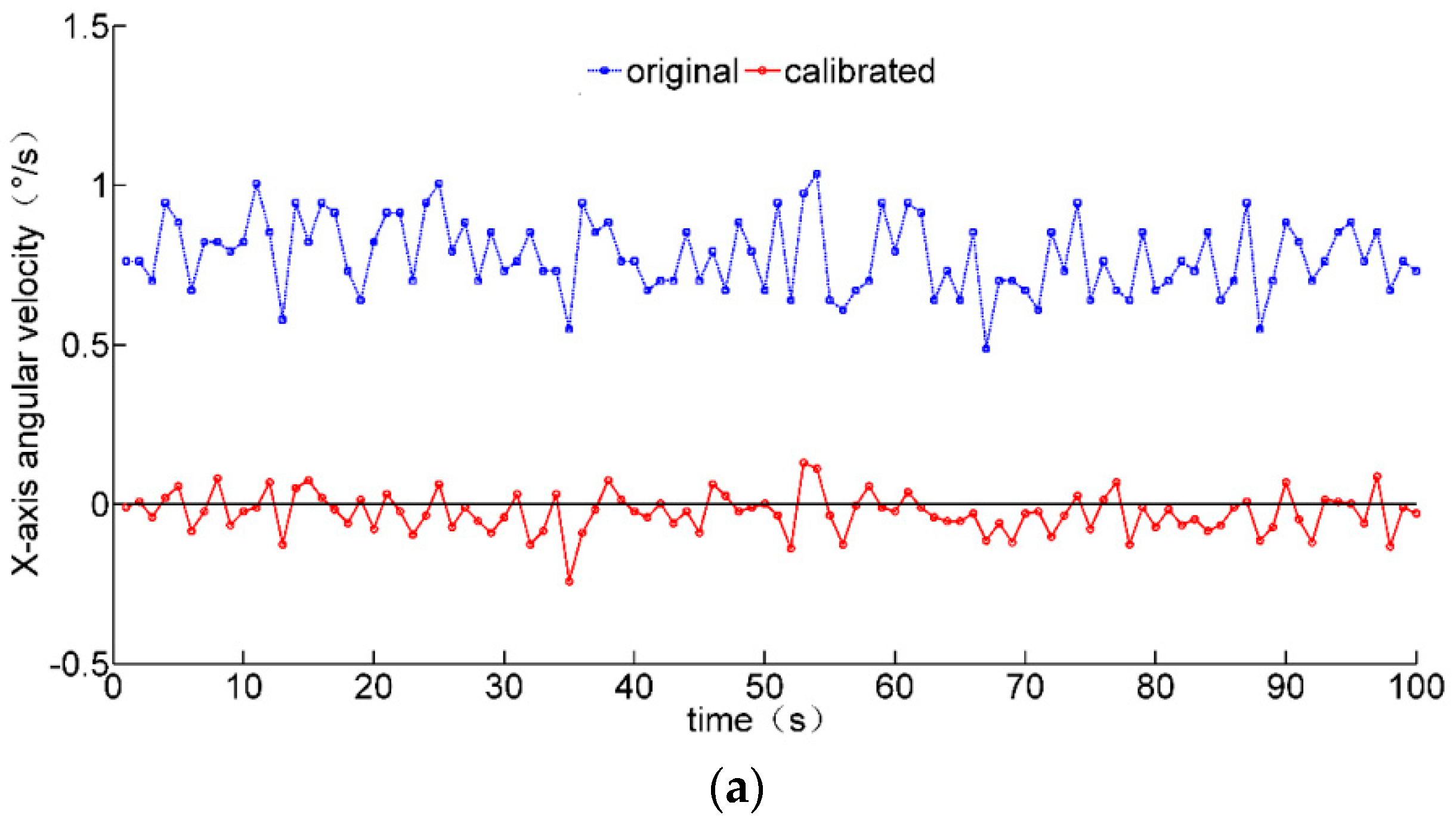
3.1. Sensor Calibration
3.2. Sensor Fusion
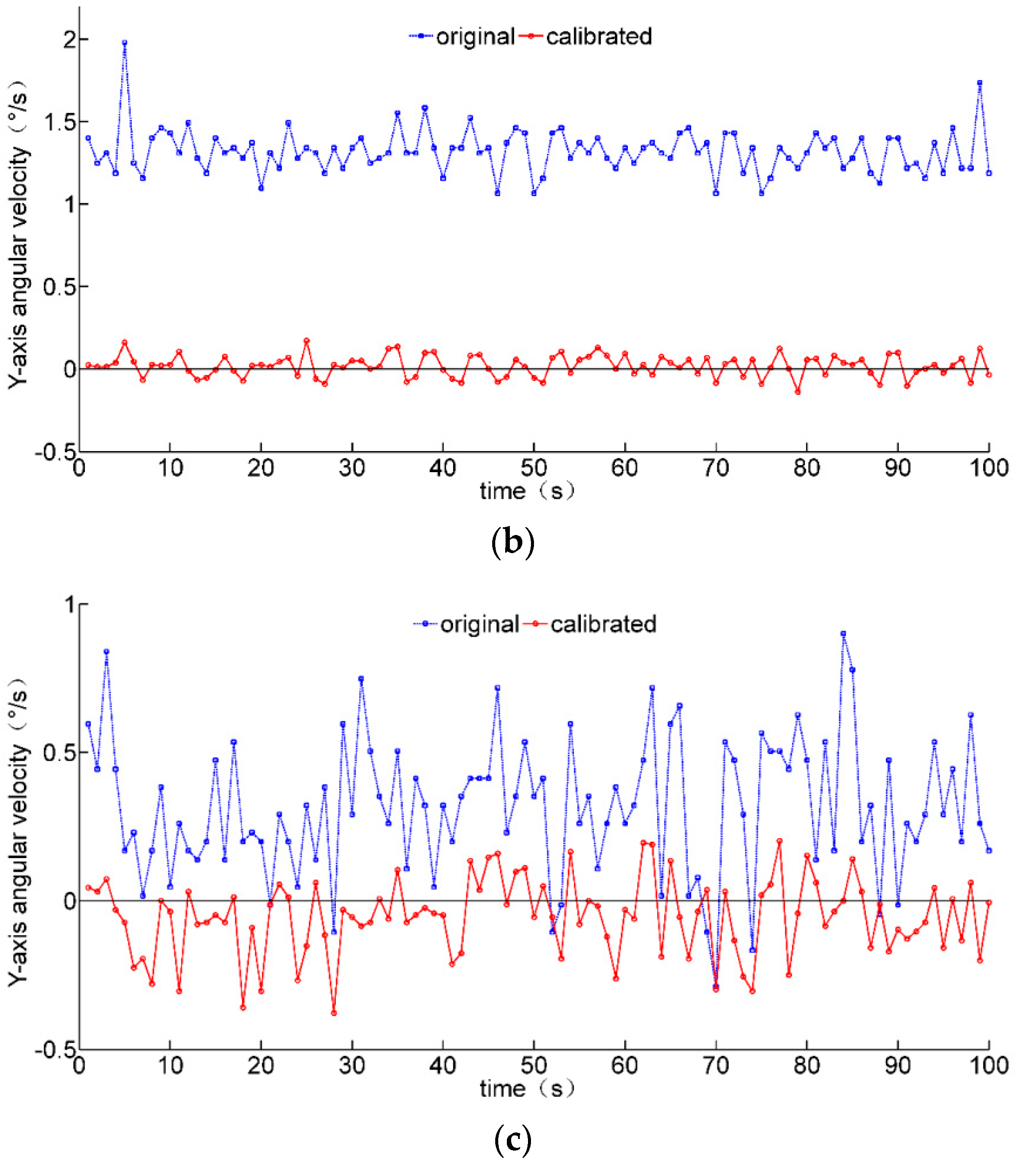
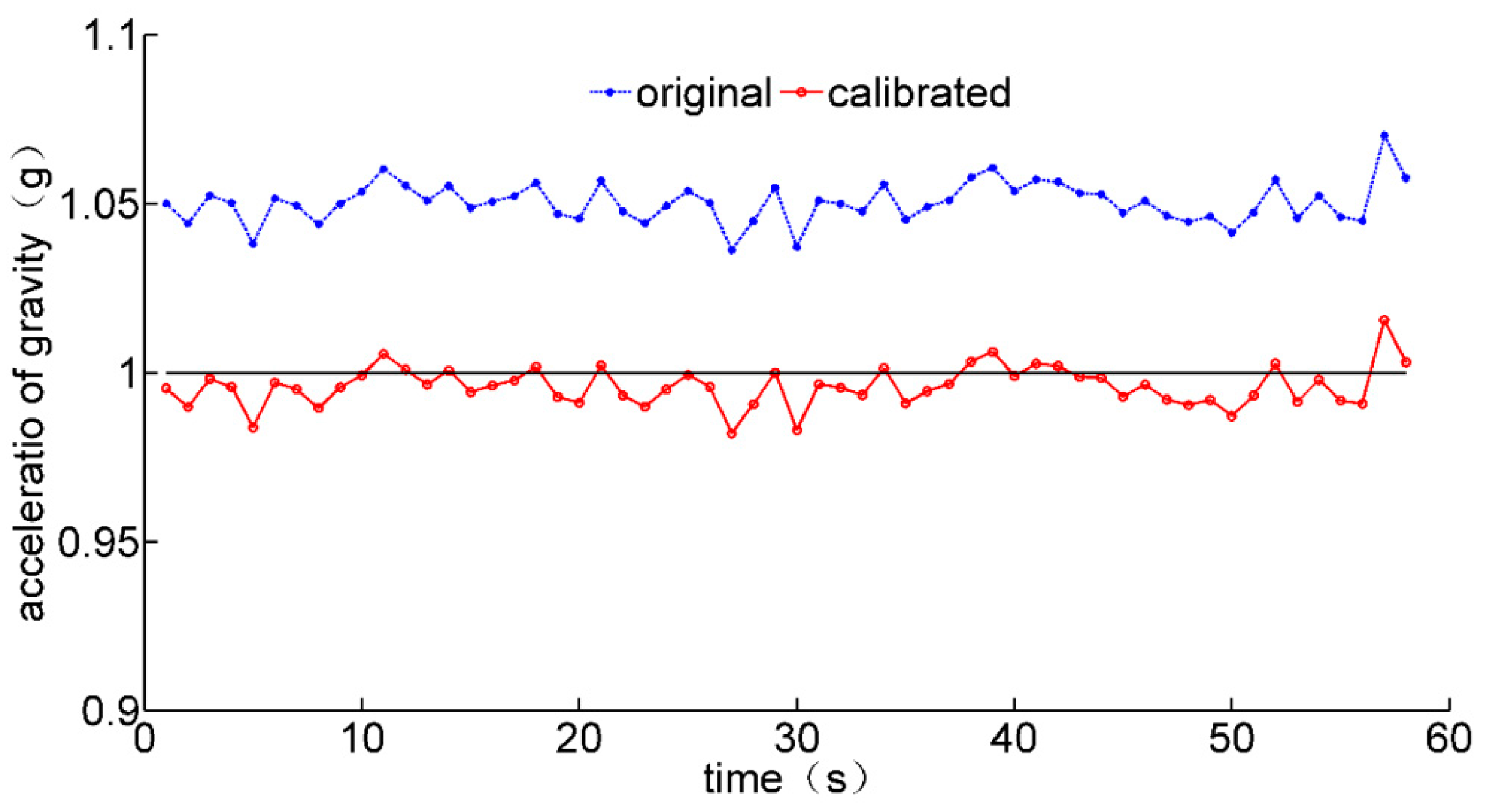
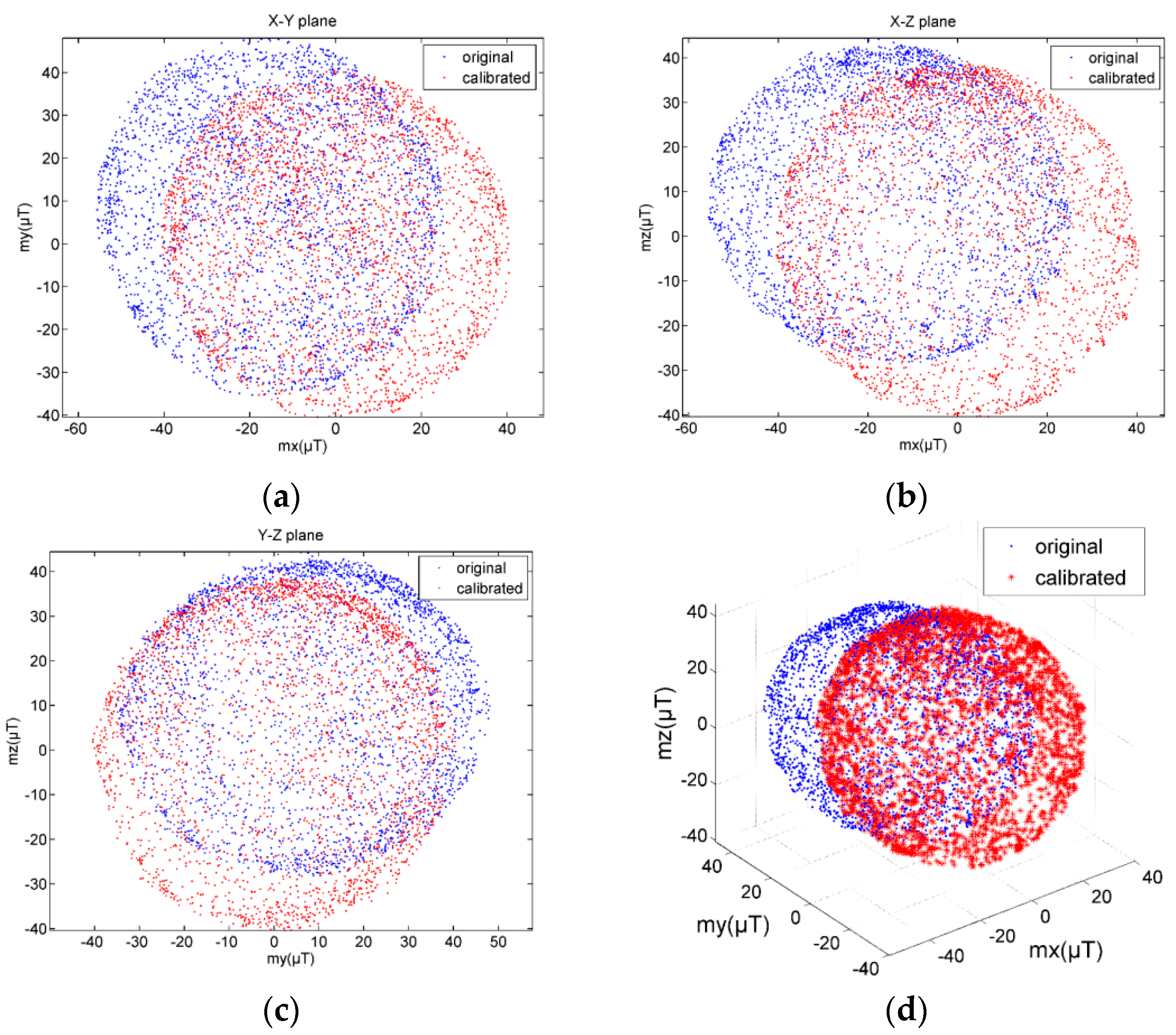
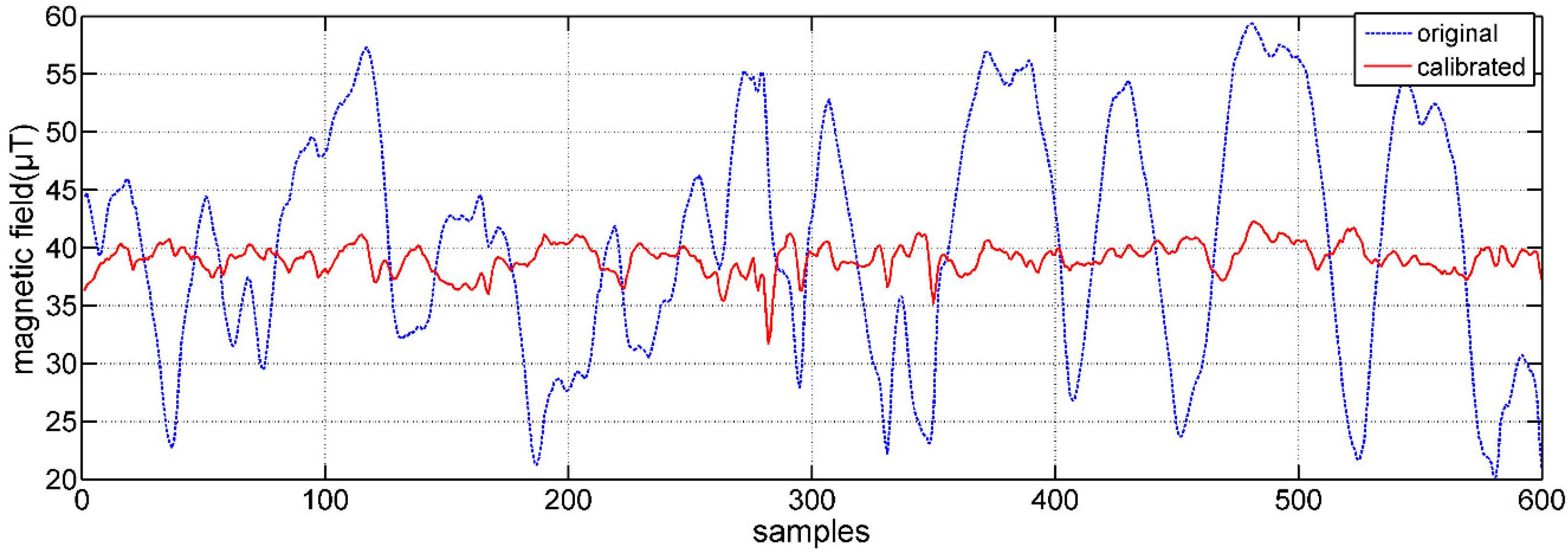
4. Experimental Results of Sensor Calibration and Fusion
5. Human–Computer Interaction Using Data Glove
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Platz, T.; Pinkowski, C.; van Wijck, F.; Kim, I.-H.; Di Bella, P.; Johnson, G. Reliability and validity of arm function assessment with standardized guidelines for the Fugl-Meyer Test, Action Research Arm Test and Box and Block Test: A multicentre study. Clin. Rehabil. 2005, 19, 404–411. [Google Scholar] [CrossRef] [PubMed]
- Yozbatiran, N.; Der-Yeghiaian, L.; Cramer, S.C. A standardized approach to performing the action research arm test. Neurorehabilit. Neural Repair 2008, 22, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Lyle, R.C. A performance test for assessment of upper limb function in physical rehabilitation treatment and research. Int. J. Rehabil. Res. 1981, 4, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Sears, E.D.; Chung, K.C. Validity and responsiveness of the jebsen–taylor hand function test. J. Hand Surg. 2010, 35, 30–37. [Google Scholar] [CrossRef]
- Nijland, R.; van Wegen, E.; Verbunt, J.; van Wijk, R.; van Kordelaar, J.; Kwakkel, G. A comparison of two validated tests for upper limb function after stroke: The Wolf Motor Function Test and the Action Research Arm Test. J. Rehabil. Med. 2010, 42, 694–696. [Google Scholar] [PubMed]
- Ren, Z.; Meng, J.; Yuan, J. Depth camera based hand gesture recognition and its applications in human-computer-interaction. In Proceedings of the 2011 8th International Conference on Information, Communications & Signal Processing, Singapore, 13–16 December 2011; pp. 1–5. [Google Scholar]
- Li, Z.; Jarvis, R. Real time hand gesture recognition using a range camera. In Proceedings of the Australasian Conference on Robotics and Automation, Sydney, Australia, 2–4 December 2009; pp. 21–27. [Google Scholar]
- Wachs, J.P.; Kölsch, M.; Stern, H.; Edan, Y. Vision-based hand-gesture applications. Commun. ACM 2011, 54, 60–71. [Google Scholar] [CrossRef]
- Skaria, S.; Huang, D.; Al-Hourani, A.; Evans, R.J.; Lech, M. Deep-Learning for Hand-Gesture Recognition with Simultaneous Thermal and Radar Sensors. In Proceedings of the 2020 IEEE Sensors, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar]
- Fan, T.; Ma, C.; Gu, Z.; Lv, Q.; Chen, J.; Ye, D.; Huangfu, J.; Sun, Y.; Li, C.; Ran, L. Wireless hand gesture recognition based on continuous-wave Doppler radar sensors. IEEE Trans. Microw. Theory Tech. 2016, 64, 4012–4020. [Google Scholar] [CrossRef]
- Sturman, D.J.; Zeltzer, D. A survey of glove-based input. IEEE Comput. Graph. Appl. 1994, 14, 30–39. [Google Scholar] [CrossRef]
- Dipietro, L.; Sabatini, A.M.; Dario, P. A survey of glove-based systems and their applications. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 461–482. [Google Scholar] [CrossRef]
- Blake, J.; Gurocak, H.B. Haptic glove with MR brakes for virtual reality. IEEE/ASME Trans. Mechatron. 2009, 14, 606–615. [Google Scholar] [CrossRef]
- Ma, Z.; Ben-Tzvi, P. Design and optimization of a five-finger haptic glove mechanism. J. Mech. Robot. 2015, 7, 041008. [Google Scholar] [CrossRef]
- Chiri, A.; Vitiello, N.; Giovacchini, F.; Roccella, S.; Vecchi, F.; Carrozza, M.C. Mechatronic design and characterization of the index finger module of a hand exoskeleton for post-stroke rehabilitation. IEEE/ASME Trans. Mechatron. 2011, 17, 884–894. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Y.; Sun, W.; Bian, Y.; Zhou, D.; Kristensson, P.O. Dexmo: An inexpensive and lightweight mechanical exoskeleton for motion capture and force feedback in VR. In Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems, San Jose, CA, USA, 7–12 May 2016; pp. 1991–1995. [Google Scholar]
- Tarchanidis, K.N.; Lygouras, J.N. Data glove with a force sensor. IEEE Trans. Instrum. Meas. 2003, 52, 984–989. [Google Scholar] [CrossRef]
- Tognetti, A.; Carbonaro, N.; Zupone, G.; De Rossi, D. Characterization of a novel data glove based on textile integrated sensors. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 2510–2513. [Google Scholar]
- Shen, Z.; Yi, J.; Li, X.; Lo, M.H.P.; Chen, M.Z.; Hu, Y.; Wang, Z. A soft stretchable bending sensor and data glove applications. Robot. Biomim. 2016, 3, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, E.; Ferreira, M.; dos Santos, M.; Suzuki, C.K. Flexible Optical Fiber Bending Transducer for Application in Glove-Based Sensors. IEEE Sens. J. 2014, 14, 3631–3636. [Google Scholar] [CrossRef]
- Da Silva, A.F.; Gonçalves, A.F.; Mendes, P.M.; Correia, J.H. FBG sensing glove for monitoring hand posture. IEEE Sens. J. 2011, 11, 2442–2448. [Google Scholar] [CrossRef]
- Lin, B.-S.; Hsiao, P.-C.; Yang, S.-Y.; Su, C.-S.; Lee, I.-J. Data glove system embedded with inertial measurement units for hand function evaluation in stroke patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 2204–2213. [Google Scholar] [CrossRef]
- Lin, B.-S.; Lee, I.; Yang, S.-Y.; Lo, Y.-C.; Lee, J.; Chen, J.-L. Design of an inertial-sensor-based data glove for hand function evaluation. Sensors 2018, 18, 1545. [Google Scholar] [CrossRef]
- Choi, Y.; Yoo, K.; Kang, S.J.; Seo, B.; Kim, S.K. Development of a low-cost wearable sensing glove with multiple inertial sensors and a light and fast orientation estimation algorithm. J. Supercomput. 2018, 74, 3639–3652. [Google Scholar] [CrossRef]
- Liu, Q.; Qian, G.; Meng, W.; Ai, Q.; Yin, C.; Fang, Z. A new IMMU-based data glove for hand motion capture with optimized sensor layout. Int. J. Intell. Robot. Appl. 2019, 3, 19–32. [Google Scholar] [CrossRef]
- Wu, G.; van der Helm, F.C.; Veeger, H.E.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef] [PubMed]
- Frosio, I.; Pedersini, F.; Borghese, N.A. Autocalibration of MEMS accelerometers. IEEE Trans. Instrum. Meas. 2008, 58, 2034–2041. [Google Scholar] [CrossRef]
- Euston, M.; Coote, P.; Mahony, R.; Kim, J.; Hamel, T. A complementary filter for attitude estimation of a fixed-wing UAV. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 340–345. [Google Scholar]
- Madgwick, S. An efficient orientation filter for inertial and inertial/magnetic sensor arrays. Rep. x-io Univ. Bristol (UK) 2010, 25, 113–118. [Google Scholar]
- Cha, Y.; Seo, J.; Kim, J.-S.; Park, J.-M. Human–computer interface glove using flexible piezoelectric sensors. Smart Mater. Struct. 2017, 26, 057002. [Google Scholar] [CrossRef]
- Li, K.; Chen, I.M.; Yeo, S.H.; Lim, C.K. Development of finger-motion capturing device based on optical linear encoder. J. Rehabil. Res. Dev. 2011, 48, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of hand kinematics using inertial and magnetic sensors. J. Neuroeng. Rehabil. 2014, 11, 1–15. [Google Scholar] [CrossRef]




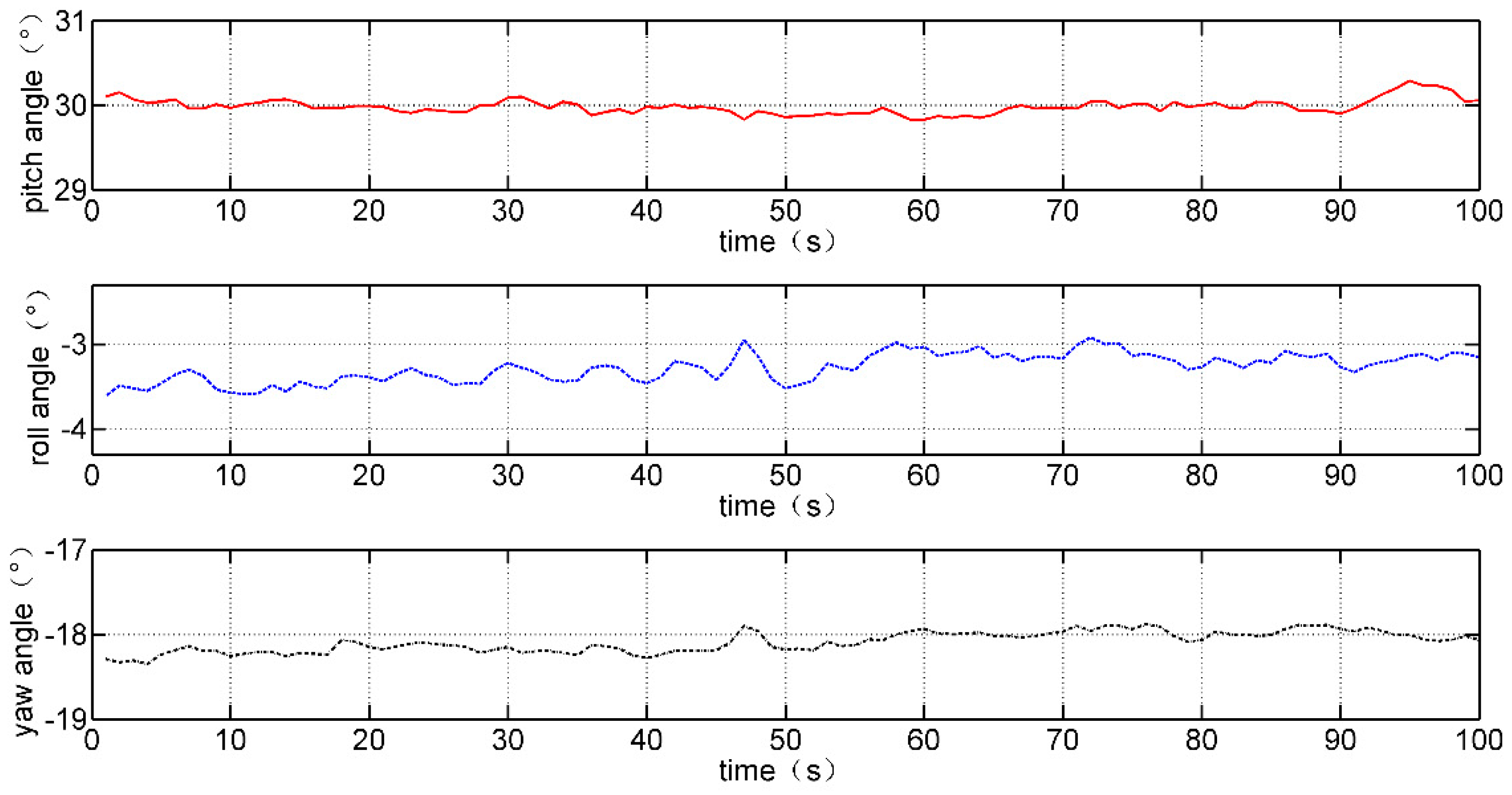





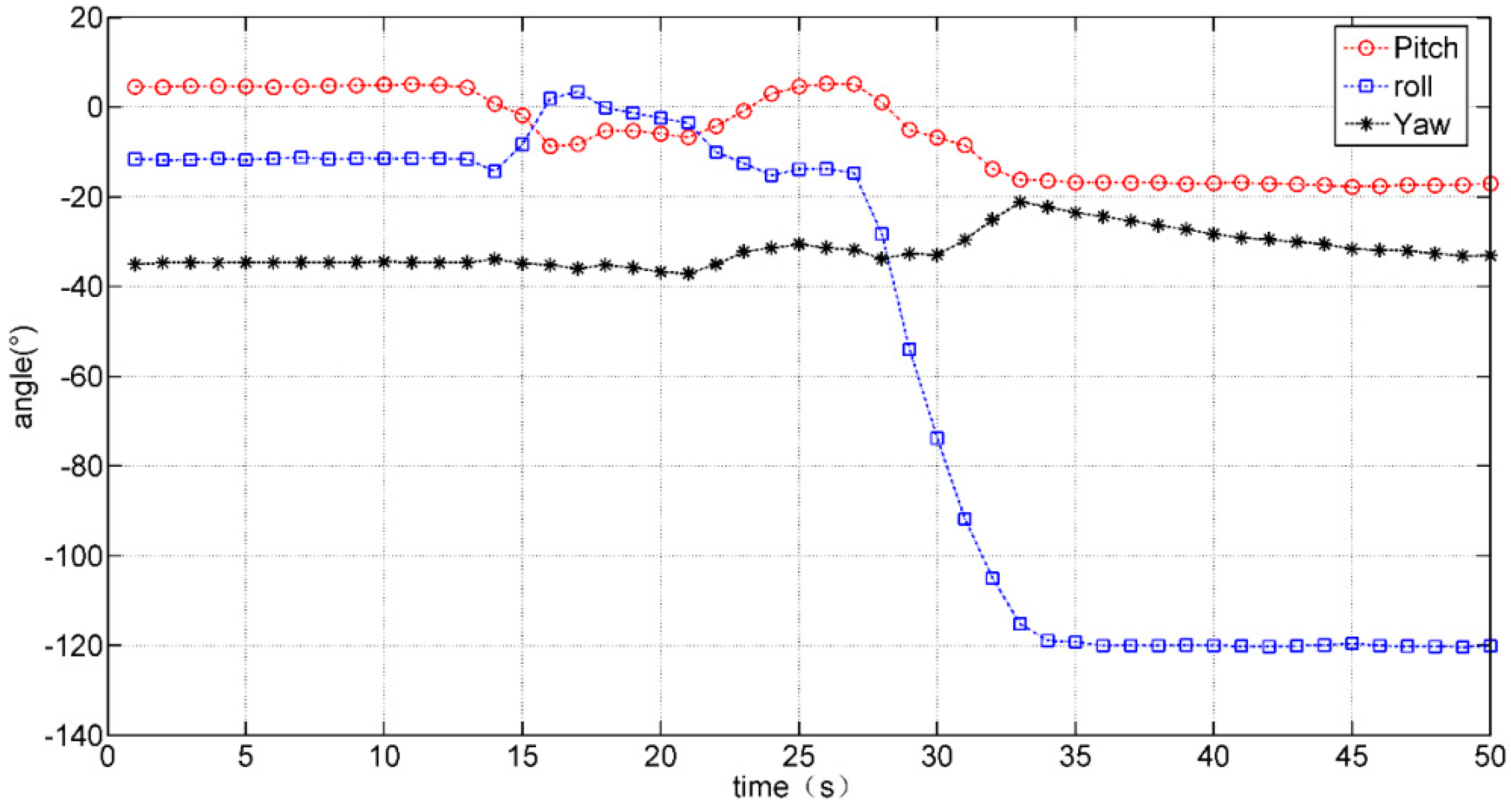
| Angle from goniometer | 112.10° | 91.20° | 80.52° | 69.65° |
| Average angle from data glove | 110.28° | 89.55° | 79.66° | 68.30° |
| Error rate | 1.6% | 1.8% | 1.1% | 1.9% |
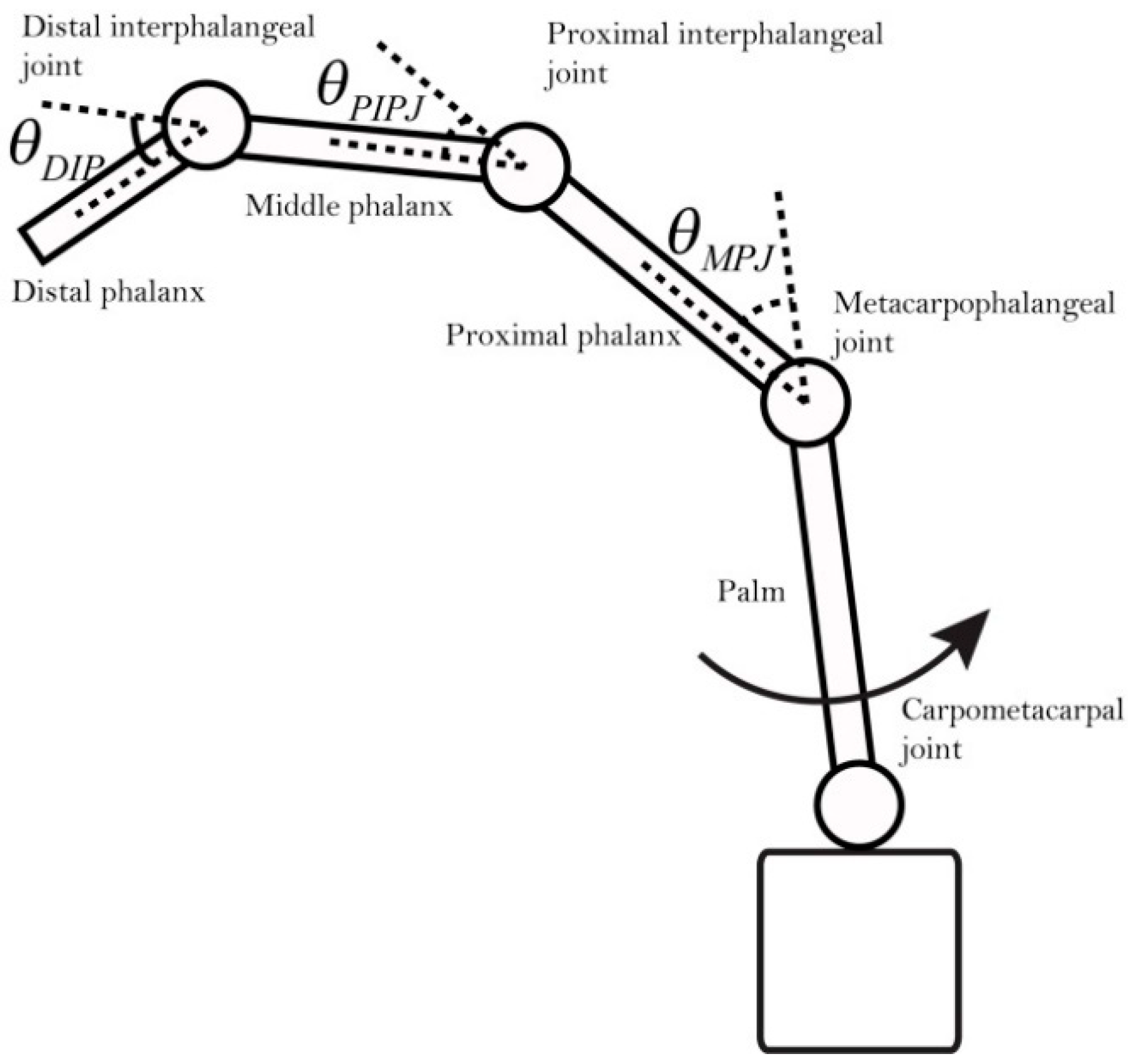
| Joint | ID | Bending Angle |
|---|---|---|
| Thumb IP joint | ||
| Thumb MP joint | ||
| Index finger PIP joint | ||
| Index finger MP joint | ||
| Middle finger PIP joint | ||
| Middle finger MP joint | ||
| Ring finger PIP joint | ||
| Ring finger MP joint | ||
| Little finger PIP joint | ||
| Little finger MP joint |
| Gesture | Index Finger | Middle Finger | Ring Finger | Little Finger | ||||
|---|---|---|---|---|---|---|---|---|
| “2” | 9.2° | 7.9° | 2.4° | 24.8° | 109.2° | 49.4° | 64.4° | 90.7° |
| “5” | 5.5° | 2.2° | 16.4° | 3.9° | 9.5° | 10.5° | 24.3° | 20.6° |
| “10” | 110.3° | 70.2° | 108.2° | 67.5° | 148.6° | 62.9° | 68.9° | 77.3° |
| Publications | Type of Sensor | Number of Sensors | Deviation of Joint Angle |
|---|---|---|---|
| Cha et al. [30] | flexible piezoelecric sensor | 19 (one hand) | 5° |
| da Silva et al. [21] | fiber bragg gratings sensor | 1 (each finger) | 2° |
| Li et al. [31] | optical linear encoder | 3 (each finger) | 1° |
| Kortier et al. [32] | IMMU | 3 (each finger) | 1.1° |
| Proposed glove system | IMMU | 12 (one hand) | 1.4° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, F.; Xian, S.; Xie, X.; Wu, C.; Yang, D.; Yin, K.; Zhang, G. Development of a Wearable Glove System with Multiple Sensors for Hand Kinematics Assessment. Micromachines 2021, 12, 362. https://doi.org/10.3390/mi12040362
Fei F, Xian S, Xie X, Wu C, Yang D, Yin K, Zhang G. Development of a Wearable Glove System with Multiple Sensors for Hand Kinematics Assessment. Micromachines. 2021; 12(4):362. https://doi.org/10.3390/mi12040362
Chicago/Turabian StyleFei, Fei, Sifan Xian, Xiaojian Xie, Changcheng Wu, Dehua Yang, Kuiying Yin, and Guanglie Zhang. 2021. "Development of a Wearable Glove System with Multiple Sensors for Hand Kinematics Assessment" Micromachines 12, no. 4: 362. https://doi.org/10.3390/mi12040362
APA StyleFei, F., Xian, S., Xie, X., Wu, C., Yang, D., Yin, K., & Zhang, G. (2021). Development of a Wearable Glove System with Multiple Sensors for Hand Kinematics Assessment. Micromachines, 12(4), 362. https://doi.org/10.3390/mi12040362






