The Influence of Crystal Orientation on Subsurface Damage of Mono-Crystalline Silicon by Bound-Abrasive Grinding
Abstract
:1. Introduction
2. Experiments
2.1. Grinding Samples
2.2. The Surface Roughness Measurement of the Ground Specimens
2.3. The Sub-Surface Damage Measurement of the Ground Specimens
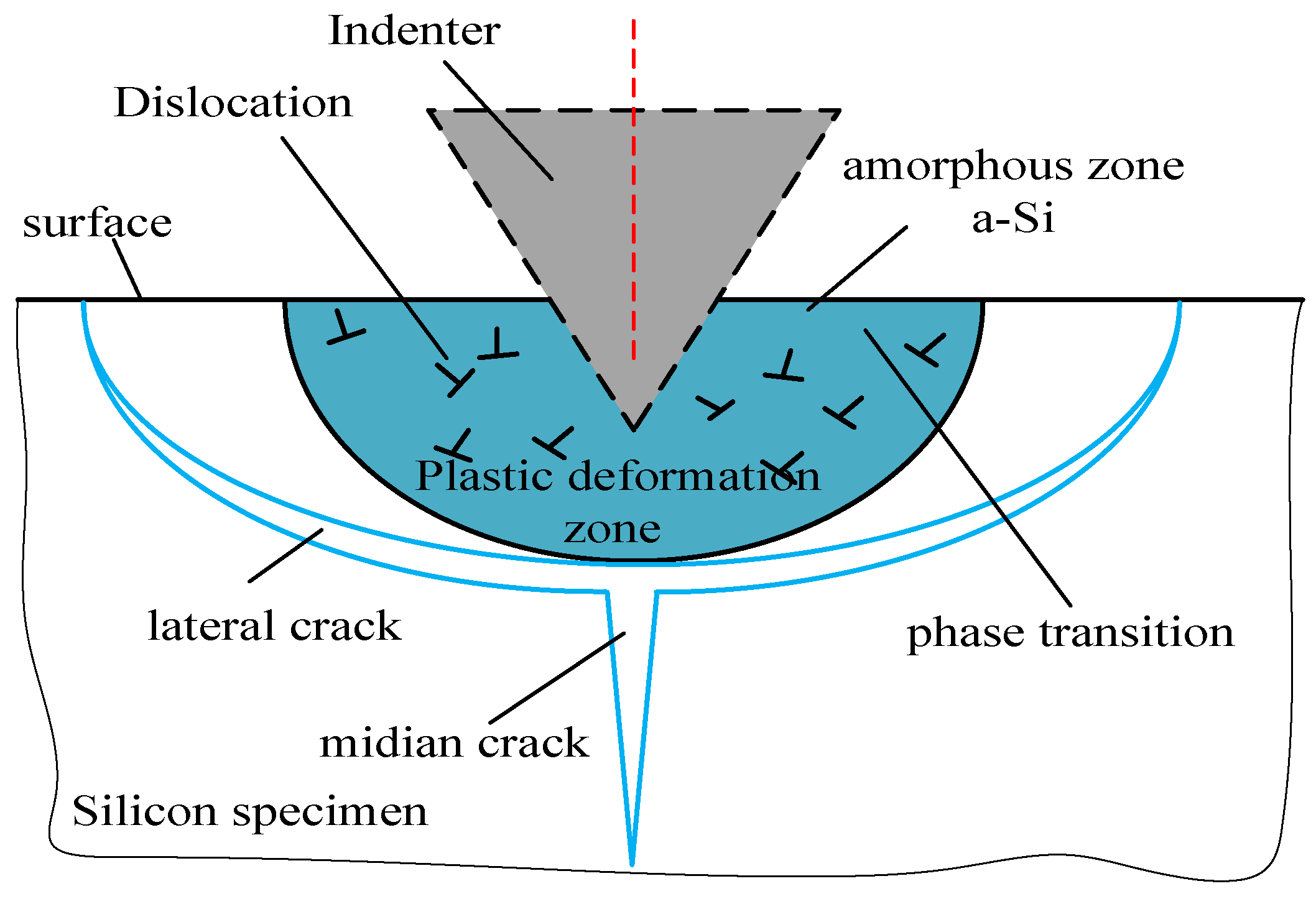
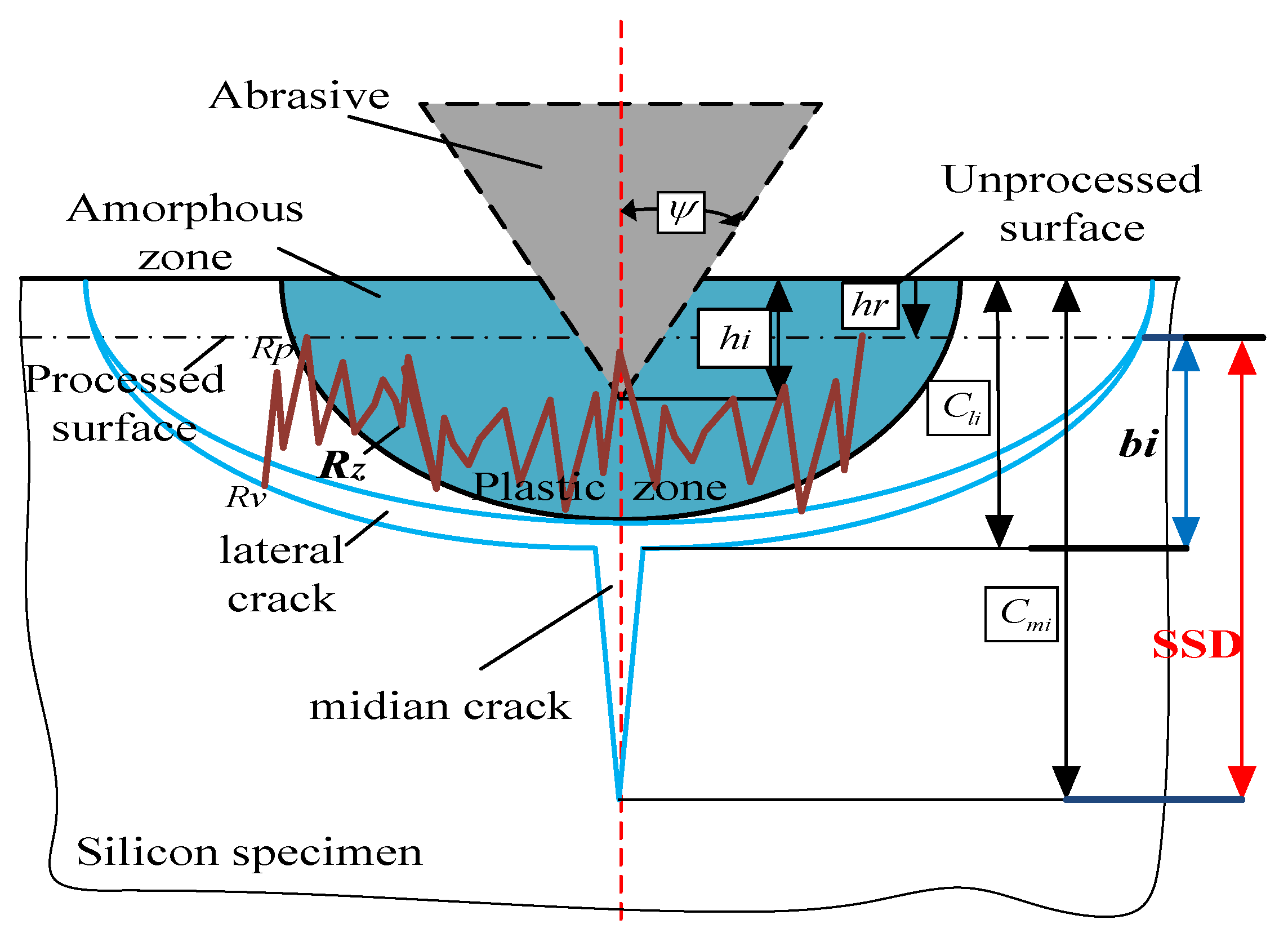
3. The Modeling of Predicting SSD
4. The Results and Discussion
4.1. Morphology of Subsurface Damage
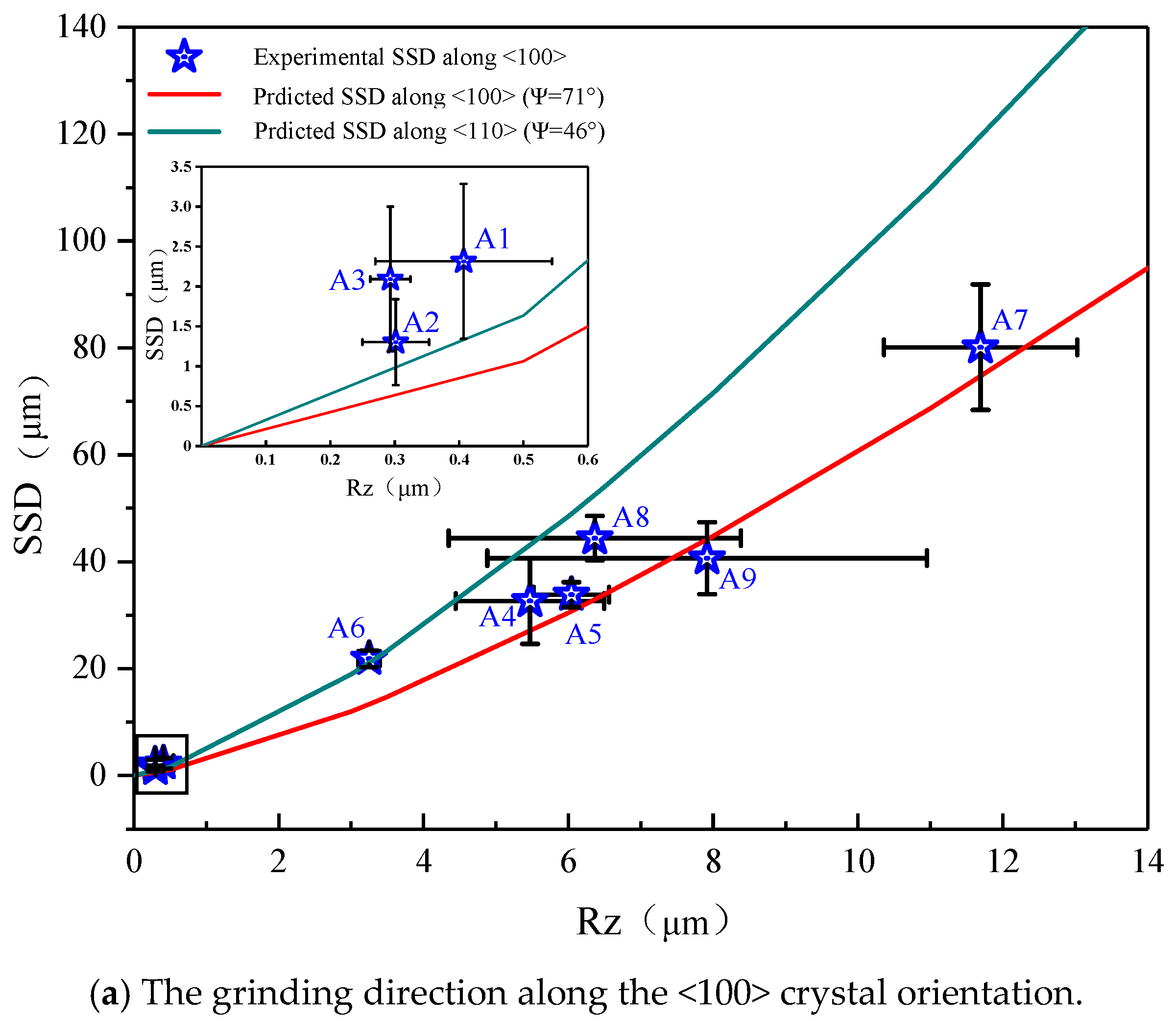
4.2. Depth of Subsurface Damage
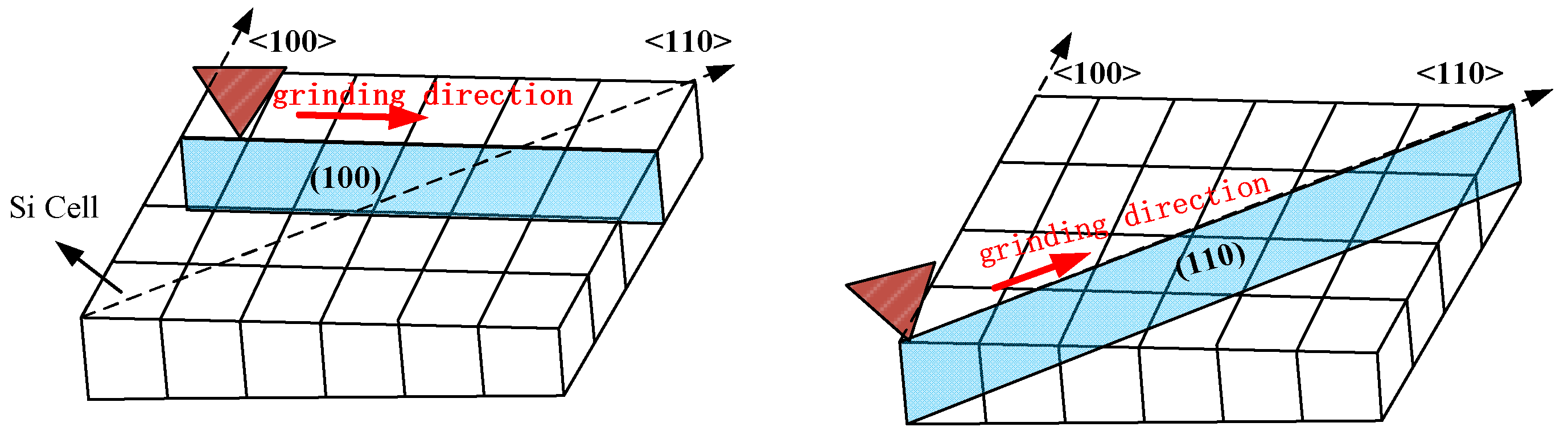
4.3. Effects of Crystal Orientation and Processing Parameters on SSD
5. Conclusions
- Except for the D15A ground samples (surface roughness (RZ) < RZC, RZ<100> < 1.5 μm, RZ<100> < 0.8 μm), where no cracks were observed on the subsurface, all the experimental results were within the theoretical prediction range. The relationship between SSD and surface roughness RZ was shown to be a proportional function and in good accordance with the proposed model.
- Grinding experiments showed that the subsurface damage depth in samples ground along the <110> crystal orientation was larger than that along the <100> crystal orientation in the same processing parameters, since the Si–Si covalent bond density on (100) plane is greater than (110) plane.
- Whether it was grinding along the <100> or <110> direction, the trend of SSD changes with process parameters is shown as the depth of SSD increasing with increasing grit size and feed rate, which decreases with the wheel speed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| ψ | the sharpness tip angle of indenter |
| KC | the fracture toughness of Mono-crystalline Silicon |
| E | the elastic modulus |
| (RZ) | ten-point mean roughness |
| SSD | subsurface damage |
| RZC | the brittle-plastic transition critical value |
| RZC<100> | the brittle-plastic transition critical value along <100> orientation |
| RZC<110> | the brittle-plastic transition critical value along <110> orientation |
| μ | the depth ratio of removal depth to cutting depth |
| m | a dimensionless quantity |
| β | the elastic recovery coefficient |
References
- Suratwala, T. Materials Science and Technology of Optical Fabrication; Lawrence Livermore National Lab: Hoboken, NJ, USA, 2018; p. 94550. [Google Scholar]
- Yin, J.; Bai, Q.; Li, Y.; Zhang, B. Formation of subsurface cracks in silicon wafers by grinding. Nanotechnol. Precis. Eng. 2018, 1, 172–179. [Google Scholar] [CrossRef]
- Chen, J.; Jinyi, C.; Tao, W. Theoretical model of brittle material removal fraction related to surface roughness and subsurface damage depth of optical glass during precision grinding. Precis. Eng. 2017, 48, 421–427. [Google Scholar]
- Yan, J.; Asami, T.; Kuriyagawa, T. Nondestructive measurement of machining-induced amorphous layers in single-crystal silicon by laser micro-Raman spectroscopy. Precis. Eng. 2008, 32, 186–195. [Google Scholar] [CrossRef]
- Liu, W.; Deng, Z.; Shang, Y.; Wan, L. Effects of grinding parameters on surface quality in silicon nitride grinding. Ceram. Int. 2017, 43, 1571–1577. [Google Scholar] [CrossRef]
- Tönshoff, H.; Karpuschewski, B.; Hartmann, M.; Spengler, C. Grinding-and-slicing technique as an advanced technology for silicon wafer slicing. Mach. Sci. Technol. 1997, 1, 33–47. [Google Scholar] [CrossRef]
- Stephens, A. Technique for measuring the depth and distribution of damage in silicon slices. J. Electrochem. Soc. 1986, 133, 106–115. [Google Scholar]
- Lundt, H.; Kerstan, M.; Huber, A.; Hahn, P. Subsurface damage of abraded silicon wafers. In Proceedings of the 7th International Symposium on Silicon Materials Science and Technology, Pennington, NJ, USA, October 1994; pp. 218–224. [Google Scholar]
- Tang, F.; Zhang, L. Subsurface nanocracking in monocrystalline Si (0 0 1) induced by nanoscratching. Eng. Fract. Mech. 2014, 124, 262–271. [Google Scholar] [CrossRef]
- Zarudi, I.; Zhang, L. Effect of ultraprecision grinding on the microstructural change in silicon monocrystals. J. Mater. Process. Technol. 1998, 84, 149–158. [Google Scholar] [CrossRef]
- Gogotsi, Y.; Zhou, G.; Ku, S.-S.; Cetinkunt, S. Raman microspectroscopy analysis of pressure-induced metallization in scratching of silicon. Semicond. Sci. Technol. 2001, 16, 345–352. [Google Scholar] [CrossRef]
- Bismayer, U.; Brinksmeier, E.; Güttler, B.; Seibt, H.; Menz, C. Measurement of subsurface damage in silicon wafers. Precis. Eng. 1994, 16, 139–144. [Google Scholar] [CrossRef]
- Lambropoulos, J.C.; Jacobs, S.D.; Ruckman, J. Material removal mechanisms from grinding to polishing. Ceram. Trans. 1999, 102, 113–128. [Google Scholar]
- Li, S.; Wang, Z.; Wu, Y. Relationship between subsurface damage and surface roughness of optical materials in grinding and lapping processes. J. Mater. Process. Technol. 2008, 205, 34–41. [Google Scholar] [CrossRef]
- Shen, N.; Suratwala, T.; Steele, W.; Wong, L.; Feit, M.D.; Miller, P.E.; Dylla-Spears, R.; Desjardin, R. Nanoscratching of Optical Glass Surfaces Near the Elastic–Plastic Load Boundary to Mimic the Mechanics of Polishing Particles. J. Am. Ceram. Soc. 2016, 99, 1477–1484. [Google Scholar] [CrossRef]
- Wojciechowski, S.; Nowakowski, Z.; Majchrowski, R.; Królczyk, G. Surface texture formation in precision machining of direct laser deposited tungsten carbide. Adv. Manuf. 2017, 5, 251–260. [Google Scholar] [CrossRef] [Green Version]
- Xiao, G.; To, S.; Zhang, G. Molecular dynamics modelling of brittle–ductile cutting mode transition: Case study on silicon carbide. Int. J. Mach. Tools Manuf. 2015, 88, 214–222. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, P.; An, T.; Dai, Y.; Qin, F. Analytical prediction for depth of subsurface damage in silicon wafer due to self-rotating grinding process. Curr. Appl. Phys. 2019, 19, 570–581. [Google Scholar] [CrossRef]
- Li, H.N.; Yu, T.B.; Da Zhu, L.; Wang, W.S. Analytical modeling of grinding-induced subsurface damage in monocrystalline silicon. Mater. Des. 2017, 130, 250–262. [Google Scholar] [CrossRef]
- Model 80# is a Product of Changxing Diamond Abrasives Co., Ltd., China; the Others Are Manufactured by Winter Diamond Tools, Saint-Gobain Diamantwerkzeuge GmbH & Co., Germany. Changxing Diamond Abrasives Co., Ltd. Available online: http://www.cxtools.com.cn (accessed on 28 March 2021).
- Zhang, Y.X.; Li, D.L.; Gao, W.; Kang, R.K. Experimental Investigation on the Detection Technique for Surface Layer Damage of Machined Silicon Wafers. J. Synth. Cryst. 2011, 40, 359–364. [Google Scholar]
- Ohta, T.; Yan, J.; Kuriyagawa, T.; Kodera, S.; Nakasuji, T. Prediction of subsurface damage depth of ground brittle materials by surface profiling. Int. J. Mach. Mach. Mater. 2007, 2, 108–124. [Google Scholar] [CrossRef]
- Helbawi, H.; Zhang, L.; Zarudi, I. Difference in subsurface damage in indented specimens with and without bonding layer. Int. J. Mech. Sci. 2001, 43, 1107–1121. [Google Scholar] [CrossRef]
- Zarudi, I.; Zhang, L. Subsurface damage in single-crystal silicon due to grinding and polishing. J. Mater. Sci. Lett. 1996, 15, 586–587. [Google Scholar] [CrossRef]
- Lu, W.K.; Sun, J.G.; Pei, Z.J. Subsurface damage measurement in silicon wafers with cross-polarisation confocal microscopy. Int. J. Nanomanuf. 2006, 1, 272–282. [Google Scholar] [CrossRef]
- Korkh, Y.V.; Burkhanov, A.M.; Rinkevich, A.B. Scanning acoustic microscope for visualization of microflaws in solids. Russ. J. Nondestruct. Test. 2009, 45, 677–684. [Google Scholar] [CrossRef]
- Abe, T.; Nakazato, Y.; Daito, M.; Kanai, A.; Miyashita, M. The ductile mode grinding technology applied to silicon wafering process. In Semiconductor Silicon: Proceedings of the Seventh International Symposium on Silicon Materials Science and Technology; The Electrochemical Society: Pennington, NJ, USA, 1994. [Google Scholar]
- Gao, S.; Kang, R.K.; Guo, D.M.; Huang, Q.S. Study on the Subsurface Damage Distribution of the Silicon Wafer Ground by Diamond Wheel. Adv. Mater. Res. 2010, 126, 113–118. [Google Scholar] [CrossRef]
- Randi, J.A.; Lambropoulos, J.C.; Jacobs, S.D. Subsurface damage in some single crystalline optical materials. Appl. Opt. 2005, 44, 2241–2249. [Google Scholar] [CrossRef] [PubMed]
- Zarudi, I.; Zou, J.; Zhang, L.C. Microstructures of phases in indented silicon: A high resolution characterization. Appl. Phys. Lett. 2003, 82, 874–876. [Google Scholar] [CrossRef] [Green Version]
- Zarudi, I.; Nguyen, T.; Zhang, L.C. Effect of temperature and stress on plastic deformation in monocrystalline silicon induced by scratching. Appl. Phys. Lett. 2005, 86, 011922. [Google Scholar] [CrossRef] [Green Version]
- Gu, W.; Yao, Z.; Li, K. Evaluation of subsurface crack depth during scratch test for optical glass BK7. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2767–2774. [Google Scholar] [CrossRef]
- Cook, R.F. Strength and sharp contact fracture of silicon. J. Mater. Sci. 2006, 41, 841. [Google Scholar] [CrossRef]
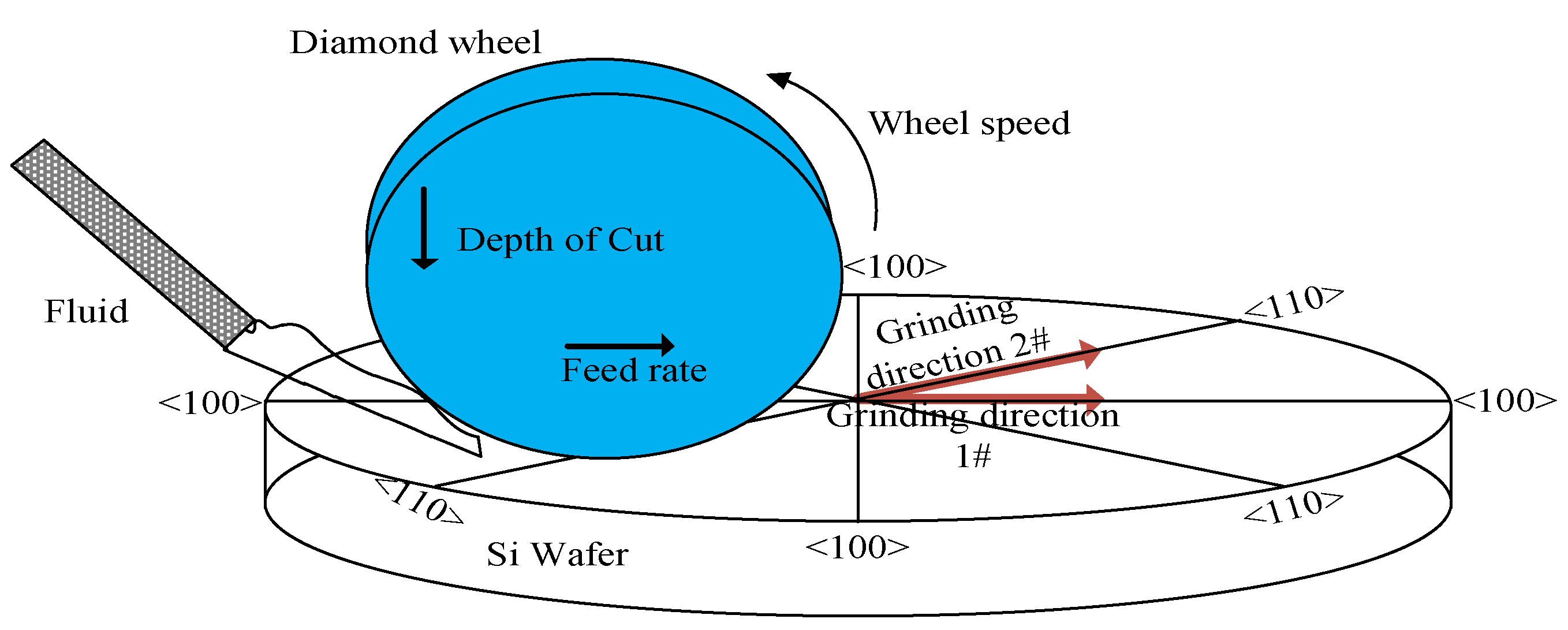
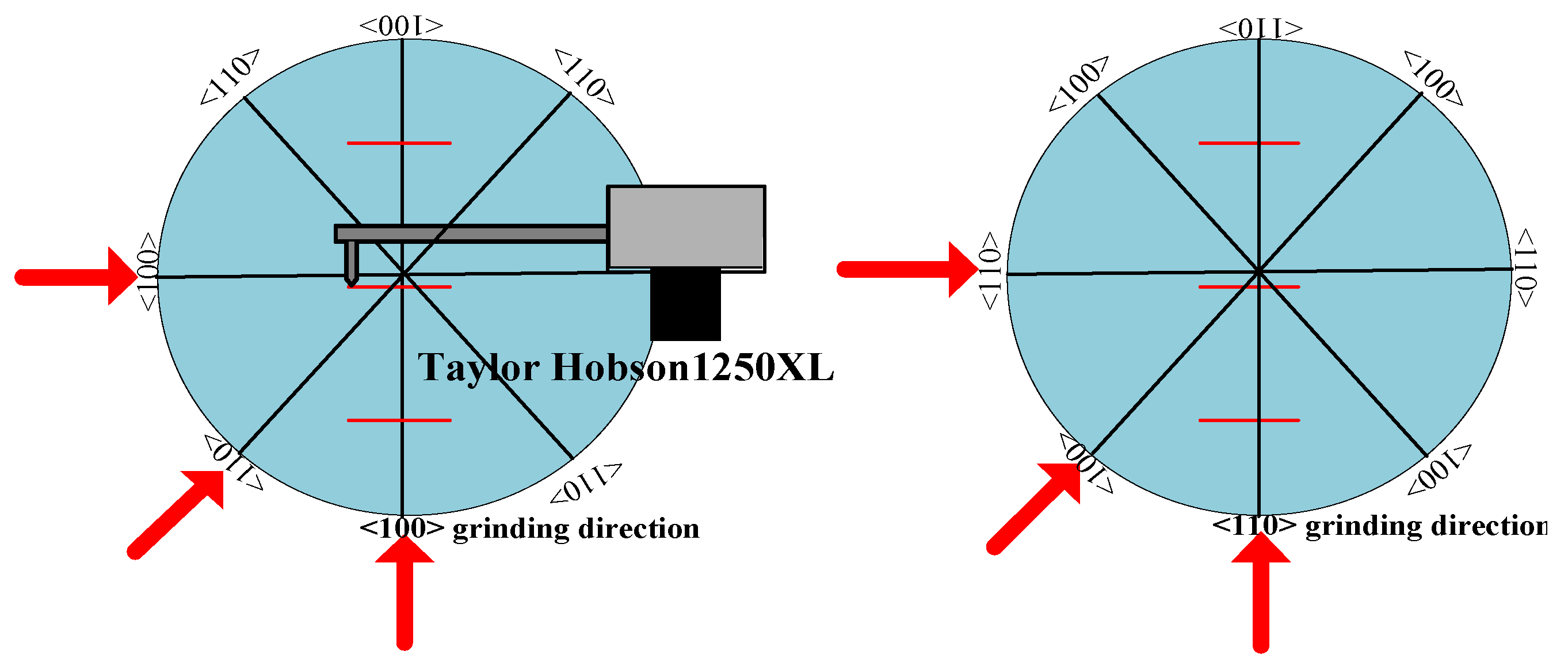
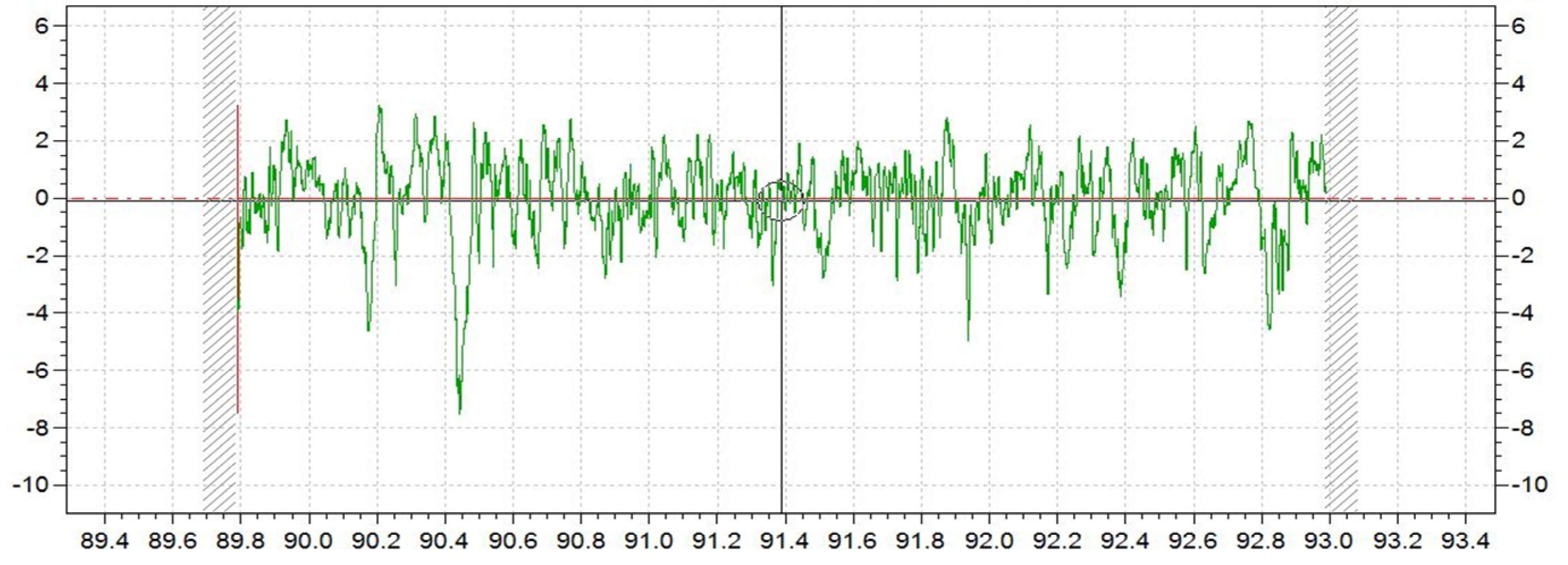
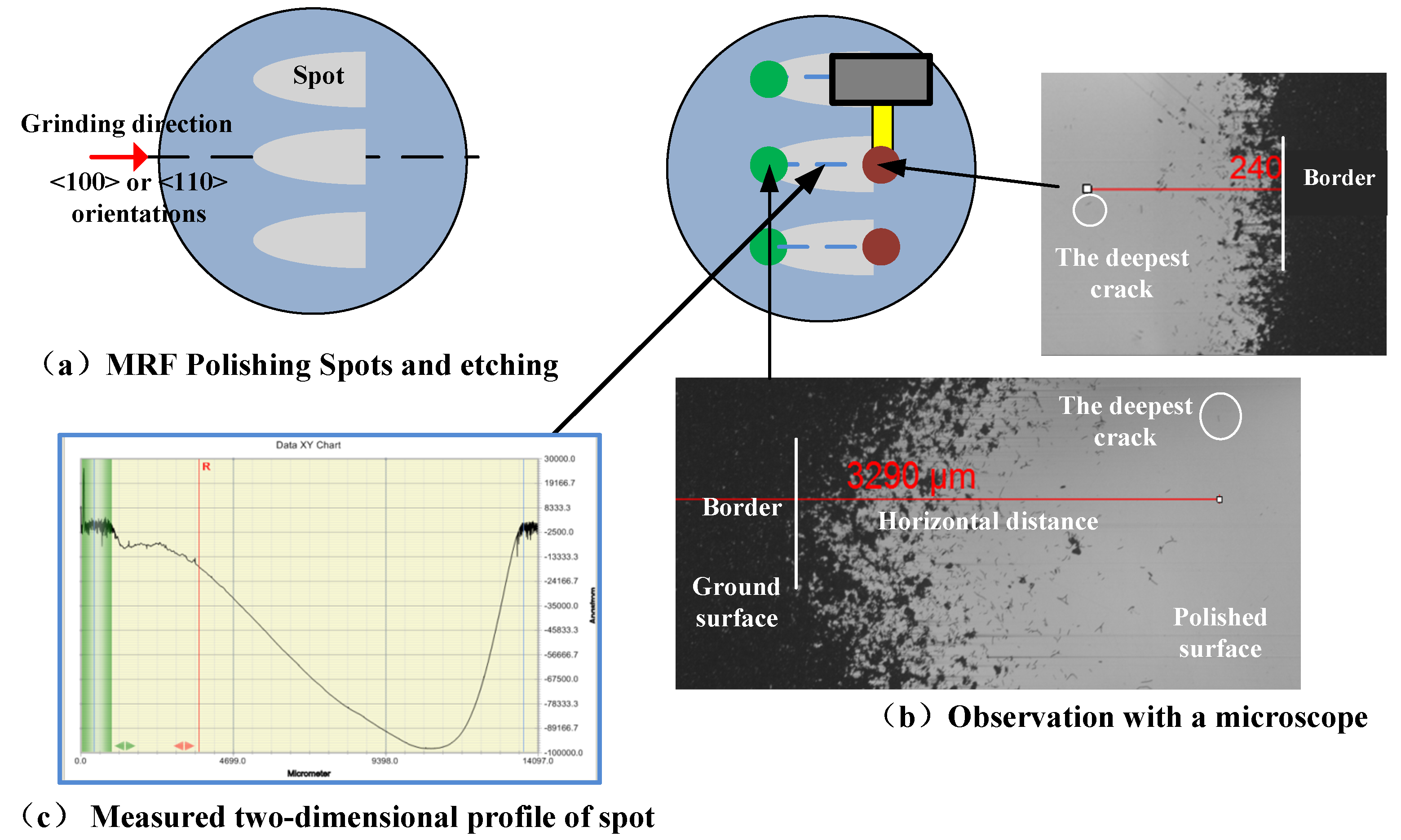



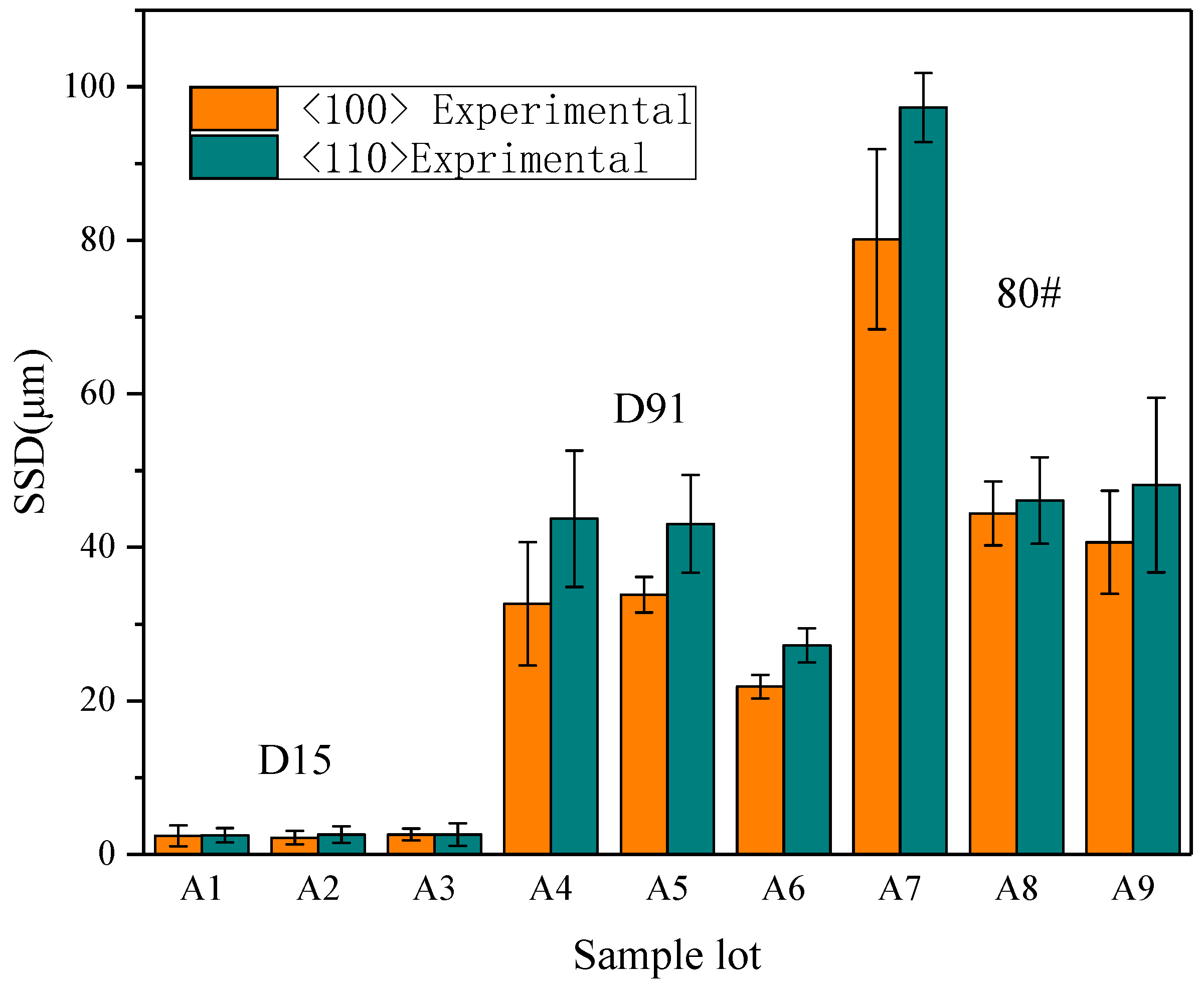
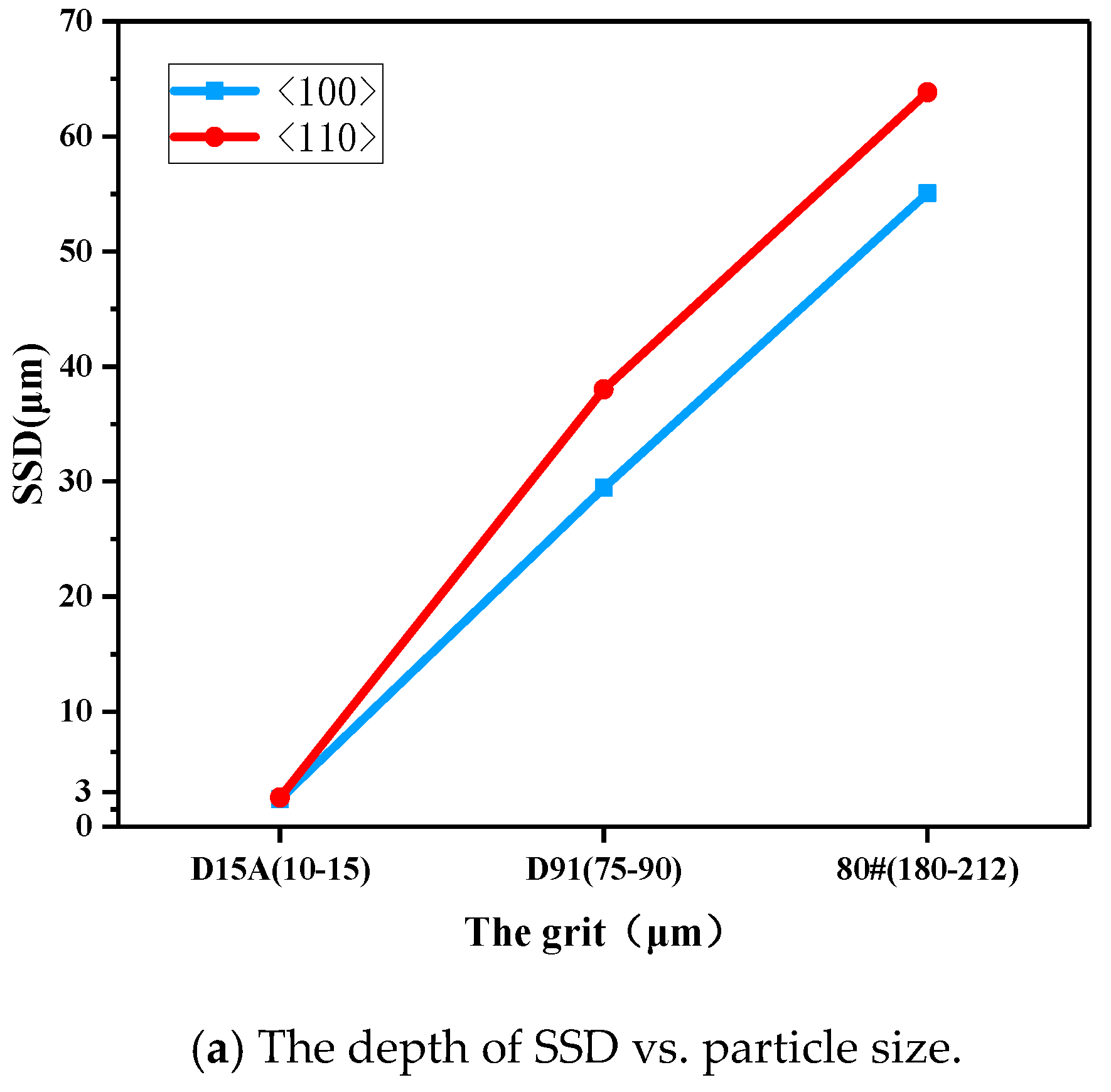
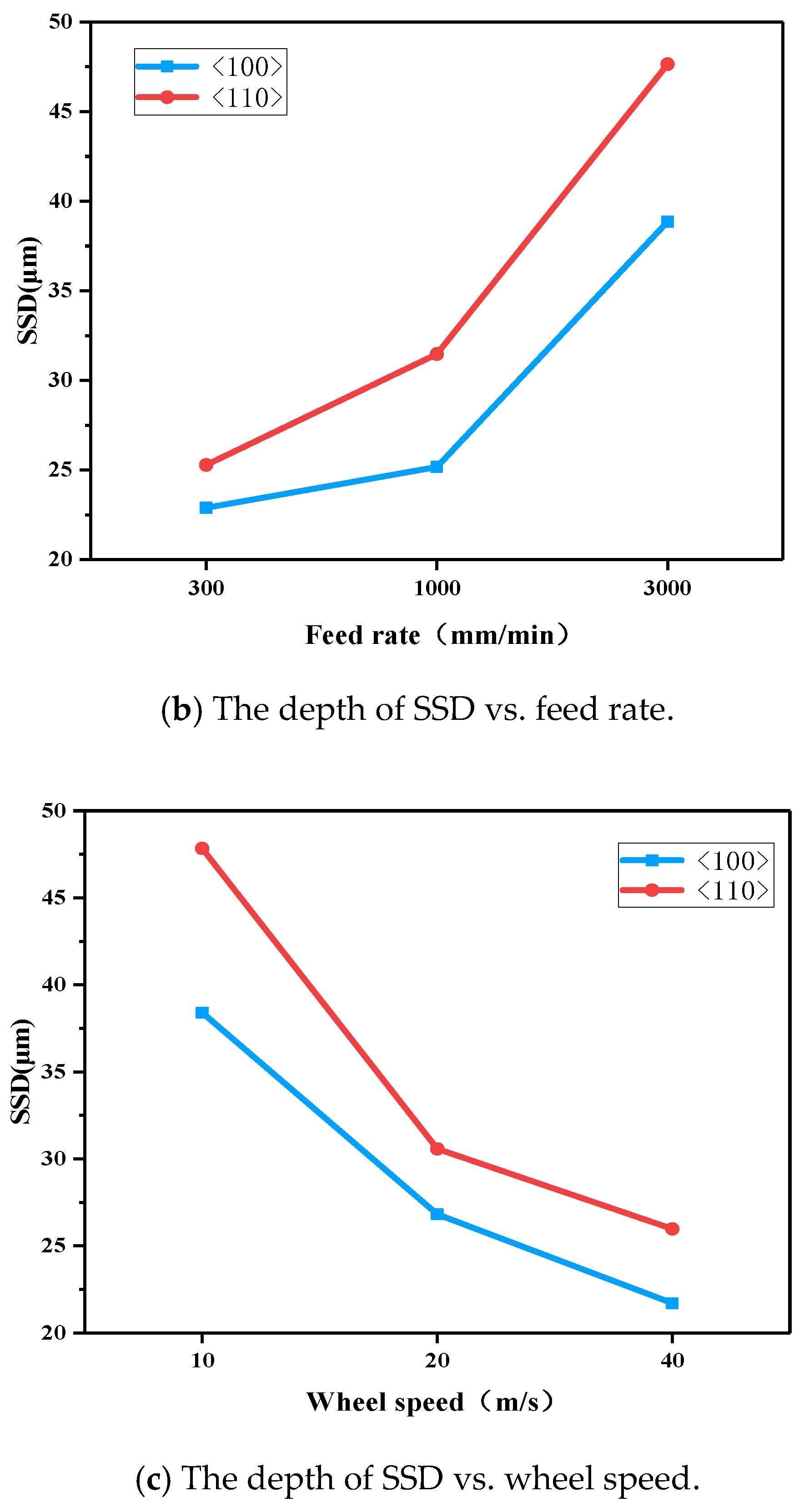
| Factors | Parameters | Levels | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| A | Grain model [10] (μm) | D15A (10–15) | D91 (75–90) | 80# (180–212) |
| B | Wheel speed (m/s) | 10 | 20 | 40 |
| C | Feed rate (mm/min) | 300 | 1000 | 3000 |
| D | Depth of cut (μm) | 5 | 10 | 15 |
| NO. | Grain Model | Wheel Speed (m/s) | Feed Rate (mm/min) | Depth of Cut (μm) | <100> RZ (μm) | <110> RZ (μm) |
|---|---|---|---|---|---|---|
| A1 B1 | D15A | 10 | 300 | 5 | 0.4071 | 0.3914 |
| A2 B2 | D15A | 20 | 1000 | 10 | 0.3061 | 0.3037 |
| A3 B3 | D15A | 40 | 3000 | 15 | 0.2933 | 0.4486 |
| A4 B4 | D91 | 10 | 1000 | 15 | 5.4685 | 6.9261 |
| A5 B5 | D91 | 20 | 3000 | 5 | 6.043 | 6.9867 |
| A6 B6 | D91 | 40 | 300 | 10 | 3.2484 | 3.675 |
| A7 B7 | 80# | 10 | 3000 | 10 | 11.6924 | 12.9087 |
| A8 B8 | 80# | 20 | 300 | 15 | 6.3651 | 6.6319 |
| A9 B9 | 80# | 40 | 1000 | 5 | 7.9160 | 6.7404 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, W.; Li, Y. The Influence of Crystal Orientation on Subsurface Damage of Mono-Crystalline Silicon by Bound-Abrasive Grinding. Micromachines 2021, 12, 365. https://doi.org/10.3390/mi12040365
Yang W, Li Y. The Influence of Crystal Orientation on Subsurface Damage of Mono-Crystalline Silicon by Bound-Abrasive Grinding. Micromachines. 2021; 12(4):365. https://doi.org/10.3390/mi12040365
Chicago/Turabian StyleYang, Wei, and Yaguo Li. 2021. "The Influence of Crystal Orientation on Subsurface Damage of Mono-Crystalline Silicon by Bound-Abrasive Grinding" Micromachines 12, no. 4: 365. https://doi.org/10.3390/mi12040365
APA StyleYang, W., & Li, Y. (2021). The Influence of Crystal Orientation on Subsurface Damage of Mono-Crystalline Silicon by Bound-Abrasive Grinding. Micromachines, 12(4), 365. https://doi.org/10.3390/mi12040365






