Optimization of Field-Free Point Position, Gradient Field and Ferromagnetic Polymer Ratio for Enhanced Navigation of Magnetically Controlled Polymer-Based Microrobots in Blood Vessel
Abstract
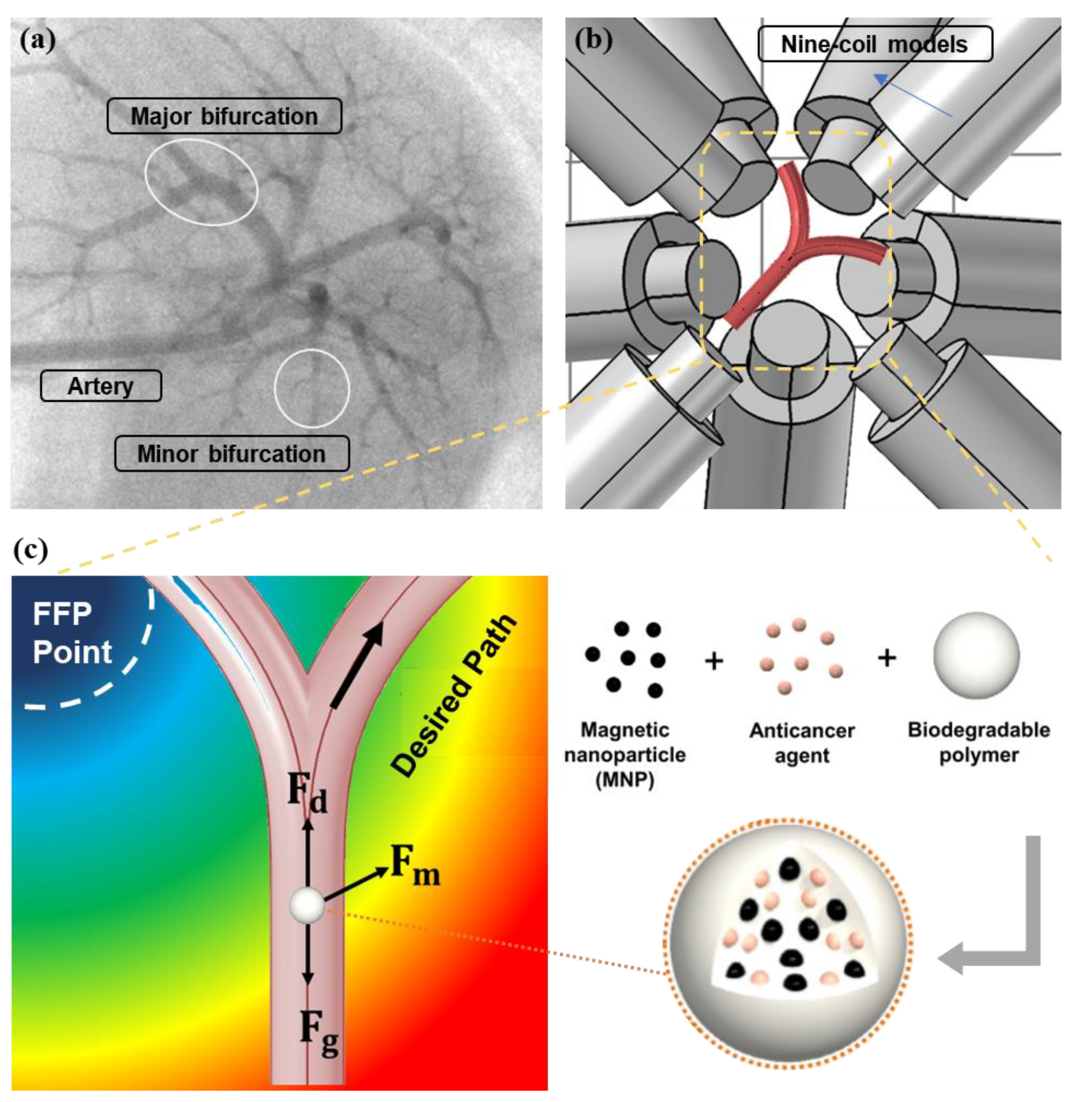
1. Introduction
2. Analytical Model
2.1. Hydrodynamic Drag Force
2.2. Magnetic Force
2.3. Gravitational Force
2.4. Contact Force
3. Results and Discussion
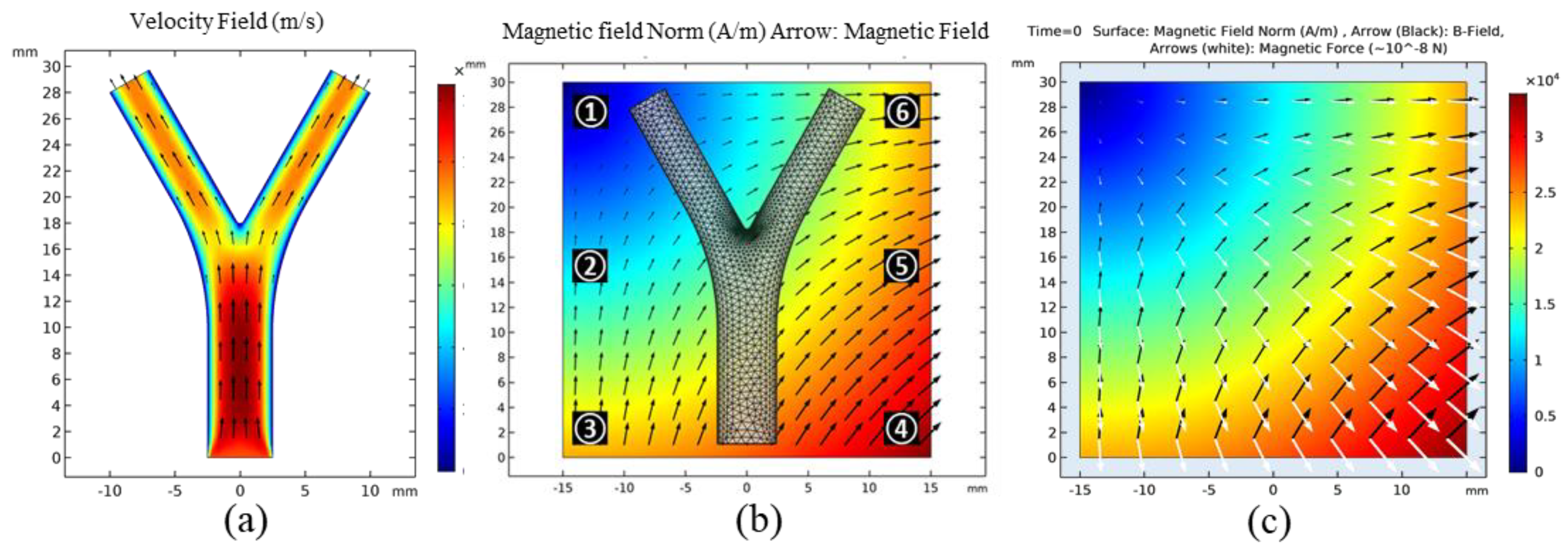
3.1. Ideal 2D Case
3.2. 3D Case
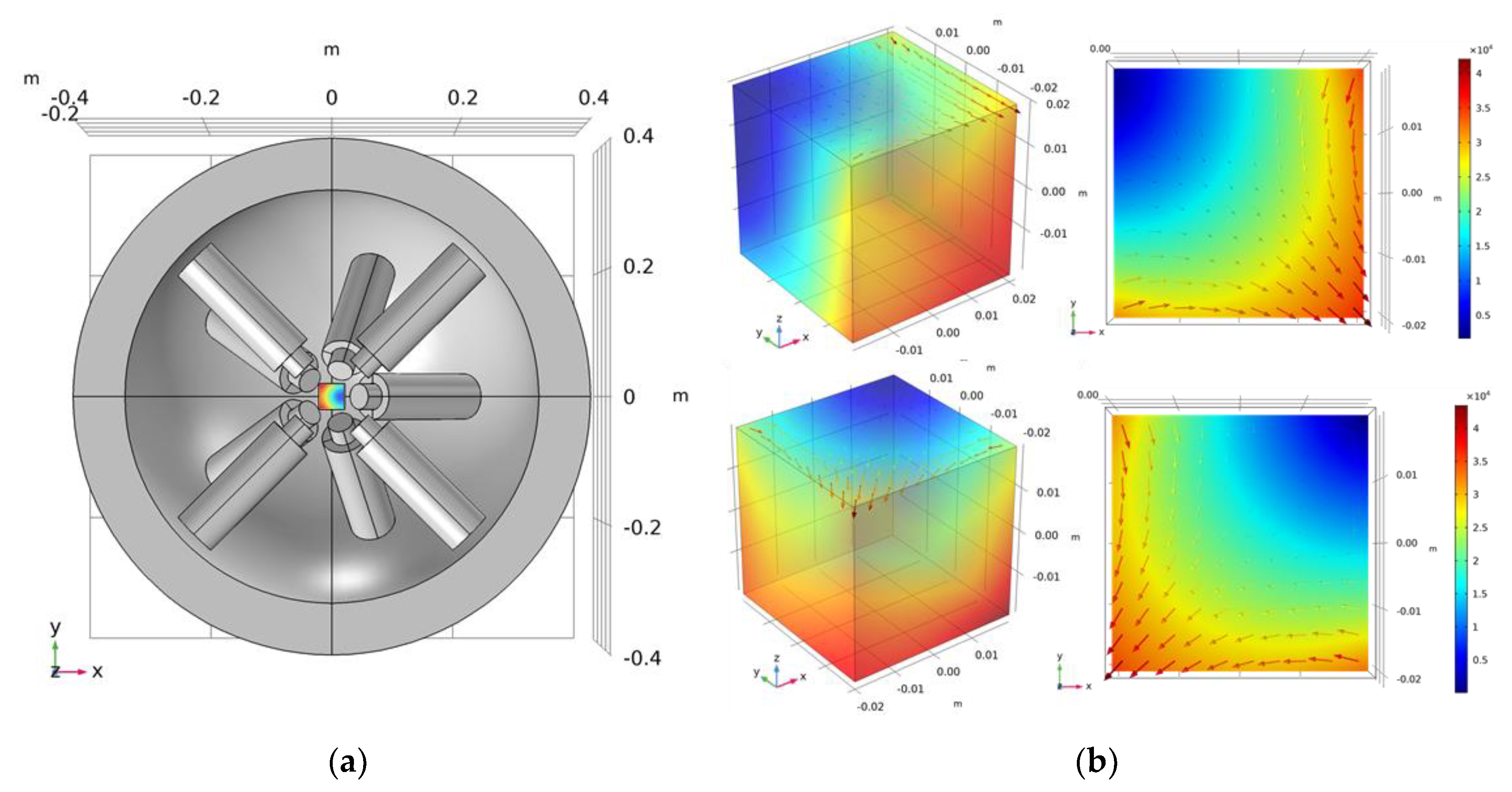
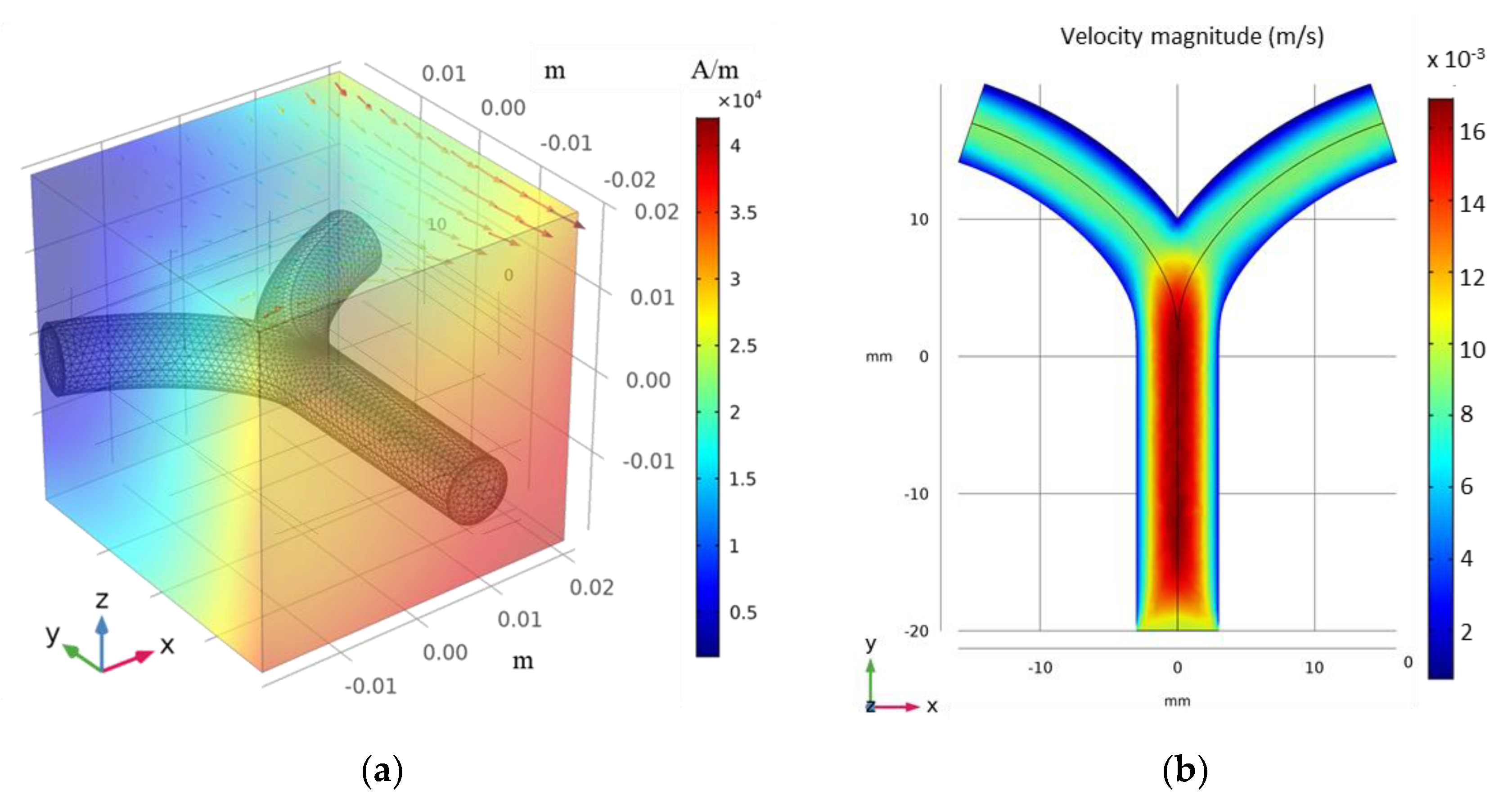
3.2.1. FFP Generation
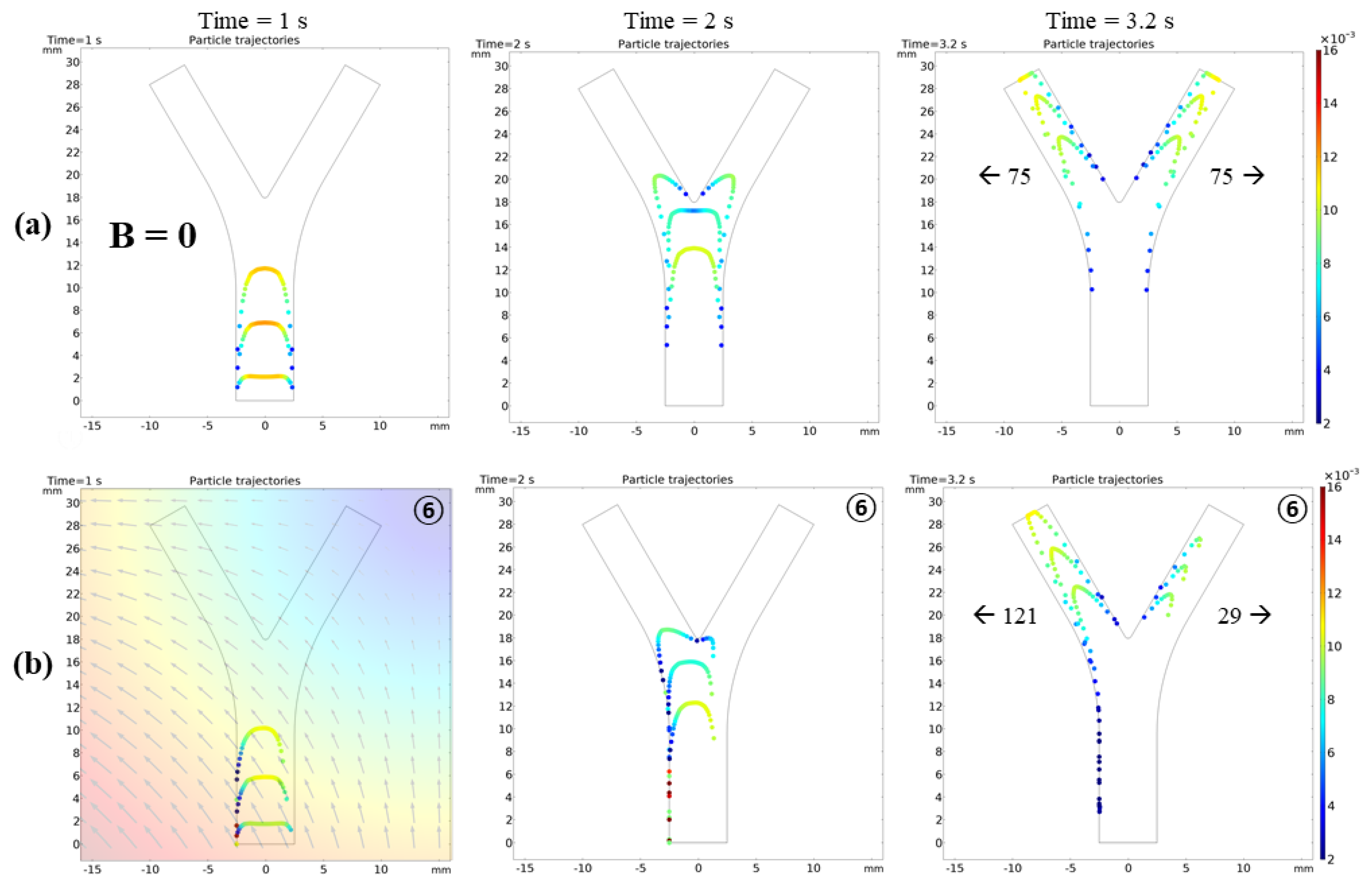
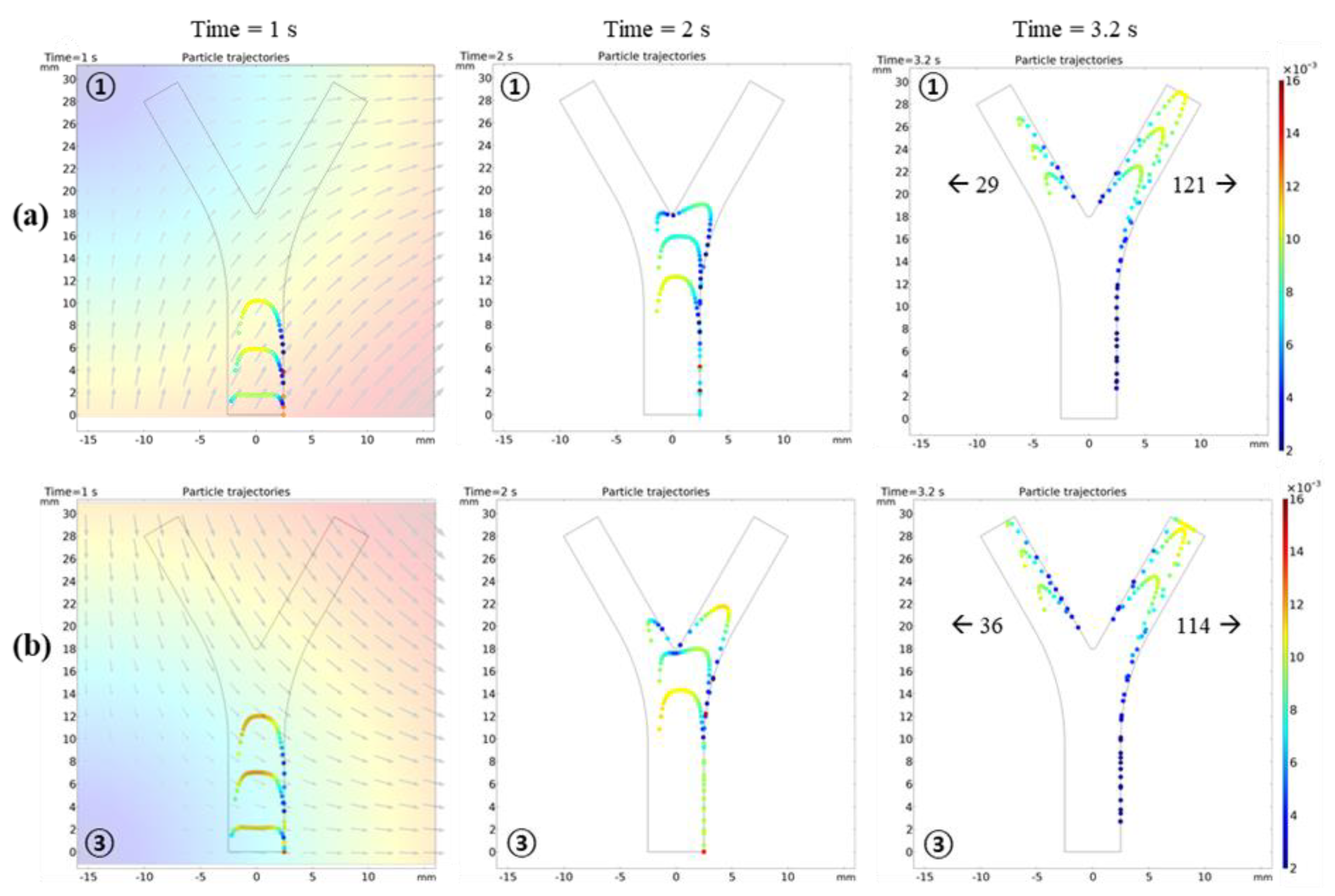
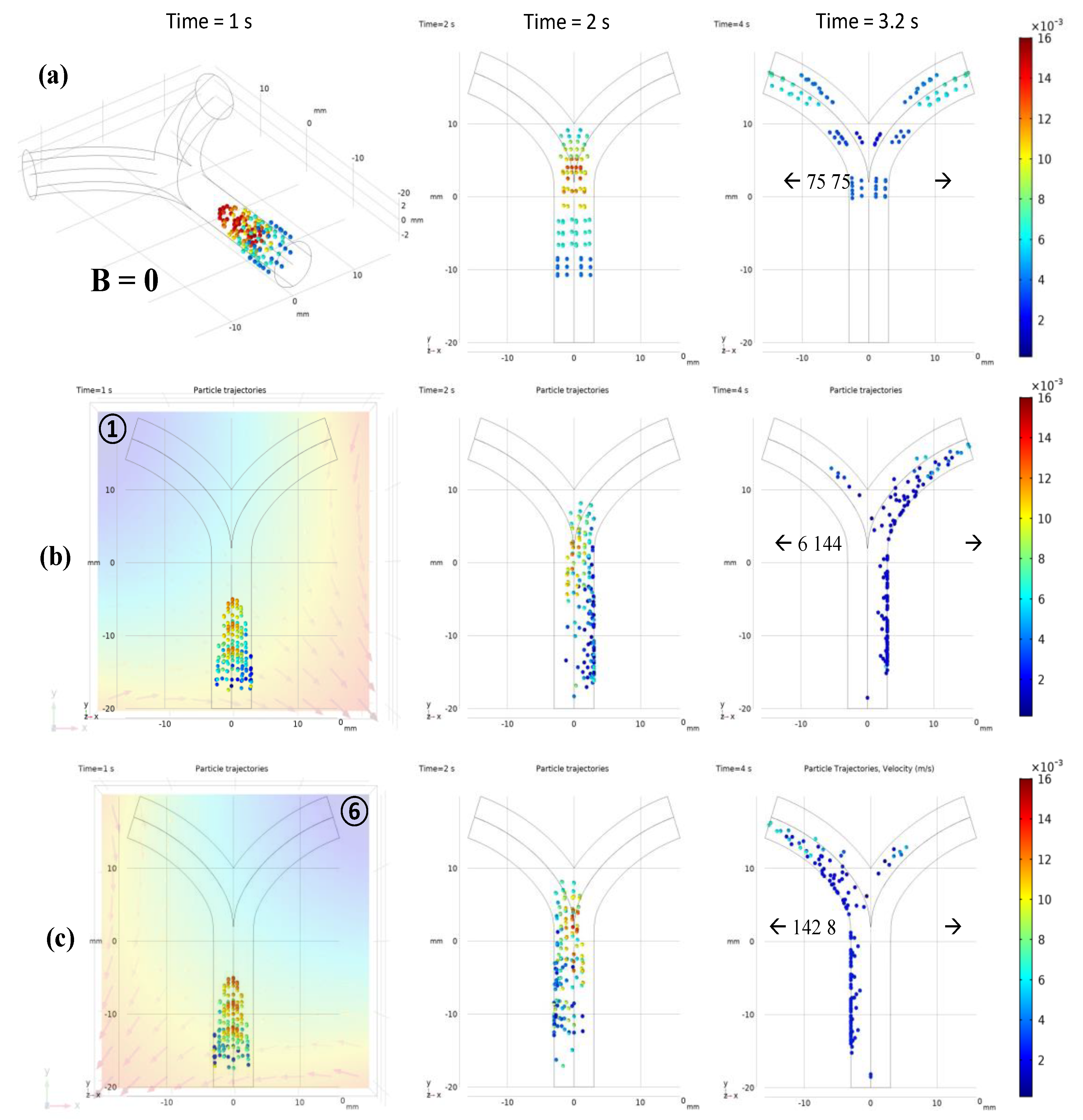
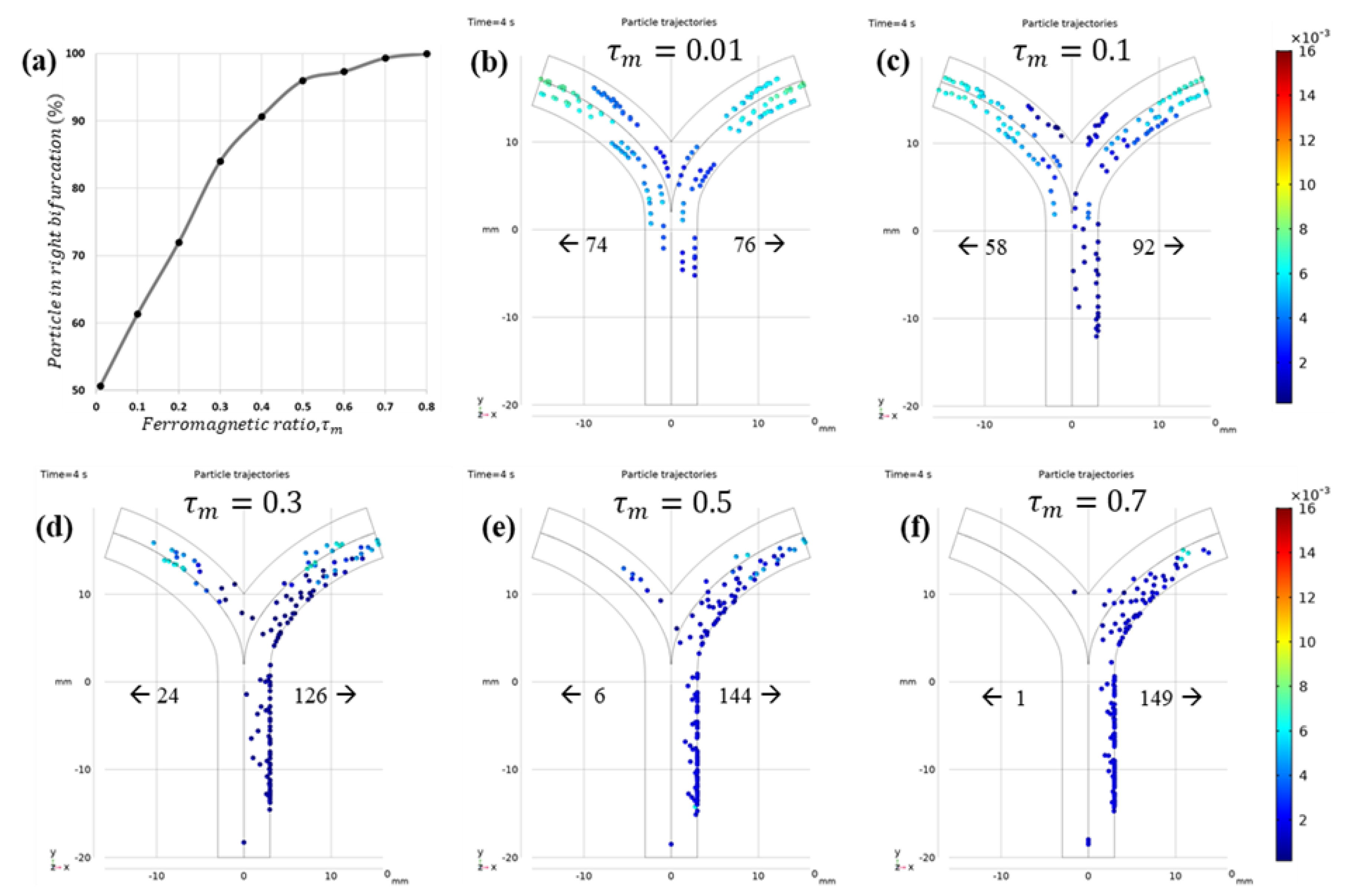
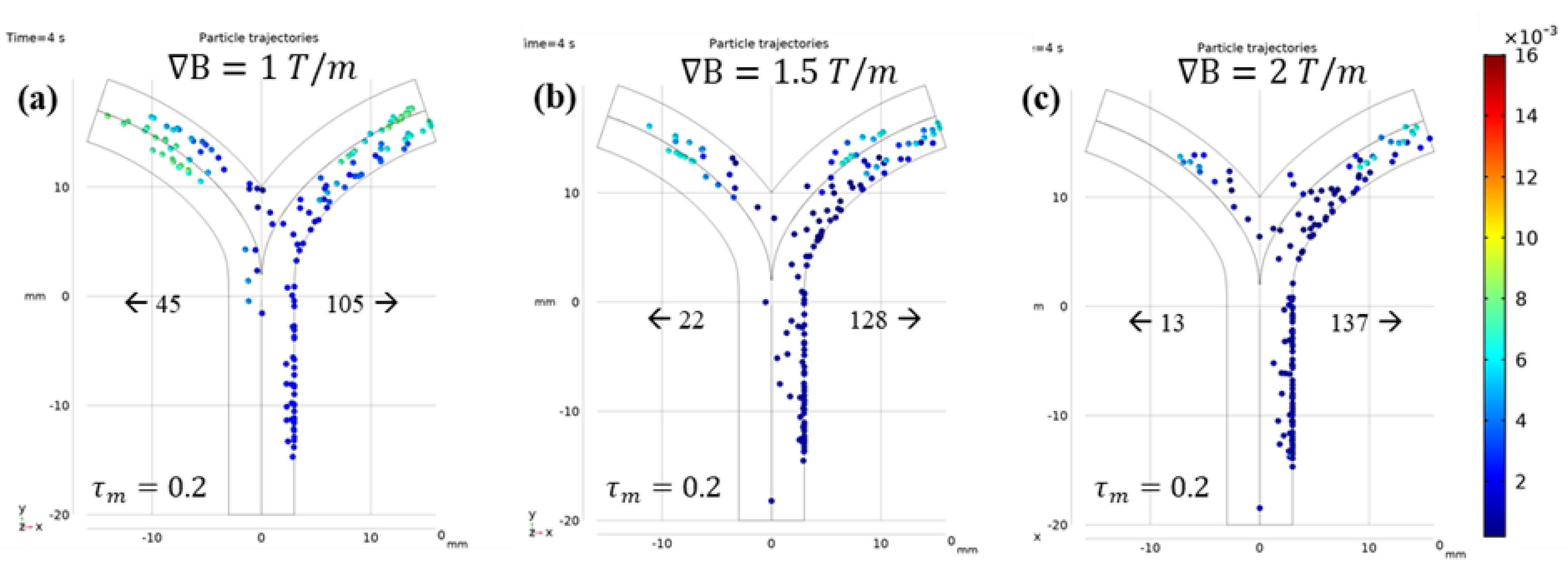
3.2.2. Microrobot Navigation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics. CA Cancer J. Clin. 2017, 67, 7–30. [Google Scholar] [CrossRef]
- Pucelik, B.; Sułek, A.; Barzowska, A.; Dąbrowski, J.M. Recent advances in strategies for overcoming hypoxia in photodynamic therapy of cancer. Cancer Lett. 2020, 492, 116–135. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.-I.; Lee, H.; Kwon, S.-H.; Choi, H.; Park, S. Magnetic nano-particles retrievable biodegradable hydrogel microrobot. Sens. Actuators B Chem. 2019, 289, 65–77. [Google Scholar] [CrossRef]
- Van der Zanden, Y.S.; Qiao, X.H.; Neefjes, J. New insights into the activities and toxicities of the old anti-cancer drug doxorubicin. FEBS J. 2020. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.E.; Chen, Z.; Shin, D.M. Nanoparticle therapeutics: An emerging treatment modality for cancer. Nat. Rev. Drug Discov. 2008, 7, 771–782. [Google Scholar] [CrossRef]
- Bertrand, N.; Wu, J.; Xu, X.; Kamaly, N.; Farokhzad, O.C. Cancer nanotechnology: The impact of passive and active targeting in the era of modern cancer biology. Adv. Drug Deliv. Rev. 2014, 66, 2–25. [Google Scholar] [CrossRef] [PubMed]
- Sung, B.; Shaffer, S.; Sittek, M.; Alboslemy, T.; Kim, C.; Kim, M.-H. Alternating Magnetic Field-Responsive Hybrid Gelatin Microgels for Controlled Drug Release. J. Vis. Exp. 2016, 2016, e53680. [Google Scholar] [CrossRef] [PubMed]
- Medina-Sánchez, M.; Magdanz, V.; Guix, M.; Fomin, V.M.; Schmidt, O.G. Swimming Microrobots: Soft, Reconfigurable, and Smart. Adv. Funct. Mater. 2018, 28. [Google Scholar] [CrossRef]
- Lee, H.S.; Go, G.; Choi, E.; Kang, B.; Park, J.-O.; Kim, C.-S. Medical Microrobot-Wireless Manipulation of a Drug Delivery Carrier through an External Ul-trasonic Actuation: Preliminary Results. Int. J. Control Autom. Syst. 2020, 18, 175–185. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Min, H.-K.; Kim, D.-H.; Kim, C.-S.; Han, J.; Park, J.-O.; Choi, E. Macrophage-Mediated Delivery of Multifunctional Nanotherapeutics for Synergistic Chemo-Photothermal Therapy of Solid Tumors. ACS Appl. Mater. Interfaces 2020, 12, 10130–10141. [Google Scholar] [CrossRef]
- Senapati, S.; Mahanta, A.K.; Kumar, S.; Maiti, P. Controlled drug delivery vehicles for cancer treatment and their performance. Signal Transduct. Target. Ther. 2018, 3, 7. [Google Scholar] [CrossRef]
- Nguyen, V.D.; Min, H.-K.; Kim, C.-S.; Han, J.; Park, J.-O.; Choi, E. Folate receptor-targeted liposomal nanocomplex for effective synergistic photothermal-chemotherapy of breast cancer in vivo. Colloids Surf. B Biointerfaces 2019, 173, 539–548. [Google Scholar] [CrossRef] [PubMed]
- Darmawan, B.A.; Lee, S.B.; Van Nguyen, D.; Go, G.; Nguyen, K.T.; Lee, H.-S.; Nan, M.; Hong, A.; Kim, C.-S.; Li, H.; et al. Self-folded microrobot for active drug delivery and rapid ultrasound-triggered drug release. Sens. Actuators B Chem. 2020, 324, 128752. [Google Scholar] [CrossRef]
- Nguyen, K.T.; Hoang, M.C.; Choi, E.; Kang, B.; Park, J.-O.; Kim, C.-S. Medical Microrobot—A Drug Delivery Capsule Endoscope with Active Locomotion and Drug Release Mechanism: Proof of Concept. Int. J. Control Autom. Syst. 2019, 18, 65–75. [Google Scholar] [CrossRef]
- Lubbe, A.S. Preclinical experiences with magnetic drug targeting: Tolerance and efficacy and clinical experiences with magnetic drug targeting: A phase I study with 4’-epidoxorubicin in 14 patients with advanced solid tumors-Reply. Cancer Res. 1997, 57, 3064–3065. [Google Scholar]
- Alcantara, C.C.J.; Kim, S.; Lee, S.; Jang, B.; Thakolkaran, P.; Kim, J.-Y.; Choi, H.; Nelson, B.J.; Pané, S. 3D Fabrication of Fully Iron Magnetic Microrobots. Small 2019, 15, 1805006. [Google Scholar] [CrossRef]
- Khalil, I.S.M.; Abelmann, L.; Misra, S. Magnetic-Based Motion Control of Paramagnetic Microparticles With Disturbance Compensation. IEEE Trans. Magn. 2014, 50, 1–10. [Google Scholar] [CrossRef]
- Chenouard, N.; Bloch, I.; Olivo-Marin, J.-C. Particle tracking in fluorescent microscopy images improved by morphological source separation. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; Institute of Electrical and Electronics Engineers (IEEE): Cairo, Egypt, 2009; pp. 821–824. [Google Scholar]
- Condeelis, J.; Weissleder, R. In Vivo Imaging in Cancer. Cold Spring Harb. Perspect. Biol. 2010, 2, a003848. [Google Scholar] [CrossRef]
- Martel, S. Combining Pulsed and DC Gradients in a Clinical MRI-Based Microrobotic Platform to Guide Thera-peutic Magnetic Agents in the Vascular Network. Int. J. Adv. Robot. Syst. 2013, 10, 30. [Google Scholar] [CrossRef]
- Martel, S.; Mathieu, J.-B.; Felfoul, O.; Chanu, A.; Aboussouan, E.; Tamaz, S.; Pouponneau, P.; Yahia, L.; Beaudoin, G.; Soulez, G.; et al. Automatic navigation of an untethered device in the artery of a living animal using a conventional clinical magnetic resonance imaging system. Appl. Phys. Lett. 2007, 90, 114105. [Google Scholar] [CrossRef]
- Gleich, B.; Weizenecker, R. Tomographic imaging using the nonlinear response of magnetic particles. Nature 2005, 435, 1214–1217. [Google Scholar] [CrossRef] [PubMed]
- Saritas, E.U.; Goodwill, P.W.; Croft, L.R.; Konkle, J.J.; Lu, K.; Zheng, B.; Conolly, S.M. Magnetic Particle Imaging (MPI) for NMR and MRI researchers. J. Magn. Reson. 2013, 229, 116–126. [Google Scholar] [CrossRef]
- Panagiotopoulos, N.; Vogt, F.M.; Barkhausen, J.; Buzug, T.M.; Duschka, R.L.; Lüdtke-Buzug, K.; Ahlborg, M.; Bringout, G.; Debbeler, C.; Graeser, M.; et al. Magnetic particle imaging: Current developments and future directions. Int. J. Nanomed. 2015, 10, 3097–3114. [Google Scholar] [CrossRef] [PubMed]
- Goodwill, P.W.; Conolly, S.M. Multidimensional X-Space Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2011, 30, 1581–1590. [Google Scholar] [CrossRef] [PubMed]
- Borgert, J.; Schmidt, J.D.; Schmale, I.; Rahmer, J.; Bontus, C.; Gleich, B.; David, B.; Eckart, R.; Woywode, O.; Weizenecker, J.; et al. Fundamentals and applications of magnetic particle imaging. J. Cardiovasc. Comput. Tomogr. 2012, 6, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Nothnagel, N.; Rahmer, J.; Gleich, B.; Halkola, A.; Buzug, T.M.; Borgert, J.; Borgert, J. Steering of Magnetic Devices with a Magnetic Particle Imaging System. IEEE Trans. Biomed. Eng. 2016, 63, 2286–2293. [Google Scholar] [CrossRef]
- Zhang, M.X.; Le, T.A.; Yoon, J. Development of a real time imaging-based guidance system of magnetic nano-particles for targeted drug delivery. J. Magn. Magn. Mater. 2017, 427, 345–351. [Google Scholar] [CrossRef]
- Griese, F.; Knopp, T.; Gruettner, C.; Thieben, F.; Müller, K.; Loges, S.; Ludewig, P.; Nadine, G. Simultaneous Magnetic Particle Imaging and Navigation of large superparamagnetic nanoparti-cles in bifurcation flow experiments. J. Magn. Magn. Mater. 2020, 498, 166206. [Google Scholar] [CrossRef]
- COMSOL, Inc. Particle Tracing Module User’s Guide; COMSOL Multiphysics®: Burlington, MA, USA, 2021. [Google Scholar]
- Jones, T.B. Dielectrophoresis and magnetophoresis. In Electromechanics of Particles; Jones, T.B., Ed.; Cambridge University Press: Cambridge, UK, 1995; pp. 34–82. [Google Scholar]
- Arcese, L.; Fruchard, M.; Ferreira, A. Endovascular Magnetically Guided Robots: Navigation Modeling and Optimization. IEEE Trans. Biomed. Eng. 2011, 59, 977–987. [Google Scholar] [CrossRef]
- Go, G.; Yoo, A.; Song, H.-W.; Min, H.-K.; Zheng, S.; Nguyen, K.T.; Kim, S.; Kang, B.; Hong, A.; Kim, C.-S.; et al. Multifunctional Biodegradable Microrobot with Programmable Morphology for Biomedical Applications. ACS Nano 2021, 15, 1059–1076. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.; Kim, J.; Park, J.-O.; Choi, E.; Kim, C.-S. Localization and Actuation for MNPs Based on Magnetic Field-Free Point: Feasibility of Movable Electromagnetic Actuations. Micromachines 2020, 11, 1020. [Google Scholar] [CrossRef] [PubMed]
- Hoang, M.C.; Nguyen, K.T.; Le, V.H.; Kim, J.; Choi, E.; Kang, B.; Park, J.-O.; Kim, C.-S. Independent Electromagnetic Field Control for Practical Approach to Actively Locomotive Wireless Capsule Endoscope. In Proceedings of the IEEE Transactions on Systems, Man, and Cybernetics, Systems, Bari, Italy, 12 June 2019; pp. 1–13. [Google Scholar]
- Pries, A.; Secomb, T.; Gaehtgens, P. Biophysical aspects of blood flow in the microvasculature. Cardiovasc. Res. 1996, 32, 654–667. [Google Scholar] [CrossRef]
| Name | Expression | Value |
|---|---|---|
| Blood viscosity | ||
| Blood density | ||
| MNP density | ||
| Polymer density | ||
| Robot diameter | ||
| Saturation magnetization | ||
| Vessel diameter (3D) | ||
| Blood pressure (Max.) | ||
| Initial velocity of blood | ||
| Initial velocity ofrobot | ||
| Turns/coil | n_coil | 1400 |
| Length of coil | l_coil | 210 mm |
| Inner radius | r_min | 21 mm |
| Outer radius | r_max | 36 mm |
| Core | Pure Iron | Fe |
| Wires | Copper | Cu |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharif, S.; Nguyen, K.T.; Bang, D.; Park, J.-O.; Choi, E. Optimization of Field-Free Point Position, Gradient Field and Ferromagnetic Polymer Ratio for Enhanced Navigation of Magnetically Controlled Polymer-Based Microrobots in Blood Vessel. Micromachines 2021, 12, 424. https://doi.org/10.3390/mi12040424
Sharif S, Nguyen KT, Bang D, Park J-O, Choi E. Optimization of Field-Free Point Position, Gradient Field and Ferromagnetic Polymer Ratio for Enhanced Navigation of Magnetically Controlled Polymer-Based Microrobots in Blood Vessel. Micromachines. 2021; 12(4):424. https://doi.org/10.3390/mi12040424
Chicago/Turabian StyleSharif, Saqib, Kim Tien Nguyen, Doyeon Bang, Jong-Oh Park, and Eunpyo Choi. 2021. "Optimization of Field-Free Point Position, Gradient Field and Ferromagnetic Polymer Ratio for Enhanced Navigation of Magnetically Controlled Polymer-Based Microrobots in Blood Vessel" Micromachines 12, no. 4: 424. https://doi.org/10.3390/mi12040424
APA StyleSharif, S., Nguyen, K. T., Bang, D., Park, J.-O., & Choi, E. (2021). Optimization of Field-Free Point Position, Gradient Field and Ferromagnetic Polymer Ratio for Enhanced Navigation of Magnetically Controlled Polymer-Based Microrobots in Blood Vessel. Micromachines, 12(4), 424. https://doi.org/10.3390/mi12040424







