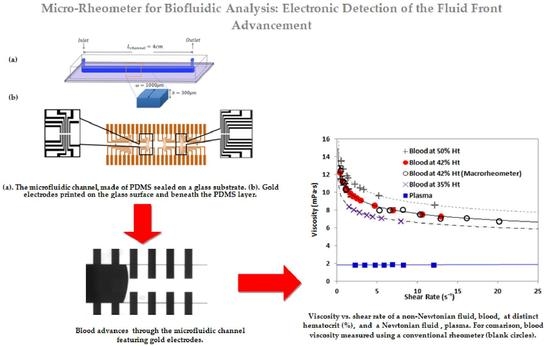
Microrheometer for Biofluidic Analysis: Electronic Detection of the Fluid-Front Advancement
Abstract
:1. Introduction
2. Materials and Methods
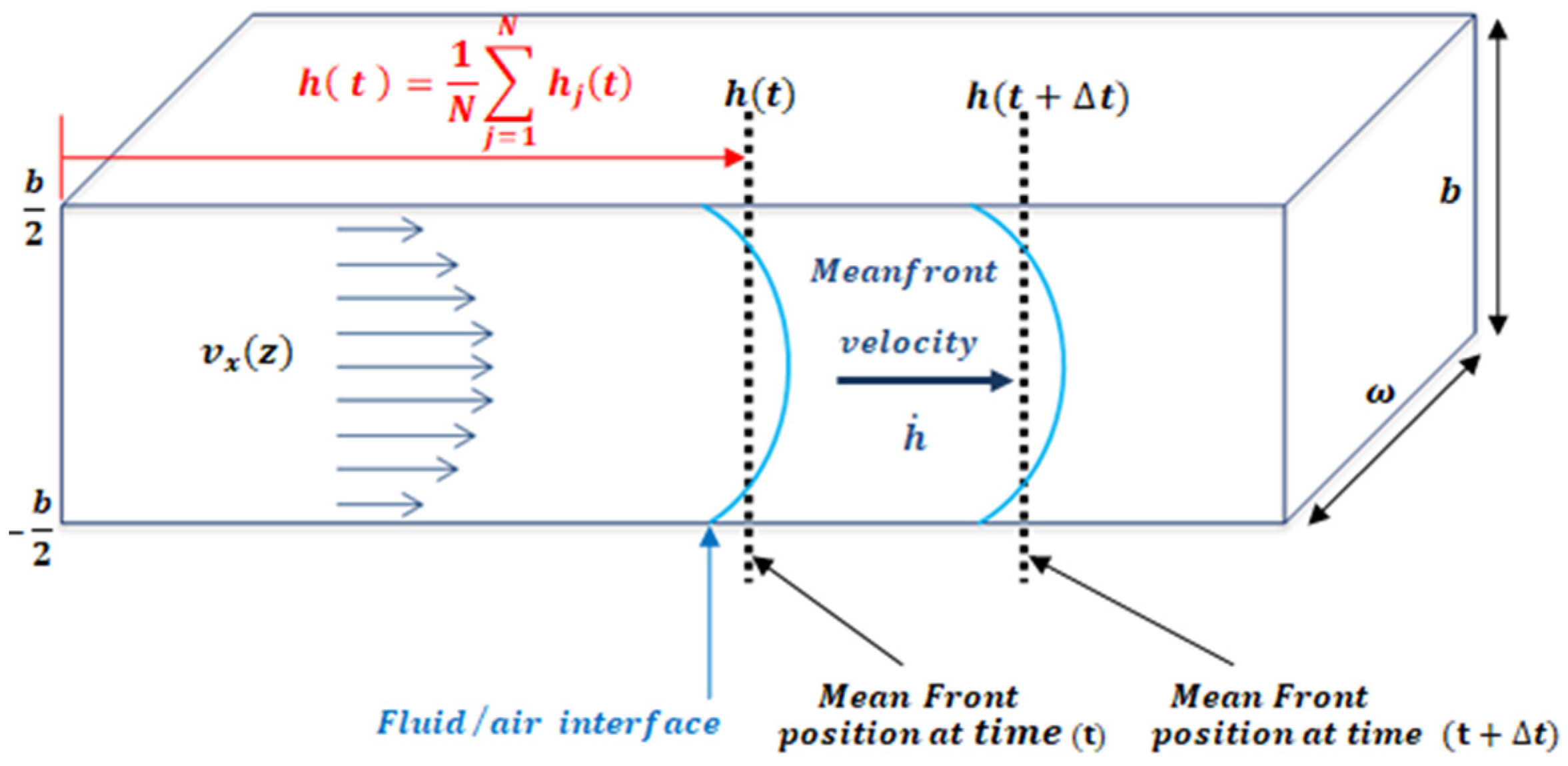
2.1. Mathematical Model
2.2. Experimental Model
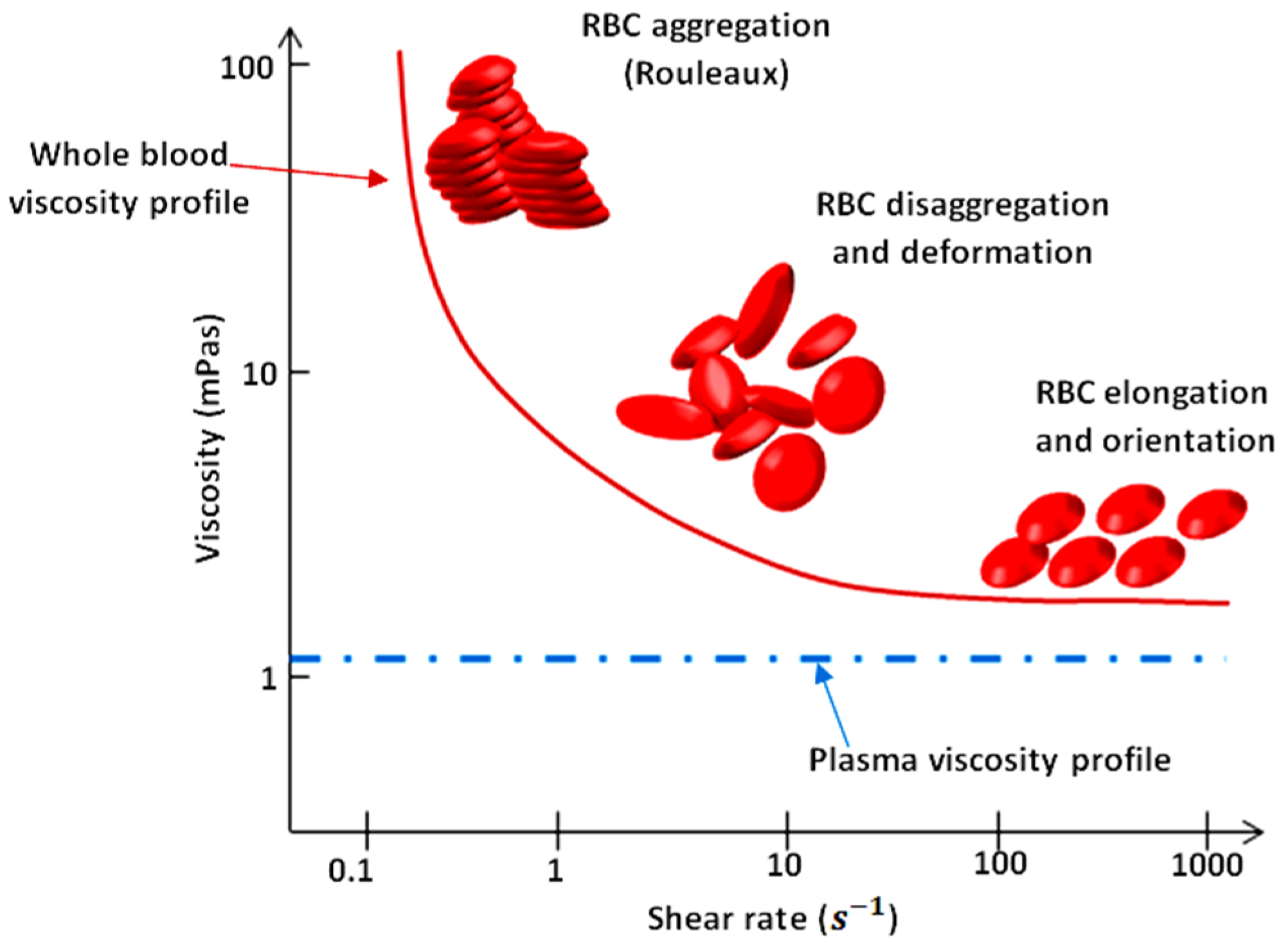
2.2.1. General Case: Non-Newtonian Fluids
2.2.2. Newtonian Fluids
2.3. Experimental Method
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
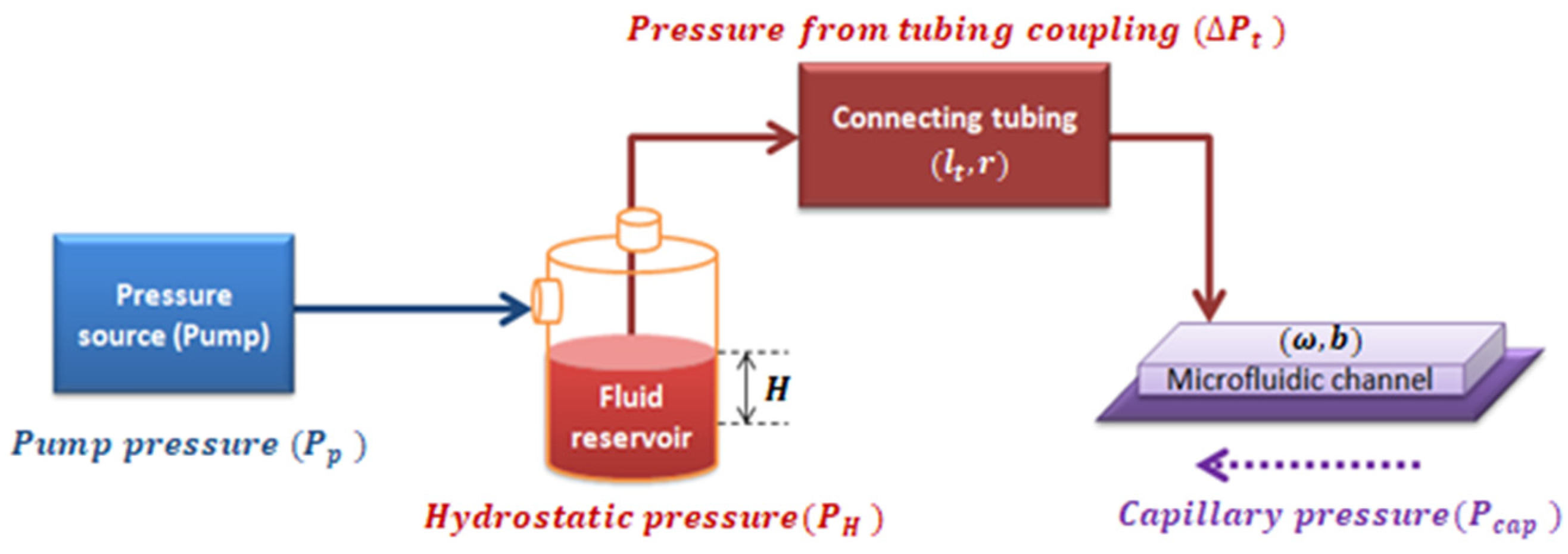
Appendix A.1. Flow Inside a Known Geometry

Appendix A.2. Pressure Drop Inside a Microfluidic System

Appendix A.3. Newtonian Fluids
Appendix B. Viscosity Data
| Fluid | Temperature(°C) | Viscosity η (m × Pas) | Reference |
| MGVS60 | 24 | 6.00 | [Paragon Scientific, Ltd.] |
| Blood plasma | 20 | 1.50–1.81 | [Baskurt, 2007] [36] |
| Water | 20 | 1.002 | [Bruus, 2008] [35] |
| Blood at 44% Ht | 22 | 9–10 at (1 s−1 ) | [Thurston and Henderson, 2006] [40] |
References
- Gupta, S.; Wang, W.S.; Vanapalli, S.A. Microfluidic viscometers for shear rheology of complex fluids and biofluids. Biomicrofluidics 2016, 10, 043402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merrill, E.W.; Gilliand, E.R.; Cokelet, G.; Shin, H.; Britten, A.; Wells, R.E. Rheology of human blood, near and at zero flow. Effects of temperature and hematocrit level. Biophys. J. 1963, 3, 199–213. [Google Scholar] [CrossRef] [Green Version]
- Merrill, E.W. Rheology of blood. Physiol. Rev. 1969, 49, 863–888. [Google Scholar] [CrossRef] [PubMed]
- Chien, S.; Usami, S.; Bertles, J.F. Abnormal rheology of oxygenated blood in sickle cell anemia. J. Clin. Investig. 1970, 49, 623–634. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thurston, G.B. Rheological parameters for the viscosity viscoelasticity and thixotropy of blood. Biorheology 1979, 16, 149–162. [Google Scholar] [CrossRef]
- Wells, R.; Schmid-Schönbein, H. Red cell deformation and fluidity of concentrated cell suspensions. J. Appl. Physiol. 1969, 27, 213–217. [Google Scholar] [CrossRef]
- Rosencranz, R.; Bogen, S.A. Clinical Laboratory Measurement of Serum, Plasma, and Blood Viscosity. Pathol. Patterns Rev. 2006, 125, S78–S86. [Google Scholar] [CrossRef]
- Tropea, C. Springer Handbook of Experimental Fluid Mechanics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fåhræus, R.; Lindqvist, T. The Viscosity of The Blood in Narrow Capillary Tubes. Am. J. Physiol. Content 1931, 96, 562–568. [Google Scholar] [CrossRef]
- Lázaro, G.R.; Hernández-Machado, A.; Pagonabarraga, I. Rheology of red blood cells under flow in highly confined microchannels. II. Effect of focusing and confinement. Soft Matter 2014, 10, 7207–7217. [Google Scholar] [CrossRef]
- Lázaro, G.R.; Hernández-Machado, A.; Pagonabarraga, I. Collective behavior of red blood cells in confined channels. Eur. Phys. J. E 2019, 42. [Google Scholar] [CrossRef]
- Doy, N.; McHale, G.; Newton, M.I.; Hardacre, C.; Ge, R.; MacInnes, J.M.; Kuvshinov, D.; Allen, R.W. Small volume laboratory on a chip measurements incorporating the quartz crystal microbalance to measure the viscosity-density product of room temperature ionic liquids. Biomicrofluidics 2010, 4, 014107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oba, T.; Kido, Y.; Nagasaka, Y. Development of laser-induced capillary wave method for viscosity measurement using pulsed carbon dioxide laser. Int. J. Thermophys. 2004, 25, 1461–1474. [Google Scholar] [CrossRef]
- Pipe, C.J.; Majmudar, T.S.; McKinley, G.H. High shear rate viscometry. Rheol. Acta 2008, 47, 621–642. [Google Scholar] [CrossRef]
- Choi, S.; Park, J.K. Microfluidic rheometer for characterization of protein unfolding and aggregation in microflows. Small 2010, 6, 1306–1310. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Yeom, E.; Lee, S.J. A microfluidic device for simultaneous measurement of viscosity and flow rate of blood in a complex fluidic network. Biomicrofluidics 2013, 7. [Google Scholar] [CrossRef] [Green Version]
- Chevalier, J.; Ayela, F. Microfluidic on chip viscometers. Rev. Sci. Instrum. 2008, 79. [Google Scholar] [CrossRef] [PubMed]
- Clasen, C.; Gearing, B.P.; McKinley, G.H. The flexure-based microgap rheometer (FMR). J. Rheol. 2006, 50, 883–905. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.A.; Liao, W.H.; Wu, Y.F.; Chen, Y.L.; Tung, Y.C. Electrofluidic Circuit-Based Microfluidic Viscometer for Analysis of Newtonian and Non-Newtonian Liquids under Different Temperatures. Anal. Chem. 2018, 90, 2317–2325. [Google Scholar] [CrossRef]
- Del Giudice, F. Simultaneous measurement of rheological properties in a microfluidic rheometer. Phys. Fluids 2020, 32, 052001. [Google Scholar] [CrossRef]
- Solomon, D.E.; Abdel-Raziq, A.; Vanapalli, S.A. A stress-controlled microfluidic shear viscometer based on smartphone imaging. Rheol. Acta 2016, 55, 727–738. [Google Scholar] [CrossRef]
- Srivastava, N.; Burns, M.A. Analysis of non-Newtonian liquids using a microfluidic capillary viscometer. Anal. Chem. 2006, 78, 1690–1696. [Google Scholar] [CrossRef]
- Jackson, G.N.B.; Ashpole, K.J.; Yentis, S.M. The TEG® vs the ROTEM® thromboelastography/thromboelastometry systems. Anaesthesia 2009, 64, 212–215. [Google Scholar] [CrossRef]
- Thakur, M.; Ahmed, A.B. A review of thromboelastography. Int. J. Perioper. Ultrasound Appl. Technol. 2012, 1, 25–29. [Google Scholar] [CrossRef]
- Bandey, H.L.; Cernosek, R.W.; Lee, W.E.; Ondrovic, L.E. Blood rheological characterization using the thickness-shear mode resonator. Biosens. Bioelectron. 2004, 19, 1657–1665. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J.; Yoon, S.Y.; Lee, K.H.; Yang, S. A highly accurate and consistent microfluidic viscometer for continuous blood viscosity measurement. Artif. Organs 2010, 34, 944–949. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, F.; Gundogdu, M. A critical review on blood flow in large arteries; relevance to blood rheology, viscosity models, and physiologic conditions. Korea-Aust. Rheol. J. 2008, 20, 197–211. [Google Scholar]
- Trejo-Soto, C.; Costa-Miracle, E.; Rodriguez-Villarreal, I.; Cid, J.; Castro, M.; Alarcon, T.; Hernandez-Machado, A. Front microrheology of the non-Newtonian behaviour of blood: Scaling theory of erythrocyte aggregation by aging. Soft Matter 2017, 13, 3042–3047. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diez-Silva, M.; Dao, M.; Han, J.; Lim, C.T.; Suresh, S. Shape and biomechanics characteristics of human red blood cells in health and disease. MRS Bull. 2010, 35, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Apostolidis, A.J.; Moyer, A.P.; Beris, A.N. Non-Newtonian effects in simulations of coronary arterial blood flow. J. Nonnewton. Fluid Mech. 2016, 233, 155–165. [Google Scholar] [CrossRef] [Green Version]
- Van Kempen, T.H.S.; Peters, G.W.M.; Van De Vosse, F.N.; Van Kempen, T.H.S.; Van De Vosse, F.N.; Peters, G.W.M. A constitutive model for the time-dependent, nonlinear stress response of fibrin networks. Biomech. Model. Mechanobiol. 2015, 14, 995–1006. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, M.; Horner, J.; Clark, M.; Deegan, M.; Hill, T.; Keith, C.; Mooradian, L. Evaluating rheological models for human blood using steady state, transient, and oscillatory shear predictions. Rheol. Acta 2018, 57, 705–728. [Google Scholar] [CrossRef]
- Ramaswamy, B.; Yeh, Y.T.T.; Zheng, S.Y. Microfluidic device and system for point-of-care blood coagulation measurement based on electrical impedance sensing. Sens. Actuators B Chem. 2013, 180, 21–27. [Google Scholar] [CrossRef]
- Trejo-Soto, C.; Costa-Miracle, E.; Rodriguez-Villarreal, I.; Cid, J.; Alarcón, T.; Hernández-Machado, A. Capillary filling at the microscale: Control of fluid front using geometry. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [Green Version]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Baskurt, O. Handbook of Hemorheology and Hemodynamics; IoS Press: Amsterdam, The Neetherlands, 2007. [Google Scholar]
- Adamson, A.W.; Gast, A.P.; Wiley, J. Physical Chemistry of Surfaces, 6th ed.; Interscience Publishers: New York, NY, USA, 1967. [Google Scholar]
- Murillo, C. Fisicoquímica, 5th ed.; Levine, I.N., Ed.; McGraw Hill: Madrid, Spain, 2004; Volume 2. [Google Scholar]
- Bruus, H. Understanding Rheology; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Thurston, G.B.; Henderson, N.M. Effects of flow geometry on blood viscoelasticity. Biorheology 2006, 43, 729–746. [Google Scholar] [PubMed]
- Colomer, J.; Hernández-Machado, A.; Alarcón Cor, T. Method and Apparatus for Measuring Rheological Properties of Newtonian and Non-Newtonian Fluids. International Patent EP3093647A1, 17 November 2016. [Google Scholar]
- Guyon, E.; Hulin, J.-P.; Petit, L.; Mitescu, C.D. Physical Hydrodynamics, 2nd ed.; Oxford University Press: Oxford, UK, 2015. [Google Scholar]


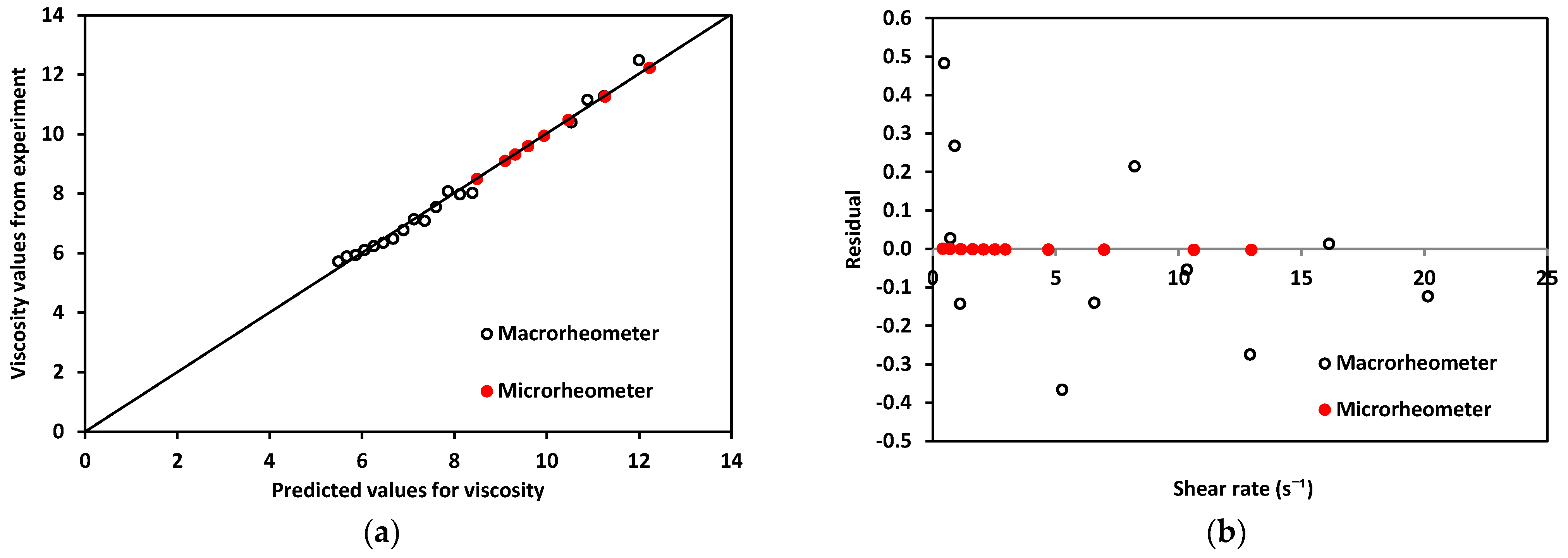
| Sample | at 25 °C | at H = 5 mm | at 25 °C | |
|---|---|---|---|---|
| Water | 102.42 | |||
| MGVS60 | 55.56 | 0.107 | 106.90 | |
| Plasma | 102.27 | |||
| Blood | * (Table 2) |
| 500 | 103.24 | 115.11 |
| 1000 | 106.94 | 146.46 |
| 1500 | 109.60 | 168.62 |
| 2000 | 111.76 | 186.35 |
| 2500 | 113.62 | 201.37 |
| 3000 | 115.27 | 214.54 |
| 3500 | 116.76 | 226.35 |
| 5000 | 120.64 | 256.22 |
| Sample | Viscosity (mPa·s) Microrheometer | Viscosity (mPa·s) Macrorheometer | |
|---|---|---|---|
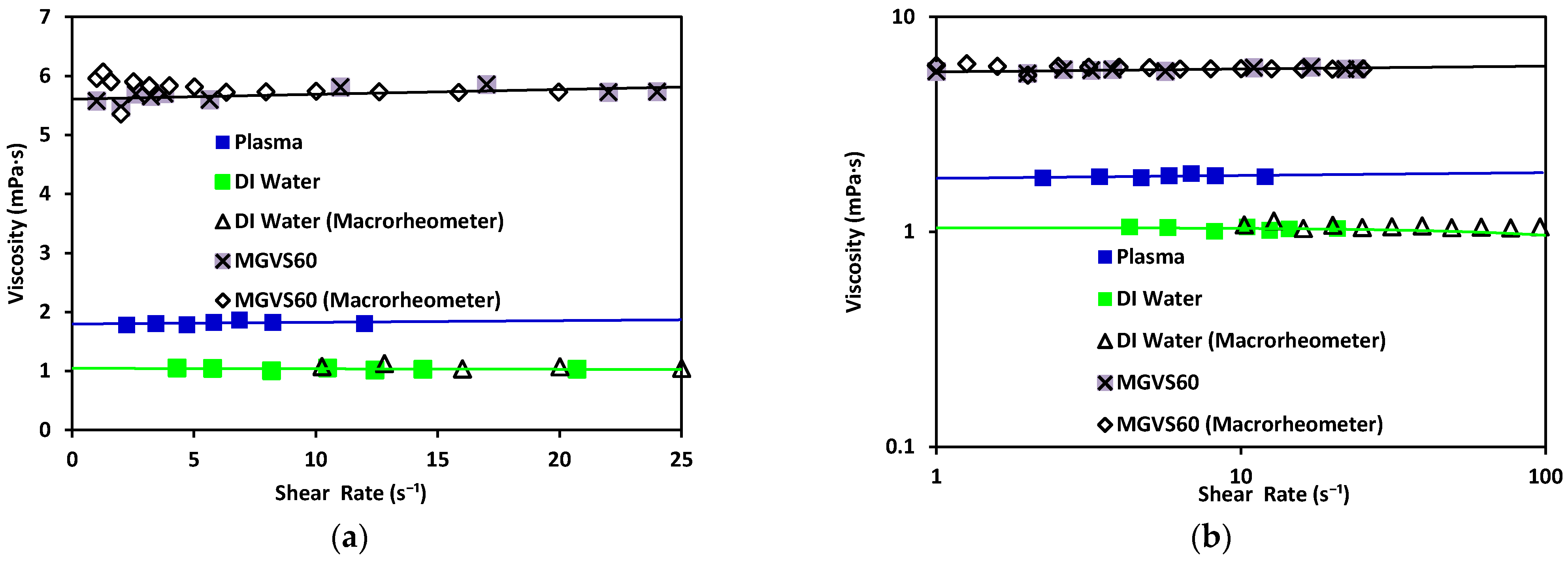
| DI water | 1.08 ± 0.03 | 1.017 | 1.02 ± 0.01 |
| MGVS60 | 5.87 ± 0.05 | 1.065 | 5.88 ± 0.02 |
| Sample | m (Pa·s) | n | |
|---|---|---|---|
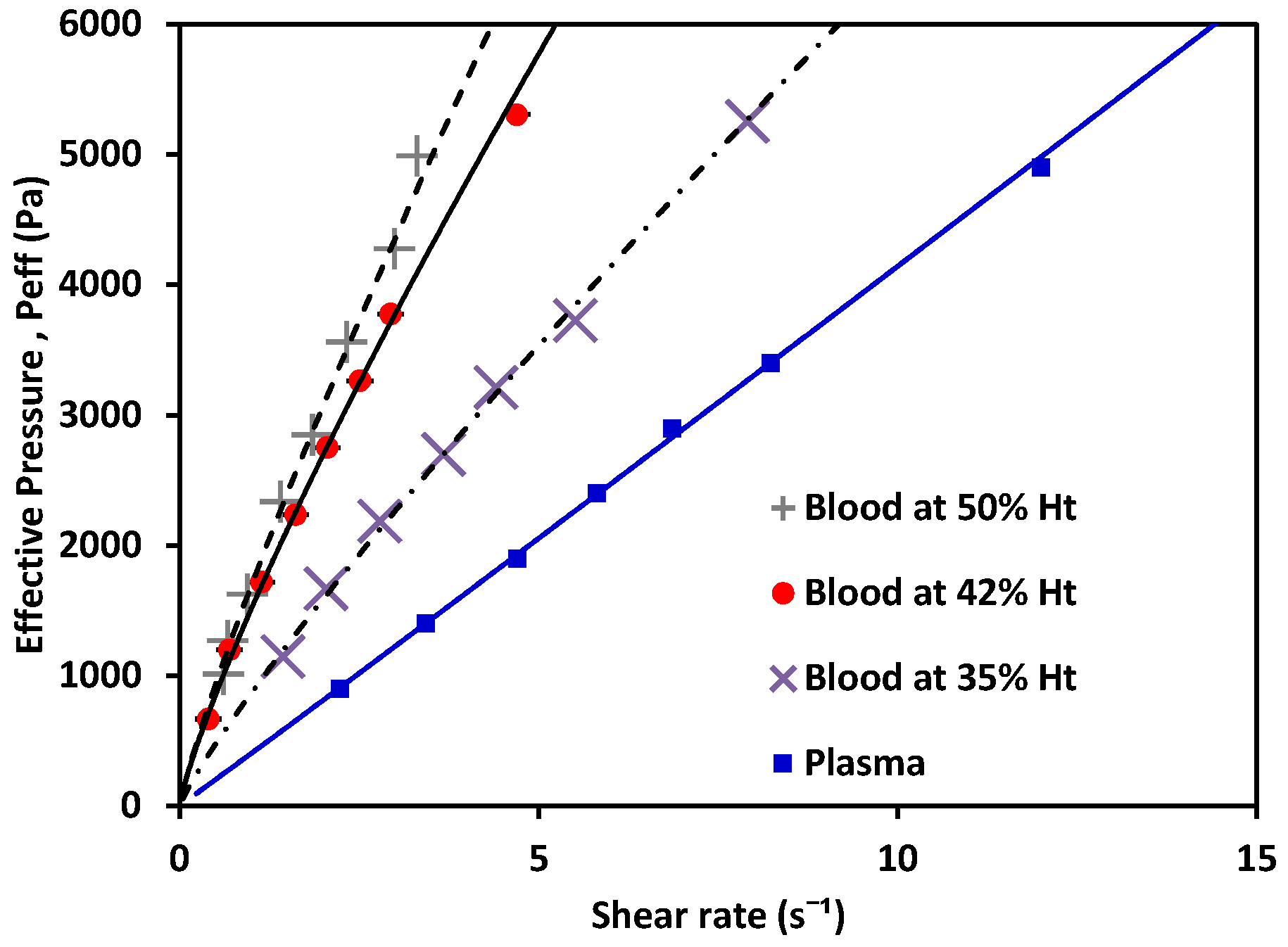
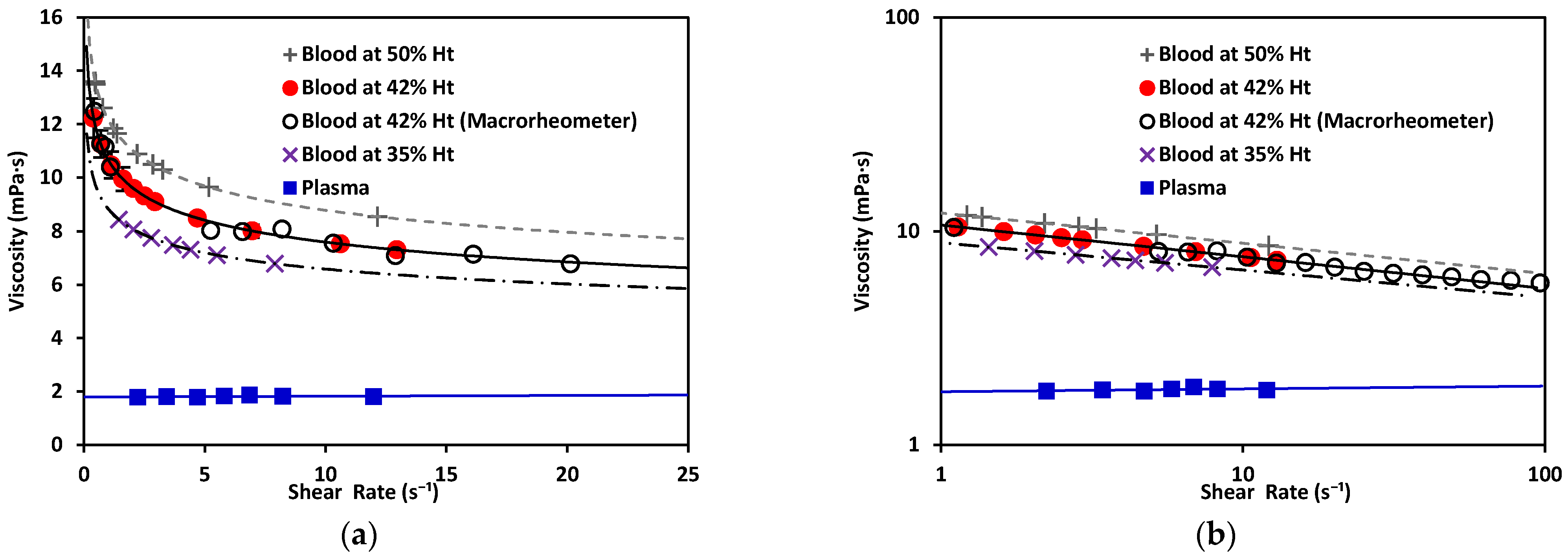
| *Blood at 50% Ht | 0.0122 | 0.8500 | |
| *Blood at 42% Ht | 0.0107 | 0.8519 | |
| *Blood at 35% Ht | 0.0088 | 0.8720 | |
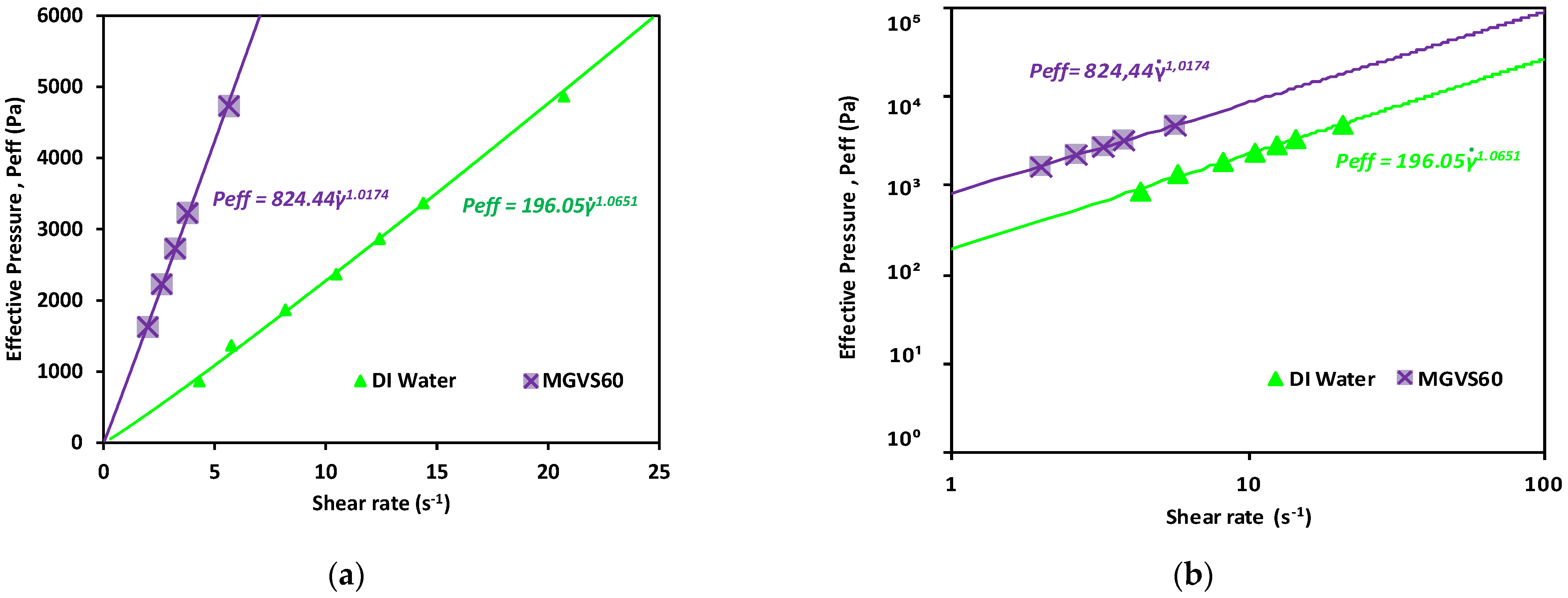
| MGVS60 | 0.0058 | 1.0174 ± 0.002 | |
| Plasma | 0.0018 ± 0.0002 | 1.0131 ± 0.028 | |
| Water | 0.0010 ± 00101 | 1.0651 ± 0651 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Méndez-Mora, L.; Cabello-Fusarés, M.; Ferré-Torres, J.; Riera-Llobet, C.; Lopez, S.; Trejo-Soto, C.; Alarcón, T.; Hernandez-Machado, A. Microrheometer for Biofluidic Analysis: Electronic Detection of the Fluid-Front Advancement. Micromachines 2021, 12, 726. https://doi.org/10.3390/mi12060726
Méndez-Mora L, Cabello-Fusarés M, Ferré-Torres J, Riera-Llobet C, Lopez S, Trejo-Soto C, Alarcón T, Hernandez-Machado A. Microrheometer for Biofluidic Analysis: Electronic Detection of the Fluid-Front Advancement. Micromachines. 2021; 12(6):726. https://doi.org/10.3390/mi12060726
Chicago/Turabian StyleMéndez-Mora, Lourdes, Maria Cabello-Fusarés, Josep Ferré-Torres, Carla Riera-Llobet, Samantha Lopez, Claudia Trejo-Soto, Tomas Alarcón, and Aurora Hernandez-Machado. 2021. "Microrheometer for Biofluidic Analysis: Electronic Detection of the Fluid-Front Advancement" Micromachines 12, no. 6: 726. https://doi.org/10.3390/mi12060726