Modeling, Validation, and Performance of Two Tandem Cylinder Piezoelectric Energy Harvesters in Water Flow
Abstract
1. Introduction
2. Physical Model and Simulation Method
- (1)
- Flow-induced force Ff can be obtained by Fluent® software at the cylinder position in flow field at time t.
- (2)
- The vibration displacement u, vibration velocity , vibration acceleration of the PEH, and electrical parameters V(t), P can be obtained by both Equations (1) and (14).
- (3)
- The cylinder position and computational grid will be updated based on the PEH displacement u in step 2.
- (4)
- One step ∆t is finished and next step t + ∆t will proceed. The performances of two tandem PEHs can then be obtained at last.
3. Experimental Setup and Simulation Verification
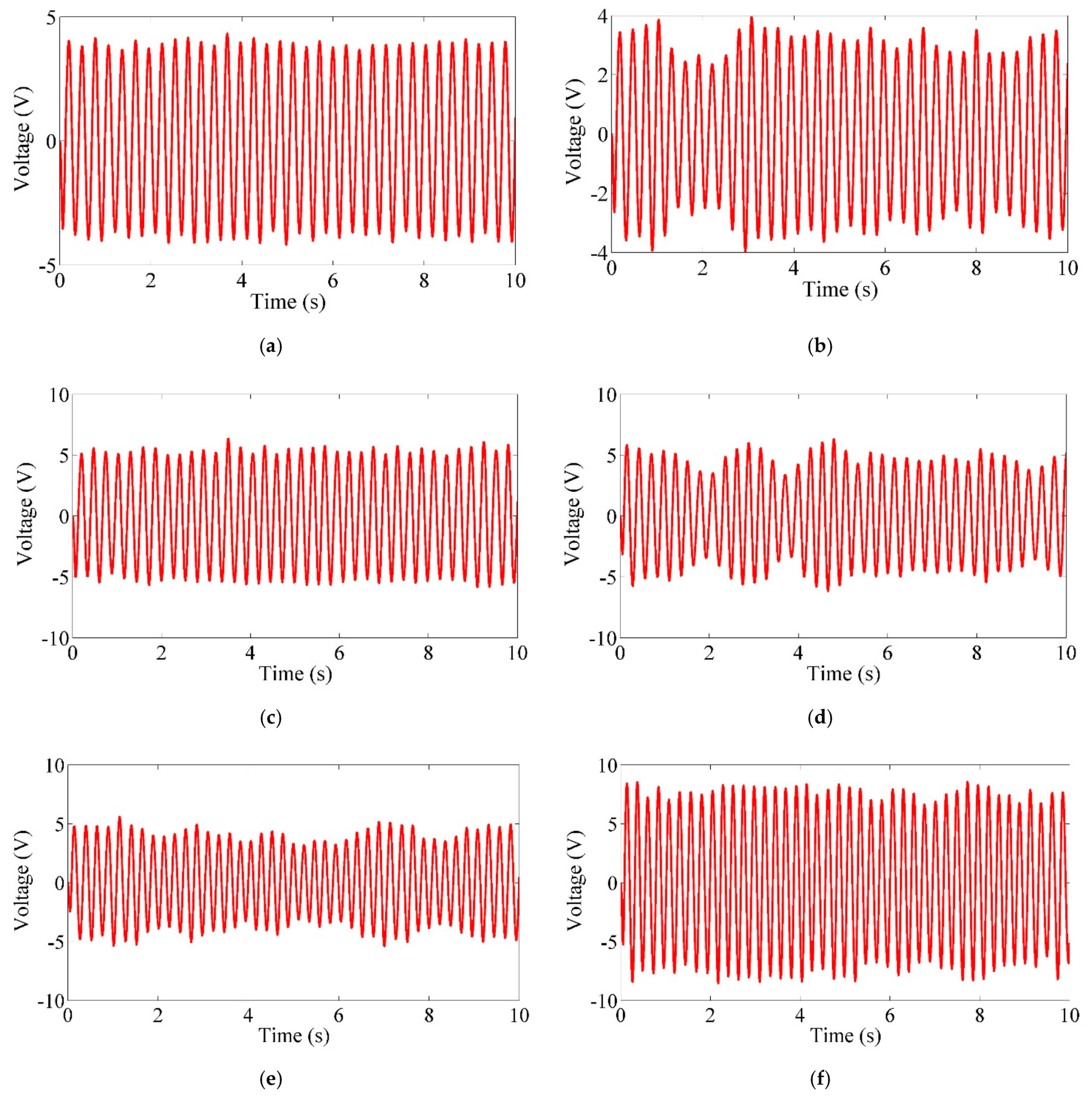
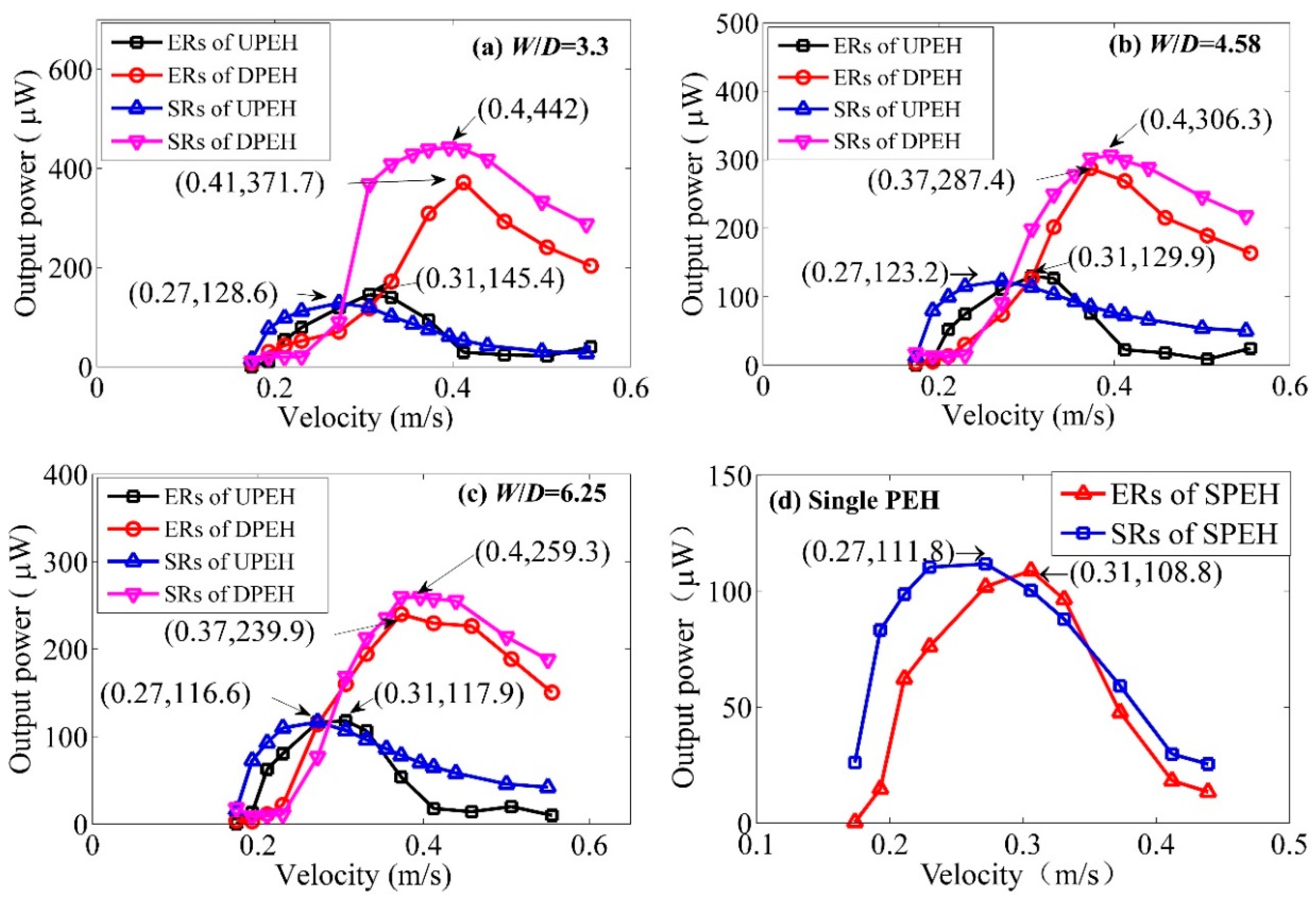
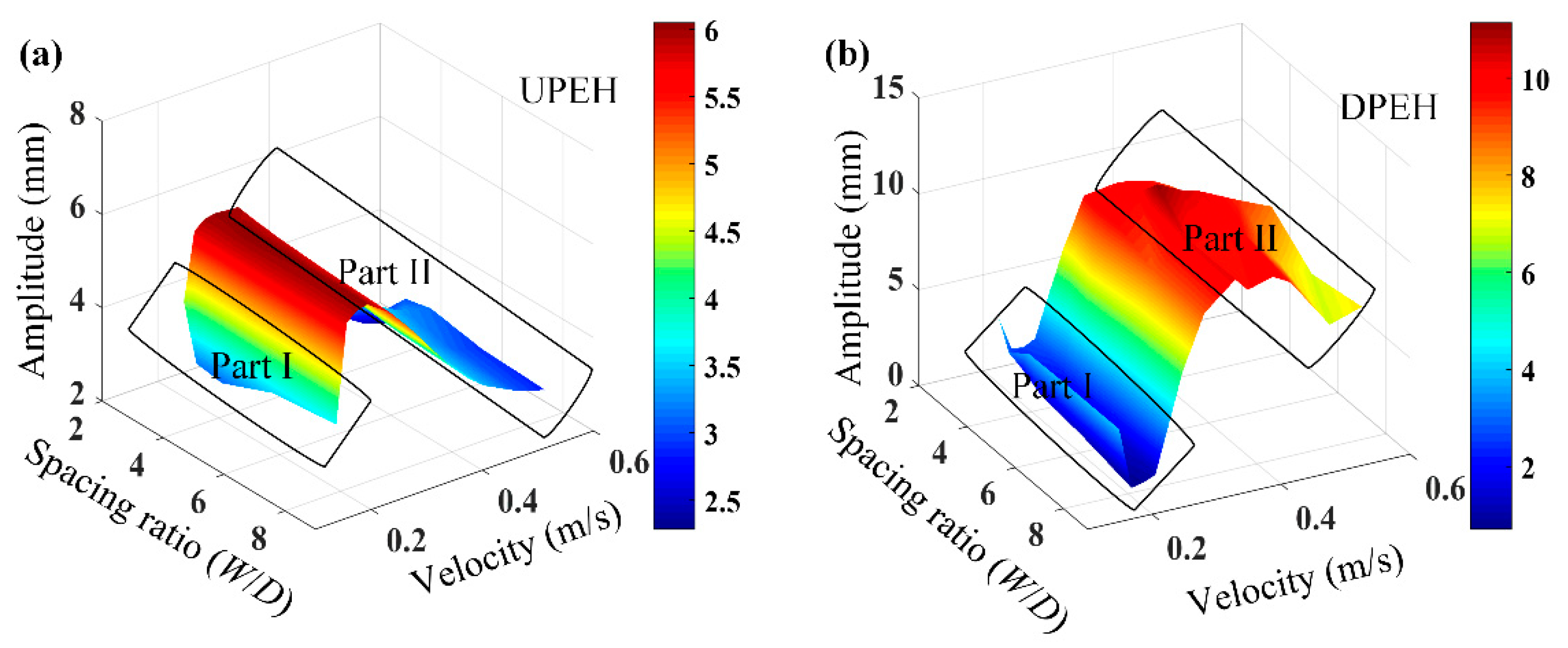
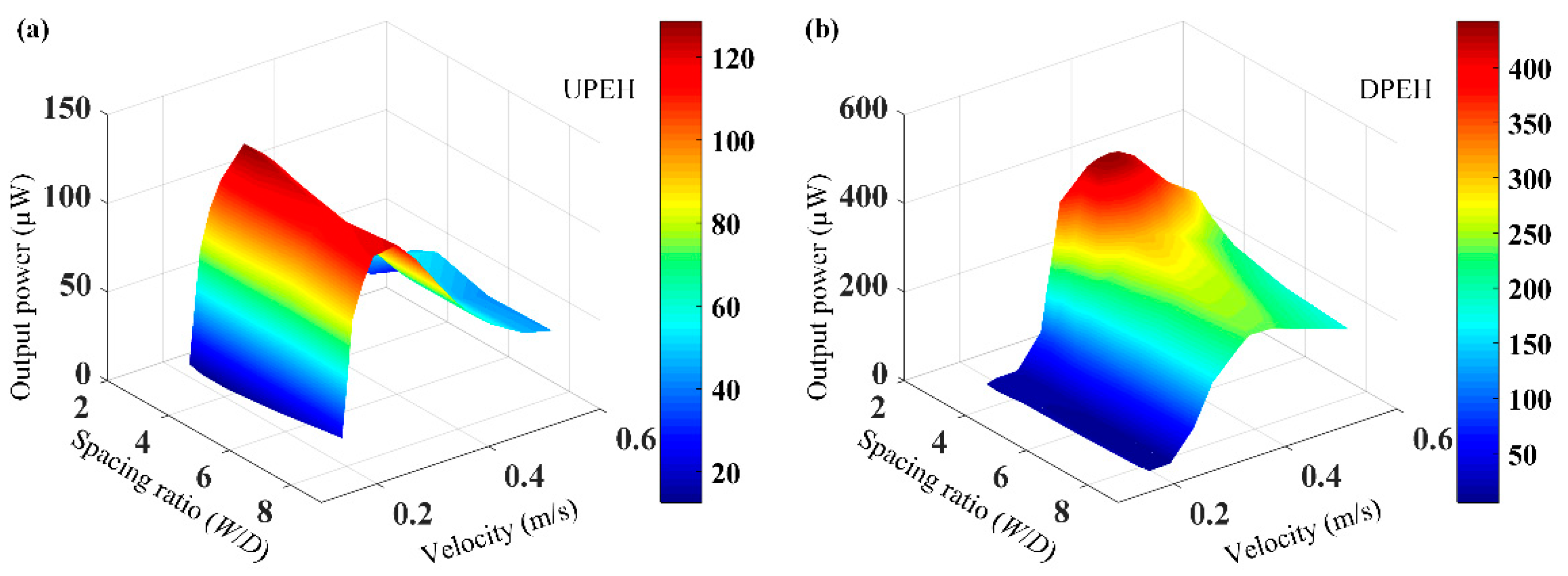
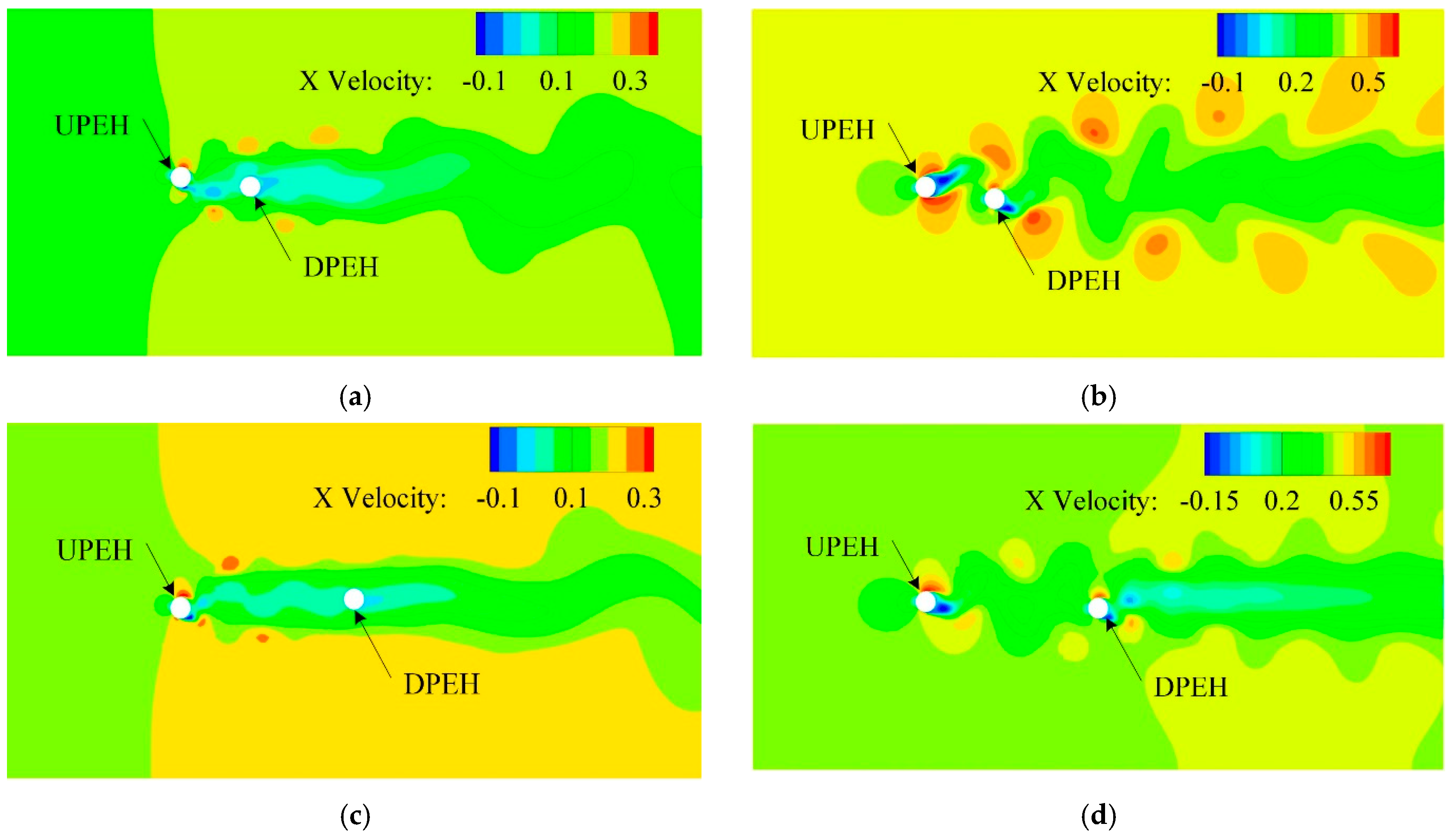
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mehr, A.S.; Mahmoudi, S.M.S.; Yari, M.; Chitsaz, A. Thermodynamic and exergoeconomic analysis of biogas fed solid oxide fuel cell power plants emphasizing on anode and cathode recycling: A comparative study. Energy Convers. Manag. 2015, 105, 596–606. [Google Scholar] [CrossRef]
- Manenti, F.; Pelosato, R.; Vallevi, P.; Leon-Garzon, A.R.; Dotelli, G.; Vita, A.; Lo Faro, M.; Maggio, G.; Pino, L.; Aricò, A.S. Biogas-fed solid oxide fuel cell (SOFC) coupled to tri-reforming process: Modelling and simulation. Int. J. Hydrogen Energy 2015, 40, 14640–14650. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Issues in mathematical modeling of piezoelectric energy harvesters. Smart Mater. Struct. 2008, 17, 065016. [Google Scholar] [CrossRef]
- Shan, X.; Tian, H.; Chen, D.; Xie, T. A curved panel energy harvester for aeroelastic vibration. Appl. Energy 2019, 249, 58–66. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Yang, Z. Resonance Mechanism of Nonlinear Vibrational Multistable Energy Harvesters under Narrow-Band Stochastic Parametric Excitations. Complexity 2019, 2019, 1–20. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Han, Q.; Litak, G. Response analysis of the nonlinear vibration energy harvester with an uncertain parameter. J. Multi-Body Dyn. 2019, 82, 376–381. [Google Scholar] [CrossRef]
- Zhou, S.; Zuo, L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting. Commun. Nonlinear Sci. Numer. Simul. 2018, 61, 271–284. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Y.; Yang, X.; Liu, J. Ring-type traveling wave ultrasonic motor using a radial bending mode. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, W.; Liu, J.; Yang, X. A High-Power Linear Ultrasonic Motor Using Bending Vibration Transducer. IEEE Trans. Ind. Electron. 2013, 60, 5160–5166. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W.; Yang, X.; Liu, J. A Rotary Piezoelectric Actuator Using the Third and Fourth Bending Vibration Modes. IEEE Trans. Ind. Electron. 2014, 61, 4366–4373. [Google Scholar] [CrossRef]
- Cheng, T.; Fu, X.; Liu, W.; Lu, X.; Chen, X.; Wang, Y.; Bao, G. Airfoil-based cantilevered polyvinylidene fluoride layer generator for translating amplified air-flow energy. Renew. Energy 2019, 135, 399–407. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y. An impact-based broadband aeroelastic energy harvester for concurrent wind and base vibration energy harvesting. Appl. Energy 2018, 212, 233–243. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, S.; Zhang, Z.; Yurchenko, D. High-performance piezoelectric wind energy harvester with Y-shaped attachments. Energy Convers. Manag. 2019, 181, 645–652. [Google Scholar] [CrossRef]
- Lai, Z.H.; Wang, J.L.; Zhang, C.L.; Zhang, G.Q.; Yurchenko, D. Harvest wind energy from a vibro-impact DEG embedded into a bluff body. Energy Convers. Manag. 2019, 199, 111993. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, Z.; Shan, X.; Sun, Y.; Xie, T.; Zi, Y. Capturing Flow Energy from Ocean and Wind. Energies 2019, 12, 2184. [Google Scholar] [CrossRef]
- van Rooij, A.C.L.M.; Nitzsche, J.; Dwight, R.P. Energy budget analysis of aeroelastic limit-cycle oscillations. J. Fluids Struct. 2017, 69, 174–186. [Google Scholar] [CrossRef][Green Version]
- Zhou, S.; Wang, J. Dual serial vortex-induced energy harvesting system for enhanced energy harvesting. AIP Adv. 2018, 8, 075221. [Google Scholar] [CrossRef]
- Xiang, J.; Wu, Y.; Li, D. Energy harvesting from the discrete gust response of a piezoaeroelastic wing: Modeling and performance evaluation. J. Sound Vib. 2015, 343, 176–193. [Google Scholar] [CrossRef]
- Wu, Y.; Li, D.; Xiang, J.; Da Ronch, A. Piezoaeroelastic energy harvesting based on an airfoil with double plunge degrees of freedom: Modeling and numerical analysis. J. Fluids Struct. 2017, 74, 111–129. [Google Scholar] [CrossRef]
- Yan, Z.; Abdelkefi, A. Nonlinear characterization of concurrent energy harvesting from galloping and base excitations. Nonlinear Dyn. 2014, 77, 1171–1189. [Google Scholar] [CrossRef]
- Yan, Z.; Abdelkefi, A.; Hajj, M.R. Piezoelectric energy harvesting from hybrid vibrations. Smart Mater. Struct. 2014, 23, 025026. [Google Scholar] [CrossRef]
- De Lorenzo, G.; Milewski, J.; Fragiacomo, P. Theoretical and experimental investigation of syngas-fueled molten carbonate fuel cell for assessment of its performance. Int. J. Hydrogen Energy 2017, 42, 28816–28828. [Google Scholar] [CrossRef]
- Farhad, S.; Hamdullahpur, F.; Yoo, Y. Performance evaluation of different configurations of biogas-fuelled SOFC micro-CHP systems for residential applications. Int. J. Hydrogen Energy 2010, 35, 3758–3768. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, G.; Wang, J. Bluff body with built-in piezoelectric cantilever for flow-induced energy harvesting. Int. J. Energy Res. 2020, 44, 3762–3777. [Google Scholar] [CrossRef]
- Kupecki, J.; Skrzypkiewicz, M.; Wierzbicki, M.; Stepien, M. Experimental and numerical analysis of a serial connection of two SOFC stacks in a micro-CHP system fed by biogas. Int. J. Hydrogen Energy 2017, 42, 3487–3497. [Google Scholar] [CrossRef]
- Baldinelli, A.; Barelli, L.; Bidini, G. Upgrading versus reforming: An energy and exergy analysis of two Solid Oxide Fuel Cell-based systems for a convenient biogas-to-electricity conversion. Energy Convers. Manag. 2017, 138, 360–374. [Google Scholar] [CrossRef]
- Bochentyn, B.; Błaszczak, P.; Gazda, M.; Fuerte, A.; Wang, S.F.; Jasiński, P. Investigation of praseodymium and samarium co-doped ceria as an anode catalyst for DIR-SOFC fueled by biogas. Int. J. Hydrogen Energy 2020, 45, 29131–29142. [Google Scholar] [CrossRef]
- De Lorenzo, G.; Fragiacomo, P. Electrical and thermal analysis of an intermediate temperature IIR-SOFC system fed by biogas. Energy Sci. Eng. 2018, 6, 60–72. [Google Scholar] [CrossRef]
- De Lorenzo, G.; Corigliano, O.; Lo Faro, M.; Frontera, P.; Antonucci, P.; Zignani, S.C.; Trocino, S.; Mirandola, F.A.; Aricò, A.S.; Fragiacomo, P. Thermoelectric characterization of an intermediate temperature solid oxide fuel cell system directly fed by dry biogas. Energy Convers. Manag. 2016, 127, 90–102. [Google Scholar] [CrossRef]
- Akaydin, H.D.; Elvin, N.; Andreopoulos, Y. Energy Harvesting from Highly Unsteady Fluid Flows using Piezoelectric Materials. J. Intell. Mater. Syst. Struct. 2010, 21, 1263–1278. [Google Scholar] [CrossRef]
- Goushcha, O.; Akaydin, H.D.; Elvin, N.; Andreopoulos, Y. Energy harvesting prospects in turbulent boundary layers by using piezoelectric transduction. J. Fluids Struct. 2015, 54, 823–847. [Google Scholar] [CrossRef]
- Hu, J.; Porfiri, M.; Peterson, S.D. Energy transfer between a passing vortex ring and a flexible plate in an ideal quiescent fluid. J. Appl. Phys. 2015, 118, 114902. [Google Scholar] [CrossRef]
- Shi, S.; New, T.H.; Liu, Y. Flapping dynamics of a low aspect-ratio energy-harvesting membrane immersed in a square cylinder wake. Exp. Therm. Fluid Sci. 2013, 46, 151–161. [Google Scholar] [CrossRef]
- Dai, H.L.; Abdelkefi, A.; Wang, L. Piezoelectric energy harvesting from concurrent vortex-induced vibrations and base excitations. Nonlinear Dyn. 2014, 77, 967–981. [Google Scholar] [CrossRef]
- Wang, J.; Ran, J.; Zhang, Z. Energy Harvester Based on the Synchronization Phenomenon of a Circular Cylinder. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Wang, J.; Tang, L.; Zhao, L.; Hu, G.; Song, R.; Xu, K. Equivalent circuit representation of a vortex-induced vibration-based energy harvester using a semi-empirical lumped parameter approach. Int. J. Energy Res. 2020, 44, 4516–4528. [Google Scholar] [CrossRef]
- Zou, Q.; Ding, L.; Wang, H.; Wang, J.; Zhang, L. Two-degree-of-freedom flow-induced vibration of a rotating circular cylinder. Ocean Eng. 2019, 191, 106505. [Google Scholar] [CrossRef]
- Wang, J.; Hu, G.; Su, Z.; Li, G.; Zhao, W.; Tang, L.; Zhao, L. A cross-coupled dual-beam for multi-directional energy harvesting from vortex induced vibrations. Smart Mater. Struct. 2019, 28, 12LT02. [Google Scholar] [CrossRef]
- Gong, Y.; Shan, X.; Luo, X.; Pan, J.; Xie, T.; Yang, Z. Direction-adaptive energy harvesting with a guide wing under flow-induced oscillations. Energy 2019, 187, 115983. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Ghommem, M.; Nuhait, A.O.; Hajj, M.R. Nonlinear analysis and enhancement of wing-based piezoaeroelastic energy harvesters. J. Sound Vib. 2014, 333, 166–177. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Nayfeh, A.H.; Hajj, M.R. Modeling and analysis of piezoaeroelastic energy harvesters. Nonlinear Dyn. 2011, 67, 925–939. [Google Scholar] [CrossRef]
- Dias, J.A.C.; De Marqui, C.; Erturk, A. Three-Degree-of-Freedom Hybrid Piezoelectric-Inductive Aeroelastic Energy Harvester Exploiting a Control Surface. AIAA J. 2015, 53, 394–404. [Google Scholar] [CrossRef]
- Shoele, K.; Mittal, R. Energy harvesting by flow-induced flutter in a simple model of an inverted piezoelectric flag. J. Fluid Mech. 2016, 790, 582–606. [Google Scholar] [CrossRef]
- Wang, J.; Geng, L.; Zhou, S.; Zhang, Z.; Lai, Z.; Yurchenko, D. Design, modeling and experiments of broadband tristable galloping piezoelectric energy harvester. Acta Mech. Sin. 2020. [Google Scholar] [CrossRef]
- Yang, K.; Wang, J.; Yurchenko, D. A double-beam piezo-magneto-elastic wind energy harvester for improving the galloping-based energy harvesting. Appl. Phys. Lett. 2019, 115, 193901. [Google Scholar] [CrossRef]
- Wang, J.; Tang, L.; Zhao, L.; Zhang, Z. Efficiency investigation on energy harvesting from airflows in HVAC system based on galloping of isosceles triangle sectioned bluff bodies. Energy 2019, 172, 1066–1078. [Google Scholar] [CrossRef]
- Tan, T.; Hu, X.; Yan, Z.; Zhang, W. Enhanced low-velocity wind energy harvesting from transverse galloping with super capacitor. Energy 2019, 187, 115915. [Google Scholar] [CrossRef]
- Taylor, G.W.; Burns, J.R.; Kammann, S.A.; Powers, W.B.; Welsh, T.R. The Energy Harvesting Eel: A small subsurface ocean/river power generator. IEEE J. Ocean. Eng. 2001, 26, 539–547. [Google Scholar] [CrossRef]
- Allen, J.J.; Smits, A.J. Energy harvesting eel. J. Fluids Struct. 2001, 15, 629–640. [Google Scholar] [CrossRef]
- Akaydın, H.D.; Elvin, N.; Andreopoulos, Y. Wake of a cylinder: A paradigm for energy harvesting with piezoelectric materials. Exp. Fluids 2010, 49, 291–304. [Google Scholar] [CrossRef]
- Weinstein, L.A.; Cacan, M.R.; So, P.M.; Wright, P.K. Vortex shedding induced energy harvesting from piezoelectric materials in heating, ventilation and air conditioning flows. Smart Mater. Struct. 2012, 21, 045003. [Google Scholar] [CrossRef]
- Li, S.; Sun, Z. Harvesting vortex energy in the cylinder wake with a pivoting vane. Energy 2015, 88, 783–792. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, Y. Flapping dynamics of a piezoelectric membrane behind a circular cylinder. J. Fluids Struct. 2015, 55, 347–363. [Google Scholar] [CrossRef]
- Song, R.; Shan, X.; Lv, F.; Li, J.; Xie, T. A Novel Piezoelectric Energy Harvester Using the Macro Fiber Composite Cantilever with a Bicylinder in Water. Appl. Sci. 2015, 5, 1942. [Google Scholar] [CrossRef]
- Li, H.; Sumner, D. Vortex shedding from two finite circular cylinders in a staggered configuration. J. Fluids Struct. 2009, 25, 479–505. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Scanlon, J.M.; McDowell, E.; Hajj, M.R. Performance enhancement of piezoelectric energy harvesters from wake galloping. Appl. Phys. Lett. 2013, 103, 033903. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J.; Su, Z.; Li, G.; Peng, H.; Kwok, K.C.S. Performance evaluation of twin piezoelectric wind energy harvesters under mutual interference. Appl. Phys. Lett. 2019, 115, 073901–073905. [Google Scholar] [CrossRef]
- Shan, X.; Song, R.; Fan, M.; Xie, T. Energy-Harvesting Performances of Two Tandem Piezoelectric Energy Harvesters with Cylinders in Water. Appl. Sci. 2016, 6, 230. [Google Scholar] [CrossRef]
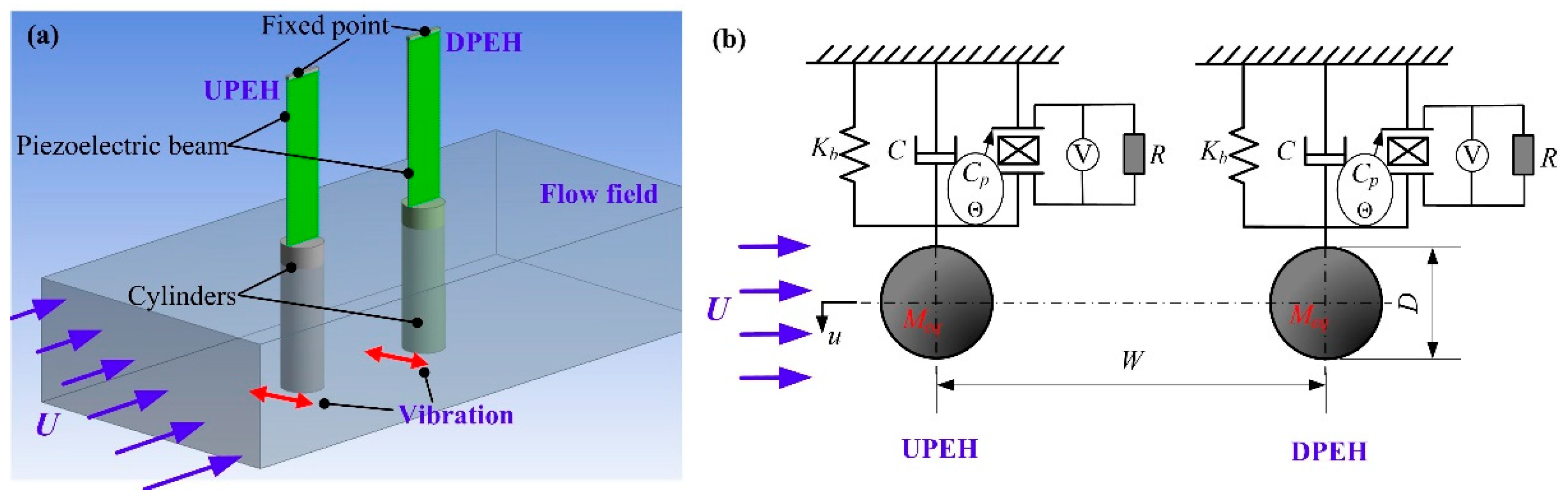
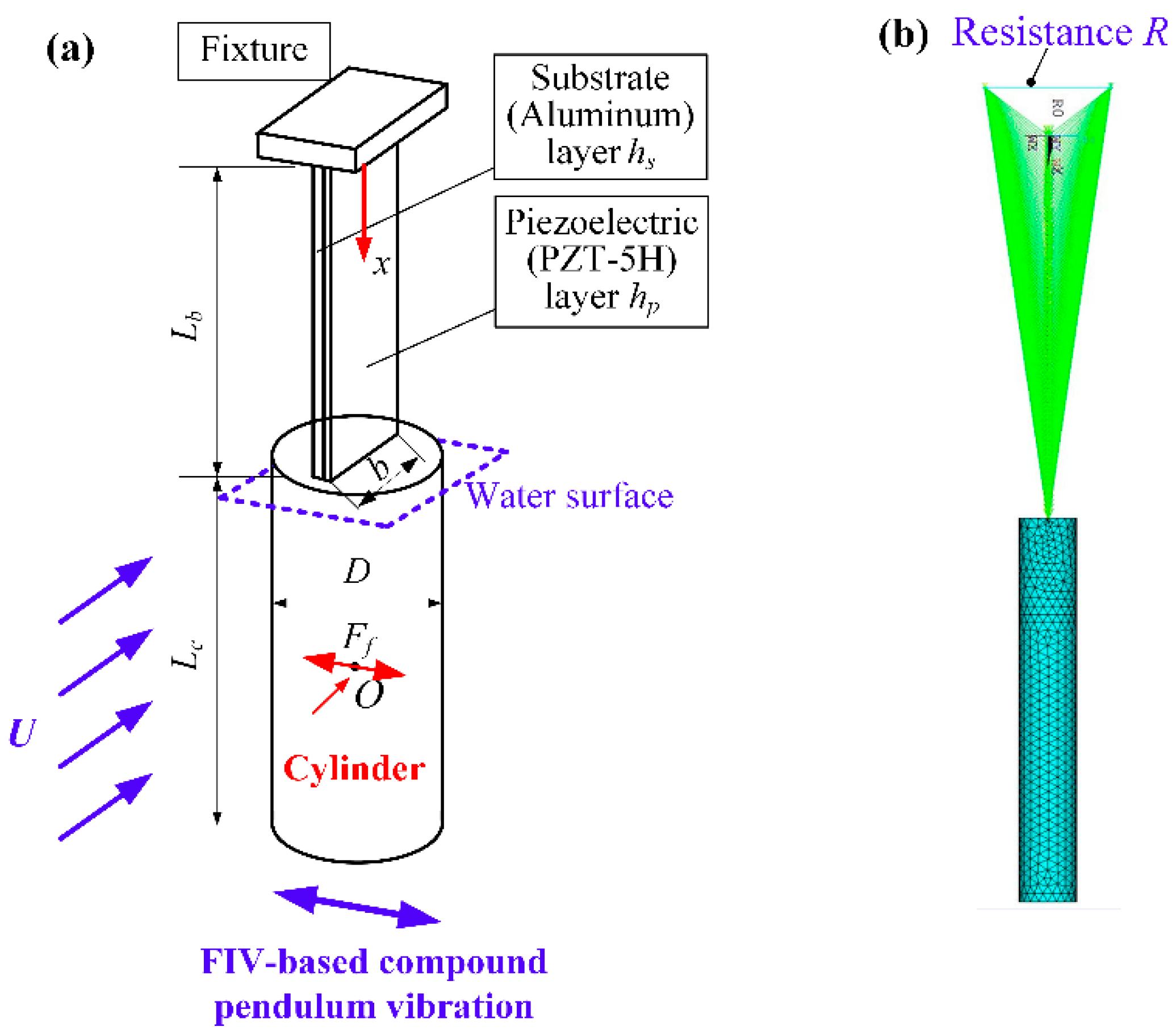

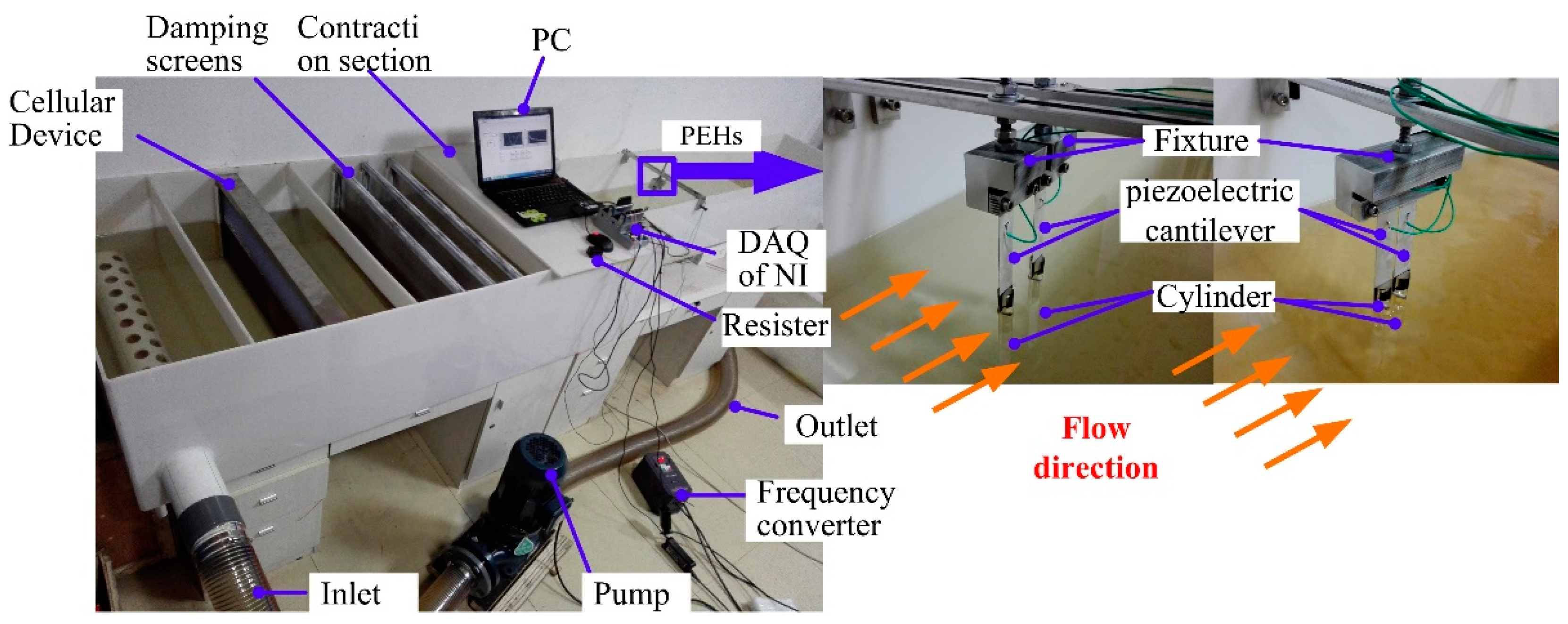

| Parameters | Values |
|---|---|
| density of PZT-5H ρp (kg/m3) | 7386 |
| density of aluminum layer ρp (kg/m3) | 2700 |
| fluid density ρp (kg/m3) | 1000 |
| Young modulus of PZT-5H Ep (GPa) | 59.77 |
| Young modulus of aluminum layer Es (GPa) | 71.7 |
| length × width × thickness of piezoelectric layer (Lb × b × hp) (mm) | 80 × 20 × 0.2 |
| length × width × thickness of substrate layer (Lb × b × hs) (mm) | 80 × 20 × 0.2 |
| piezoelectric constant e31 (C/m2) | −13.74 |
| dielectric constant (F/m) | 4.178 × 10−8 |
| load resistance R (kΩ) | 100 |
| Cylinder diameter D (mm) | 12 |
| length of cylinder immersed in water Lf (mm) | 55 |
| first mode damping ratio | 0.0499 |
| open circuit resonance frequency ωnoc (rad) | 26.25 |
| short circuit resonance frequency ωnsc(rad) | 25.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, R.; Hou, C.; Yang, C.; Yang, X.; Guo, Q.; Shan, X. Modeling, Validation, and Performance of Two Tandem Cylinder Piezoelectric Energy Harvesters in Water Flow. Micromachines 2021, 12, 872. https://doi.org/10.3390/mi12080872
Song R, Hou C, Yang C, Yang X, Guo Q, Shan X. Modeling, Validation, and Performance of Two Tandem Cylinder Piezoelectric Energy Harvesters in Water Flow. Micromachines. 2021; 12(8):872. https://doi.org/10.3390/mi12080872
Chicago/Turabian StyleSong, Rujun, Chengwei Hou, Chongqiu Yang, Xianhai Yang, Qianjian Guo, and Xiaobiao Shan. 2021. "Modeling, Validation, and Performance of Two Tandem Cylinder Piezoelectric Energy Harvesters in Water Flow" Micromachines 12, no. 8: 872. https://doi.org/10.3390/mi12080872
APA StyleSong, R., Hou, C., Yang, C., Yang, X., Guo, Q., & Shan, X. (2021). Modeling, Validation, and Performance of Two Tandem Cylinder Piezoelectric Energy Harvesters in Water Flow. Micromachines, 12(8), 872. https://doi.org/10.3390/mi12080872






