A Vacuum-Powered Artificial Muscle Designed for Infant Rehabilitation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Vacuum Actuator Design
2.2. Fabrication
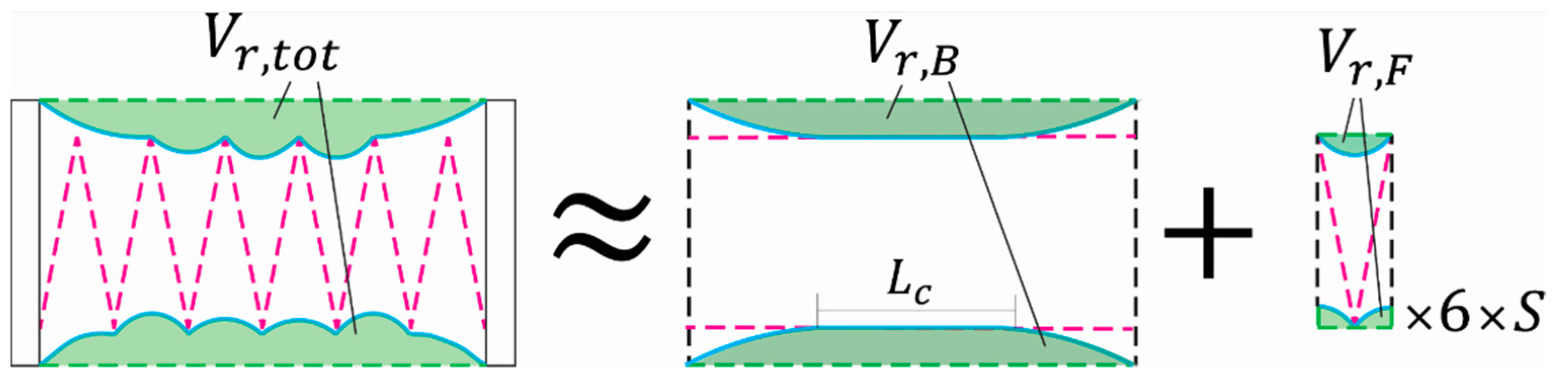
2.3. Finite Element Modeling of the Structure
2.4. Modelling Actuator Force Output
2.5. Actuator Restoring Force Experiment
2.6. Quasi-Static Characterization of the Actuator
2.7. Dynamic Response of the Actuator
2.8. Case Application in Rehabilitation Exercise
3. Results
3.1. Finite Element Modeling Results
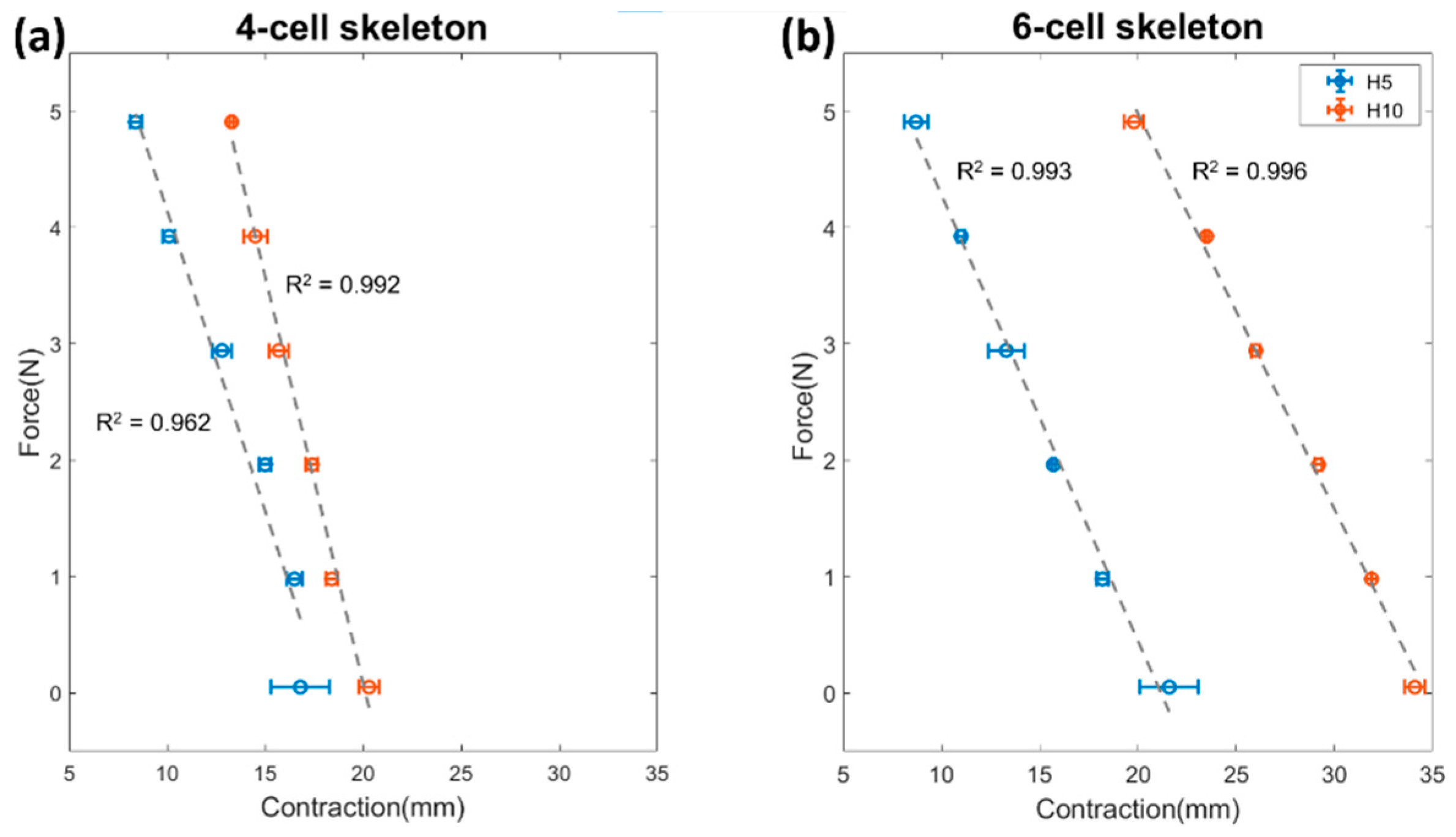
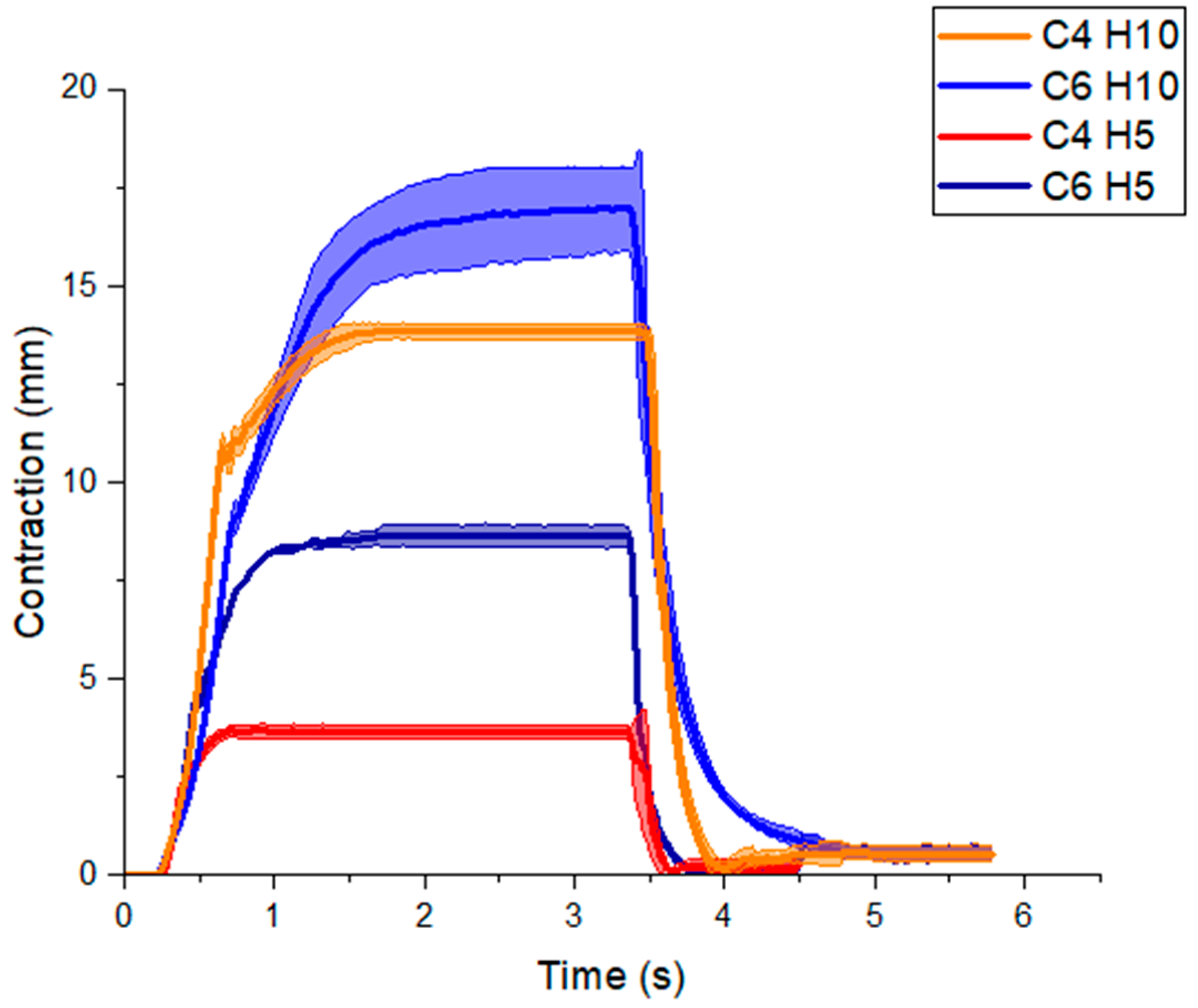
3.2. Actuator Force-Contraction Profile
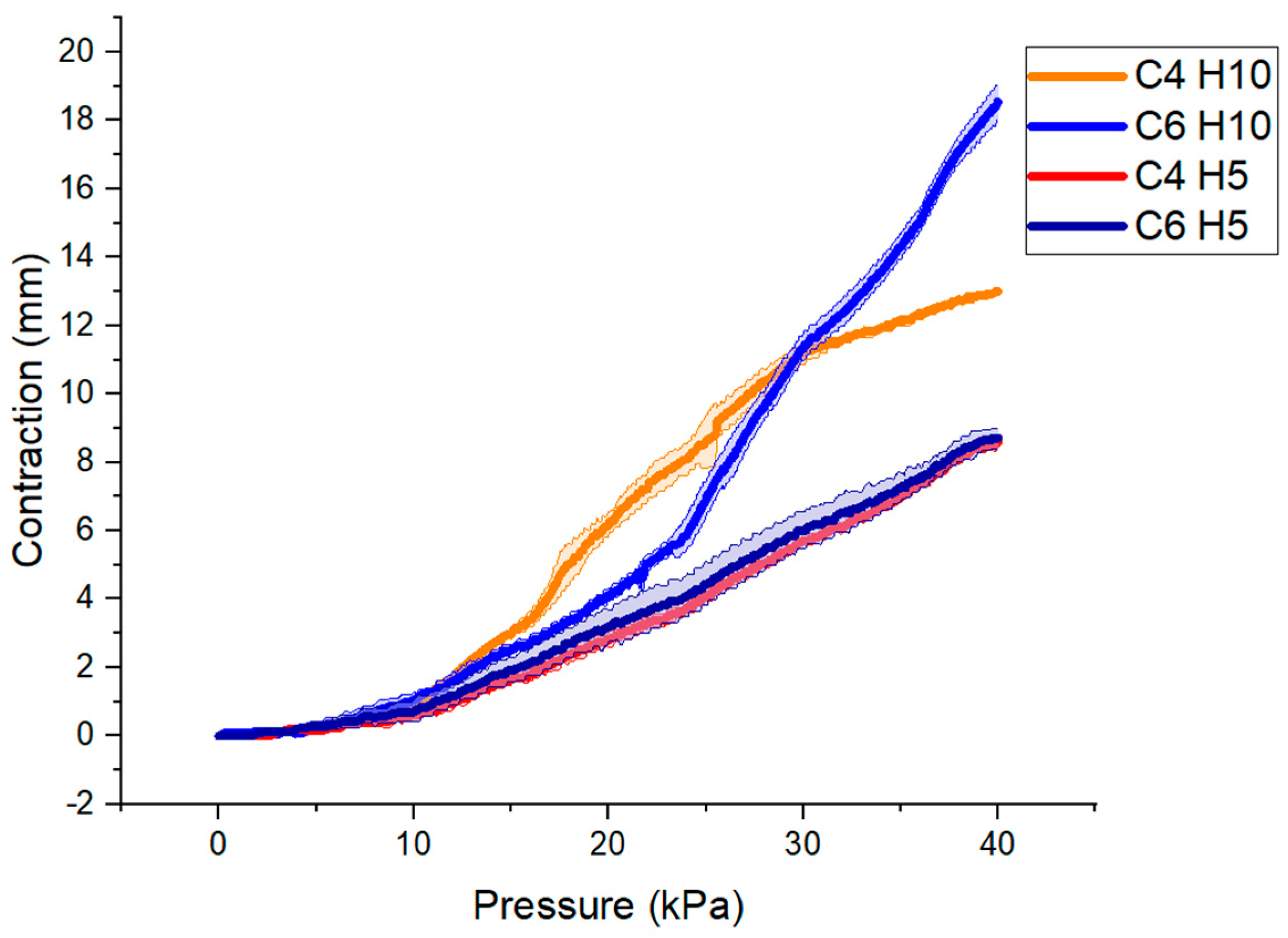
3.3. Quasi-Static Characterization of the Actuator
3.4. Dynamic Response of the Actuator
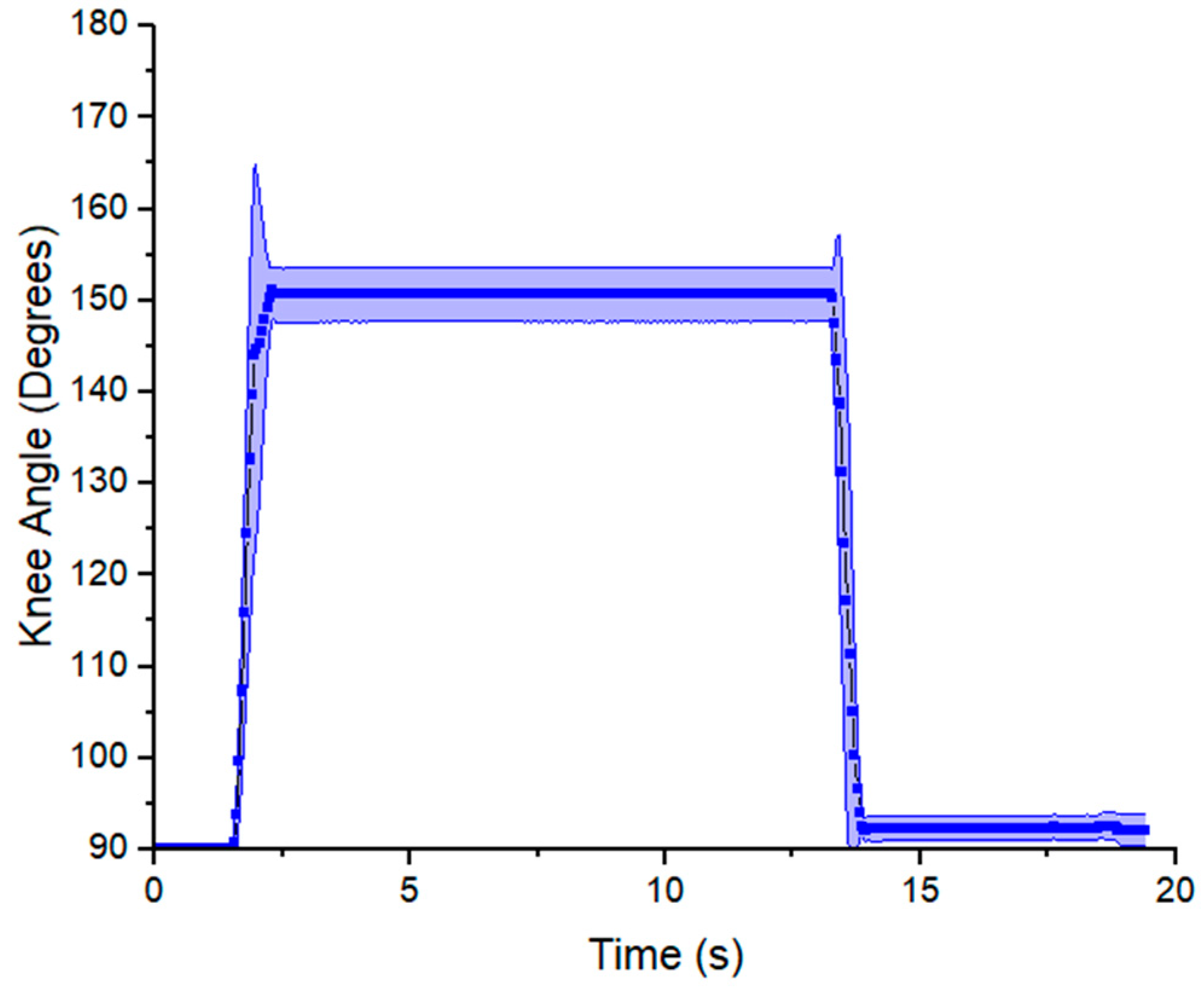
3.5. Case Application in Rehabilitation Exercise
4. Discussion
4.1. FEM of Different Skeleton Parameters
4.2. Actuator Force-Contraction Profile
4.3. Characterization of the Actuator
4.4. Dynamic Response of the Actuator
4.5. Case Application in Rehabilitation Exercise
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Okoro, C.A.; Hollis, N.; Cyrus, A.C.; Griffin-Blake, S. Prevalence of Disabilities and Health Care Access by Disability Status and Type Among Adults—United States, 2016. Morb. Mortal. Wkly. Rep. MMWR 2018, 67, 882–887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asbeck, A.T.; Schmidt, K.; Walsh, C.J. Soft exosuit for hip assistance. Rob. Auton. Syst. 2015, 73, 102–110. [Google Scholar] [CrossRef]
- Asbeck, A.T.; Dyer, R.J.; Larusson, A.F.; Walsh, C.J. Biologically-inspired soft exosuit. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013. [Google Scholar]
- Goher, K.M.; Fadlallah, S.O. Chapter 11. Assistive Devices for Elderly Mobility and Rehabilitation: Review and Reflection; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Park, Y.L.; Santos, J.; Galloway, K.G.; Goldfield, E.C.; Wood, R.J. A soft wearable robotic device for active knee motions using flat pneumatic artificial muscles. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4805–4810. [Google Scholar]
- Subramanyam, K.; Rogers, E.; Kulesza, M.; Holland, D.; Gafford, J.; Goldfield, E.; Walsh, C. Soft Wearable Orthotic Device for Assisting Kicking Motion in Developmentally Delayed Infants. J. Med. Devices 2015, 9, 030913. [Google Scholar] [CrossRef] [Green Version]
- Hadders-Algra, M. Early human motor development: From variation to the ability to vary and adapt. Neurosci. Biobehav. Rev. 2018, 90, 411–427. [Google Scholar] [CrossRef]
- Domellöf, E.; Rönnqvist, L.; Hopkins, B. Functional asymmetries in the stepping response of the human newborn: A kinematic approach. Exp. Brain Res. 2007, 177, 324–335. [Google Scholar] [CrossRef]
- Barbu-Roth, M.; Anderson, D.I.; Desprès, A.; Streeter, R.J.; Cabrol, D.; Trujillo, M.; Campos, J.J.; Provasi, J. Air stepping in response to optic flows that move Toward and Away from the neonate. Dev. Psychobiol. 2014, 56, 1142–1149. [Google Scholar] [CrossRef] [PubMed]
- Goldfield, E.C.; Park, Y.L.; Chen, B.R.; Hsu, W.H.; Young, D.; Wehner, M.; Kelty-Stephen, D.G.; Stirling, L.; Weinberg, M.; Newman, D.; et al. Bio-Inspired Design of Soft Robotic Assistive Devices: The Interface of Physics, Biology, and Behavior. Ecol. Psychol. 2012, 24, 300–327. [Google Scholar] [CrossRef]
- Apkon, S.D.; Grady, R.; Hart, S.; Lee, A.; McNalley, T.; Niswander, L.; Petersen, J.; Remley, S.; Rotenstein, D.; Shurtleff, H.; et al. Advances in the Care of Children with Spina Bifida. Adv. Pediatr. 2014, 61, 33–74. [Google Scholar] [CrossRef]
- Sansom, J.K.; Teulier, C.; Smith, B.A.; Moerchen, V.; Muraszko, K.; Ulrich, B.D. Muscle activation patterns in infants with myelomeningocele stepping on a treadmill. Pediatr. Phys. Ther. 2013, 25, 278–289. [Google Scholar] [CrossRef] [Green Version]
- Instituto Mexicano del Seguro Social Guía De Práctica Clínica. Prevención, Diagnóstico y Tratamiento de la Espina Bífida en Niños. IMSS 2013, IMSS-269-13. [Google Scholar]
- Aizawa, C.Y.P.; Morales, M.P.; Lundberg, C.; Moura, M.C.D.; Pinto, F.C.; Voos, M.C.; Hasue, R.H. Conventional physical therapy and physical therapy based on reflex stimulation showed similar results in children with myelomeningocele. Arq. Neuropsiquiatr. 2017, 75, 160–166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michmizos, K.P.; Rossi, S.; Castelli, E.; Cappa, P.; Krebs, H.I. Robot-Aided Neurorehabilitation: A Pediatric Robot for Ankle Rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 1056–1067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, Y.; Zhang, D. FEXO knee: A rehabilitation device for knee joint combining functional electrical stimulation with a compliant exoskeleton. In Proceedings of the 5th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics, Sao Paulo, Brazil, 12–15 August 2014; pp. 683–688. [Google Scholar]
- Neuhaus, P.D.; Noorden, J.H.; Craig, T.J.; Torres, T.; Kirschbaum, J.; Pratt, J.E. Design and evaluation of Mina: A robotic orthosis for paraplegics. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011. [Google Scholar]
- Mohanta, J.K.; Mohan, S.; Deepasundar, P.; Kiruba-Shankar, R. Development and control of a new sitting-type lower limb rehabilitation robot. Comput. Electr. Eng. 2018, 67, 330–347. [Google Scholar] [CrossRef]
- Beyl, P.; Naudet, J.; van Ham, R.; Lefeber, D. Mechanical Design of an Active Knee Orthosis for Gait Rehabilitation. In Proceedings of the 2007 IEEE 10th International Conference on Rehabilitation Robotics, Noordwijk, The Netherlands, 13–15 June 2007; pp. 100–105. [Google Scholar]
- Sancho-Pérez, J.; Pérez, M.; García, E.; Sanz-Merodio, D.; Plaza, A.; Cestari, M. Mechanical description of ATLAS 2020, a 10-DOF paediatric exoskeleton. Adv. Coop. Robot. 2016, 814–822. [Google Scholar] [CrossRef]
- Nickel, V.L.; Perry, J.; Garrett, A.L. Development of Useful Function in the Severely Paralyzed Hand. J. Bone Jt. Surg. 1963, 45, 933–952. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Galloway, K.C.; Wood, R.J.; Walsh, C.J. Soft robotic glove for combined assistance and at-home rehabilitation. Rob. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Connolly, F.; Walsh, C.J.; Bertoldi, K. Automatic design of fiber-reinforced soft actuators for trajectory matching. Proc. Natl. Acad. Sci. USA 2017, 114, 51–56. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Greenspan, B.; Mascitelli, T.; Raccuglia, M.; Denner, K.; Duda, R.; Lobo, M.A. Design of the Playskin AirTM: A User-Controlled, Soft Pneumatic Exoskeleton. Front. Biomed. Devices 2019. [Google Scholar] [CrossRef] [Green Version]
- Kokkoni, E.; Liu, Z.; Karydis, K. Development of a Soft Robotic Wearable Device to Assist Infant Reaching. J. Eng. Sci. Med. Diagn. Ther. 2020, 3, 021109. [Google Scholar] [CrossRef]
- Kang, J.; Martelli, D.; Vashista, V.; Martinez-Hernandez, I.; Kim, H.; Agrawal, S.K. Robot-driven downward pelvic pull to improve crouch gait in children with cerebral palsy. Sci. Robot. 2017, 2, 2634. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lobo, M.A.; Koshy, J.; Hall, M.L.; Erol, O.; Cao, H.; Buckley, J.M.; Galloway, J.C.; Higginson, J. Playskin Lift: Development and Initial Testing of an Exoskeletal Garment to Assist Upper Extremity Mobility and Function. Phys. Ther. 2016, 96, 390. [Google Scholar] [CrossRef] [Green Version]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Verma, M.S.; So, J.H.; Mosadegh, B.; Keplinger, C.; Lee, B.; Khashai, F.; Lossner, E.; Suo, Z.; Whitesides, G.M. Buckling Pneumatic Linear Actuators Inspired by Muscle. Adv. Mater. Technol. 2016, 1, 1600055. [Google Scholar] [CrossRef]
- Greer, J.D.; Morimoto, T.K.; Okamura, A.M.; Hawkes, E.W. Series pneumatic artificial muscles (sPAMs) and application to a soft continuum robot. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5503–5510. [Google Scholar]
- Nguyen, P.H.; Zhang, W. Design and Computational Modeling of Fabric Soft Pneumatic Actuators for Wearable Assistive Devices. Sci. Rep. 2020, 10, 66. [Google Scholar] [CrossRef] [PubMed]
- Drotman, D.; Ishida, M.; Jadhav, S.; Tolley, M.T. Application-driven design of soft, 3-d printed, pneumatic actuators with bellows. IEEE/ASME Trans. Mechatron. 2019, 24, 78–87. [Google Scholar] [CrossRef]
- Mosadegh, B.; Polygerinos, P.; Keplinger, C.; Wennstedt, S.; Shepherd, R.F.; Gupta, U.; Shim, J.; Bertoldi, K.; Walsh, C.J.; Whitesides, G.M. Pneumatic Networks for Soft Robotics that Actuate Rapidly. Adv. Funct. Mater. 2014, 24, 2163–2170. [Google Scholar] [CrossRef]
- Hu, W.; Alici, G. Bioinspired Three-Dimensional-Printed Helical Soft Pneumatic Actuators and Their Characterization. Soft Robot. 2020, 7, 267–282. Available online: https://home.liebertpub.com/soro (accessed on 9 February 2021). [CrossRef]
- Tawk, C.; Spinks, G.M.; Panhuis, M.I.H.; Alici, G. 3D Printable Linear Soft Vacuum Actuators: Their Modeling, Performance Quantification and Application in Soft Robotic Systems. IEEE/ASME Trans. Mechatron. 2019, 24, 2118–2129. [Google Scholar] [CrossRef]
- Wang, T.; Ge, L.; Gu, G. Programmable design of soft pneu-net actuators with oblique chambers can generate coupled bending and twisting motions. Sens. Actuators A Phys. 2018, 271, 131–138. [Google Scholar] [CrossRef]
- Yang, H.D.; Greczek, B.T.; Asbeck, A.T. Modeling and Analysis of a High-Displacement Pneumatic Artificial Muscle with Integrated Sensing. Front. Robot. AI 2019, 5, 136. [Google Scholar] [CrossRef]
- Belforte, G.; Eula, G.; Ivanov, A.; Visan, A.L. Bellows textile muscle. J. Text. Inst. 2014, 105, 356–364. [Google Scholar] [CrossRef]
- Niiyama, R.; Rus, D.; Kim, S. Pouch Motors: Printable/inflatable soft actuators for robotics. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6332–6337. [Google Scholar]
- Tawk, C.; Panhuis, M.I.H.; Spinks, G.M.; Alici, G. Bioinspired 3d printable soft vacuum actuators for locomotion robots, grippers and artificial muscles. Soft Robot. 2018, 5, 685–694. [Google Scholar] [CrossRef]
- Felt, W.; Robertson, M.A.; Paik, J. Modeling vacuum bellows soft pneumatic actuators with optimal mechanical performance. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 534–540. [Google Scholar]
- Yang, D.; Mosadegh, B.; Ainla, A.; Lee, B.; Khashai, F.; Suo, Z.; Bertoldi, K.; Whitesides, G.M. Buckling of Elastomeric Beams Enables Actuation of Soft Machines. Adv. Mater. 2015, 27, 6323–6327. [Google Scholar] [CrossRef]
- Yang, D.; Verma, M.S.; Lossner, E.; Stothers, D.; Whitesides, G.M. Negative-Pressure Soft Linear Actuator with a Mechanical Advantage. Adv. Mater. Technol. 2017, 2, 1600164. [Google Scholar] [CrossRef]
- Jiao, Z.; Ji, C.; Zou, J.; Yang, H.; Pan, M. Vacuum-Powered Soft Pneumatic Twisting Actuators to Empower New Capabilities for Soft Robots. Adv. Mater. Technol. 2019, 4, 1800429. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-G.; Rodrigue, H. Origami-Based Vacuum Pneumatic Artificial Muscles with Large Contraction Ratios. Soft Robot. 2019, 6, 109–117. Available online: https://home.liebertpub.com/soro (accessed on 25 January 2021). [CrossRef]
- Li, S.; Vogt, D.M.; Rus, D.; Wood, R.J. Fluid-driven origami-inspired artificial muscles. Proc. Natl. Acad. Sci. USA 2017, 114, 13132–13137. [Google Scholar] [CrossRef] [Green Version]
- Kulasekera, A.L.; Arumathanthri, R.B.; Chathuranga, D.S.; Lalitharatne, T.D.; Gopura, R.C. A Low-Profile Vacuum Actuator: Towards a Sit-to-Stand Assist Exosuit. In Proceedings of the 2020 3rd IEEE International Conference on Soft Robotics (RoboSoft), New Haven, CT, USA, 15 May–15 July 2020; pp. 110–115. [Google Scholar]
- Sargent, B.; Scholz, J.; Reimann, H.; Kubo, M.; Fetters, L. Development of infant leg coordination: Exploiting passive torques. Infant Behav. Dev. 2015, 40, 108–121. [Google Scholar] [CrossRef] [PubMed]
- Hawkes, E.W.; Christensen, D.L.; Okamura, A.M. Design and implementation of a 300% strain soft artificial muscle. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4022–4029. [Google Scholar]
- Gollob, S.D.; Park, C.; Koo, B.H.B.; Roche, E.T. A Modular Geometrical Framework for Modelling the Force-Contraction Profile of Vacuum-Powered Soft Actuators. Front. Robot. AI 2021, 8, 606938. [Google Scholar] [CrossRef]
- Sun, H.; Jensen, R. Body segment growth during infancy. J. Biomech. 1994, 27, 265–275. [Google Scholar] [CrossRef]
- Wells, J.; Hyler-Both, D.; Danley, T.; Wallace, G. Biomechanics of growth and development in the healthy human infant: A pilot study. J. Osteopath. Med. 2002, 102, 313–319. [Google Scholar]
- Ding, Y.; Kim, M.; Kuindersma, S.; Walsh, C.J. Human-in-the-loop optimization of hip assistance with a soft exosuit during walking. Sci. Robot. 2018, 3, eaar5438. [Google Scholar] [CrossRef] [PubMed] [Green Version]

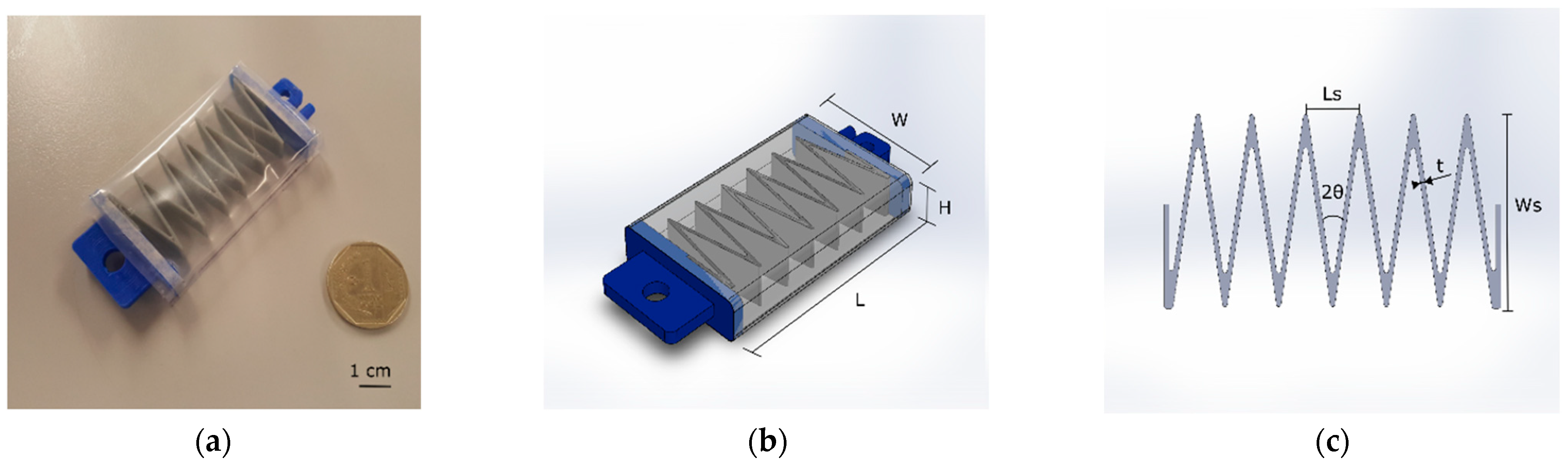






| N° Cells C | Ws (mm) | H (mm) | Ls (mm) | W (mm) |
|---|---|---|---|---|
| 4 | 30 | 5 | 10 | 38 |
| 6 | 30 | 5 | 10 | 38 |
| 4 | 30 | 10 | 10 | 38 |
| 6 | 30 | 10 | 10 | 38 |
| Four-Cell | Six-Cell | |
|---|---|---|
| 30xH5 | 520 | 380 |
| 30xH10 | 700 | 340 |
| Reference | Maximum Force (N) | Scaled Force Output (N/(kPa·mm2)) | Contraction (%) |
|---|---|---|---|
| Magazine [47] | 21 | 1.02 | 50 |
| FOAM [46] | 145 | 2.28 | 50 |
| Bellows [41] | 14.9 | 5.36 | 71 |
| LP-VPAM | 26.4 | 1.73 | 61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendoza, M.J.; Gollob, S.D.; Lavado, D.; Koo, B.H.B.; Cruz, S.; Roche, E.T.; Vela, E.A. A Vacuum-Powered Artificial Muscle Designed for Infant Rehabilitation. Micromachines 2021, 12, 971. https://doi.org/10.3390/mi12080971
Mendoza MJ, Gollob SD, Lavado D, Koo BHB, Cruz S, Roche ET, Vela EA. A Vacuum-Powered Artificial Muscle Designed for Infant Rehabilitation. Micromachines. 2021; 12(8):971. https://doi.org/10.3390/mi12080971
Chicago/Turabian StyleMendoza, Mijaíl Jaén, Samuel Dutra Gollob, Diego Lavado, Bon Ho Brandon Koo, Segundo Cruz, Ellen T. Roche, and Emir A. Vela. 2021. "A Vacuum-Powered Artificial Muscle Designed for Infant Rehabilitation" Micromachines 12, no. 8: 971. https://doi.org/10.3390/mi12080971







