Ab Initio Quantum-Mechanical Predictions of Semiconducting Photocathode Materials
Abstract
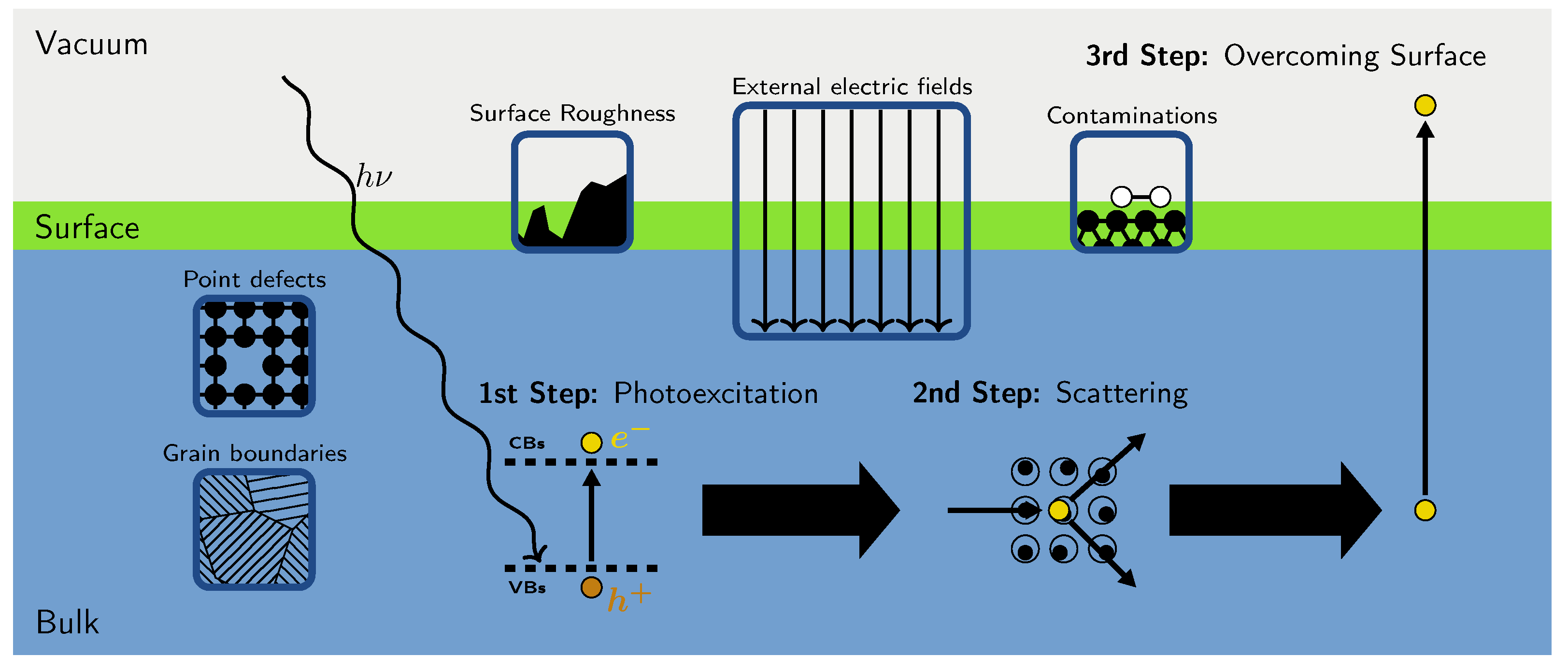
:1. Introduction
2. Methods
2.1. Theoretical Background
2.2. Computational Costs
3. Results and Discussion
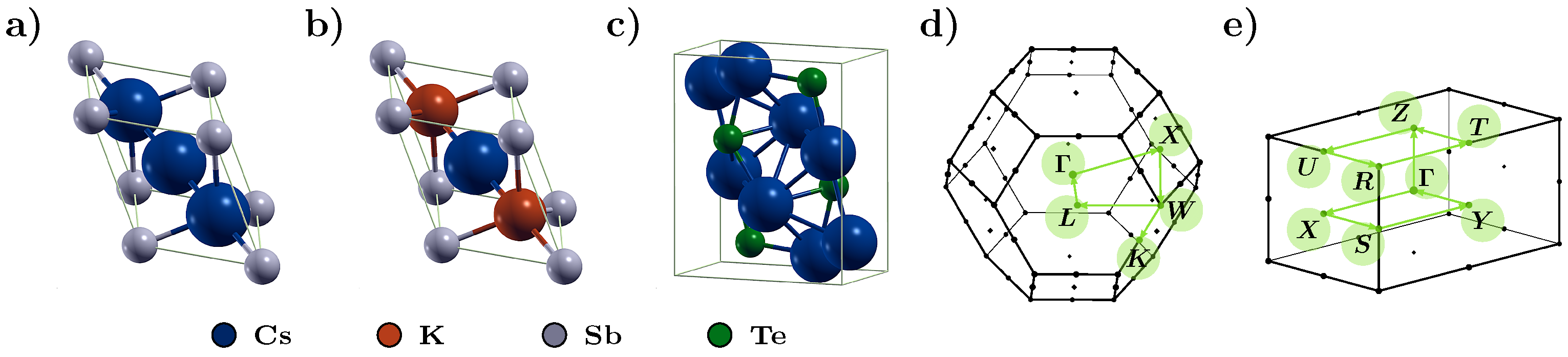
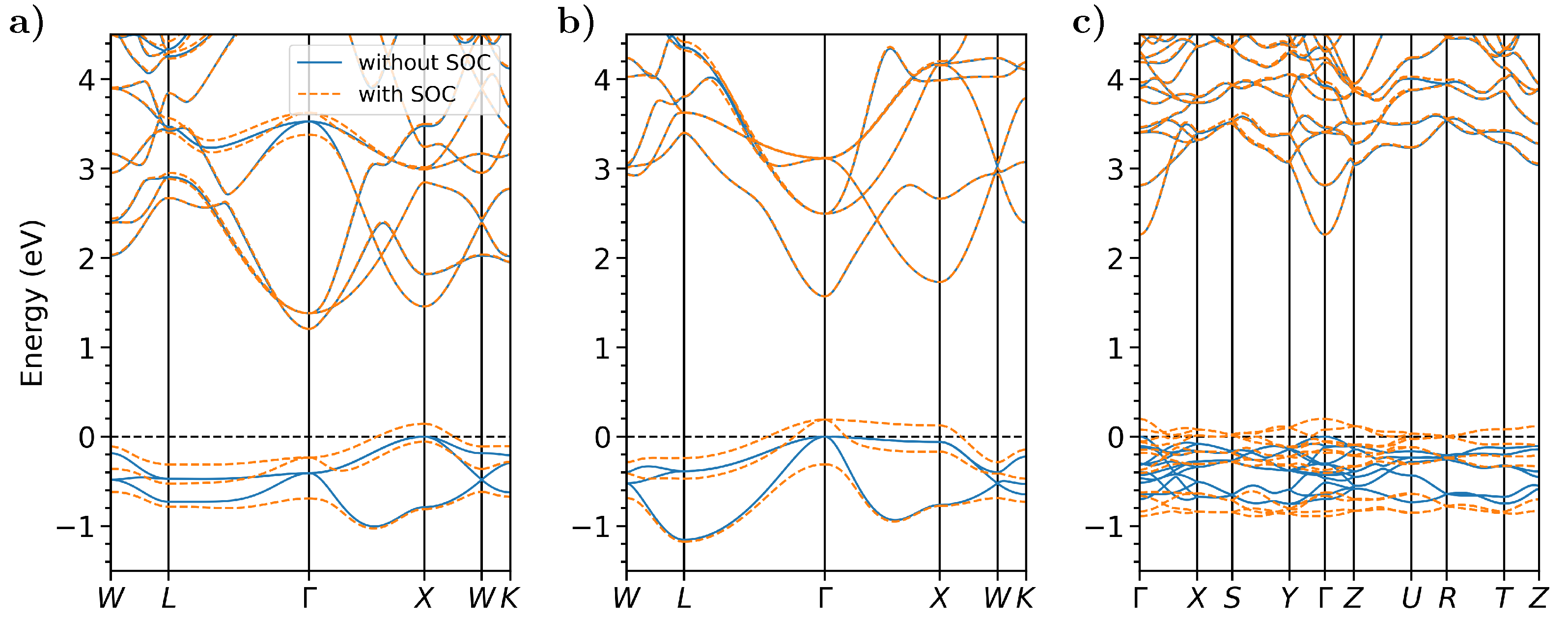
3.1. Electronic Structure
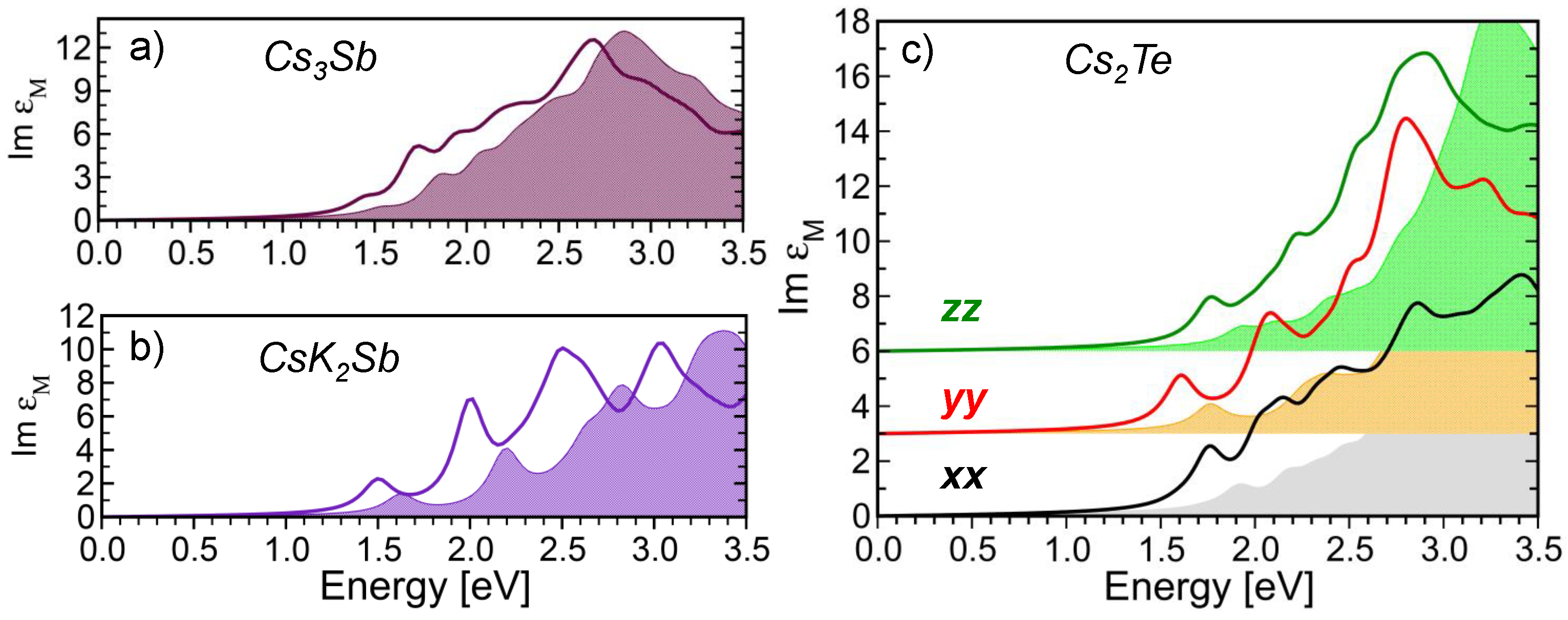
3.2. Optical Spectroscopy
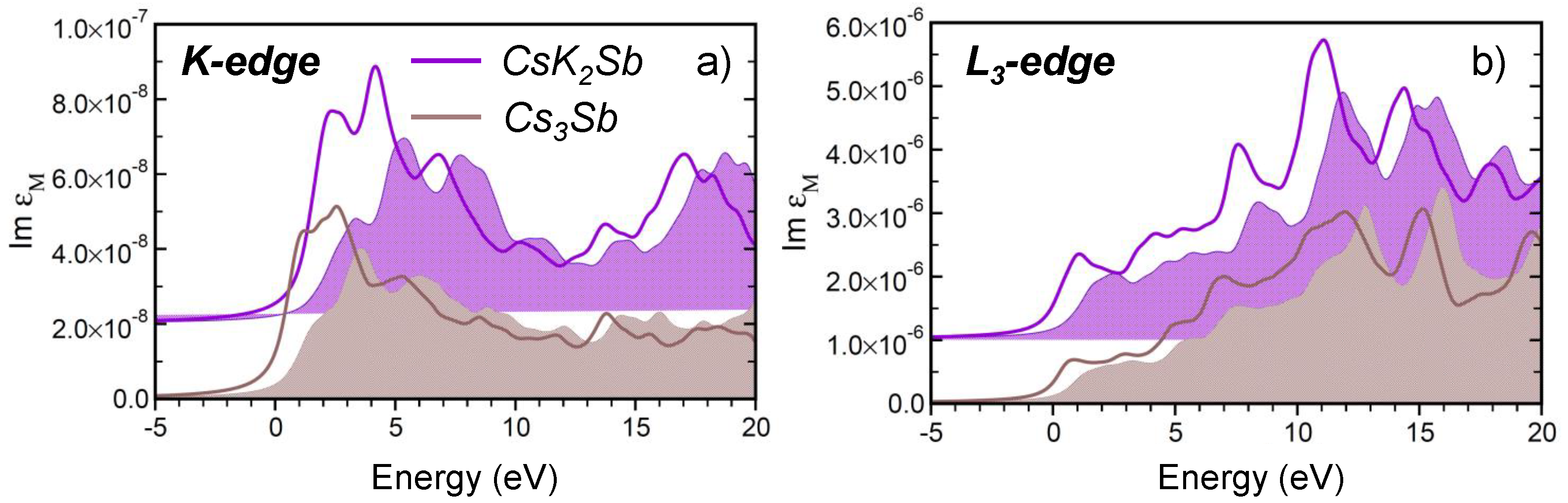
3.3. Core-Level Spectroscopy
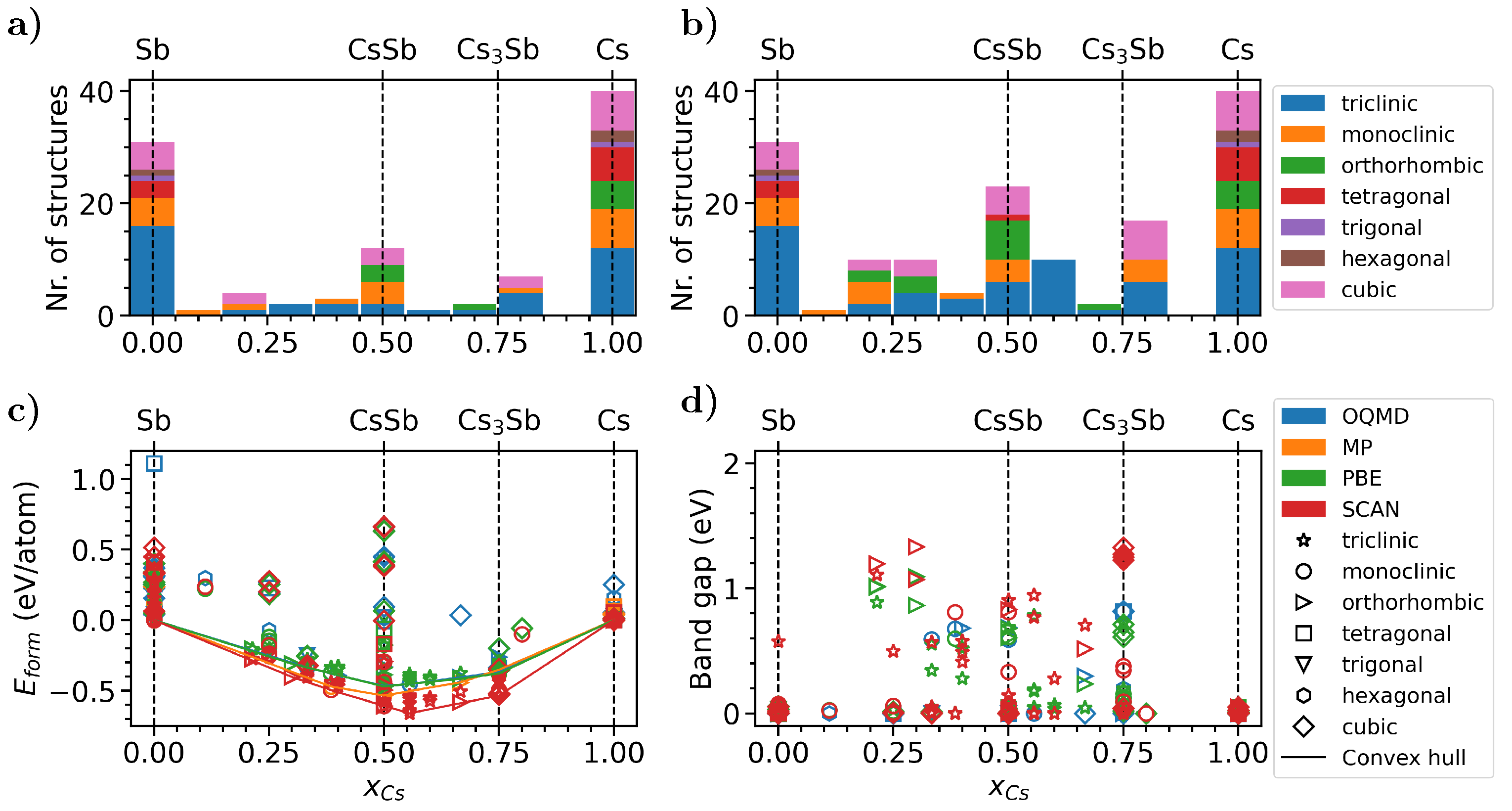
3.4. High-Throughput Material Screening
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Computational Details
References
- Callegari, C.; Grum-Grzhimailo, A.N.; Ishikawa, K.L.; Prince, K.C.; Sansone, G.; Ueda, K. Atomic, molecular and optical physics applications of longitudinally coherent and narrow bandwidth Free-Electron Lasers. Phys. Rep. 2021, 904, 1–59. [Google Scholar] [CrossRef]
- Hada, M.; Nishina, Y.; Kato, T. Exploring Structures and Dynamics of Molecular Assemblies: Ultrafast Time-Resolved Electron Diffraction Measurements. ACC Chem. Res. 2020, 54, 731–743. [Google Scholar] [CrossRef]
- Zhu, Y.; Durr, H. The future of electron microscopy. Phys. Today 2015, 68, 32. [Google Scholar] [CrossRef] [Green Version]
- Ding, T.; Rebholz, M.; Aufleger, L.; Hartmann, M.; Meyer, K.; Stooß, V.; Magunia, A.; Wachs, D.; Birk, P.; Mi, Y.; et al. Nonlinear Coherence Effects in Transient-Absorption Ion Spectroscopy with Stochastic Extreme-Ultraviolet Free-Electron Laser Pulses. Phys. Rev. Lett. 2019, 123, 103001. [Google Scholar] [CrossRef] [Green Version]
- Qian, H.; Li, C.; Du, Y.; Yan, L.; Hua, J.; Huang, W.; Tang, C. Experimental investigation of thermal emittance components of copper photocathode. Phys. Rev. Spec. Top.-Accel. Beams 2012, 15, 040102. [Google Scholar] [CrossRef]
- Musumeci, P.; Navarro, J.G.; Rosenzweig, J.; Cultrera, L.; Bazarov, I.; Maxson, J.; Karkare, S.; Padmore, H. Advances in bright electron sources. Nucl. Instrum. Methods Phys. Res. A 2018, 907, 209–220. [Google Scholar] [CrossRef]
- Hernandez-Garcia, C.; O’Shea, P.G.; Stutzman, M.L. Electron sources for accelerators. Phys. Today 2008, 61, 44. [Google Scholar] [CrossRef] [Green Version]
- Schreiber, S.; Faatz, B. The free-electron laser FLASH. High Power Laser Sci. Eng. 2015, 3, e20. [Google Scholar] [CrossRef] [Green Version]
- Gaowei, M.; Sinsheimer, J.; Strom, D.; Xie, J.; Cen, J.; Walsh, J.; Muller, E.; Smedley, J. Codeposition of ultrasmooth and high quantum efficiency cesium telluride photocathodes. Phys. Rev. Accel. Beams 2019, 22, 073401. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, C.; Varma, B. Preparation and study of properties of a few alkali antimonide photocathodes. J. Appl. Phys. 1978, 49, 4549–4553. [Google Scholar] [CrossRef] [Green Version]
- Lyashenko, A.; Breskin, A.; Chechik, R.; Dias, T. Ion-induced secondary electron emission from K–Cs–Sb, Na–K–Sb, and Cs–Sb photocathodes and its relevance to the operation of gaseous avalanche photomultipliers. J. Appl. Phys. 2009, 106, 044902. [Google Scholar] [CrossRef]
- Schubert, S.; Ruiz-Osés, M.; Ben-Zvi, I.; Kamps, T.; Liang, X.; Muller, E.; Müller, K.; Padmore, H.; Rao, T.; Tong, X.; et al. Bi-alkali antimonide photocathodes for high brightness accelerators. APL Mater. 2013, 1, 032119. [Google Scholar] [CrossRef]
- Cultrera, L.; Karkare, S.; Lee, H.; Liu, X.; Bazarov, I.; Dunham, B. Cold electron beams from cryocooled, alkali antimonide photocathodes. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 113401. [Google Scholar] [CrossRef] [Green Version]
- Aryshev, A.; Shevelev, M.; Honda, Y.; Terunuma, N.; Urakawa, J. Femtosecond response time measurements of a Cs2Te photocathode. Appl. Phys. Lett. 2017, 111, 033508. [Google Scholar] [CrossRef] [Green Version]
- Mamun, M.; Hernandez-Flores, M.; Morales, E.; Hernandez-Garcia, C.; Poelker, M. Temperature dependence of alkali-antimonide photocathodes: Evaluation at cryogenic temperatures. Phys. Rev. Accel. Beams 2017, 20, 103403. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Kuriki, M.; Yokota, A.; Urano, M.; Negishi, K. Substrate dependence of CsK2Sb photo-cathode performance. Prog. Theor. Exp. Phys. 2017, 2017, 033G01. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, H.; Liu, F.; DeFazio, J.; Gaowei, M.; Narvaez Villarrubia, C.W.; Xie, J.; Sinsheimer, J.; Strom, D.; Pavlenko, V.; Jensen, K.L.; et al. Free-Standing Bialkali Photocathodes Using Atomically Thin Substrates. Adv. Mater. Interfaces 2018, 5, 1800249. [Google Scholar] [CrossRef] [Green Version]
- Schmeißer, M.A.; Mistry, S.; Kirschner, H.; Schubert, S.; Jankowiak, A.; Kamps, T.; Kühn, J. Towards the operation of Cs-K-Sb photocathodes in superconducting rf photoinjectors. Phys. Rev. Accel. Beams 2018, 21, 113401. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Ding, Y.; Ruan, C.; Xu, X.; Liu, H. High Photocurrent Density and Continuous Electron Emission Characterization of a Multi-Alkali Antimonide Photocathode. Electronics 2020, 9, 1991. [Google Scholar] [CrossRef]
- Wang, E.; Litvinenko, V.; Pinayev, I.; Gaowei, M.; Skaritka, J.; Belomestnykh, S.; Ben-Zvi, I.; Brutus, J.; Jing, Y.; Biswas, J.; et al. Long lifetime of bialkali photocathodes operating in high gradient superconducting radio frequency gun. Sci. Rep. 2021, 11, 4477. [Google Scholar] [CrossRef]
- Panuganti, H.; Chevallay, E.; Fedosseev, V.; Himmerlich, M. Synthesis, surface chemical analysis, lifetime studies and degradation mechanisms of Cs-K-Sb photocathodes. Nucl. Instrum. Methods Phys. Res. A 2021, 986, 164724. [Google Scholar] [CrossRef]
- Di Bona, A.; Sabary, F.; Joly, S.; Michelato, P.; Sertore, D.; Pagani, C.; Valeri, S. Development, operation and analysis of bialkali antimonide photocathodes for high-brightness photo-injectors. Nucl. Instrum. Methods Phys. Res. A 1997, 385, 385–390. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Qian, Y.; Feng, C.; Zhang, J.; Jiang, Y.; Pan, Z. Spectral response characteristics of transmission-mode alkali telluride photocathodes working from vacuum-ultraviolet to ultraviolet band. J. Vac. Sci. Technol. B 2017, 35, 061202. [Google Scholar] [CrossRef]
- Ding, Z.; Karkare, S.; Feng, J.; Filippetto, D.; Johnson, M.; Virostek, S.; Sannibale, F.; Nasiatka, J.; Gaowei, M.; Sinsheimer, J.; et al. Temperature-dependent quantum efficiency degradation of K-Cs-Sb bialkali antimonide photocathodes grown by a triple-element codeposition method. Phys. Rev. Accel. Beams 2017, 20, 113401. [Google Scholar] [CrossRef] [Green Version]
- Yusof, Z.; Denchfield, A.; Warren, M.; Cardenas, J.; Samuelson, N.; Spentzouris, L.; Power, J.; Zasadzinski, J. Photocathode quantum efficiency of ultrathin Cs2Te layers on Nb substrates. Phys. Rev. Accel. Beams 2017, 20, 123401. [Google Scholar] [CrossRef] [Green Version]
- Michelato, P. Photocathodes for RF photoinjectors. Nucl. Instrum. Methods Phys. Res. A 1997, 393, 455–459. [Google Scholar] [CrossRef]
- Pavlenko, V.; Liu, F.; Hoffbauer, M.A.; Moody, N.A.; Batista, E.R. Kinetics of alkali-based photocathode degradation. AIP Adv. 2016, 6, 115008. [Google Scholar] [CrossRef] [Green Version]
- Schubert, S.; Wong, J.; Feng, J.; Karkare, S.; Padmore, H.; Ruiz-Osés, M.; Smedley, J.; Muller, E.; Ding, Z.; Gaowei, M.; et al. Bi-alkali antimonide photocathode growth: An X-ray diffraction study. J. Appl. Phys. 2016, 120, 035303. [Google Scholar] [CrossRef]
- Feng, J.; Karkare, S.; Nasiatka, J.; Schubert, S.; Smedley, J.; Padmore, H. Near atomically smooth alkali antimonide photocathode thin films. J. Appl. Phys. 2017, 121, 044904. [Google Scholar] [CrossRef]
- Gaowei, M.; Ding, Z.; Schubert, S.; Bhandari, H.; Sinsheimer, J.; Kuehn, J.; Nagarkar, V.; Marshall, M.; Walsh, J.; Muller, E.; et al. Synthesis and X-ray characterization of sputtered bi-alkali antimonide photocathodes. APL Mater. 2017, 5, 116104. [Google Scholar] [CrossRef]
- Gevorkyan, G.; Karkare, S.; Emamian, S.; Bazarov, I.; Padmore, H. Effects of physical and chemical surface roughness on the brightness of electron beams from photocathodes. Phys. Rev. Accel. Beams 2018, 21, 093401. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Demarteau, M.; Wagner, R.; Schubert, S.; Gaowei, M.; Attenkofer, K.; Walsh, J.; Smedley, J.; Wong, J.; Feng, J.; et al. Synchrotron X-ray study of a low roughness and high efficiency K2CsSb photocathode during film growth. J. Phys. D 2017, 50, 205303. [Google Scholar] [CrossRef] [Green Version]
- Galdi, A.; Balajka, J.; DeBenedetti, W.J.I.; Cultrera, L.; Bazarov, I.V.; Hines, M.A.; Maxson, J.M. Reduction of surface roughness emittance of Cs3Sb photocathodes grown via codeposition on single crystal substrates. Appl. Phys. Lett. 2021, 118, 244101. [Google Scholar] [CrossRef]
- Vecchione, T.; Ben-Zvi, I.; Dowell, D.; Feng, J.; Rao, T.; Smedley, J.; Wan, W.; Padmore, H. A low emittance and high efficiency visible light photocathode for high brightness accelerator-based X-ray light sources. Appl. Phys. Lett. 2011, 99, 034103. [Google Scholar] [CrossRef]
- Ding, Z.; Gaowei, M.; Sinsheimer, J.; Xie, J.; Schubert, S.; Padmore, H.; Muller, E.; Smedley, J. In-situ synchrotron X-ray characterization of K2CsSb photocathode grown by ternary co-evaporation. J. Appl. Phys. 2017, 121, 055305. [Google Scholar] [CrossRef]
- Kane, E.O. Theory of photoelectric emission from semiconductors. Phys. Rev. 1962, 127, 131. [Google Scholar] [CrossRef]
- Berglund, C.N.; Spicer, W.E. Photoemission studies of copper and silver: Theory. Phys. Rev. 1964, 136, A1030. [Google Scholar] [CrossRef]
- Spicer, W.E. Photoemissive, Photoconductive, and Optical Absorption Studies of Alkali-Antimony Compounds. Phys. Rev. 1958, 112, 114–122. [Google Scholar] [CrossRef]
- Powell, R.A.; Spicer, W.E.; Fisher, G.B.; Gregory, P. Photoemission Studies of Cesium Telluride. Phys. Rev. B 1973, 8, 3987–3995. [Google Scholar] [CrossRef]
- Yu, L.; Wan, W.; Tang, W.X.; Feng, J. Systematic analysis of a compact setup to measure the photoemitted electron beam transverse momentum and emittance. Rev. Sci. Instrum. 2021, 92, 013302. [Google Scholar] [CrossRef]
- Jensen, K.L.; Jensen, B.L.; Montgomery, E.J.; Feldman, D.W.; O’Shea, P.G.; Moody, N. Theory of photoemission from cesium antimonide using an alpha-semiconductor model. J. Appl. Phys. 2008, 104, 044907. [Google Scholar] [CrossRef] [Green Version]
- Jensen, K.L.; Shabaev, A.; Lambrakos, S.G.; Finkenstadt, D.; Petillo, J.J.; Alexander, A.M.; Smedley, J.; Moody, N.A.; Yamaguchi, H.; Liu, F.; et al. An extended moments model of quantum efficiency for metals and semiconductors. J. Appl. Phys. 2020, 128, 015301. [Google Scholar] [CrossRef]
- Karkare, S.; Dimitrov, D.; Schaff, W.; Cultrera, L.; Bartnik, A.; Liu, X.; Sawyer, E.; Esposito, T.; Bazarov, I. Monte Carlo charge transport and photoemission from negative electron affinity GaAs photocathodes. J. Appl. Phys. 2013, 113, 104904. [Google Scholar] [CrossRef]
- Gupta, P.; Cultrera, L.; Bazarov, I. Monte Carlo simulations of electron photoemission from cesium antimonide. J. Appl. Phys. 2017, 121, 215702. [Google Scholar] [CrossRef]
- Dimitrov, D.; Bell, G.; Smedley, J.; Ben-Zvi, I.; Feng, J.; Karkare, S.; Padmore, H. Modeling quantum yield, emittance, and surface roughness effects from metallic photocathodes. J. Appl. Phys. 2017, 122, 165303. [Google Scholar] [CrossRef]
- Antoniuk, E.R.; Yue, Y.; Zhou, Y.; Schindler, P.; Schroeder, W.A.; Dunham, B.; Pianetta, P.; Vecchione, T.; Reed, E.J. Generalizable density functional theory based photoemission model for the accelerated development of photocathodes and other photoemissive devices. Phys. Rev. B 2020, 101, 235447. [Google Scholar] [CrossRef]
- Marzari, N.; Ferretti, A.; Wolverton, C. Electronic-structure methods for materials design. Nat. Mater. 2021, 20, 736–749. [Google Scholar] [CrossRef]
- Louie, S.G.; Chan, Y.H.; Felipe, H.; Li, Z.; Qiu, D.Y. Discovering and understanding materials through computation. Nat. Mater. 2021, 20, 728–735. [Google Scholar] [CrossRef]
- Peeters, E.; Mackie, C.; Candian, A.; Tielens, A.G. A Spectroscopic View on Cosmic PAH Emission. Acc. Chem. Res. 2021, 54, 1921–1933. [Google Scholar] [CrossRef] [PubMed]
- Konold, P.E.; Arik, E.; Weißenborn, J.; Arents, J.C.; Hellingwerf, K.J.; van Stokkum, I.H.; Kennis, J.T.; Groot, M.L. Confinement in crystal lattice alters entire photocycle pathway of the Photoactive Yellow Protein. Nat. Commun. 2020, 11, 4248. [Google Scholar] [CrossRef] [PubMed]
- Drexler, A.; He, S.; Razumovskiy, V.; Romaner, L.; Ecker, W.; Pippan, R. Verification of the generalised chemical potential for stress-driven hydrogen diffusion in nickel. Philos. Mag. Lett. 2020, 100, 513–523. [Google Scholar] [CrossRef]
- Fortino, M.; Berselli, A.; Stone-Weiss, N.; Deng, L.; Goel, A.; Du, J.; Pedone, A. Assessment of interatomic parameters for the reproduction of borosilicate glass structures via DFT-GIPAW calculations. J. Am. Ceram. Soc. 2019, 102, 7225–7243. [Google Scholar] [CrossRef]
- Guerra, C.F.; Snijders, J.; te Velde, G.T.; Baerends, E.J. Towards an order-N DFT method. Theor. Chem. Acta 1998, 99, 391–403. [Google Scholar]
- Shimojo, F.; Kalia, R.K.; Nakano, A.; Vashishta, P. Linear-scaling density-functional-theory calculations of electronic structure based on real-space grids: Design, analysis, and scalability test of parallel algorithms. Comput. Phys. Commun. 2001, 140, 303–314. [Google Scholar] [CrossRef]
- Li, T.; Rickman, B.L.; Schroeder, W.A. Density functional theory analysis of hexagonal close-packed elemental metal photocathodes. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 073401. [Google Scholar] [CrossRef] [Green Version]
- Camino, B.; Noakes, T.; Surman, M.; Seddon, E.; Harrison, N. Photoemission simulation for photocathode design: Theory and application to copper and silver surfaces. Comp. Mater. Sci. 2016, 122, 331–340. [Google Scholar] [CrossRef]
- Napier, I.; Chang, V.; Noakes, T.; Harrison, N. From Electronic Structure to Design Principles for Photocathodes: Cu–Ba Alloys. Phys. Rev. Appl. 2019, 11, 064061. [Google Scholar] [CrossRef]
- Ettema, A. Li2CsSb: A highly-efficient photocathode material. Appl. Phys. Lett. 2003, 82, 3988–3990. [Google Scholar] [CrossRef]
- Kalarasse, L.; Bennecer, B.; Kalarasse, F. Optical properties of the alkali antimonide semiconductors Cs3Sb, Cs2KSb, CsK2Sb and K3Sb. J. Phys. Chem. Solids 2010, 71, 314–322. [Google Scholar] [CrossRef]
- Kalarasse, L.; Bennecer, B.; Kalarasse, F.; Djeroud, S. Pressure effect on the electronic and optical properties of the alkali antimonide semiconductors Cs3Sb, KCs2Sb, CsK2Sb and K3Sb: Ab initio study. J. Phys. Chem. Solids 2010, 71, 1732–1741. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, L.; Dong, Y.; Zhang, S.; Xu, S.; Qian, Y. Density functional theory studies on Cs activation mechanism between GaN (0001) and Al0.25Ga0.75N (0001) surface. J. Vac. Sci. Technol. B 2015, 33, 051214. [Google Scholar] [CrossRef]
- Murtaza, G.; Ullah, M.; Ullah, N.; Rani, M.; Muzammil, M.; Khenata, R.; Ramay, S.M.; Khan, U. Structural, elastic, electronic and optical properties of bi-alkali antimonides. Bull. Mater. Sci. 2016, 39, 1581–1591. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Pandey, R.; Moody, N.A.; Batista, E.R. Degradation of alkali-based photocathodes from exposure to residual gases: A first-principles study. J. Phys. Chem. C 2017, 121, 8399–8408. [Google Scholar] [CrossRef]
- Wang, G.; Yang, P.; Moody, N.A.; Batista, E.R. Overcoming the quantum efficiency-lifetime tradeoff of photocathodes by coating with atomically thin two-dimensional nanomaterials. NPJ 2D Mater. Appl. 2018, 2, 17. [Google Scholar] [CrossRef]
- Cocchi, C.; Mistry, S.; Schmeißer, M.; Kühn, J.; Kamps, T. First-principles many-body study of the electronic and optical properties of CsK2Sb, a semiconducting material for ultra-bright electron sources. J. Phys. Condens. Matter 2018, 31, 014002. [Google Scholar] [CrossRef] [PubMed]
- Cocchi, C.; Mistry, S.; Schmeißer, M.; Amador, R.; Kühn, J.; Kamps, T. Electronic structure and core electron fingerprints of caesium-based multi-alkali antimonides for ultra-bright electron sources. Sci. Rep. 2019, 9, 18276. [Google Scholar] [CrossRef] [PubMed]
- Cocchi, C. X-ray Absorption Fingerprints from Cs Atoms in Cs3Sb. Phys. Status Solidi (RRL) 2020, 14, 2000194. [Google Scholar] [CrossRef]
- Khan, Z.; Murtaza, G.; Khan, A.A.; Laref, A.; Kattan, N.A.; Haneef, M. Different physical properties of bi-alkali pnictogen compounds using density functional theory. Int. J. Energy Res. 2021, 45, 7703–7718. [Google Scholar] [CrossRef]
- Zhong, Q.; Dai, Z.; Wang, W.; Zhao, Y.; Meng, S. Quartic anharmonicity and ultra-low lattice thermal conductivity of alkali antimonide compounds M3Sb (M = K, Rb and Cs). Int. J. Energy Res. 2021, 45, 6958–6965. [Google Scholar] [CrossRef]
- Saßnick, H.D.; Cocchi, C. Electronic structure of cesium-based photocathode materials from density functional theory: Performance of PBE, SCAN, and HSE06 functionals. Electr. Struct. 2021, 3, 027001. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneus Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W. Nobel Lecture: Electronic structure of matter—Wave functions and density functionals. Rev. Mod. Phys. 1999, 71, 1253. [Google Scholar] [CrossRef] [Green Version]
- Stowasser, R.; Hoffmann, R. What do the Kohn–Sham orbitals and eigenvalues mean? J. Am. Chem. Soc. 1999, 121, 3414–3420. [Google Scholar] [CrossRef]
- Baerends, E.; Gritsenko, O.; Van Meer, R. The Kohn–Sham gap, the fundamental gap and the optical gap: The physical meaning of occupied and virtual Kohn–Sham orbital energies. Phys. Chem. Chem. Phys. 2013, 15, 16408–16425. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tran, F.; Blaha, P. Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Xiao, B. Crystal structures, optical properties, and effective mass tensors of CH3NH3PbX3 (X = I and Br) phases predicted from HSE06. J. Phys. Chem. Lett. 2014, 5, 1278–1282. [Google Scholar] [CrossRef] [PubMed]
- Kitchaev, D.A.; Peng, H.; Liu, Y.; Sun, J.; Perdew, J.P.; Ceder, G. Energetics of MnO2 polymorphs in density functional theory. Phys. Rev. B 2016, 93, 045132. [Google Scholar] [CrossRef] [Green Version]
- Buda, I.G.; Lane, C.; Barbiellini, B.; Ruzsinszky, A.; Sun, J.; Bansil, A. Characterization of thin film materials using SCAN meta-GGA, an accurate nonempirical density functional. Sci. Rep. 2017, 7, 44766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chakraborty, A.; Dixit, M.; Aurbach, D.; Major, D.T. Predicting accurate cathode properties of layered oxide materials using the SCAN meta-GGA density functional. NPJ Comput. Mater. 2018, 4, 60. [Google Scholar] [CrossRef]
- Li, W.; Sabino, F.P.; de Lima, F.C.; Wang, T.; Miwa, R.H.; Janotti, A. Large disparity between optical and fundamental band gaps in layered In 2Se3. Phys. Rev. B 2018, 98, 165134. [Google Scholar] [CrossRef] [Green Version]
- Patra, A.; Patra, B.; Constantin, L.A.; Samal, P. Electronic band structure of layers within meta generalized gradient approximation of density functionals. Phys. Rev. B 2020, 102, 045135. [Google Scholar] [CrossRef]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601. [Google Scholar] [CrossRef] [Green Version]
- Hedin, L. New method for calculating the one-particle Green’s function with application to the electron gas problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Hanke, W.; Sham, L.J. Many-particle effects in the optical spectrum of a semiconductor. Phys. Rev. B 1980, 21, 4656–4673. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. First-principles theory of quasiparticles: Calculation of band gaps in semiconductors and insulators. Phys. Rev. Lett. 1985, 55, 1418. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 1986, 34, 5390–5413. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237. [Google Scholar] [CrossRef] [Green Version]
- Salpeter, E.E.; Bethe, H.A. A relativistic equation for bound-state problems. Phys. Rev. 1951, 84, 1232. [Google Scholar] [CrossRef]
- Strinati, G. Application of the Green’s Functions Method to the Study of the Optical Properties of Semiconductors. Riv. Nuovo Cim. 1988, 11, 1–86. [Google Scholar] [CrossRef]
- Laskowski, R.; Blaha, P. Understanding the L2,3 X-ray absorption spectra of early 3d transition elements. Phys. Rev. B 2010, 82, 205104. [Google Scholar] [CrossRef]
- Vorwerk, C.; Cocchi, C.; Draxl, C. Addressing electron-hole correlation in core excitations of solids: An all-electron many-body approach from first principles. Phys. Rev. B 2017, 95, 155121. [Google Scholar] [CrossRef] [Green Version]
- Vorwerk, C.; Aurich, B.; Cocchi, C.; Draxl, C. Bethe–Salpeter equation for absorption and scattering spectroscopy: Implementation in the exciting code. Electr. Struct. 2019, 1, 037001. [Google Scholar] [CrossRef]
- Olovsson, W.; Tanaka, I.; Mizoguchi, T.; Puschnig, P.; Ambrosch-Draxl, C. All-electron Bethe-Salpeter calculations for shallow-core X-ray absorption near-edge structures. Phys. Rev. B 2009, 79, 041102. [Google Scholar] [CrossRef] [Green Version]
- Olovsson, W.; Tanaka, I.; Puschnig, P.; Ambrosch-Draxl, C. Near-edge structures from first principles all-electron Bethe–Salpeter equation calculations. J. Phys. Condens. Matter 2009, 21, 104205. [Google Scholar] [CrossRef]
- Olovsson, W.; Tanaka, I.; Mizoguchi, T.; Radtke, G.; Puschnig, P.; Ambrosch-Draxl, C. Al L2,3 edge X-ray absorption spectra in III–V semiconductors: Many-body perturbation theory in comparison with experiment. Phys. Rev. B 2011, 83, 195206. [Google Scholar] [CrossRef] [Green Version]
- Olovsson, W.; Weinhardt, L.; Fuchs, O.; Tanaka, I.; Puschnig, P.; Umbach, E.; Heske, C.; Draxl, C. The Be K-edge in beryllium oxide and chalcogenides: Soft X-ray absorption spectra from first-principles theory and experiment. J. Phys. Condens. Matter 2013, 25, 315501. [Google Scholar] [CrossRef] [Green Version]
- Cocchi, C.; Draxl, C. Bound excitons and many-body effects in X-ray absorption spectra of azobenzene-functionalized self-assembled monolayers. Phys. Rev. B 2015, 92, 205105. [Google Scholar] [CrossRef] [Green Version]
- Cocchi, C.; Zschiesche, H.; Nabok, D.; Mogilatenko, A.; Albrecht, M.; Galazka, Z.; Kirmse, H.; Draxl, C.; Koch, C.T. Atomic signatures of local environment from core-level spectroscopy in β-Ga2O3. Phys. Rev. B 2016, 94, 075147. [Google Scholar] [CrossRef] [Green Version]
- Vorwerk, C.; Hartmann, C.; Cocchi, C.; Sadoughi, G.; Habisreutinger, S.N.; Félix, R.; Wilks, R.G.; Snaith, H.J.; Bär, M.; Draxl, C. Exciton-Dominated Core-Level Absorption Spectra of Hybrid Organic-Inorganic Lead Halide Perovskites. J. Phys. Chem. Lett. 2018, 9, 1852–1858. [Google Scholar] [CrossRef] [Green Version]
- Rohlfing, M.; Louie, S.G. Electron-hole excitations and optical spectra from first principles. Phys. Rev. B 2000, 62, 4927–4944. [Google Scholar] [CrossRef]
- Wiser, N. Dielectric constant with local field effects included. Phys. Rev. 1963, 129, 62. [Google Scholar] [CrossRef]
- Aspnes, D. Local-field effects and effective-medium theory: A microscopic perspective. Am. J. Phys. 1982, 50, 704–709. [Google Scholar] [CrossRef]
- Genovese, L.; Videau, B.; Ospici, M.; Deutsch, T.; Goedecker, S.; Méhaut, J.F. Daubechies wavelets for high performance electronic structure calculations: The BigDFT project. Comptes Rendus Mécanique 2011, 339, 149–164. [Google Scholar] [CrossRef]
- Andrade, X.; Strubbe, D.; De Giovannini, U.; Larsen, A.H.; Oliveira, M.J.T.; Alberdi-Rodriguez, J.; Varas, A.; Theophilou, I.; Helbig, N.; Verstraete, M.J.; et al. Real-space grids and the Octopus code as tools for the development of new simulation approaches for electronic systems. Phys. Chem. Chem. Phys. 2015, 17, 31371–31396. [Google Scholar] [CrossRef] [Green Version]
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys 2020, 152, 194103. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef] [Green Version]
- Gulans, A.; Kontur, S.; Meisenbichler, C.; Nabok, D.; Pavone, P.; Rigamonti, S.; Sagmeister, S.; Werner, U.; Draxl, C. Exciting: A full-potential all-electron package implementing density-functional theory and many-body perturbation theory. J. Phys. Condens. Matter 2014, 26, 363202. [Google Scholar] [CrossRef] [PubMed]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.; Marks, L.D. WIEN2k: An APW+ lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Govoni, M.; Galli, G. Large scale GW calculations. J. Chem. Theory Comput. 2015, 11, 2680–2696. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sangalli, D.; Ferretti, A.; Miranda, H.; Attaccalite, C.; Marri, I.; Cannuccia, E.; Melo, P.; Marsili, M.; Paleari, F.; Marrazzo, A.; et al. Many-body perturbation theory calculations using the yambo code. J. Phys. Condens. Matter 2019, 31, 325902. [Google Scholar] [CrossRef] [PubMed]
- Del Ben, M.; Yang, C.; Li, Z.; Felipe, H.; Louie, S.; Deslippe, J. Accelerating large-scale excited-state GW calculations on leadership HPC systems. In Proceedings of the 2020 International Conference for High Performance Computing, Networking, Storage and Analysis (SC20), Atlanta, GA, USA, 9–19 November 2020; pp. 36–46. [Google Scholar]
- Ettema, A.; De Groot, R. Bandstructure calculations of the hexagonal and cubic phases of K3Sb. J. Phys. Condens. Matter 1999, 11, 759. [Google Scholar] [CrossRef]
- Ettema, A.; de Groot, R. Electronic structure of Cs2KSb and K2CsSb. Phys. Rev. B 2002, 66, 115102. [Google Scholar] [CrossRef]
- Guo, S.D. Electronic structures and elastic properties of X3Sb (X = Li, K, Cs) from the first-principles calculations. Mater. Res. Express 2014, 1, 015906. [Google Scholar] [CrossRef]
- Jack, K.H.; Wachtel, M. The characterization and crystal structure of caesium antimonide, a photo-electric surface material. Proc. R. Soc. Lond. A 1957, 239, 46–60. [Google Scholar]
- Wei, S.H.; Zunger, A. Electronic structure of M3I Sb-type filled tetrahedral semiconductors. Phys. Rev. B 1987, 35, 3952. [Google Scholar] [CrossRef]
- Kokalj, A. XCrySDen—A new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 1999, 17, 176–179. [Google Scholar] [CrossRef]
- Amador, R.; Saßnick, H.D.; Cocchi, C. Electronic structure and optical properties of Na2KSb and NaK2Sb from first-principles many-body theory. J. Phys. Condens. Matter 2021, 33, 365502. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Kim, B.; Chen, X.Q.; Sarma, D.; Kresse, G.; Franchini, C. Relativistic GW + BSE study of the optical properties of Ruddlesden-Popper iridates. Phys. Rev. Mater. 2018, 2, 075003. [Google Scholar] [CrossRef] [Green Version]
- Laskowski, R.; Christensen, N.E.; Santi, G.; Ambrosch-Draxl, C. Ab initio calculations of excitons in GaN. Phys. Rev. B 2005, 72, 035204. [Google Scholar] [CrossRef]
- Schleife, A.; Rödl, C.; Fuchs, F.; Furthmüller, J.; Bechstedt, F. Optical and energy-loss spectra of MgO, ZnO, and CdO from ab initio many-body calculations. Phys. Rev. B 2009, 80, 035112. [Google Scholar] [CrossRef] [Green Version]
- Arnaud, B.; Lebègue, S.; Rabiller, P.; Alouani, M. Huge Excitonic Effects in Layered Hexagonal Boron Nitride. Phys. Rev. Lett. 2006, 96, 026402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aggoune, W.; Cocchi, C.; Nabok, D.; Rezouali, K.; Belkhir, M.A.; Draxl, C. Dimensionality of excitons in stacked van der Waals materials: The example of hexagonal boron nitride. Phys. Rev. B 2018, 97, 241114. [Google Scholar] [CrossRef] [Green Version]
- Cocchi, C.; Moldt, T.; Gahl, C.; Weinelt, M.; Draxl, C. Optical properties of azobenzene-functionalized self-assembled monolayers: Intermolecular coupling and many-body interactions. J. Chem. Phys. 2016, 145, 234701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swallow, J.E.N.; Vorwerk, C.; Mazzolini, P.; Vogt, P.; Bierwagen, O.; Karg, A.; Eickhoff, M.; Schörmann, J.; Wagner, M.R.; Roberts, J.W.; et al. Influence of Polymorphism on the Electronic Structure of Ga2O3. Chem. Mater. 2020, 32, 8460–8470. [Google Scholar] [CrossRef]
- Curtarolo, S.; Setyawan, W.; Hart, G.L.; Jahnatek, M.; Chepulskii, R.V.; Taylor, R.H.; Wang, S.; Xue, J.; Yang, K.; Levy, O.; et al. AFLOW: An automatic framework for high-throughput materials discovery. Comp. Mater. Sci. 2012, 58, 218–226. [Google Scholar] [CrossRef] [Green Version]
- Pizzi, G.; Cepellotti, A.; Sabatini, R.; Marzari, N.; Kozinsky, B. AiiDA: Automated interactive infrastructure and database for computational science. Comp. Mater. Sci. 2016, 111, 218–230. [Google Scholar] [CrossRef] [Green Version]
- Mathew, K.; Montoya, J.H.; Faghaninia, A.; Dwarakanath, S.; Aykol, M.; Tang, H.; Heng Chu, I.; Smidt, T.; Bocklund, B.; Horton, M.; et al. Atomate: A high-level interface to generate, execute, and analyze computational materials science workflows. Comp. Mater. Sci. 2017, 139, 140–152. [Google Scholar] [CrossRef] [Green Version]
- Curtarolo, S.; Setyawan, W.; Wang, S.; Xue, J.; Yang, K.; Taylor, R.H.; Nelson, L.J.; Hart, G.L.; Sanvito, S.; Buongiorno-Nardelli, M.; et al. AFLOWLIB.ORG: A distributed materials properties repository from high-throughput ab initio calculations. Comp. Mater. Sci. 2012, 58, 227–235. [Google Scholar] [CrossRef] [Green Version]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Draxl, C.; Scheffler, M. The NOMAD laboratory: From data sharing to artificial intelligence. J. Phys. Mater. 2019, 2, 036001. [Google Scholar] [CrossRef]
- Talirz, L.; Kumbhar, S.; Passaro, E.; Yakutovich, A.V.; Granata, V.; Gargiulo, F.; Borelli, M.; Uhrin, M.; Huber, S.P.; Zoupanos, S.; et al. Materials Cloud, a platform for open computational science. Sci. Data 2020, 7, 299. [Google Scholar] [CrossRef] [PubMed]
- Qu, X.; Jain, A.; Rajput, N.N.; Cheng, L.; Zhang, Y.; Ong, S.P.; Brafman, M.; Maginn, E.; Curtiss, L.A.; Persson, K.A. The Electrolyte Genome project: A big data approach in battery materials discovery. Comp. Mater. Sci. 2015, 103, 56–67. [Google Scholar] [CrossRef] [Green Version]
- Körbel, S.; Marques, M.A.L.; Botti, S. Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations. J. Mater. Chem. C 2016, 4, 3157–3167. [Google Scholar] [CrossRef]
- Emery, A.A.; Wolverton, C. High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites. Sci. Data 2017, 4, 170153. [Google Scholar] [CrossRef] [Green Version]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. NPJ Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, J.; Shi, J.; Borlido, P.; Chen, L.; Botti, S.; Marques, M.A.L. Predicting the Thermodynamic Stability of Solids Combining Density Functional Theory and Machine Learning. Chem. Mater. 2017, 29, 5090–5103. [Google Scholar] [CrossRef]
- Oganov, A.R.; Valle, M. How to quantify energy landscapes of solids. J. Chem. Phys. 2009, 130, 104504. [Google Scholar] [CrossRef] [PubMed]
- Bergerhoff, G.; Hundt, R.; Sievers, R.; Brown, I.D. The inorganic crystal structure data base. J. Chem. Inform. Comput. Sci. 1983, 23, 66–69. [Google Scholar] [CrossRef]
- Zagorac, D.; Müller, H.; Ruehl, S.; Zagorac, J.; Rehme, S. Recent developments in the Inorganic Crystal Structure Database: Theoretical crystal structure data and related features. J. Appl. Crystallogr. 2019, 52, 918–925. [Google Scholar] [CrossRef] [Green Version]
- Togo, A.; Tanaka, I. Spglib: A software library for crystal symmetry search. arXiv 2018, arXiv:1808.01590. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Wang, A.; Kingsbury, R.; McDermott, M.; Horton, M.; Jain, A.; Ong, S.P.; Dwaraknath, S.; Persson, K.A. A framework for quantifying uncertainty in DFT energy corrections. Sci. Rep. 2021, 11, 15496. [Google Scholar] [CrossRef]
- Zhang, Y.; Kitchaev, D.A.; Yang, J.; Chen, T.; Dacek, S.T.; Sarmiento-Pérez, R.A.; Marques, M.A.L.; Peng, H.; Ceder, G.; Perdew, J.P.; et al. Efficient first-principles prediction of solid stability: Towards chemical accuracy. NPJ Comput. Mater. 2018, 4, 9. [Google Scholar] [CrossRef]
- Yang, J.H.; Kitchaev, D.A.; Ceder, G. Rationalizing accurate structure prediction in the meta-GGA SCAN functional. Phys. Rev. B 2019, 100, 035132. [Google Scholar] [CrossRef] [Green Version]
- Cultrera, L.; Bazarov, I.; Bartnik, A.; Dunham, B.; Karkare, S.; Merluzzi, R.; Nichols, M. Thermal emittance and response time of a cesium antimonide photocathode. Appl. Phys. Lett. 2011, 99, 152110. [Google Scholar] [CrossRef] [Green Version]
- Huhn, W.P.; Blum, V. One-hundred-three compound band-structure benchmark of post-self-consistent spin-orbit coupling treatments in density functional theory. Phys. Rev. Mater. 2017, 1, 033803. [Google Scholar] [CrossRef] [Green Version]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hutter, J. GTH. 2021. Available online: https://github.com/juerghutter/GTH/tree/master/SCAN (accessed on 24 August 2021).
- Huber, S.P.; Zoupanos, S.; Uhrin, M.; Talirz, L.; Kahle, L.; Häuselmann, R.; Gresch, D.; Müller, T.; Yakutovich, A.V.; Andersen, C.W.; et al. AiiDA 1.0, a scalable computational infrastructure for automated reproducible workflows and data provenance. Sci. Data 2020, 7, 300. [Google Scholar] [CrossRef] [PubMed]
- Uhrin, M.; Huber, S.P.; Yu, J.; Marzari, N.; Pizzi, G. Workflows in AiiDA: Engineering a high-throughput, event-based engine for robust and modular computational workflows. Comp. Mater. Sci. 2021, 187, 110086. [Google Scholar] [CrossRef]
- aiida-cp2k. 2021. Available online: https://github.com/aiidateam/aiida-cp2k (accessed on 24 August 2021).

| PBE | SCAN | SCAN + SOC | PBE | BSE | Exp. | |
|---|---|---|---|---|---|---|
| CsSb | ||||||
| 0.65 | 1.21 | 1.06 | 1.19 | |||
| (k-point) | 1.02 () | 1.46 (X) | 1.31 (X) | 1.53 () | 1.44 () | 1.6 [38] |
| CsKSb | ||||||
| 0.88 | 1.57 | 1.38 | 1.62 | |||
| (k-point) | 0.88 () | 1.57 () | 1.38 () | 1.62 () | 1.50 () | 1.2 [10] |
| CsTe | ||||||
| 1.76 | 2.26 | 2.06 | 2.45 | |||
| (k-point) | 1.76 () | 2.26 () | 2.06 () | 2.45 () | 1.60 () | 3.3 [39] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cocchi, C.; Saßnick, H.-D. Ab Initio Quantum-Mechanical Predictions of Semiconducting Photocathode Materials. Micromachines 2021, 12, 1002. https://doi.org/10.3390/mi12091002
Cocchi C, Saßnick H-D. Ab Initio Quantum-Mechanical Predictions of Semiconducting Photocathode Materials. Micromachines. 2021; 12(9):1002. https://doi.org/10.3390/mi12091002
Chicago/Turabian StyleCocchi, Caterina, and Holger-Dietrich Saßnick. 2021. "Ab Initio Quantum-Mechanical Predictions of Semiconducting Photocathode Materials" Micromachines 12, no. 9: 1002. https://doi.org/10.3390/mi12091002
APA StyleCocchi, C., & Saßnick, H.-D. (2021). Ab Initio Quantum-Mechanical Predictions of Semiconducting Photocathode Materials. Micromachines, 12(9), 1002. https://doi.org/10.3390/mi12091002






