An Improved Difference Temperature Compensation Method for MEMS Resonant Accelerometers
Abstract
:1. Introduction
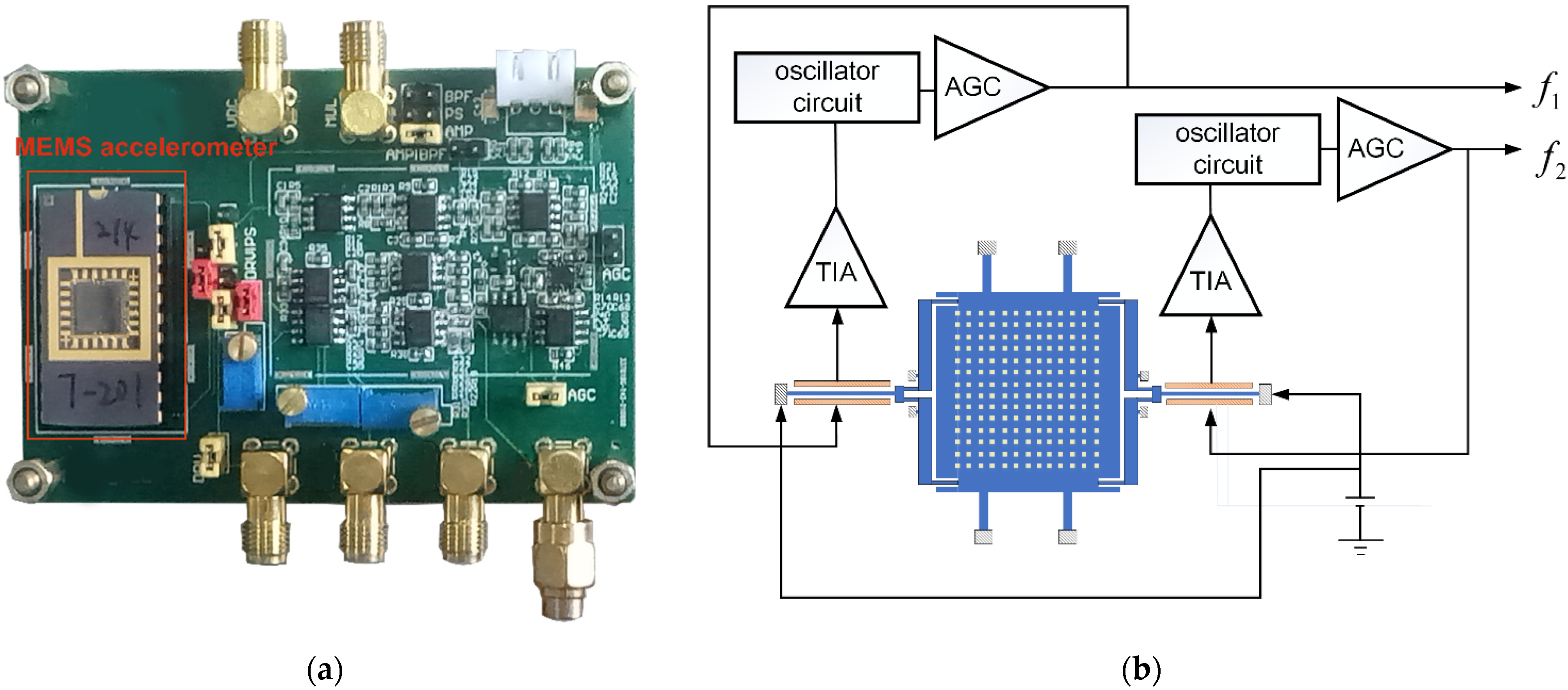
2. Architecture and Temperature Sensitivity Analysis of the Sensor
3. Temperature Compensation
3.1. Temperature Model of Sensor and Method for Temperature Compensation
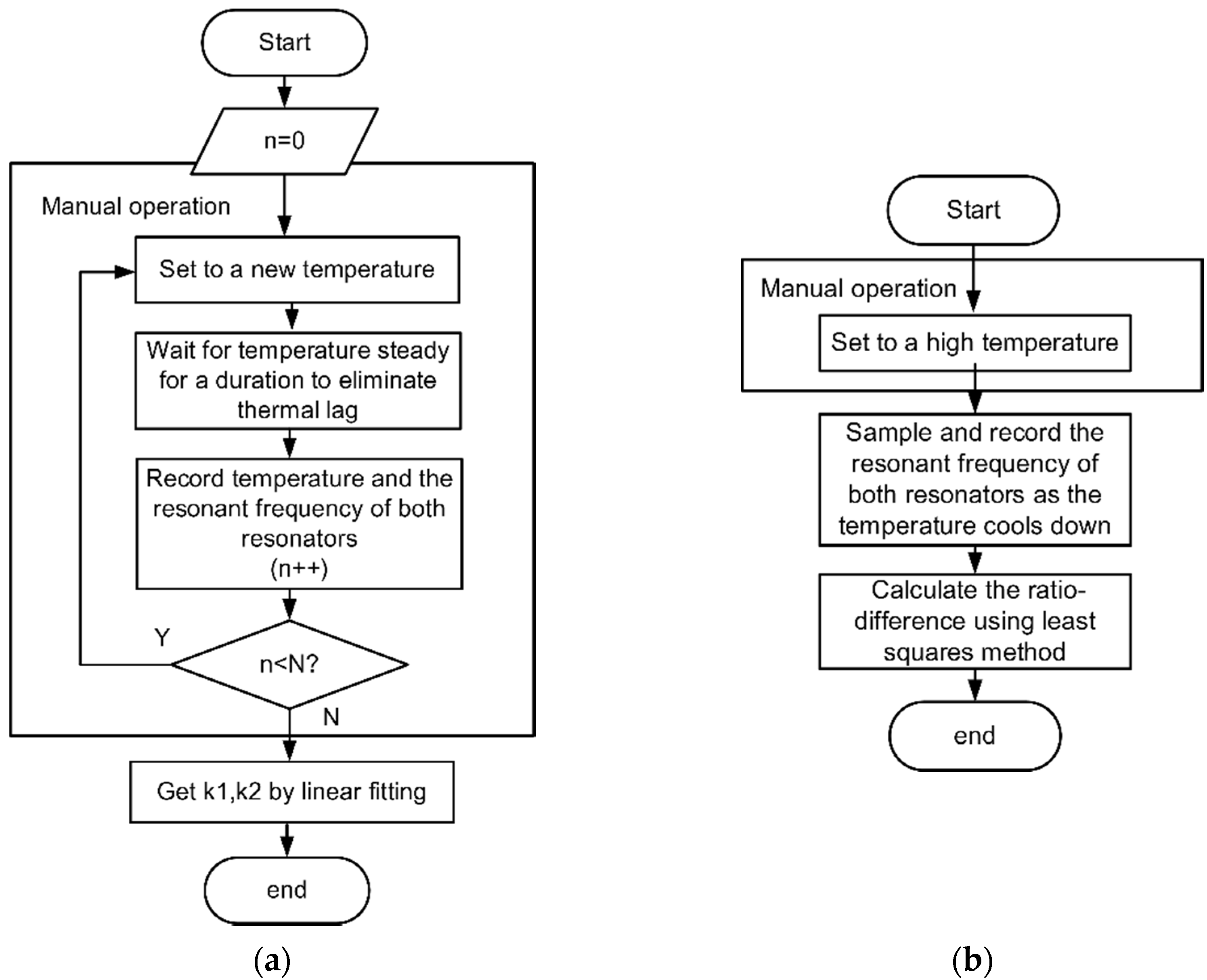
3.2. Calibration of Temperature Difference Ratio
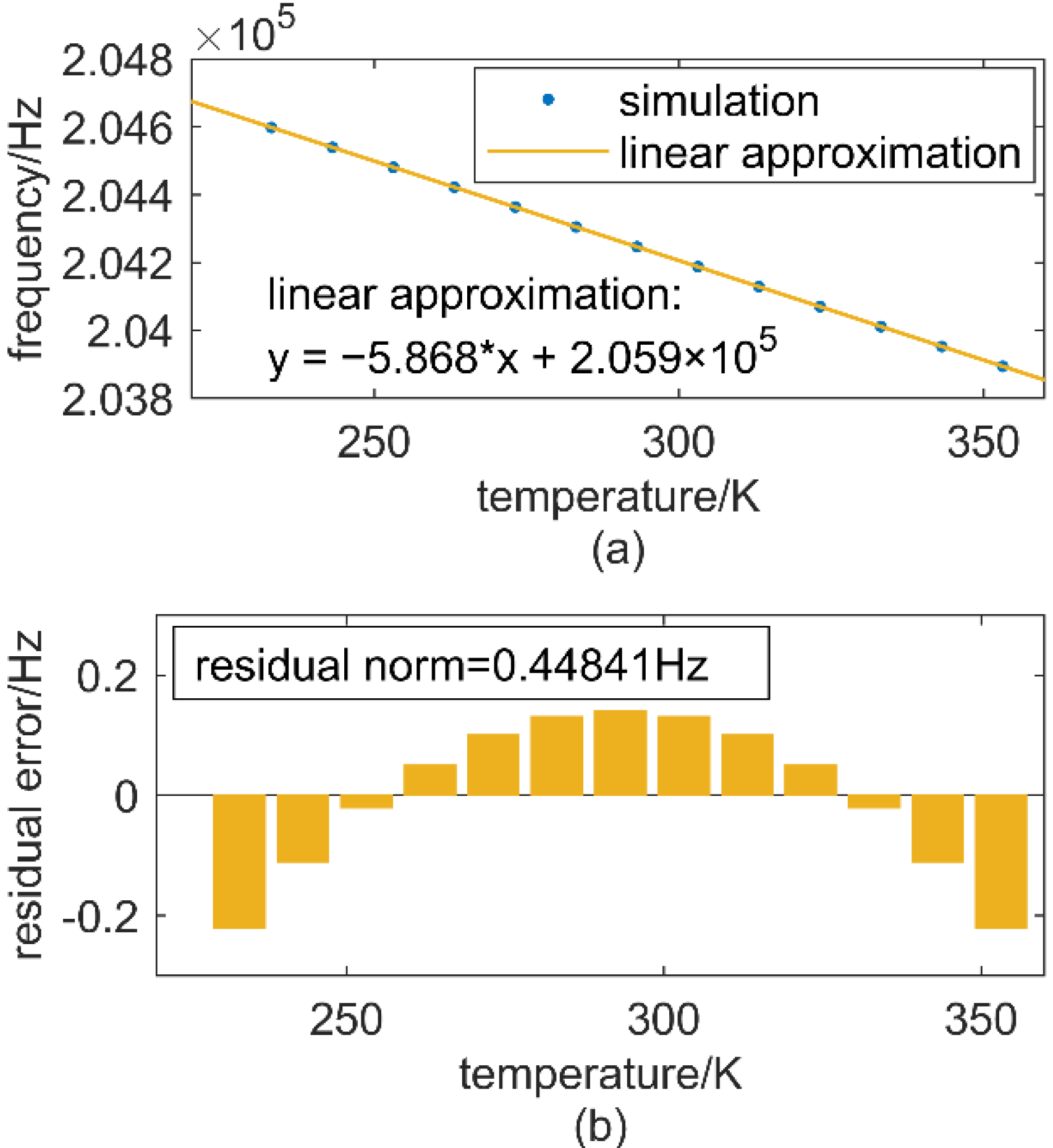
4. Experiments and Results
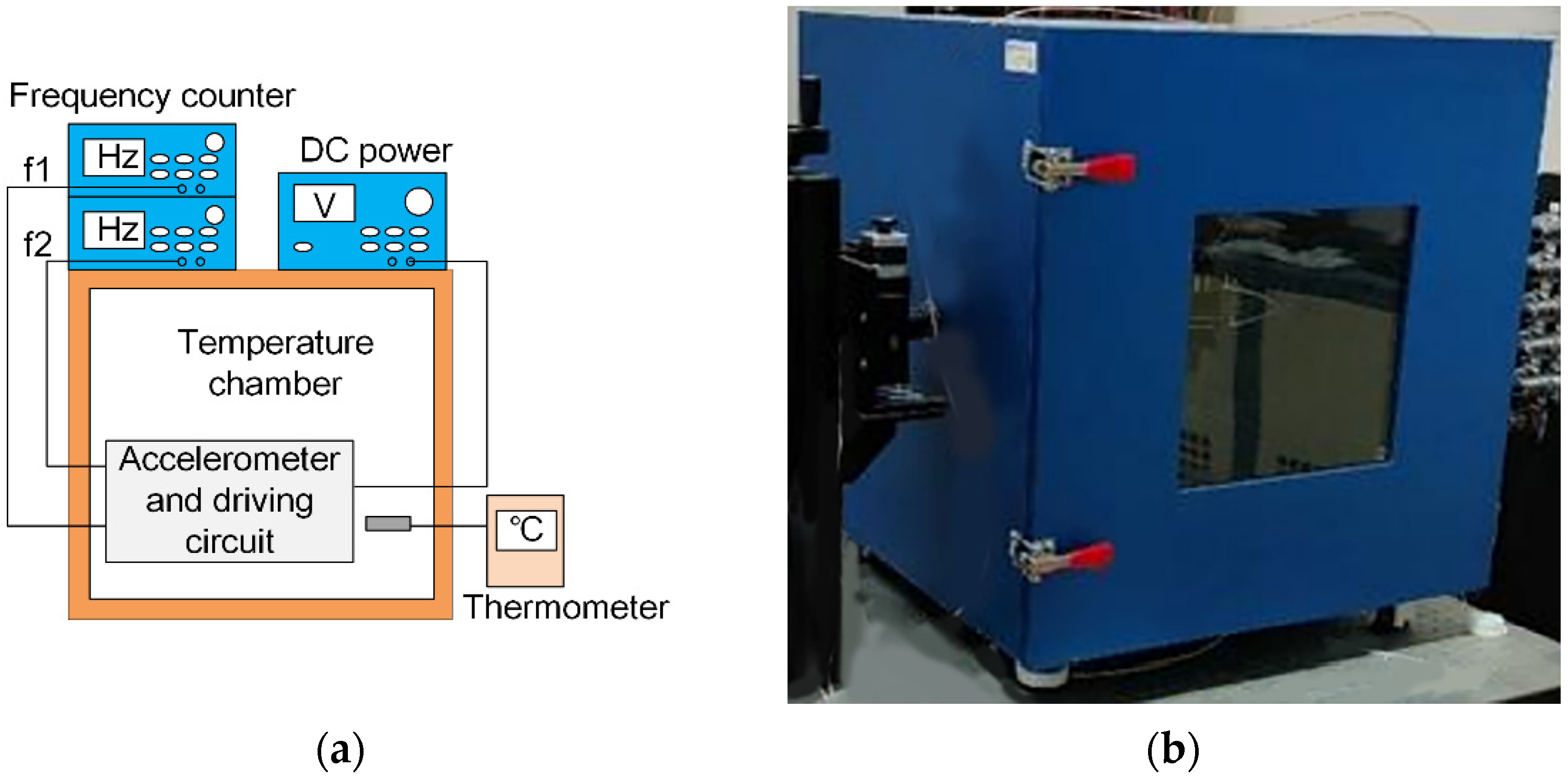
4.1. Experimental Setup
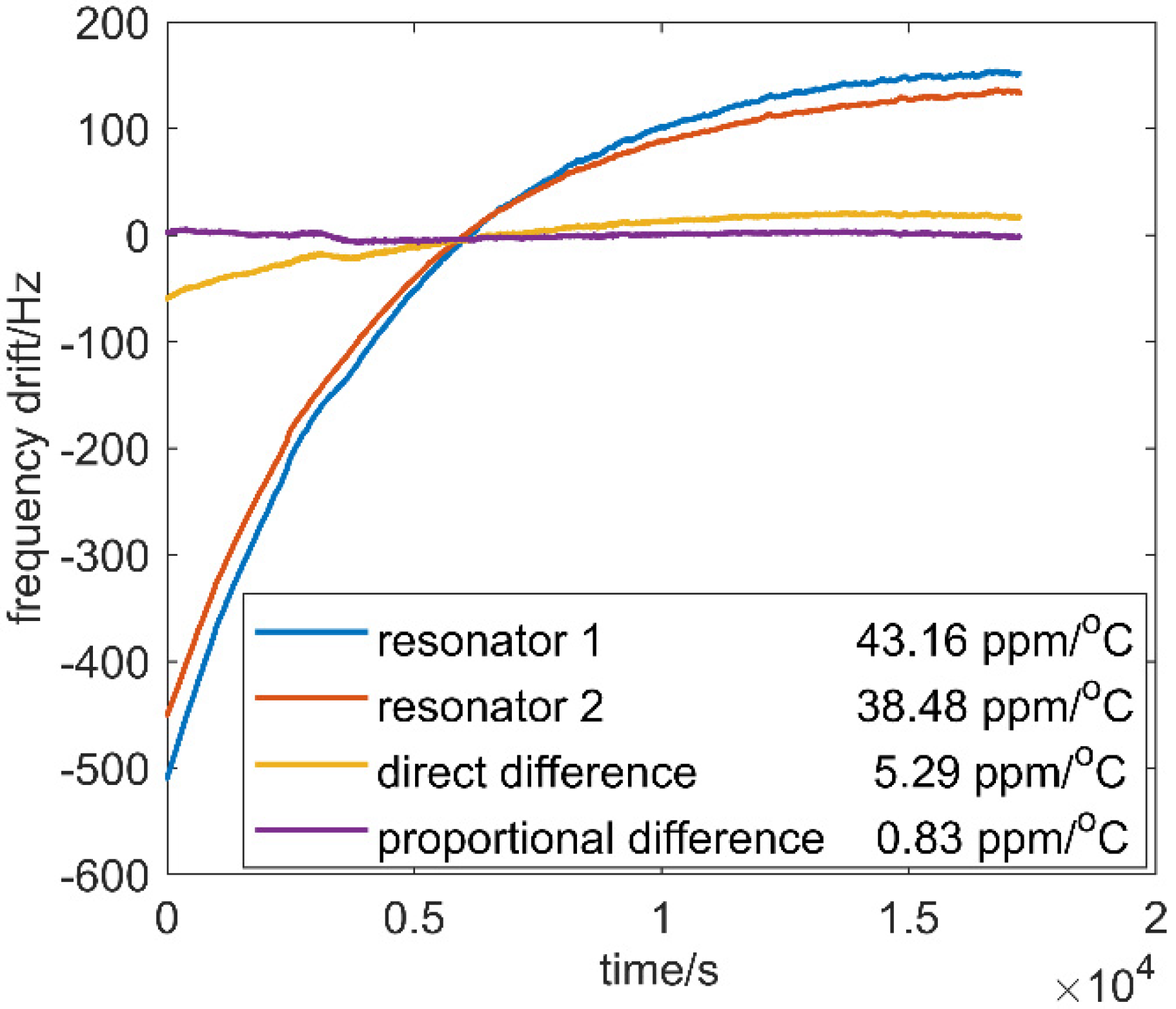
4.2. Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Judy, M.W. Evolution of Integrated Inertial Mems Technology. In Proceedings of the 2004 Solid-State, Actuators, and Microsystems Workshop, Hilton Head Island, SC, USA, 6–10 June 2004. [Google Scholar]
- Marek, J. MEMS for automotive and consumer electronics. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference—(ISSCC), Bucharest, Romania, 16–20 September 2010. [Google Scholar]
- Weinberg, M.S.; Bernstein, J.; Borenstein, J.T.; Campbell, J.; Sohn, J.B. Micromachining inertial instruments. In Proceedings of the SPIE—The International Society for Optical Engineering, Austin, TX, USA, 23 September 1996. [Google Scholar]
- Hopkins, R.; Miola, J.; Setterlund, R. The silicon oscillating accelerometer: A high-performance MEMS accelerometer for precision navigation and strategic guidance applications. In Proceedings of the 2005 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 24–26 January 2006. [Google Scholar]
- Zou, X.; Thiruvenkatanathan, P.; Seshia, A.A. Micro-electro-mechanical resonant tilt sensor. In Proceedings of the IEEE International Frequency Control Symposium, Baltimore, MD, USA, 21–24 May 2012. [Google Scholar]
- Zwahlen, P.; Nguyen, A.M.; Dong, Y.; Rudolf, F.; Schmid, H. Navigation grade MEMS accelerometer. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems, Hong Kong, China, 24–28 January 2010. [Google Scholar]
- Shan, X.; Zou, T.; Forbes, J.R.; Angeles, J. Design Specifications for Biaxial Navigation-Grade MEMS Accelerometers. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Zhao, C.; Pandit, M.; Sobreviela, G.; Steinmann, P.; Mustafazade, A.; Zou, X.; Seshia, A. JMEMS Letters A Resonant MEMS Accelerometer With 56ng Bias Stability and 98ng/Hz1/2 Noise Floor. J. Microelectromech. Syst. 2019, 28, 324–326. [Google Scholar] [CrossRef]
- Rao, K.; Liu, H.; Wei, X.; Wu, W.; Tu, L.C. A High-resolution Area-change-based Capacitive MEMS Accelerometer for Tilt Sensing. In Proceedings of the 2020 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 23–26 March 2020. [Google Scholar]
- Comi, C.; Corigliano, A.; Langfelder, G.; Longoni, A.; Tocchio, A.; Simoni, B. A Resonant Microaccelerometer With High Sensitivity Operating in an Oscillating Circuit. J. Microelectromech. Syst. 2010, 19, 1140–1152. [Google Scholar] [CrossRef]
- Seshia, A.A.; Palaniapan, M.; Roessig, T.A.; Howe, R.T.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromech. Syst. 2003, 11, 784–793. [Google Scholar] [CrossRef] [Green Version]
- Omura, Y.; Nonomura, Y.; Tabata, O. New resonant accelerometer based on rigidity change. In Proceedings of the International Conference on Solid State Sensors & Actuators, Chicago, IL, USA, 19 June 1999. [Google Scholar]
- Seo, Y.H.; Cho, Y.-H. Design, fabrication, static test and uncertainty analysis of a resonant microaccelerometer. Sens. Mater. 2002, 14, 91–108. [Google Scholar]
- Wang, Y.; Zhang, J.; Yao, Z.; Lin, C.; Tong, Z.; Su, Y.; Zhao, J. A MEMS Resonant Accelerometer With High Performance of Temperature Based on Electrostatic Spring Softening and Continuous Ring-Down Technique. IEEE Sens. J. 2018, 18, 7023–7031. [Google Scholar] [CrossRef]
- Meldrum, M.A. Application of vibrating beam technology to digital acceleration measurement. Sens. Actuators A Phys. 1990, 21, 377–380. [Google Scholar] [CrossRef]
- Liu, G.J.; Jiang, T.; Jiang, Q.K.; Wang, A.L. Characterization of a MEMS Accelerometer Considering Environmental Temperature Fluctuations. Mater. Sci. Forum 2011, 697–698, 801–804. [Google Scholar] [CrossRef]
- Watanabe, H.; Yamada, N.; Okaji, M. Linear Thermal Expansion Coefficient of Silicon from 293 to 1000 K. Int. J. Thermophys. 2004, 25, 221–236. [Google Scholar] [CrossRef]
- Yang, D.; Woo, J.K.; Lee, S.; Mitchell, J.; Challoner, A.D.; Najafi, K. A Micro Oven-Control System for Inertial Sensors. J. Microelectromech. Syst. 2017, 26, 507–518. [Google Scholar] [CrossRef]
- Kwon, H.K.; Ortiz, L.C.; Vukasin, G.D.; Chen, Y.; Kenny, T.W. An Oven-Controlled MEMS Oscillator (OCMO) With Sub 10mw, ± 1.5 PPB Stability Over Temperature. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019. [Google Scholar]
- Xu, C.; Segovia-Fernandez, J.; Kim, H.J.; Piazza, G. Temperature-Stable Piezoelectric MEMS Resonators Using Integrated Ovens and Simple Resistive Feedback Circuits. J. Microelectromech. Syst. 2017, 26, 187–195. [Google Scholar] [CrossRef]
- Salvia, J.C.; Melamud, R.; Chandorkar, S.A.; Lord, S.F.; Kenny, T.W. Real-Time Temperature Compensation of MEMS Oscillators Using an Integrated Micro-Oven and a Phase-Locked Loop. J. Microelectromech. Syst. 2010, 19, 192–201. [Google Scholar] [CrossRef]
- Li, B.; Li, C.; Zhao, Y.; Han, C.; Zhang, Q. An integrated packaged resonant accelerometer with temperature compensation. Rev. Sci. Instrum. 2020, 91, 105004. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.; Graham, A.B.; Lee, B.J.; Ahn, C.H.; Kenny, T.W. Resonant pressure sensor with on-chip temperature and strain sensors for error correction. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January 2013. [Google Scholar]
- Lee, J.; Rhim, J. Temperature compensation method for the resonant frequency of a differential vibrating accelerometer using electrostatic stiffness control. J. Micromech. Microeng. 2012, 22, 95016–95026+95011. [Google Scholar] [CrossRef]
- Behbahani, A.H.; Kim, D.; Stupar, P.; Denatale, J.; M’Closkey, R.T. Tailored Etch Profiles for Wafer-Level Frequency Tuning of Axisymmetric Resonators. J. Microelectromech. Syst. 2017, 26, 333–343. [Google Scholar] [CrossRef] [Green Version]
- Ge, H.H.; Behbahani, A.H.; Closkey, R.T.M. MEMS gyro drift compensation using multiple rate measurements derived from a single resonator. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 288–293. [Google Scholar]
- Lee, S.; Nguyen, T.C. Influence of automatic level control on micromechanical resonator oscillator phase noise. In Frequency Control Symposium and PDA Exhibition Jointly with the 17th European Frequency and Time Forum, 2003, Proceedings of the 2003 IEEE International, Tampa, FL, USA, 4–8 May 2003; IEEE: Tampa, FL, USA, 2003. [Google Scholar]

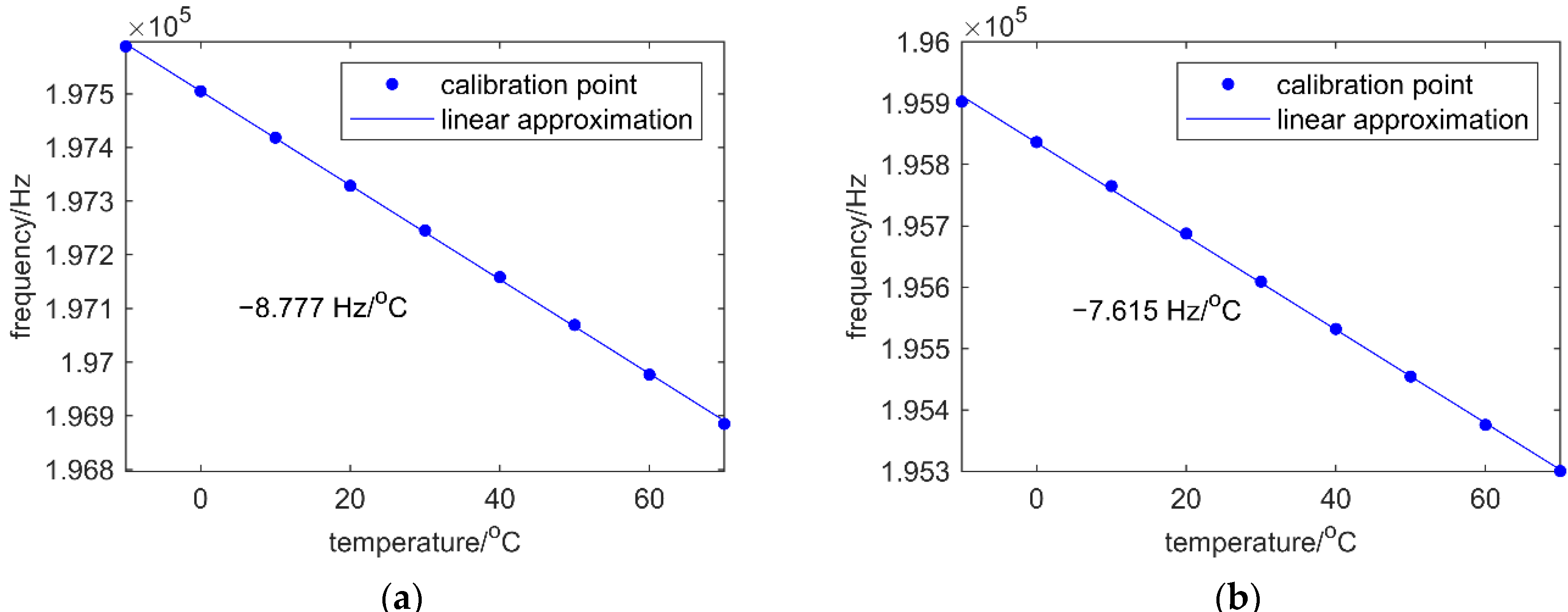

| Parameter | Value |
|---|---|
| Device thickness | 40 µm |
| Length of CC resonant beam | 400 µm |
| Width of CC resonant beam | 6 µm |
| Gap of resonant beam | 2 µm |
| Quality of proof mass | 1.50 mg |
| Quality factor | 15,600 |
| Resonant frequency 1 (at 30 °C) | 197.2495 kHz |
| Resonant frequency 2 (at 30 °C) | 195.6092 kHz |
| Scale factor of resonator 1 | 512 Hz/g |
| Scale factor of resonator 2 | 508 Hz/g |
| Temperature Factor 1 | Temperature Factor 2 | Temperature Difference Ratio | |
|---|---|---|---|
| −8.777 | −7.615 | 0.867 | |
| proposed | ~ | ~ | 0.878 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, P.; Xiong, X.; Wang, K.; Wang, J.; Zou, X. An Improved Difference Temperature Compensation Method for MEMS Resonant Accelerometers. Micromachines 2021, 12, 1022. https://doi.org/10.3390/mi12091022
Cai P, Xiong X, Wang K, Wang J, Zou X. An Improved Difference Temperature Compensation Method for MEMS Resonant Accelerometers. Micromachines. 2021; 12(9):1022. https://doi.org/10.3390/mi12091022
Chicago/Turabian StyleCai, Pengcheng, Xingyin Xiong, Kunfeng Wang, Jiawei Wang, and Xudong Zou. 2021. "An Improved Difference Temperature Compensation Method for MEMS Resonant Accelerometers" Micromachines 12, no. 9: 1022. https://doi.org/10.3390/mi12091022
APA StyleCai, P., Xiong, X., Wang, K., Wang, J., & Zou, X. (2021). An Improved Difference Temperature Compensation Method for MEMS Resonant Accelerometers. Micromachines, 12(9), 1022. https://doi.org/10.3390/mi12091022






