Fabrication of Multifocal Microlens Array by One Step Exposure Process
Abstract
:1. Introduction
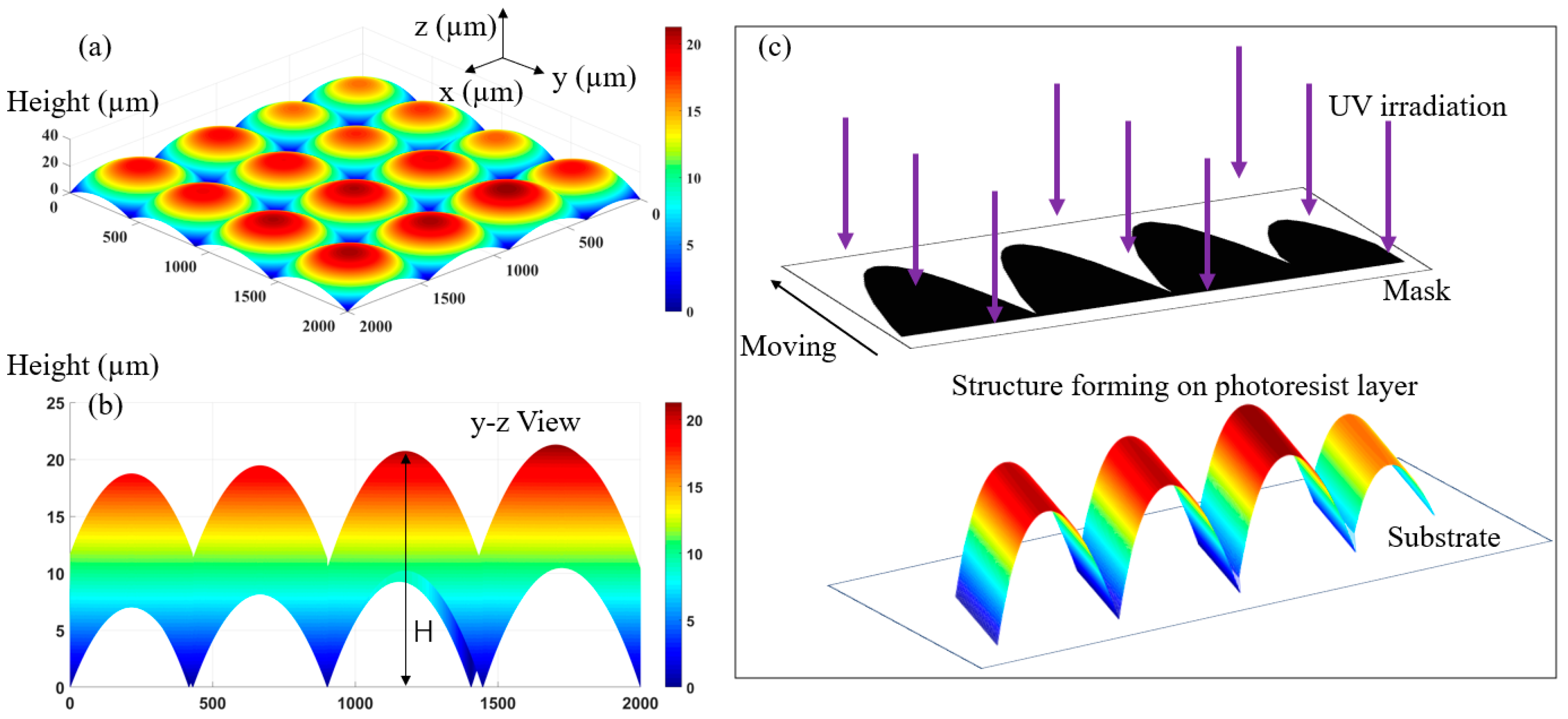
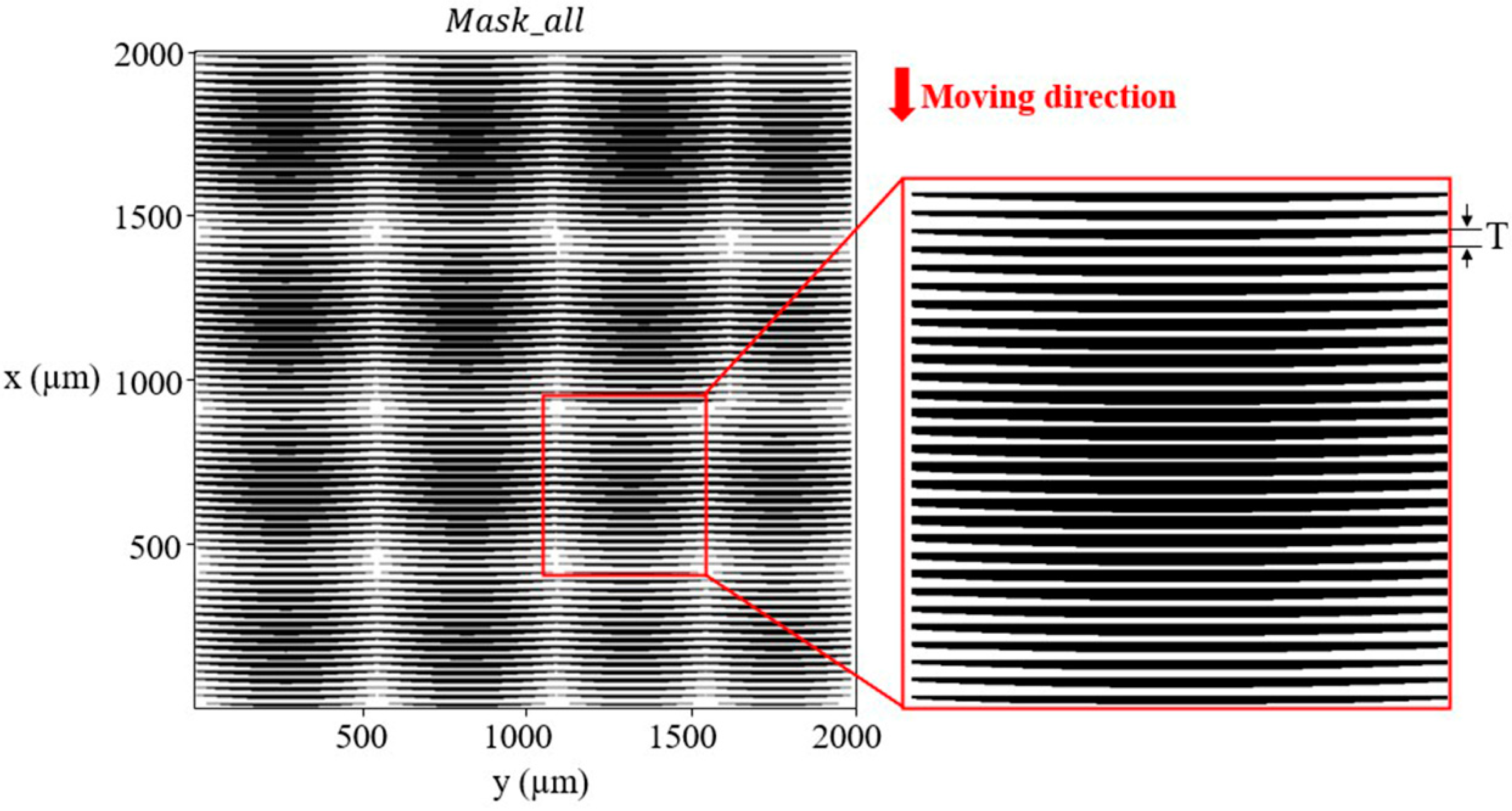
2. Fabrication Principle
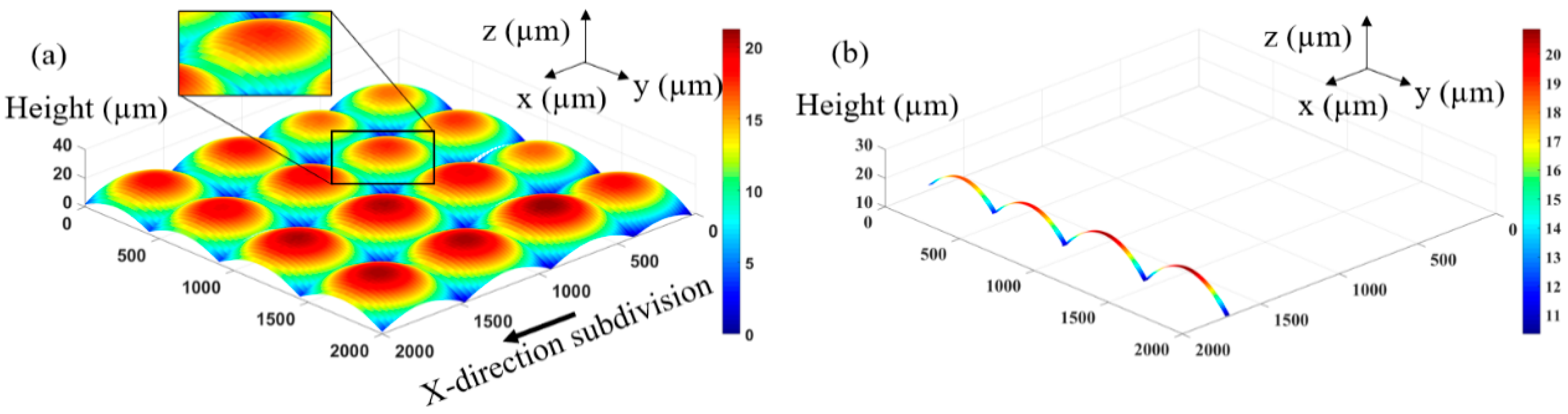
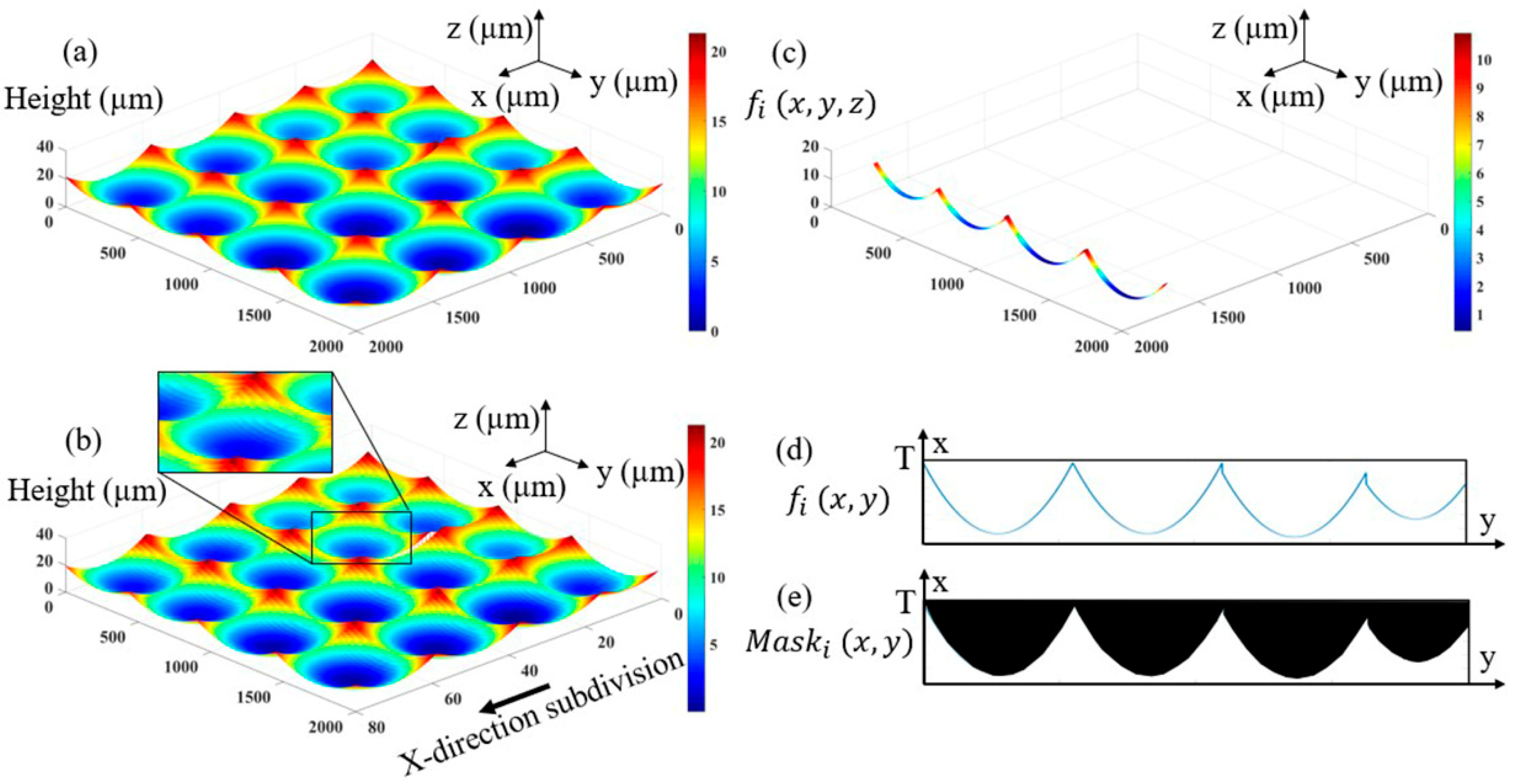
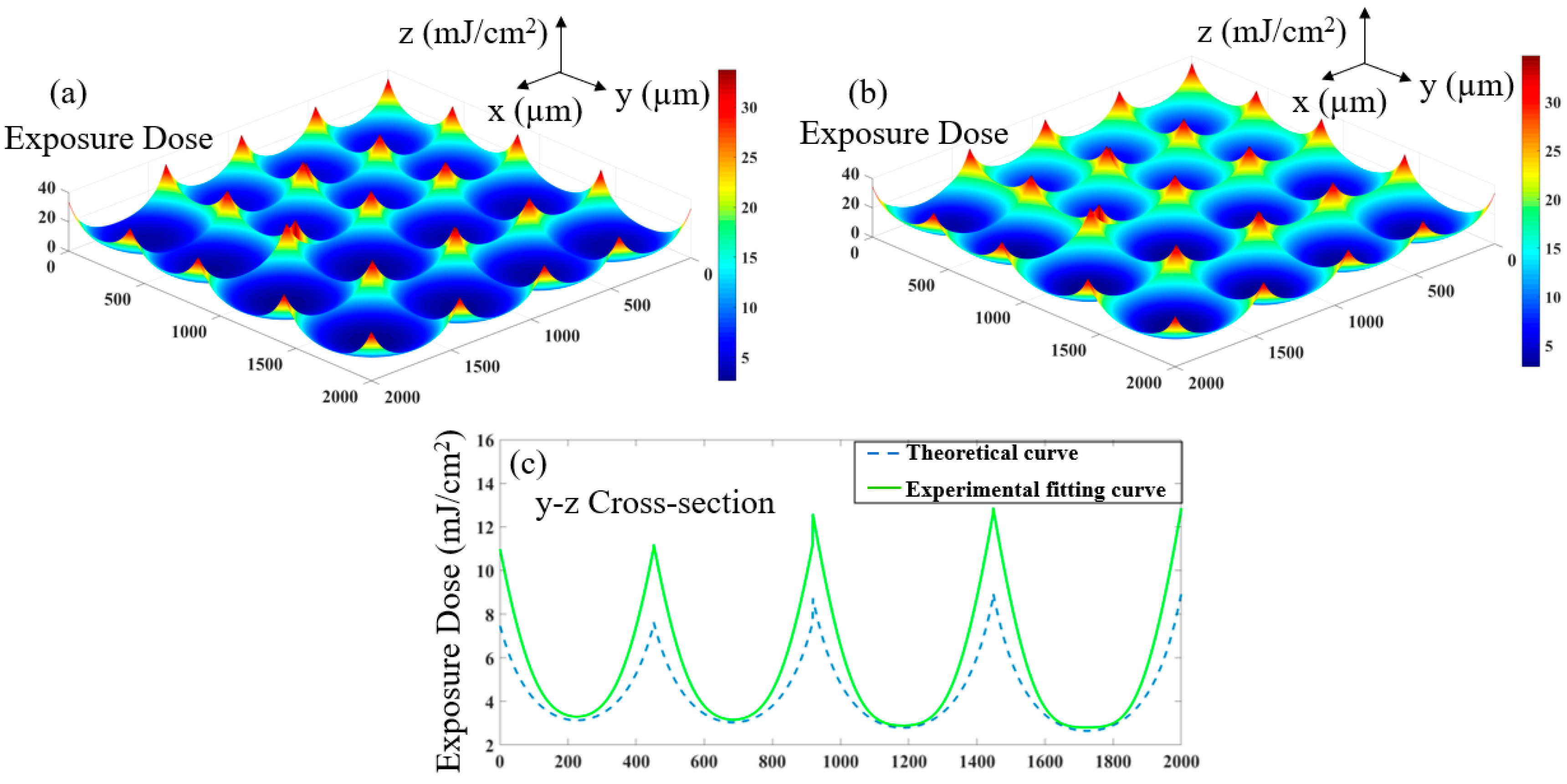
3. Nonlinear Effect Correction
4. Fabrication Process, Testing and Characterization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, X.; Peng, Y.; Peng, R.; Zeng, X.; Zhang, Y.-A.; Guo, T. Fabrication of Large-Scale Microlens Arrays Based on Screen Printing for Integral Imaging 3D Display. ACS Appl. Mater. Interfaces 2016, 8, 24248–24255. [Google Scholar] [CrossRef]
- Wang, W.; Chen, G.; Weng, Y.; Weng, X.; Zhou, X.; Wu, C.; Guo, T.; Yan, Q.; Lin, Z.; Zhang, Y. Large-scale microlens arrays on flexible substrate with improved numerical aperture for curved integral imaging 3D display. Sci. Rep. 2020, 10, 11741. [Google Scholar] [CrossRef] [PubMed]
- Lee, X.-H.; Moreno, I.; Sun, C.-C. High-performance LED street lighting using microlens arrays. Opt. Express 2013, 21, 10612–10621. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Hassan, A.; Jiang, Y. Freeform microlens array homogenizer for excimer laser beam shaping. Opt. Express 2016, 31, 24846–24858. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Xu, C.; Xue, L.; Pang, H.; Cao, A.; Fu, Y.; Deng, Q. Integrated Double-Sided Random Microlens Array Used for Laser Beam Homogenization. Micromachines 2021, 12, 673. [Google Scholar] [CrossRef]
- Dickey, F.M.; Holswade, S.C. Laser beam shaping. SPIE 2000, 4095, 101–216. [Google Scholar]
- Jin, Y.; Zhao, Y.; Jiang, Y. Microlens beam homogenizer for excimer laser processing. J. Laser Appl. 2016, 28, 22601. [Google Scholar] [CrossRef]
- Cao, A.; Shi, L.; Yu, J.; Pang, H.; Zhang, M.; Deng, Q. Laser Beam Homogenization Method Based on Random Microlens Array. Appl. Laser 2015, 35, 124–128. [Google Scholar]
- Liu, Z.; Liu, H.; Lu, Z.; Li, Q.; Li, J. A beam homogenizer for digital micromirror device lithography system based on random freeform microlenses. Opt. Commun. 2019, 443, 211–215. [Google Scholar] [CrossRef]
- Ducharme, A.D. Microlens diffusers for efficient laser speckle generation. Opt. Express 2007, 15, 14573–14579. [Google Scholar] [CrossRef]
- Jung, H.; Jeong, K.-H. Monolithic Polymer Microlens Arrays with High Numerical Aperture and High Packing Density. ACS Appl. Mater. Interfaces 2015, 7, 2160–2165. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.I.; Kim, K.; Yang, S.; Jang, K.W.; Jeong, K.H. Multi-focus microlens arrays using multilayer photolithography. Opt. Express 2020, 28, 9082–9088. [Google Scholar] [CrossRef]
- Nieto, D.; Gómez-Varela, A.I.; Martín, Y.C.; O’Connor, G.M.; Flores-Arias, M.T. Improvement of the optical and morphological properties of microlens arrays fabricated by laser using a sol–gel coating. Appl. Surf. Sci. 2015, 351, 697–703. [Google Scholar] [CrossRef]
- Kostyuk, G.K.; Zakoldaev, R.A.; Sergeev, M.; Yakovlev, E.B. Microlens array fabrication on fused silica influenced by NIR laser. Appl. Phys. A 2016, 122, 99. [Google Scholar] [CrossRef]
- Lin, C.H.; Jiang, L.; Chai, Y.H.; Xiao, H.; Chen, S.J.; Tsai, H.L. Fabrication of microlens arrays in photosensitive glass by femtosecond laser direct writing. Appl. Phys. A 2009, 97, 751–757. [Google Scholar] [CrossRef]
- Florian, C.; Piazza, S.; Diaspro, A.; Serra, P.; Duocastella, M. Direct Laser Printing of Tailored Polymeric Microlenses. ACS Appl. Mater. Interfaces 2016, 8, 17028–17032. [Google Scholar] [CrossRef]
- Simon, T.; Kathrin, A.; Timo, G.; Harald, G. 3D-printed eagle eye: Compound microlens system for foveated imaging. Sci. Adv. 2017, 2, 15. [Google Scholar]
- Geng, Q.; Wang, D.; Chen, P.; Chen, S.-C. Ultrafast multi-focus 3-D nano-fabrication based on two-photon polymerization. Nat. Commun. 2019, 10, 2179. [Google Scholar] [CrossRef]
- Romanenko, O.; Havranek, V.; Mackova, A.; Davidkova, M.; Cutroneo, M.; Ponomarev, A.G.; Nagy, G.; Stammers, J.; Rajta, I. Performance and application of heavy ion nuclear microbeam facility at the Nuclear Physics Institute in Řež, Czech Republic. Rev. Sci. Instrum. 2019, 90, 013701. [Google Scholar] [CrossRef]
- Nagy, G.U.L.; Lavrentiev, V.; Bányász, I.; Szilasi, S.Z.; Havranek, V.; Vosecek, V.; Huszánk, R.; Rajta, I. Compaction of poly-dimethylsiloxane due to nitrogen ion irradiation and its application for creating microlens arrays. Thin Solid Films 2017, 636, 634–638. [Google Scholar] [CrossRef]
- Wu, N.; Chen, Q.-D.; Niu, L.-G.; Jiao, J.; Xia, H.; Song, J.-F.; Sun, H.-B. 100% Fill-Factor Aspheric Microlens Arrays (AMLA) with Sub-20-nm Precision. IEEE Photon Technol. Lett. 2009, 21, 1535–1537. [Google Scholar] [CrossRef] [Green Version]
- Xue, L.; Pang, Y.; Liu, W.; Liu, L.; Pang, H.; Cao, A.; Shi, L.; Fu, Y.; Deng, Q. Fabrication of Random Microlens Array for Laser Beam Homogenization with High Efficiency. Micromachines 2020, 11, 338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, P.-C.; Chang, Y.-P.; Zhang, R.-H.; Wu, C.-C.; Tang, G.-R. Microfabricated microfluidic platforms for creating microlens array. Opt. Express 2017, 25, 16101–16115. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Dai, B.; Zhuo, R.; Yuan, X.; Gao, X.; Wen, J.; Sheng, B.; Zhang, D. Focal-length-tunable elastomer-based liquid-filled plano–convex mini lens. Opt. Lett. 2016, 41, 404–407. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Dai, B.; Huang, Y.; Wang, H.; Yang, Z.; Wang, K.; Zhuang, S.; Zhang, D. Fabrication of polymer microlens array with controllable focal length by modifying surface wettability. Opt. Express 2018, 26, 4172–4182. [Google Scholar] [CrossRef]
- Liu, C.; Wang, D.; Wang, Q.-H.; Xing, Y. Multifunctional optofluidic lens with beam steering. Opt. Express 2020, 28, 7734–7745. [Google Scholar] [CrossRef]
- Long, Y.; Song, Z.; Pan, M.; Tao, C.; Hong, R.; Dai, B.; Zhang, D. Fabrication of uniform-aperture multi-focus microlens array by curving microfluid in the microholes with inclined walls. Opt. Express 2021, 29, 12763–12771. [Google Scholar] [CrossRef]
- Wu, M.; Park, C. Fabrication of arrays of microlenses with controlled profiles using gray-scalemicrolens projection photo-lithography. Langmuir 2002, 18, 9312–9318. [Google Scholar] [CrossRef]
- Kuang, D.; Zhang, X.; Gui, M.; Fang, Z. Hexagonal microlens array fabricated by direct laser writing and inductively coupled plasma etching on organic light emitting devices to enhance the outcoupling efficiency. Appl. Opt. 2009, 48, 974–978. [Google Scholar] [CrossRef]
- Bruce, W.; Smith, K.S. Microlithography Science and Technology; CRC Press: Boca Raton, FL, USA, 2007; p. 864. [Google Scholar]
- Hur, J.-G. Maskless fabrication of three-dimensional microstructures with high isotropic resolution: Practical and theoretical considerations. Appl. Opt. 2011, 50, 2383–2390. [Google Scholar] [CrossRef]

| Lithography Process | Parameter |
|---|---|
| Pretreatment of quartz substrate | Wash with acetone and dry |
| Spin coated photoresist | 700 rpm, 100 rpm/s, 25 μm |
| Pre drying | 90 °C, 5 min |
| Exposure | 365 nm, 3.5 mW/cm2, 1 s–13 s |
| Development | AZ 400K: Deionized H2O, 1:1, 30 s |
| Clean | Deionized H2O |
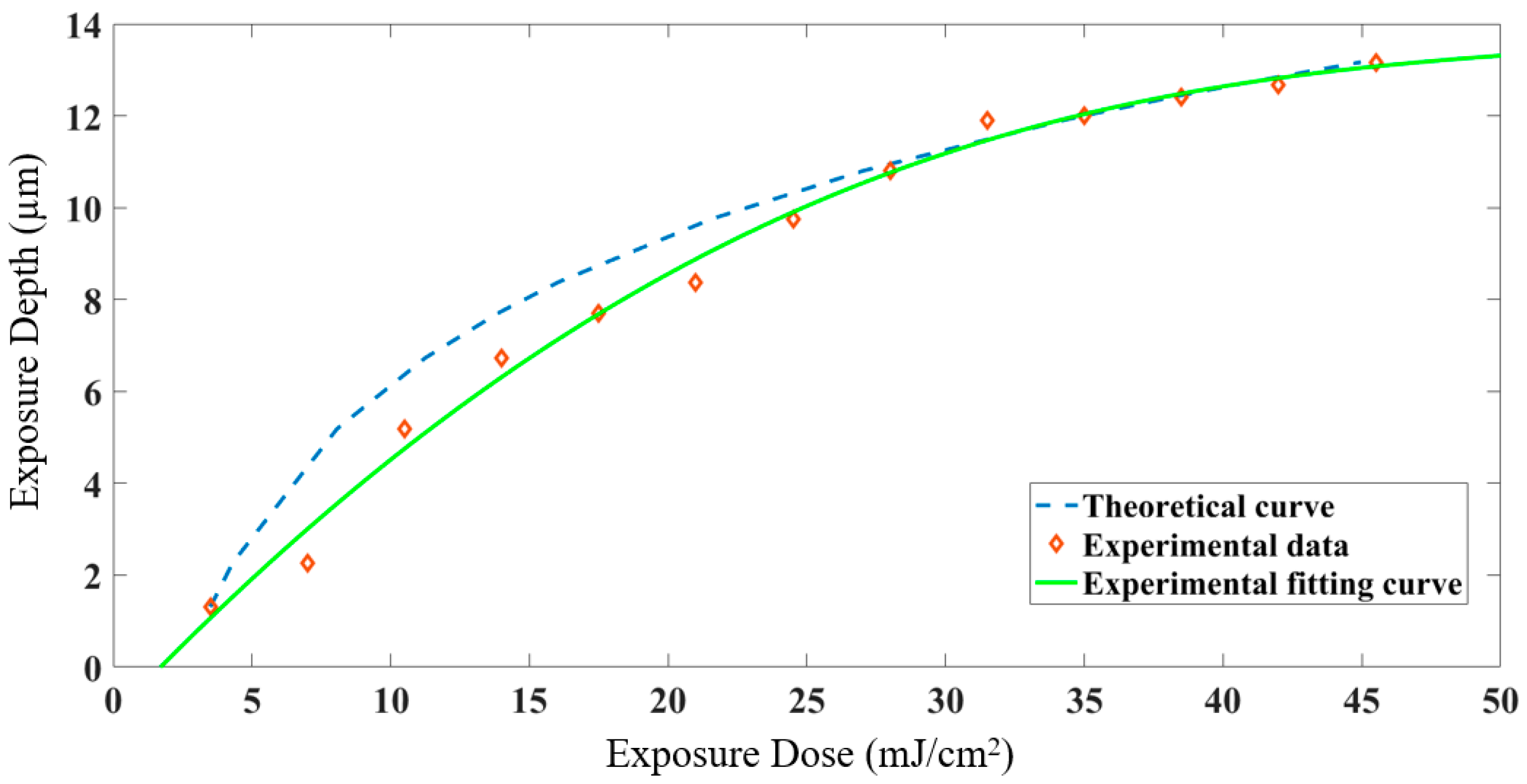
| Time of Exposure (s) | Exposure Dose (mJ/cm2) | Average Exposure Depth (μm) | Standard Deviation (μm) | Confidence Interval (μm) |
|---|---|---|---|---|
| 1 | 3.5 | 1.31 | 0.02 | (1.296,1.324) |
| 2 | 7.0 | 2.27 | 0.10 | (2.199,2.341) |
| 3 | 10.5 | 5.18 | 0.07 | (5.130,5.230) |
| 4 | 14.0 | 6.73 | 0.07 | (6.680,6.780) |
| 5 | 17.5 | 7.70 | 0.08 | (7.643,7.757) |
| 6 | 21.0 | 8.37 | 0.02 | (8.356,8.384) |
| 7 | 24.5 | 9.75 | 0.08 | (9.693,9.807) |
| 8 | 28.0 | 10.80 | 0.03 | (10.779,10.821) |
| 9 | 31.5 | 11.90 | 0.11 | (11.821,11.979) |
| 10 | 35.0 | 12.00 | 0.08 | (11.943,12.057) |
| 11 | 38.5 | 12.40 | 0.08 | (12.343,12.457) |
| 12 | 42.0 | 12.66 | 0.06 | (12.617,12.703) |
| 13 | 45.5 | 13.16 | 0.04 | (13.131,13.189) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, W.; Cai, Y.; Xu, C.; Pang, H.; Cao, A.; Fu, Y.; Deng, Q. Fabrication of Multifocal Microlens Array by One Step Exposure Process. Micromachines 2021, 12, 1097. https://doi.org/10.3390/mi12091097
Yuan W, Cai Y, Xu C, Pang H, Cao A, Fu Y, Deng Q. Fabrication of Multifocal Microlens Array by One Step Exposure Process. Micromachines. 2021; 12(9):1097. https://doi.org/10.3390/mi12091097
Chicago/Turabian StyleYuan, Wei, Yajuan Cai, Cheng Xu, Hui Pang, Axiu Cao, Yongqi Fu, and Qiling Deng. 2021. "Fabrication of Multifocal Microlens Array by One Step Exposure Process" Micromachines 12, no. 9: 1097. https://doi.org/10.3390/mi12091097
APA StyleYuan, W., Cai, Y., Xu, C., Pang, H., Cao, A., Fu, Y., & Deng, Q. (2021). Fabrication of Multifocal Microlens Array by One Step Exposure Process. Micromachines, 12(9), 1097. https://doi.org/10.3390/mi12091097






