Rate-Dependent Modeling of Piezoelectric Actuators for Nano Manipulation Based on Fractional Hammerstein Model
Abstract
:1. Introduction
- In terms of PEA rate-dependent modeling, this paper proposes a modeling method based on the improved Bouc-Wen model and fractional-order model consisting of a separate Hammerstein model, which achieves a more accurate description of the dynamic characteristics of PEA rate-dependent hysteresis. At present, most Hammerstein models adopt a combination of traditional hysteresis models and integer-order or linear autoregressive models to model PEA. When using integer-order or linear autoregressive models to describe the dynamic characteristics of PEA, the accuracy is far inferior to that of fractional-order models. Compared with the integer-order or linear autoregressive models, it is more in line with engineering reality and can contain richer amplitude-frequency information.
- In terms of model parameter identification, this paper proposes an artificial bee colony algorithm based on differential evolution (DE-ABC), and uses it for the first time for the parameter identification of the fractional Hammerstein model. By adding the mutation strategy and chaos search for genetic algorithm into the previous ABC, the convergence speed of the algorithm is faster and the identification accuracy is higher, and the simultaneous identification of order and coefficient of fractional model is realized.
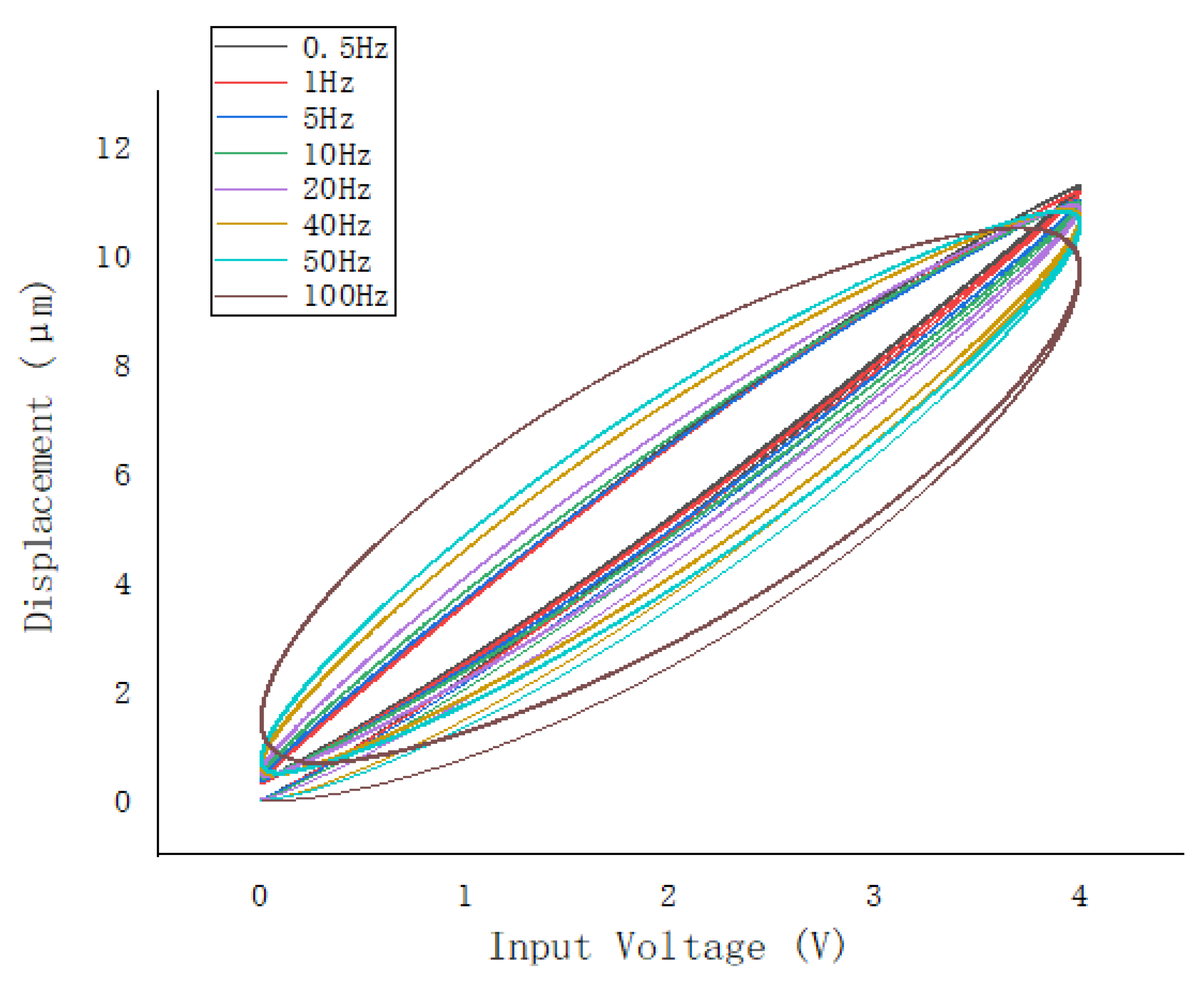
- Through experimental data collection and analysis, the proposed model has a good frequency generalization ability within 1–100 Hz, and can better reflect the true characteristics of piezoelectric ceramic actuators than the traditional static hysteresis model.
2. Fractional Hammerstein Model of PEA
2.1. The Improved Bouc-Wen Model
2.2. Fractional Dynamic Model
3. Artificial Bee Colony Algorithm Based on Differential Evolution (DE-ABC)
- Obtain the input and output data of the experiment.
- Set the initial conditions and the number of parameters.
- Parameter identification based on DE-ABC.
- Verification. If the fitness does not meet the requirements, return to step 2 to continue identification.
- The initial value of the chaotic sequence generated according to Formula (11);
- Generate chaotic sequence according to Formula (10);
- Generate a new solution according to Formula (12), calculate its fitness value, compare it with the original solution, and keep the best solution;
- If the maximum number of chaotic iterations is reached, the search ends, otherwise go to step 2.
4. Model Verification
4.1. Experimental Setup
4.2. Comparison of Model Identification Effects
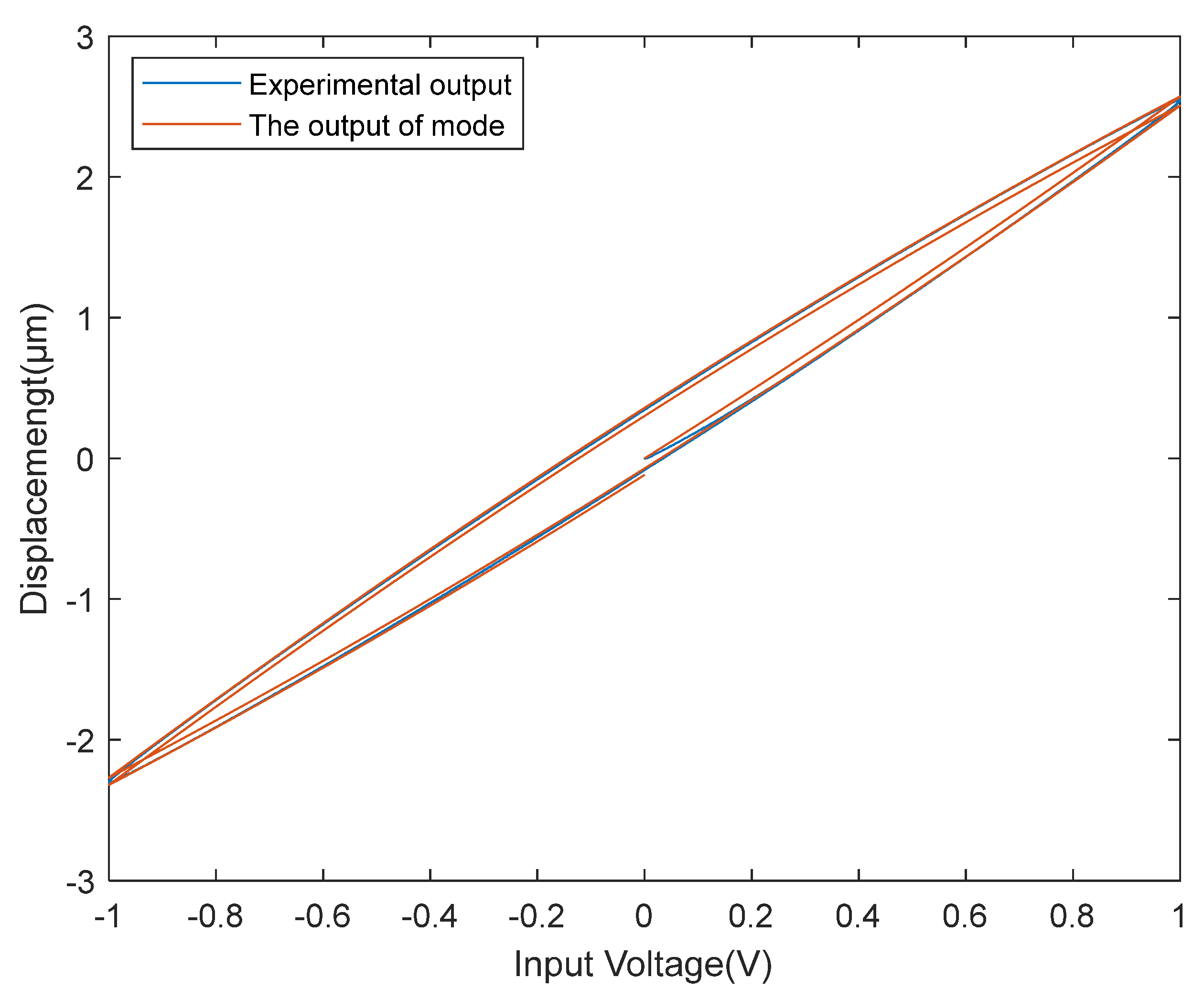
4.3. Fractional Hammerstein Model
- Identification of the fractional-order model, which mainly reflects the linear dynamic characteristics of the PEA. A sine frequency sweep signal with a frequency range of 1–100 Hz is generated by Matlab as the input of the Bouc-Wen model. The output data of the Bouc-Wen model is used as the input of the fractional-order model, and the collected output data of the experimental equipment of the frequency sweep signal is used as the output of the fractional-order model. Through the input and output data of the aforementioned fractional model, the DE-ABC is used to identify the parameters of the fractional model. Through the DE-ABC, the fractional linear dynamic model is:
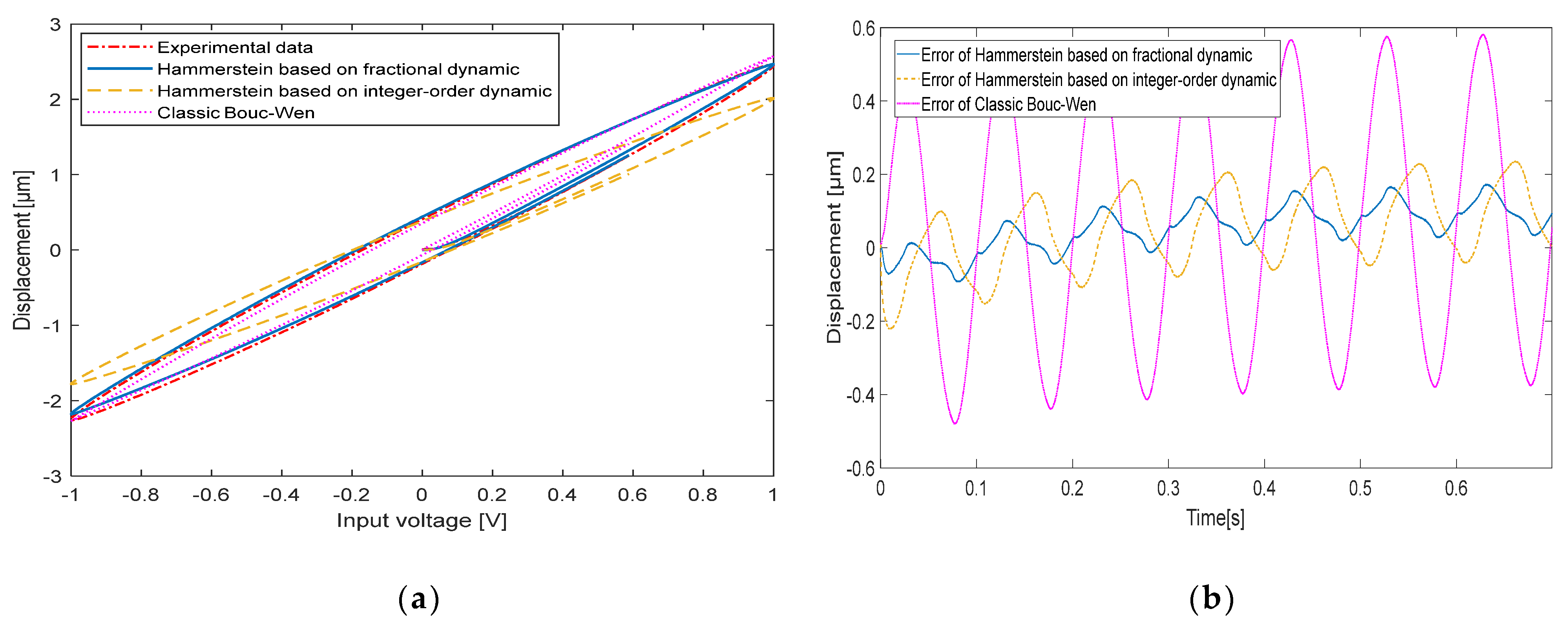
4.4. Model Examination
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, Z.; Liu, H.H.T.; Zhu, B.; Gao, H.; Kaynak, O. Nonlinear Robust Attitude Tracking Control of a Table-Mount Experimental Helicopter Using Output Feedback. IEEE Trans. Ind. Electron. 2015, 62, 5665–5676. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Shi, B.; Huo, Z.; Zhou, K.; Tian, Y.; Zhang, D. Design and control of a novel asymmetrical piezoelectric actuated microgripper for micromanipulation. Sens. Actuators A Phys. 2018, 269, 227–237. [Google Scholar] [CrossRef]
- Karpelson, M.; Wei, G.-Y.; Wood, R.J. Driving high voltage piezoelectric actuators in microrobotic applications. Sens. Actuators A Phys. 2012, 176, 78–89. [Google Scholar] [CrossRef]
- Hu, B.; Tang, X.; Hu, S.; Yan, W.; Hu, Z. Research on micro-displacement driving technology based on piezoelectric ceramic. In Proceedings of the 6th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Design, Manufacturing, and Testing of Smart Structures, Micro- and Nano-Optical Devices, and Systems, Xiamen, China, 26–29 April 2012; Volume 8418, p. 84180Z. [Google Scholar] [CrossRef]
- Fan, Y.; Collet, M.; Ichchou, M.; Li, L.; Bareille, O.; Dimitrijevic, Z. A wave-based design of semi-active piezoelectric composites for broadband vibration control. Smart Mater. Struct. 2016, 25, 055032. [Google Scholar] [CrossRef]
- Koven, R.; Mills, M.; Gale, R.; Aksak, B. Low-Frequency and Broadband Vibration Energy Harvesting Using Base-Mounted Piezoelectric Transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2017, 64, 1735–1743. [Google Scholar] [CrossRef]
- Su, H.; Li, G.; Rucker, C.; Iii, R.J.W.; Fischer, G.S. A Concentric Tube Continuum Robot with Piezoelectric Actuation for MRI-Guided Closed-Loop Targeting. Ann. Biomed. Eng. 2016, 44, 2863–2873. [Google Scholar] [CrossRef]
- Liu, Y.F.; Li, J.; Hu, X.H.; Zhang, Z.M.; Cheng, L.; Lin, Y.; Zhang, W.J. Modeling and control of piezoelectric inertia–friction actuators: review and future research directions. Mech. Sci. 2015, 6, 95–107. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Liu, H.; Wu, H.; Zou, D. Modelling and compensation of hysteresis in piezoelectric actuators based on Maxwell approach. Electron. Lett. 2016, 52, 188–190. [Google Scholar] [CrossRef]
- Oh, J.; Bernstein, D.S. Piecewise Linear Identification for the Rate-Independent and Rate-Dependent Duhem Hysteresis Models. IEEE Trans. Autom. Control. 2007, 52, 576–582. [Google Scholar] [CrossRef] [Green Version]
- Du, H.F.; Du, A. The hysteresis curves of nanoparticles obtained by Monte Carlo method based on the Stoner-Wohlfarth model. J. Appl. Phys. 2006, 99, 104306. [Google Scholar] [CrossRef]
- Kamlah, M.; Böhle, U. Finite element analysis of piezoceramic components taking into account ferroelectric hysteresis behavior. Int. J. Solids Struct. 2001, 38, 605–633. [Google Scholar] [CrossRef]
- Arockiarajan, A.; Delibas, B.; Menzel, A.; Seemann, W. Studies on rate-dependent switching effects of piezoelectric materials using a finite element model. Comput. Mater. Sci. 2006, 37, 306–317. [Google Scholar] [CrossRef] [Green Version]
- Pruvost, S.; Hajjaji, A.; Lebrun, L.; Guyomar, D.; Boughaleb, Y. Domain Switching and Energy Harvesting Capabilities in Ferroelectric Materials. J. Phys. Chem. C 2010, 114, 20629–20635. [Google Scholar] [CrossRef]
- Rong, C.; He, Z.; Li, D.; Xue, G.; Yang, Z. Online parameter identification of a giant magnetostrictive actuator based on the dynamic Jiles–Atherton model. RSC Adv. 2016, 6, 114208–114218. [Google Scholar] [CrossRef]
- Song, X.; Duggen, L.; Lassen, B.; Mangeot, C. Modeling and identification of hysteresis with modified Preisach model in piezoelectric actuator. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1538–1543. [Google Scholar] [CrossRef]
- Na, J.; Chen, Q.; Ren, X. Hysteresis Dynamics and Modeling. In Adaptive Identification and Control of Uncertain Systems with Non-smooth Dynamics; Academic Press: Cambridge, MA, USA, 2018; ISBN 9780128136836. [Google Scholar]
- Gu, G.; Li, C.-X.; Zhu, L.-M.; Su, C.-Y. Modeling and Identification of Piezoelectric-Actuated Stages Cascading Hysteresis Nonlinearity With Linear Dynamics. IEEE/ASME Trans. Mechatron. 2015, 21, 1792–1797. [Google Scholar] [CrossRef]
- Dong, R.; Tan, Y.; Chen, H.; Xie, Y. A neural networks based model for rate-dependent hysteresis for piezoceramic actuators. Sens. Actuators A Phys. 2008, 143, 370–376. [Google Scholar] [CrossRef]
- Wong, P.-K.; Xu, Q.; Vong, C.-M.; Wong, H.-C. Rate-Dependent Hysteresis Modeling and Control of a Piezostage Using Online Support Vector Machine and Relevance Vector Machine. IEEE Trans. Ind. Electron. 2011, 59, 1988–2001. [Google Scholar] [CrossRef]
- Liu, P.; Wang, Z.-Y.; Zhang, Z.; Mao, J.-Q.; Zhou, K.-M. Modeling and H ∞ Robust Control of a Smart Structure with Rate-dependent Hysteresis Nonlinearity. Int. J. Autom. Comput. 2014, 11, 51–58. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Wang, J. Research on Hysteresis of Piezoceramic Actuator Based on the Duhem Model. Sci. World J. 2013, 2013, 814919. [Google Scholar] [CrossRef]
- Yu, S.; Feng, Y.; Yang, X. Extended state observer–based fractional order sliding-mode control of piezoelectric actuators. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2020, 235, 095965182093435. [Google Scholar] [CrossRef]
- Wang, Z.; Zhen, Z.; Mao, J.; Zhou, K. A Hammerstein-based model for rate-dependent hysteresis in piezoe-lectric actuator. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 1931–1936. [Google Scholar] [CrossRef]
- Wang, G.; Chen, G.; Bai, F. Modeling and identification of asymmetric Bouc–Wen hysteresis for piezoelectric actuator via a novel differential evolution algorithm. Sens. Actuators A Phys. 2015, 235, 105–118. [Google Scholar] [CrossRef]
- Zhu, Y.Y. System identification for process control: recent experience and outlook. Int. J. Model. Identif. Control. 2009, 6, 89–103. [Google Scholar] [CrossRef]
- Eskinat, E.; Johnson, S.H.; Luyben, W.L. Use of Hammerstein models in identification of nonlinear systems. AIChE J. 1991, 37, 255–268. [Google Scholar] [CrossRef]
- Jia, L.; Li, X.L. Identification of Hammerstein model: Review and prospect. Control. Theory Appl. 2014, 31, 1–10. [Google Scholar] [CrossRef]
- Bouc, R. Forced Vibration of Mechanical Systems with Hysteresis. In Proceedings of the Fourth Conference on Nonlinear Oscillations, Prague, Czech Republic, 5–9 September 1967. [Google Scholar]
- Wen, Y.K. Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Li, Z.; Xue, S.; Lin, W.; Tong, M. Training a robust reinforcement learning controller for the uncertain system based on policy gradient method. Neurocomputing 2018, 316, 313–321. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Sang, Y.; Yu, L.; Shu, H.; Li, S.; He, T.; Yang, L.; Zhang, X.; Yu, T. Applications of supercapacitor energy storage systems in microgrid with distributed generators via passive fractional-order sliding-mode control. Energy 2019, 187, 115905. [Google Scholar] [CrossRef]
- Chen, L.; Saikumar, N.; HosseinNia, S.H. Development of Robust Fractional-Order Reset Control. IEEE Trans. Control. Syst. Technol. 2019, 28, 1404–1417. [Google Scholar] [CrossRef] [Green Version]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (abc) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Lampinen, J.; Zelinka, I. On stagnation of the differential evolution algorithm. In Proceedings of the Mendel, 6th International Mendel Conference on Soft Computing 2000, Brno, Czech Republic, 7–9 June 2000. [Google Scholar]
- Available online: https://www.pi-china.cn/zh_cn/products/nanopositioning-piezo-flexure-stages/multi-axis-piezo-flexure-stages/p-7332-p-7333-xyz-piezo-nanopositioning-stage-201200/ (accessed on 10 December 2021).




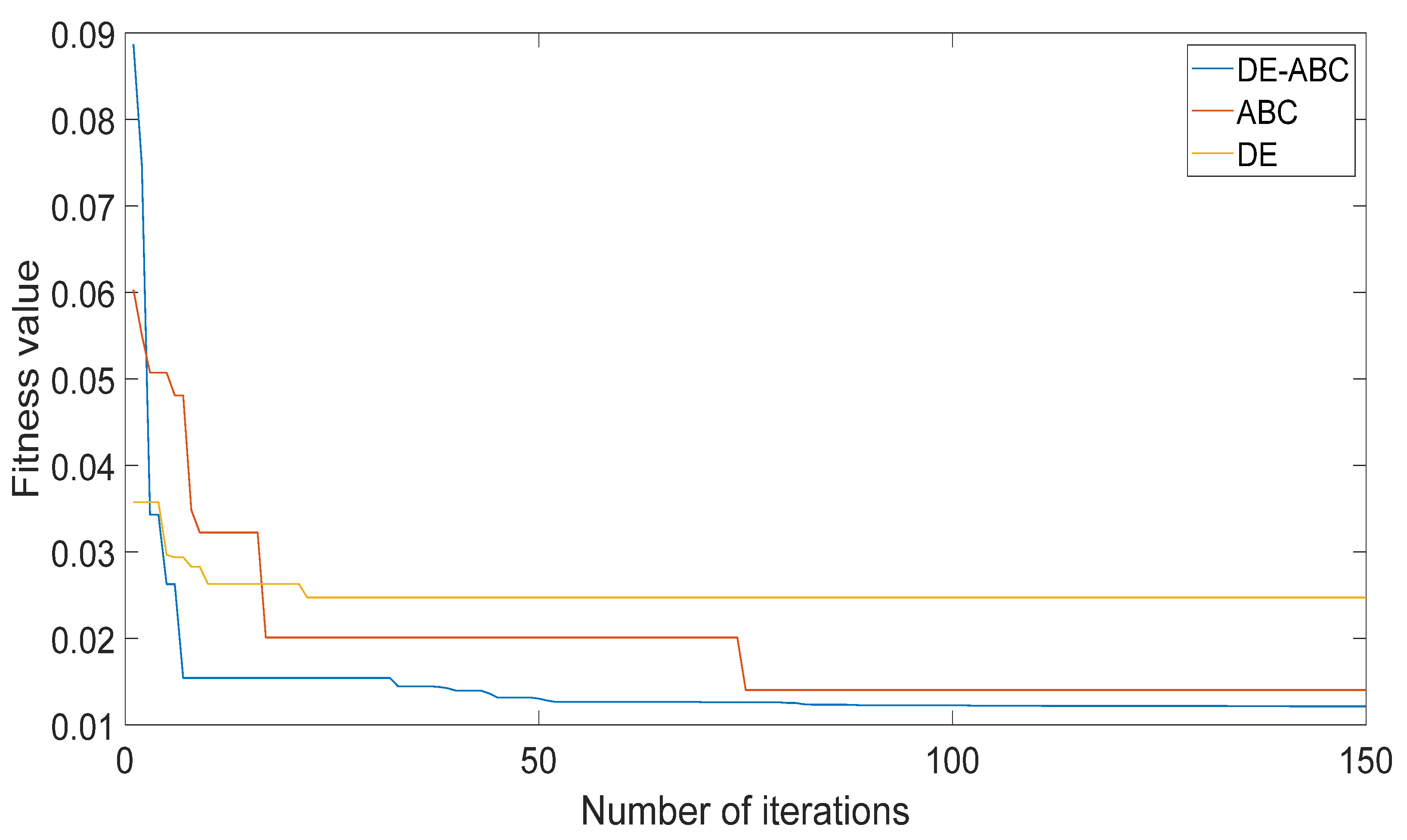

| Algorithms | Best Fitness Value |
|---|---|
| DE | 0.0247 |
| ABC | 0.0144 |
| DE-ABC | 0.0120 |
| x | y | α | β | γ | RE | RMSE |
|---|---|---|---|---|---|---|
| 0.0031 | 2.0000 | −1.2039 | 0.1111 | 0.0024 | 0.0208 | 0.0120 |
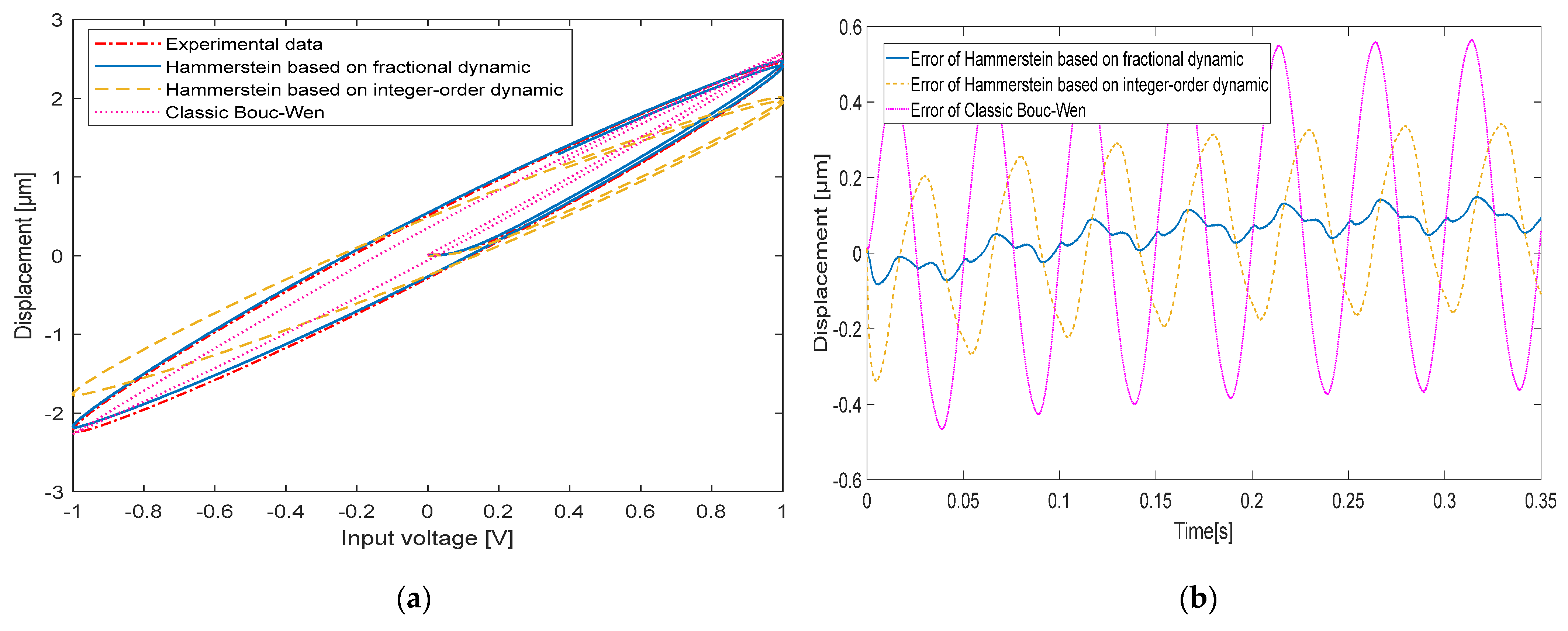
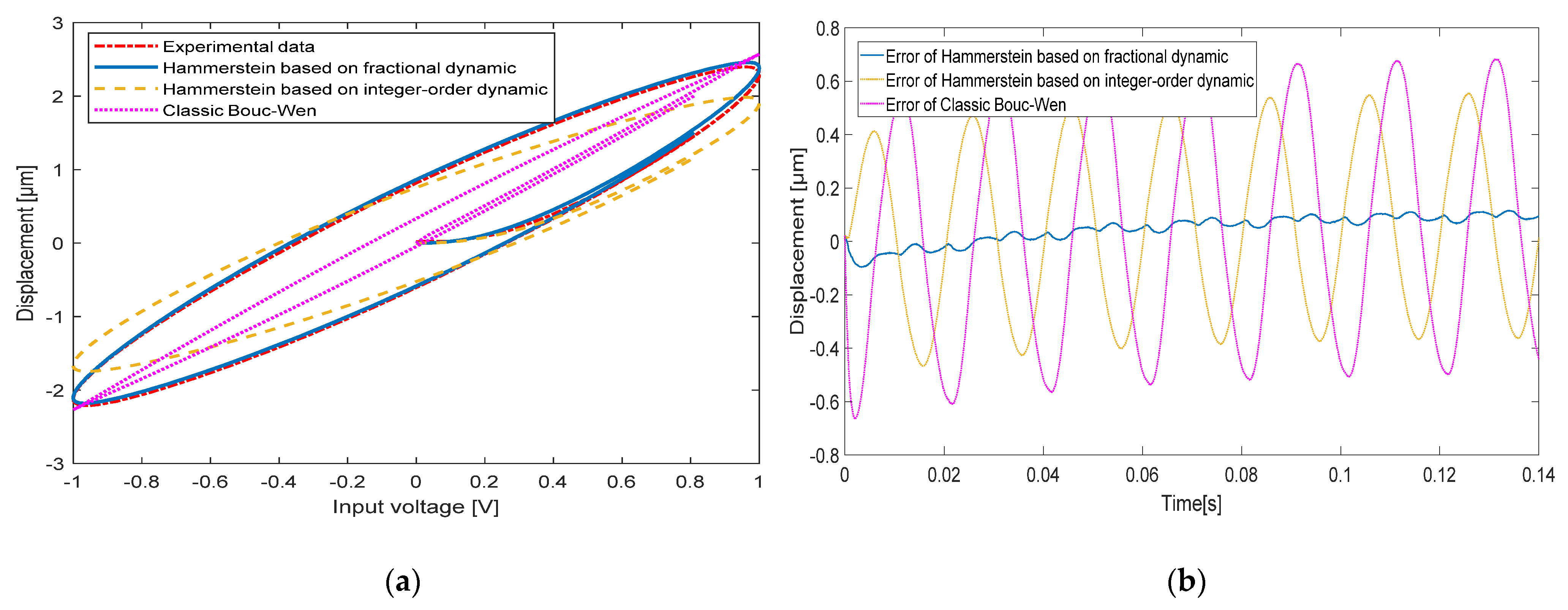
| Frequency | Model | Max Error | RMSE |
|---|---|---|---|
| 10 Hz | Classic Bouc-Wen | 0.5000 μm | 0.1127 |
| Hammerstein based on integer-order dynamic | 0.1144 μm | 0.0413 | |
| Hammerstein based on fractional dynamic | 0.0753 μm | 0.0264 | |
| 20 Hz | Classic Bouc-Wen | 0.5161 μm | 0.1095 |
| Hammerstein based on integer-order dynamic | 0.2572 μm | 0.0627 | |
| Hammerstein based on fractional dynamic | 0.0915 μm | 0.0244 | |
| 50 Hz | Classic Bouc-Wen | 0.6292 μm | 0.1411 |
| Hammerstein based on integer-order dynamic | 0.5266 μm | 0.1086 | |
| Hammerstein based on fractional dynamic | 0.0788 μm | 0.0228 | |
| 100 Hz | Classic Bouc-Wen | 1.2012 μm | 0.2698 |
| Hammerstein based on integer-order dynamic | 0.5039 μm | 0.1101 | |
| Hammerstein based on fractional dynamic | 0.0727 μm | 0.0221 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhao, Z.; Zhang, Y.; Li, D. Rate-Dependent Modeling of Piezoelectric Actuators for Nano Manipulation Based on Fractional Hammerstein Model. Micromachines 2022, 13, 42. https://doi.org/10.3390/mi13010042
Yang L, Zhao Z, Zhang Y, Li D. Rate-Dependent Modeling of Piezoelectric Actuators for Nano Manipulation Based on Fractional Hammerstein Model. Micromachines. 2022; 13(1):42. https://doi.org/10.3390/mi13010042
Chicago/Turabian StyleYang, Liu, Zhongyang Zhao, Yi Zhang, and Dongjie Li. 2022. "Rate-Dependent Modeling of Piezoelectric Actuators for Nano Manipulation Based on Fractional Hammerstein Model" Micromachines 13, no. 1: 42. https://doi.org/10.3390/mi13010042





