A Temperature Drift Suppression Method of Mode-Matched MEMS Gyroscope Based on a Combination of Mode Reversal and Multiple Regression
Abstract
:1. Introduction
2. Honeycomb Disk Resonator Gyroscope
3. Zero-Bias Temperature Drift Compensation Method
3.1. Zero-Bias Drift Principle
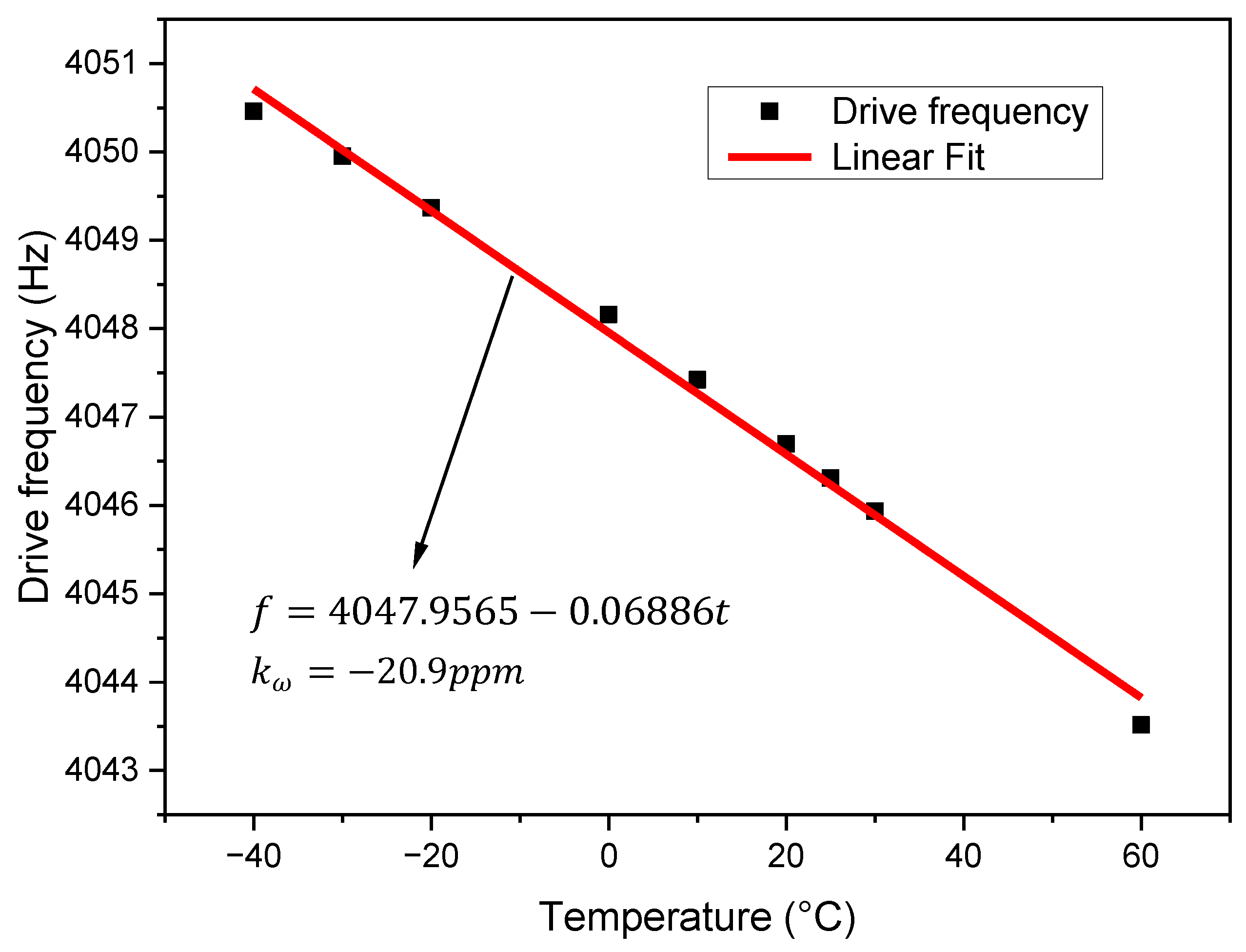
3.2. Temperature Self-Sensing Based on the Frequency of the Gyroscope
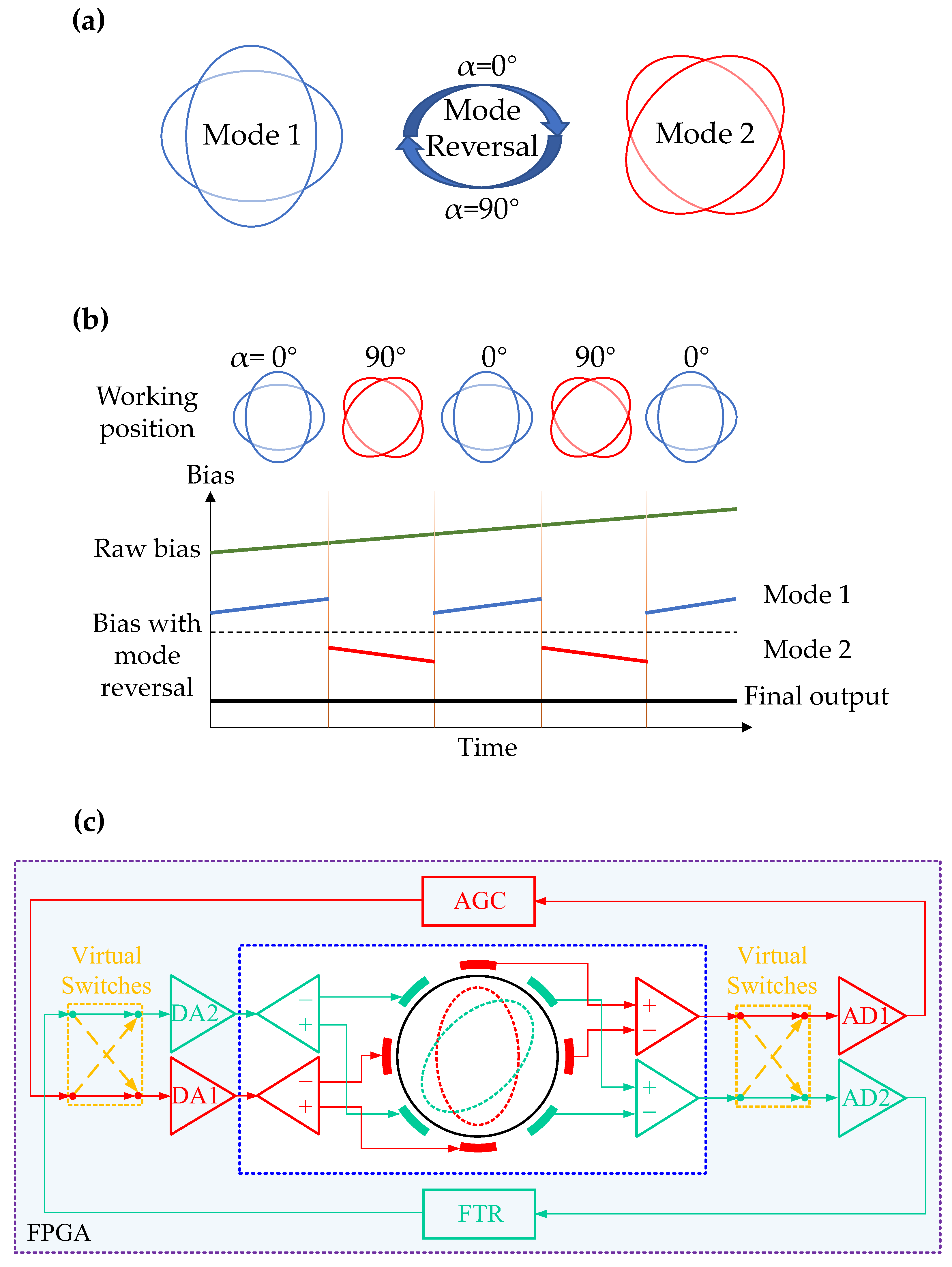
3.3. Suppression of Zero Bias Drift by Mode Reversal
3.4. Real-Time Rapid Temperature Change Compensation Scheme in Mode Reversal
4. Temperature Compensation Experiments
4.1. The Experimental Setup
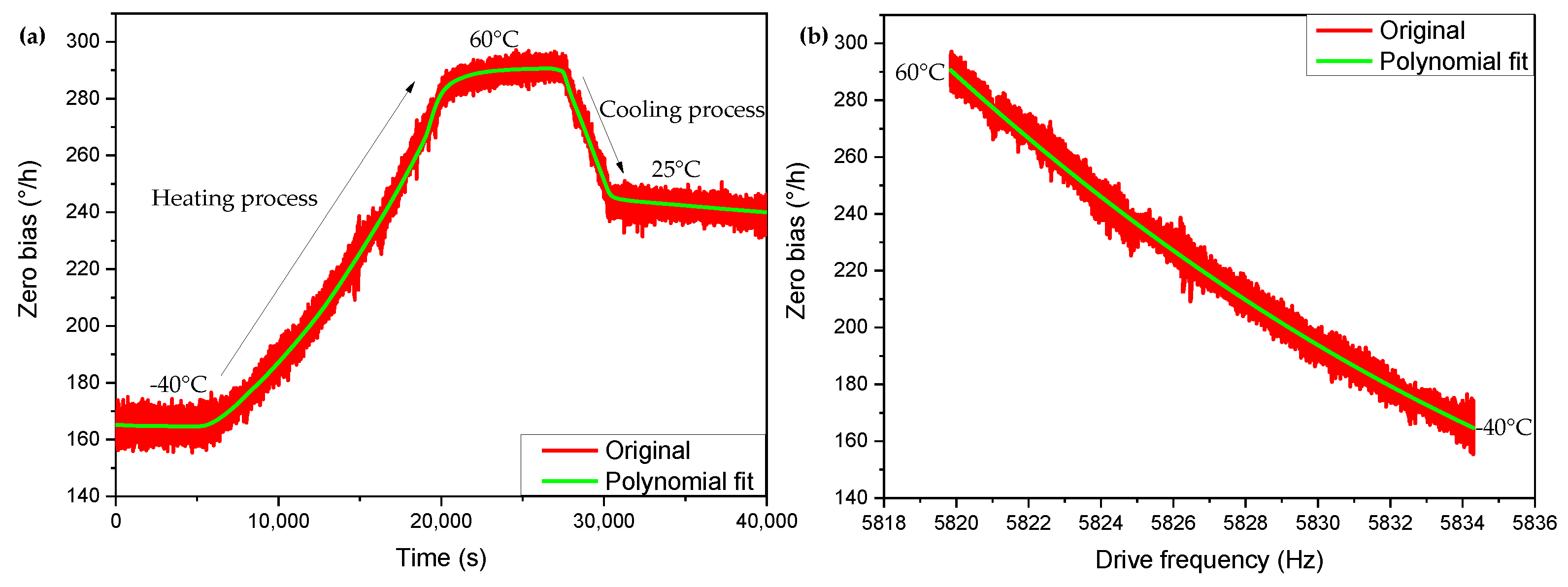
4.2. Polynomial Compensation in Slowly Varying Temperature Condition
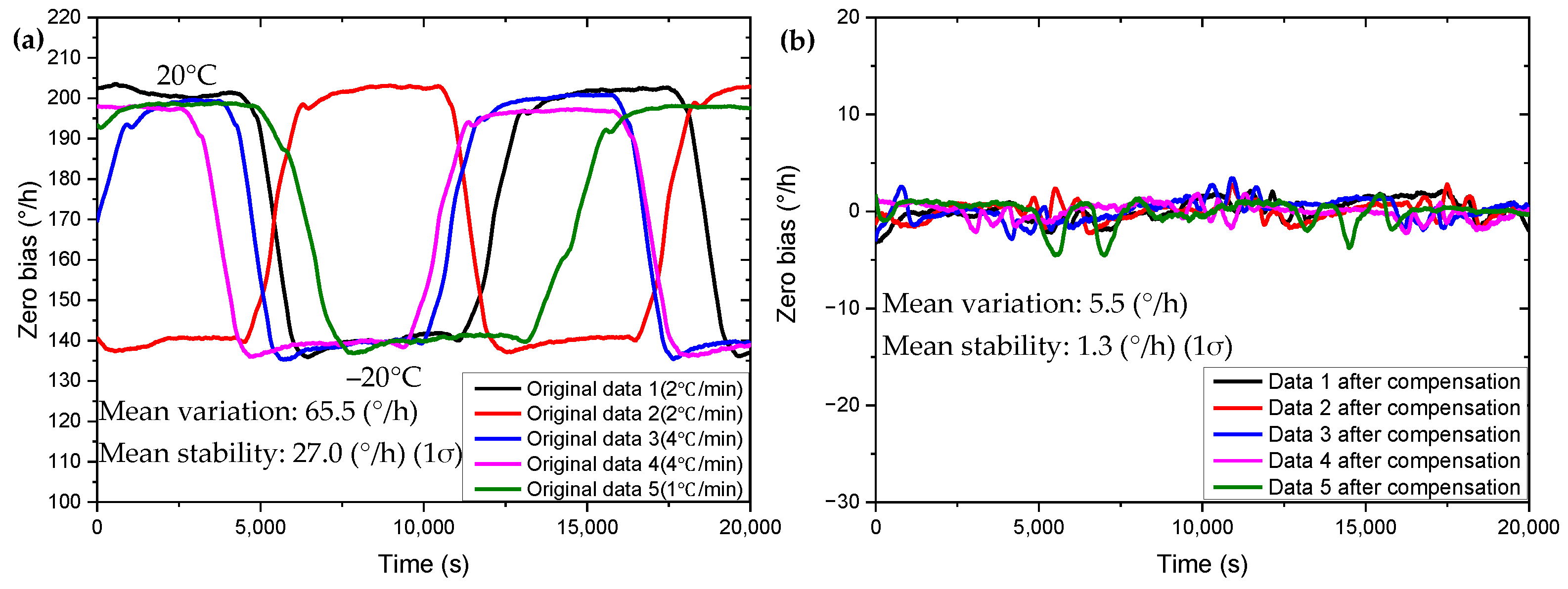
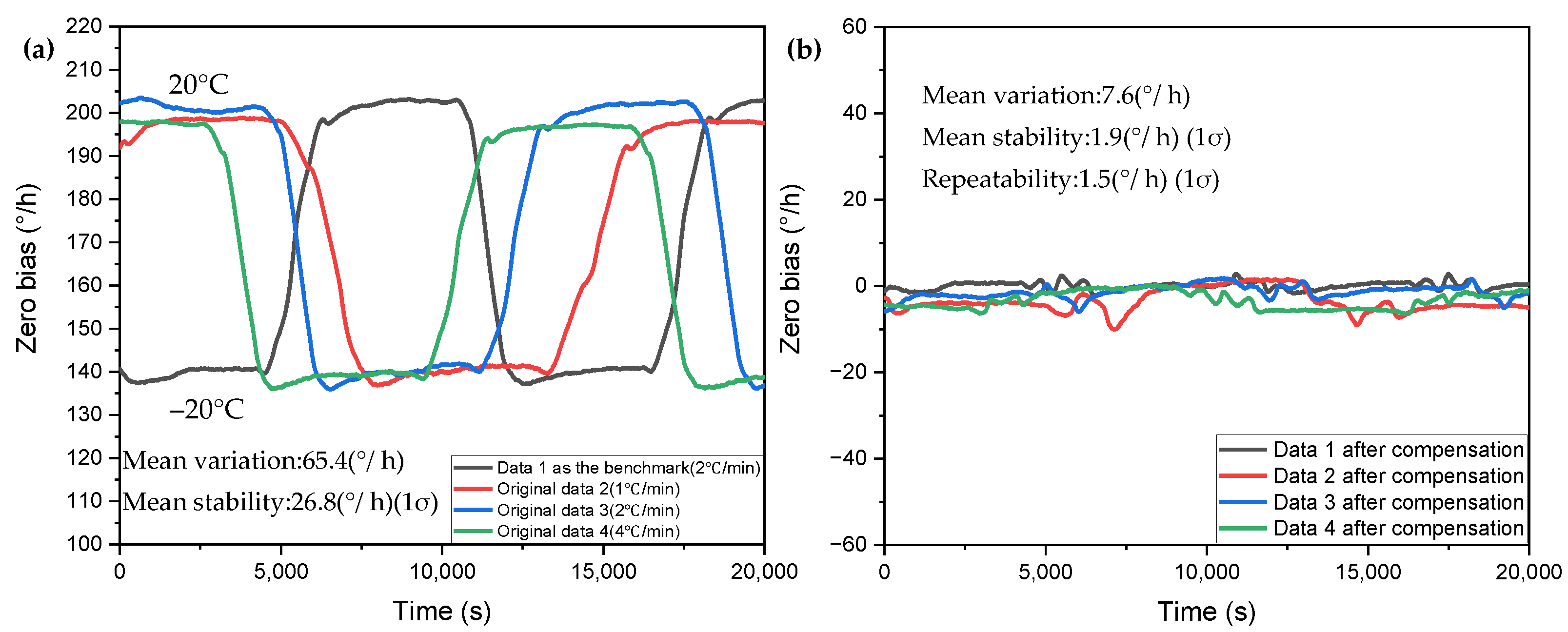
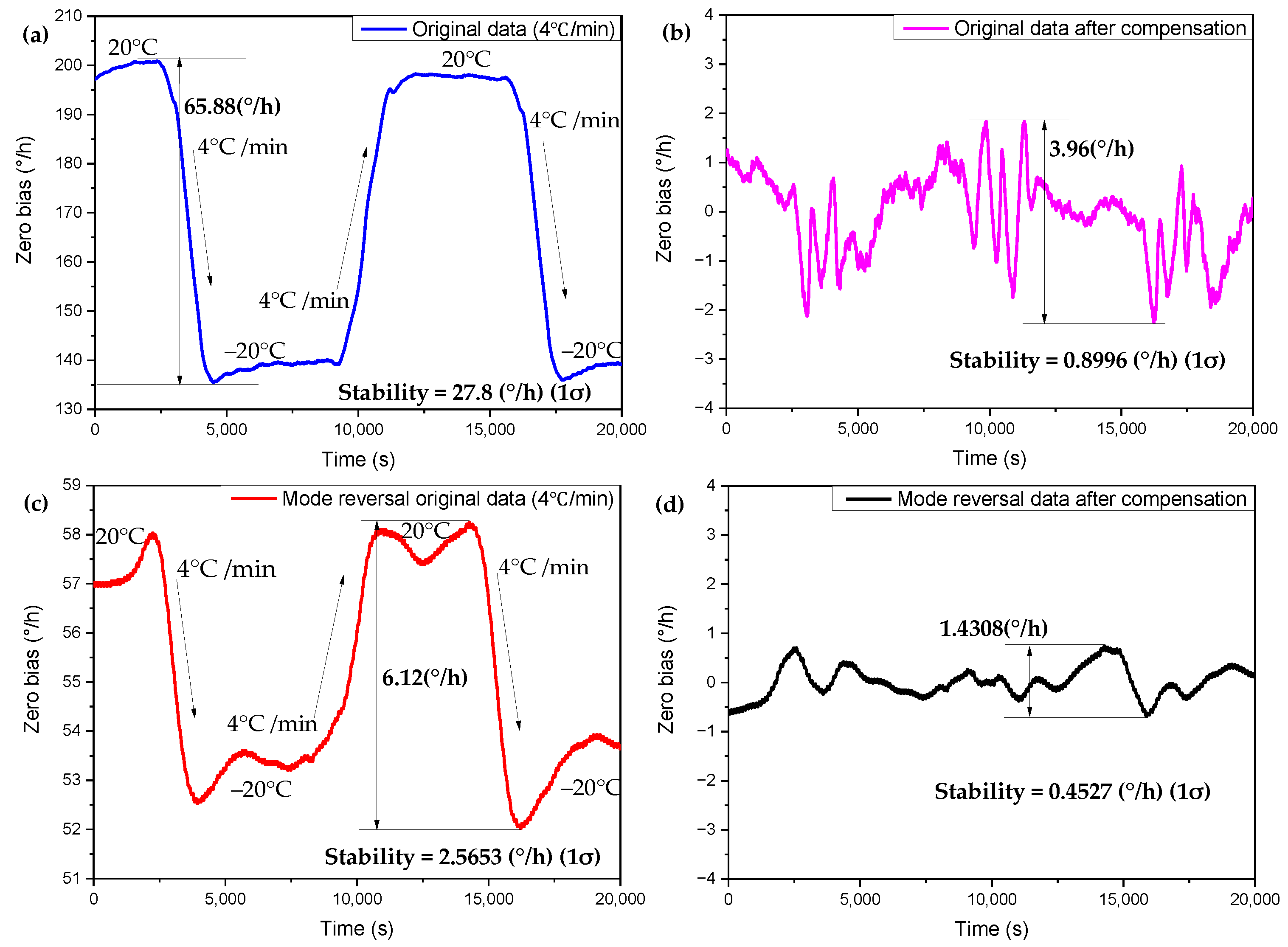
4.3. Multiple Regression Compensation under Temperature Cycling Condition
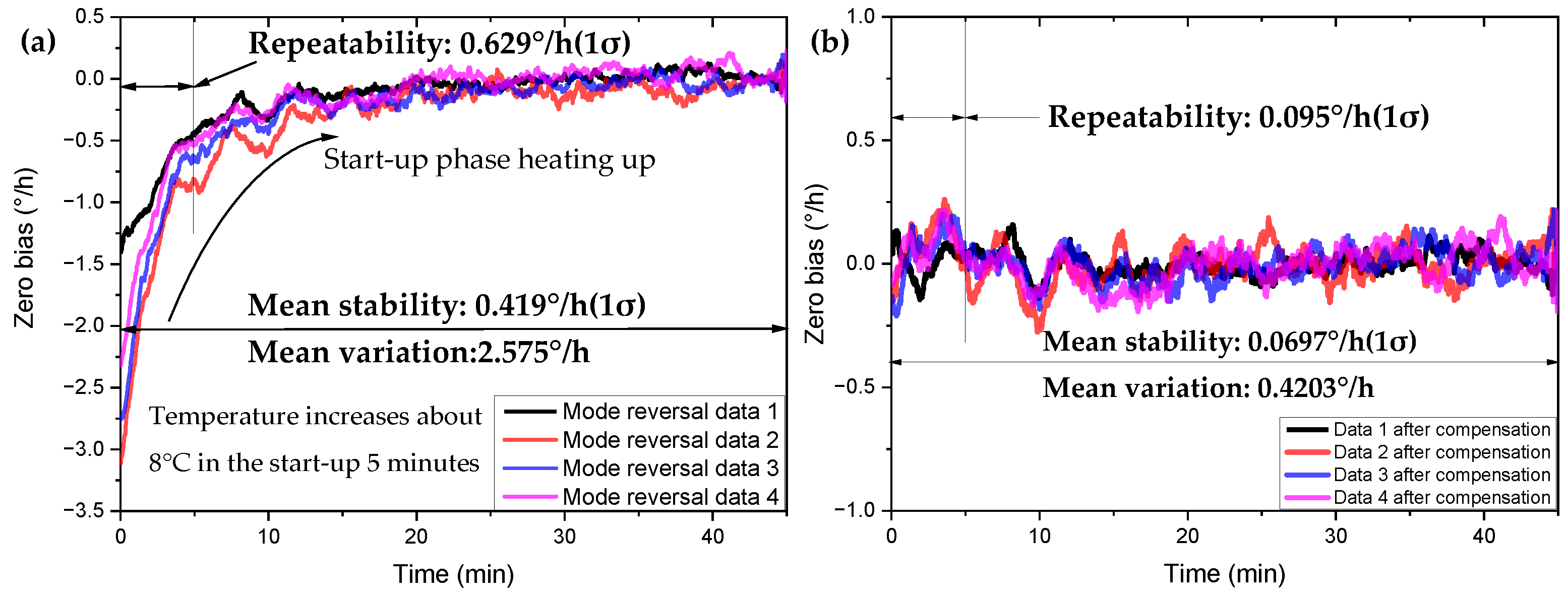
4.4. Rapid Temperature Change Compensation in Mode Reversal
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tazartes, D. An historical perspective on inertial navigation systems. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 25–26 February 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Wahlstrom, J.; Skog, I. Fifteen Years of Progress at Zero Velocity: A Review. IEEE Sens. J. 2020, 21, 1139–1151. [Google Scholar] [CrossRef]
- Passaro, V.M.N.; Cuccovillo, A.; Vaiani, L.; De Carlo, M.; Campanella, C.E. Gyroscope Technology and Applications: A Review in the Industrial Perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Cheng, F.; Li, B.; Le, C.; Chao, L.; Ke, S. Research development of silicon MEMS gyroscopes: A review. Microsyst. Technol. 2015, 21, 2053–2066. [Google Scholar] [CrossRef]
- Piyabongkarn, D.; Rajamani, R.; Greminger, M. The development of a MEMS gyroscope for absolute angle measurement. IEEE Trans. Control Syst. Technol. 2005, 13, 185–195. [Google Scholar] [CrossRef]
- Guo, Z.; Fu, P.; Liu, D.; Huang, M. Design and FEM simulation for a novel resonant silicon MEMS gyroscope with temperature compensation function. Microsyst. Technol. 2017, 24, 1453–1459. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Sheng, X.; Wang, S.; Yang, B.; Huang, L. A Novel Temperature Compensation Method for a MEMS Gyroscope Oriented on a Periphery Circuit. Int. J. Adv. Robot. Syst. 2013, 10, 327. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Y.; Han, Z.; Shao, X.; Gao, J.; Huang, K.; Shi, Y.; Tang, J.; Shen, C.; Liu, J. Pole-Zero Temperature Compensation Circuit Design and Experiment for Dual-Mass MEMS Gyroscope Bandwidth Expansion. IEEE/ASME Trans. Mechatron. 2019, 24, 677–688. [Google Scholar] [CrossRef]
- Cui, M.; Huang, Y.; Wang, W.; Cao, H. MEMS Gyroscope Temperature Compensation Based on Drive Mode Vibration Characteristic Control. Micromachines 2019, 10, 248. [Google Scholar] [CrossRef]
- Ahn, C.; Hong, V.; Park, W.; Yang, Y.; Chen, Y.; Ng, E.; Huynh, J.; Challoner, A.; Goodson, K.; Kenny, T. On-chip ovenization of encapsulated Disk Resonator Gyroscope (drg). In Proceedings of the 2015 Transducers—2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 39–42. [Google Scholar]
- Yang, D.; Woo, J.-K.; Lee, S.; Mitchell, J.; Challoner, A.D.; Najafi, K. A Micro Oven-Control System for Inertial Sensors. J. Microelectromechanical Syst. 2017, 26, 507–518. [Google Scholar] [CrossRef]
- Shcheglov, K.; Evans, C.; Gutierrez, R.; Tang, T. Temperature dependent characteristics of the JPL silicon MEMS gyroscope. In Proceedings of the 2000 IEEE Aerospace Conference. Proceedings (Cat. No.00TH8484), Big Sky, MT, USA, 25 March 2000. [Google Scholar] [CrossRef]
- Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing. Sens. Actuators A Phys. 2013, 201, 517–524. [Google Scholar] [CrossRef]
- Gunhan, Y.; Unsal, D. Polynomial degree determination for temperature dependent error compensation of inertial sensors. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 1209–1212. [Google Scholar] [CrossRef]
- Cui, J.; Yan, G.; Zhao, Q. Enhanced temperature stability of scale factor in MEMS gyroscope based on multi parameters fusion compensation method. Measurement 2019, 148, 106947. [Google Scholar] [CrossRef]
- Shiau, J.K.; Ma, D.M.; Huang, C.X.; Chang, M.Y. MEMS Gyroscope Null Drift and Compensation Based on Neural Network. Adv. Mater. Res. 2011, 255–260, 2077–2081. [Google Scholar] [CrossRef]
- Araghi, G.; Landry, R.J. Temperature compensation model of MEMS inertial sensors based on neural network. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 301–309. [Google Scholar]
- Chong, S.; Rui, S.; Jie, L.; Xiaoming, Z.; Jun, T.; Yunbo, S.; Jun, L.; Huiliang, C. Temperature drift modeling of MEMS gyroscope based on genetic-Elman neural network. Mech. Syst. Signal Process. 2016, 72, 897–905. [Google Scholar] [CrossRef]
- Gu, H.; Liu, X.; Zhao, B.; Zhou, H. The In-Operation Drift Compensation of MEMS Gyroscope Based on Bagging-ELM and Improved CEEMDAN. IEEE Sens. J. 2019, 19, 5070–5077. [Google Scholar] [CrossRef]
- Tu, Y.-H.; Peng, C.-C. An ARMA-Based Digital Twin for MEMS Gyroscope Drift Dynamics Modeling and Real-Time Compensation. IEEE Sens. J. 2020, 21, 2712–2724. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Y.; Shen, C.; Liu, Y.; Wang, X. Temperature Energy Influence Compensation for MEMS Vibration Gyroscope Based on RBF NN-GA-KF Method. Shock Vib. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Xu, C. Temperature Drift Compensation of MEMS Inertial Sensor Based on IA-BP Algorithm. In Proceedings of the 2021 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 27–28 August 2021; pp. 547–550. [Google Scholar] [CrossRef]
- Feng, Y.; Li, X.; Zhang, X. An Adaptive Compensation Algorithm for Temperature Drift of Micro-Electro-Mechanical Systems Gyroscopes Using a Strong Tracking Kalman Filter. Sensors 2015, 15, 11222–11238. [Google Scholar] [CrossRef]
- Chang, L.; Cao, H.; Shen, C. Dual-Mass MEMS Gyroscope Parallel Denoising and Temperature Compensation Processing Based on WLMP and CS-SVR. Micromachines 2020, 11, 586. [Google Scholar] [CrossRef]
- Miao, T.; Xu, Y.; Li, Q.; Sun, J.; Wu, X.; Xiao, D.; Hu, X. Temperature Drift Self-calibration for Honeycomb-like Disk Resonator Gyroscope. In Proceedings of the 2022 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Avignon, France, 8–11 May 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Miao, T.; Li, Q.; Hu, X.; Wu, X.; Wu, W.; Xiao, D. Virtual Rotating MEMS Gyrocompassing with Honeycomb Disk Resonator Gyroscope. IEEE Electron. Device Lett. 2022, 43, 1331–1334. [Google Scholar] [CrossRef]
- Hou, Z.; Xiao, D.; Wu, X.; Dong, P.; Niu, Z.; Zhou, Z.; Zhang, X. Effect of parasitic resistance on a MEMS vibratory gyroscopes due to temperature fluctuations. In Proceedings of the 2011 6th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Kaohsiung, Taiwan, 20–23 February 2011; pp. 293–296. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Zhang, Y.; Zhou, X.; Wu, X.; Xiao, D. Honeycomb-Like Disk Resonator Gyroscope. IEEE Sens. J. 2019, 20, 85–94. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.; Wang, P.; Zhang, Y.; Zhou, X.; Yu, L.; Wu, X.; Xiao, D. 0.015 Degree-Per-Hour Honeycomb Disk Resonator Gyroscope. IEEE Sens. J. 2020, 21, 7326–7338. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, S.; Sun, J.; Lu, K.; Xu, Y.; Li, Q.; Wu, X.; Xiao, D. A Rate-Integrating Honeycomb Disk Resonator Gyroscope With 0.038°/h Bias Instability and °7000°/s Measurement Range. IEEE Electron. Device Lett. 2021, 42, 581–584. [Google Scholar] [CrossRef]
- Hopcroft, M.A.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectromechanical Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef]
- Trusov, A.A.; Phillips, M.R.; Mccammon, G.H.; Rozelle, D.M.; Meyer, A.D. Continuously self-calibrating CVG system using hemispherical resonator gyroscopes. In Proceedings of the 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings, Hapuna Beach, HI, USA, 23–26 March 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Ge, H.H.; Liu, J.Y.; Buchanan, B. Bias self-calibration techniques using silicon disc resonator gyroscope. In Proceedings of the 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings, Hapuna Beach, HI, USA, 23–26 March 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Wibbeler, J.; Pfeifer, G.; Hietschold, M. Parasitic charging of dielectric surfaces in capacitive microelectromechanical systems (MEMS). Sens. Actuators A Phys. 1998, 71, 74–80. [Google Scholar] [CrossRef]
- Liu, N.; Su, Y.; Tong, X.; Han, G.; Si, C.; Li, Z.; Ning, J. The effect of parasitic charge on the output stability of MEMS gyroscopes. J. Semicond. 2018, 39, 084002. [Google Scholar] [CrossRef]
- Norouzpour-Shirazi, A.; Ayazi, F. A Dual-Mode Actuation and Sensing Scheme for In-Run Calibration of Bias and Scale Factor Errors in Axisymmetric Resonant Gyroscopes. IEEE Sens. J. 2017, 18, 1993–2005. [Google Scholar] [CrossRef]
- Shen, Q.; Chang, H.; Wu, Y.; Xie, J. Turn-on bias behavior prediction for micromachined Coriolis vibratory gyroscopes. Measurement 2018, 131, 380–393. [Google Scholar] [CrossRef]
- Bu, F.; Guo, S.; Fan, B.; Wang, Y. Effect of Quadrature Control Mode on ZRO Drift of MEMS Gyroscope and Online Compensation Method. Micromachines 2022, 13, 419. [Google Scholar] [CrossRef]
- Challoner, A.D.; Ge, H.H.; Liu, J.Y. Boeing Disc Resonator Gyroscope. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014. [Google Scholar]
- Johnson, B.; Albrecht, C.; Braman, T.; Christ, K.; Duffy, P.; Endean, D.; Gnerlich, M.; Reinke, J. Development of a Navigation-Grade MEMS IMU. In Proceedings of the 2021 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kailua-Kona, HI, USA, 22–25 March 2021; pp. 1–4. [Google Scholar] [CrossRef]




| Type of Data Processing | Zero-Bias Variation (°/h) | Zero-Bias Stability (°/h) | Zero-Bias Mean (°/h) |
|---|---|---|---|
| original data | 129.4627 | 15.7944 | - |
| First-order polynomial compensation | 18.7559 | 3.9337 | |
| Quadratic polynomial compensation | 13.1759 | 2.4561 | |
| Cubic polynomial compensation | 13.1440 | 2.4649 | |
| Quartic polynomial compensation | 13.9183 | 2.3488 | 0.0024 |
| Quintic polynomial compensation | 13.9168 | 2.3489 | 0.0053 |
| Sixth degree polynomial compensation | 14.2046 | 2.3323 | 0.5081 |
| Seventh degree polynomial compensation | 14.6513 | 2.3204 | 0.1665 |
| Eighth degree polynomial compensation | 14.5726 | 2.3096 | 0.1142 |
| Ninth degree polynomial compensation | 14.7923 | 2.3076 | −0.0344 |
| 10th degree polynomial compensation | 14.7265 | 2.3053 | 0.0996 |
| Type of Data Processing | Zero-Bias Variation (°/h) | Zero-Bias Stability (°/h) | Zero-Bias Mean (°/h) |
|---|---|---|---|
| Original data 1 (2 °C/min) Data 1 after compensation | 67.68 5.40 | 27.8405 1.1256 | - −0.1474 |
| Original data 2 (2 °C/min) Data 2 after compensation | 66.24 5.04 | 28.3720 1.1557 | - 0.0298 |
| Original data 3 (4 °C/min) Data 3 after compensation | 65.88 6.48 | 27.8385 1.1943 | - 0.1296 |
| Original data 4 (4 °C/min) Data 4 after compensation | 65.52 3.96 | 27.4579 0.8996 | - −0.0535 |
| Original data 5 (1 °C/min) Data 5 after compensation | 62.28 6.48 | 23.5128 1.9715 | - 0.0956 |
| Type of Data Processing | Zero-Bias Variation (°/h) | Zero-Bias Stability (°/h) | Zero-Bias Mean (°/h) |
|---|---|---|---|
| Benchmark-data 1 (2 °C/min) Data 1 after compensation | 66.24 5.04 | 28.3720 1.1557 | - 0.0298 |
| Original data 2 (1 °C/min) Data 2 after compensation | 62.28 11.06 | 23.5128 3.3215 | - −3.5240 |
| Original data 3 (2 °C/min) Data 3 after compensation | 67.6 87.92 | 27.8405 1.6827 | - −1.3837 |
| Original data 4 (4 °C/min) Data 4 after compensation | 65.5 26.48 | 27.4579 1.5994 | - −2.6233 |
| Type of Data Processing | Zero-Bias Variation (°/h) | Zero Bias Stability (°/h) (1σ) | Zero-Bias Mean (°/h) |
|---|---|---|---|
| Mode reversal data 1 Data 1 after compensation | 1.5424 0.3031 | 0.2890 0.0463 | - |
| Mode reversal data 2 Data 2 after compensation | 3.2637 0.5375 | 0.5184 0.0838 | - |
| Mode reversal data 3 Data 3 after compensation | 2.9499 0.4296 | 0.4678 0.0708 | - |
| Mode reversal data 4 Data 4 after compensation | 2.5438 0.4111 | 0.4009 0.0780 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Miao, T.; Li, Q.; Wang, P.; Wu, X.; Xi, X.; Xiao, D. A Temperature Drift Suppression Method of Mode-Matched MEMS Gyroscope Based on a Combination of Mode Reversal and Multiple Regression. Micromachines 2022, 13, 1557. https://doi.org/10.3390/mi13101557
Chen L, Miao T, Li Q, Wang P, Wu X, Xi X, Xiao D. A Temperature Drift Suppression Method of Mode-Matched MEMS Gyroscope Based on a Combination of Mode Reversal and Multiple Regression. Micromachines. 2022; 13(10):1557. https://doi.org/10.3390/mi13101557
Chicago/Turabian StyleChen, Liangqian, Tongqiao Miao, Qingsong Li, Peng Wang, Xuezhong Wu, Xiang Xi, and Dingbang Xiao. 2022. "A Temperature Drift Suppression Method of Mode-Matched MEMS Gyroscope Based on a Combination of Mode Reversal and Multiple Regression" Micromachines 13, no. 10: 1557. https://doi.org/10.3390/mi13101557
APA StyleChen, L., Miao, T., Li, Q., Wang, P., Wu, X., Xi, X., & Xiao, D. (2022). A Temperature Drift Suppression Method of Mode-Matched MEMS Gyroscope Based on a Combination of Mode Reversal and Multiple Regression. Micromachines, 13(10), 1557. https://doi.org/10.3390/mi13101557






