Structure Design and Working Characteristics Analysis of Direct-Drive Giant Magnetostrictive Injector
Abstract
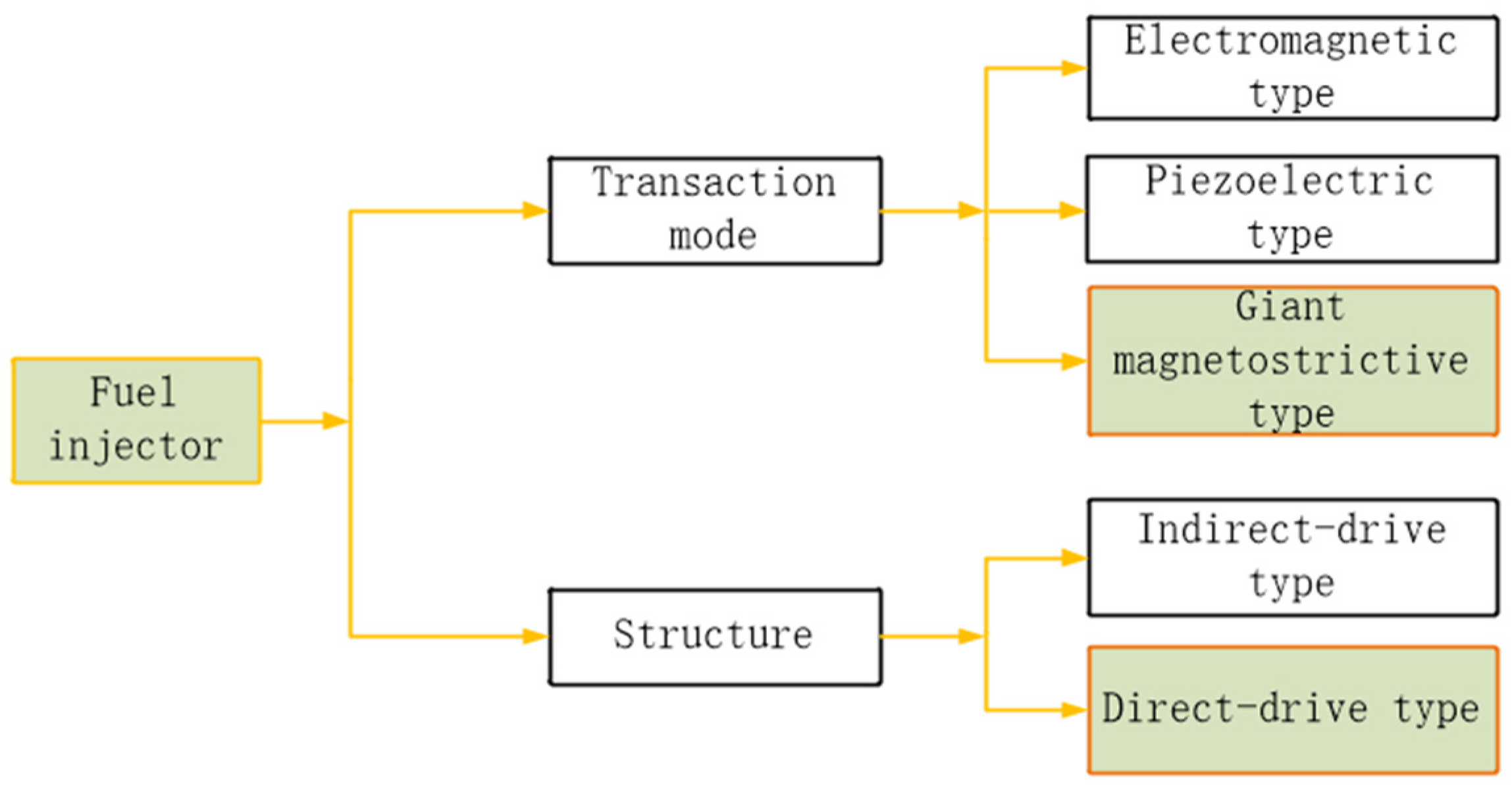
:1. Introduction
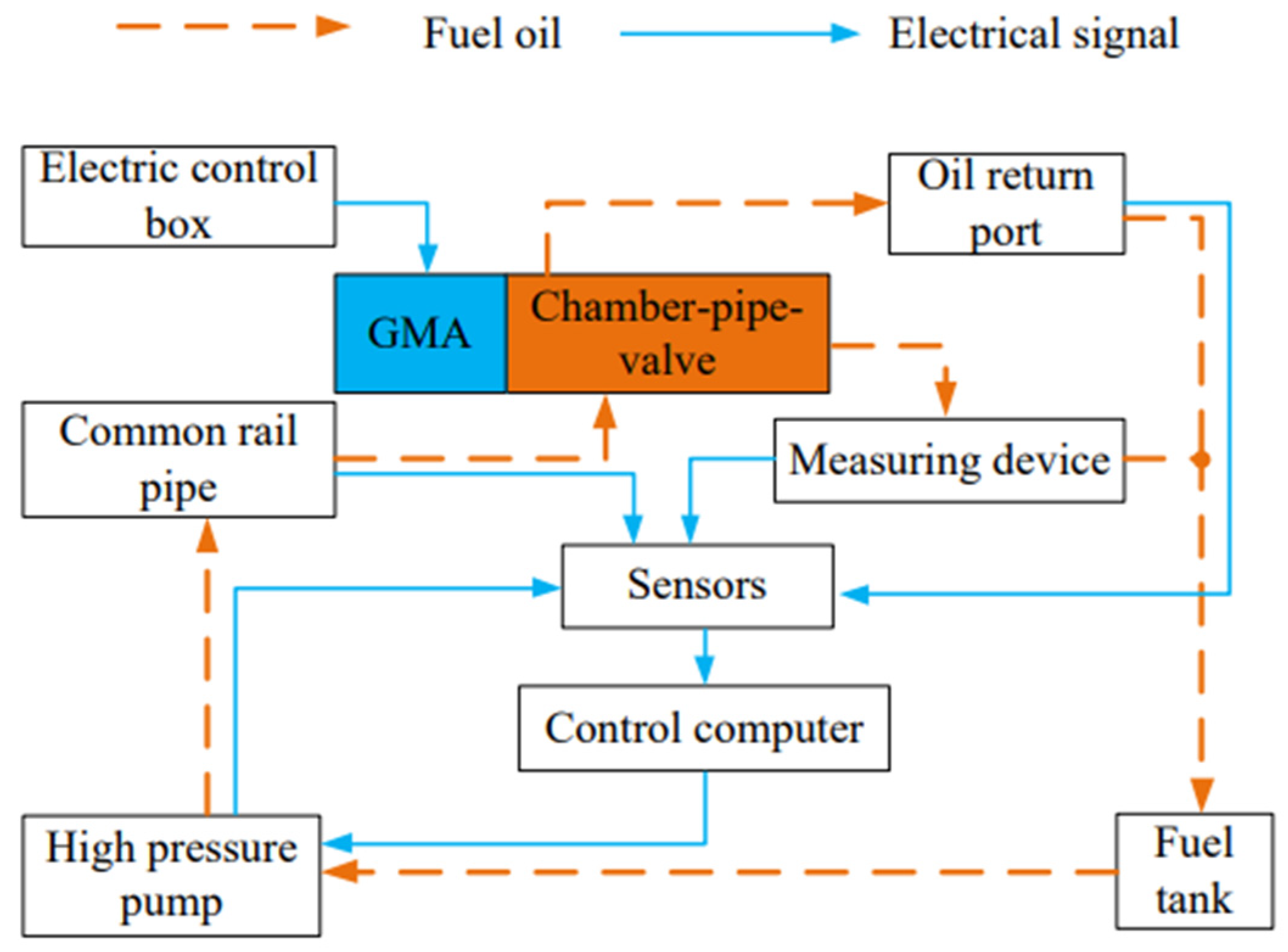
2. Structure Design and Theoretical Model
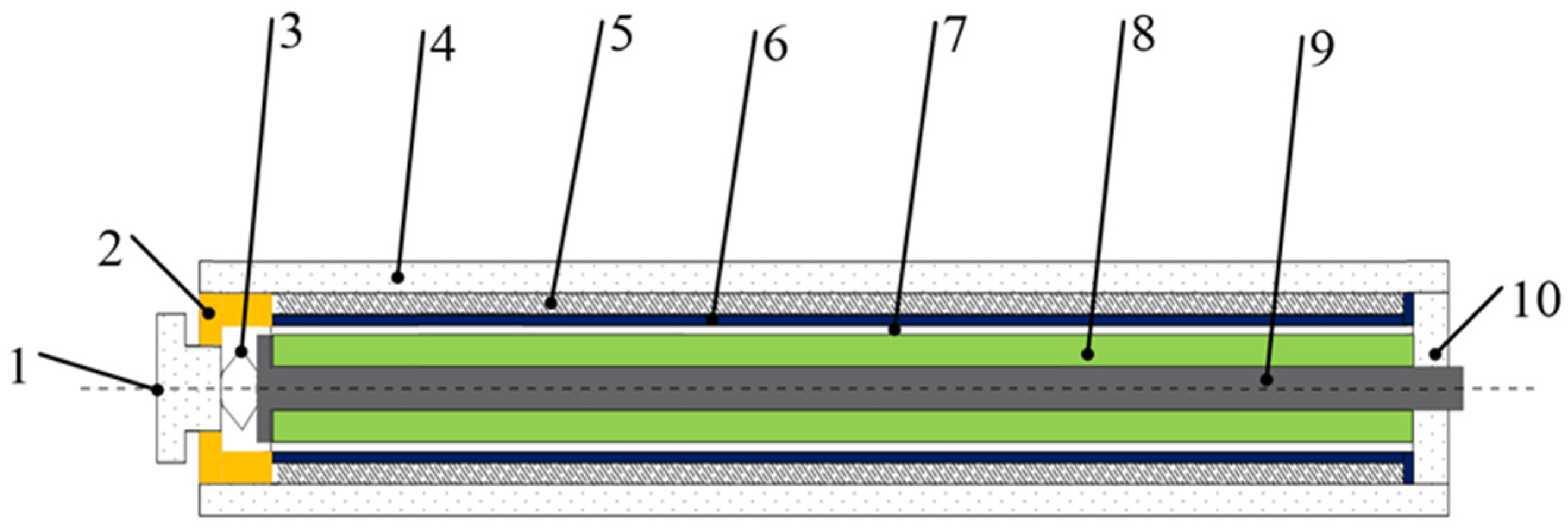
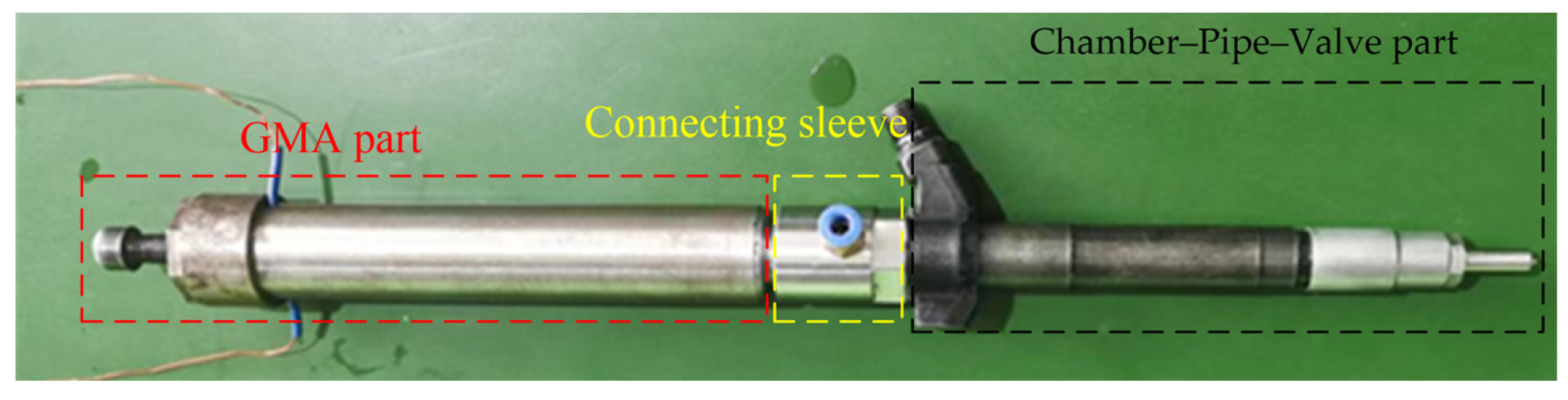
2.1. GMI Structure Design
2.2. GMA Model
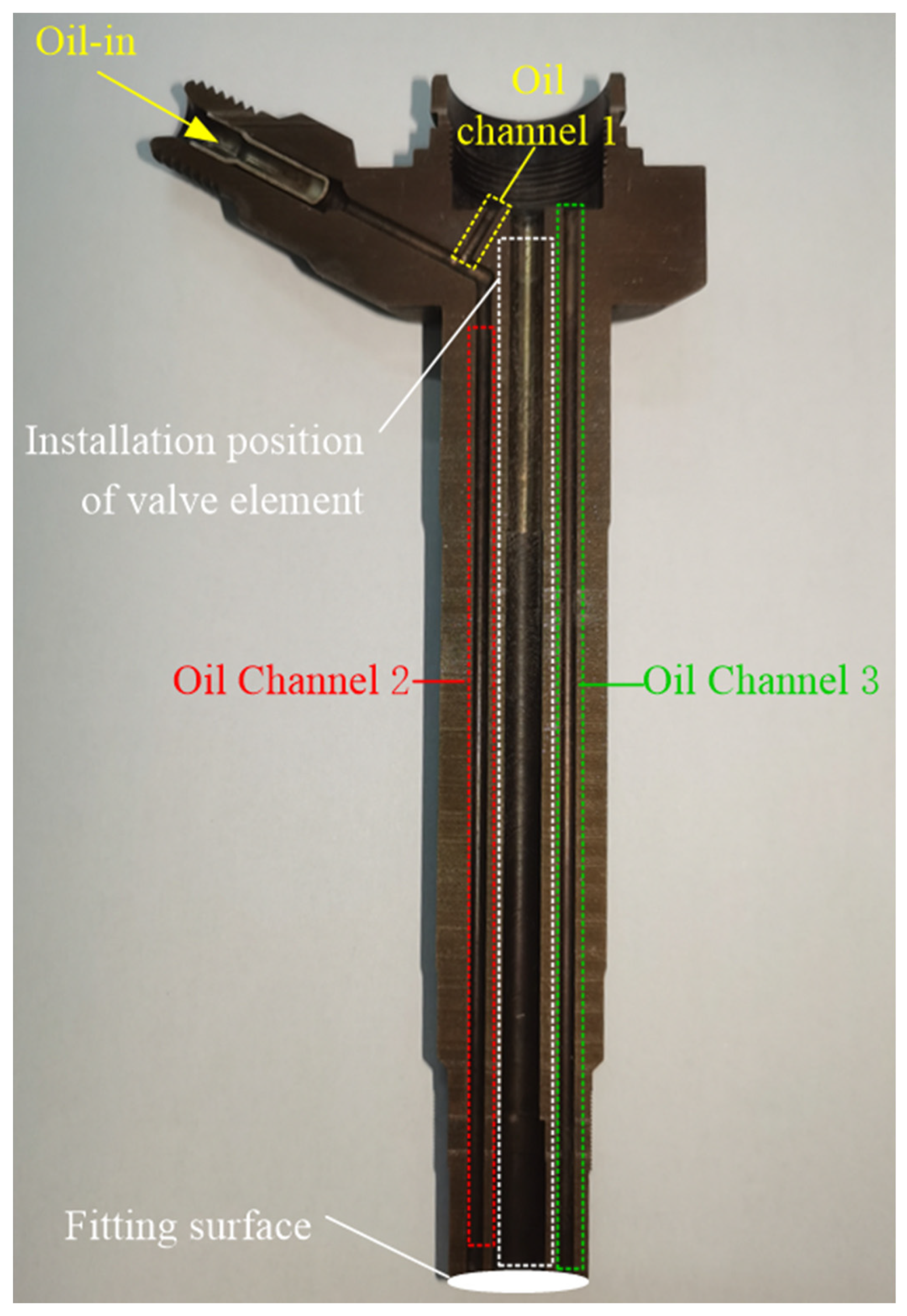
2.3. Model of Chamber–Pipe–Valve
2.3.1. Cavity Model
2.3.2. Pipeline Model
2.3.3. Valve Element Model
2.3.4. Leak Module Model
2.3.5. Throttle Model
3. AMESim Simulation Model Building and Experimental Verification
3.1. Introduction to Software
3.2. Establishment of Direct-Drive GMI Simulation Model
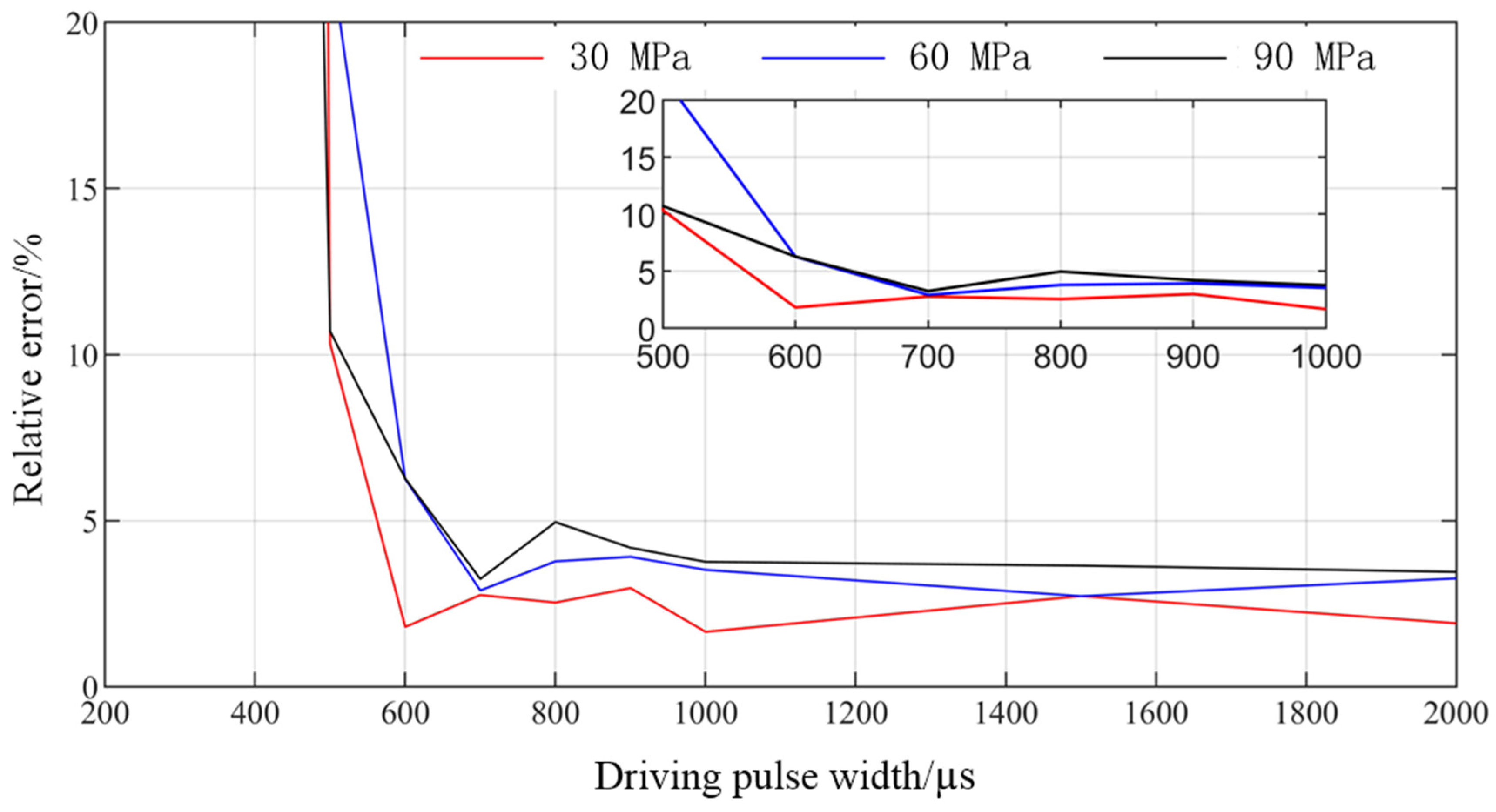
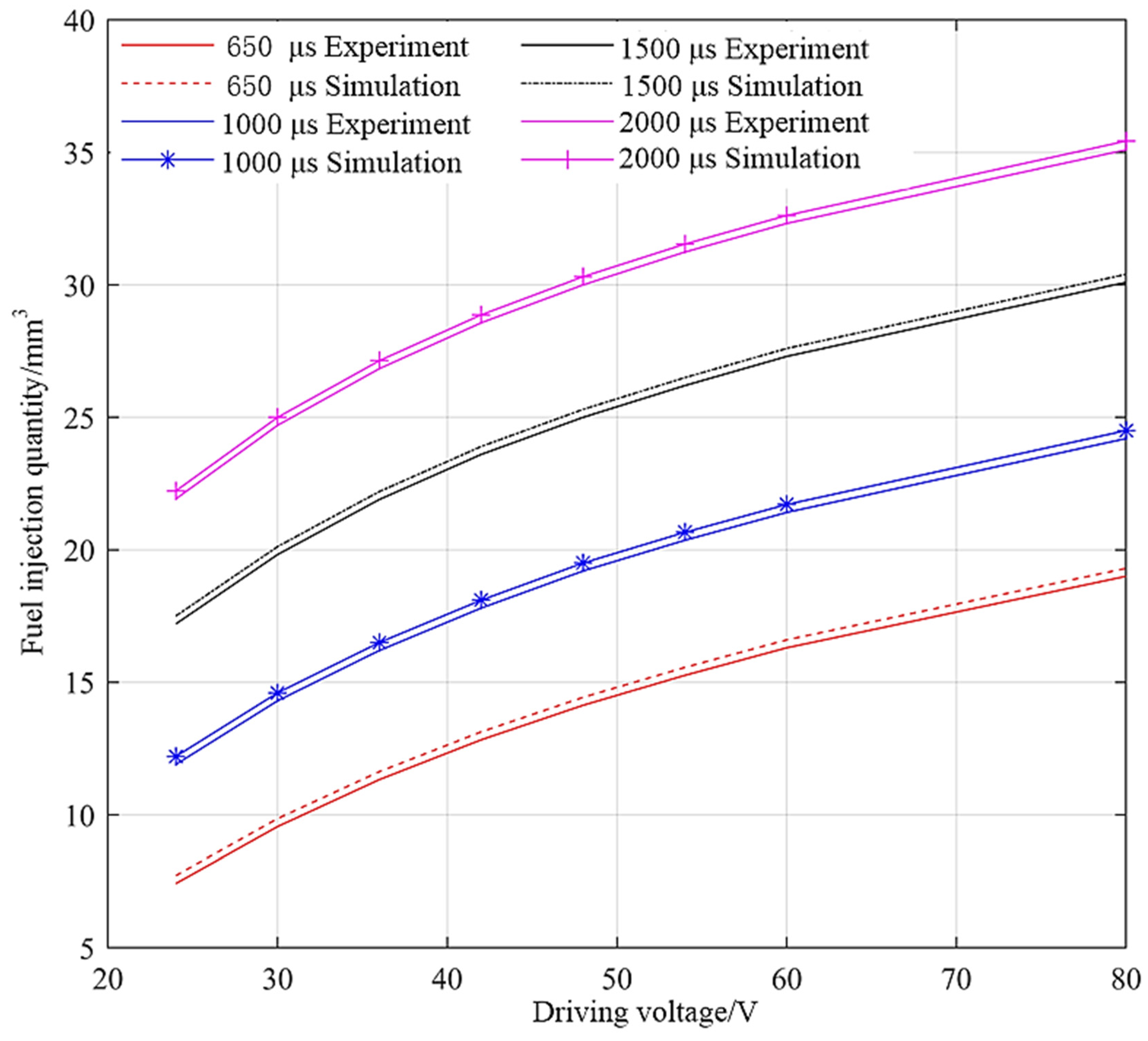
3.3. Experimental Verification
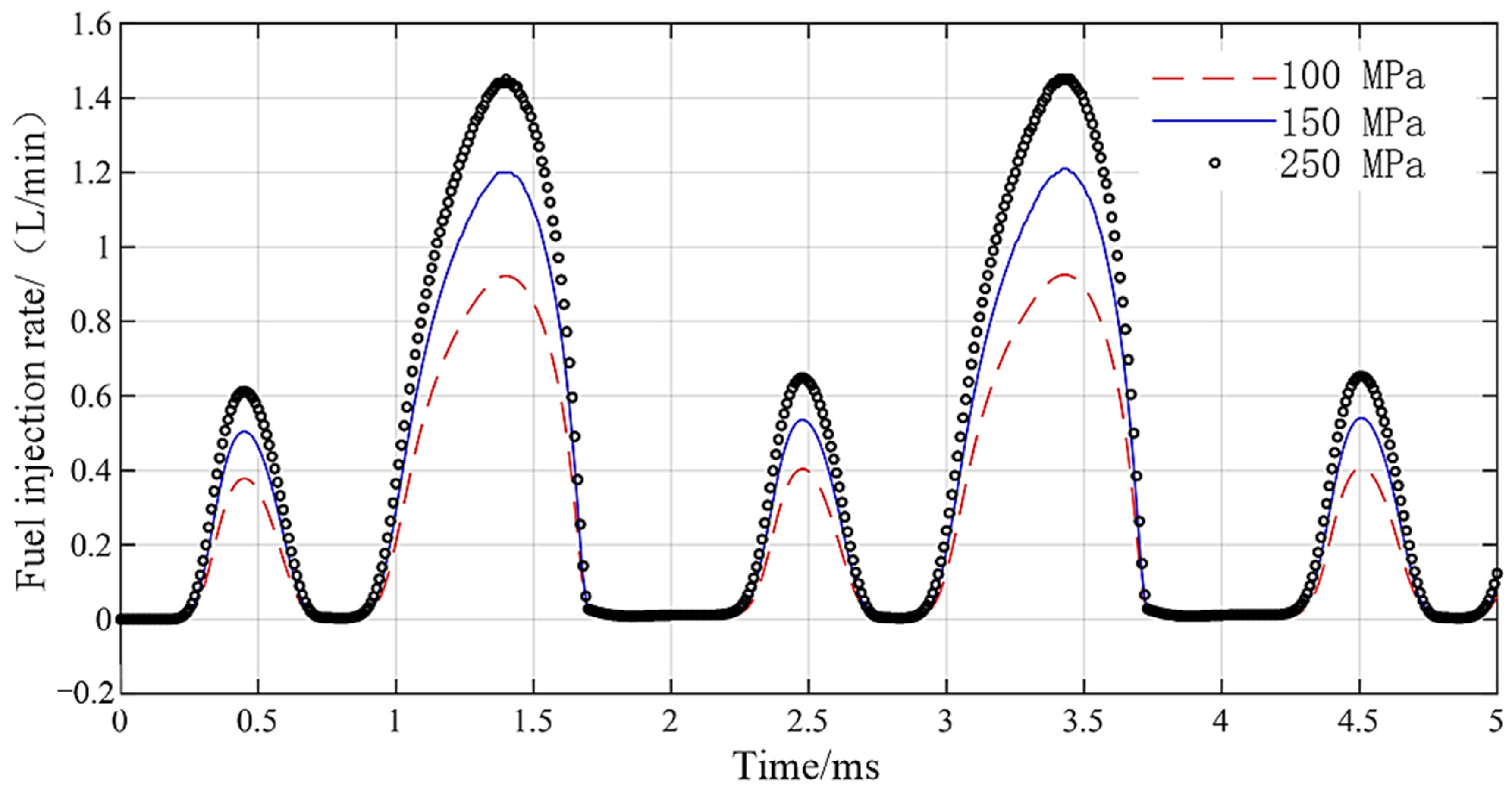
4. GMI Fuel Injection Performance Analysis
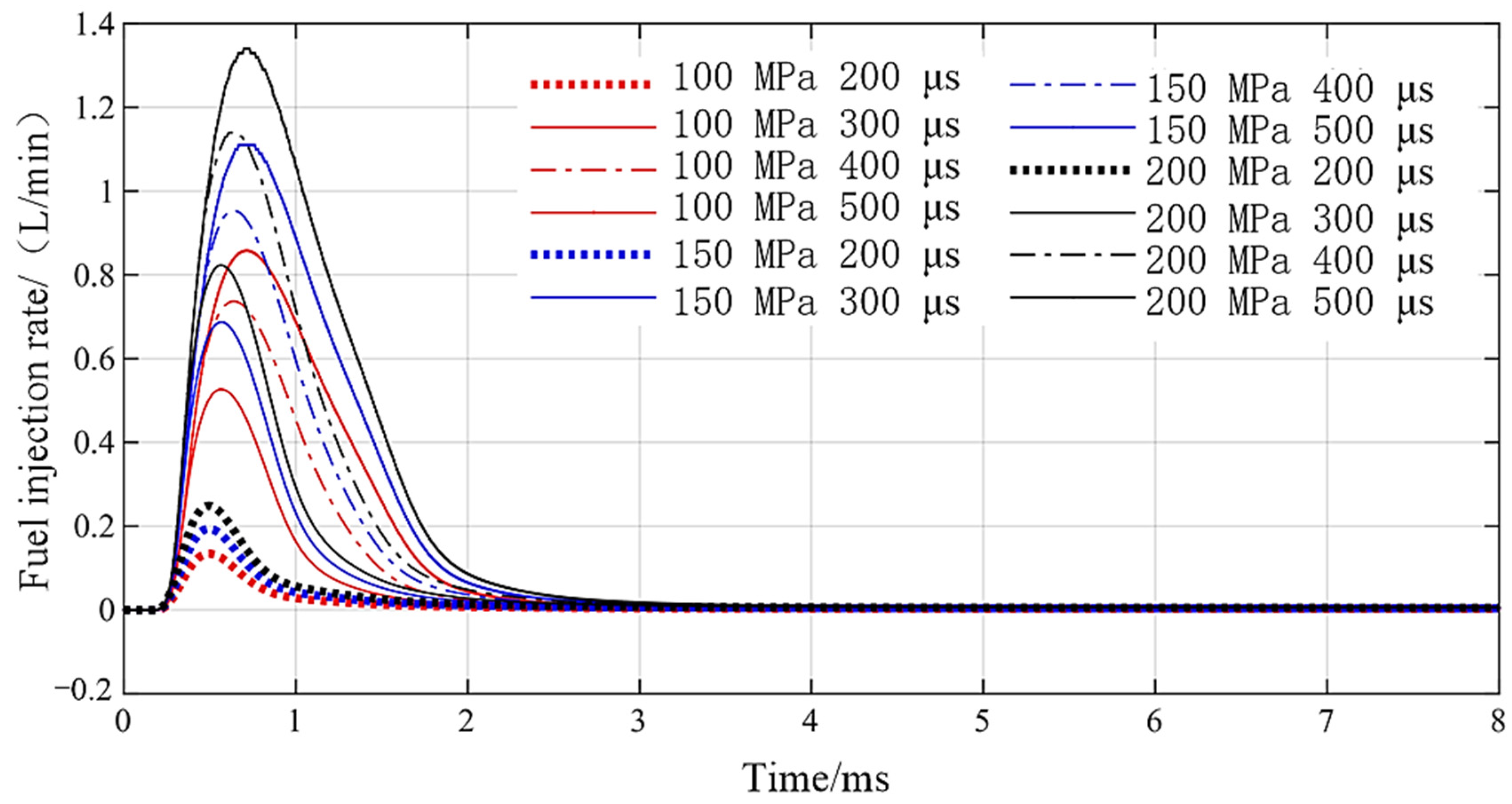
4.1. Large Pulse Width and Long Spray
4.2. Small Pulse Width and Short Jet
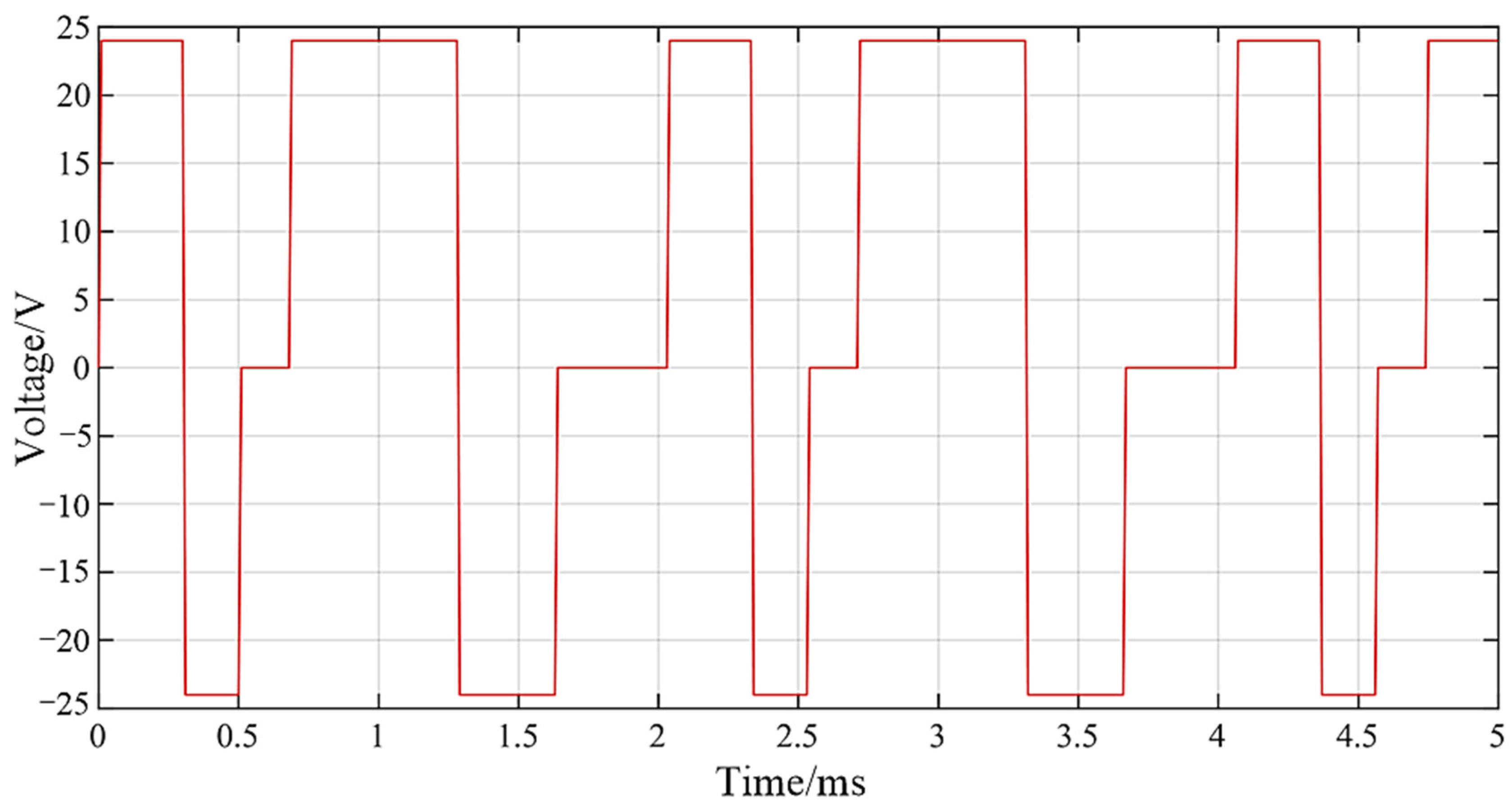
4.3. Multiple Injection
5. Conclusions
- The simulation model of DD-GMI was built. According to the different hydrodynamic characteristics, DD-GMI cavity–pipeline–valve part model was divided into cavity model, pipeline model, valve model, leakage module model, and throttle model for modeling. This part model was combined with the GMA model to complete the integrated modeling of DD-GMI.
- The experimental verification of DD-GMI integrated model was carried out. When the driving pulse width was larger than 650 µs, the relative error between DD-GMI integrated model and experimental results was less than 5%. By changing the driving voltage, the single injection quantity of DD-GMI under different driving pulse widths (≥650 µs) was tested. The relative error between the model calculation results and the experimental test results was less than 5%, and when the driving pulse width is 2000 µs and the voltage amplitude was 80V, the relative error between them was able to reach 1%. The results show that the model can accurately describe the fuel injection performance of DD-GMI. At the same time, the minimum injection quantity measured by the injector is about 5.9 mm3, which shows good injection accuracy.
- Based on DD-GMI integrated model, fuel injection performance was analyzed. With the increase of driving pulse width, the duration of fuel injection was prolonged, and under the same rail pressure, the rising speed and falling speed of fuel injection rate were basically the same, which indicates that DD-GMI has good working stability. The shortest injection pulse width of DD-GMI was about 200 µs, and its response speed was fast. In 5 ms, DD-GMI completed five complete injection processes by using the waveform drive of short and long square waves and has good multiple injection ability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, J. Electronic control fuel injection technology of diesel engine. Fuel Inject. Control. Intern. Combust. Engine 2001, 1, 4–13. [Google Scholar]
- China will fully implement the national six emission standards for heavy diesel vehicles from July. Heavy Veh. 2021, 3, 1.
- Zhou, Z.; He, Z.; Xue, G.; Zhou, J.; Rong, C.; Liu, G. Development status of giant magnetostrictive actuator for electronically controlled fuel injector. Hydraul. Pneum. 2022, 46, 147–155. [Google Scholar]
- Shen, W.Z.; Bo, W.H.; Hui, L.X. Dynamic response of the output force of giant magnetostrictive materials. Int. J. Mech. Mater. Des. 2020, 16, 685–691. [Google Scholar] [CrossRef]
- Domenjoud, M.; Berthelot, É.; Galopin, N.; Corcolle, R.; Bernard, Y.; Daniel, L. Characterization of giant magnetostrictive materials under static stress: Influence of loading boundary conditions. Smart Mater. Struct. 2019, 28, 095012. [Google Scholar] [CrossRef]
- Liu, G.; He, Z.; Bai, G.; Zheng, J.; Zhou, J.; Dai, B. Modeling and experimental study of oil-cooled stacked giant magnetostrictive actuator for servo valve. Actuators 2020, 9, 37. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, C.M. Development of variable preload system for machine tool spindle using giant magnetostrictive material Terfenol-D actuator. J. Intell. Mater. Syst. Struct. 2020, 31, 2304–2311. [Google Scholar] [CrossRef]
- Zhou, S.Z.; Gao, X.X. Magnetostrictive Material; Metallurgical Industry Press: Beijing, China, 2017. [Google Scholar]
- Tanaka, H.; Sato, Y.; Urai, T. Development of a Common-Rail Proportional Injector Controlled by a Tandem Arrayed Giant-Magnetostrictive-Actuator; 2001-01-3182, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2001. [Google Scholar]
- Sato, Y.; Tanaka, H.; Fuseya, T. Characteristics of a Proportional Injector for Common Rail Injection System: 1st Report, Injection Characteristics by a Switching Pilot-valve. Trans. JSME Ser. C 2000, 66, 1857–1860. [Google Scholar] [CrossRef] [Green Version]
- Xue, G.; Zhang, P.; He, Z.; Li, Y.; Xu, C.; Wu, X. Design and modeling of giant magnetostrictive fuel injector. J. Intern. Combust. Engine 2019, 37, 337–342. [Google Scholar]
- Xue, G.; Zhang, P.; Li, X.; He, Z.; Wang, H.; Li, Y.; Ce, R.; Zeng, W.; Li, B. A review of giant magnetostrictive injector (GMI). Sens. Actuators A Phys. 2018, 273, 159–181. [Google Scholar] [CrossRef]
- Xu, B. Structure Design and Characteristic Analysis of High Pressure Common Rail Injector Based on GMA. Master’s Thesis, Anhui University of Science and Technology, Huainan, China, 2020. [Google Scholar]
- Allocca, L.; Davino, D.; Montanaro, A.; Visone, C. Proof of principle of a fuel injector based on a magnetostrictive actuator. Actuators 2021, 10, 237. [Google Scholar] [CrossRef]
- Patil, M.A. Design and Static Magnetic Analysis of Magnetostrictive (Tb0. 3Dy0. 7Fe1. 95) Fuel Injector with Flexible Piston Hydraulic Displacement Amplification. Adv. Eng. Forum 2016, 18, 66–74. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, J.; Wang, W.; Gao, Z. Study on Model and Characteristics Analysis of the Magnetostrictive Drive Component of Automotive Fuel Injection System. Chin. J. Sens. Actuators 2016, 29, 1797–1803. [Google Scholar]
- Wang, W.; Han, H.; Han, L.; Zhang, Y. A Model of Giant Magnetostrictive Actuator Used in Automobile Engine Fuel Injection System. Int. J. Serv. Comput. Oriented Manuf. 2013, 1, 154–166. [Google Scholar] [CrossRef]
- Bright, C.B.; Garza, J.C. Possible Very High Speed Rate Shaping Fuel Injector; 2007-01-4113, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Bright, C.B.; Faidley, L.; Witthauer, A.; Rickels, E.; Donlin, T. Programmable Diesel Injector Transducer Test Results; 2011-01-0381, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2011. [Google Scholar]
- Yan, R.; Wang, Z.; Zhu, L. Research of the Giant Magnetostrictive Fuel Injector. Adv. Mater. Res. 2014, 889–890, 916–919. [Google Scholar] [CrossRef]
- Zhou, Z.; He, Z.; Xue, G.; Zhou, J.; Rong, C.; Liu, G. Analysis of working characteristics of giant magnetostrictive actuator for direct-drive fuel injector. AIP Adv. 2022, 12, 075216. [Google Scholar] [CrossRef]
- Wang, L. Study on Injection Characteristics and Structure Optimization of High-Pressure Common Rail Electromagnetic Injector. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2016. [Google Scholar]
- Liu, T. Study on Characteristics of Needle Valve Movement of High Pressure Common Rail Injector. Master’s Thesis, Beijing University of Technology, Beijing, China, 2018. [Google Scholar]
- Fu, Y.; Qi, X. AMESim System Modeling and Simulation Reference Manual; Beihang University Press: Beijing, China, 2011. [Google Scholar]






| Material | Giant Magnetostrictive Materials | Piezoelectric Ceramic Material | Traditional Magnetostrictive Material |
|---|---|---|---|
| Terfenol-D | PZT | Ni | |
| Saturated magnetostriction coefficient [λS]/(ppm) | 1500~2000 | 100~600 | −35~40 |
| Magnetic coupling coefficient [K33] | 0.7~0.72 | 0.45~0.72 | 0.3 |
| Energy density [ω]/(kJ·m−3) | 30~50 | 0.23~1.0 | 0.03 |
| Workplace (V/cm) or (kA/m) | ~800 | 124 | 0.1 |
| Young’s modulus [E]/(GPa) | 25~35 | 4.6~6.0 | 21 |
| Curie point [Tc]/(℃) | 380 | 40~180 | 376 |
| Simulation Model Icon | Explanation |
|---|---|
 ; ;  ; ;  ; ;  ; ; ; ;  ; ;  ; ;  | Material defined by parameter settings; basic magnetoresistive unit; radial magnetoresistive unit; zero magnetic potential node; three-terminal magnetic circuit connector; ammeter; magnetic potential sensor; magnetic flux sensor |
 ; ;  ; ;  ; ;  ; ; | Signal source; gain; three-terminal subtractive connector; convention function |
 ; ;  ; ;  ; ; ; ;  ; ;  | Electromagnetic force function; ideal mechanical spring; zero velocity source; linear translation node that transfers velocity and displacement; damper; mass block with configurable dead center |
 ; ;  ; ;  ; ;  | Nozzle; leakage and viscous damping; hydraulic chamber; hydraulic port |
| Parameter [Symbol]/Unit | Value | Parameter[Symbol]/Unit | Value | ||
|---|---|---|---|---|---|
| Size parameters | Enameled wire diameter [φ]/mm | 0.6 | Mechanical parameters | Saturation magnetostrictive strain [λS] | 800 |
| GMM cylinder length[l]/mm | 160 | GMM bulk density [ρ]/(kg/m3) | 9500 | ||
| GMM cylinder cross-sectional area[A]/mm2 | 48 | GMM damping [CD]/(N·s/m) | 700 | ||
| Coil winding inner diameter [Ra]/mm | 6 | GMM elastic modulus [E]/(N/m 2) | 3 × 1010 | ||
| Coil winding outer diameter [Rb]/mm | 11.5 | “T” plunger mass [m2]/g | 23 | ||
| Coil winding length [Lc]/mm | 160 | Spring rate [k2]/(N/m) | 3 × 105 | ||
| Equivalent damping [c2]/(N·s/m) | 200 | ||||
| Magnetic parameters | Circuit parameters | ||||
| Pinning loss factor [k]/(A/m) | 1300 | ||||
| Shape parameter [a]/(A/m) | 9800 | Coil turns [N] | 2000 | ||
| Domain Wall Interaction Coefficient [α] | −1.0 × 10−3 | ||||
| Reversible coefficient [c] | 0.28 | Equivalent inductance [L]/mH | 8.4 | ||
| Saturation magnetization [MS]/(A/m) | 8.0×105 | Equivalent resistance [R]/mΩ | 8.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; He, Z.; Xue, G.; Zhou, J.; Rong, C.; Liu, G. Structure Design and Working Characteristics Analysis of Direct-Drive Giant Magnetostrictive Injector. Micromachines 2022, 13, 1721. https://doi.org/10.3390/mi13101721
Zhou Z, He Z, Xue G, Zhou J, Rong C, Liu G. Structure Design and Working Characteristics Analysis of Direct-Drive Giant Magnetostrictive Injector. Micromachines. 2022; 13(10):1721. https://doi.org/10.3390/mi13101721
Chicago/Turabian StyleZhou, Zhaoqi, Zhongbo He, Guangming Xue, Jingtao Zhou, Ce Rong, and Guoping Liu. 2022. "Structure Design and Working Characteristics Analysis of Direct-Drive Giant Magnetostrictive Injector" Micromachines 13, no. 10: 1721. https://doi.org/10.3390/mi13101721
APA StyleZhou, Z., He, Z., Xue, G., Zhou, J., Rong, C., & Liu, G. (2022). Structure Design and Working Characteristics Analysis of Direct-Drive Giant Magnetostrictive Injector. Micromachines, 13(10), 1721. https://doi.org/10.3390/mi13101721






