Machine-Learning-Enabled Design and Manipulation of a Microfluidic Concentration Gradient Generator
Abstract
:1. Introduction
2. Theory of the Design
3. Materials and Methods
3.1. Building a Database of the Concentration Gradient Generators with Different Inlet Configurations
3.2. Training an ANN for Predicting the Two Boundaries of the Reactive Region
3.3. Completion of the Concentration Profile by Interpolation Algorithm
4. Results and Discussion
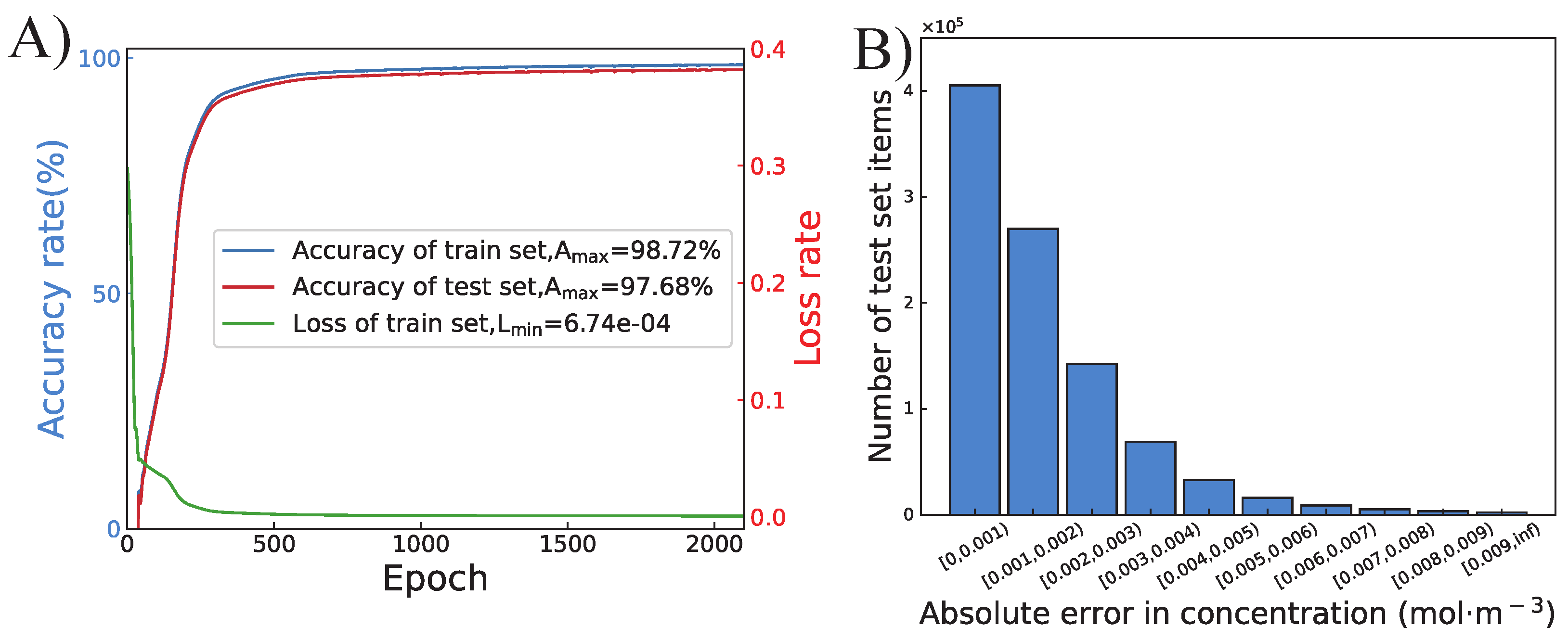
4.1. Training of the Proposed ANN
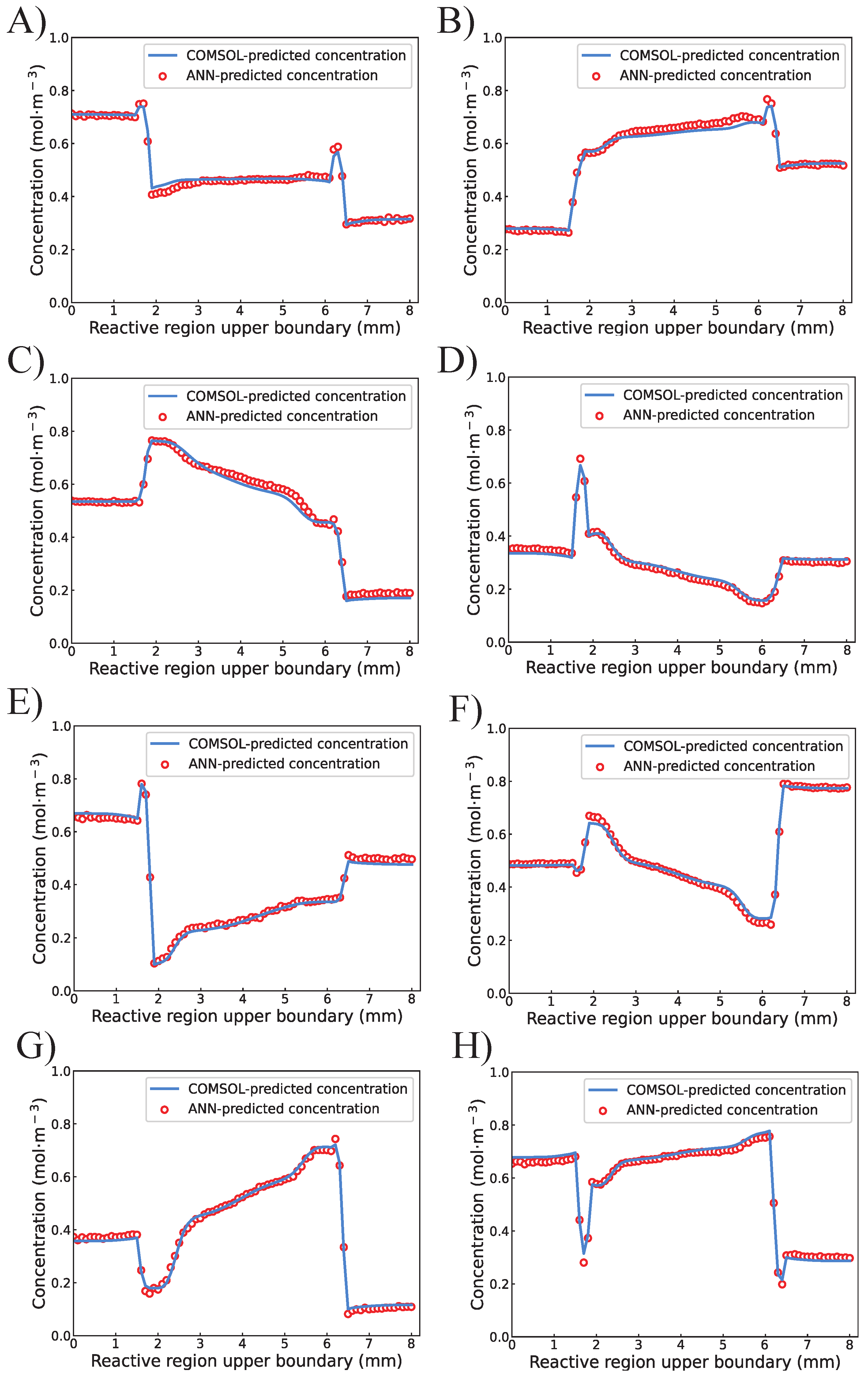
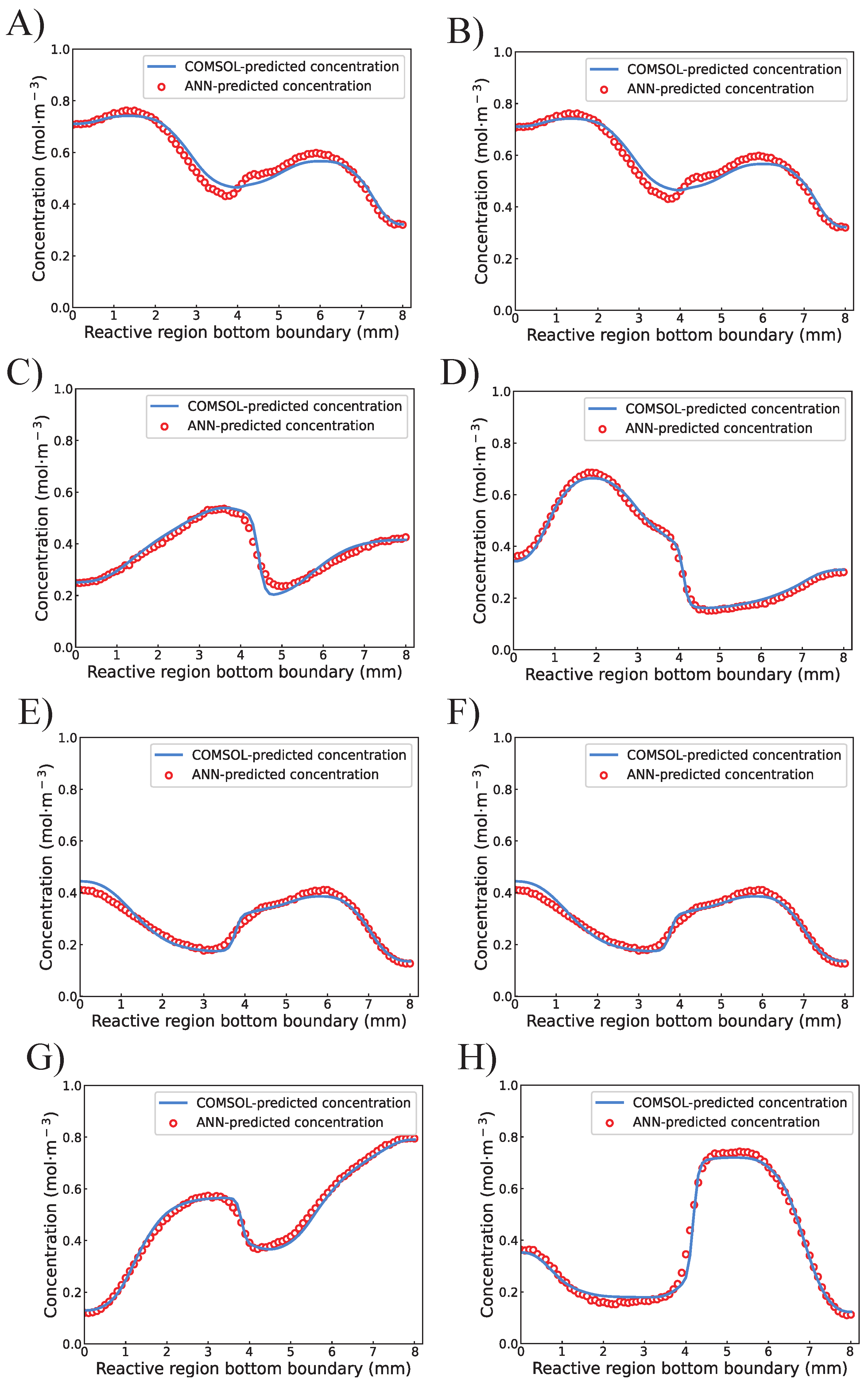
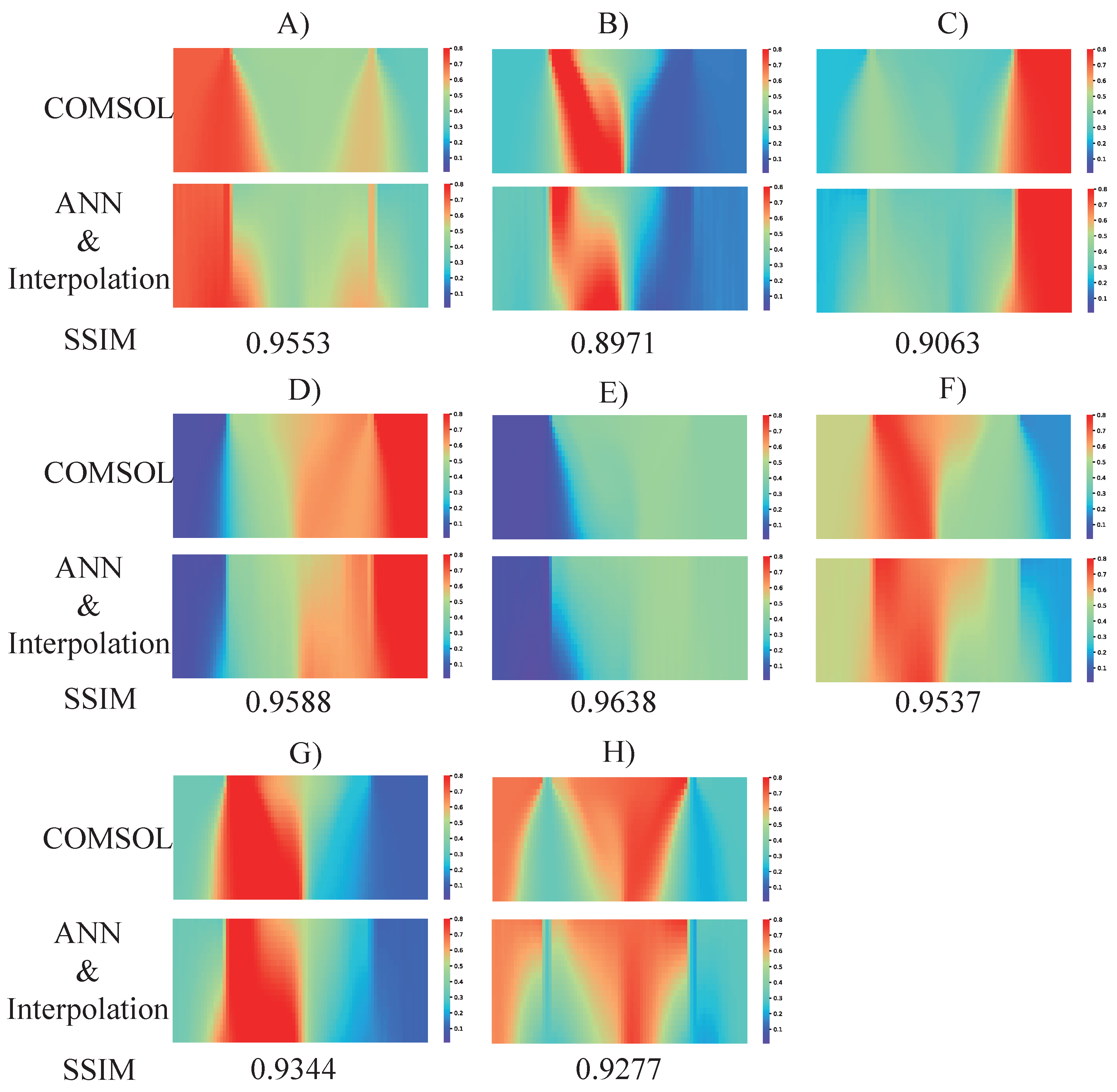
4.2. Completion of the Concentration Profile by Interpolation Algorithm
5. Conclusions
Potential Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allard, C.A.; Opalko, H.E.; Moseley, J.B. Stable Pom1 clusters form a glucose-modulated concentration gradient that regulates mitotic entry. ELife 2019, 8, e46003. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, A.; Ladage, D.; Schinköthe, T.; Klausmann, U.; Ulrichs, C.; Klinz, F.J.; Brixius, K.; Arnhold, S.; Desai, B.; Mehlhorn, U.; et al. Basic fibroblast growth factor controls migration in human mesenchymal stem cells. Stem Cells 2006, 24, 1750–1758. [Google Scholar] [CrossRef] [PubMed]
- Rifes, P.; Isaksson, M.; Rathore, G.S.; Aldrin-Kirk, P.; Møller, O.K.; Barzaghi, G.; Lee, J.; Egerod, K.L.; Rausch, D.M.; Parmar, M.; et al. Modeling neural tube development by differentiation of human embryonic stem cells in a microfluidic WNT gradient. Nat. Biotechnol. 2020, 38, 1265–1273. [Google Scholar] [CrossRef] [PubMed]
- Manfrin, A.; Tabata, Y.; Paquet, E.R.; Vuaridel, A.R.; Rivest, F.R.; Naef, F.; Lutolf, M.P. Engineered signaling centers for the spatially controlled patterning of human pluripotent stem cells. Nat. Methods 2019, 16, 640–648. [Google Scholar] [CrossRef] [PubMed]
- Sokol, C.L.; Camire, R.B.; Jones, M.C.; Luster, A.D. The chemokine receptor CCR8 promotes the migration of dendritic cells into the lymph node parenchyma to initiate the allergic immune response. Immunity 2018, 49, 449–463. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.X.; Choi, S.Y.; Niu, X.; Kang, N.; Xue, H.; Killam, J.; Wang, Y. Lactic acid and an acidic tumor microenvironment suppress anticancer immunity. Int. J. Mol. Sci. 2020, 21, 8363. [Google Scholar] [CrossRef] [PubMed]
- Lyu, J.; Chen, L.; Zhang, J.; Kang, X.; Wang, Y.; Wu, W.; Tang, H.; Wu, J.; He, Z.; Tang, K. A microfluidics-derived growth factor gradient in a scaffold regulates stem cell activities for tendon-to-bone interface healing. Biomater. Sci. 2020, 8, 3649–3663. [Google Scholar] [CrossRef]
- Velnar, T.; Gradisnik, L. Tissue augmentation in wound healing: The role of endothelial and epithelial cells. Med. Arch. 2018, 72, 444. [Google Scholar] [CrossRef]
- Lin, Z.; Luo, G.; Du, W.; Kong, T.; Liu, C.; Liu, Z. Recent advances in microfluidic platforms applied in cancer metastasis: Circulating tumor cells’(CTCs) isolation and tumor-on-a-chip. Small 2020, 16, 1903899. [Google Scholar] [CrossRef]
- Ruzycka, M.; Cimpan, M.R.; Rios-Mondragon, I.; Grudzinski, I.P. Microfluidics for studying metastatic patterns of lung cancer. J. Nanobiotechnol. 2019, 17, 71. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Pang, Y. Concentration gradient generation methods based on microfluidic systems. RSC Adv. 2017, 7, 29966–29984. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.G.; Wu, Y.F.; Xu, Z.R.; Wang, J.H. A radial microfluidic concentration gradient generator with high-density channels for cell apoptosis assay. Lab Chip 2011, 11, 3305–3312. [Google Scholar] [CrossRef]
- Sugiyama, H.; Osaki, T.; Takeuchi, S.; Toyota, T. Role of negatively charged lipids achieving rapid accumulation of water-soluble molecules and macromolecules into cell-sized liposomes against a concentration gradient. Langmuir 2021, 38, 112–121. [Google Scholar] [CrossRef]
- Hong, B.; Xue, P.; Wu, Y.; Bao, J.; Chuah, Y.J.; Kang, Y. A concentration gradient generator on a paper-based microfluidic chip coupled with cell culture microarray for high-throughput drug screening. Biomed. Microdevices 2016, 18, 21. [Google Scholar] [CrossRef]
- Lim, W.; Park, S. A microfluidic spheroid culture device with a concentration gradient generator for high-throughput screening of drug efficacy. Molecules 2018, 23, 3355. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Zhang, X.; Li, Y.; Deng, J.; Li, X.; Qu, Y.; Lu, Y.; Liu, T.; Gao, Z.; Lin, B. High-glucose 3D INS-1 cell model combined with a microfluidic circular concentration gradient generator for high throughput screening of drugs against type 2 diabetes. RSC Adv. 2018, 8, 25409–25416. [Google Scholar] [CrossRef] [Green Version]
- Mulholland, T.; McAllister, M.; Patek, S.; Flint, D.; Underwood, M.; Sim, A.; Edwards, J.; Zagnoni, M. Drug screening of biopsy-derived spheroids using a self-generated microfluidic concentration gradient. Sci. Rep. 2018, 8, 14672. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Gao, Z.; Liu, Y.; Li, S.; Zhu, J.; Chen, P.; Liu, B.F. Multichannel synchronous hydrodynamic gating coupling with concentration gradient generator for high-throughput probing dynamic signaling of single cells. Anal. Chem. 2020, 92, 12062–12070. [Google Scholar] [CrossRef]
- Rismanian, M.; Saidi, M.S.; Kashaninejad, N. A microfluidic concentration gradient generator for simultaneous delivery of two reagents on a millimeter-sized sample. J. Flow Chem. 2020, 10, 615–625. [Google Scholar] [CrossRef]
- Yang, C.G.; Xu, Z.R.; Lee, A.P.; Wang, J.H. A microfluidic concentration gradient droplet array generator for the production of multi-color nanoparticles. Lab Chip 2013, 13, 2815–2820. [Google Scholar] [CrossRef]
- Tang, M.; Huang, X.; Chu, Q.; Ning, X.; Wang, Y.; Kong, S.K.; Zhang, X.; Wang, G.; Ho, H.P. A linear concentration gradient generator based on multi-layered centrifugal microfluidics and its application in antimicrobial susceptibility testing. Lab Chip 2018, 18, 1452–1460. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, N.; Chen, J.; Rodgers, V.G.; Brisk, P.; Grover, W.H. Finding the optimal design of a passive microfluidic mixer. Lab Chip 2019, 19, 3618–3627. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Brisk, P.; Grover, W.H. Random design of microfluidics. Lab Chip 2016, 16, 4212–4219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McIntyre, D.; Lashkaripour, A.; Fordyce, P.; Densmore, D. Machine learning for microfluidic design and control. Lab Chip 2022, 22, 2925–2937. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.H.; Yang, H.; Wang, Y. Inverse design of microfluidic concentration gradient generator using deep learning and physics-based component model. Microfluid. Nanofluid. 2020, 24, 44. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, N.; Chen, J.; Su, G.; Yao, H.; Ho, T.Y.; Sun, L. Predicting the fluid behavior of random microfluidic mixers using convolutional neural networks. Lab Chip 2021, 21, 296–309. [Google Scholar] [CrossRef]
- Cunningham, P.; Cord, M.; Delany, S.J. Supervised learning. In Machine Learning Techniques for Multimedia; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. [Google Scholar]
- Akossou, A.; Palm, R. Impact of data structure on the estimators R-square and adjusted R-square in linear regression. Int. J. Math. Comput. 2013, 20, 84–93. [Google Scholar]
- Davis, P.J. Interpolation and Approximation; Courier Corporation: Chelmsford, MA, USA, 1975. [Google Scholar]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Sara, U.; Akter, M.; Uddin, M.S. Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study. J. Comput. Commun. 2019, 7, 8–18. [Google Scholar] [CrossRef] [Green Version]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Fu, L.; Yu, L.; Huang, X.; Brisk, P.; Grover, W.H. Accelerating Simulation of Particle Trajectories in Microfluidic Devices by Constructing a Cloud Database. In Proceedings of the 2018 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Hong Kong, China, 8–11 July 2018; pp. 666–671. [Google Scholar]
- Smits, A.J.; McKeon, B.J.; Marusic, I. High–Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 2011, 43, 353–375. [Google Scholar] [CrossRef]
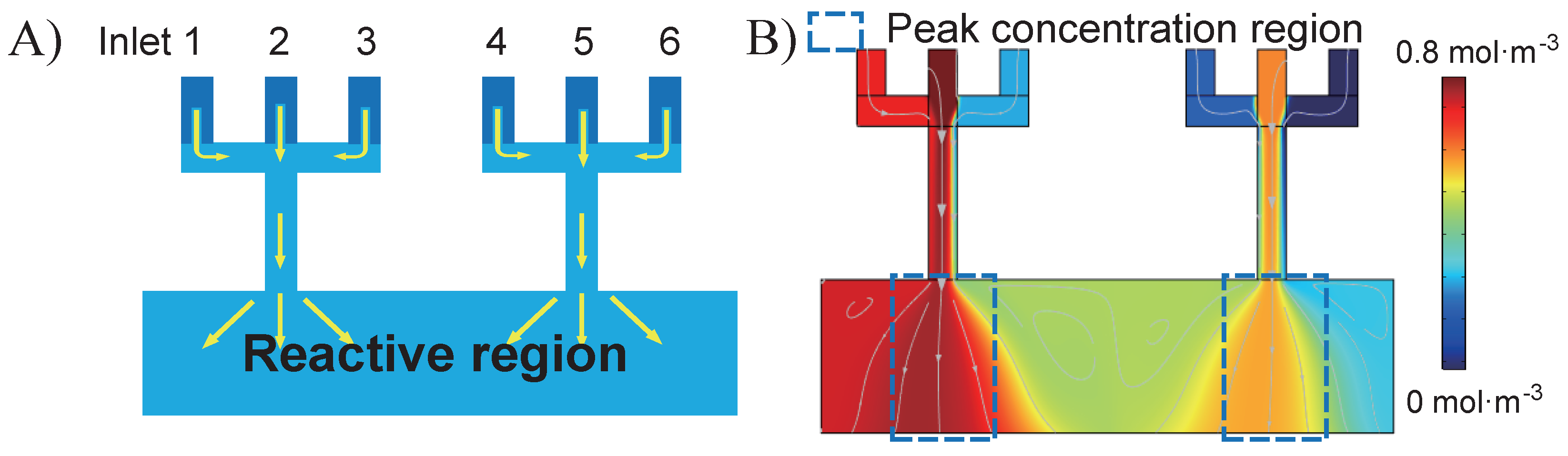
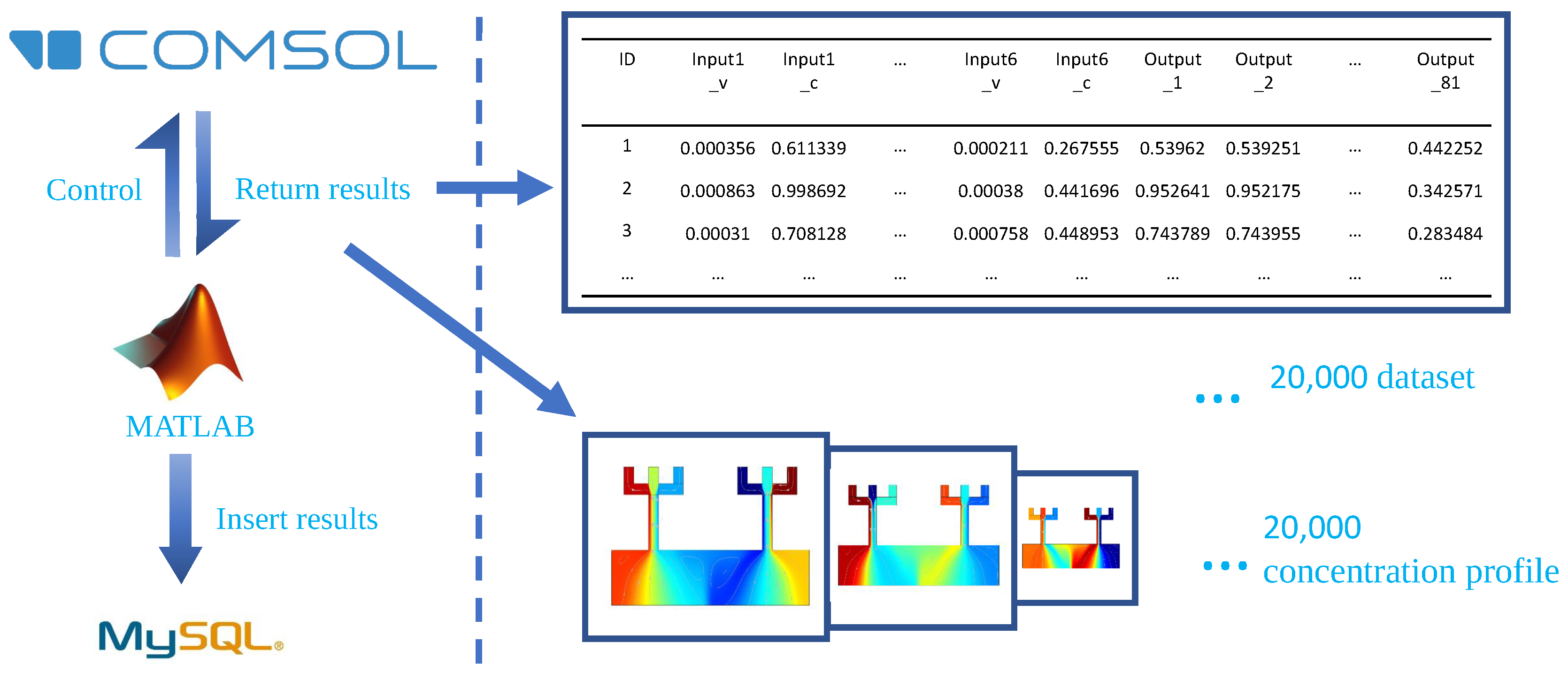
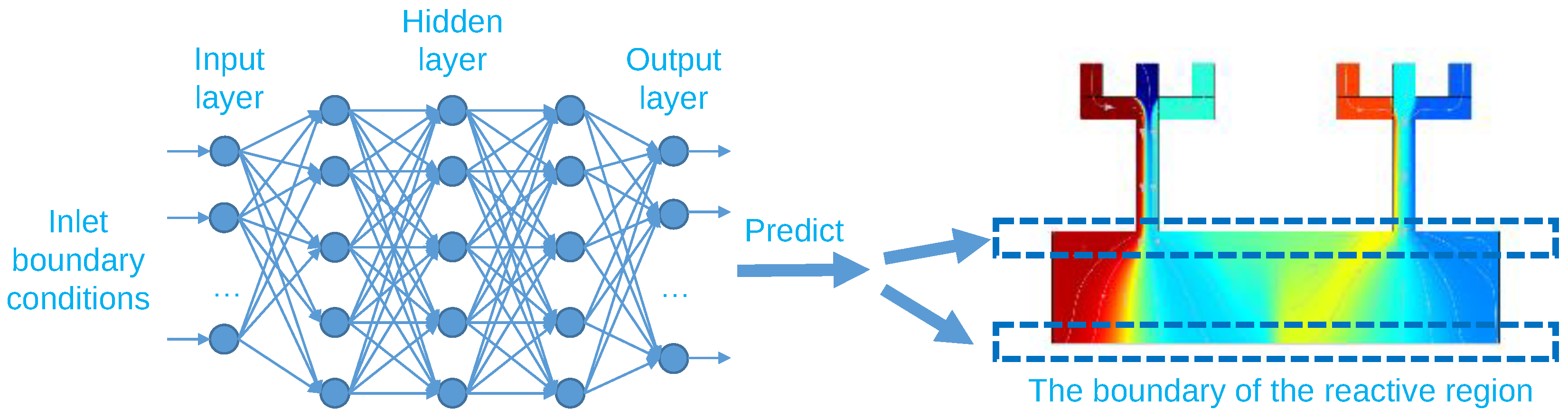
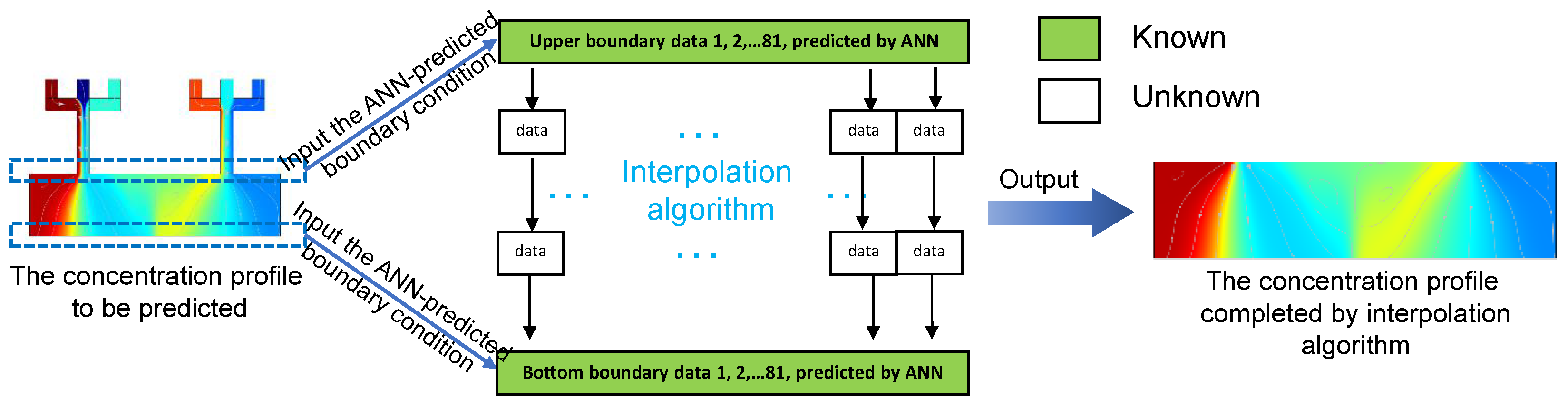
| N/A | Inlet 1 | Inlet 2 | Inlet 3 | Inlet 4 | Inlet 5 | Inlet 6 |
|---|---|---|---|---|---|---|
| Flow rate (mm) | 0.68 | 0.87 | 0.41 | 0.15 | 0.91 | 0.28 |
| Concentration (mol) | 0.69 | 0.77 | 0.29 | 0.22 | 0.59 | 0.083 |
| Parameter | Value |
|---|---|
| Inlet flow rate | Randomly generated from 0 to 1 mm |
| Inflow concentration from six inlets | Randomly generated from 0 to 1 mol |
| Diffusion coefficient | · |
| Mesh max element size | 175 μm |
| Mesh min element size | 5 μm |
| Mesh max element growth rate | 1.13 |
| Mesh curvature factor | 0.3 |
| Mesh resolution of narrow regions | 1 |
| Tolerance to convergence | 0.001 |
| Layer | Type | Depth | Activation |
|---|---|---|---|
| 1 | Input layer | 12 | Linear |
| 2 | Fully-connected layer | 120 | ReLU |
| 3 | Fully-connected layer | 120 | ReLU |
| 4 | Fully-connected layer | 120 | ReLU |
| 5 | Output layer | 162 (81 + 81) | Linear |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Liu, Z.; Wang, J. Machine-Learning-Enabled Design and Manipulation of a Microfluidic Concentration Gradient Generator. Micromachines 2022, 13, 1810. https://doi.org/10.3390/mi13111810
Zhang N, Liu Z, Wang J. Machine-Learning-Enabled Design and Manipulation of a Microfluidic Concentration Gradient Generator. Micromachines. 2022; 13(11):1810. https://doi.org/10.3390/mi13111810
Chicago/Turabian StyleZhang, Naiyin, Zhenya Liu, and Junchao Wang. 2022. "Machine-Learning-Enabled Design and Manipulation of a Microfluidic Concentration Gradient Generator" Micromachines 13, no. 11: 1810. https://doi.org/10.3390/mi13111810
APA StyleZhang, N., Liu, Z., & Wang, J. (2022). Machine-Learning-Enabled Design and Manipulation of a Microfluidic Concentration Gradient Generator. Micromachines, 13(11), 1810. https://doi.org/10.3390/mi13111810







