Relationship between Onset of Sliding Behavior and Size of Droplet on Inclined Solid Substrate
Abstract
:1. Introduction
2. Evaluation of Adhesiveness
2.1. Models for Adhesiveness of Droplet
2.2. Wolfram and Faust’s (WF) Model
2.3. Furmidge’s Model
2.4. Alternative Evaluation for WF and Furmidge’s Models
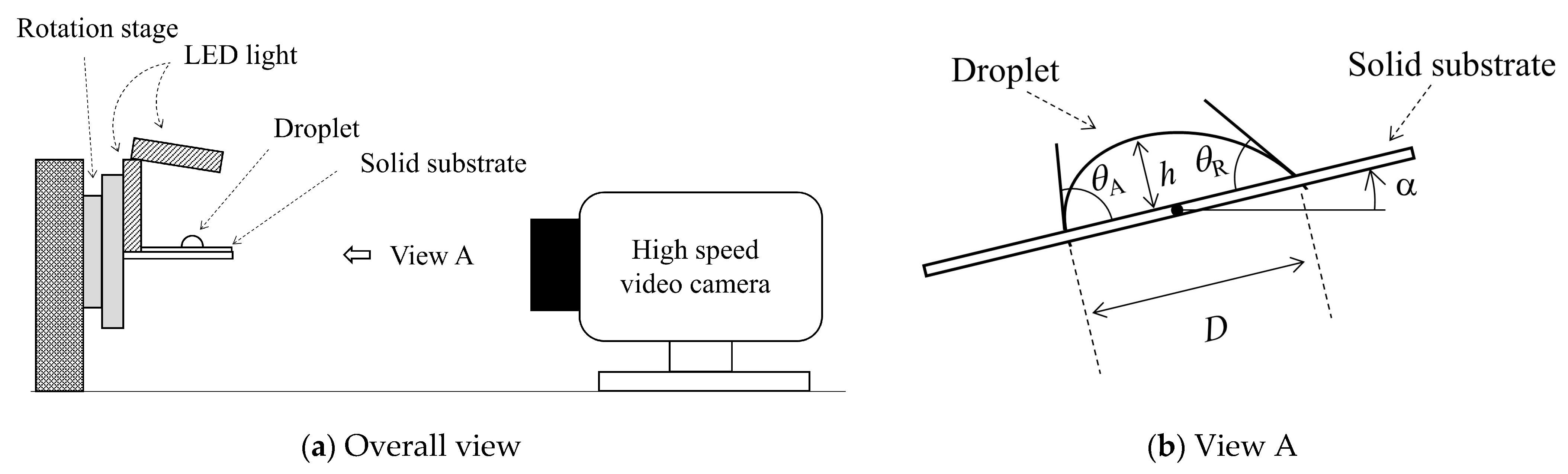
3. Experiment
4. Results and Discussion
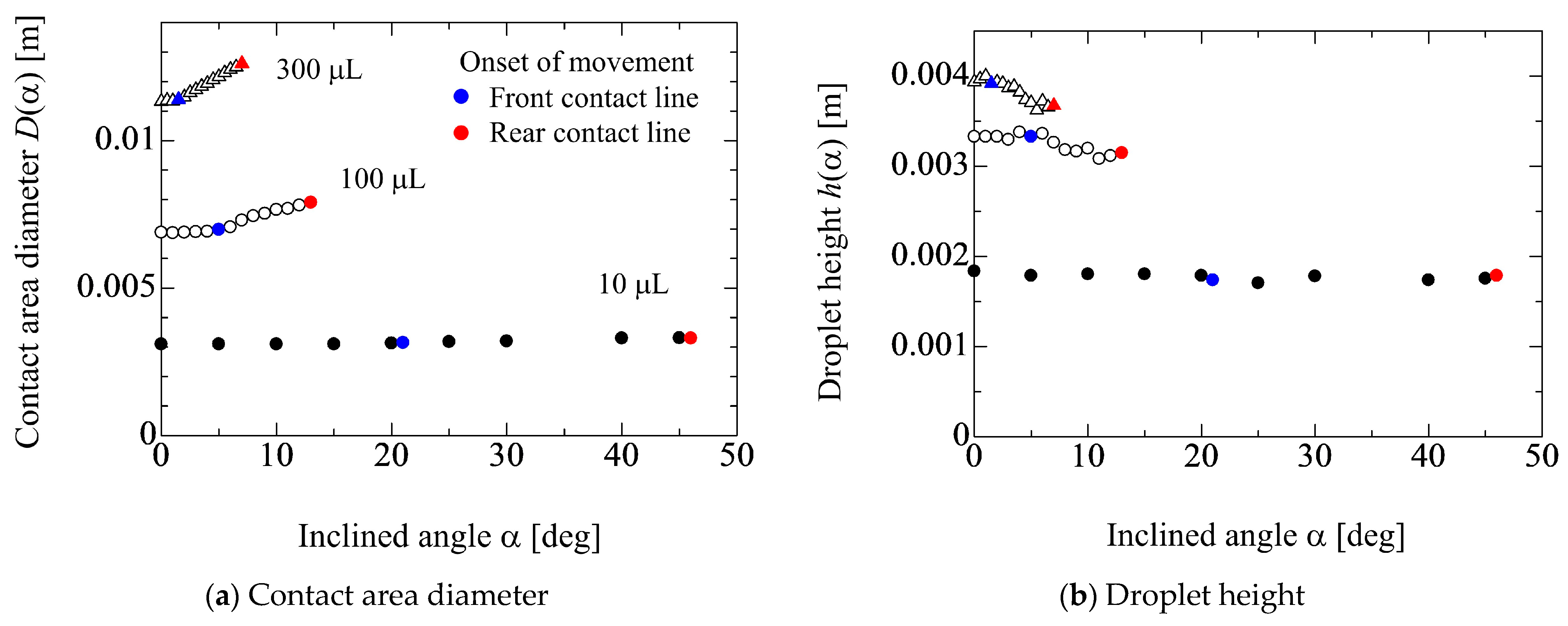
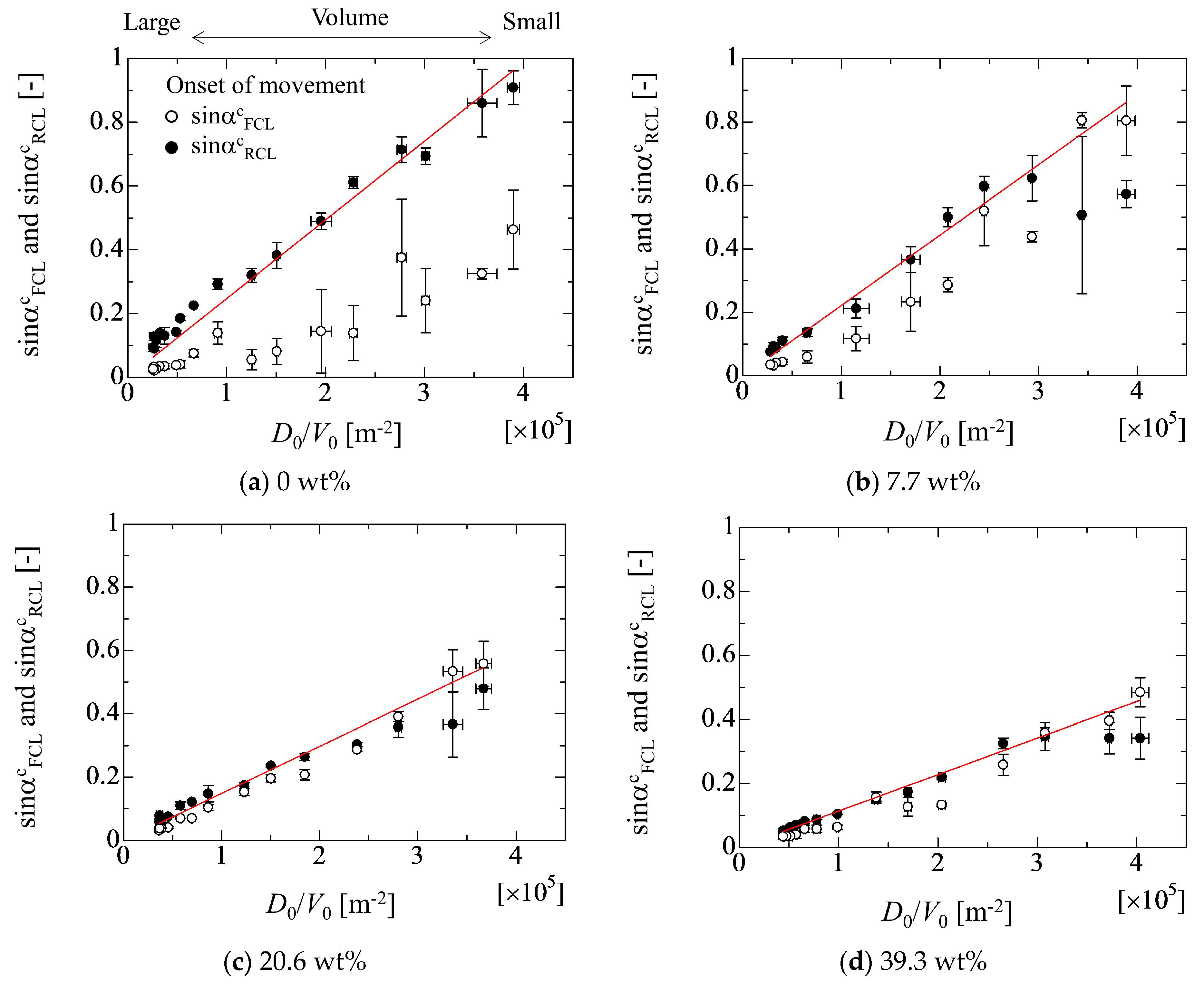
4.1. Inclined Angle Dependency of Geometrical Parameters of Droplet
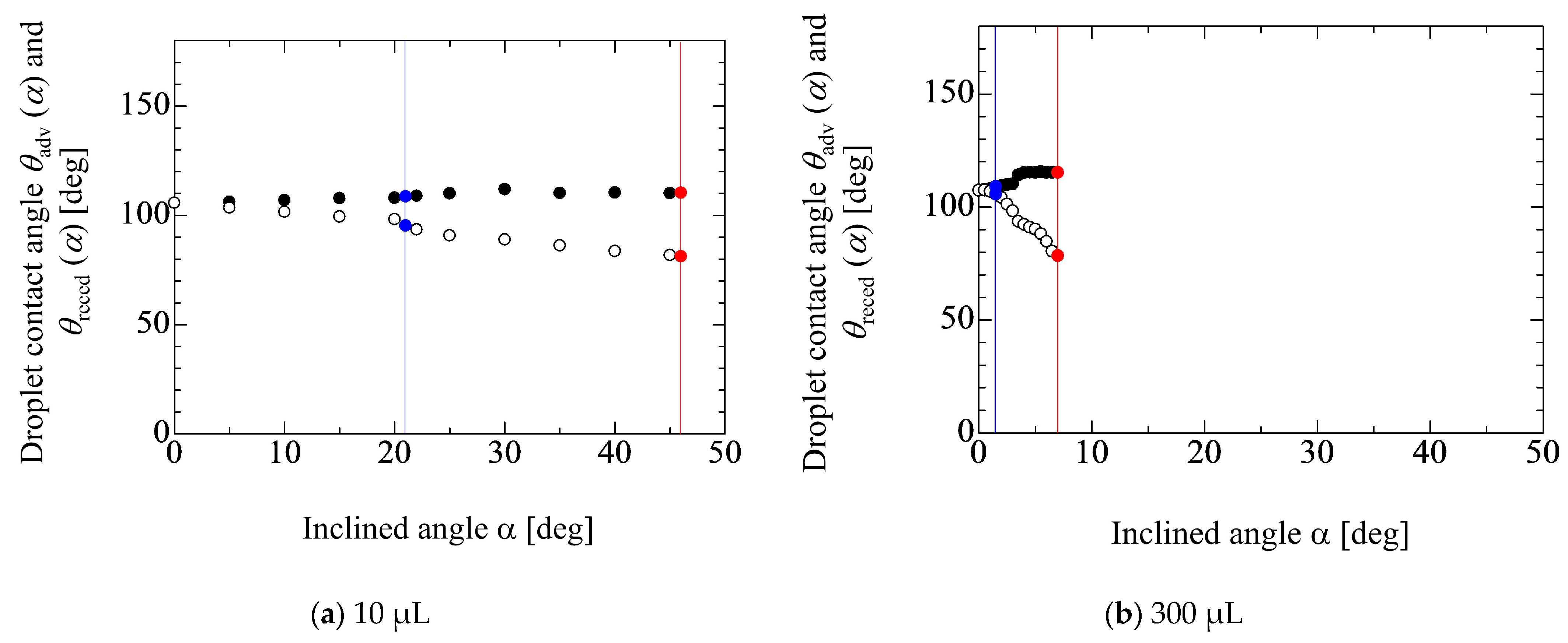
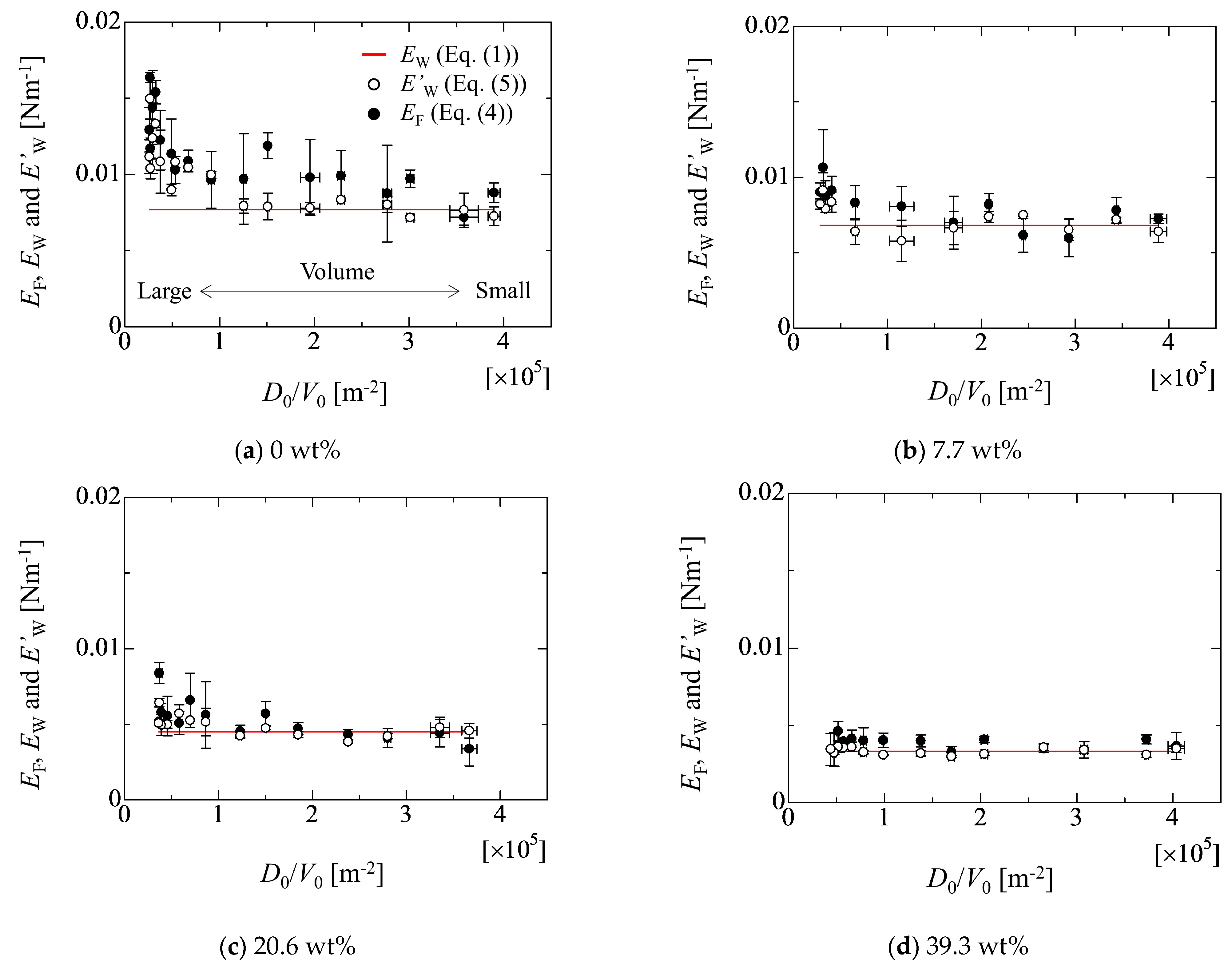
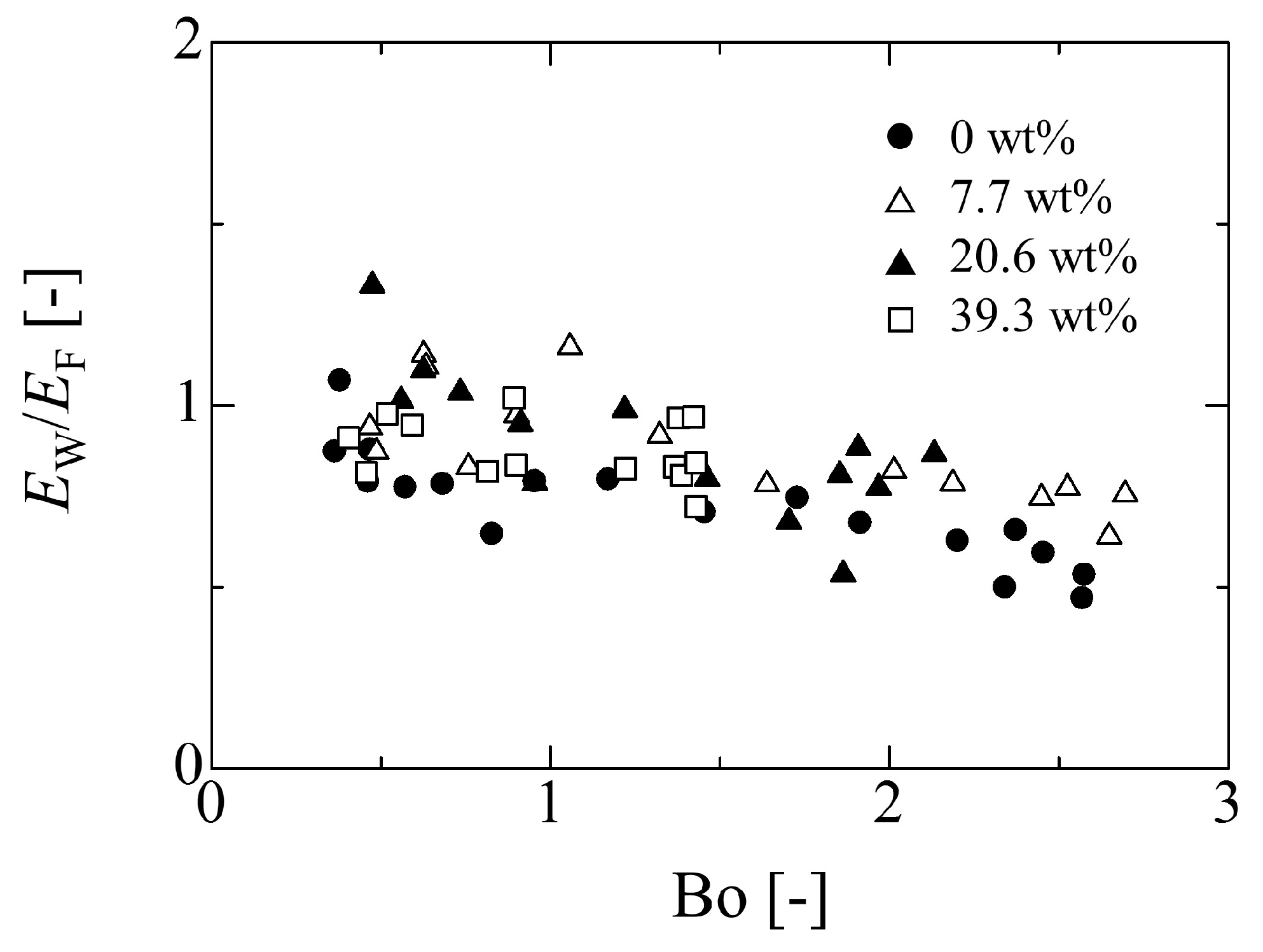
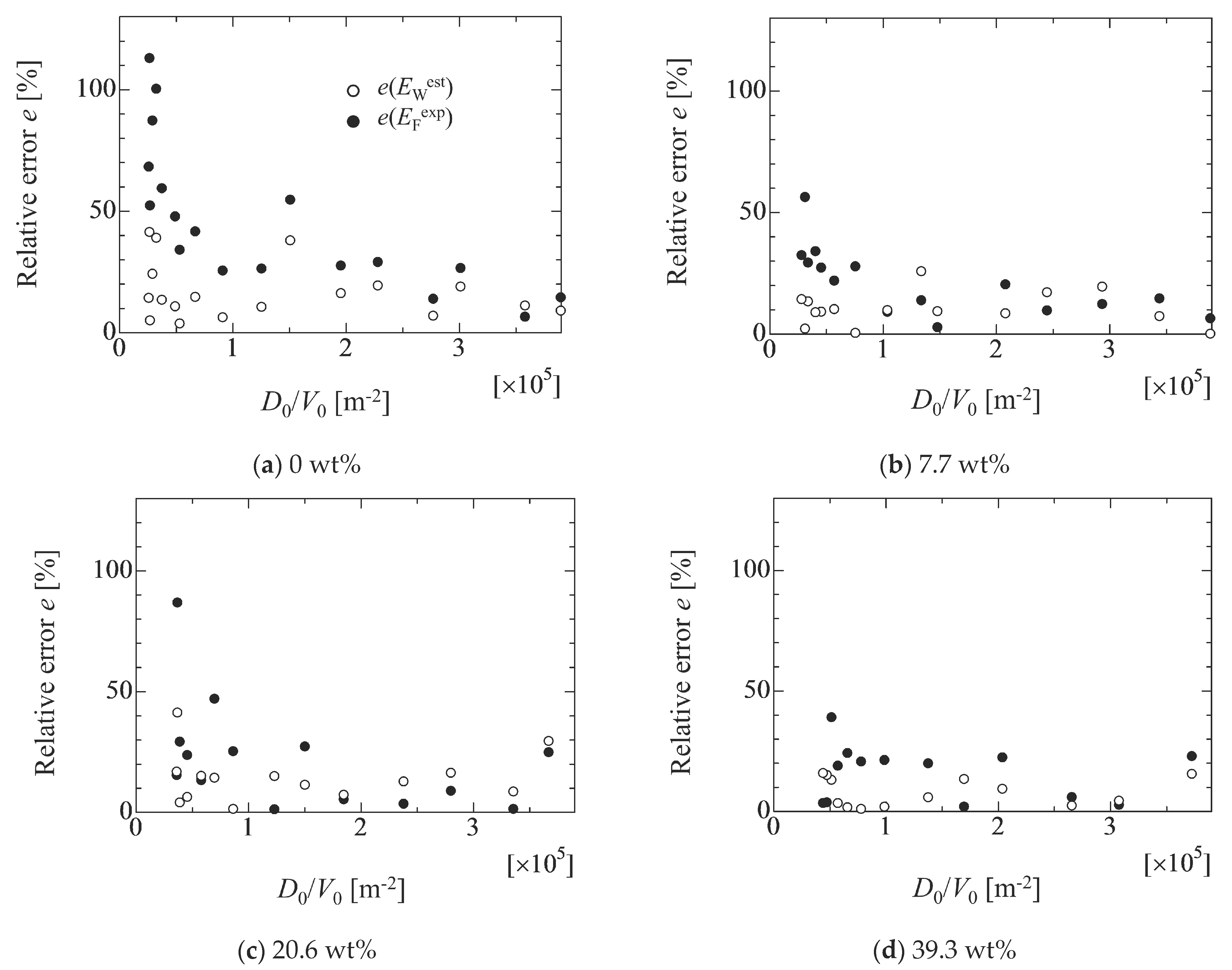
4.2. Evaluation of Adhesion Forces
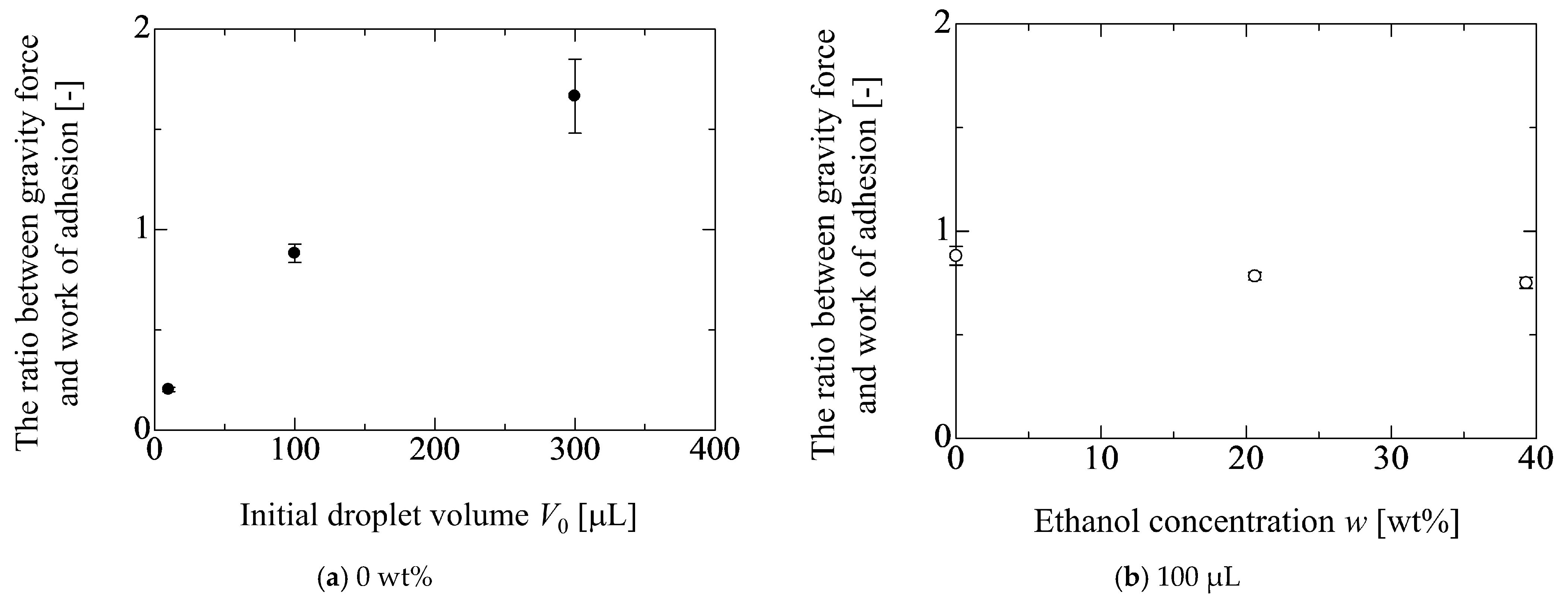
4.3. Effect of Droplet Size on Adhesion Force
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Bo | Bond number [-] |
| a, b | Parameters in Equation (6) [-] |
| cf | Pre-factor in Furmidge’s relation [-] |
| D | Contact area diameter of droplet [m] |
| E | Adhesion force [Nm−1] |
| e | Relative error [%] |
| g | Gravitational acceleration [m s−2] |
| h | Droplet height [m] |
| k | Gradient of linear fitting relation for Wolfram and Faust’s model [m2] |
| lwidth | Width of the contact area of droplet [m]’ |
| V | Droplet volume [m3] |
| Greek Symbols | |
| α | Inclined angle of solid substrate [deg] |
| θ | Contact angle [deg] |
| ρ | Density [kg m−3] |
| σ | Surface tension [N m−1] |
| ω | Angular velocity of rotation for solid substrate [deg s−1] |
| Superscripts | |
| c | Critical |
| est | Estimation |
| exp | Experiment |
| Subscripts | |
| 0 | Initial condition |
| A | Advancing |
| ap | Apparent |
| F | Furmidge’s model |
| FCL | Front contact line |
| l | Liquid |
| lg | Liquid–gas interface |
| R | Receding |
| RCL | Rear contact line |
| W | Wolfram model |
References
- Kim, J. Spray cooling heat transfer: The state of the art. Int. J. Heat Fluid Flow 2007, 28, 753–767. [Google Scholar] [CrossRef]
- Hsu, H.-W.; Liu, C.-L. Spray-coating semiconducting conjugated polymers for organic thin film transistor applications. RSC Adv. 2014, 4, 30145–30149. [Google Scholar] [CrossRef]
- Yan, K.; Li, J.; Pan, L.; Shi, Y. Inkjet printing for flexible and wearable electronics. APL Mater. 2020, 8, 120705-1–120705-22. [Google Scholar] [CrossRef]
- Das, P.K.; Grippin, A.; Kwong, A.; Weber, A.Z.; Luo, D.; Lan, L.; Xu, M.; Xu, H.; Li, M.; Wang, L.; et al. Liquid-Water-Droplet Adhesion-Force Measurements on Fresh and Aged Fuel-Cell Gas-Diffusion Layers. J. Electrochem. Soc. 2012, 159, B489–B496. [Google Scholar] [CrossRef]
- Wang, X.; Xu, B.; Chen, Z.; Del Col, D.; Li, D.; Zhang, L.; Mou, X.; Liu, Q.; Yang, Y.; Cao, Q. Review of droplet dynamics and dropwise condensation enhancement: Theory, experiments and applications. Adv. Colloid Interface Sci. 2022, 305, 102684. [Google Scholar] [CrossRef]
- Wang, X.; Xu, W.; Chen, Z.; Xu, B. Dropwise condensation heat transfer on nanostructured superhydrophobic surfaces with different inclinations and surface subcoolings. Int. J. Heat Mass Transf. 2021, 181, 121898. [Google Scholar] [CrossRef]
- Yilbas, B.S.; A-Sharafi, A.; Ali, H.; A-Aqeeli, N. Dynamics of a water droplet on a hydrophobic inclined surface: Influence of droplet size and surface inclination angle on droplet rolling. RSC Adv. 2017, 7, 48806. [Google Scholar] [CrossRef] [Green Version]
- Lv, C.; Yang, C.; Hao, P.; He, F.; Zheng, Q. Sliding of Water Droplets on Microstructured Hydrophobic Surfaces. Langmuir 2010, 26, 8704–8708. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Li, Y.; Qin, Y.; Yin, Y.; Zhang, J.; Che, Z. Water droplet detachment characteristics on surfaces of gas diffusion layers in PEMFCs. Int. J. Hydrogen Energy 2022, 47, 10341–10351. [Google Scholar] [CrossRef]
- Xie, J.; Xu, J.; Shang, W.; Zhang, K. Mode selection between sliding and rolling for droplet on inclined surface: Effect of surface wettability. Int. J. Heat Mass Transf. 2018, 122, 45–58. [Google Scholar] [CrossRef]
- Park, J.; Kumar, S. Droplet Sliding on an Inclined Substrate with a Topographical Defect. Langmuir 2017, 33, 7352–7363. [Google Scholar] [CrossRef] [PubMed]
- Al-Sharafi, A.; Yilbas, B.S.; Ali, H.; Alaqeeli, N. A Water Droplet Pinning and Heat Transfer Characteristics on an Inclined Hydrophobic Surface. Sci. Rep. 2018, 8, 3061. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, C.; Shi, S. Wetting states of two-dimensional drops under gravity. Phys. Rev. E 2018, 98, 042802. [Google Scholar] [CrossRef] [Green Version]
- Furmidge, C. Studies at phase interfaces. I. The sliding of liquid drops on solid surfaces and a theory for spray retention. J. Colloid Sci. 1962, 17, 309–324. [Google Scholar] [CrossRef]
- Wolfram, E.; Faust, R. Chapter 10 in Wetting, Spreading and Adhesion; Padday, J.F., Ed.; Academic Press: London, UK, 1978; pp. 213–222. [Google Scholar]
- Tadmor, R. Open Problems in Wetting Phenomena: Pinning Retention Forces. Langmuir 2021, 37, 6357–6372. [Google Scholar] [CrossRef]
- Qin, Y.; Li, Y.; Zhang, D.; Xu, N.; Zhu, X. Wettability, durability and corrosion properties of slippery laser-textured aluminum alloy surface under water impact. Surf. Coat. Technol. 2020, 394, 125856. [Google Scholar] [CrossRef]
- Peta, K.; Bartkowiak, T.; Galek, P.; Mendak, M. Contact angle analysis of surface topographies created by electric discharge machining. Tribol. Int. 2021, 163, 107139. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Islamova, A.G.; Orlova, E.G.; Ivashutenko, A.S.; Shanenkov, I.I.; Zykov, I.Y.; Feoktistov, D.V. Influence o roughness on polar and dispersed components of surface free energy and wettability properties of copper and steel surfaces. Surf. Coat. Technol. 2021, 422, 127518. [Google Scholar] [CrossRef]
- Annapragada, S.R.; Murthy, J.Y.; Garimella, S.V. Prediction of droplet dynamics on an incline. Int. J. Heat Mass Transf. 2012, 55, 1466–1474. [Google Scholar] [CrossRef] [Green Version]
- Goswami, A.; Alen, S.K.; Farhat, N.; Rahman, A. Numerical study of wetting stability and sliding behavior of liquid droplets on microgrooved surfaces. Colloid Polym. Sci. 2019, 297, 989–1000. [Google Scholar] [CrossRef]
- Fernández-Toledano, J.-C.; Blake, T.; De Coninck, J. Taking a closer look: A molecular-dynamics investigation of microscopic and apparent dynamic contact angles. J. Colloid Interface Sci. 2021, 587, 311–323. [Google Scholar] [CrossRef]
- Blake, T.D. The physics of moving wetting lines. J. Colloid Interface Sci. 2006, 299, 1–13. [Google Scholar] [CrossRef]
- Voinov, O.V. Hydrodynamics of wetting. Fluid Dyn. 1977, 11, 714–721. [Google Scholar] [CrossRef]
- Bonn, D.; Eggers, J.; Indekew, J.; Meunier, J.; Rolley, E. Wetting and spreading. Rev. Mod. Phys. 2009, 81, 739–805. [Google Scholar] [CrossRef]
- Yonemoto, Y.; Kunugi, T. Analytical consideration of liquid droplet impingement on solid surfaces. Sci. Rep. 2017, 7, 2362. [Google Scholar] [CrossRef] [Green Version]
- Snoeijer, J.H.; Andreotti, B. Moving Contact Lines: Scales, Regimes, and Dynamical Transitions. Annu. Rev. Fluid Mech. 2013, 45, 269–292. [Google Scholar] [CrossRef] [Green Version]
- McHale, G.; Gao, N.; Wells, G.G.; Barri-Zhang, H.; Ledesma-Aguilar, R. Friction coefficient for droplets on solids: The liq-uid-solid amontons’ laws. Langmuir 2022, 38, 4425–4433. [Google Scholar] [CrossRef]
- Kim, Y.H.; Kim, K.; Jeong, J.H. Determination of the adhesion energy of liquid droplets on a hydrophobic flat surface con-sidering the contact area. Int. J. Heat Mass Transf. 2016, 102, 826–832. [Google Scholar] [CrossRef]
- Yonemoto, Y.; Kunugi, T. Experimental and theoretical investigation of contact-angle variation for water-ethanol mixture droplets on a low-surface-energy solid. Int. J. Heat Mass Transf. 2016, 96, 614–626. [Google Scholar] [CrossRef]
- Extrand, C.W.; Kumagai, Y. Liquid Drops on an Inclined Plane: The Relation between Contact Angles, Drop Shape, and Retentive Force. J. Colloid Interface Sci. 1995, 170, 515–521. [Google Scholar] [CrossRef]
- Pierce, E.; Carmona, F.J.; Amirfazli, A. Understanding of sliding and contact angle results in tilted plate experiments. Colloids Surfaces A: Physicochem. Eng. Asp. 2008, 323, 73–82. [Google Scholar] [CrossRef]
- Bouteau, M.; Cantin, S.; Benhabib, F.; Perrot, F. Sliding behavior of liquid droplets on tilted Langmuir–Blodgett surfaces. J. Colloid Interface Sci. 2008, 317, 247–254. [Google Scholar] [CrossRef] [PubMed]
- Kibar, A.; Ozbay, R.; Sarshar, M.A.; Kang, Y.T.; Choi, C.-H. Bubble Movement on Inclined Hydrophobic Surfaces. Langmuir 2017, 33, 12016–12027. [Google Scholar] [CrossRef] [PubMed]
- Yonemoto, Y.; Suzuki, S.; Uenomachi, S.; Kunugi, T. Sliding behavior of water-ethanol mixture droplets on inclined low-surface-energy solid. Int. J. Heat Mass Transf. 2018, 120, 1315–1324. [Google Scholar] [CrossRef]
- Kubiak, K.J.; Mathia, T.G. Anisotropic Wetting of Hydrophobic and Hydrophilic Surfaces–Modelling by Lattice Boltzmann Method. Procedia Eng. 2014, 79, 45–48. [Google Scholar] [CrossRef] [Green Version]
- Prajitno, D.H.; Maulana, A.; Syarif, D.G. Effect of Surface Roughness on Contact Angle Measurement of Nanofluid on Surface of Stainless Steel 304 by Sessile Drop Method. J. Physics: Conf. Ser. 2016, 739, 012029. [Google Scholar] [CrossRef]
- Yonemoto, Y.; Tomimitsu, I.; Shimizu, K.; Kunugi, T. Wettability model for water-ethanol binary mixture droplet on roughened low-surface-energy solids. Int. J. Multiph. Flow 2021, 137, 103569. [Google Scholar] [CrossRef]
- Yonemoto, Y.; Tashiro, K.; Shimizu, K.; Kunugi, T. Predicting the splash of a droplet impinging on solid substrates. Sci. Rep. 2022, 12, 5093. [Google Scholar] [CrossRef]
- de Gennes, P.G.; Brochard-Wyard, F.; Quere, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer: New York, NY, USA, 2003. [Google Scholar]






| Liquids [wt%] | Volumes [μL] | Initial Contact Are Diameter D0 [m] | Initial Droplet Height h0 [m] |
|---|---|---|---|
| 0 | 7–600 | 2.7 × 10−3–15.5 × 10−3 | 1.6 × 10−3–4.3 × 10−3 |
| 7.7 | 8–600 | 3.1 × 10−3–16.9 × 10−3 | 1.6 × 10−3–3.7 × 10−3 |
| 20.6 | 10–500 | 3.7 × 10−3–18.5 × 10−3 | 1.4 × 10−3–2.7 × 10−3 |
| 39.3 | 10–400 | 4.0 × 10−3–17.6 × 10−3 | 1.2 × 10−3–2.2 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yonemoto, Y.; Fujii, Y.; Sugino, Y.; Kunugi, T. Relationship between Onset of Sliding Behavior and Size of Droplet on Inclined Solid Substrate. Micromachines 2022, 13, 1849. https://doi.org/10.3390/mi13111849
Yonemoto Y, Fujii Y, Sugino Y, Kunugi T. Relationship between Onset of Sliding Behavior and Size of Droplet on Inclined Solid Substrate. Micromachines. 2022; 13(11):1849. https://doi.org/10.3390/mi13111849
Chicago/Turabian StyleYonemoto, Yukihiro, Yosuke Fujii, Yoshiki Sugino, and Tomoaki Kunugi. 2022. "Relationship between Onset of Sliding Behavior and Size of Droplet on Inclined Solid Substrate" Micromachines 13, no. 11: 1849. https://doi.org/10.3390/mi13111849
APA StyleYonemoto, Y., Fujii, Y., Sugino, Y., & Kunugi, T. (2022). Relationship between Onset of Sliding Behavior and Size of Droplet on Inclined Solid Substrate. Micromachines, 13(11), 1849. https://doi.org/10.3390/mi13111849







