Next Article in Journal
Dynamic Behaviours of Monodisperse Double Emulsion Formation in a Tri-Axial Capillary Device
Previous Article in Journal
Influence of Filler Materials on Wettability and Mechanical Properties of Basalt/E-Glass Woven Fabric–Reinforced Composites for Microfluidics
Previous Article in Special Issue
Development of NIR-Based ANN Models for On-Line Monitoring of Glycerol Concentration during Biodiesel Production in a Microreactor
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Micromachines
Volume 13
Issue 11
10.3390/mi13111876
micromachines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Near-Infrared Spectroscopy Coupled with Chemometrics and Artificial Neural Network Modeling for Prediction of Emulsion Droplet Diameters

by
Filip Grgić
,
Tamara Jurina
,
Davor Valinger
,
Jasenka Gajdoš Kljusurić
,
Ana Jurinjak Tušek
* and
Maja Benković
Faculty of Food Technology and Biotechnology, University of Zagreb, Pierottijeva ul. 6, 10000 Zagreb, Croatia
*
Author to whom correspondence should be addressed.
Micromachines 2022, 13(11), 1876; https://doi.org/10.3390/mi13111876
Submission received: 30 September 2022 / Revised: 24 October 2022 / Accepted: 26 October 2022 / Published: 31 October 2022
(This article belongs to the Special Issue Implementation of Microreactor Technology in Biotechnology 2022 (IMTB 2022))
Browse Figures
Versions Notes

Abstract

:
There is increased interest in the food industry for emulsions as delivery systems to preserve the stability of sensitive biocompounds with the aim of improving their bioavailability, solubility, and stability; maintaining their texture; and controlling their release. Emulsification in continuously operated microscale devices enables the production of emulsions of controllable droplet sizes and reduces the amount of emulsifier and time consumption, while NIR, as a nondestructive, noninvasive, fast, and efficient technique, represents an interesting aspect for emulsion investigation. The aim of this work was to predict the average Feret droplet diameter of oil-in-water and oil-in-aqueous mint extract emulsions prepared in a continuously operated microfluidic device with different emulsifiers (PEG 1500, PEG 6000, and PEG 20,000) based on the combination of near-infrared (NIR) spectra with chemometrics (principal component analysis (PCA) and partial least-squares (PLS) regression) and artificial neural network (ANN) modeling. PCA score plots for average preprocessed NIR spectra show the specific grouping of the samples into three groups according to the emulsifier used, while the PCA analysis of the emulsion samples with different emulsifiers showed the specific grouping of the samples based on the amount of emulsifier used. The developed PLS models had higher R2 values for oil-in-water emulsions, ranging from 0.6863 to 0.9692 for calibration, 0.5617 to 0.8740 for validation, and 0.4618 to 0.8692 for prediction, than oil-in-aqueous mint extract emulsions, with R2 values that were in range of 0.8109–0.8934 for calibration, 0.5017–0.6620, for validation and 0.5587–0.7234 for prediction. Better results were obtained for the developed nonlinear ANN models, which showed R2 values in the range of 0.9428–0.9917 for training, 0.8515–0.9294 for testing, and 0.7377–0.8533 for the validation of oil-in-water emulsions, while for oil-in-aqueous mint extract emulsions R2 values were higher, in the range of 0.9516–0.9996 for training, 0.9311–0.9994 for testing, and 0.8113–0.9995 for validation.

1. Introduction

The consumption of medicinal plants is inversely related to the occurrence of diseases such as several types of cancer, cardiovascular, cerebrovascular, and neurodegenerative diseases. The high presence of antioxidants in plants, in the form of bioactive compounds, represents an important basis for the health-protecting effects connected with their consumption [1]. Due to their beneficial effects, these bioactive compounds extracted from medicinal plants have been successfully incorporated into food systems [2].
In order to increase the use of extracts with compounds isolated from medicinal plants in food matrices, several technologies should be considered: nanoemulsions, nanocapsules, vapors, and edible films [2]. There is increased interest in the food industry for emulsions as delivery systems to maintain the completeness of sensitive biocompounds with the aim to improve their bioavailability, solubility, stability, and texture and the control of their release [3]. Therefore, the industrial use of emulsions has emerged in recent years with the aim to ameliorate certain product characteristics or to create completely new ones [4,5].
Emulsions are multiphase systems comprising two or more liquids that are insoluble in one another [6]. One phase is a continuous phase in which small droplets of another phase are dispersed [7,8]. According to the droplet size range, emulsions can be divided into macroemulsions (0.1–100 µm), microemulsions (5–100 µm), and nanoemulsions (20–200 nm) [9,10]. Emulsions typically consist of oil, water, and emulsifier [3,11]. Emulsifiers are surface-active substances (surfactants) that are used for avoiding emulsion destabilization such as flocculation, coalescence, and Ostwald ripening [12]. They are normally soluble in one phase, consisting of functional groups capable of interaction with the other phase at the interfacial surface [6]. Emulsifiers are amphiphilic molecules that are used with the aim to maintain the emulsion stability for a long period of time by preventing droplet coalescence at the liquid–liquid interface [8].
Emulsification is a process of emulsion formation; however, this process is unspontaneous and requires energy input for droplet production [13]. Conventional high-energy methods include colloid mills, high-pressure homogenizers, and sonicators [5,14,15,16]. Major obstacles of these methods are the relatively expensive equipment and the regulation of process parameters such as the temperature, applied force, and droplet size of an emulsion [5,17]. To overcome the above-mentioned limitations, the use of microfluidic technology has the potential to eliminate the existing problems. According to the literature, transferring the emulsification to a smaller scale enables the production of emulsions with controllable droplet sizes and reduces the amount of emulsifier and time consumption [18,19,20]. The microchannel geometry allows the control of shear forces; high shear forces act on a small liquid volume (several nanoliters), allowing the precise adjustment of the emulsion droplet size. The prevailing surface tension in microchannels ensures the continuous generation of droplets with the same droplet size and shape [21]. To produce monodispersed droplets using various microfluidics, different techniques have been described, including T-junctions, Y-junctions, and flow-focusing cross-junctions [22]. According to Vidovič et al. [23], the characteristics of the dispersion being dispersed as well as the working conditions and the device being utilized determine the form and distribution of the droplets. When working to generate droplets using continuously operated microfluidic devices, the size of the droplets depends on the channel geometry, channel length, shape–flow-rate ratio, and velocity. Furthermore, the droplet size also depends on the contact and injection angle as well as the surfactant addition [24]. According to Wang et al. [25], changing the contact angle between the dispersed phase and the channel wall is the most practical way to modify the droplet size. Microchannels are mostly produced form glass and poly(dimethylsiloxane), and the effect of the wettability of those materials on the contact angle has to be taken into consideration [26]. Due to the significance of the contact angle in the design of microdroplet preparation machinery as well as its role in the selection of appropriate raw materials for industrial processes, it is crucial to understand how it affects step emulsification. In experimental work, applying different surfactants frequently alters a fluid’s interfacial tension and contact angle.
Maintaining emulsion stability is one of the greatest challenges during the emulsification process. As mentioned, the mixing speed, mixing time, emulsification method, oil composition, oil-to-water ratio, emulsifier type, and concentration are parameters that influence the droplet size distribution [10,27]. Therefore, it is necessary to develop a rapid and nondestructive method for monitoring the emulsification process. According to the literature, the application of near-infrared spectroscopy (NIRs) has emerged for monitoring variables influencing the formation of emulsions [10,28,29,30].
Near-infrared spectroscopy (NIRs), as a nondestructive, noninvasive, fast, and efficient technique, has a long history of application in the food industry [31,32,33]. The advantages of its application include having little or no need for sample preparation; the lower cost compared to conventional analytical techniques, and the capability to analyze a wide range of products [33]. NIRs is based on the absorption of NIR radiation in the wavelength range from 780 nm to 2500 nm [34]. The absorbance of light is mainly caused by overtones and the combination vibrations of some hydrogen-based functional groups such as O–H, C–H, C–O, and N–H [24]. Due to the large number of recorded spectra, it is imperative to analyze the acquired spectral data. In order to extract important information and to identify significant patterns in NIR spectra, various mathematical and statistical methods (principal component analysis, (PCA), partial least-squares regression (PLSR), canonical correlation analysis (CCA), and principal component regression (PCR)) can be used [10,23]. The big advantage of these statistical methods includes exploring these spectral data for qualitative and quantitative applications [35]. However, due to the complex nature of food, nonlinear techniques, compared to multivariate methods, have proved to be a good solution. Artificial neural networks (ANNs) coupled with NIR spectroscopy have been identified as an excellent tool for monitoring emulsion droplet dimeter prediction [10], the prediction of the physical and chemical properties of plant extracts [36], and honey adulteration detection and quantification [37]. For all three mentioned experiments, developed ANN models described the experimental data with high accuracy (the coefficients of determination were greater than 0.8).
The aim of this work was to predict the average Feret droplet diameters of oil-in-water and oil-in-aqueous mint extract emulsions based on the combination of NIR spectra with PLS regression and ANN modeling. Emulsification was performed in a microfluidic system including a static teardrop micromixer with the addition of three emulsifiers (PEG 1500, PEG 6000, and PEG 20,000) at three different concentrations (2%, 4%, and 6%). To the best of our knowledge this is the first application of NIR spectra and PLS and ANN modeling for the analysis of oil-in-aqueous mint extract emulsions prepared using a microfluidic device, motivated by the fact that emulsion technology is generally applied for the encapsulation of bioactives in aqueous solutions, which can either be used directly in the liquid state or can be dried to form powders [38]. Different spectral preprocessing methods (first-order Savitzky–Golay derivative (SG1), standard normal variate (SNV), multiplicative scatter corrections (MSC), first-order Savitzky–Golay derivative followed by standard normal variate (SG1+SNV), and first-order Savitzky–Golay derivative followed by multiplicative scatter corrections (SG1+MSC)) were applied in order to determine the predictive ability of the models used.

2. Materials and Methods

2.1. Materials

Edible sunflower oil (Zvijezda plus d.o.o., Zagreb, Croatia) was purchased from a local supermarket. Polyethylene glycols with average molecular weights of 1500 g/mol (PEG 1500) and 6000 g/mol (PEG 6000) were purchased from Acros Organics (Geel, Belgium), while the 20,000 g/mol polyethylene glycol (PEG 20,000) was obtained from Sigma-Aldrich (Taufkirchen, Germany). Dried mint leaves (Mentha piperita L.) were purchased from Suban, Croatia. Plant materials were collected during the flowering season of 2019 in the north-western part of Croatia, dried naturally, and stored in ambient conditions before use.

2.2. Methods

2.2.1. Mint Extract Preparation

First, 1 g of dry plant material was placed in a 200 mL glass with 50 mL of deionized water, and solid–liquid extraction was performed using an Ika HBR4 digital oil bath (IKA-Werk GmbH & Co., KG, Staufen, Germany) at 80 °C and 250 rpm for 30 min. After the extraction, samples were filtered through a 100% cellulose paper filter (LLG Labware, Meckenheim, Germany) with 5–13 µm pores and stored at 4 °C until analyzed. The dry matter content of the aqueous mint extract was 0.85%.

2.2.2. Emulsification in a Microfluidic System

Glass microchips with laser-engraved microchannels were placed in stainless-steel holders, which provided leak-free connections (Micronit Microfluidics B.V., Enschede, The Netherlands). Experiments were performed in microchannels with the following dimensions: width/height/length = 250 μm: 150 μm: 55.3 mm. The microchannels were equipped with static teardrop micromixers. Emulsion droplets were generated in a borosilicate glass microfluidic device. Two syringe pumps (NE -1000 Syringe Pump, New Era Pump Systems, New York, NY, USA) with high-pressure stainless-steel syringes (8 mL, Harvard Apparatus) were used for solution delivery. Two phases, oil and aqueous mint extract, were introduced separately into microchannels through a fused silica connection (375 µm o.d., 150 µm i.d., Micronit Microfluidics B.V., Enschede, The Netherlands). The emulsification experiments were performed according to the design of experiments previously described by Grgić et al. [39] (Table 1).

2.2.3. Average Feret Diameter

The prepared samples of oil-in-aqueous mint extract emulsions were photographed using a microscope equipped with a camera (BTC type LCD-35, Bresser, Germany) at 4× magnification. The average Feret diameter of the droplets was measured using the software tool ImageJ (v.1.8.0. National Institutes of Health, Bethesda, MD, USA). The Feret diameter was defined as the perpendicular distance between two tangents located on opposite sides of a particle [39]. The average Feret diameter of oil-in-water emulsions prepared in the same microfluidic system according to the same experimental design (Table 1) was previously published in an article by Grgić et al. [39].

2.2.4. Near-Infrared Spectra of Emulsions

The near-infrared (NIR) spectra of all oil-in-water and oil-in-aqueous mint extract emulsions were recorded in the wavelength range from 904 nm to 1699 nm using an NIR spectrometer (NIR—128—1.7—USB/6.25/50 µm Control Development Inc., South Bend, IN, USA). The NIR spectra were recorded in disposable plastic cuvettes with a liquid sample measurement setup. The NIR spectra were recorded in three parallel runs.

2.2.5. NIR Spectra Processing and Modeling

The effects of preprocessing methods of NIR spectra on sample grouping were analyzed using the Unscrambler X software (Version 10.1. CAMO AS, Oslo, Norway). Oil-in-water emulsions and oil-in-aqueous mint extract emulsions were analyzed separately. The performances of the following preprocessing methods were tested: (i) raw spectra, (ii) first-order Savitzky–Golay derivative (SG1), (iii) standard normal variate (SNV), (iv) multiplicative scatter corrections (MSC), (v) first-order Savitzky–Golay derivative followed by standard normal variate (SG1+SNV), and (vi) first-order Savitzky–Golay derivative followed by multiplicative scatter corrections (SG1+MSC). The same software was also used for a principal component analysis (PCA) and a partial least-squares (PLS) regression.
For the prediction of the average droplet sizes of the oil-in-water emulsions and oil-in-aqueous mint extract emulsions with PEG 1500, PEG 6000, or PEG 20,000 as emulsifiers, PLS regression models were developed. The PLS model input data were the triplicates of the spectra of each sample. Each PLS model used seven latent variables (factors) and a random cross-validation method based on splitting the input data into 20 segments. No normalization method was used before the data transformation. The applicability of the PLS models developed using raw and preprocessed NIR spectra was estimated based on: (i) the coefficients of determination for calibration (R2cal) and cross-validation (R2cval), (ii) the root-mean-square error for calibration (RMSEC) and cross-validation (RMSECV), (iii) the average value of the difference between the predicted and observed values (bias), and (iv) the ratio of the predicted deviation (RPD) and the range error ratio (RER) [10,37].
The average droplet sizes of the oil-in-water emulsions and oil-in-aqueous mint extract emulsions with PEG 1500, PEG 6000, or PEG 20,000 as an emulsifier based on NIR spectra were also predicted using artificial neural network (ANN) modeling in Statistica v.13.0 software (Tibco Software Inc., Tulsa, OT, USA). Multiple layer perceptron network (MLP network) models consisted of an input layer, a hidden layer, and an output layer (Figure 1). The first five factors from the PCA analysis were represented by the five neurons in the input layer. ANN inputs were chosen from the first five principal components, which accounted for more than 99.99% of the data variability. A PCA based on the raw spectra and a PCA based on the selected preprocessing method were used separately. The following set of alternatives was randomly chosen as the hidden activation function and the output activation function: identity, logistic, hyperbolic tangent, and exponential. The MLP chose a random number between 3 and 11 neurons for the hidden layer.
The data matrix for ANN modeling comprised 51 rows representing emulsion samples prepared using an individual emulsifier and 6 columns referring to five PCA coordinates (factors) and the measured average droplet sizes. During the construction, data were randomly divided into 70% for network training, 15% for network testing, and 15% for model validation. For each emulsifier, 1000 networks were generated. Model training was carried out using a back error propagation algorithm and the sum-of-squares error function implemented in Statistica v.13.0 (Tibco Software Inc., Tulsa, OT, USA) automated neural networks. The proposed ANN model performance was estimated based on the R2 and root-mean-square error (RMSE) values for the training, testing, and validation.

3. Results and Discussion

3.1. The Average Feret Diameters of Oil-in-Aqueous Mint Emulsions: Comparison with the Average Feret Diameters of Oil-in-Water Emulsions

This research examined the applicability of a microfluidic device for generating oil–aqueous mint extract emulsions utilizing emulsifiers such as PEG 1500, PEG 6000, and PEG 20,000. The prepared emulsions were observed under a microscope at the microfluidic device outlet. Photos were taken and used for the average Feret diameter measurements. The gathered photos of the prepared emulsions and measured average Feret diameters are presented in Figure 2.
It can be observed that spherical oil droplets of a dispersed phase were generated in the continuous aqueous mint extract (Figure 2(a1–a3)). As previously described by Shah et al. [40], in contrast to bulk emulsification techniques, an emulsion is carefully manufactured one drop at a time in a microfluidic device, and therefore a monodisperse emulsion is the end product of this procedure. A microfluidic device’s ability to create controlled-sized emulsion [41,42] droplets depends on a number of factors, including the flow rates, the fluid viscosity, the emulsifier, and the geometry of the microfluidic channels [10,34]. All of the mentioned factors have to be taken into consideration when optimizing the emulsification process [39].
For oil-in-aqueous mint extract emulsions, the smallest droplets were generated with the emulsifier PEG 6000 (Figure 2(a2,b2)), with an average Feret dimeter in the range from 52.36 ± 16.50 µm to 149.99 ± 39.15 µm, followed by the emulsions with PEG 1500 (Figure 2(a1,b1)) and with PEG 20,000 (Figure 2(a3,b3)). For PEG 1500 emulsions, the average droplet Feret dimeter was in the range from 112.26 ± 16.24 µm to 163.77 ± 16.93 µm, while for the PEG 20,000 emulsions the average droplet Feret dimeter was in the range from 109.81 ± 1.74 µm to 169.99 ± 1.06 µm. When comparing the measured data with the results presented by Grgić et al. [39] for oil-in-water emulsions produced with the same emulsifiers and using the same process conditions, the droplet size followed approximately the same trend. For PEG 1500 and PEG 20,000 oil-in-mint extracts, the emulsion droplets were larger than the oil-in-water emulsion droplets for all experiments. For PEG 6000 oil-in-mint extracts, the emulsion droplets were larger than the oil-in-water emulsion droplets for experiments with 30% oil phase.

3.2. NIR Spectra of Oil-in-Water and Oil-in-Aqueous Mint Extract Emulsions: Preprocessing and PCA Analysis

The NIR spectra of the oil-in-water and oil-in-aqueous mint extract emulsions prepared with different emulsifiers (PEG 1500, PEG 6000, and PEG 20,000) were recorded continuously in the wavelength range from 904 to 1699 nm. The average spectra of individual samples, grouped according to the continuous phase, are given in Figure 3(a1,a2), while the SNV preprocessed spectra of the oil-in-water emulsions and the MSC preprocessed spectra of oil-in-mint aqueous extract emulsions are given in Figure 3(b1,b2). Despite variations in spectral absorbance, the majority of the spectra obtained from the emulsion samples followed a similar pattern. Additive effects (spectral shifts) characteristic of the different droplet sizes present in the samples can be seen. A similar observation was made in a study by Bampi et al. [28], where a discrepancy in the spectral baseline was observed that could be attributed to different light scattering due to the different water droplet sizes in the emulsions. The largest differences in the spectral peaks of both sample types are seen for the wavelength range from 1300 to 1699 nm, which is specific for the superposition of the O-H bonds. Moreover, the differences in this part of the spectrum can be easily correlated with the water present in the samples [36].
According to Borges et al. [29], NIR spectroscopy is a method that allows the efficient determination of the average diameter and water content of oil-in-water emulsions and offers great potential for the online qualitative analysis of biodiesel during storage. Furthermore, according to Bi et al. [43] and Grisanti et al. [44], the implication that numerous interferences frequently cause spectra to be altered during the signal acquisition process is a practical issue for the implementation of NIR technology. The sample thickness, measurement geometry, or physical characteristics of the samples can influence the light path length, and therefore preprocessing is an essential step in NIR spectral modeling [45]. As described by Feng et al. [46], spectral preprocessing is used to eliminate systemic noise and highlight the changes between the samples. In this work, the efficiency of the first-order Savitzky–Golay derivative (SG1), standard normal variate (SNV), multiplicative scatter corrections (MSC), first-order Savitzky–Golay derivative followed by standard normal variate (SG1+SNV), and first-order Savitzky–Golay derivative followed by multiplicative scatter corrections (SG1+MSC) was analyzed. The results showed that SNV and MSC were the most efficient methods for the analysis of the NIR spectra of oil-in-water and oil-in-aqueous mint extract emulsions prepared in a continuously operated microfluidic device. The standard normal variate (SNV) and multiplicative signal correction (MSC) methods was analyzed (Figure 3(b1,b2)). By deducting the complete spectrum’s mean value, the standard normal variate (SNV) eliminates a constant offset component and scales down all spectra by dividing the result by the full spectrum’s standard deviation [47]. On the other hand, by employing the linear least-squares approach to construct a linear model between a reference spectrum and other spectra in the dataset, the multiplicative scatter correction reduces spectral deviations. The dataset’s average spectrum, known as the reference spectrum, is frequently selected [48]. However, without the application of chemometric methods that can extract significant data from the spectra, few conclusions can be drawn from either the raw or preprocessed spectral data. For this reason, a PCA analysis was applied to the raw spectral data and preprocessed data as one of the most widely used chemometric methods to detect the differences between samples [10]. The results for the oil-in-water emulsions are shown in Figure 4, and the results for the oil-in-aqueous mint extract emulsions are shown in Figure 5. Based on the PCA results, SNV was selected as the optimal preprocessing method for individual oil-in-water emulsion NIR spectra and MSC was selected as the optimal preprocessing method for individual oil-in-aqueous mint extract emulsion NIR spectra. The selected preprocessing methods resulted in the best discrimination of the sample and the highest explanation of the data in the first two principal components [49]. PCA score plots for average NIR preprocessed spectra (Figure 4a and Figure 5a) show the specific grouping of the samples in three groups according to the emulsifier used (PEG 1500, PEG 6000, and PEG 20,000). As expected, the grouping was more evident for the oil-in-water emulsions. Mint extracts, as the continuous phase for the second type of emulsion, scarcely influenced the sample grouping. The chart of the principal components (x-axis) and the percentage of explained variance (y-axis) shows its inflection point at the third PC, which is an indication of the most important PCs to investigate the observed system. As presented for both types of emulsions, the first three principal components (PCs) explained most of the sample variability. For the oil-in-water emulsions, the first three PCs explained 75.92% of the data variability, while for the oil-in-aqueous mint extract emulsions the first three PCs explained 87.06% of the data variability. The compressed variance difference in PC1–PC3 for the oil-in-water emulsions and oil-in-aqueous mint extract emulsions could be explained by the color difference of the continuous phases used and the larger effect of color in PC1–PC3 of the oil-in-aqueous mint extract emulsions. The detection of significant variables (variables with large variances) and correlations between variables [50] was made by the analysis of the loading spectra (Figure 4b and Figure 5b). Even though both positive and negative contributions are displayed in the loading plots (Figure 4b and Figure 5b), the spectral shape of the pure PC1 loading vector displays the majority of the distinctive absorption peaks observed in Figure 2a and Figure 3a. Moreover, the intensity maximum of the pure PC1 spectrum is shifted toward the actual spectrum by the positive and negative contributions from PC2 and PC3, as previously presented by Zhang et al. [51]. For the oil-in-water emulsions, the maximum loading peaks were noticed at 941 nm (C−H bond, 3rd overtone) and 1631 nm (C−H, 1st overtone), while for the oil-in-aqueous mint extract emulsions the maximum loading peaks were noticed at 960 nm (C−H bond, 3rd overtone), 1437 nm (O−H, 1st overtone), and 1631 nm (C−H, 1st overtone). Furthermore, a PCA analysis was applied for the analysis of the emulsion samples according to the emulsifier used. As presented in Figure 4c,e,g and Figure 5c,e,g, the specific grouping of the samples based on the amount of the emulsifier used can be noticed. It can be seen that sample grouping was more pronounced for the oil-in-water emulsions. Furthermore, the emulsions with the highest amount of emulsifier (6%) were specifically grouped, while there was some overlap of the samples with 2% and 4% emulsifier. That was especially evident for the oil-in-aqueous mint extract emulsions (Figure 5c,e,g). Moreover, the first three factors explained 75.31% (PEG 1500), 89.11% (PEG 6000), and 89.11% (PEG 20,000) of the variability between the oil-in-water emulsion samples and 83.85% (PEG 1500), 89.24% (PEG 6000), and 96.23% (PEG 20,000) of the variability between the oil-in-aqueous mint extract emulsion samples. The obtained results indicate that those samples were also separated based on the mixing rate, oil phase, and particle size. The loading plot shows that for oil-in-water emulsions the maximum loading peaks were noticed as follows: (i) for PEG1500 at 941 nm (C−H bond, 3rd overtone) and 1631 nm (C−H, 1st overtone) (Figure 4d); (ii) for PEG 6000 at 941 nm (C-H bond, 3rd overtone), 1218 nm (C−H, 2nd overtone), and 1687 nm (C−H, 1st overtone) (Figure 4f); and (iii) for PEG 20,000 at 1631 nm (C−H, 1st overtone) (Figure 4h). Moreover, for the oil-in-aqueous mint extract emulsions, maximum loading peaks were noticed as follows: (i) for PEG1500 at 1469 nm (O−H, 1st overtone) and 1631 nm(C−H, 1st overtone) (Figure 5d); (ii) for PEG 6000 at 1438 nm (O−H, 1st overtone), 1469 nm (O−H, 1st overtone), and 1631 nm (C−H, 1st overtone) (Figure 5f); and (iii) for PEG 20000 at 960 nm (C−H bond, 3rd overtone), 1437 nm (O−H, 1st overtone), 1631 nm (C−H, 1st overtone), and 1687 nm (C−H, 1st overtone) (Figure 5h). The high percentages of explained variance in both cases are indicative that NIR coupled with chemometrics can be successfully used for the rapid and nondestructive discrimination of emulsion samples. These results are consistent with studies by Borges et al. [29], Bampi et al. [28], and Dinache et al. [52], who also successfully used NIR spectroscopy coupled with chemometrics to analyze emulsions.

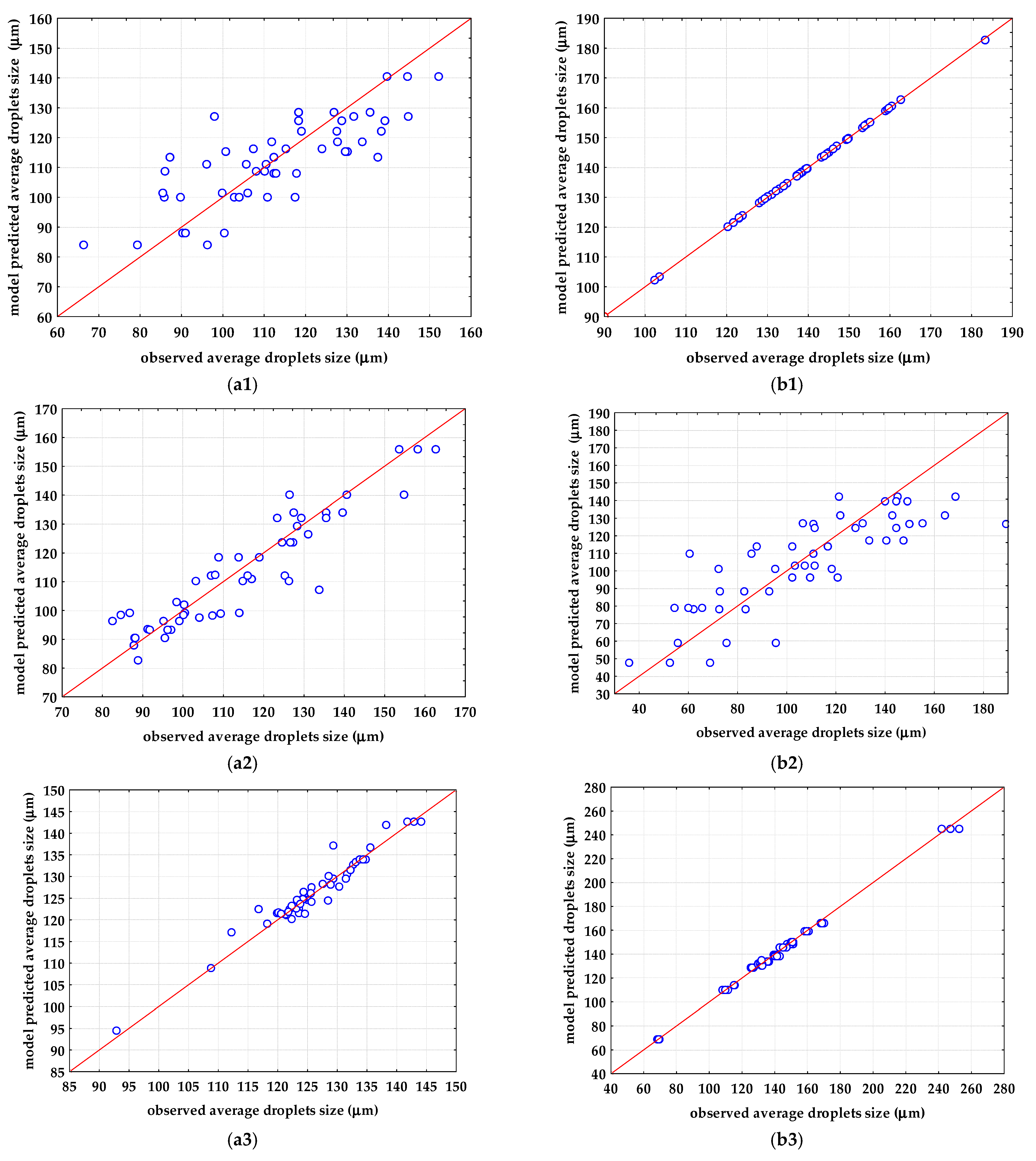
3.3. PLS Modeling of the Average Feret Diameters of Emulsions

The aim of this work was to analyze the applicability of NIR spectroscopy to distinguishing the emulsion droplet sizes, expressed as the average Feret diameter at the microfluidics device outflow. For that purpose, partial least-squares (PLS) modeling was applied (Table 2).
The performances of the different preprocessing methods were tested, including the first-order Savitzky–Golay derivative, standard normal variate, multiplicative scatter corrections, first-order Savitzky–Golay derivative in combination with standard normal variate, and first-order Savitzky–Golay derivative in combination with multiplicative scatter corrections. The applicability of the developed PLS models was evaluated using R2cal, R2cval, RMSEC, RMSECV, bias, RPD, and RER. As for the PCA analysis, the SNV preprocessing method was shown to be the most efficient for the PLS modeling using the NIR spectra of the oil-in-water emulsions, whereas the MSC was the most efficient for the PLS modeling using the NIR spectra of the oil-in-aqueous mint extract emulsions.
From the results summarized in Table 2 and Figure 6, it can be seen that the PLS model for oil-in-water emulsions using SNV preprocessed NIR spectra showed strong correlations (R2 > 0.7) [53] for the coefficient of calibration (R2cal), cross-validation (R2cval), and prediction (R2pred) with the addition of PEG 20000 (R2cal of 0.9692, R2cval of 0.8740, and R2pred of 0.8692). For PEG 15000, the PLS model correlation was moderate (R2cal of 0.6863, R2cval of 0.5617, and R2pred of 0.4618). For PEG 6000, a strong correlation was achieved for the coefficient of calibration (R2cal of 0.9601), while for cross-validation and prediction the correlations were moderate (R2cval of 0.6204 and R2pred of 0.6254). It can also be noticed that there were variations in RMSEC, RMSECV, and RMSEP for a number of PLS model factors. The results indicate that PLS models for oil-in-aqueous mint extract emulsions showed lower accuracy in comparison to those for oil-in-water emulsions. The highest R2pred of 0.7234 was obtained for emulsions prepared with PEG 1500, followed by PEG 20000, with an R2pred of 0.7062, and PEG 6000, with an R2pred of 0.5587. These poor values can be attributed to the indirect measurement of the average Feret diameter [54]. The quality of the developed PLS models was also evaluated based on residual predictive deviation (RPD) index and the range-to-error ratio (RER). Ideal and robust models need to possess higher R2pred coefficients and RPD indexes [55]. Based on the obtained RPD values, the only model for oil-in-water emulsion with PEG 20000 with RPD = 7.4581 was the one that can be used for process control (RPD > 6.5) [56]. The other developed PLS models, except the model for oil-in-aqueous mint extract emulsions with PEG 6000, can be used for screening (1.5 < RPD < 2.5) [57]. The bias, which is the discrepancy between the means of the true values and the estimated values, additionally known as the error of means, was strongly affected by the measurement error and the number of predictor variables [58]. Comparing the developed PLS models, it could be noticed that lower bias values were obtained for the oil-in-mint aqueous extract emulsions.
The efficient use of NIR spectroscopy coupled with PLS modeling was presented by Mishra et al. [59] for the at-line and in-line monitoring of droplet size in mayonnaise. The authors developed PLS models that achieved prediction errors for droplets in the range of 0.38 to 0.68 µm. Moreover, Amsaraj et al. [60] combined Fourier-transform infrared spectroscopy with a partial least-squares discriminant analysis of milk adulteration and achieved a 100% accurate classification. Bampi et al. [28] proposed PLS models with 9.53% mean error for the external validation of the average droplet size of water–biodiesel emulsions, while Jurinjak Tušek et al. [10] applied PLS modeling to predict the average Feret diameter of oil-in-water emulsions with two different emulsifiers (Tween 20 and PEG 2000).

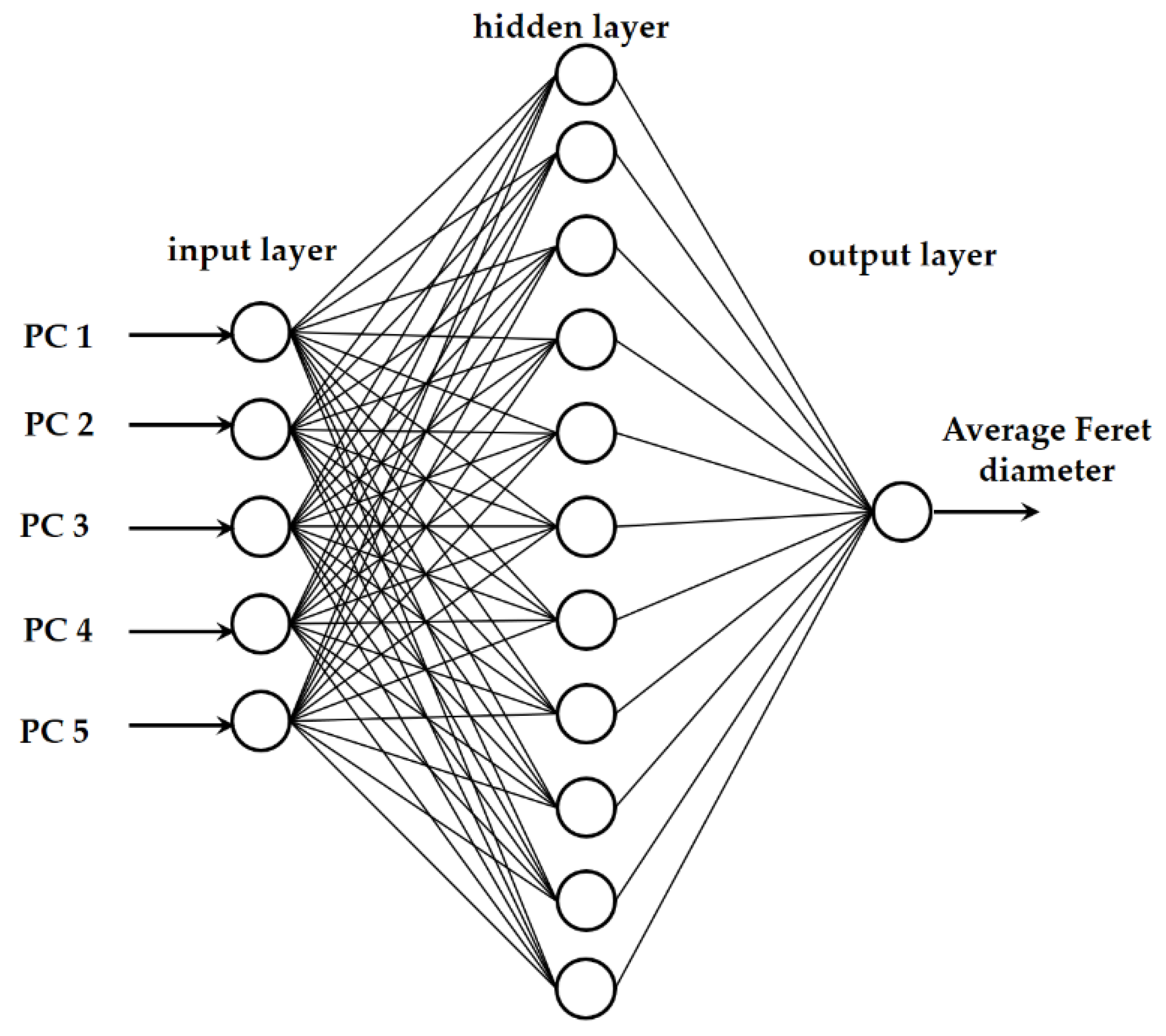
3.4. ANN Modeling of the Average Feret Diameters of Emulsions

A multilayer feed-forward neural network or multilayer perceptron (MLP) was fitted using the training dataset of the average droplet Feret diameter of each individual produced emulsion. The model inputs were the first five PCs, which contributed 99% of the data variability selected after the preprocessing that ensured efficient sample grouping. For the oil-in-water emulsions, five PCs after SNV preprocessing were used, and for the oil-in-aqueous mint extract emulsions, five PCs after MSC preprocessing were used, as in the case of PLS modeling. The performances of selected ANNs are given in Table 3 and in Figure 6. Based on the obtained R2 and RMSE values for training, testing, and validation, it can be noticed that ANN modeling ensured better agreement between the experimental data and the model-predicted data than PLS modeling. This can be simply explained by the nature of the model; PLS models include linear regressions, while ANN models include highly nonlinear expressions.
The optimal ANN architecture was selected based on the number of neurons in the hidden layer (less neurons in the hidden layer means a simpler and more stable network). For the oil-in-water emulsions, the highest R2validation was obtained for the emulsion with PEG 20000 (Figure 7(a3)). For the prediction of the average droplet Feret diameters in the oil-in-water emulsion with PEG 20000, MLP 5-5-1 was selected. The selected ANN was characterized by five neurons in the input layer, five neurons in the hidden layer, and one neuron in the output layer. A hidden activation function and output activation function was the exponential function. MLP 5-5-1 achieved an R2training of 0.9917, an RMSEtraining of 0.0002, an R2test of 0.9294, an RMSEtraining of 0.00184, an R2validation of 0.8533, and an RMSEvalidation of 0.0027. The ANN models used for the description of the average droplet Feret diameter of oil-in-aqueous mint extract emulsions showed significant improvement regarding R2validation in comparison to the developed PLS models. For oil-in-aqueous mint extract emulsions, the highest R2validation was obtained for emulsions with PEG 1500 (Figure 7(b1)) using MLP 5-8-1 with five neurons in the input layer, eight neurons in the hidden layer, and one neuron in the output layer. The selected ANN included a logistic function as a hidden activation function and an identity function as an output activation function. This ANN achieved an R2training of 0.9996, an RMSEtraining of 0.0004, an R2test of 0.9994, an RMSEtraining of 0.0006, an R2validation of 0.9995, and an RMSEvalidation of 0.0005.
The effectiveness of ANN modeling vs PLS modeling was estimated using R2 and RMSE, and based on those criteria, the developed ANN models showed higher effectiveness for the prediction of the average Feret diameter of both oil-in-water and oil in mint aqueous emulsions. However, the proposed models were limited in their applicability to the range of the trained variables and therefore do not have a wider application. As previously described, the superior performance of the ANN model is attributed to its nonlinear mapping capability, which is a feature lacking in the PLS models [61,62], and it is in agreement with previously presented results where ANN modeling was also applied for the prediction of emulsion droplets using NIR spectra [10,28]. Furthermore, ANN modeling was shown to be more efficient than PLS modeling for the rapid detection of the microbial spoilage of beef fillets based on Fourier-transform infrared spectra [63], for the prediction of soil organic carbon using UV-VIS-NIR spectra [64], for the quantitative analysis of quartz in the presence of mineral interferences using FTIR spectra [62], for nondestructive grape texture prediction using NIR spectra [49], and for the prediction of bioactive component contents in olive leaf extracts using NIR spectra [36].

4. Conclusions

This is the first application of NIR spectra and PLS and ANN modeling for the analysis of oil-in-aqueous mint extract emulsions prepared using a microfluidic device. Based on the presented results, it can be concluded that, for all emulsifiers used, oil-in-aqueous mint extract emulsion droplets were larger than those generated in oil-in-water emulsions. The results also showed that NIR spectroscopy coupled with chemometrics can be used for the distinctive qualitative and quantitative grouping of the samples according to the emulsifier used for its production. The obtained results for the ANN models a showed higher ability to predict the average droplet sizes than the PLS models, especially in case of PEG 1500 oil-in-aqueous mint extract emulsions, where R2 values of 0.9996, 0.9994, and 0.9995 were obtained for training, testing, and validation, respectively. This was attributed to the ANN’s nonlinear mapping capability, which is a feature lacking in the examined PLS models.

Author Contributions

Conceptualization, M.B. and A.J.T.; methodology, D.V.; validation, D.V.; formal analysis, F.G.; writing—original draft preparation, T.J. and F.G.; writing—review and editing, J.G.K. and A.J.T.; visualization, M.B. and D.V.; supervision, J.G.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Speisky, H.; Rocco, C.; Carrasco, C.; Lissi, E.A.; López-Alarcón, C. Antioxidant screening of medicinal herbal teas. Phytother. Res. 2006, 20, 462–467. [Google Scholar] [CrossRef] [PubMed]
  2. Ortega-Ramirez, L.A.; Rodriguez-Garcia, I.; Leyva, J.M.; Cruz-Valenzuela, M.R.; Silva-Espinoza, B.A.; Gonzalez-Aguilar, G.A.M.W.; Ayala-Zavala, J.F. Potential of medicinal plants as antimicrobial and antioxidant agents in food industry: A hypothesis. J. Food Sci. 2014, 79, R129–R137. [Google Scholar] [CrossRef] [PubMed]
  3. Al-Maqtari, Q.A.A.; Ghaleb, A.D.S.; Mahdi, A.A.; Al-Ansi, W.; Noman, A.E.; Wei, M.; Al-Adeeb, A.; Yao, W. Stabilization of water-in-oil emulsion of Pulicaria jaubertii extract by ultrasonication: Fabrication, characterization, and storage stability. Food Chem. 2021, 350, 129249. [Google Scholar] [CrossRef] [PubMed]
  4. Gothsch, T.; Finke, J.H.; Beinert, S.; Lesche, C.; Schur, J.; Buttgenbach, S.; Muller-Goymann, C.; Kwade, A. Effect of mi-crochannel geometry on high-pressure dispersion and emul-sification. Chem. Eng. Technol. 2011, 34, 335–343. [Google Scholar] [CrossRef]
  5. Komaiko, J.; Sastrosubroto, A.; McClements, D.J. Formation of oil-in-water emulsions from natural emulsifiers using spontaneous emulsification: Sunflower phospholipids. J. Agric. Food Chem. 2015, 63, 10078–10088. [Google Scholar] [CrossRef]
  6. Al-Bukhaiti, W.Q.; Noman, A.; Wang, H. Emulsions: Micro and nano-emulsions and their applications in industries—A mini-review. Int. J. Agric. Innov. Res. 2018, 7, 69–73. [Google Scholar]
  7. Jurkin, T.; Gotić, M. Uvod u mikroemulzije. Kem. Ind. 2013, 62, 389–399. [Google Scholar]
  8. Čulo, I.; Grgić, F.; Jurina, T.; Šalić, A.; Benković, M.; Valinger, D.; Gajdoš Kljusurić, J.; Jurinjak Tušek, A.; Zelić, B. Emulsification on a microscale: Faster, better, and more effective. Kem. Ind. 2022, 71, 653–659. [Google Scholar] [CrossRef]
  9. Adheeb Usaid, A.S.; Premkumar, J.; Ranganathan, T.V. Emulsion and it’s applications in food industry—A review. Int. J. Eng. Res. Appl. 2014, 4, 241–248. [Google Scholar]
  10. Jurinjak Tušek, A.; Jurina, T.; Čulo, I.; Valinger, D.; Gajdoš Kljusurić, J.; Benković, M. Application of NIRs coupled with PLS and ANN modelling to predict average droplet size in oil- in-water emulsions prepared with different microfluidic devices. Spectrochim. Acta A Mol. 2022, 270, 120860. [Google Scholar] [CrossRef]
  11. Goodarzi, F.; Zendehboudi, S. A comprehensive review on emulsions and emulsion stability in chemical and energy industries. Can. J. Chem. Eng. 2019, 97, 281–309. [Google Scholar] [CrossRef] [Green Version]
  12. Ravera, F.; Dziza, K.; Santini, E.; Cristofolini, L.; Liggieri, L. Emulsification and emulsion stability: The role of the interfacial properties. Adv. Colloid Interface Sci. 2021, 288, 102344. [Google Scholar] [CrossRef] [PubMed]
  13. Porras, M.; Solans, C.; González, C.; Gutiérrez, J.M. Properties of water-in-oil (W/O) nano-emulsions prepared by a low-energy emulsification method. Colloids Surf. A Physicochem. Eng. 2008, 324, 181–188. [Google Scholar] [CrossRef]
  14. Usón, N.; Garcia, M.J.; Solans, C. Formation of water-in-oil (W/O) nanoemulsions in a water/mixed non-ionic surfactant/oil systems prepared by a lowenergy emulsification method. Colloids Surf. A Physicochem. Eng. 2004, 250, 415–421. [Google Scholar] [CrossRef]
  15. Tadros, F.T. Emulsion formation, stability, and industrial application. In Emulsion, Formation, Industrial Applications; Tadros, F.T., Ed.; De Gruyter: Berlin, Germany, 2016; pp. 1–8. [Google Scholar]
  16. Hadžiabdić, J.; Orman, D.; Elezović, A.; Vranić, E.; Rahić, O. Preparation of nanoemulsions by high-energy and low-energy emulsification methods. IFMBE Proc. 2017, 62, 317–322. [Google Scholar] [CrossRef]
  17. Maan, A.A.; Nazir, A.; Khan, M.K.I.; Boom, R.; Shroen, K. Microfluidic emulsification in food processing. J. Food Eng. 2015, 147, 1–7. [Google Scholar] [CrossRef]
  18. Dobhal, A.; Kulkarni, A.; Dandekar, P.; Jain, R. A microreactor-based continuous process for controlled synthesis of poly-methyl-methacrylate-methacrylic acid (PMMA) nanoparticles. J. Mater. Chem. B 2017, 5, 3404–3417. [Google Scholar] [CrossRef]
  19. Khalid, N.; Kobayashi, I.; Neves, M.A.; Uemura, K.; Nakajima, M.; Nabetani, H. Microchannel emulsification study on formulation and stability characterization of monodisperse oil-in-water emulsions encapsulating quercetin. Food Chem. 2016, 212, 27–34. [Google Scholar] [CrossRef]
  20. Vladisavljević, G.; Al Nuumani, R.; Nabavi, S. Microfluidic production of multiple emulsions. Micromachines 2017, 8, 75. [Google Scholar] [CrossRef]
  21. Azarmanesh, M.; Bawazeer, S.; Mohamad, A.A.; Sanati-Nezhad, A. Rapid and highly controlled generation of monodisperse multiple emulsions via a onestep hybrid microfluidic device. Sci. Rep. 2019, 9, 12694. [Google Scholar] [CrossRef] [Green Version]
  22. Ibrahim, A.M.; Padovani, J.I.; Howe, R.T.; Anis, Y.H. Modeling of Droplet Generation in a Microfluidic Flow-Focusing Junction for Droplet Size Control. Micromachines 2021, 12, 590. [Google Scholar] [CrossRef] [PubMed]
  23. Vidovič, S.; Bizjak, A.; Sitar, A.; Horvat, M.; Janković, B.; Golobič, I. Development of a semi-empirical model for droplet size determination of a three-channel spray nozzle for pellet coating based on the optical method concept. Processes 2022, 10, 86. [Google Scholar] [CrossRef]
  24. Sohrabi, S.; Kassir, N.; Keshavarz Moraveji, M. Droplet microfluidics: Fundamentals and its advanced applications. RSC Adv. 2020, 23, 27560–27574. [Google Scholar] [CrossRef] [PubMed]
  25. Wang, M.; Kong, C.; Liang, Q.; Zhao, J.; Wen, M.; Xu, Z.; Ruan, X. Numerical simulations of wall contact angle effects on droplet size during step emulsification. RSC Adv. 2018, 8, 33042–33047. [Google Scholar] [CrossRef] [Green Version]
  26. Xu, J.H.; Li, S.W.; Lan, W.J.; Luo, G.S. Microfluidic approach for rapid interfacial tension measurement. Langmuir 2008, 24, 11287–11292. [Google Scholar] [CrossRef] [PubMed]
  27. Alade, O.S.; Mahmoud, M.; Al Shehri, D.A.; Sultan, A.S. Rapid determination of emulsion stability using turbidity measurement incorporating artificial neural network (ANN): Experimental validation using video/optical microscopy and kinetic modelling. ASC Omega 2021, 6, 5910–5920. [Google Scholar] [CrossRef] [PubMed]
  28. Bampi, M.; Scheer, A.D.P.; de Castilhos, F. Application of near infrared spectroscopy to predict the average droplet size and water content in biodiesel emulsions. Fuel 2013, 113, 546–552. [Google Scholar] [CrossRef] [Green Version]
  29. Borges, G.R.; Farias, G.B.; Braz, T.M.; Santos, L.M.; Amaral, M.J.; Fortuny, M.; Franceschi, E.; Dariva, C.; Santos, A.F. Use of near infrared for evaluation of droplet size distribution and water content in water-in-crude oil emulsions in pressurized pipeline. Fuel 2015, 147, 43–52. [Google Scholar] [CrossRef]
  30. Rizkin, B.A.; Popovic, F.G.; Hartman, R.L. Review article: Spectroscopic microreactors for heterogeneous catalysis. J. Vac. Sci. Technol. A 2019, 37, 050801. [Google Scholar] [CrossRef] [Green Version]
  31. Holroyd, S.E. The use of near infrared spectroscopy on milk and milk products. J. Near Infrared Spectrosc. 2013, 21, 311–322. [Google Scholar] [CrossRef]
  32. Grossi, M.; Di Lecce, G.; Arru, M.; Toschi, T.G.; Riccò, B. An opto-electronic system for in-situ determination of peroxide value and total phenol content in olive oil. J. Food Eng. 2015, 146, 1–7. [Google Scholar] [CrossRef]
  33. Zareef, M.; Chen, Q.; Hassan, M.M.; Arslan, M.; Hashim, M.M.; Ahmad, W.; Kutsanedzie, F.Y.H.; Agyekum, A.A. An Overview on the applications of typical non-linear algorithms coupled with NIR spectroscopy in food analysis. Food Eng. Rev. 2020, 12, 173–190. [Google Scholar] [CrossRef]
  34. Chen, Q.; Zhang, D.; Pan, W.; Ouyang, Q.; Li, H.; Urmila, K.; Zhao, J. Recent developments of green analytical techniques in analysis of tea’s quality and nutrition. Trends Food Sci. Technol. 2015, 43, 63–82. [Google Scholar] [CrossRef]
  35. Wulandari, L.; Retnaningtyas, Y.; Lukman, H. Analysis of flavonoid in medicinal plant extract using infrared spectroscopy and chemometrics. J. Anal. Methods Chem. 2016, 2016, 4696803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Valinger, D.; Kušen, M.; Jurinjak Tušek, A.; Panić, M.; Jurina, T.; Benković, M.; Radojčić Redovniković, I.; Gajdoš Kljusurić, J. Development of near infrared spectroscopy models for quantitative prediction of the content of bioactive compounds in olive leaves. Chem. Biochem. Eng. Q. 2018, 32, 535–543. [Google Scholar] [CrossRef]
  37. Valinger, D.; Longin, L.; Grbeš, F.; Banković, M.; Jurina, T.; Gajdoš Kljusurić, J.; Jurinjak Tušek, A. Detection of honey adulteration—The potential of UV-VIS and NIR spectroscopy coupled with multivariate analysis. LWT 2021, 145, 111316. [Google Scholar] [CrossRef]
  38. Fang, Z.; Bhandari, B. Encapsulation of polyphenols-A review. Trends Food Sci. Tech. 2010, 21, 510–523. [Google Scholar] [CrossRef]
  39. Grgić, F.; Benković, M.; Valinger, D.; Jurina, T.; Gajodš Kljusurić, J.; Jurinjak Tušek, A. Macro-batch and continuously operated microfluidic emulsification—Differences, Similarities and Optimization. Processes 2022, 10, 449. [Google Scholar] [CrossRef]
  40. Shah, R.K.; Shzm, H.C.; Rowat, A.C.; Lee, D.; Agresti, J.J.; Utada, A.S.; Chu, L.-Y.; Kim, J.-W.; Fernadez-Nieves, A.; Martinez, C.J.; et al. Designer emulsions using microfluidics. Mater. Today 2008, 11, 18–27. [Google Scholar] [CrossRef]
  41. Wang, J.; Li, Y.; Wang, X.; Wang, J.; Tian, H.; Zhao, P.; Tian, Y.; Gu, Y.; Wang, L.; Wang, C. Droplet microfluidics for the production of microparticles and nanoparticles. Micromachines 2017, 8, 22. [Google Scholar] [CrossRef]
  42. Park, D.; Kim, H.; Kim, J.W. Microfluidic production of monodisperse emulsions for cosmetics. Biomicrofluidics 2021, 15, 051302. [Google Scholar] [CrossRef] [PubMed]
  43. Bi, Y.; Yuan, K.; Xiao, W.; Jizhoug, W.; Shi, C.; Chu, G.; Zhang, G.; Zhiu, G. A local pre-processing method for near-infrared spectra, combined with spectral segmentation and standard normal variate transformation. Anal. Chim. Acta 2016, 909, 30–40. [Google Scholar] [CrossRef] [PubMed]
  44. Grisanti, E.; Totska, M.; Huber, S.; Calderon, C.K.; Hohmann, M.; Lingenfelser, D.; Otto, M. Dynamic localized SNV, Peak SNV, and partial peak SNV: Novel standardization methods for preprocessing of spectroscopic data used in predictive modeling. J. Spectrosc. 2018, 2018, 5037572. [Google Scholar] [CrossRef]
  45. Sohn, S.-I.; Pandian, S.; Oh, Y.-J.; Zaukuu, J.-L.Z.; Na, C.-S.; Lee, Y.-H.; Shin, E.-K.; Kang, H.-J.; Ryu, T.-H.; Cho, W.-S.; et al. Vis-NIR spectroscopy and machine learning methods for the discrimination of transgenic Brassica napus L. and their hybrids with B. juncea. Processes 2022, 10, 240. [Google Scholar] [CrossRef]
  46. Feng, X.; Peng, C.; Chen, Y.; Liu, X.; Feng, X.; He, Y. Discrimination of CRISPR/Cas9-induced mutants of rice seeds using near-infrared hyperspectral imaging. Sci. Rep. 2017, 7, 15934. [Google Scholar] [CrossRef] [Green Version]
  47. Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. TrAC Trend Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
  48. Winding, W.; Shaver, J.; Bro, R. Loopy MSC: A simple way to improve multiplicative scatter correction. J. Appl. Spectrospc. 2008, 62, 1153–1159. [Google Scholar] [CrossRef]
  49. Basile, T.; Marsico, A.D.; Perniola, R. Use of Artificial Neural Networks and NIR Spectroscopy for Non-Destructive Grape Texture Prediction. Foods 2022, 11, 281. [Google Scholar] [CrossRef]
  50. Balage, J.M.; e Silva, S.D.L.; Gomide, C.A.; Bonin Mde, N.; Figueira, A.C. Predicting pork quality using Vis/NIR spectroscopy. Meat Sci. 2015, 108, 37–43. [Google Scholar] [CrossRef]
  51. Zhang, F.; Zhang, R.; Ge, J.; Chen, W.; Yang, W.; Du, Y. Calibration transfer based on the weight matrix (CTWM) of PLS for near infrared (NIR) spectral analysis. Anal. Methods 2018, 10, 2169–2179. [Google Scholar] [CrossRef]
  52. Dinache, A.; Tozar, T.; Smarandache, A.; Andrei, I.R.; Nistorescu, S.; Nastasa, V.; Staicu, A.; Pascu, M.-L.; Romanitan, M.O. Spectroscopic characterization of emulsions generated with a new laser-assisted device. Molecules 2020, 25, 1729. [Google Scholar] [CrossRef] [PubMed]
  53. Kawasaki, A.; Kawamura, G.; Zin, W.W. A local level relationship between floods and poverty: A case in Myanmar. Int. J. Disaster Risk Reduct. 2020, 42, 101348. [Google Scholar] [CrossRef]
  54. Rambo, M.K.D.; Ferreira, M.M.C.; de Melo, P.M.; Santana Junior, C.C.; Bertuol, D.A.; Rambo, M.C.D. Prediction of quality parameters of food residues using NIR spectroscopy and PLS models based on proximate analysis. Food Sci. Technol. 2020, 40, 444–450. [Google Scholar] [CrossRef]
  55. Hayati, R.; Zulfahrizal, Z.; Munawar, A. A Robust prediction performance of inner quality attributes in intact cocoa beans using near infrared spectroscopy and multivariate analysis. Heliyon 2021, 7, e06286. [Google Scholar] [CrossRef] [PubMed]
  56. Willimas, P.C.; Sobering, D.C. Comparison of commercial near infrared transmittance and reflectance instruments for analysis of whole grains and seeds. J. Near Infrared Spectrosc. 2010, 1, 25–32. [Google Scholar] [CrossRef]
  57. Parrini, S.; Staglianò, N.; Bozzi, R.; Argenti, G. Can grassland chemical quality be quantified using transform near-infrared spectroscopy? Animals 2022, 12, 86. [Google Scholar] [CrossRef]
  58. Eskildsen, E.C.; Næs, T. Sample-specific prediction error measures in spectroscopy. Appl. Spectrosc. 2020, 74, 791–798. [Google Scholar] [CrossRef]
  59. Mishra, P.; van Dijk, M.; Wintermeyer, C.; Sabater, C.; Bot, A.; Verkleij, T.; Broeze, J. At-line and inlin epredisction of droplet size in mayonnaise with near-infrared spectroscopy. Infrared Phys. Technol. 2022, 123, 104155. [Google Scholar] [CrossRef]
  60. Amsaraj, R.; Ambade, N.D.; Muzzuri, S. Variable selection coupled to PLS2, ANN and SVM for simultaneous detection of multiple adulterants in milk using spectral data. Int. Dairy J. 2021, 123, 105172. [Google Scholar] [CrossRef]
  61. Lin, M.B.; Groves, W.A.; Freivalds, A.; Lee, E.G.; Harper, M. Comparison of artificial neural network (ANN) and partial least squares (PLS) regression models for predicting respiratory ventilation: An exploratory study. Eur. J. Appl. Physiol. 2012, 112, 1603–1611. [Google Scholar] [CrossRef]
  62. Panagou, E.Z.; Mohareb, F.R.; Argyri, A.A.; Bessant, C.B.; Nychas, G.-J.E. A comparison of artificial neural networks and partial least squares modelling for the rapid detection of the microbial spoilage of beef fillets based on Fourier transform infrared spectral fingerprints. Food Microbiol. 2011, 28, 782–790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  63. Tekin, Y.; Tűmsavas, Z.; Mouazen, A.M. Comparing the artificial neural network with partial least squares for prediction of soil organic carbon and pH at different moisture content levels using visible and near-infrared spectroscopy. Rev. Bras. Ciênc. Solo. 2014, 38, 1794–1804. [Google Scholar] [CrossRef] [Green Version]
  64. Salehi, M.; Zare, A.; Taheri, A. Artificial neural networks (ANNs) and partial least squares (PLS) regression in the quantitative analysis of respirable crystalline silica by Fourier-transform infrared spectroscopy (FTIR). Ann. Work Expo. Health 2021, 65, 346–357. [Google Scholar] [CrossRef] [PubMed]
Micromachines 13 01876 g001 550
Figure 1. Graphical representation of the neural network model.
Figure 1. Graphical representation of the neural network model.
Micromachines 13 01876 g001
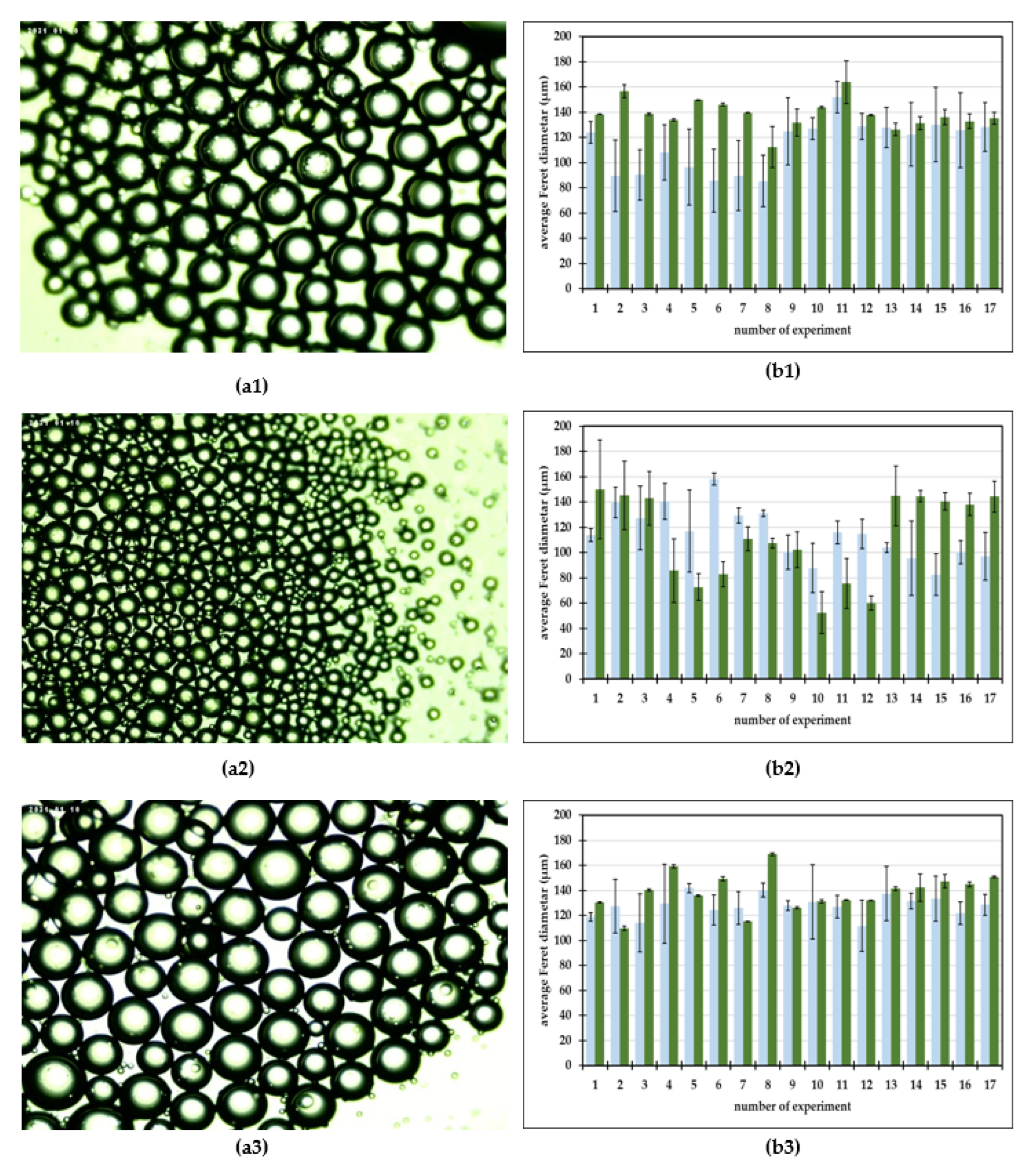
Micromachines 13 01876 g002 550
Figure 2. (a) Photos of oil-in-aqueous mint extract emulsions. (b) Average Feret diameters of oil-in-water emulsions (Micromachines 13 01876 i001) and oil-in-aqueous mint extract emulsions (Micromachines 13 01876 i002). (a1,b1) PEG 1500, (a2,b2) PEG 6000, (a3,b3) PEG 20,000.
Figure 2. (a) Photos of oil-in-aqueous mint extract emulsions. (b) Average Feret diameters of oil-in-water emulsions (Micromachines 13 01876 i001) and oil-in-aqueous mint extract emulsions (Micromachines 13 01876 i002). (a1,b1) PEG 1500, (a2,b2) PEG 6000, (a3,b3) PEG 20,000.
Micromachines 13 01876 g002
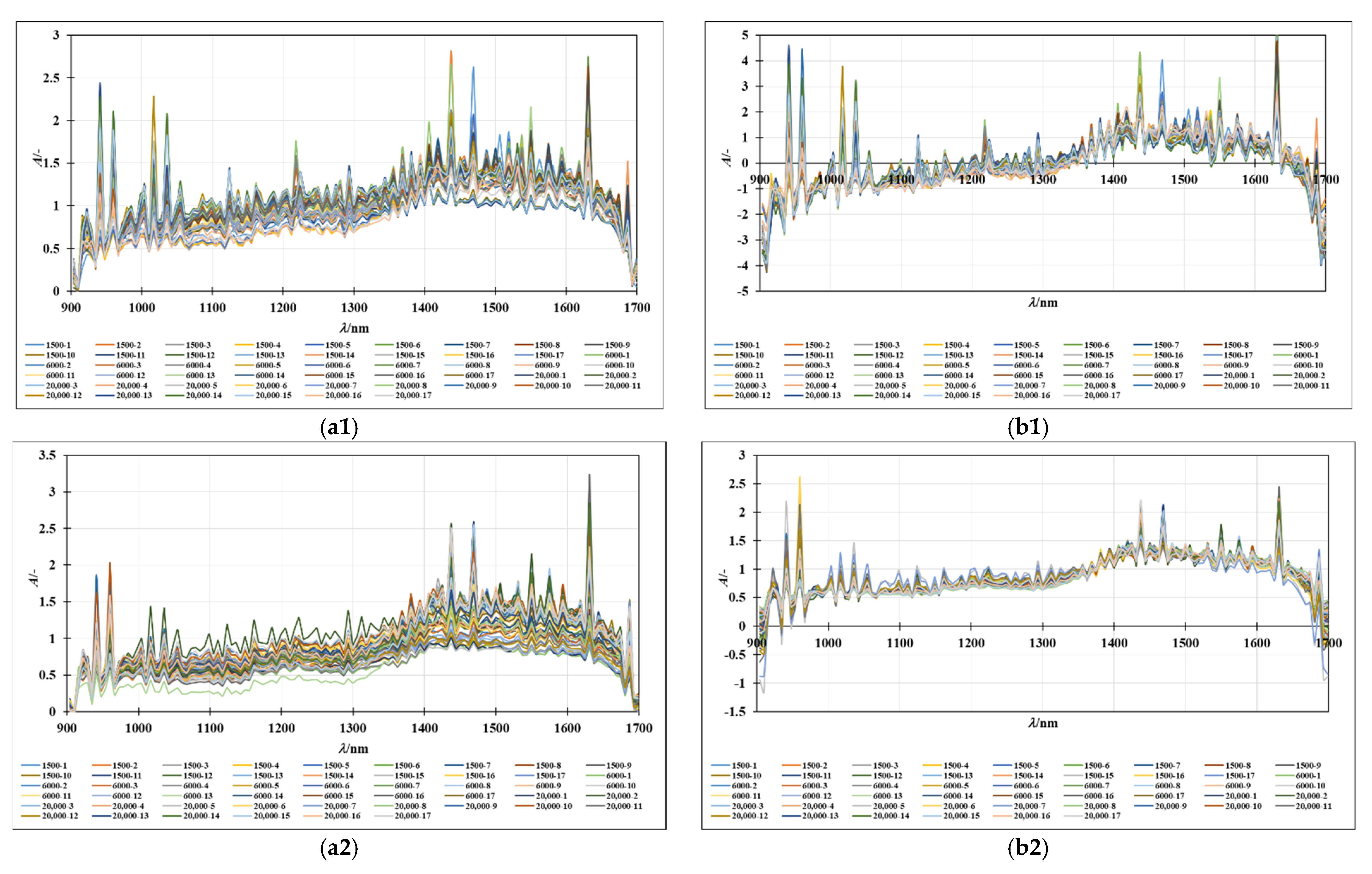
Micromachines 13 01876 g003 550
Figure 3. (a) Raw spectra of (a1) oil-in-water and (a2) oil-in-mint aqueous extracts. (b) (b1) SNV preprocessed spectra of oil-in-water emulsions and (b2) MSC preprocessed spectra of oil-in-mint aqueous extract emulsions.
Figure 3. (a) Raw spectra of (a1) oil-in-water and (a2) oil-in-mint aqueous extracts. (b) (b1) SNV preprocessed spectra of oil-in-water emulsions and (b2) MSC preprocessed spectra of oil-in-mint aqueous extract emulsions.
Micromachines 13 01876 g003
Micromachines 13 01876 g004 550
Figure 4. (a) PCA score plot of all average oil-in-water emulsion NIR spectra after SNV preprocessing (Micromachines 13 01876 i006 PEG 1500, Micromachines 13 01876 i007 PEG 6000, Micromachines 13 01876 i008 PEG 20,000). (b) PCA loading of all average oil-in-water emulsion NIR spectra after SNV preprocessing. PCA score plot of NIR spectra of oil-in-water emulsion NIR spectra after SNV preprocessing with (c) PEG 1500, (e) PEG 6000, and (g) PEG 20,000 (Micromachines 13 01876 i005 2% emulsifier, Micromachines 13 01876 i003 4% emulsifier, Micromachines 13 01876 i004 6% emulsifier). PCA loading of NIR spectra of oil-in water emulsion NIR spectra after SNV preprocessing with (d) PEG 1500, (f) PEG 6000, and (h) PEG 20,000.
Figure 4. (a) PCA score plot of all average oil-in-water emulsion NIR spectra after SNV preprocessing (Micromachines 13 01876 i006 PEG 1500, Micromachines 13 01876 i007 PEG 6000, Micromachines 13 01876 i008 PEG 20,000). (b) PCA loading of all average oil-in-water emulsion NIR spectra after SNV preprocessing. PCA score plot of NIR spectra of oil-in-water emulsion NIR spectra after SNV preprocessing with (c) PEG 1500, (e) PEG 6000, and (g) PEG 20,000 (Micromachines 13 01876 i005 2% emulsifier, Micromachines 13 01876 i003 4% emulsifier, Micromachines 13 01876 i004 6% emulsifier). PCA loading of NIR spectra of oil-in water emulsion NIR spectra after SNV preprocessing with (d) PEG 1500, (f) PEG 6000, and (h) PEG 20,000.
Micromachines 13 01876 g004
Micromachines 13 01876 g005 550
Figure 5. (a) PCA score plot of all average oil-in-aqueous mint extract emulsion NIR spectra after MSC preprocessing (Micromachines 13 01876 i006 PEG 1500, Micromachines 13 01876 i007 PEG 6000, Micromachines 13 01876 i008 PEG 20,000). (b) PCA loading of all average oil-in-aqueous mint extract emulsion NIR spectra after MSC preprocessing. PCA score plot of NIR spectra of oil-in-aqueous mint extract emulsion NIR spectra after SNV preprocessing with (c) PEG 1500, (e) PEG 6000, and (g) PEG 20,000 (Micromachines 13 01876 i005 2% emulsifier, Micromachines 13 01876 i003 4% emulsifier, Micromachines 13 01876 i004 6% emulsifier). PCA loading of NIR spectra of oil-in-aqueous mint extract emulsion NIR spectra after SNV preprocessing with (d) PEG 1500, (f) PEG 6000, and (h) PEG 20,000.
Figure 5. (a) PCA score plot of all average oil-in-aqueous mint extract emulsion NIR spectra after MSC preprocessing (Micromachines 13 01876 i006 PEG 1500, Micromachines 13 01876 i007 PEG 6000, Micromachines 13 01876 i008 PEG 20,000). (b) PCA loading of all average oil-in-aqueous mint extract emulsion NIR spectra after MSC preprocessing. PCA score plot of NIR spectra of oil-in-aqueous mint extract emulsion NIR spectra after SNV preprocessing with (c) PEG 1500, (e) PEG 6000, and (g) PEG 20,000 (Micromachines 13 01876 i005 2% emulsifier, Micromachines 13 01876 i003 4% emulsifier, Micromachines 13 01876 i004 6% emulsifier). PCA loading of NIR spectra of oil-in-aqueous mint extract emulsion NIR spectra after SNV preprocessing with (d) PEG 1500, (f) PEG 6000, and (h) PEG 20,000.
Micromachines 13 01876 g005
Micromachines 13 01876 g006 550
Figure 6. Variation in RMSEC, RMSECV, and RMSEP as a function of the latent variable number for the best PLS models for (a) oil-in-water emulsions and (b) oil-in-mint extract emulsions.
Figure 6. Variation in RMSEC, RMSECV, and RMSEP as a function of the latent variable number for the best PLS models for (a) oil-in-water emulsions and (b) oil-in-mint extract emulsions.
Micromachines 13 01876 g006
Micromachines 13 01876 g007 550
Figure 7. Comparisons between observations and ANN model predictions for the average droplets sizes of (a) oil-in-water emulsions and (b) oil-in-aqueous mint extract emulsions: (a1,b1) PEG 1500, (a2,b2) PEG 6000, (a3,b3) PEG 20,000.
Figure 7. Comparisons between observations and ANN model predictions for the average droplets sizes of (a) oil-in-water emulsions and (b) oil-in-aqueous mint extract emulsions: (a1,b1) PEG 1500, (a2,b2) PEG 6000, (a3,b3) PEG 20,000.
Micromachines 13 01876 g007
Table
Table 1. Design of emulsification experiments. Levels of each input variable are given in brackets (−1, 1, and 0: low, medium, and high levels).
Table 1. Design of emulsification experiments. Levels of each input variable are given in brackets (−1, 1, and 0: low, medium, and high levels).
Exp.Emulsifier Concentration (%)Oil Concentration (%)Total Flow Rate (µL/min)
1.2 (−1)30 (0)200 (−1)
2.6 (1)30 (0)200 (−1)
3.2 (−1)30 (0)400 (1)
4.6 (1)30 (0)400 (1)
5.2 (−1)25 (−1)300 (0)
6.6 (1)25 (−1)300 (0)
7.2 (−1)35 (1)300 (0)
8.6 (1)35 (1)300 (0)
9.4 (0)25 (−1)200 (−1)
10.4 (0)25 (−1)400 (1)
11.4 (0)35 (1)200 (−1)
12.4 (0)35 (1)400 (1)
13.4 (0)30 (0)300 (0)
14.4 (0)30 (0)300 (0)
15.4 (0)30 (0)300 (0)
16.4 (0)30 (0)300 (0)
17.4 (0)30 (0)300 (0)
Table
Table 2. Parameters of partial least-squares (PLS) models for the prediction of the average droplet size, expressed as the average Feret diameter of oil-in-water emulsions and oil-in-aqueous mint extract (green shading) emulsions prepared in a microfluidic device at different flow rates using different emulsifiers based on different NIR spectra pretreatments. Preprocessing methods: raw spectra (No), first-order Savitzky–Golay derivative (SG1), standard normal variate (SNV), multiplicative scatter corrections (MSC), first-order Savitzky–Golay derivative followed by standard normal variate (SG1+SNV), and first-order Savitzky–Golay derivative followed by multiplicative scatter corrections (SG1+MSC). Model applicability: the coefficients of determination for calibration (R2cal) and cross-validation (R2cval), the root-mean-square error for calibration (RMSEC) and cross-validation (RMSECV), the average value of the difference between the predicted and observed values (bias), the ratio of predicted deviation (RPD), and the range error ratio (RER). Seven factors were included in each model.
Table 2. Parameters of partial least-squares (PLS) models for the prediction of the average droplet size, expressed as the average Feret diameter of oil-in-water emulsions and oil-in-aqueous mint extract (green shading) emulsions prepared in a microfluidic device at different flow rates using different emulsifiers based on different NIR spectra pretreatments. Preprocessing methods: raw spectra (No), first-order Savitzky–Golay derivative (SG1), standard normal variate (SNV), multiplicative scatter corrections (MSC), first-order Savitzky–Golay derivative followed by standard normal variate (SG1+SNV), and first-order Savitzky–Golay derivative followed by multiplicative scatter corrections (SG1+MSC). Model applicability: the coefficients of determination for calibration (R2cal) and cross-validation (R2cval), the root-mean-square error for calibration (RMSEC) and cross-validation (RMSECV), the average value of the difference between the predicted and observed values (bias), the ratio of predicted deviation (RPD), and the range error ratio (RER). Seven factors were included in each model.
EmulsifierPretreatmentR2calRSECR2valRMSECVR2predRMSEPBiasRPDRER
PEG 1500No0.690011.30850.549614.53780.535713.55566.26891.62659.2493
SG10.580313.15870.458915.69160.350914.56545.20331.51388.6081
SNV0.686311.37650.561713.48100.461813.42676.80441.64219.3381
MSC0.689111.43750.515414.24840.458214.88756.84391.48108.4218
SG1-SNV0.610512.67520.487115.28770.364016.99201.15151.29767.3788
SG1-MSC0.612712.63960.447915.24020.206518.50271.65471.19166.7763
PEG 6000No0.94674.68150.586513.28910.587413.05132.28841.68057.4023
SG0.95754.18330.730411.95650.483114.87741.57551.47426.4937
SNV0.96014.05360.620413.00930.625412.43602.54241.76367.7686
MSC0.95874.12300.623912.64380.586213.07042.27821.67807.3915
SG1-SNV0.95671.04020.87332.78530.610513.21212.47871.66007.3122
SG1-MSC0.94594.71510.657212.05210.691514.89312.13561.47276.4869
PEG 20,000No0.97661.50390.56957.19780.55345.26284.86152.445513.2401
SG10.78984.50890.37518.36230.396311.59981.81051.10956.0070
SNV0.96921.7570.87407.46390.86921.72571.72577.45819.3778
MSC0.96821.75320.48217.22930.51176.11762.76962.103811.3901
SG1-SNV0.99910.30240.99730.53940.91651.85622.86386.933737.5391
SG1-MSC0.78534.55650.33048.42330.380811.71331.17131.09885.9488
PEG 1500No0.84124.89590.64547.55790.690110.29620.49211.43797.8740
SG10.82965.07060.66138.02530.440017.15424.10510.86314.7261
SNV0.83854.93690.62627.20360.72619.71190.48141.52448.2477
MSC0.83195.03660.66207.33420.72349.77070.40761.51538.2975
SG1-SNV0.83854.93690.62217.27930.72619.71190.48141.52448.1477
SG1-MSC0.83175.04040.51828.62450.460719.95877.46580.74184.0620
PEG 6000No0.89319.35040.418422.15240.552427.06951.99721.32275.6627
SG10.866110.46820.186425.57650.167841.41236.40730.86463.7015
SNV0.89329.34760.523221.00920.557626.88322.15301.33195.7019
MSC0.89349.34110.501720.50990.558726.84572.11101.33375.7099
SG1-SNV0.88029.90170.259523.79590.139648.69936.53990.73523.1476
SG1-MSC0.90348.88820.294924.01480.208748.27725.81810.74173.1751
PEG 20,000No0.564823.05350.316131.03970.221829.63695.78221.17066.2226
SG0.615521.66890.241831.29970.200433.83833.94011.02535.4500
SNV0.589122.40060.310629.28110.239329.30176.04201.18406.2938
MSC0.810915.19720.512324.17650.706218.61263.57651.86409.9083
SG-SNV0.791615.95120.477230.38060.136441.06878.98470.84484.4905
SG-MSC0.98943.59410.433431.42400.106444.12659.08420.78624.1793
Table
Table 3. Characteristics of ANN networks selected for the prediction of the average droplet sizes of oil-in-water and oil-in-aqueous mint extract (green shading) emulsions prepared in a microfluidic device at different flow rates using different emulsifiers based on different NIR spectra pretreatments.
Table 3. Characteristics of ANN networks selected for the prediction of the average droplet sizes of oil-in-water and oil-in-aqueous mint extract (green shading) emulsions prepared in a microfluidic device at different flow rates using different emulsifiers based on different NIR spectra pretreatments.
Emulsifier/
Pretreatment		MLPTraining Perf./
Training Error		Test Perf./
Test Error		Validation Perf./
Validation Error		Hidden ActivationOutput Activation
PEG 1500/
SNV		MLP 5-10-10.9843
0.0073		0.8085
0.0101		0.7443
0.0128		IdentityExponential
MLP 5-9-10.9844
0.0041		0.8496
0.0100		0.7364
0.0161		IdentityIdentity
MLP 5-10-10.9828
0.0058		0.8508
0.0125		0.7348
0.0172		ExponentialExponential
MLP 5-8-10.9836
0.0072		0.8515
0.0079		0.7615
0.0121		LogisticIdentity
MLP 5-5-10.9835
0.0032		0.8115
0.0120		0.7358
0.0166		ExponentialExponential
PEG 6000/
SNV		MLP 5-4-10.9374
0.0048		0.9083
0.0064		0.7160
0.0074		TanhExponential
MLP 5-8-10.9428
0.0044		0.8675
0.0044		0.7377
0.0119		ExponentialIdentity
MLP 5-8-10.9270
0.0056		0.8551
0.0056		0.7094
0.0145		TanhIdentity
MLP 5-8-10.9261
0.0057		0.8287
0.0057		0.7176
0.0149		ExponentialExponential
MLP 5-6-10.9297
0.0054		0.8689
0.0054		0.7101
0.0103		ExponentialExponential
PEG 20000/
SNV		MLP 5-7-10.9912
0.0003		0.7979
0.0028		0.7501
0.0061		ExponentialExponential
MLP 5-4-10.8970
0.0036		0.8056
0.0052		0.7808
0.0064		ExponentialIdentity
MLP 5-7-10.8329
0.0046		0.8036
0.0043		0.7844
0.0068		LogisticTanh
MLP 5-7-10.8154
0.0043		0.8042
0.0054		0.6151
0.0091		LogisticTanh
MLP 5-5-10.9917
0.0002		0.9294
0.00184		0.8533
0.0027		ExponentialExponential
PEG 1500/
MSC		MLP 5-11-10.9998
0.0002		0.9994
0.0005		0.9985
0.0015		ExponentialIdentity
MLP 5-11-10.9993
0.0007		0.9988
0.0012		0.9972
0.0028		ExponentialIdentity
MLP 5-10-10.9966
0.0034		0.9921
0.0079		0.9920
0.0080		ExponentialIdentity
MLP 5-11-10.9997
0.0003		0.9996
0.0004		0.9993
0.0007		LogisticIdentity
MLP 5-8-10.9996
0.0004		0.9994
0.0006		0.9995
0.0005		LogisticIdentity
PEG 6000/
MSC		MLP 5-3-10.9516
0.0044		0.9311
0.0075		0.8113
0.0096		TanhLogistic
MLP 5-11-10.9227
0.0042		0.8667
0.0086		0.7257
0.0185		TanhTanh
MLP 5-10-10.7311
0.0092		0.7104
0.0128		0.6716
0.0167		LogisticLogistic
MLP 5-5-10.7693
0.0092		0.7285
0.0113		0.7182
0.0142		TanhLogistic
MLP 5-4-10.8271
0.0087		0.7577
0.0125		0.7192
0.0128		TanhLogistic
PEG 20000/
MSC		MLP 5-5-10.9924
0.0003		0.8273
0.0031		0.6731
0.0091		LogisticIdentity
MLP 5-5-10.9990
0.0003		0.9915
0.005		0.9978
0.0008		ExponentialTanh
MLP 5-9-10.9868
0.0001		0.9691
0.0007		0.9528
0.0016		ExponentialLogistic
MLP 5-5-10.9969
0.0004		0.7644
0.0055		0.7234
0.0084		LogisticLogistic
MLP 5-11-10.9908
0.0005		0.9392
0.0006		0.9281
0.0023		ExponentialIdentity
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Grgić, F.; Jurina, T.; Valinger, D.; Gajdoš Kljusurić, J.; Jurinjak Tušek, A.; Benković, M. Near-Infrared Spectroscopy Coupled with Chemometrics and Artificial Neural Network Modeling for Prediction of Emulsion Droplet Diameters. Micromachines 2022, 13, 1876. https://doi.org/10.3390/mi13111876

AMA Style

Grgić F, Jurina T, Valinger D, Gajdoš Kljusurić J, Jurinjak Tušek A, Benković M. Near-Infrared Spectroscopy Coupled with Chemometrics and Artificial Neural Network Modeling for Prediction of Emulsion Droplet Diameters. Micromachines. 2022; 13(11):1876. https://doi.org/10.3390/mi13111876

Chicago/Turabian Style

Grgić, Filip, Tamara Jurina, Davor Valinger, Jasenka Gajdoš Kljusurić, Ana Jurinjak Tušek, and Maja Benković. 2022. "Near-Infrared Spectroscopy Coupled with Chemometrics and Artificial Neural Network Modeling for Prediction of Emulsion Droplet Diameters" Micromachines 13, no. 11: 1876. https://doi.org/10.3390/mi13111876

APA Style

Grgić, F., Jurina, T., Valinger, D., Gajdoš Kljusurić, J., Jurinjak Tušek, A., & Benković, M. (2022). Near-Infrared Spectroscopy Coupled with Chemometrics and Artificial Neural Network Modeling for Prediction of Emulsion Droplet Diameters. Micromachines, 13(11), 1876. https://doi.org/10.3390/mi13111876

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop