A Piezoelectric MEMS Microgripper for Arbitrary XY Trajectory
Abstract
:1. Introduction
2. Analytical Model
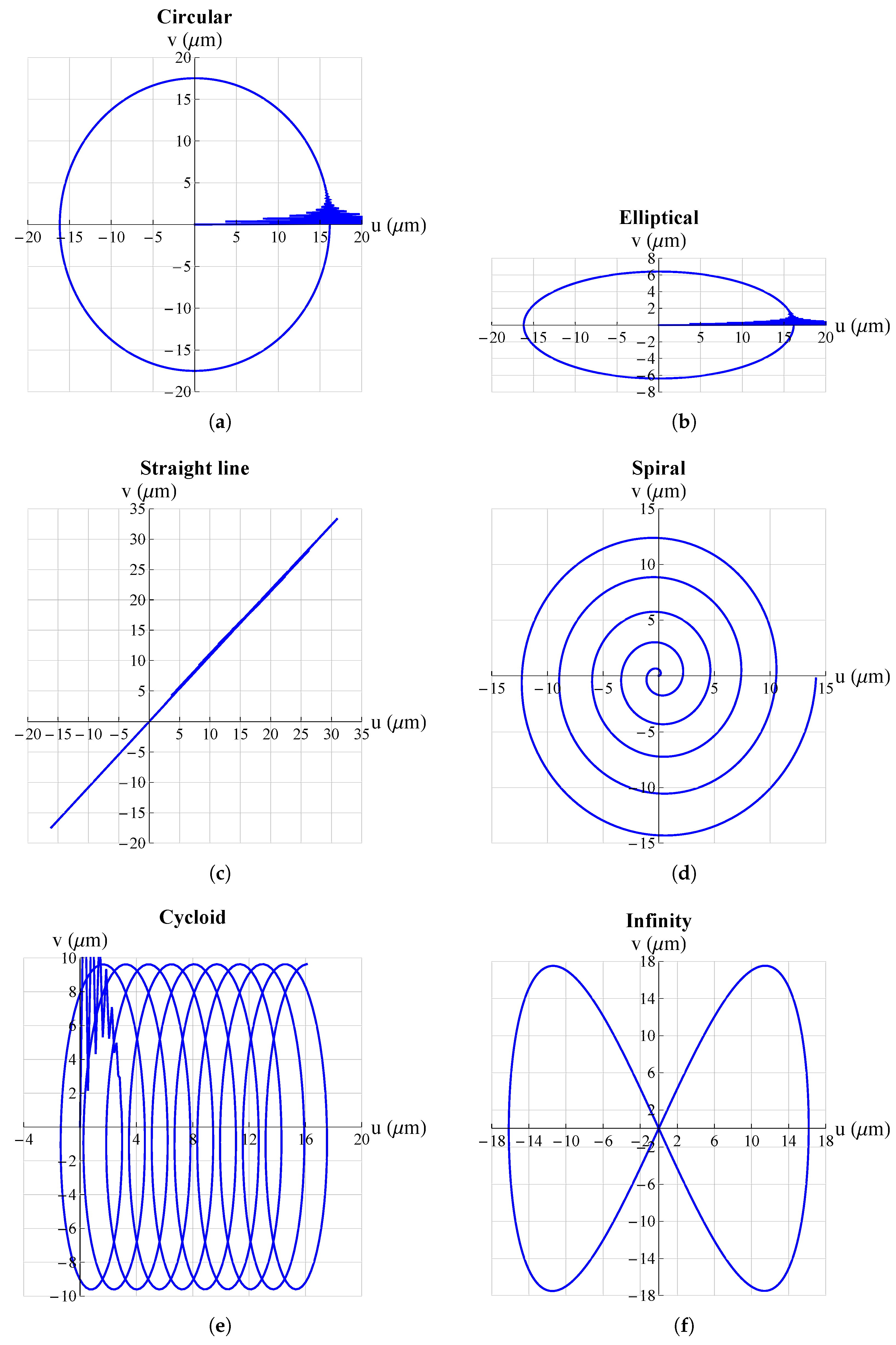
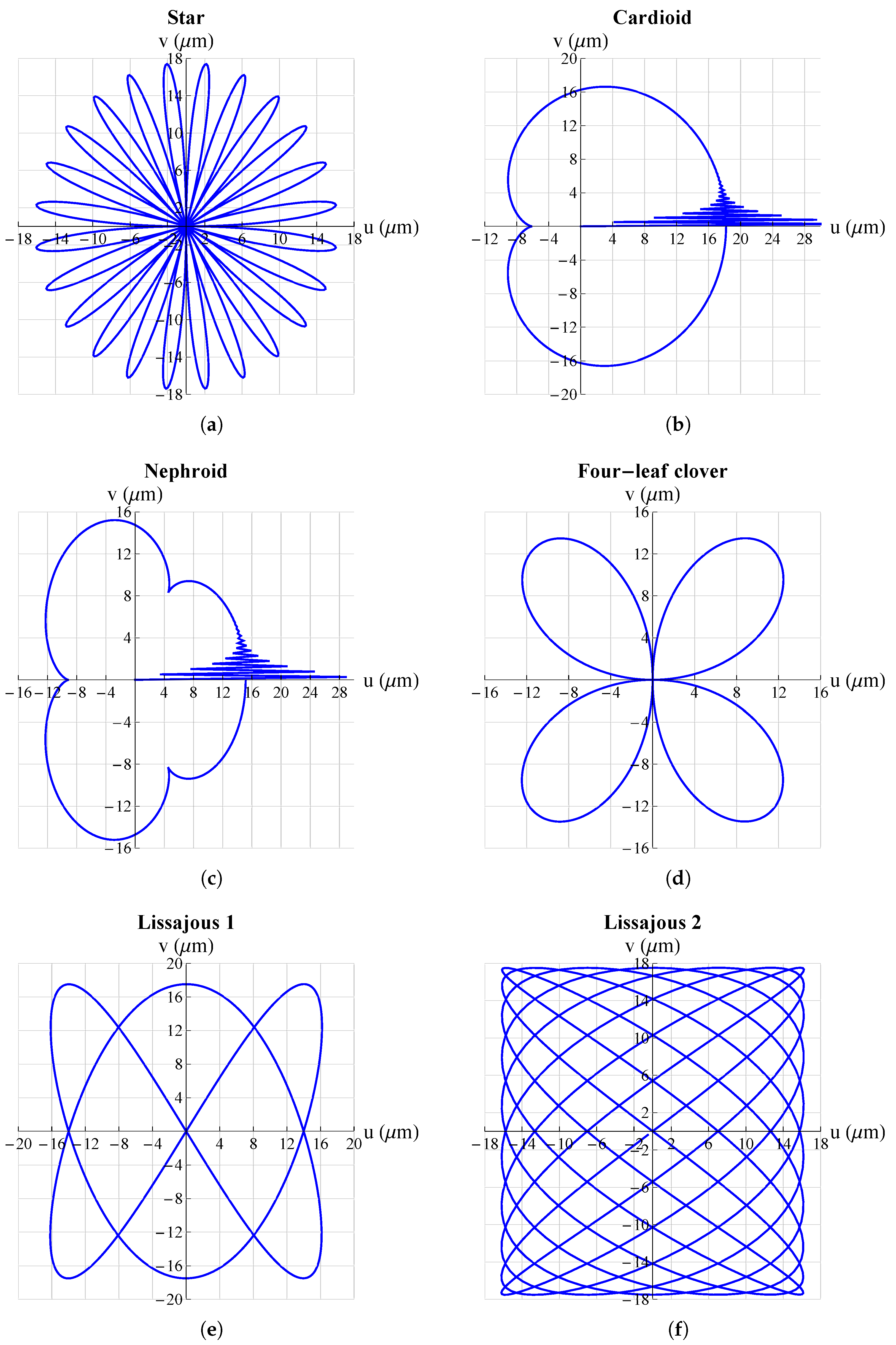
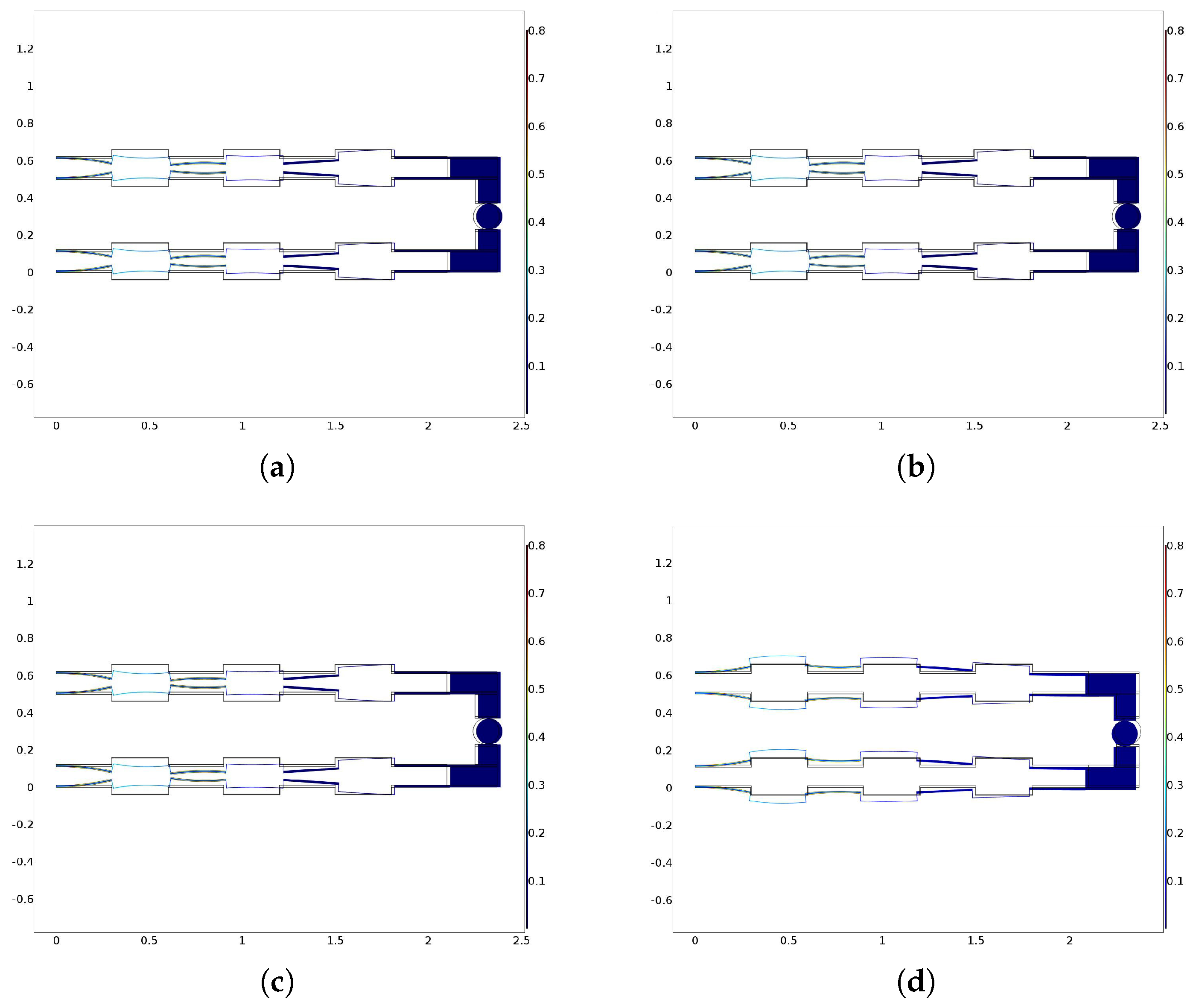
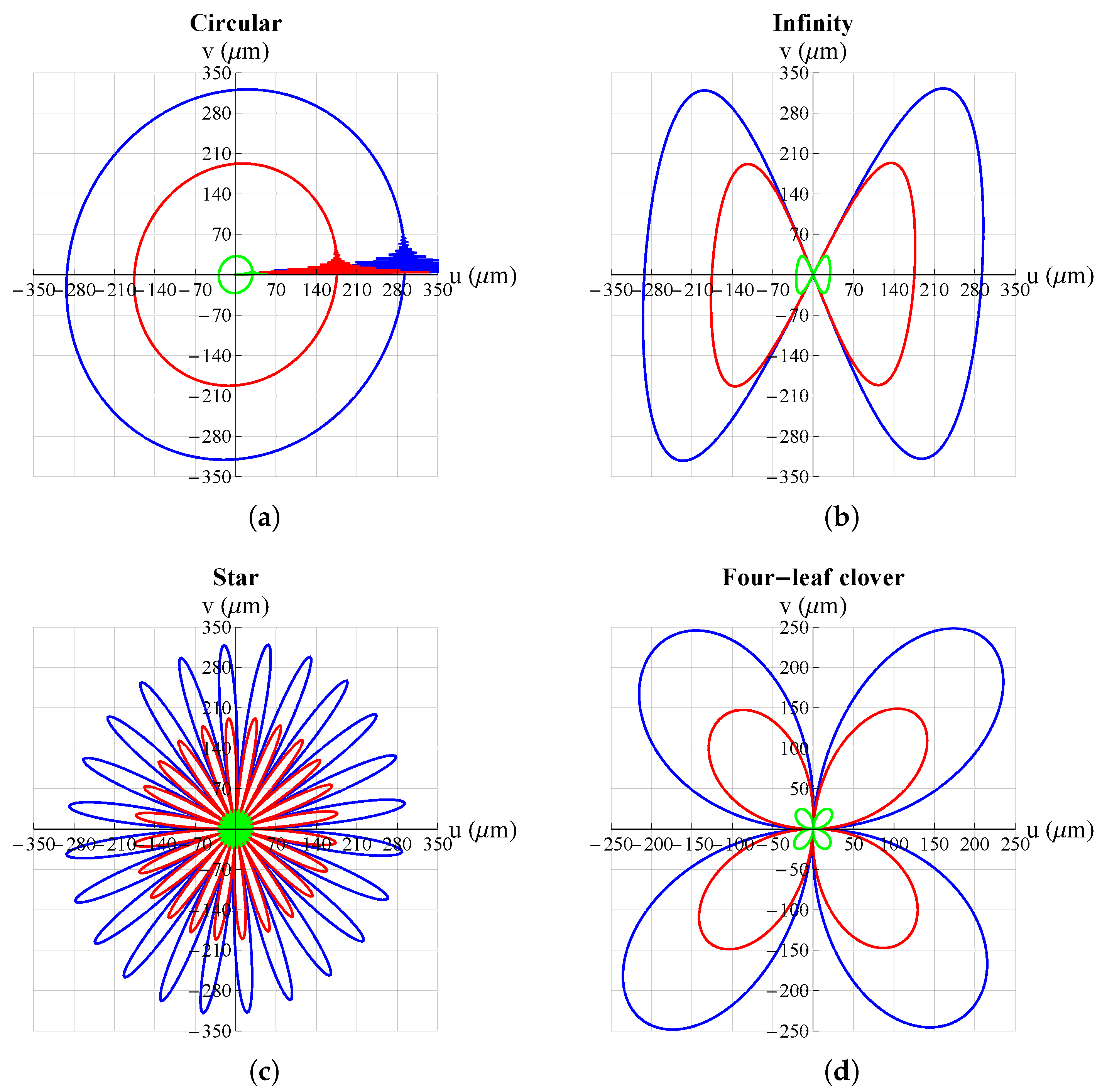
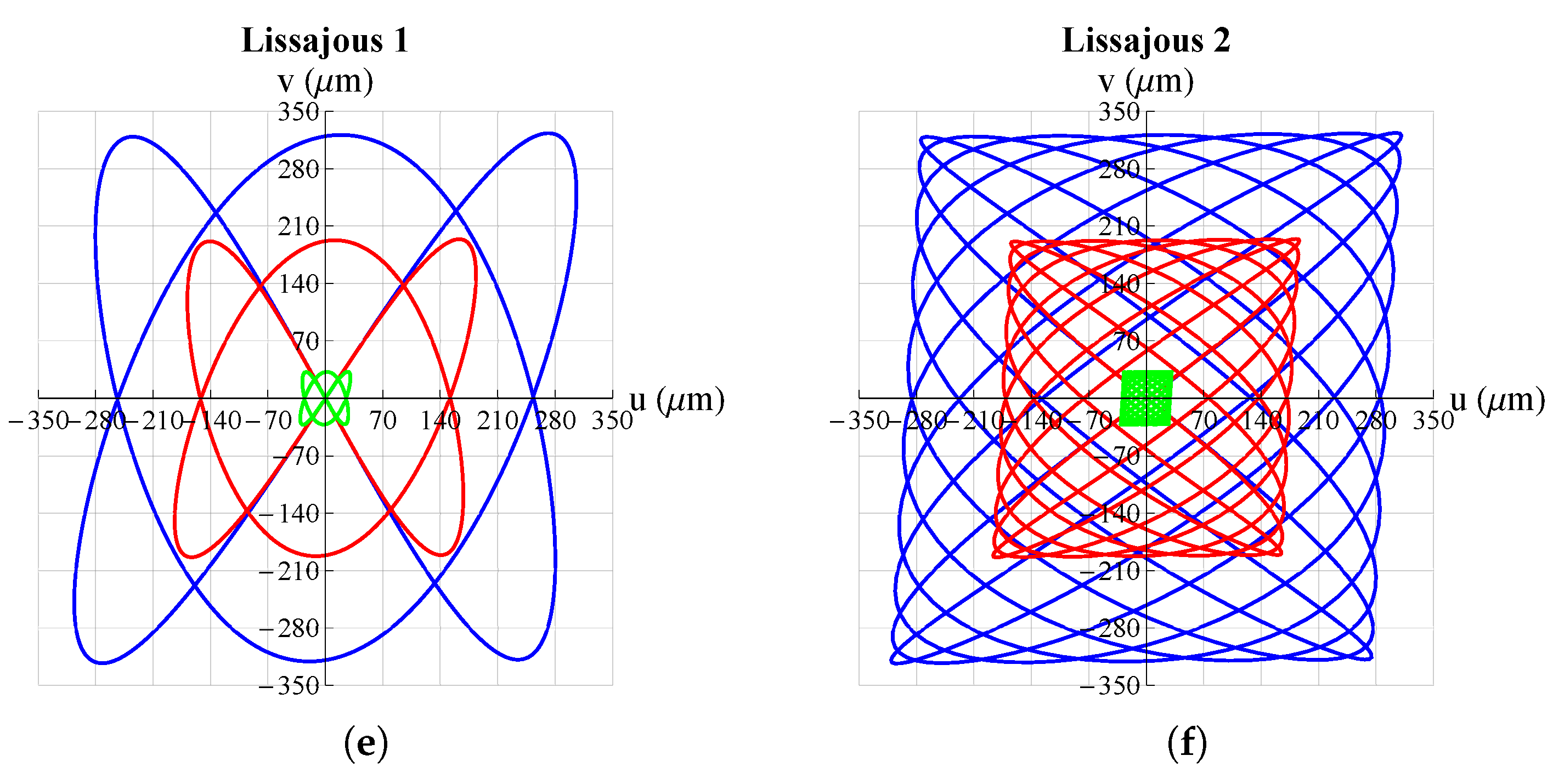
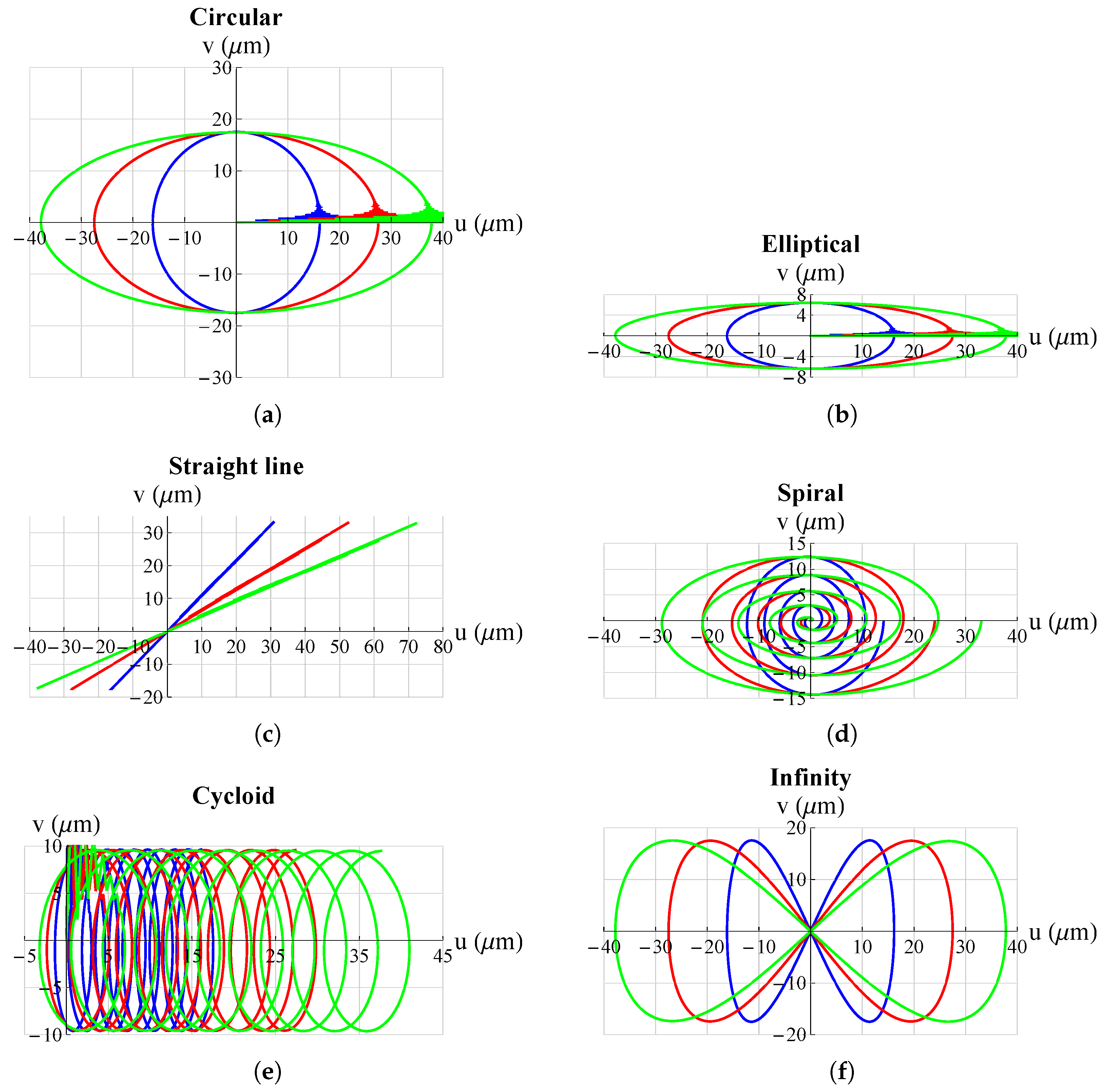
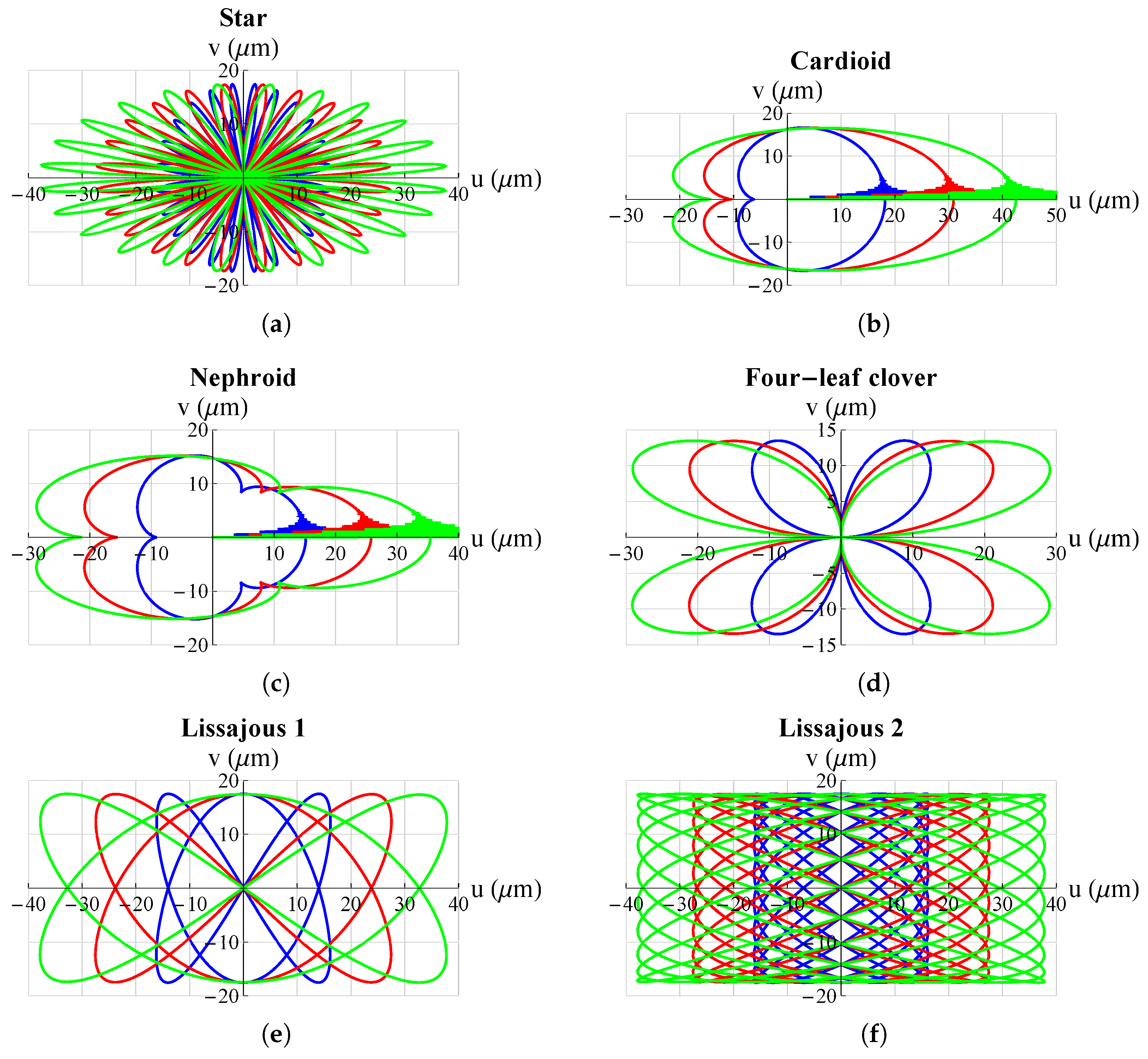
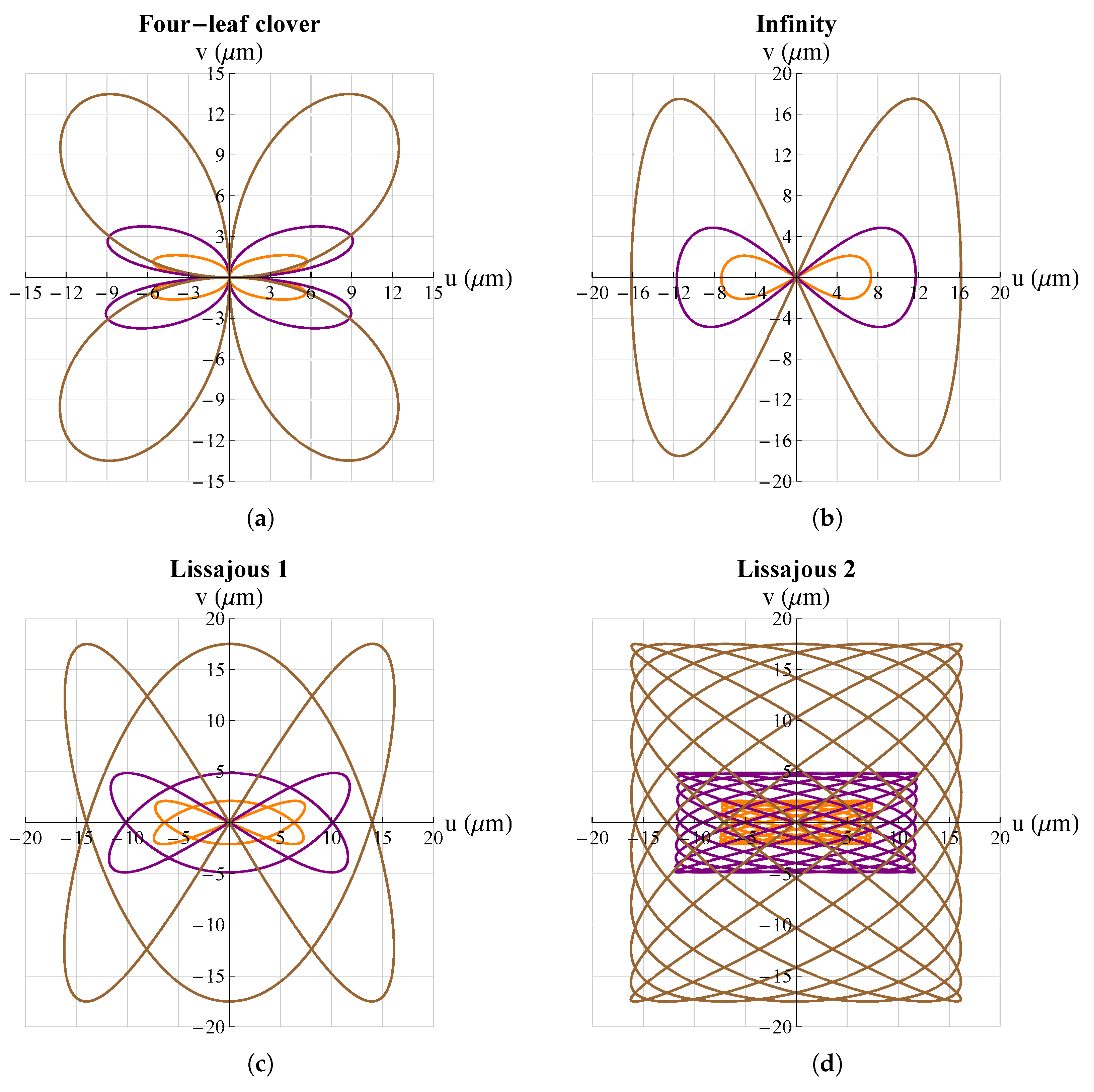
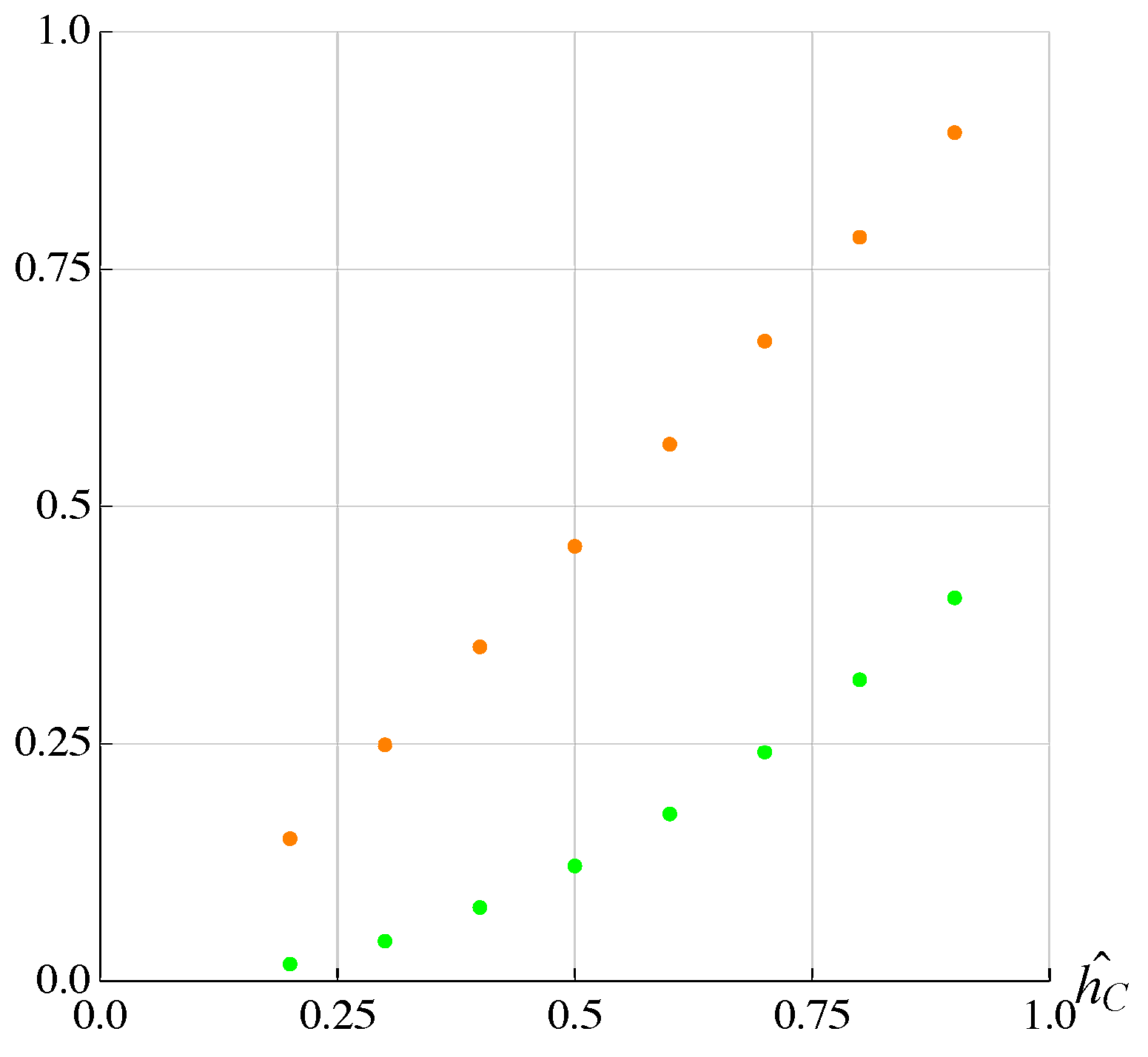
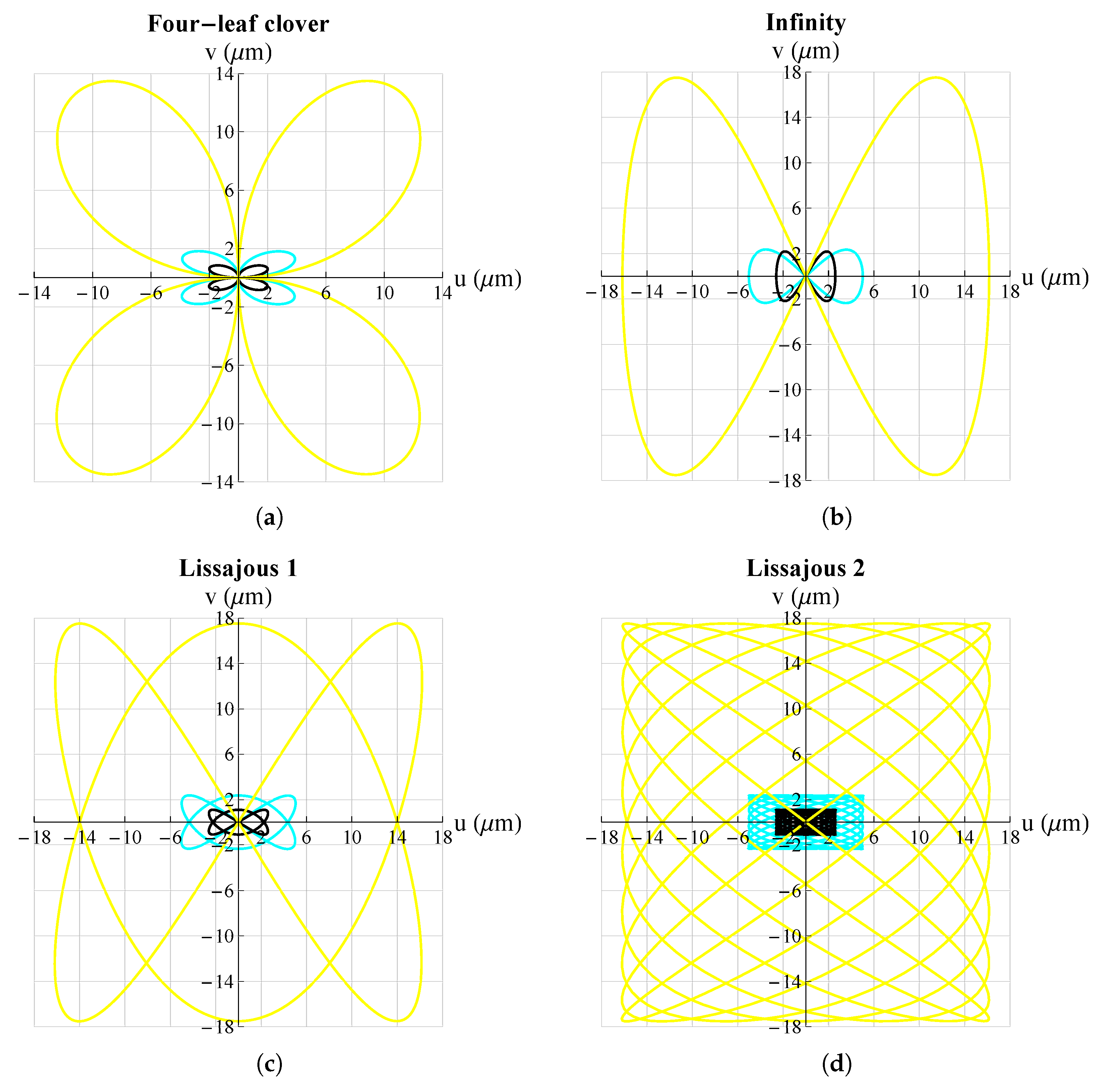
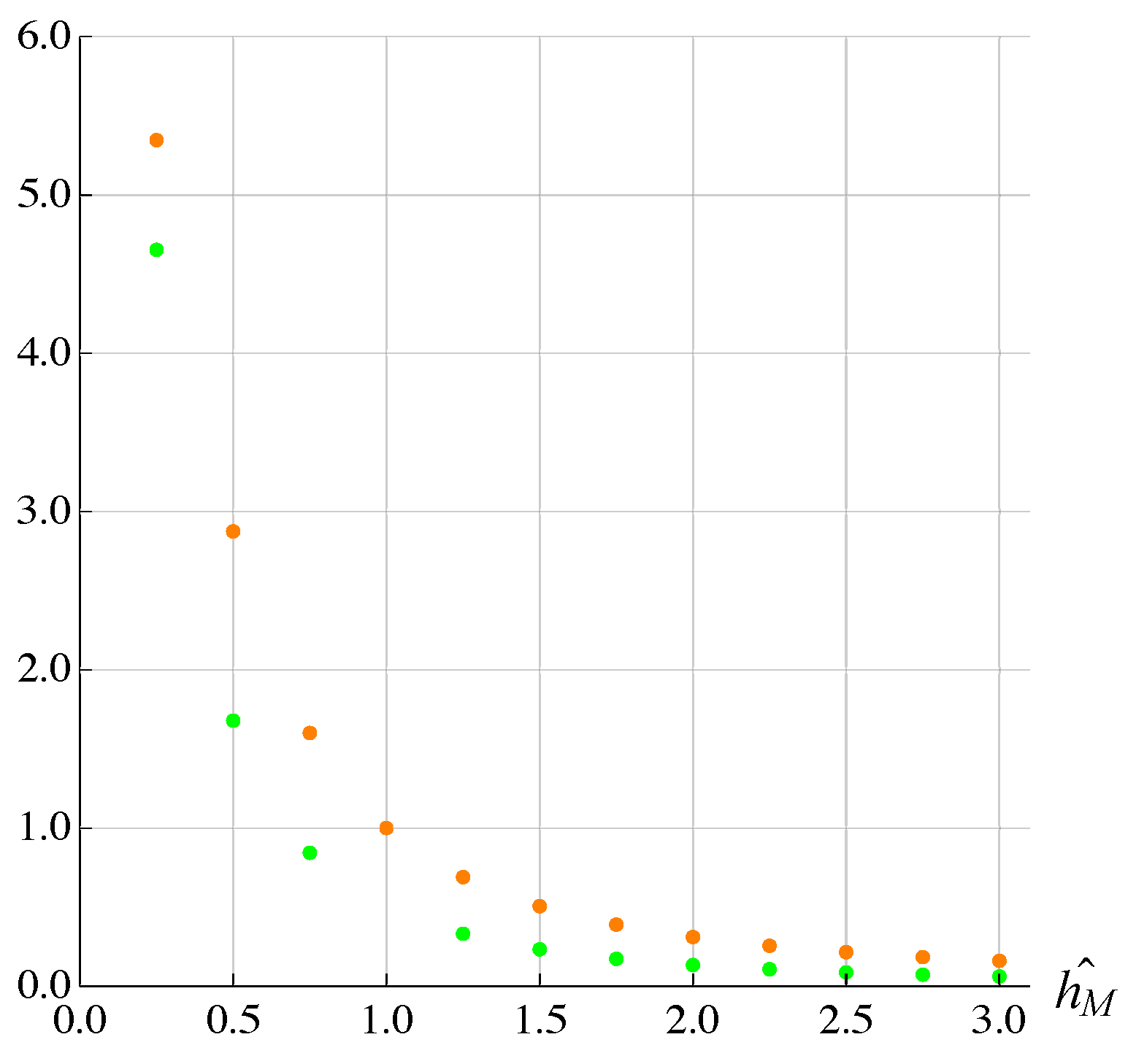
3. Results and Discussion
4. Conclusions
Funding
Conflicts of Interest
Nomenclature
| b | out of plane thickness |
| Young’s modulus of silicon | |
| Young’s modulus of PZT | |
| thickness of silicon | |
| thickness of PZT | |
| bending moment applied by PZTs | |
| u | displacement of the specimen along the x-axis |
| v | displacement of the specimen along the y-axis |
| electrical voltages supplied to PZTs | |
| parametric equations of the wanted trajectory |
References
- Dong, J.; Mukhopadhyay, D.; Ferreira, P.M. Design, fabrication and testing of a silicon-on-insulator (SOI) MEMS parallel kinematics XY stage. J. Micromech. Microeng. 2007, 17, 1154–1161. [Google Scholar] [CrossRef]
- Botta, F.; Verotti, M.; Bagolini, A.; Bellutti, P.; Belfiore, N.P. Mechanical response of four-bar linkage microgrippers with bidirectional electrostatic actuation. Actuators 2018, 7, 78. [Google Scholar] [CrossRef] [Green Version]
- Otic, C.J.C.; Yonemura, S. Thermally Induced Knudsen Forces for Contactless Manipulation of a Micro-Object. Micromachines 2022, 13, 1092. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Huang, X.; Liu, Y.; Wang, G.; Hong, K. Design and Control of a Piezoelectric-Driven Microgripper Perceiving Displacement and Gripping Force. Micromachines 2020, 11, 121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dawson, H.; Elias, J.; Etienne, P.; Calas-Etienne, S. The Rise of the OM-LoC: Opto-Microfluidic Enabled Lab-on-Chip. Micromachines 2021, 12, 1467. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Zheng, F.; Leng, H.; Zhang, C.; Luo, K.; Cao, Y.; Yang, X. Simplified Method of Microcontact Force Measurement by Using Micropressure Sensor. Micromachines 2021, 12, 515. [Google Scholar] [CrossRef]
- Tian, W.; Ling, Z.; Yu, W.; Shi, J. A Review of MEMS Scale Piezoelectric Energy Harvester. Appl. Sci. 2018, 8, 645. [Google Scholar] [CrossRef] [Green Version]
- Gu, G.Y.; Zhu, L.M.; Su, C.Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Design and analysis of a totally decoupled flexure-based XY parallel micromanipulator. IEEE Trans. Robot. 2009, 25, 645–657. [Google Scholar]
- Zhu, W.L.; Zhu, Z.; Shi, Y.; Wang, X.; Guan, K.; Ju, B.F. Design, modeling, analysis and testing of a novel piezo-actuated XY compliant mechanism for large workspace nano-positioning. Smart Mater. Struct. 2016, 25, 115033. [Google Scholar] [CrossRef]
- Yong, Y.K.; Aphale, S.S.; Moheimani, S.R. Design, identification, and control of a flexure-based XY stage for fast nanoscale positioning. IEEE Trans. Nanotechnol. 2008, 8, 46–54. [Google Scholar] [CrossRef]
- Laszczyk, K.; Bargiel, S.; Gorecki, C.; Krężel, J.; Dziuban, P.; Kujawińska, M.; Callet, D.; Frank, S. A two directional electrostatic comb-drive X–Y micro-stage for MOEMS applications. Sens. Actuators A Phys. 2010, 163, 255–265. [Google Scholar] [CrossRef]
- Lin, C.; Shen, Z.; Wu, Z.; Yu, J. Kinematic characteristic analysis of a micro-/nano positioning stage based on bridge-type amplifier. Sens. Actuators A Phys. 2018, 271, 230–242. [Google Scholar] [CrossRef]
- Zubir, M.N.M.; Shirinzadeh, B.; Tian, Y. Development of a novel flexure-based microgripper for high precision micro-object manipulation. Sens. Actuators A Phys. 2009, 150, 257–266. [Google Scholar] [CrossRef]
- Yao, Q.; Dong, J.; Ferreira, P.M. Design, analysis, fabrication and testing of a parallel-kinematic micropositioning XY stage. Int. J. Mach. Tools Manuf. 2007, 47, 946–961. [Google Scholar] [CrossRef]
- Zhou, M.; Fan, Z.; Ma, Z.; Zhao, H.; Guo, Y.; Hong, K.; Li, Y.; Liu, H.; Wu, D. Design and experimental research of a novel stick-slip type piezoelectric actuator. Micromachines 2017, 8, 150. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Li, Y. Design and analysis of a new high precision decoupled XY compact parallel micromanipulator. Micromachines 2017, 8, 82. [Google Scholar] [CrossRef] [Green Version]
- Pang, J.; Liu, P.; Yan, P.; Zhang, Z. Modeling and experimental testing of a composite bridge type amplifier based nano-positioner. In Proceedings of the 2016 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Chongqing, China, 18–22 July 2016; pp. 25–30. [Google Scholar]
- Botta, F.; Rossi, A.; Belfiore, N.P. A feasibility study of a novel piezo MEMS tweezer for soft materials characterization. Appl. Sci. 2019, 9, 2277. [Google Scholar] [CrossRef] [Green Version]
- Botta, F.; Rossi, A.; Belfiore, N.P. A novel method to fully suppress single and bi-modal excitations due to the support vibration by means of piezoelectric actuators. J. Sound Vib. 2021, 510, 116260. [Google Scholar] [CrossRef]
- Botta, F.; Marx, N.; Gentili, S.; Schwingshackl, C.; Di Mare, L.; Cerri, G.; Dini, D. Optimal placement of piezoelectric plates for active vibration control of gas turbine blades: Experimental results. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; SPIE: San Diego, CA, USA, 2012; Volume 8345, pp. 655–665. [Google Scholar]
- Botta, F.; Marx, N.; Schwingshackl, C.; Cerri, G.; Dini, D. A wireless vibration control technique for gas turbine blades using piezoelectric plates and contactless energy transfer. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: San Antonio, TX, USA, 2013; Volume 55263, p. V07AT32A006. [Google Scholar]
- Botta, F.; Scorza, A.; Rossi, A. Optimal Piezoelectric Potential Distribution for Controlling Multimode Vibrations. Appl. Sci. 2018, 8, 551. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, Y.; Peng, Y.; Kaneko, J.; Azuma, T.; Ito, S.; Gao, W.; Lu, T.F. Design and construction of the motion mechanism of an XY micro-stage for precision positioning. Sens. Actuators A Phys. 2013, 201, 395–406. [Google Scholar] [CrossRef]
- Ai, W.; Xu, Q. New Structural Design of a Compliant Gripper Based on the Scott-Russell Mechanism. Int. J. Adv. Robot. Syst. 2014, 11, 192. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Liu, H.; Zhao, H. A compact 2-DOF piezoelectric-driven platform based on “z-shaped” flexure hinges. Micromachines 2017, 8, 245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Huang, H. Parasitic Motion Principle (PMP) Piezoelectric Actuators: Definition and Recent Developments; IntechOpen: London, UK, 2021. [Google Scholar]
- DeVoe, D.L.; Pisano, A.P. Modeling and optimal design of piezoelectric cantilever microactuators. J. Microelectromech. Syst. 1997, 6, 266–270. [Google Scholar] [CrossRef]
- El-Sayed, A.M.; Abo-Ismail, A.; El-Melegy, M.T.; Hamzaid, N.A.; Abu Osman, N.A. Development of a micro-gripper using piezoelectric bimorphs. Sensors 2013, 13, 5826–5840. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, S.; Ratha, S.; Rout, C.S.; Nayak, S.K. Self-charging supercapacitors for smart electronic devices: A concise review on the recent trends and future sustainability. J. Mater. Sci. 2022, 57, 4399–4440. [Google Scholar] [CrossRef]
- Aaryashree; Sahoo, S.; Walke, P.; Nayak, S.K.; Rout, C.S.; Late, D.J. Recent developments in self-powered smart chemical sensors for wearable electronics. Nano Res. 2021, 14, 3669–3689. [Google Scholar] [CrossRef]
- Sahoo, S.; Krishnamoorthy, K.; Pazhamalai, P.; Mariappan, V.K.; Manoharan, S.; Kim, S.J. High performance self-charging supercapacitors using a porous PVDF-ionic liquid electrolyte sandwiched between two-dimensional graphene electrodes. J. Mater. Chem. A 2019, 7, 21693–21703. [Google Scholar] [CrossRef]
- Crawley, E.F.; de Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA J. 1987, 25, 1373–1385. [Google Scholar] [CrossRef]
- Botta, F.; Toccaceli, F. Piezoelectric plates distribution for active control of torsional vibrations. Actuators 2018, 7, 23. [Google Scholar] [CrossRef]


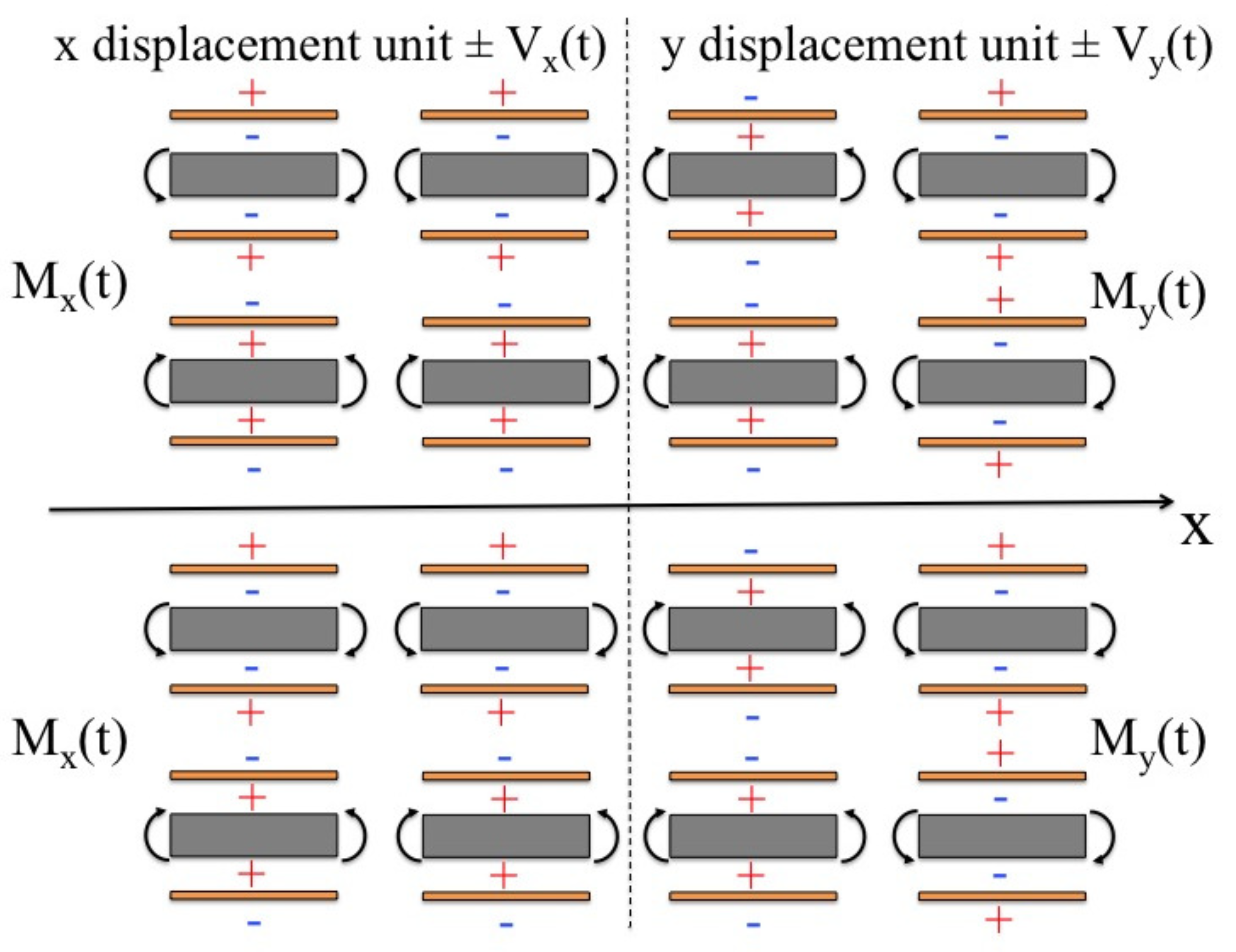

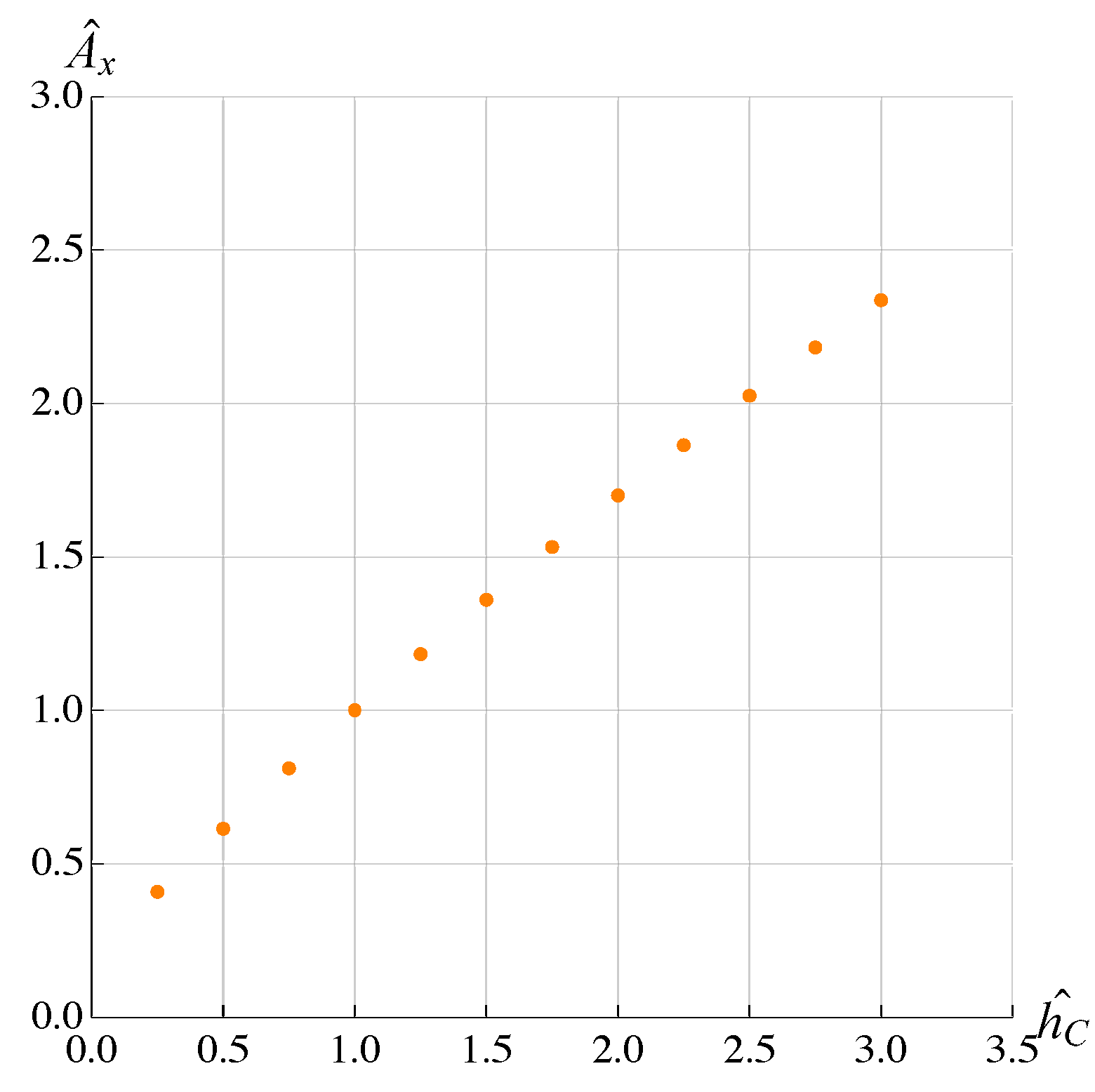
| Property | Silicon | PZT-5A | Unit |
|---|---|---|---|
| Density | 2329 | 7750 | kg/m3 |
| Poisson’s ratio | 0.28 | – | – |
| Young’s modulus | 170 | – | GPa |
| – | −1.71 | C/N | |
| – | 3.74 | C/N | |
| – | 5.84 | C/N |
| Label | Value (μm) | Label | Value (μm) |
|---|---|---|---|
| 300 | 10 | ||
| 270 | 36 | ||
| 100 | 119 | ||
| 500 | 120 | ||
| Out-of-plane thickness | 10 | ||
| Trajectory | Voltage Functions | |||
|---|---|---|---|---|
| Label | ||||
| Circular | ||||
| Elliptical | ||||
| Straight line | ||||
| Spiral | ||||
| Cycloidal | ||||
| Infinity | ||||
| Star | ||||
| Cardioid | ||||
| Nephroid | ||||
| Four-leaf clover | ||||
| Lissajous 1 | ||||
| Lissajous 2 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Botta, F. A Piezoelectric MEMS Microgripper for Arbitrary XY Trajectory. Micromachines 2022, 13, 1888. https://doi.org/10.3390/mi13111888
Botta F. A Piezoelectric MEMS Microgripper for Arbitrary XY Trajectory. Micromachines. 2022; 13(11):1888. https://doi.org/10.3390/mi13111888
Chicago/Turabian StyleBotta, Fabio. 2022. "A Piezoelectric MEMS Microgripper for Arbitrary XY Trajectory" Micromachines 13, no. 11: 1888. https://doi.org/10.3390/mi13111888
APA StyleBotta, F. (2022). A Piezoelectric MEMS Microgripper for Arbitrary XY Trajectory. Micromachines, 13(11), 1888. https://doi.org/10.3390/mi13111888







