Correlation of Superlattice Cross-Plane Thermal Conductivity with Emission Wavelength in InAlAs/InGaAs Quantum Cascade Lasers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theoretical Approach
2.2. Experimental Approach
COMSOL Thermal Simulation
3. Results
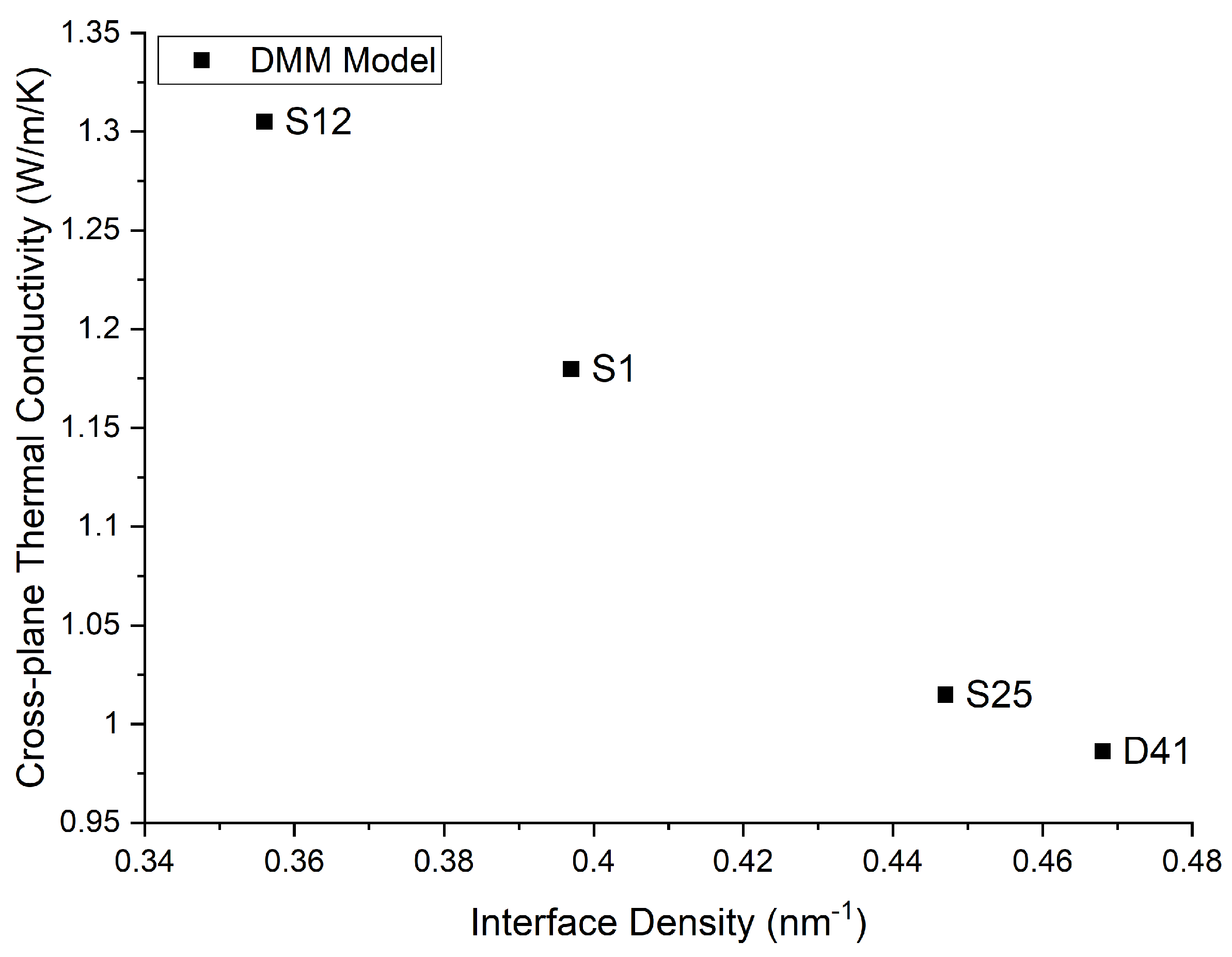
3.1. Theoretical Results
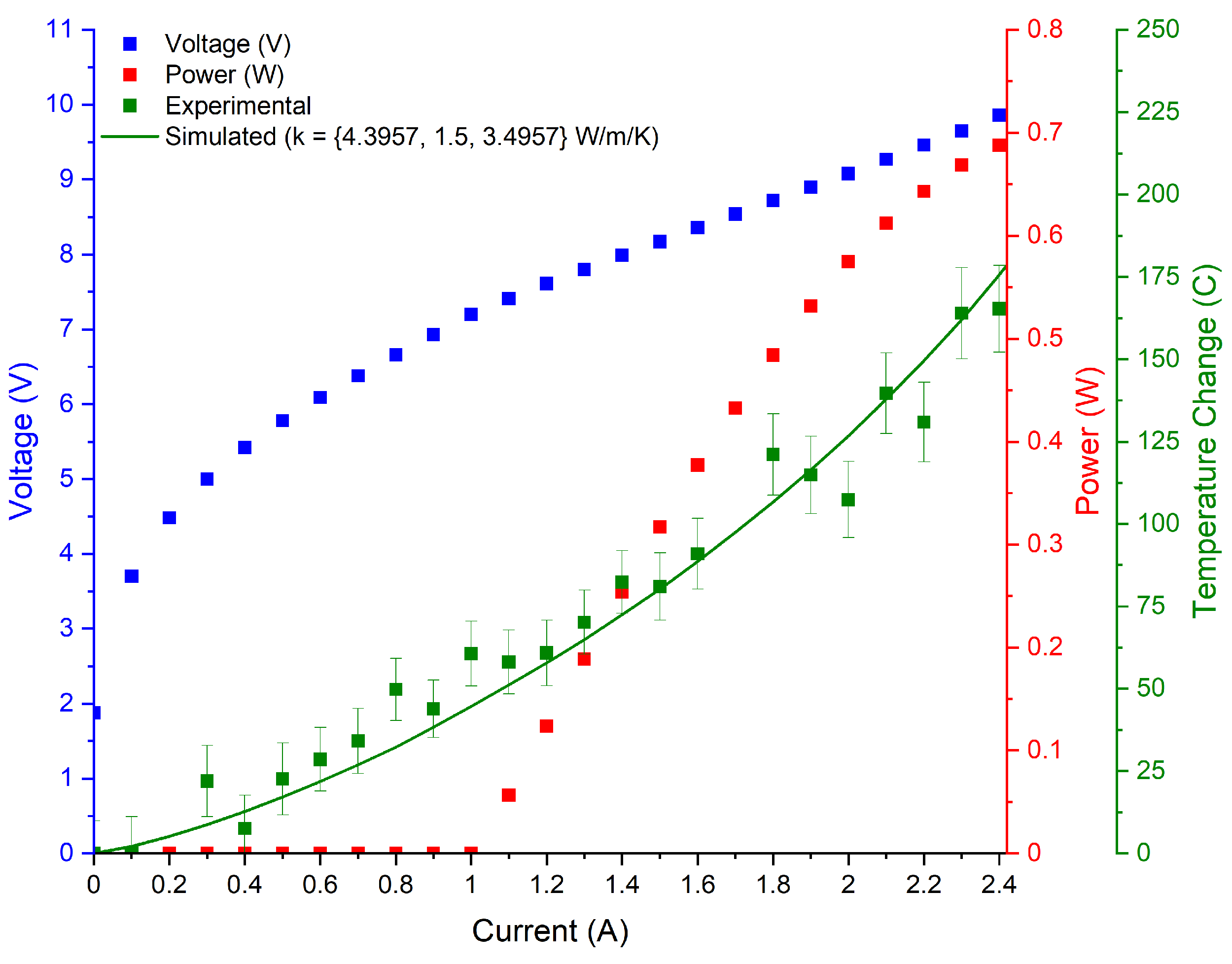
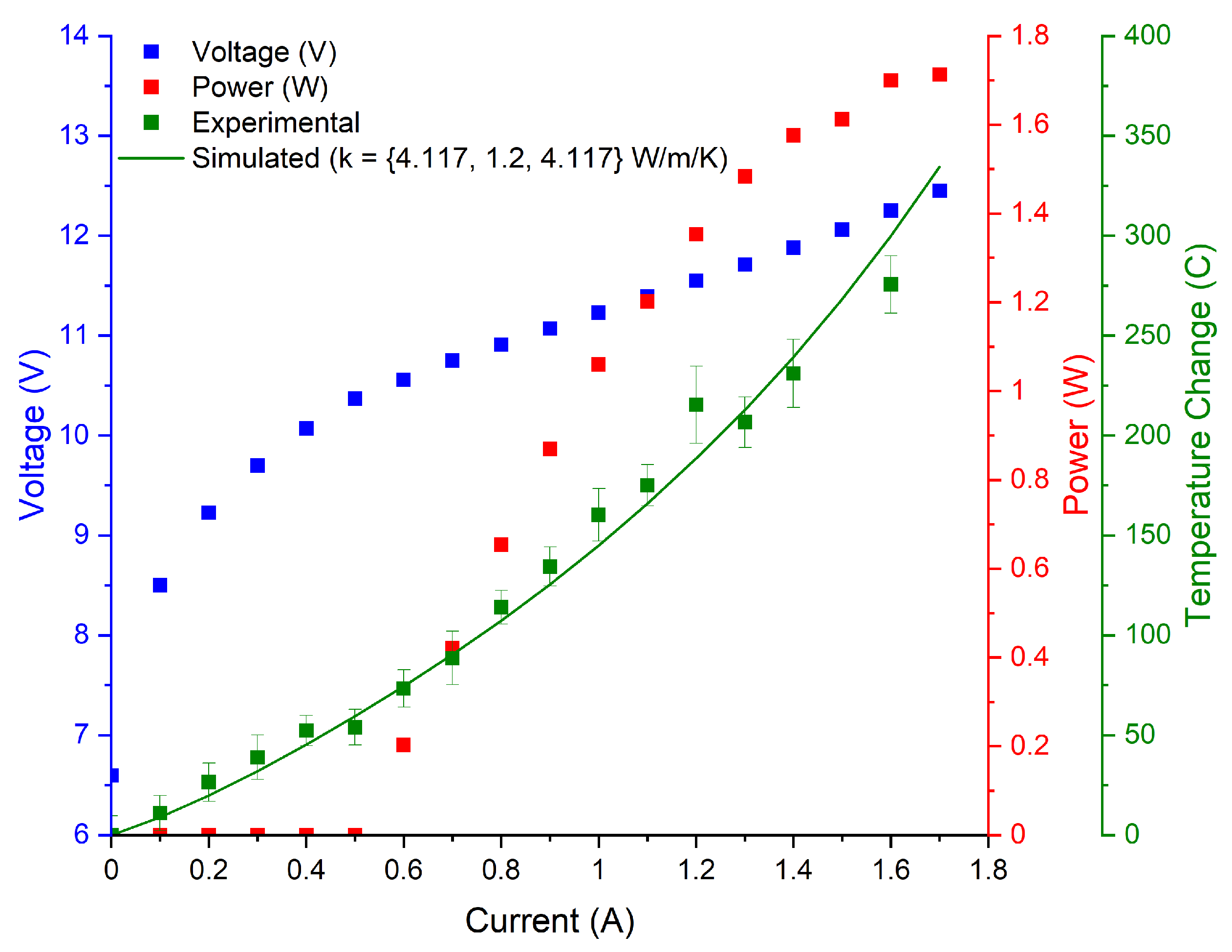
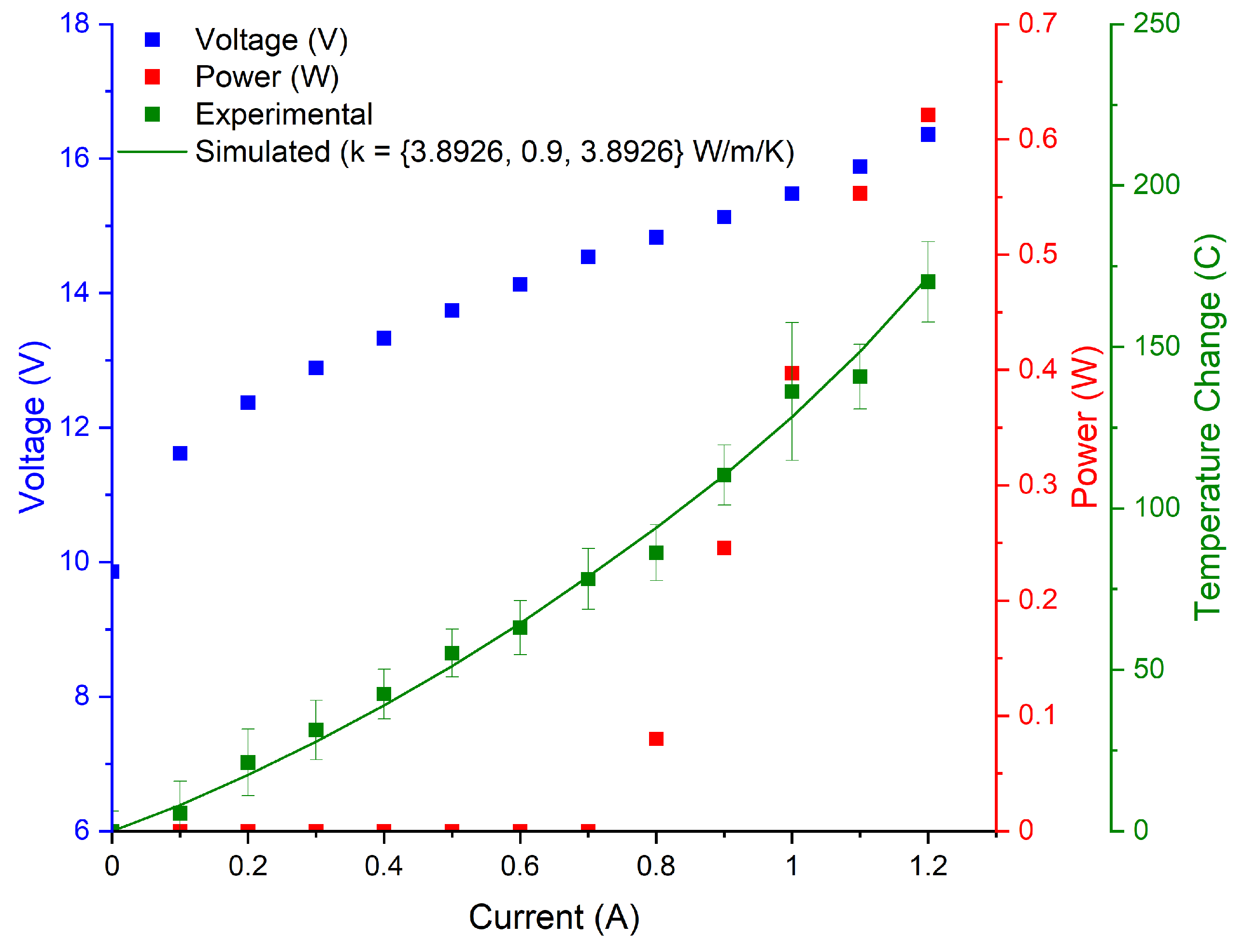
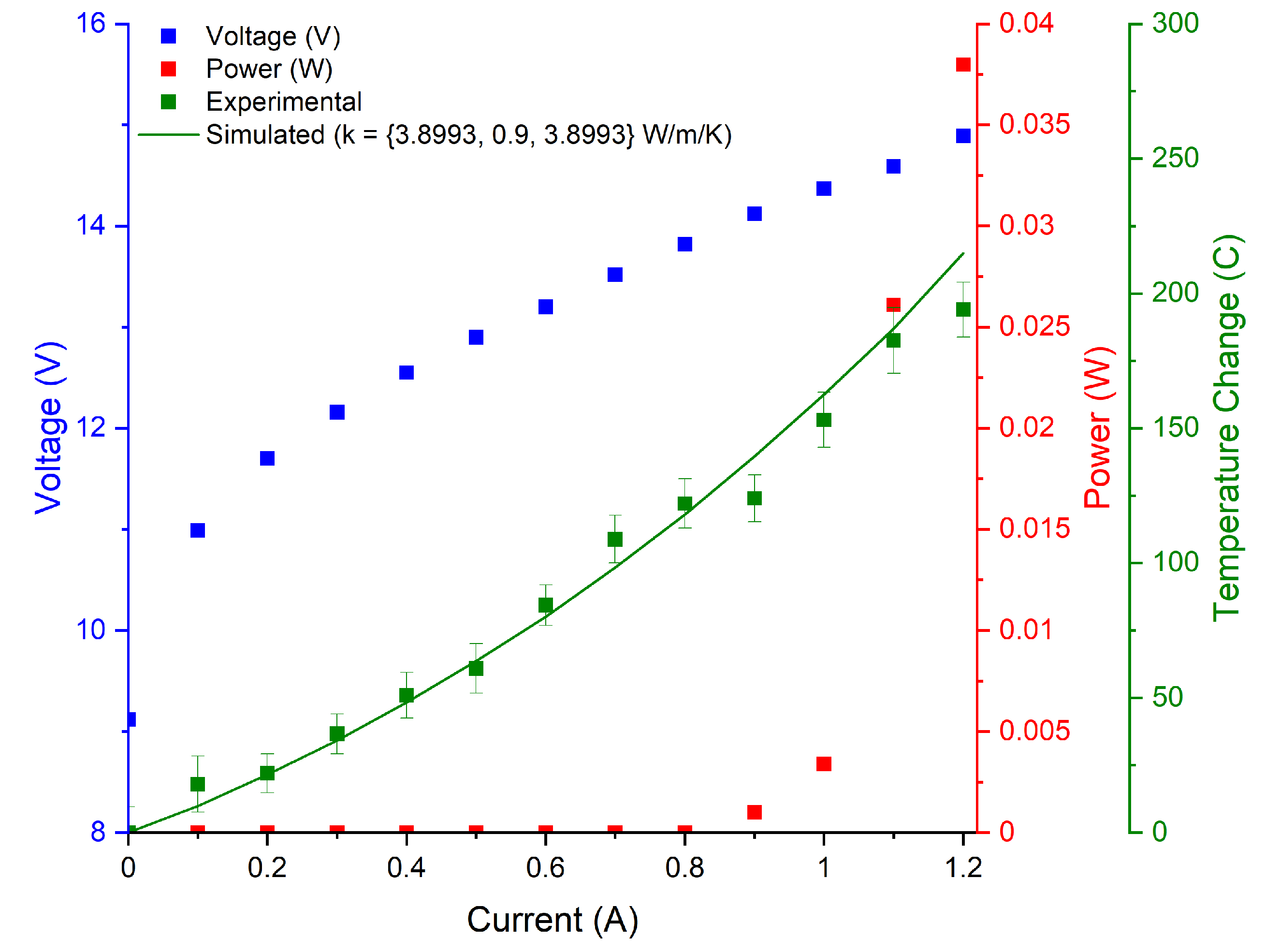
3.2. Experimental Results
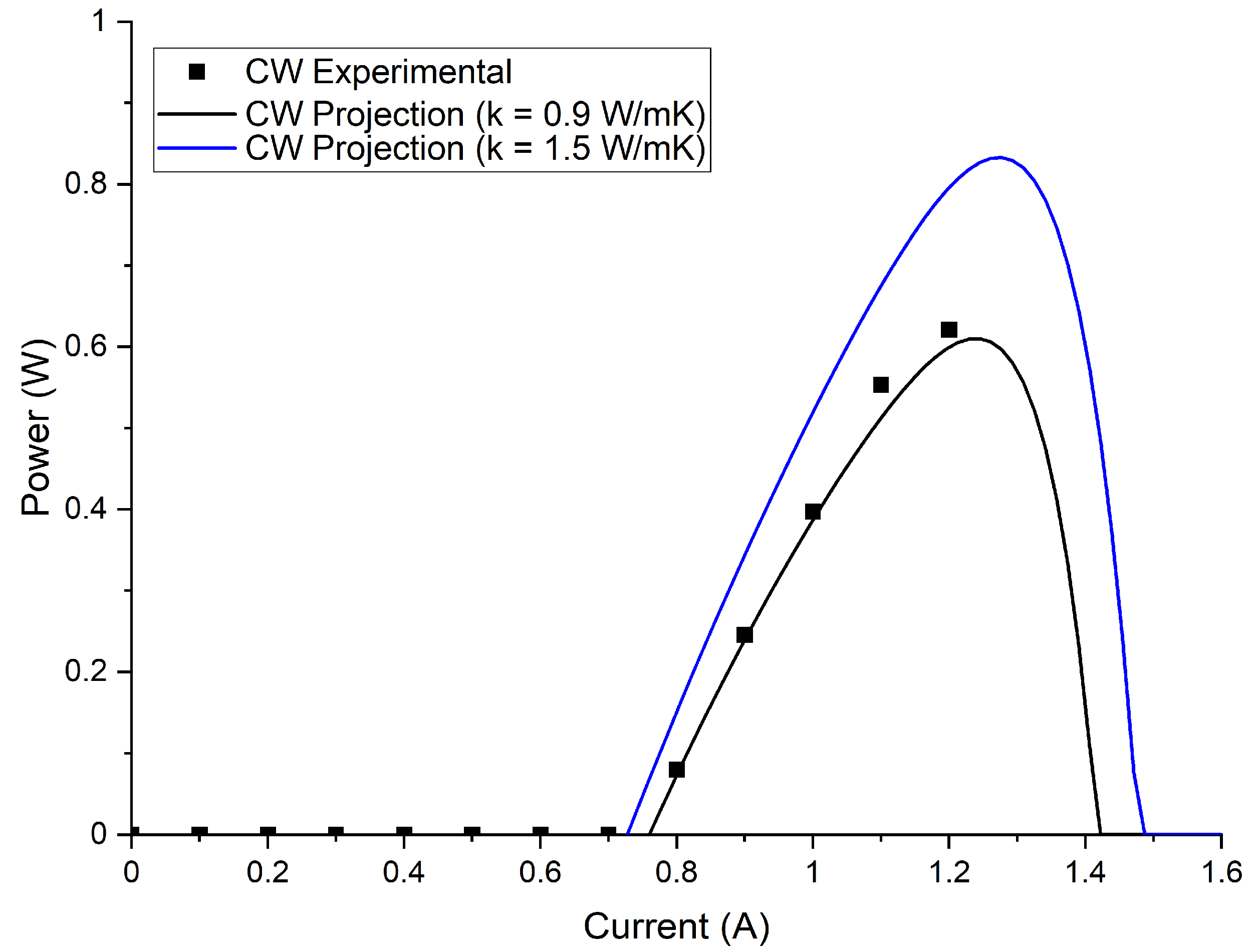
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lops, A.; Spagnolo, V.; Scamarcio, G. Thermal Modeling of GaInAs/AlInAs Quantum Cascade Lasers. J. Appl. Phys. 2006, 100, 043109. [Google Scholar] [CrossRef]
- Szymański, M. Calculation of the Cross-Plane Thermal Conductivity of a Quantum Cascade Laser Active Region. J. Phys. D Appl. Phys. 2011, 44, 085101. [Google Scholar] [CrossRef]
- Mei, S.; Knezevic, I. Thermal Conductivity of III-V Semiconductor Superlattices. J. Appl. Phys. 2015, 118, 175101. [Google Scholar] [CrossRef] [Green Version]
- Mawst, L.J.; Botez, D. High-Power Mid-Infrared (λ∼3–6 µm) Quantum Cascade Lasers. IEEE Photon. J. 2022, 14, 1508025. [Google Scholar] [CrossRef]
- Jaffe, G.R.; Mei, S.; Boyle, C.; Kirch, J.D.; Savage, D.E.; Botez, D.; Mawst, L.J.; Knezevic, I.; Lagally, M.G.; Eriksson, M.A. Measurements of the Thermal Resistivity of InAlAs, InGaAs, and InAlAs/InGaAs Superlattices. ACS Appl. Mater. Interfaces 2019, 11, 11970–11975. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Zhang, Y.; Li, A.; Tian, Z. Analysis of Key Parameters Affecting the Thermal Behavior and Performance of Quantum Cascade Lasers. J. Appl. Phys. 2006, 100, 053105. [Google Scholar] [CrossRef]
- Spagnolo, V.; Troccoli, M.; Scamarcio, G.; Gmachl, C.; Capasso, F.; Tredicucci, A.; Sergent, A.M.; Hutchinson, A.L.; Sivco, D.L.; Cho, A.Y. Temperature Profile of GaInAs/AlInAs/InP Quantum Cascade-Laser Facets Measured by Microprobe Photoluminescence. Appl. Phys. Lett. 2001, 78, 2095–2097. [Google Scholar] [CrossRef]
- Le, K.Q.; Kim, S. Model for Cross-Plane Thermal Conductivity of Layered Quantum Semiconductor Structures and Application for Thermal Modeling of GaInAs/AlInAs-Based Quantum Cascade Lasers. Phys. Status Solidi A 2008, 205, 392–396. [Google Scholar] [CrossRef]
- Abbas, F.; Pandey, B.J.; Clark, K.; Lascola, K.; Dikmelik, Y.; Robbins, D.; Hinojos, D.; Hodges, K.L.; Roodenko, K.; Gu, Q. Thermal Modeling of Quantum Cascade Lasers with 3D Anisotropic Heat Transfer Analysis. Proc. SPIE 2020, 11288, 1128808. [Google Scholar]
- Lyakh, A.; Suttinger, M.; Go, R.; Figueiredo, P.; Todi, A. 5.6 Μm Quantum Cascade Lasers Based on a Two-Material Active Region Composition with a Room Temperature Wall-Plug Efficiency Exceeding 28%. Appl. Phys. Lett. 2016, 109, 121109. [Google Scholar] [CrossRef]
- Goldberg, Y.A.; Schmidt, N.M. Handbook Series on Semiconductor Parameters, Vol. 2: Ternary and Quaternary III–V Compounds; Levinshtein, M., Rumyantsev, S., Shur, M.S., Eds.; World Scientific: Singapore, 1999; Volume 2. [Google Scholar]
- Kothari, K.; Maldovan, M. Analysis of In-Plane Thermal Phonon Transport in III–V Compound Semiconductor Superlattices. Nanoscale Microscale Thermophys. Eng. 2018, 22, 239–253. [Google Scholar] [CrossRef]
- Szymański, M.; Kozłowska, A.; Tomm, J.; Huk, R.; Maląg, A.; Rusek, M. From Two- to Three-Dimensional Model of Heat Flow in Edge-Emitting Laser: Theory, Experiment and Numerical Tools. Energies 2021, 14, 7006. [Google Scholar] [CrossRef]
- Pierścińska, D.; Pierściński, K.; Gutowski, P.; Badura, M.; Sobczak, G.; Serebrennikova, O.; Ściana, B.; Tłaczała, M.; Sobczak, G.; Bugajski, M. Heat Dissipation Schemes in AlInAs/InGaAs/InP Quantum Cascade Lasers Monitored by CCD Thermoreflectance. Photonics 2017, 4, 47. [Google Scholar] [CrossRef] [Green Version]
- Hathaway, D.; Shahzad, M.; Sakthivel, T.S.; Suttinger, M.; Go, R.; Sanchez, E.; Seal, S.; Shu, H.; Lyakh, A. Output Facet Heating Mechanism for Uncoated High Power Long Wave Infrared Quantum Cascade Lasers. AIP Adv. 2020, 10, 085104. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, L.; Zhang, J.; Li, L.; Liu, J.; Liu, F.; Wang, Z. Facet Temperature Distribution of a Room Temperature Continuous-Wave Operating Quantum Cascade Laser. J. Phys. D Appl. Phys. 2012, 45, 325103. [Google Scholar] [CrossRef]
- Swartz, E.T.; Pohl, R.O. Thermal Boundary Resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Chen, J.; Xu, X.; Zhou, J.; Li, B. Interfacial Thermal Resistance: Past, Present, and Future. Rev. Mod. Phys. 2022, 94, 025002. [Google Scholar] [CrossRef]
- Nalwa, H.S. Encyclopedia of Nanoscience and Nanotechnology; American Scientific Publishers: Stevenson Ranch, CA, USA, 2004; Volume 10. [Google Scholar]
- Sood, A.; Rowlette, J.A.; Caneau, C.G.; Bozorg-Grayeli, E.; Asheghi, M.; Goodson, K.E. Thermal Conduction in Lattice–Matched Superlattices of InGaAs/InAlAs. Appl. Phys. Lett. 2014, 105, 051909. [Google Scholar] [CrossRef] [Green Version]
- Suttinger, M.; Go, R.; Figueiredo, P.; Todi, A. Power Scaling and Experimentally Fitted Model for Broad Area Quantum Cascade Lasers in Continuous Wave Operation. Opt. Eng. 2017, 57, 011011. [Google Scholar] [CrossRef]

| Structure | Wavelength (µm) | Number of Interfaces | Total Stage Thickness (Å) | Laser Core Dimensions | Barrier Composition/Total Thickness (Å) | Quantum Well Composition/Total Thickness (Å) |
|---|---|---|---|---|---|---|
| D41 | 3.7 | 20 | 427 | 5 mm × 8 µm | 188 | 239 |
| S25 | 3.7 | 20 | 447 | 5 mm × 7.2 µm | 198 | 249 |
| S1 | 5.7 | 18 | 453 | 3.15 mm × 7 µm | 160 | 293 |
| S12 | 8.7 | 16 | 449 | 5 mm × 9 µm | 115 | 334 |
| Parameter | ||
|---|---|---|
| (8.34 + 3.68x) × 1010 | (8.34 + 3.56x) × 1010 | |
| (3.95 + 1.94x) × 1010 | (3.95 + 2.01x) × 1010 | |
| 5680 − 1920x | 5680 − 370x | |
| 280 + 166x | 280 + 110x | |
| 2.5 | 5.0 | |
| Wavelength (µm) | Interface Density N/L (nm−1) | DMM Thermal Boundary Resistance (m2K/W) | AMM Thermal Boundary Resistance (m2K/W) | DMM Cross-Plane Thermal Conductivity (W/m/K) | AMM Cross-Plane Thermal Conductivity (W/m/K) |
|---|---|---|---|---|---|
| 3.7 | 0.468 | 1.549 × 10−9 | 9.765 × 10−9 | 0.986 | 1.341 |
| 3.7 | 0.447 | 1.557 × 10−9 | 9.83 × 10−9 | 1.015 | 1.373 |
| 5.7 | 0.397 | 1.452 × 10−9 | 8.9 × 10−9 | 1.18 | 1.602 |
| 8.7 | 0.356 | 1.445 × 10−9 | 8.4 × 10−9 | 1.305 | 1.816 |
| Wavelength (µm) | |||
|---|---|---|---|
| 3.7 | 0.176 | 0.112 | 0.726 |
| 3.7 | 0.177 | 0.111 | 0.697 |
| 5.7 | 0.141 | 0.13 | 0.577 |
| 8.7 | 0.102 | 0.149 | 0.515 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villalobos Meza, A.M.; Shahzad, M.; Hathaway, D.; Shu, H.; Lyakh, A. Correlation of Superlattice Cross-Plane Thermal Conductivity with Emission Wavelength in InAlAs/InGaAs Quantum Cascade Lasers. Micromachines 2022, 13, 1934. https://doi.org/10.3390/mi13111934
Villalobos Meza AM, Shahzad M, Hathaway D, Shu H, Lyakh A. Correlation of Superlattice Cross-Plane Thermal Conductivity with Emission Wavelength in InAlAs/InGaAs Quantum Cascade Lasers. Micromachines. 2022; 13(11):1934. https://doi.org/10.3390/mi13111934
Chicago/Turabian StyleVillalobos Meza, Alejandro M., Monas Shahzad, Dagan Hathaway, Hong Shu, and Arkadiy Lyakh. 2022. "Correlation of Superlattice Cross-Plane Thermal Conductivity with Emission Wavelength in InAlAs/InGaAs Quantum Cascade Lasers" Micromachines 13, no. 11: 1934. https://doi.org/10.3390/mi13111934
APA StyleVillalobos Meza, A. M., Shahzad, M., Hathaway, D., Shu, H., & Lyakh, A. (2022). Correlation of Superlattice Cross-Plane Thermal Conductivity with Emission Wavelength in InAlAs/InGaAs Quantum Cascade Lasers. Micromachines, 13(11), 1934. https://doi.org/10.3390/mi13111934





