A High Quality-Factor Optical Modulator with Hybrid Graphene-Dielectric Metasurface Based on the Quasi-Bound States in the Continuum
Abstract
:1. Introduction
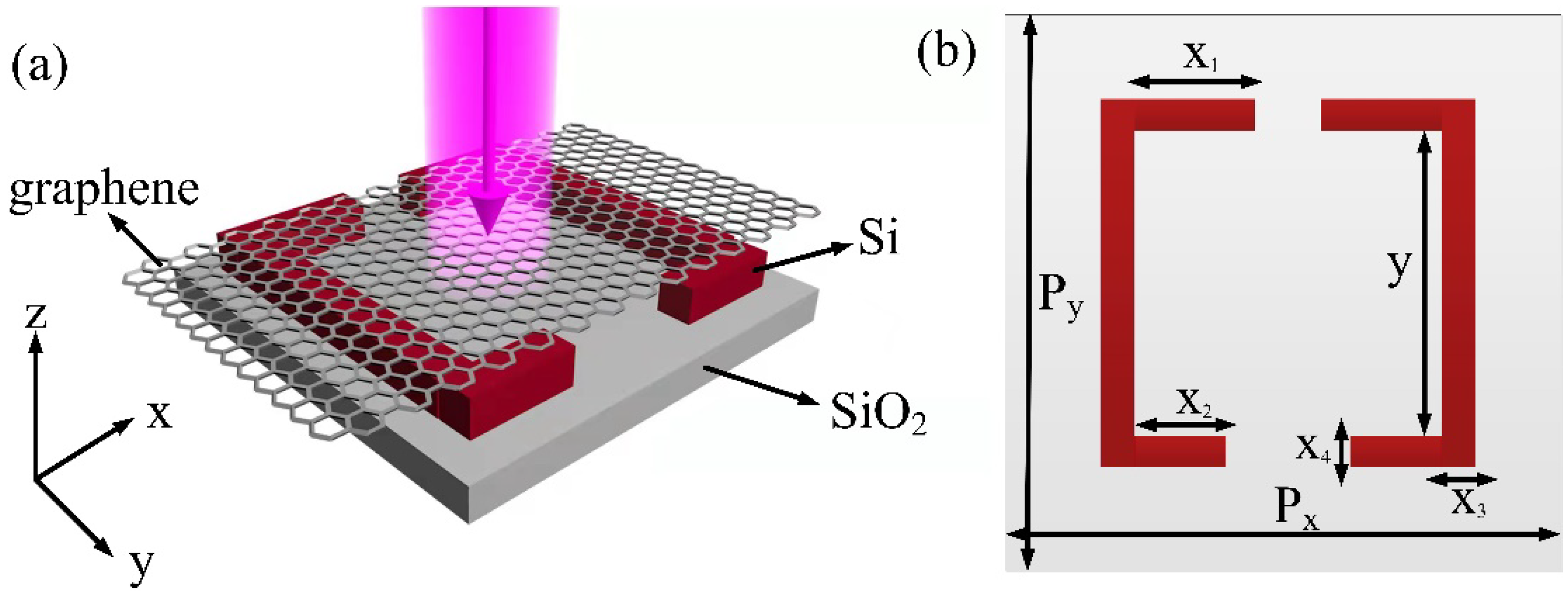
2. Structure and Model
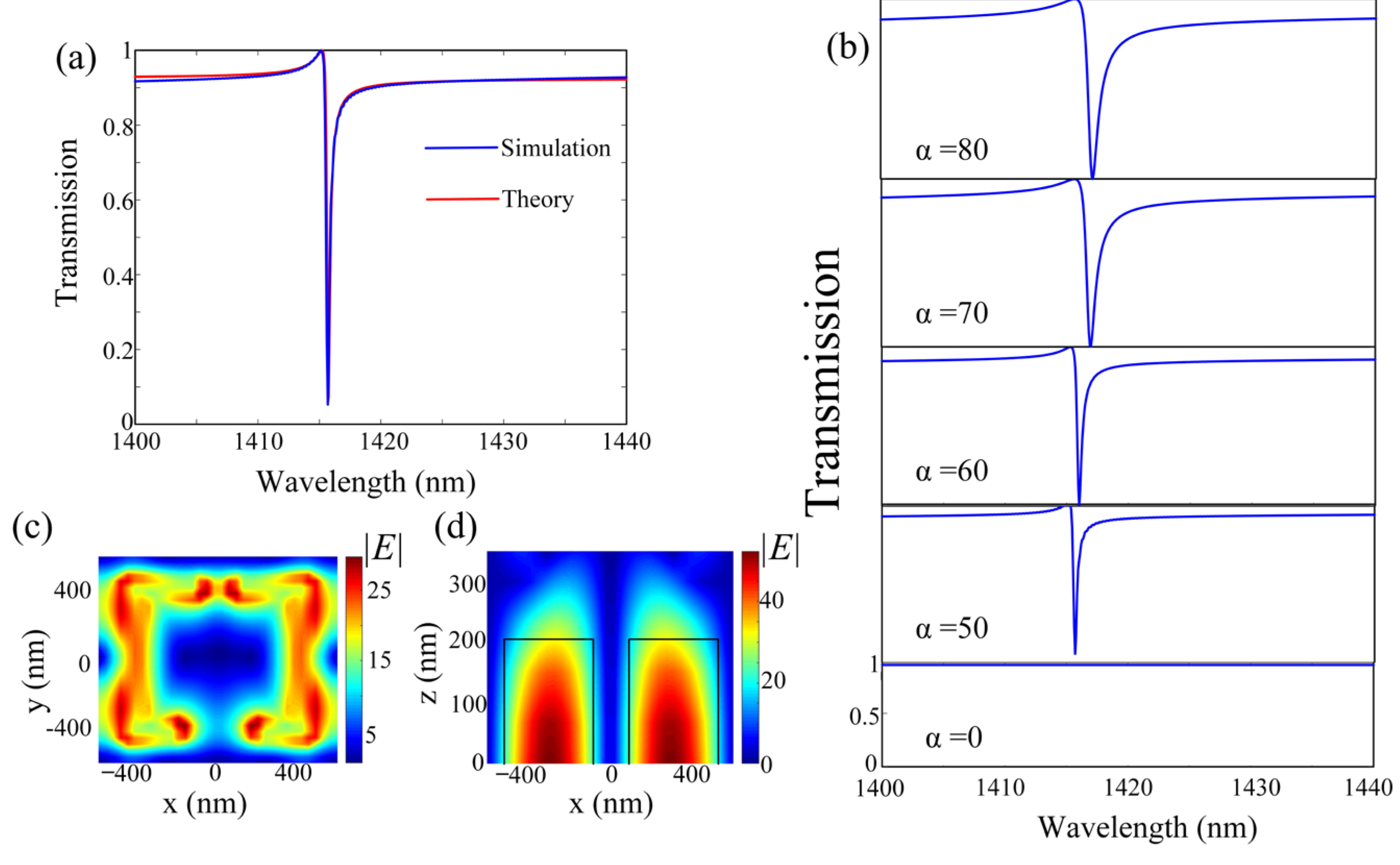
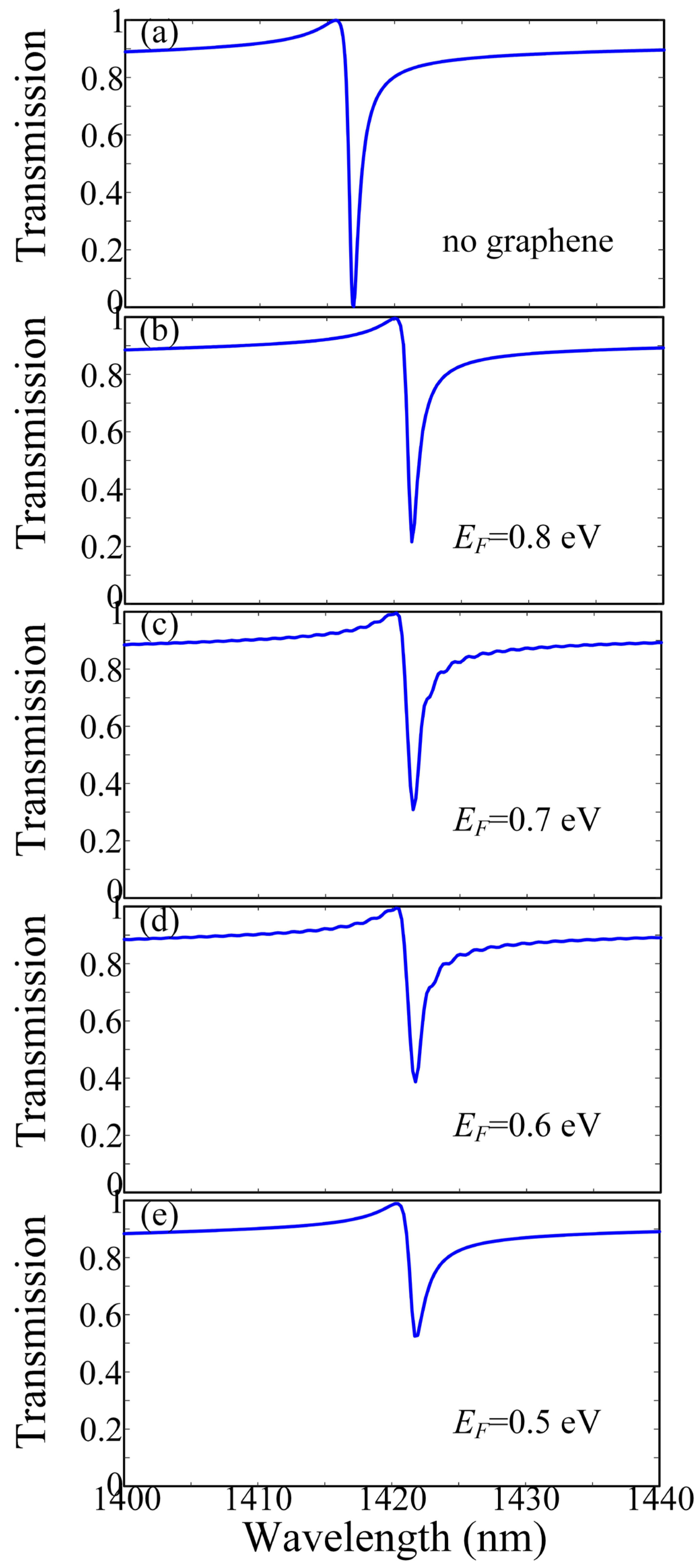
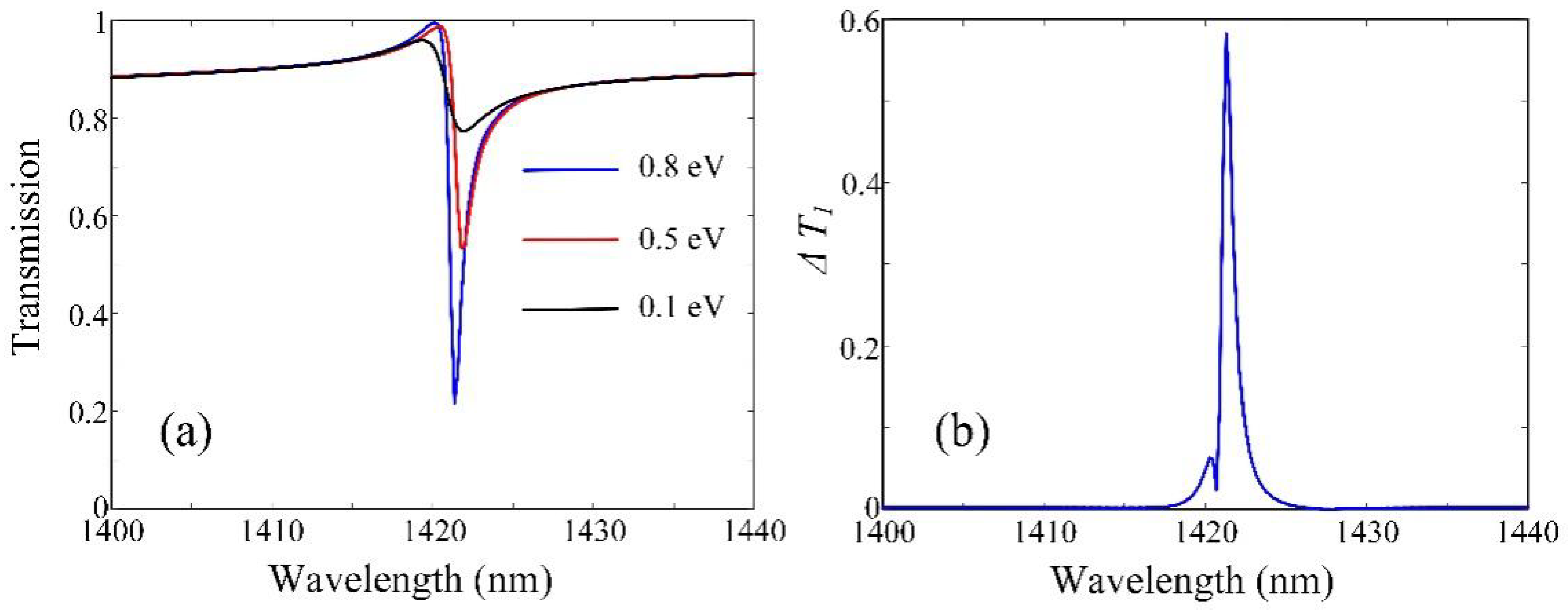
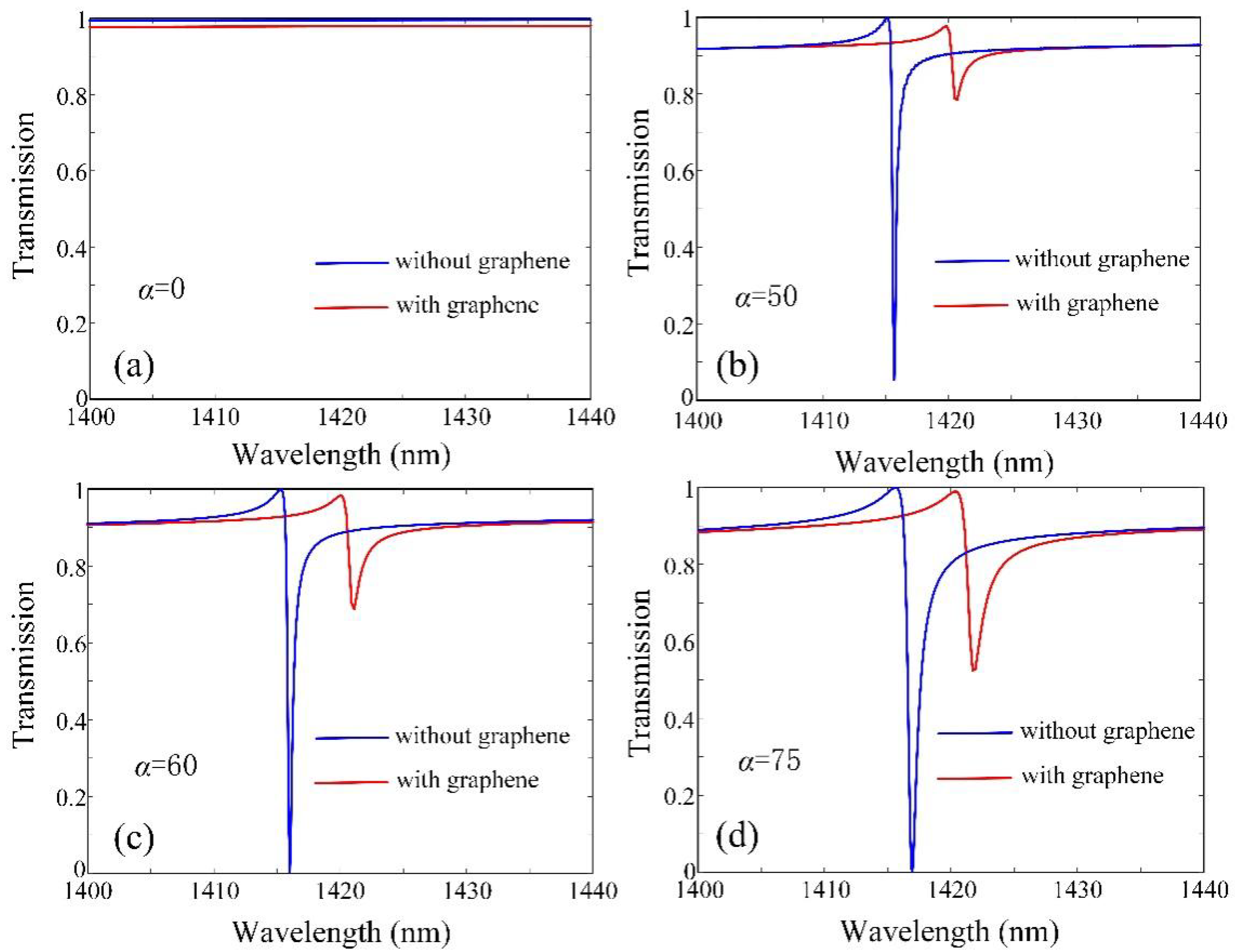
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soukoulis, C.M.; Wegener, M. Past achievements and future challenges in the development of three-dimensional photonic metamaterials. Nat. Photonics 2011, 5, 523–530. [Google Scholar] [CrossRef] [Green Version]
- Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M. 3D metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Zhou, C.; Jiang, X.; Zhang, J. Active metamaterials and metadevices: A review. J. Phys. D Appl. Phys. 2020, 53, 503002. [Google Scholar] [CrossRef]
- Xu, M.; He, Q.; Pu, M.; Zhang, F.; Li, L.; Sang, D.; Guo, Y.; Zhang, R.; Li, X.; Ma, X.; et al. Emerging Long-Range Order from a Freeform Disordered Metasurface. Adv. Mater. 2022, 34, 2108709. [Google Scholar] [CrossRef] [PubMed]
- Sang, D.; Xu, M.; Pu, M.; Zhang, F.; Guo, Y.; Li, X.; Ma, X.; Fu, Y.; Luo, X. Toward High-Efficiency Ultrahigh Numerical Aperture Freeform Metalens: From Vector Diffraction Theory to Topology Optimization. Laser Photonics Rev. 2022, 16, 202200265. [Google Scholar] [CrossRef]
- Chen, H.-T.; Taylor, A.J.; Yu, N. A review of metasurfaces: Physics and applications. Rep. Prog. Phys. 2016, 79, 076401. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Zhou, C.; Yuan, S.; Qiu, X.; Zhu, L.; Wang, Y.; Xia, J. Multiple Fano resonances in symmetry-breaking silicon metasurface for manipulating light emission. ACS Photonics 2018, 5, 4074–4080. [Google Scholar] [CrossRef]
- Tian, J.; Li, Q.; Belov, P.A.; Sinha, R.K.; Qian, W.; Qiu, M. High-Q All-Dielectric Metasurface: Super and Suppressed Optical Absorption. ACS Photonics 2020, 7, 1436. [Google Scholar] [CrossRef]
- Piper, J.R.; Fan, S. Total absorption in a graphene monolayer in the optical regime by critical coupling with a photonic crystal guided resonance. ACS Photonics 2014, 1, 347–353. [Google Scholar] [CrossRef]
- Luo, X.; Liu, Z.; Wang, L.; Liu, J.; Lin, Q. Tunable ultra-narrowband and wide-angle graphene-based perfect absorber in the optical communication region. Appl. Phys. Express 2018, 11, 105102. [Google Scholar] [CrossRef]
- Liu, G.D.; Zhai, X.; Xia, S.X.; Lin, Q.; Zhao, C.J.; Wang, L.L. Toroidal resonance based optical modulator employing hybrid graphene-dielectric metasurface. Opt. Express 2017, 25, 26045–26054. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, F.; Shen, N.H.; Fu, Q.; Wei, Z.; Li, H.; Soukoulis, C.M. Achieving a high-Q response in metamaterials by manipulating the toroidal excitations. Phys. Rev. A 2018, 97, 033816. [Google Scholar] [CrossRef] [Green Version]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef] [Green Version]
- Rybin, M.V.; Koshelev, K.L.; Sadrieva, Z.F.; Samusev, K.B.; Bogdanov, A.A.; Limonov, M.F.; Kivshar, Y.S. High-Q supercavity modes in subwavelength dielectric resonators. Phys. Rev. Lett. 2017, 119, 243901. [Google Scholar] [CrossRef] [Green Version]
- Neumann, J.V.; Wigner, E.P. Uber das Verhalten von Eigenwerten bei Adiabatischen Prozessen. Phys. Z 1929, 30, 467. [Google Scholar]
- Ursell, F. Trapping modes in the theory of surface waves. Math. Proc. Camb. Philos. Soc. 1951, 47, 347–358. [Google Scholar] [CrossRef]
- Parker, R. Resonance effects in wake shedding from parallel plates: Some experimental observations. J. Sound Vib. 1966, 4, 62–72. [Google Scholar] [CrossRef]
- Parker, R. Resonance effects in wake shedding from parallel plates: Calculation of resonant frequencies. J. Sound Vib. 1967, 5, 330–343. [Google Scholar] [CrossRef]
- Marinica, D.C.; Borisov, A.G.; Shabanov, S.V. Bound States in the Continuum in Photonics. Phys. Rev. Lett. 2008, 100, 183902. [Google Scholar] [CrossRef]
- Gomis-Bresco, J.; Artigas, D.; Torner, L. Anisotropy-induced photonic bound states in the continuum. Nat. Photonics 2017, 11, 232–236. [Google Scholar] [CrossRef]
- Sadrieva, Z.F.; Sinev, I.S.; Koshelev, K.L.; Samusev, A.; Iorsh, I.V.; Takayama, O.; Malureanu, R.; Bogdanov, A.A.; Lavrinenko, A.V. Transition from Optical Bound States in the Continuum to Leaky Resonances: Role of Substrate and Roughness. ACS Photonics 2017, 4, 723–727. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Lu, L.; Stone, A.D.; Soljačić, M. Topological Nature of Optical Bound States in the Continuum. Phys. Rev. Lett. 2014, 113, 257401. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, C.; Hugonin, J.-P.; Sauvan, C. Fano resonances in photonic crystal slabs near optical bound states in the continuum. Phys. Rev. B 2016, 94, 155303. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Tong, Y.; Tsang, H.K.; Sun, X. High-dimensional communication on etchless lithium niobate platform with photonic bound states in the continuum. Nat. Commun. 2020, 11, 2602. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Liu, W.; Zhao, M.; Wang, J.; Zhang, Y.; Chen, A.; Zi, J. Generating optical vortex beams by momentum-space polarization vortices centred at bound states in the continuum. Nat. Photonics 2020, 14, 623–628. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, Y.; Zhang, X.; Tang, H.; Song, Q.; Han, J.; Xiao, S. Highly controllable etchless perovskite microlasers based on bound states in the continuum. ACS Nano 2021, 15, 7386–7391. [Google Scholar] [CrossRef]
- Doskolovich, L.L.; Bezus, E.A.; Bykov, D.A. Integrated flat-top reflection filters operating near bound states in the continuum. Photonics Res. 2019, 7, 1314–1322. [Google Scholar] [CrossRef] [Green Version]
- Ndao, A.; Hsu, L.; Cai, W.; Ha, J.; Park, J.; Contractor, R.; Lo, Y.; Kanté, B. Differentiating and quantifying exosome secretion from a single cell using quasi-bound states in the continuum. Nanophotonics 2020, 9, 1081–1086. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Guo, G.; Feng, T.; Xu, Y.; Miroshnichenko, A.E. Toroidal dipole bound states in the continuum. Phys. Rev. B 2018, 98, 161112. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [Green Version]
- Ju, L.; Geng, B.; Horng, J.; Girit, Ç.; Martin, M.; Hao, Z.; Bechtel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R.; et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630–634. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, Z.; Yan, S.; Ye, L.; Zhu, J. Ultraviolet absorption band engineering of graphene by integrated plasmonic structures. Opt. Mater. Express 2018, 8, 3295–3306. [Google Scholar] [CrossRef]
- Cai, Y.; Guo, Y.; Zhou, Y.; Wang, Y.; Zhu, J.; Chen, C. Ultracompact and chipless terahertz identification tags using multi-resonant metasurface based on graphene. J. Phys. D Appl. Phys. 2019, 53, 015105. [Google Scholar] [CrossRef]
- Zeng, T.-Y.; Liu, G.-D.; Wang, L.-L.; Lin, Q. Light-matter interactions enhanced by quasi-bound states in the continuum in a graphene-dielectric metasurface. Opt. Express 2021, 29, 40177. [Google Scholar] [CrossRef]
- Luo, X.; Cheng, Z.-Q.; Zhai, X.; Liu, Z.-M.; Li, S.-Q.; Liu, J.-P.; Wang, L.-L.; Lin, Q.; Zhou, Y.-H. A Tunable Dual-Band and Polarization-Insensitive Coherent Perfect Absorber Based on Double-Layers Graphene Hybrid Waveguide. Nanoscale Res. Lett. 2019, 14, 337. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Zhou, Y.; Cai, Y.; Cheng, Z.; Liu, Z.; Wan, W. A review of perfect absorbers based on the two dimensional materials in the visible and near-infrared regimes. J. Phys. D Appl. Phys. 2021, 55, 093002. [Google Scholar] [CrossRef]
- Luo, X.; Cheng, Z.-Q.; Liu, Z.; Xu, L.; Zhai, X.; Wan, W.; Zhou, Y.-H. Dual-band perfect absorber based on a graphene/hexagonal boron nitride van der Waals hybrid structure. J. Phys. D Appl. Phys. 2021, 54, 375303. [Google Scholar] [CrossRef]
- Xia, S.-X.; Zhai, X.; Wang, L.-L.; Sun, B.; Liu, J.-Q.; Wen, S.-C. Dynamically tunable plasmonically induced transparency in sinusoidally curved and planar graphene layers. Opt. Express 2016, 24, 17886–17899. [Google Scholar] [CrossRef]
- Luo, X.; Zhai, X.; Wang, L.; Lin, Q. Narrow-Band Plasmonic Filter Based on Graphene Waveguide with Asymmetrical Structure. Plasmonics 2015, 10, 1427–1431. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Jiang, X.; Yan, X.; Cheng, L.; Wang, B.; Xu, C. Strong interaction between graphene layer and Fano resonance in terahertz metamaterials. J. Phys. D Appl. Phys. 2017, 50, 195101. [Google Scholar] [CrossRef] [Green Version]
- Bao, Q.; Loh, K.P. Graphene Photonics, Plasmonics, and Broadband Optoelectronic Devices. ACS Nano 2012, 6, 3677–3694. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Huang, B.; Mao, X.; Zhang, Z.; Zhang, Z.; Geng, Z.; Xue, P.; Chen, H. Frequency conversion with nonlinear graphene photodetectors. Nanoscale 2017, 9, 4082–4089. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.H.; Kholmanov, I.; Alici, K.B.; Purtseladze, D.; Arju, N.; Tatar, K.; Fozdar, D.Y.; Suk, J.W.; Hao, Y.; Khanikaev, A.B.; et al. Inductive Tuning of Fano-Resonant Metasurfaces Using Plasmonic Response of Graphene in the Mid-Infrared. Nano Lett. 2013, 13, 1111–1117. [Google Scholar] [CrossRef] [PubMed]
- Shangguan, Q.; Chen, Z.; Yang, H.; Cheng, S.; Yang, W.; Yi, Z.; Wu, X.; Wang, S.; Yi, Y.; Wu, P. Design of Ultra-Narrow Band Graphene Refractive Index Sensor. Sensors 2022, 22, 6483. [Google Scholar] [CrossRef] [PubMed]
- Horng, J.; Chen, C.-F.; Geng, B.; Girit, C.; Zhang, Y.; Hao, Z.; Bechtel, H.A.; Martin, M.; Zettl, A.; Crommie, M.F. Drude Conductivity of Dirac Fermions in Graphene. Phys. Rev. B 2010, 86, 165113. [Google Scholar] [CrossRef]
- Suk, J.W.; Kitt, A.; Magnuson, C.W.; Hao, Y.; Ahmed, S.; An, J.; Swan, A.K.; Goldberg, B.B.; Ruoff, R.S. Transfer of CVD-Grown Monolayer Graphene onto Arbitrary Substrates. ACS Nano 2011, 5, 6916–6924. [Google Scholar] [CrossRef]
- Fan, S.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. JOSA A 2003, 20, 569–572. [Google Scholar] [CrossRef] [Green Version]
- Vakil, A.; Engheta, N. Transformation Optics Using Graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef] [Green Version]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science Business Media: New York, NY, USA, 2007. [Google Scholar]
- Argyropoulos, C. Enhanced transmission modulation based on dielectric metasurfaces loaded with graphene. Opt. Express 2015, 23, 23787–23797. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Shu, J.; Qiu, C.; Xu, Q. Excitation of Plasmonic Waves in Graphene by Guided-Mode Resonances. ACS Nano 2012, 6, 7806–7813. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Yan, X.; Li, Z.; Xu, C. Active modulation of electromagnetically induced transparency analogue in terahertz hybrid metal-graphene metamaterials. Carbon 2018, 126, 271–278. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W. Study of the interaction between graphene and planar terahertz metamaterial with toroidal dipolar resonance. Opt. Lett. 2017, 42, 2034–2037. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Cheng, H.; Luo, X.; Cheng, Z.; Zhai, X. A High Quality-Factor Optical Modulator with Hybrid Graphene-Dielectric Metasurface Based on the Quasi-Bound States in the Continuum. Micromachines 2022, 13, 1945. https://doi.org/10.3390/mi13111945
Li C, Cheng H, Luo X, Cheng Z, Zhai X. A High Quality-Factor Optical Modulator with Hybrid Graphene-Dielectric Metasurface Based on the Quasi-Bound States in the Continuum. Micromachines. 2022; 13(11):1945. https://doi.org/10.3390/mi13111945
Chicago/Turabian StyleLi, Chaolong, Hongbo Cheng, Xin Luo, Ziqiang Cheng, and Xiang Zhai. 2022. "A High Quality-Factor Optical Modulator with Hybrid Graphene-Dielectric Metasurface Based on the Quasi-Bound States in the Continuum" Micromachines 13, no. 11: 1945. https://doi.org/10.3390/mi13111945
APA StyleLi, C., Cheng, H., Luo, X., Cheng, Z., & Zhai, X. (2022). A High Quality-Factor Optical Modulator with Hybrid Graphene-Dielectric Metasurface Based on the Quasi-Bound States in the Continuum. Micromachines, 13(11), 1945. https://doi.org/10.3390/mi13111945




