A Study on the Resolution and Depth of Focus of ArF Immersion Photolithography
Abstract
1. Introduction
2. Materials and Methods
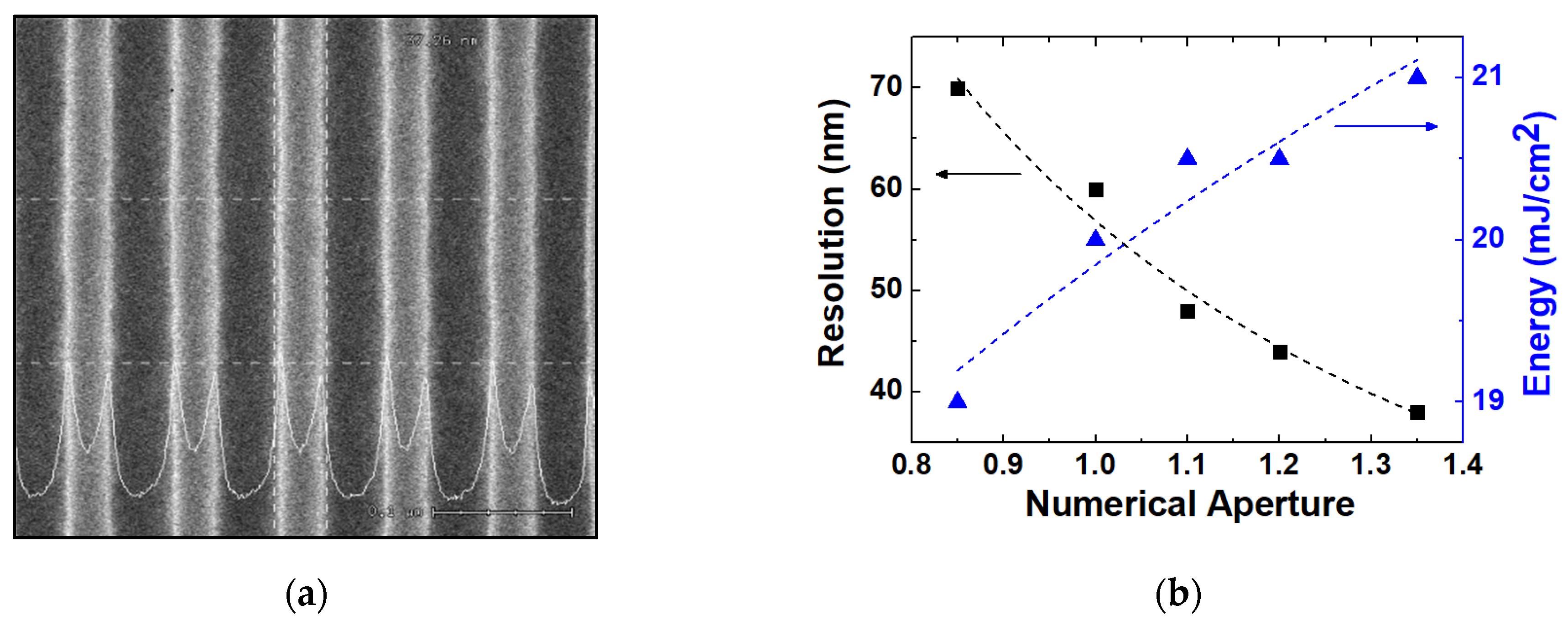
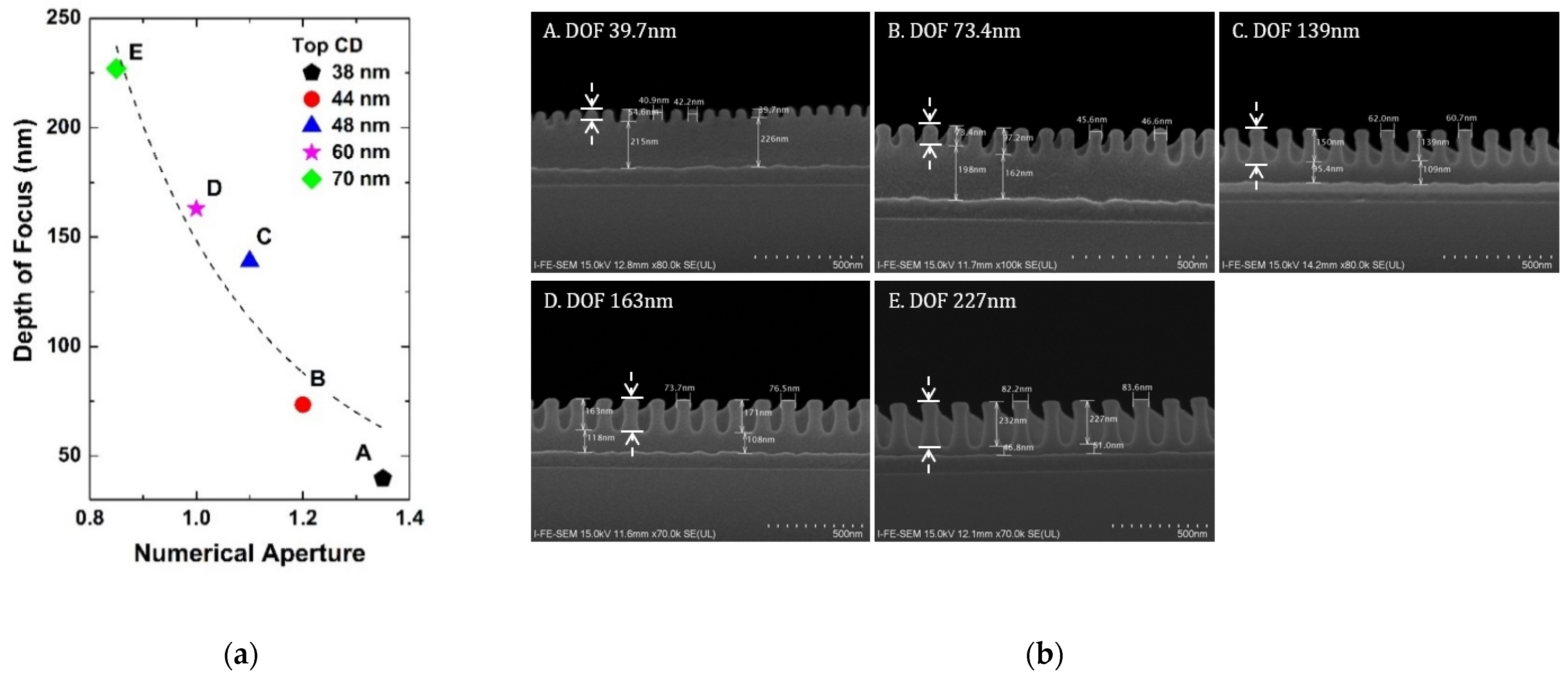
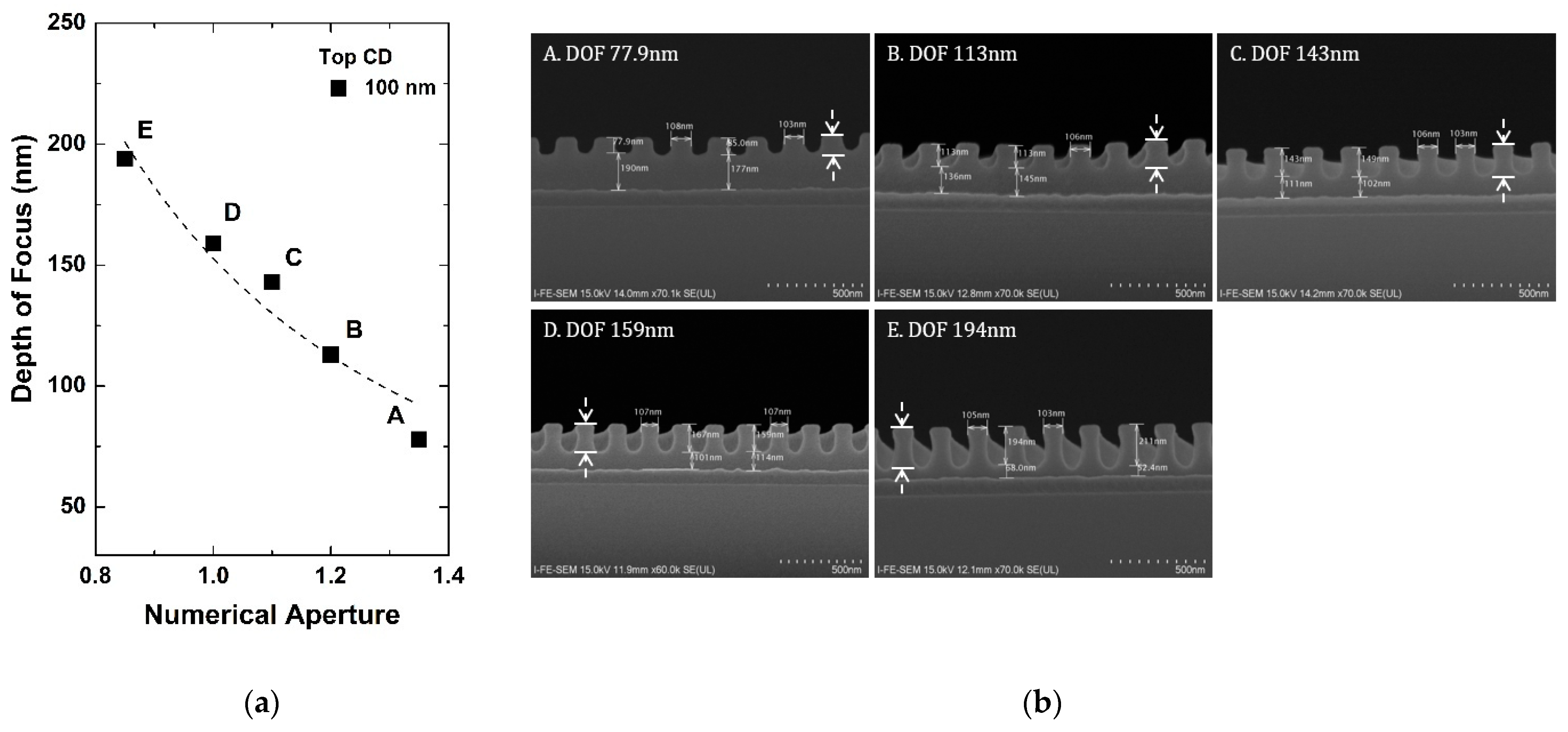
2.1. Resolution and Depth of Focus according to NA
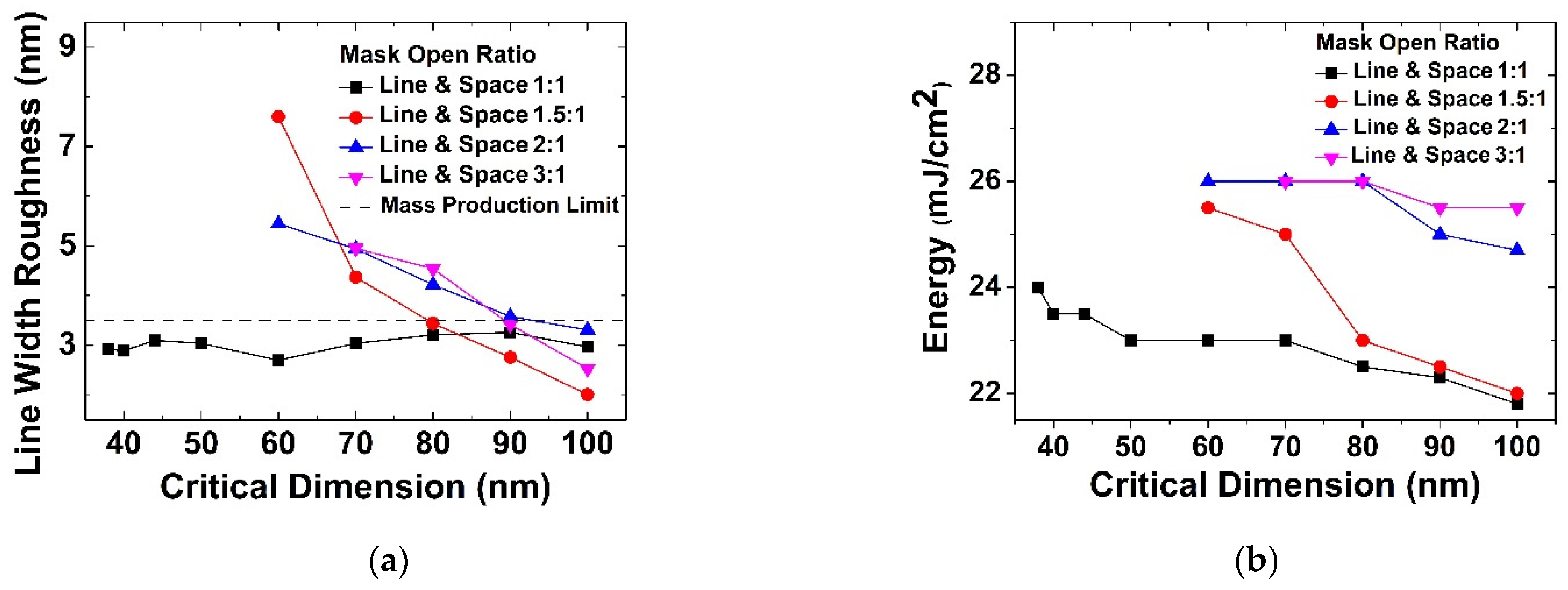
2.2. Resolution according to Mask Open Area Ratio
3. Results and Discussion
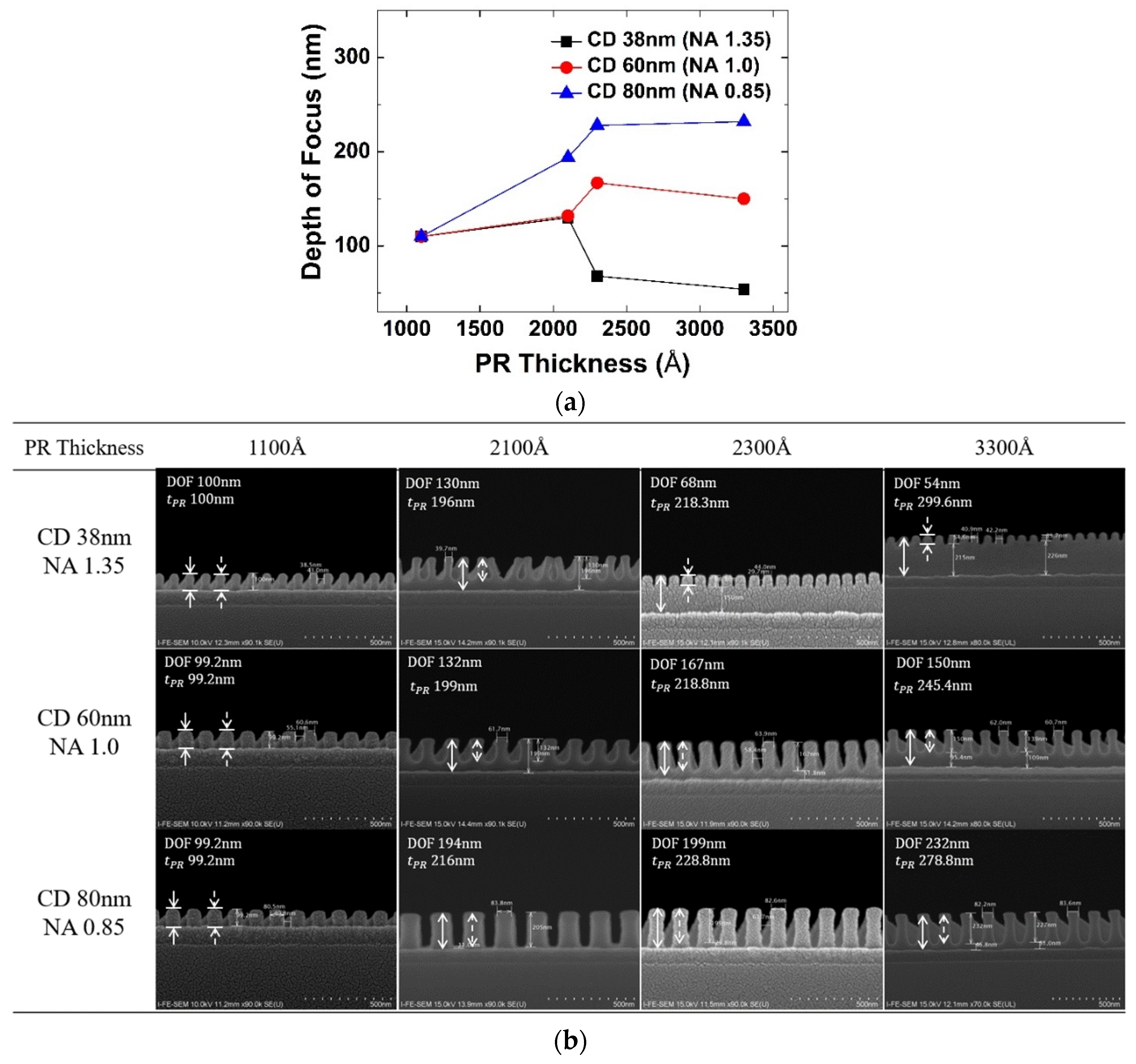
Photoresist Thickness and Depth of Focus
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pirati, A.; van Schoot, J.; Troost, K.; van Ballegoij, R.; Krabbendam, P.; Stoeldraijer, J.; Loopstra, E.; Benschop, J.; Finders, J.; Meilin, H.G.; et al. The future of EUV lithography: Enabling Moore’s Law in the next decade. In Extreme Ultraviolet (EUV) Lithography VIII; SPIE: Bellingham, DC, USA, 2017; pp. 57–72. [Google Scholar]
- Smith, B.W.; Kang, H.; Bourov, A.; Cropanese, F.; Fan, Y. Water immersion optical lithography for the 45-nm node. In Optical Microlithography XVI; SPIE: Bellingham, DC, USA, 2003; pp. 679–689. [Google Scholar] [CrossRef]
- Wu, Q.; Li, Y.; Zhao, Y. The Evolution of photolithography technology, process standards and future outlook. In Proceedings of the 2020 IEEE 15th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Kunming, China, 3–6 November 2020. [Google Scholar]
- Brunner, T.A. Impact of lens aberrations on optical lithography. IBM J. Res. Dev. 1997, 41, 57–67. [Google Scholar] [CrossRef]
- Switkes, M.; Rothschild, M. Immersion Lithography at 157 nm. J. Vacuum Sci. Technol. B Microelectron. Nanometer Struct. Proc. Meas. Phenomena 2001, 19, 2353–2356. [Google Scholar] [CrossRef]
- Lin, B.J. Semiconductor foundry, lithography, and partners. In Emerging Lithographic Technologies VI; SPIE: Bellingham, DC, USA, 2002; Volume 4688. [Google Scholar]
- Sato, T.; Endo, A.; Mimotogi, A.; Mimotogi, S.; Sato, K.; Tanaka, S. Impact of polarization on an attenuated phase shift mask with ArF hyper-numerical aperture lithography. J. Micro/Nanolithography MEMS MOEMS 2006, 5, 043001. [Google Scholar] [CrossRef]
- Sugawara, M.; Chiba, A.; Nishiyama, I. Effect of incident angle of off-axis illumination on pattern printability in extreme ultraviolet lithography. J. Vac. Sci. Technol. B 2003, 21, 2701–2705. [Google Scholar] [CrossRef]
- Kazanskiy, N.; Skidanov, R. Technological line for creation and research of diffractive optical elements. In Optical Technologies for Telecommunications 2018; SPIE: Bellingham, DC, USA, 2019; pp. 237–247. [Google Scholar]
- Kanga, W.E.; Tanakab, H.; Kimurab, K.; Padmanabana, M.; Funatoa, S.; Kinoshitaa, Y.; Kudoa, T.; Nozakia, Y.; Pawlowskia, G. Bottom Anti-Reflective Coatings for DUV Lithography. J. Photopolym. Sci. Technol. 1997, 10, 3. [Google Scholar] [CrossRef]
- Owa, S.; Nagasaka, H. Immersion lithography: Its potential performance and issues. In Optical Microlithography XVI; SPIE: Bellingham, DC, USA, 2003; pp. 724–733. [Google Scholar] [CrossRef]
- Brun, J.L. The k3 coefficient in nonparaxial λ/NA scaling equations for resolution, depth of focus, and immersion lithography. J. Micro/Nanolithography MEMS MOEMS 2002, 1, 7–12. [Google Scholar]
- Smith, B.W.; Bourov, A.; Fan, Y.; Zavyalova, L.V.; Lafferty, N.V.; Cropanese, F.C. Approaching the numerical aperture of water immersion lithography at 193-nm. In Optical Microlithography XVII; SPIE: Bellingham, DC, USA, 2004; Volume 5377, pp. 273–284. [Google Scholar]
- Kim, B.; Suh, S.S.; Kim, B.; Woo, S.; Cho, H.; Tolani, V.; Dai, G.; Irby, D.; Wang, K.; Xiao, G.; et al. Trade-off between inverse lithography mask complexity and lithographic performance. In Photomask and Next-Generation Lithography Mask Technology XVI; SPIE: Bellingham, DC, USA, 2009; pp. 458–468. [Google Scholar]
- Azamouche, L.; Pargon, E.; Menguelti, K.; Fouchier, M.; Fuard, D.; Gouraud, P.; Verove, C.; Joubert, O. Unbiased line width roughtness measurements with critical dimension scanning electron microscopy and critical dimension atomic force microscopy. J. Appl. Phys. 2012, 111, 084318. [Google Scholar] [CrossRef]
- Kawata, H.; James, M.C.; Yen, A.; Smith, H.I. Optical projection lithography using lenses with numerical apertures greater than unity. Microelectron. Eng. 1989, 9, 31–36. [Google Scholar] [CrossRef]
- Burn, J.L. Depth of focus in multilayered media—A long-neglected phenomenon aroused by immersion lithography. J. Microlitho. 2003, 3, 21–27. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Kim, C.-H.; Lee, G.-W. A Study on the Resolution and Depth of Focus of ArF Immersion Photolithography. Micromachines 2022, 13, 1971. https://doi.org/10.3390/mi13111971
Song J, Kim C-H, Lee G-W. A Study on the Resolution and Depth of Focus of ArF Immersion Photolithography. Micromachines. 2022; 13(11):1971. https://doi.org/10.3390/mi13111971
Chicago/Turabian StyleSong, Jungchul, Chae-Hwan Kim, and Ga-Won Lee. 2022. "A Study on the Resolution and Depth of Focus of ArF Immersion Photolithography" Micromachines 13, no. 11: 1971. https://doi.org/10.3390/mi13111971
APA StyleSong, J., Kim, C.-H., & Lee, G.-W. (2022). A Study on the Resolution and Depth of Focus of ArF Immersion Photolithography. Micromachines, 13(11), 1971. https://doi.org/10.3390/mi13111971







