Next Article in Journal
Towards Transient Electronics through Heat Triggered Shattering of Off-the-Shelf Electronic Chips
Previous Article in Journal
Resonant Raman Scattering in Boron-Implanted GaN
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Micromachines
Volume 13
Issue 2
10.3390/mi13020241
micromachines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Research Progress of Graphene Nano-Electromechanical Resonant Sensors—A Review

by
Shang-Chun Fan
1,2,*,
Yang Lu
1,
Peng-Cheng Zhao
1,
Fu-Tao Shi
1,
Zhan-She Guo
1,* and
Wei-Wei Xing
1
1
School of Instrumentation Science and Opto-Electronics Engineering, Beihang University, Beijing 100191, China
2
Key Laboratory of Quantum Sensing Technology, Ministry of Industry and Information Technology, Beijing 100191, China
*
Authors to whom correspondence should be addressed.
Micromachines 2022, 13(2), 241; https://doi.org/10.3390/mi13020241
Submission received: 14 January 2022 / Revised: 24 January 2022 / Accepted: 26 January 2022 / Published: 31 January 2022
Browse Figures
Versions Notes

Abstract

:
Graphene nano-electromechanical resonant sensors have wide application in areas such as seawater desalination, new energy, biotechnology, and aerospace due to their small size, light weight, and high sensitivity and resolution. This review first introduces the physical and chemical properties of graphene and the research progress of four preparation processes of graphene. Next, the principle prototype of graphene resonators is analyzed, and three main methods for analyzing the vibration characteristics of a graphene resonant sheet are described: molecular structural mechanics, non-local elastic theory and molecular dynamics. Then, this paper reviews research on graphene resonator preparation, discussing the working mechanism and research status of the development of graphene resonant mass sensors, pressure sensors and inertial sensors. Finally, the difficulties in developing graphene nano-electromechanical resonant sensors are outlined and the future trend of these sensors is described.

1. Introduction

As the core device in measurements, silicon micro-resonant sensors play an important role in atmospheric parameter measurement system, aerospace ground test system, industrial automation production, consumer electronic products, etc. [1,2,3,4,5]. These sensors are featured by a resonant state of sensitive elements modulated by measurement, and by direct output of frequency signals to realize stable and repeatable measurements [6,7,8,9,10,11]. Limited by the properties of silicon, the size of traditional silicon microstructure sensors cannot be further reduced; otherwise, material failure will be caused. Therefore, it is difficult for these sensors to accurately measure weak force changes for space exploration, biomedical measurement, and ultra-micro-fine processing. This problem can be addressed by the birth of new materials, which has facilitated sensor development at a nanometer level. An outstanding new material is graphene with excellent structural and electromechanical properties. Nowadays, newly developed resonators have used graphene as sensor sensitive materials to realize physical quantity detection.
In 2004, Konstantin Novoselov and Andre Geim of Manchester University used mechanical exfoliation to exfoliate a single-layer graphene sheet (SLGS) from graphite [12], triggering a wave of research on graphene materials and their applications. As shown in Figure 1, graphene is a two-dimensional honeycomb crystal, composed only of carbon atoms [13]. Due to this unique crystal structure, graphene has excellent electromechanical and mechanical properties. Research has shown that at present an SLGS is the thinnest material with a thickness of only 0.335 nm [14]. Its Young’s modulus is up to 1 TPa, and its breaking strength is about 130 GPa [15], 100 times more than that of stainless steel and far superior to the overload capacity of silicon, carbon nanotubes and other materials [16]. The density of graphene is about 2200 kg/m3, which is lower than that of single crystal silicon. When graphene has a size of micron, its fundamental frequency can reach megahertz [17]. In recent years, scholars have carried out in-depth theoretical and experimental research on the mechanical, electrical [18,19,20,21], optical [19,22,23,24,25,26], thermal [27] and chemical properties of graphene [28,29], predicting its application potential for high-performance sensors [30,31,32,33,34,35,36,37,38].
Because graphene has excellent crystallinity, the preparation process of single-layer and multi-layer graphene has been rather mature. There are mainly four preparation methods: micromechanical exfoliation [12], SiC epitaxial growth [39,40], chemical reduction [41,42,43], and Chemical Vapor Deposition(CVD). CVD is currently the most effective method for producing large-area graphene sheets with a guaranteed thickness. The graphene sheets produced in batches have the same excellent mechanical and electrical properties as those obtained by micromechanical exfoliation. The preparation process of CVD is compatible with the current integrated circuit process, and has become the mainstream process for preparing graphene devices [16,44,45,46,47,48,49], and the defects still need to be detected [50,51].
The present review focuses on the application of graphene in nano-electromechanical resonators. Herein, the birth of graphene and its physical and chemical properties are introduced, and the principle prototype of graphene resonators is presented. Three theoretical model of graphene sheets: molecular structural mechanics, non-local elastic theory and molecular dynamics. The preparation of graphene resonators is reviewed, followed by the application of graphene resonant mass, pressure and inertial sensors. This paper highlights high-performance graphene resonators, paving the way for future research on graphene nano-electromechanical resonant sensors.

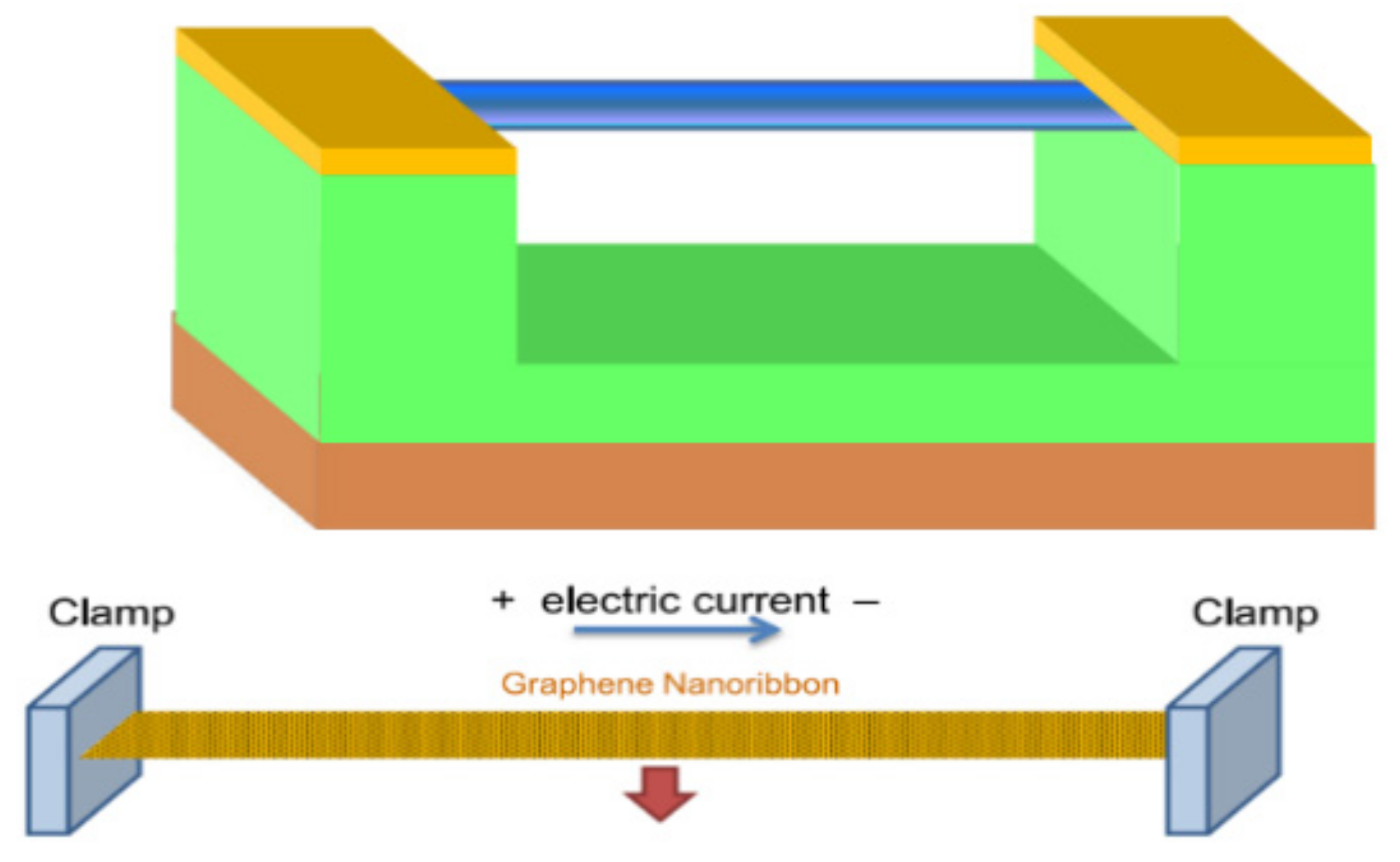
2. Principle Prototype of Graphene Resonator

After the emergence of the SLGS in 2004, the prototype of the nanoelectromechanical resonator is produced by Bunch with single-layer and multi-layer graphene sheets in 2007, providing an important experimental and theoretical basis for designing and examining graphene resonators (Figure 2). The single-layer or multi-layer graphene sheets obtained by mechanical exfoliation method is adsorbed on the etched SiO2 insulating layer with shallow grooves through intermolecular van der Waals force to form a double-clamped beam. Gold electrodes are arranged at both ends of the SiO2 layer, which can vibrate the resonator in MHz through electrical excitation. The frequency of a single-layer graphene resonator is 70.5 MHz, detected by optical interferometry, and the quality factor Q is about 78 in the experiment. This frequency is much larger than the resonant frequency when graphene is natural bending, indicating the presence of internal tension in the resonator. This result may be due to the friction between the graphene and the substrate during device preparation [33].
In Figure 3, with using scanning probe microscope, the mechanical vibration of suspended graphene is detected, and the maximum vibration amplitude of the eigenmode occurred at the free edge rather than at the center of the graphene resonant beam. Finite element simulations show that this phenomenon is caused by the non-uniform stress inside the resonator, meaning that external vibration and corresponding tension must be considered in future experiments and applications. This finding indicates the direction for the future development of graphene tunable frequency resonators [51].
In 2009 a single-layer graphene resonator with electrical signal output is shown in Figure 4 [52]. The variation of the resonant frequency of the graphene resonator with additional mass, external temperature, silicon electrode voltage and other factors are tested. Experiments show that the resonant frequency and Q of graphene resonators increase as the temperature decreases, and that the frequency offset can be used to measure the thermal expansion coefficient of graphene. In addition, the Q value of the graphene resonator increases with the decrease of temperature (about 3000 at 100 K). Below 100 K, the energy dissipation of the resonator slows down, and Q can reach 10,000 at 5 K. Samples of different sizes, electronic properties and degrees of cleanliness all show almost the same results, but the reason for the effect of temperature on energy dissipation is not clear.
The resonator with suspended the graphene sheet on the surface of the SU-8 rubber substrate is shown in Figure 5, using the thermal expansion and contraction effect of SU-8 to change the tension of the graphene sheet [53]. Experiments show that the resonant frequency and Q value of the resonator increase to a certain extent after cooling. On the basis of this idea, a peripherally fixed drum resonator used SU-8 resist is fabricated [54]. Through experiments, it is found that the additional SU-8 resist doesn’t reduce the electrical properties of graphene, but increase its mechanical stiffness and improve the electromechanical response of the resonator.
The above explorations of the structural design, signal detection, and additional factors of the graphene resonator prototype have laid an important foundation for the subsequent application of graphene resonators in the field of sensing technology. In order to examine the resonant characteristics of graphene in depth, researchers have carried out comprehensive research from multiple perspectives such as the simulation and experiment of graphene resonant beams, graphene resonator processing, and applications of graphene resonators.

3. Vibration Characteristics of Graphene Resonant Sheet

Graphene resonators mostly use a single-layer graphene beam as sensitive element. The measured state can be reflected by the change of the output frequency of graphene beams. The thickness of single-layer graphene is only 0.335 nm. The establishment of the ultra-thin material graphene resonant beam model and the choice of analysis method affect the design of the graphene resonator structure and the experimental structural analysis. In this section, we will introduce three main analysis methods of graphene resonant sheets.

3.1. Molecular Structural Mechanics

Single-layer graphene is at the magnitude of microscopic atom and molecule. Molecular structural mechanics equates atoms to individual nodes. Using Cauchy-Born rule, the force between atoms is equivalent to that between nodes, and the vibration potential energy between atoms is converted to the strain energy in mechanics. Structural mechanical equations are established to obtain mechanical parameters, and molecular structural mechanics first needs to determine the model for graphene modeling.
In 2008, Juan et al. approximated a single graphene sheet to an elastic thin plate using the continuous elastic theory. The equilibrium shape and motion equation of the graphene sheet under external forces were derived. The static and dynamic responses of defect-free quadrilateral supported graphene were studied, and the formula for calculating the resonant frequency was deduced [55].
In 2009, Scarpa et al. proposed a truss-type analysis model and studied the in-plane linear elastic properties of graphene monolayers based on the theory of cell material mechanics. This study provids not only information about the mechanical properties of an SLGS, but also the results of the equivalent mechanical deformation mechanism when an SLGS is subjected to uniaxial small strain and pure shear load. Pure shear load exerts a tensile effect on the carbon-carbon bond of an SLGS [56]. In 2011, Georgantzinos et al. proposed a spring-based nonlinear finite element method to study the nonlinear mechanical behavior of graphene nanoribbons. An appropriate nonlinear spring was used to simulate the interaction between each atom, with the force-displacement curves of atoms following the potential energy differential equation of the bond deformation under the corresponding interaction. The results indicate that linear and non-linear mechanical properties depend on the chiral structure of graphene and the size of the graphene sheet [57]. In 2012, Rouhi et al. studied the buckling and vibration characteristics of the SLGS based on a cylindrical beam model. They regarded an SLGS as a spatial frame structure, which retains the discrete nature of graphene sheets, and used three-dimensional elastic beam elements to model the sheets. The critical compressive force and fundamental resonant frequency of the SLGS with different boundary conditions and geometric shapes are obtained and compared. The results show that the compressive buckling force decreases with the increase of the aspect ratio of a graphene sheet. At a low aspect ratio, an increase in aspect ratio results in a significant decrease in critical buckling load [58].
In 2013, Sakhacee et al. used molecular structural mechanics to simulate the vibration behavior of flawless SLGS at a constant temperature. The fundamental frequencies of the zigzag and armchair SLGS with different chiral configurations were obtained under the cantilever and fixed-support boundary conditions by simulating the carbon atoms in graphene lattices with equivalent structure beams and centralized mass units [59]. In 2013, Li et al. conducted a modeling analysis of the SLGS based on atomic potential energy. The graphene membrane, covalent bonds between atoms, and carbon atoms were considered as a frame-like structure, beam members, and nodes, respectively. The FE code of ANSYS commercial software was used to calculate the finite element model composed of beam elements, and the three-dimensional elastic Beam4 element was used for bonding modeling. The energy equivalence concept proposed by Rouhi and Anari was employed to establish the relationship between stiffness of beam elements in structural mechanics and force constants in molecular mechanics. The position of the mass attached to the graphene sheet and the influence of the different constraints of the sheet on the frequency and sensitivity of the resonator were analyzed [60]. In 2017, based on hexagonal network topology and single-electron tunneling model, Guo et al. proposed a single-electronic device network model based on graphene. The model describes the boundary constraints and the connection and coupling relationship matrix based on the graphene sensor. A simple expression of the detection molecule based on the graphene sensor is also introduced, which reduces the computational complexity of the model [61].

3.2. Non-Local Elastic Theory

Non-local elastic theory, an extension of classical continuum theory proposes that the conservation laws of mass, energy, and momentum are valid for an object as a whole, but that arbitrarily small voxels divided by the object may not hold. Additionally, the stress component of an arbitrarily small voxel as a reference point x depends on the strain components at position x, at all the other points of the object [62]. This theory can explain some atomic and molecular scaled phenomena that cannot be explained by continuum theory, such as high-frequency vibration and wave dispersion. Meanwhile, non-local elastic theory plays an important role in calculating of mechanical properties of components using graphene and carbon nanotubes as materials. This method has been widely used for graphene research.
In 2009, Murmu et al. studied the vibration characteristics of monolayer graphene sheets, using non-local elastic theory. The theory takes into account the small size effect introduced in the nanoscale structure. With a small size of an SLGS, it is found that the resonant fundamental frequency of an SLGS is rather sensitive to size changes [63]. In 2011, Wang et al. combined non-local slab model and molecular dynamics to study the vibration characteristics of single-layer and double-layer graphene sheets. The results show that the resonant frequency calculated by the classic graphene elastic model is relatively high, and that the small-scale effect, boundary conditions, and graphene size have a greater impact on the vibration characteristics of single-layer and double-layer graphene. The non-local slab model is important for the vibration analysis of graphene sheets with an edge length less than 8 nm [64].
In 2014, Chang et al. explored the possibility of using peripherally clamped double-layer circular graphene as a nano-mechanical resonator based on non-local elastic theory. The frequency equation of the resonant cavity with attached mass at any position was derived and the influence of the parameters on the vibration frequency and sensitivity of the resonator was studied. The results show that the farther the attachment mass is from the center of the resonator, the higher the frequency and the lower the sensitivity, that the frequency and sensitivity of the double-layer graphene resonator decrease with the increase of the aspect ratio, and that the sensitivity increases with the increase of the local nano-meter parameters [65]. In 2016, Shen et al. used the Galerkin method to derive the vibration frequency of the SLGS based on the non-local Kirchhoff plate theory [66]. In 2018, they used non-local theory to study the feasibility of a double-layer graphene sheet as a mass sensor resonator. These results show that the in-phase mode between single-layer graphene sheets and double-layer graphene sheets is similar. The sensitivity of the mass sensor can be improved by reducing the non-local parameters, making the attached nanoparticles close to the center of the double-layer graphene sheet and reducing the size of the graphene sheet. This finding is helpful for designing graphene mass sensors [67].

3.3. Molecular Dynamics

Molecular dynamics is an analytical method based on classical mechanics. The object of molecular dynamics is atoms, and this model is composed of several atoms. The core idea of molecular dynamics is to calculate the positions and trajectories of all atoms in the simulation system, using statistical analysis to obtain the macroscopic physical quantities of the system. Statistical physics holds that macro physical phenomena are intrinsically related to the movement of microscopic particles, and that the macroscopic quantity is equal to the statistical average of the microscopic quantities. Therefore, by knowing the relevant laws and trajectories of all atoms in the system, macroscopic physical quantities can be obtained.
Molecular dynamics examines atoms, and its model is composed of several atoms. The core idea of molecular dynamics is to calculate the positions and trajectories of all atoms in a simulation system, and obtain the macroscopic physical quantities of the system with statistical analysis. According to statistical physics, macro physical phenomena are intrinsically related to the movement of microscopic particles, and the macroscopic quantity is equal to the statistical average of microscopic quantities. Therefore, knowledge of the relevant laws and trajectories of all atoms in a system can generate macroscopic physical quantities.
With molecular dynamics, Kwon et al. studied a nano-scale graphene-nanoribbon-resonator in 2012, finding that the resonant frequency of graphene is greatly affected by driving force and axial strain, and that the tunable range of resonant frequency decreases exponentially with the increase of axial strain or driving force, as shown in Figure 6 [68,69]. Because most graphene bending deflection is in the elastic region of graphene, the function between resonant frequency and tension can be explained by classical continuum mechanics. The modeling technology used in these studies can be applied to other graphene-based nanoelectromechanical devices.
In 2013, Kang et al. studied suspended graphene nanoribbons resonators using molecular dynamics. The simulation results show that the resonant frequency of graphene nanoribbons depends on the average tension on both sides of the ribbons. The tension comes from two aspects. One is the deformation caused by the electrostatic force generated by the grid voltage; the other is the initial strain caused by the mismatch between the negative thermal expansion coefficient of graphene and the positive thermal expansion coefficient of the substrate when the ambient temperature changes. As the initial strain increases, the tunability and frequency tuning range of the graphene nanoribbons decrease. Therefore, if the axial tension can be changed by pending measurement, the graphene resonator will have the potential for the measurement of physical quantities such as high sensitivity mass, acceleration and pressure [70].
In 2013, Kim et al. used classical molecular dynamics simulation to study the mechanical response of nano-scale graphene resonators [71]. In 2014, Jiang et al. established a two-dimensional slab model, and analyzed the vibration characteristics of a graphene sheet using the finite element method [72]. In the same year, they used the finite element method to study the influence of the pressure difference between the inside and outside of the cavity on the four-side clamped graphene resonator, revealing the effect of the pre-tension and the number of layers on the resonant frequency and tunable range of the graphene resonator [73].
In 2016, Zhang used molecular dynamics simulation to study the vibration characteristics of an SLGS, including its free vibration resonant frequency and mode, and the effect of boundary conditions on the resonant frequency, such as size, initial strain, initial displacement, aspect ratio and chirality. It is found that the fundamental frequency of single graphene nanoribbons can reach GHz. When the size of graphene is small, there is a non-linear relationship between the resonant frequency and the size. With the increase of the size, the resonant frequency changes approximately linearly with the size. The strain change of graphene has greater influence on the fundamental frequency while the width and chirality of graphene have less influence on the change of the resonant fundamental frequency [74,75].

3.4. Summary

At present, there is no perfect theoretical model for the research on the resonant characteristics of graphene. Among the existing models, molecular dynamics is used to simulate the movement of molecules or atoms, and the result is closer to the experimental data. However, this method is usually used for nano-scale structure. For micron-sized structure, calculation is extremely time-consuming and complex, so it is necessary to find new solutions.
For multilayer graphene, macroscopic continuum theory can be used to approximate the model by using thin plate, shell and other continuous media models. Then the mechanical behavior and mechanical properties of graphene such as bending, stretching and vibration can be analyzed by Euler beam theory, Timoshenko plate and shell theory, etc. [76]. The numerical model can also be carried out by using commercial finite element analysis software such as COMSOL/ANSYS. However, the small-scale effect of an SLGS cannot be ignored. The semi-continuum model of graphene resonant beams proposed by Sun et al. can be used under specific conditions, which takes into account the dispersion characteristics of the material particles brought by the direction of graphene thickness entering the nanoscale [77].
The results of the above-mentioned studies show that for small size graphene sheets, the resonant frequency calculated by the classical continuous model is higher than that calculated by molecular dynamics or non-local elastic theory. This is because the small-scale effect of graphene is not taken into account by classical mechanical model. A comparison of molecular dynamics and non-local elastic theory shows that the small-scale effect of graphene depends on the boundary conditions and vibration modes of graphene, and that the small-scale effect has the least influence on the resonant frequency under the four-sided clamping. Thus, graphene nanoribbons with an appropriate size, aspect ratio, and boundary conditions are expected to be used to make high-sensitivity sensors detecting weak pressure, acceleration, and additional nano-mass.

4. Preparation of Graphene Resonators

The research of graphene resonator technology is the key to ensuring stable output of graphene resonators and their quantitative production. In recent years, the preparation process of graphene and graphene resonators has also been extensively studied.
In 2008, Jeremy et al. pioneered the preparation of large-scale and few-layer reduced graphene oxide sheets through oxidation and exfoliation, and the drum-shaped graphene resonator is produced, as shown in Figure 7 [78].
A method is reported to fabricate a large-scale double-clamped suspended epitaxy single-layer graphene resonator by wet chemical etching, providing experimental and theoretical basis for the implementation of graphene resonator array. The size of the double-clamped graphene beam in Figure 8 is 8 μm × (0.5–3.5) μm [39]. To improve the transfer efficiency of large-area single-layer graphene grown on copper foil by CVD, reusable dry transfer and wet transfer technologies have been developed. The graphene can be transferred to substrates covered with shallow depressions, perforated substrates and flat substrates guaranteeing the integrity of the graphene, with fewer cracks and tears [79,80].
In 2010, Paul L. McEuen et al. produced large scale single-layer graphene sheets by CVD, and fabricated suspended graphene resonator array, as shown in Figure 9. The performance of the resonator was tested by electro-excitation and light detection. It was found that the graphene sheet resonator can be equivalent to a sheet with initial tension. The test results also show that the graphene sheets grown by CVD have the same excellent mechanical and electrical properties as the graphene sheets grown by mechanical peeling method, and that a large number of graphene sheets with the same properties can be produced by CVD method in batch [81].
The above-mentioned literature on the method for fabricating graphene resonators seldom discusses how to fabricate high-quality graphene sheets. In recent years, growing single-layer or multi-layer graphene on the surface of metal Cu and Ni foil or SiO2 film has been developed by CVD. The quality of the prepared graphene has been significantly improved, the size of the substrate is not limited, the cost is greatly reduced, and the transfer is easy to achieve [82]. The Institute of Physics of the Chinese Academy of Sciences studied the controllable epitaxy growth of graphene on metal surfaces. The epitaxy preparation process and structure characteristics of graphene on various metal single crystals (Ru, Pt, Ni, Ir, Cu, Pd, etc.) have been studied in detail [83]. Among these metal single crystals, a continuous defect-free SLGS with millimeter size and high quality has been obtained on the surface of Ru (0001) [84]. However, since etching is isotropic, the SiO2 under the metal electrode contact will be removed, resulting in mechanical structural instability in the process of using buffered hydrofluoric acid (BHF) to remove part of the SiO2. The manufacturing process of suspended graphene devices by using LOR etchant effectively solves this problem. The polymer under the graphene layer was effectively removed by using organic solvents irresponsive to inorganic materials such as metals and insulators, and a desirable effect and a stable mechanical structure have been obtained [85].
These preparation and transfer technologies have opened up possibilities for manufacturing various graphene devices with unique configurations and enhanced performance.

5. Application of Graphene Resonators in NEMS

As soon as the graphene resonator was developed, research on its application to sensors has been reported. As early as 2007, Bunch et al. pointed out the great potential of graphene resonators in quality and mechanical quantity detection during the experimental study of graphene nano-electromechanical resonant sensors (NEMS) [33]. In this section, the application of graphene in nano-electromechanical systems is reviewed. The development of three NEMS is introduced: graphene resonant mass sensors, pressure sensors and some inertial sensors.

5.1. Graphene Resonant Mass Sensor

The fundamental vibrational frequency of micron-level single-layer graphene has reached MHz [17], and any additional mass or adsorbed gaseous substance will change the vibration state of an SLGS inspires a new design direction in the detection field that requires sensitive extremely weak mass. Mass sensors based on graphene resonant nanoelectromechanical devices are expected to detect tiny particles such as bacteria (a single mass of about 10–12 g) and viruses (a single mass of about 10–15 g).
In 2008, using molecular structural mechanics, Sakhaee et al. studied the influence of single-point mass and atomic dust on the resonant frequency of an SLGS. The numerical results show that the SLGS is sensitive to adsorption mass, and that the sensitivity of mass detection is as high as 10–21 g. For the same size of the additional mass, the frequency offset of a graphene sheet increases with the increase of the length-width ratio of the sheet [59].
In 2013, Kwon et al. used molecular dynamics simulation method to study the relationship between the fundamental frequency and additional mass of a double-clamped suspended graphene resonator, as shown in Figure 10. The additional mass ∆m deposited on the graphene sheet changes the equivalent mass Meq of the sheet, thereby changing the natural vibration frequency of the graphene sheet. The simulation shows that the double-clamped graphene resonator can achieve a mass resolution of 10–24 g. The frequency-mass response curve of the resonator reveals a strong linear relationship when the additional mass is in the range of 10–21~10–19 g. It should be noted that the molecular dynamics simulation used by Kwon et al. was carried out at ultra-low temperature of 1 K, without considering the effect of thermal diffusion on the vibration characteristics and measurement sensitivity of graphene sheets in the actual working environment [86].
In 2014, Fazelzadeh et al. studied a nano-size mass sensor based on an SLGS in a thermal environment, using rectangular nano-sheets simply supported on four sides as structural model. The non-local slab model and Galerkin numerical calculation method were used to derive the analytical solution of the frequency deviation of the SLGS with respect to variables such as nanoparticles (i.e., additional mass), temperature, and nanoparticle position. Numerical calculation shows that the relative frequency deviation of the SLGS increases with the increase of temperature, the sensitivity also increases. The closer the additional nanoparticles are to the center of the sheet, the greater the relative frequency shift becomes [87]. In 2015, Karličić et al. studied the influence of the in-plane magnetic field on the graphene resonant mass sensor. With non-local Kirchhoff theory, they analyzed the vibration characteristics of the SLGS, finding that with the increase of the external magnetic field strength, the vibration frequency of the sheet increases, and that the sensitivity of mass detection also increases [88].
In 2013, Natsuki et al. studied the feasibility of simply supported double-layer graphene sheets for mass sensing. The frequency-additional mass response of single-layer and double-layer graphene sheets is compared and analyzed by the continuum model, as shown in Figure 11. It can be seen that, in the case of the same size and additional mass, the double-layer graphene sheet has a larger frequency deviation than the SLGS and has a wider logarithmic linear range. Therefore, compared with an SLGS, a double-layer structure can achieve higher measurement sensitivity; that is, it is easier to use the resonant frequency to calculate the size of the additional mass [89]. Other graphene resonant mass sensors have been designed by continuum model simulation. It is found that the graphene sheet has higher mass detection sensitivity in nonlinear vibration state, with the sensitivity affected by the initial in-plane tension of the graphene sheet [90].
In 2019, Xiao studied the relationship between the resonant frequencies of peripherally supported graphene sheets and the adsorption mass by molecular dynamics simulation. The effects of different high-order modes, the size and the position of the adsorption mass were studied, and a mass solution method based on high-order modes was proposed [91]. In 2021, the influence of the local mode of the double-clamped graphene sheet on mass sensitivity was studied. The different responses of the local and the basic modes to adsorption mass, and the effects of the local modes on the quality factor of mechanical vibration were examined. The results show that increasing the aspect ratio and pre-stressing of graphene sheets can effectively improve the quality factor of the graphene resonant mass sensor [92].
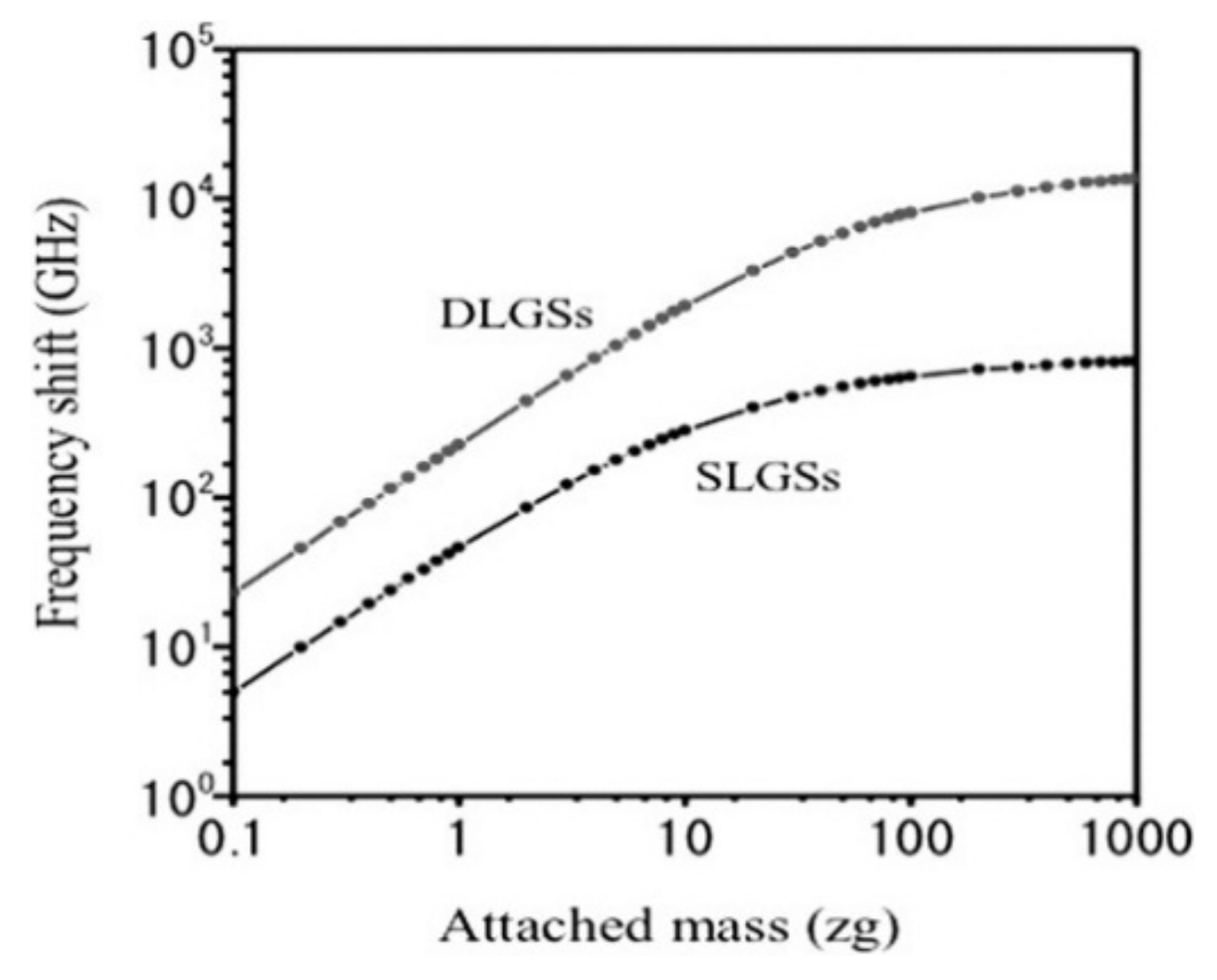
Taken together, single or double-layer graphene resonators have the potential for ultra-high sensitivity of mass detection. However, current research mainly involves theoretical analysis and simulation calculation, lacking necessary experimental data. This will pose difficulties for practical application of the graphene resonant mass sensor.

5.2. Graphene Resonant Pressure Sensor

Pressure sensors are one of the most widely used sensors in industry, and many physical quantities of these sensors are shown by pressure. Graphene is a sensitive element in graphene resonant pressure sensors, and has two main shapes: drum shape and beam shape. When subjected to pressure, graphene changes its resonant frequency, and detecting this change can help measure pressure. The difference of the theoretical model lies in the modal analysis of peripheral fixed support and double-clamped of graphene. Table 1 shows the comparison of the structure, analysis method and index of several graphene resonant pressure sensors.
In the design of drum-shaped graphene resonant pressure sensors, Raj eliminated parasitic capacitance with high-resistance sapphire (resistivity > 1014 Ωm) substrate. Through direct radio frequency drive and detection, the resonant frequency of the multilayer graphene sheet becomes as high as 200 MHz and the mechanical quality factor is close to 500, as shown in Figure 12 [93]. The graphene pressure “micro-drum” sensor designed by Wang was realized by transferring large-area, multilayer graphene on a suspended silicon nitride film perforated by a periodic micro-pore array [94]. This study used the optical interference principle of the Fabry-Perot light cavity to detect the resonant frequency of the graphene sheet, and calculated the measured pressure value in Figure 13 [95].
For graphene resonant pressure sensors with a double-clamped beam structure, the secondary sensitivity method has been mostly used to avoid direct contact between the graphene beam and the medium, mainly in the stage of finite element simulation. The structure designed by Jiang employed the concept of classic silicon micro-resonant pressure sensor compound sensitivity. The square silicon diaphragm was used as the primary sensitive element to directly sense the measured pressure. This pressure acted on the silicon diaphragm to deform the silicon diaphragm, causing the axial strain and stress change of the graphene beam, while the rectangular graphene beam suspended above the cavity acted as a secondary sensitive element to indirectly sense the pressure as shown in Figure 14 [96]. With the single graphene beam resonant pressure sensor in Figure 15 [97], Fan designed a dual-beam graphene resonant pressure sensor [98], which can realize differential detection and reduce common mode interference.
The experiment and simulation of the structure of graphene resonant pressure sensors enable the detection of a series of physical quantities that can be output through changes in force. On this basis, inertial force and Coriolis force have been effectively expressed.

5.3. Graphene Resonant Inertial Sensor

Inertia is the inherent property of all objects. They have inertia whether they are solid, liquid or gas, and whether they are moving or stationary. Inertial measurement is to detect the state of an object by using inertial sensitive elements such as gyroscope and accelerometer to determine the relative position and state of an object. This measurement is used in many fields such as navigation positioning, consumer electronics, and motion carrier control. Inertial sensors are divided into two categories: angular velocity gyroscope and accelerometer. The detection principle of the gyroscope is mainly based on: Coriolis effect and Sagnac effect. For Coriolis effect, Coriolis force is proportional to the input angular rate; for Sagnac effect, phase difference is proportional to the input angular rate. The detection principle of the accelerometer is mainly based on Newton’s second law, in which the magnitude of the acceleration of an object is proportional to the force and inversely proportional to the mass of the object, and the direction of acceleration is the same as that of the force. Graphene resonant inertial sensors can achieve high sensitivity signal output due to the mechanical property of graphene, but the structure design of the sensor itself is the basis for effective, reliable and high-quality signal detection.
After 2007, Bunch et al. examined graphene resonators, through experimental analysis, and proved that graphene has a strong adhesion to the surface of SiO2 substrate through intermolecular van der Waals force. This adhesion is also reflected in the proof mass of graphene to SiO2/Si, which can realize the adhesion of small mass at the bottom of suspended graphene [99,100,101]. Such characteristics make graphene sensitive to pressure changes, further realizing the sensitivity of graphene to inertia.
In 2012, Kang et al. designed a graphene nanoribbon acceleration sensor, as shown in Figure 16. In this design, graphene nanoribbons are suspended on the substrate and form an equivalent parallel plate capacitor with the substrate. The inertial force produced by external acceleration will change the mechanical vibration state of graphene nanoribbons, resulting in changes in the capacitance of parallel plate capacitor and the conductivity of graphene nanoribbons. The measured acceleration can be calculated by measuring the capacitance change or vibration frequency offset through the current oscillation circuit [102]. In 2015, Kang et al. studied the dynamic characteristics of accelerometers based on suspended cross graphene resonators through molecular dynamics simulation. It is found that the deflection motion of the transverse graphene resonator under the action of the driving force is similar to that of the graphene nanoribbon resonator [103].
In 2015, Lee et al. combined graphene drum resonator and SU-8 resist proof mass to create a graphene accelerometer, as shown in Figure 17. In this structure, the gate is generated on the silicon substrate by deep UV lithography and the gate surface is covered with a layer of the SiO2 insulating film. The layer is polished by CMP method and the graphene sheet is transferred on the layer, and then the periphery of the graphene film is fixed on the SU-8 resist substrate to form a drum resonator. On this basis, the cylindrical SU-8 resist proof mass is placed at the center of the graphene sheet. The proof mass senses the acceleration to change the deflection of the graphene sheet and change the conductivity of the graphene sheet. The acceleration value is obtained by measuring the change of conductivity. Although the detection method is non-resonant, the preparation method of drum resonator provides a reference process route for preparing graphene resonant accelerometer [53,104].
In 2017, Jie et al. simulated and analyzed the sensitivity of the graphene resonator to acceleration by using COMSOL Multiphysics finite element software. The sensitive structure is shown in Figure 18. The rectangular graphene sheet with mass block constitutes a double-clamped resonator, and the graphene sheet is suspended above the U-shaped SiO2 insulating layer. Under the action of external acceleration, the additional mass senses the inertial force and causes the deformation of the graphene sheet, resulting in the change of the resonant frequency of the graphene sheet [105]. In 2018, Shi et al. designed the structure of differential graphene resonant accelerometer through COMSOL, and calculated the differential mode in double beam working states. This study improves the acceleration detection sensitivity and measurement accuracy and suppresses conjugate interference [106].
In the design of a graphene resonant acceleration sensor, sensitive mass block is usually introduced as a sensitive element for acceleration detection to change the vibration state of graphene. This introduction enables graphene to generate residual stress during the transfer of graphene to the mass block. In 2020, Fan uses SOI wafer to release the process flow of mass block by sacrificially removing the box layer, combining dry etching with steam HF etching. The weight of sensitive mass block Si is three orders of magnitude greater than that of SU-8 [107], six orders of magnitude greater than that of gold [108], and seven orders of magnitude greater than that of carbon [104]. The weight of suspended mass block increases significantly, which has potential significance for miniaturized NEMS inertial sensor applications [47].
In 2021, Lu et al. designed a graphene resonant gyroscope structure with direct output frequency. The variation law of resonant frequency of graphene with different structure parameters and angular velocities is calculated by finite element simulation. The ultra-high sensitivity of diagonal velocity can realize the sensitivity to extremely weak angular velocity [109].
In summary, the graphene resonator can realize the detection of mass, force and other physical quantities based on the measured modulation law of the vibration characteristics of graphene sheets. The preparation technology of graphene materials and related resonators has achieved great progress and has made corresponding progress in the fields of quantum effects and optoelectronic devices [23,24,25,26,37]. However, the current research on graphene resonant sensing technology is in the stage of theoretical analysis and numerical simulation, and there is still a lack of sufficient literature reports on the overall structural design and related experimental research of the sensor.

6. Conclusions

This paper has reviewed the properties of single-layer graphene, four common graphene material preparation technologies, and the development of graphene resonators from the perspectives of experiments, vibration characteristic analysis and preparation process. This review focuses on the application of graphene resonators in mass, pressure and inertial measurements. Since the research on graphene nano-electromechanical resonant sensors is still in its infancy, two main challenging problems remain to be solved before the fabrication of graphene resonant sensor products:
(1)
Process. It is still difficult to prepare high-quality graphene with a regular shape, but it is easy to introduce initial stress and strain in the process of graphene matrix transfer. This affects the tunability of graphene resonators. In addition, the effect of electrostatic force, temperature and other interference factors should be fully considered.
(2)
Overall structure design. The existing literature mainly studies the effect of sensing on graphene resonators from the perspective of the graphene resonator itself, but the research related to the overall structure modeling and optimization analysis of the sensor is not sufficient. A perfect structure is helpful in improving the measurement sensitivity and measurement range of the sensor, and is thus convenient for the design of device processing technology. Overall structure design of graphene resonant NEMS sensors needs to adequately consider the reasonable processing technology, boundary conditions and actual working conditions, reasonably using the theoretical and simulation analysis methods.
In addition, the graphene resonant sensor works in a resonant state, so the realization of closed-loop self-excited system and weak signal detection are also the key to technical issues. Graphene resonant sensor cannot replace MEMS sensor at the current level of processing and detection
To sum up, graphene plays an important role in the field of nano-electromechanical resonators, and graphene resonators has developed rapidly due to their high quality with preparation optimization and high sensitivity detection. In the future, graphene nano-electromechanical resonant sensors will have broader prospects in such fields as biological detection, energy and chemical industry, and inertial navigation.

Author Contributions

S.-C.F. conceived the idea for the research; Y.L. made an in-depth analysis and classification, wrote the paper; P.-C.Z. and F.-T.S. provided relevant research results; Z.-S.G. and W.-W.X. proof-read the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant number 61773045.

Data Availability Statement

The data is included in the main text.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Burrer, C.; Esteve, J. A novel resonant silicon accelerometer in bulk-micromachining technology. Sens. Actuators A Phys. 1995, 46, 185–189. [Google Scholar] [CrossRef]
  2. Aikele, M.; Bauer, K.; Ficker, W.; Neubauer, F.; Prechtel, U.; Schalk, J.; Seidel, H. Resonant accelerometer with self-test. Sens. Actuators A Phys. 2001, 92, 161–167. [Google Scholar] [CrossRef]
  3. Bauer, K.; Aikele, M.; Ficker, W.; Koppenhagen, K.; Schalk, J. Self-Test for Resonant Structure Sensors Applied to a Tuning Fork Gyro and a Resonant Accelerometer; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
  4. Jeong, C.; Seok, S.; Lee, B.; Kim, H.; Chun, K. A study on resonant frequency and Q factor tunings for MEMS vibratory gyroscopes. J. Micromech. Microeng. 2004, 14, 1530–1536. [Google Scholar] [CrossRef]
  5. Yan, L.; Shangchun, F.; Zhanshe, G.; Jing, L.; Le, C. Study of dynamic characteristics of resonators for MEMS resonant vibratory gyroscopes. Microsyst. Technol. 2012, 18, 639–647. [Google Scholar] [CrossRef]
  6. Eernisse, E.P.; Ward, R.W.; Wiggins, R.B. Survey of quartz bulk resonator sensor technologies. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 323–330. [Google Scholar] [CrossRef]
  7. Brand, O.; Baltes, H. Micromachined Resonant Sensors—An Overview. Sens. Update 1998, 4, 3–51. [Google Scholar] [CrossRef]
  8. Cheng, R.; Zhao, Y.; Li, C.; Tian, B.; Yu, Z.; Liu, K. Design and fabrication of a resonant pressure sensor by combination of DETF quartz resonator and silicon diaphragm. Microsyst. Technol. 2015, 21, 631–640. [Google Scholar] [CrossRef]
  9. Reza, A.; Behraad, B.; Joshua, L.; Frederic, N. Micromachined Resonators: A Review. Micromachines 2016, 7, 160. [Google Scholar]
  10. Zhao, C.; Montaseri, M.H.; Wood, G.; Pu, S.H.; Seshia, A.; Kraft, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sens. Actuators A Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]
  11. Platz, D.; Schmid, U. Vibrational modes in MEMS resonators. J. Micromech. Microeng. 2019, 29, 123001. [Google Scholar] [CrossRef]
  12. Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
  13. Zhang, Y.; Liang, Y.; Zhou, J. Recent Progress of Graphene Doping. Acta Chim. Sin. 2014, 72, 367. [Google Scholar] [CrossRef] [Green Version]
  14. Ni, Z.H.; Wang, H.M.; Kasim, J.; Fan, H.M.; Yu, T.; Wu, Y.H.; Feng, Y.P.; Shen, Z.X. Graphene thickness determination using reflection and contrast spectroscopy. Nano Lett. 2007, 7, 2758–2763. [Google Scholar] [CrossRef]
  15. Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
  16. Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.-H.; Kim, P.; Choi, J.-Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef]
  17. Khan, Z.H.; Kermany, A.R.; Öchsner, A.; Iacopi, F. Mechanical and electromechanical properties of graphene and their potential application in MEMS. J. Phys. D Appl. Phys. 2017, 50, 053003. [Google Scholar] [CrossRef] [Green Version]
  18. Novoselov, K.S.; Jiang, Z.; Zhang, Y.; Morozov, S.V.; Stormer, H.L.; Zeitler, U.; Maan, J.C.; Boebinger, G.S.; Kim, P.; Geim, A.K. Room-Temperature Quantum Hall Effect in Graphene. Science 2007, 315, 1379. [Google Scholar] [CrossRef] [Green Version]
  19. Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [Green Version]
  20. Chen, J.-H.; Jang, C.; Xiao, S.; Ishigami, M.; Fuhrer, M.S. Intrinsic and extrinsic performance limits of graphene devices on SiO2. Nat. Nanotechnol. 2008, 3, 206–209. [Google Scholar] [CrossRef]
  21. Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef] [Green Version]
  22. Zhang, Y.; Tang, T.-T.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 2009, 459, 820–823. [Google Scholar] [CrossRef] [PubMed]
  23. Xia, S.-X.; Zhai, X.; Wang, L.-L.; Wen, S.-C. Polarization-independent plasmonic absorption in stacked anisotropic 2D material nanostructures. Opt. Lett. 2020, 45, 93–96. [Google Scholar] [CrossRef]
  24. Zhang, J.; Wei, X.; Rukhlenko, I.D.; Chen, H.-T.; Zhu, W. Electrically Tunable Metasurface with Independent Frequency and Amplitude Modulations. ACS Photonics 2019, 7, 265–271. [Google Scholar] [CrossRef]
  25. Chen, Z.; Chen, H.; Yin, J.; Zhang, R.; Jile, H.; Xu, D.; Yi, Z.; Zhou, Z.; Cai, S.; Yan, P. Multi-band, tunable, high figure of merit, high sensitivity single-layer patterned graphene—Perfect absorber based on surface plasmon resonance. Sci. Direct Diam. Relat. Mater. 2021, 116, 108393. [Google Scholar] [CrossRef]
  26. Xu, K.-D.; Li, J.; Zhang, A.; Chen, Q. Tunable multi-band terahertz absorber using a single-layer square graphene ring structure with T-shaped graphene strips. Opt. Express 2020, 28, 11482–11492. [Google Scholar] [CrossRef]
  27. Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
  28. Liu, X. Study on the Biocompatibility of Carboxyl Ion Implanted Graphene and Carboxyl Functionalized Graphene. Master’s Thesis, Tianjin Normal University, Tianjin, China, 2015. [Google Scholar]
  29. Bunch, J.S.; Verbridge, S.S.; Alden, J.S.; van der Zande, A.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Impermeable Atomic Membranes from Graphene Sheets. Nano Lett. 2008, 8, 2458–2462. [Google Scholar] [CrossRef] [Green Version]
  30. Ponomarenko, L.A.; Schedin, F.; Katsnelson, M.I.; Yang, R.; Hill, E.W.; Novoselov, K.S.; Geim, A.K. Chaotic Dirac Billiard in Graphene Quantum Dots. Science 2008, 320, 356–358. [Google Scholar] [CrossRef] [Green Version]
  31. Lau, C.N.; Bao, W.; Velasco, J. Properties of suspended graphene membranes. Mater. Today 2012, 15, 238–245. [Google Scholar] [CrossRef]
  32. Castellanos-Gomez, A.; Singh, V.; van der Zant, H.S.J.; Steele, G.A. Mechanics of freely-suspended ultrathin layered materials. Ann. Phys. 2014, 527, 27–44. [Google Scholar] [CrossRef] [Green Version]
  33. Bunch, J.S.; van der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical Resonators from Graphene Sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef] [Green Version]
  34. Zang, X.; Zhou, Q.; Chang, J.; Liu, Y.; Lin, L. Graphene and carbon nanotube (CNT) in MEMS/NEMS applications. Microelectron. Eng. 2015, 132, 192–206. [Google Scholar] [CrossRef]
  35. Chen, C.; Hone, J. Graphene nanoelectromechanical systems. Proc. IEEE 2013, 101, 1766–1779. [Google Scholar] [CrossRef]
  36. Liu, J.; Jalali, M.; Mahshid, S.; Wachsmann-Hogiu, S. Are plasmonic optical biosensors ready for use in point-of-need applications? Analyst 2019, 145, 364–384. [Google Scholar] [CrossRef] [Green Version]
  37. Al Jahdaly, B.; Elsadek, M.; Ahmed, B.; Farahat, M.; Taher, M.; Khalil, A. Outstanding Graphene Quantum Dots from Carbon Source for Biomedical and Corrosion Inhibition Applications: A Review. Sustainability 2021, 13, 2127. [Google Scholar] [CrossRef]
  38. Zheng, X.; Khaoulani, S.; Ktari, N.; Lo, M.; Khalil, A.; Zerrouki, C.; Fourati, N.; Chehimi, M. Towards Clean and Safe Water: A Review on the Emerging Role of Imprinted Polymer-Based Electrochemical Sensors. Sensors 2021, 21, 4300. [Google Scholar] [CrossRef]
  39. Shivaraman, S.; Barton, R.A.; Yu, X.; Alden, J.; Herman, L.; Chandrashekhar, M.; Park, J.; Mceuen, P.L.; Parpia, J.M.; Craighead, H.G. Free-standing epitaxial graphene. Nano Lett. 2009, 9, 3100–3105. [Google Scholar] [CrossRef] [Green Version]
  40. Riedl, C.; Coletti, C.; Iwasaki, T.; Zakharov, A.A.; Starke, U. Quasi-Free-Standing Epitaxial Graphene on SiC Obtained by Hydrogen Intercalation. Phys. Rev. Lett. 2009, 103, 246804. [Google Scholar] [CrossRef] [Green Version]
  41. Luo, D.; Zhang, G.; Liu, J.; Sun, X. Evaluation Criteria for Reduced Graphene Oxide. J. Phys. Chem. C 2011, 115, 11327–11335. [Google Scholar] [CrossRef]
  42. Pei, S.; Cheng, H.M. The reduction of graphene oxide. Carbon 2012, 50, 3210–3228. [Google Scholar] [CrossRef]
  43. Eda, G.; Fanchini, G.; Chhowalla, M. Large-area ultrathin films of reduced graphene oxide as a transparent and flexible electronic material. Nat. Nanotechnol. 2008, 3, 270–274. [Google Scholar] [CrossRef]
  44. Alfonso, R.; Xiaoting, J.; John, H.; Daniel, N.; Hyungbin, S.; Vladimir, B.; Dresselhaus, M.S.; Jing, K. Large area, few-layer graphene films on arbitrary substrates by chemical vapor deposition. Nano Lett. 2009, 9, 30–35. [Google Scholar]
  45. Kong, J.; Cecco, A.R.; Dresselhaus, M.S. Large-Area Single- and Few-Layer Graphene on Arbitrary Substrates. U.S. Patent 8,535,533, 17 September 2013. [Google Scholar]
  46. Hwangbo, Y.; Lee, C.-K.; Kim, S.-M.; Kim, J.-H.; Kim, K.-S.; Jang, B.; Lee, H.-J.; Lee, S.-K.; Kim, S.S.; Ahn, J.-H.; et al. Fracture Characteristics of Monolayer CVD-Graphene. Sci. Rep. 2014, 4, 4439. [Google Scholar] [CrossRef] [Green Version]
  47. Fan, X.; Smith, A.D.; Forsberg, F.; Wagner, S.; Schröder, S.; Akbari, S.S.A.; Fischer, A.C.; Villanueva, L.G.; Östling, M.; Lemme, M.C.; et al. Manufacture and characterization of graphene membranes with suspended silicon proof masses for MEMS and NEMS applications. Microsyst. Nanoeng. 2020, 6, 17. [Google Scholar] [CrossRef] [Green Version]
  48. Lee, G.-H.; Cooper, R.C.; An, S.J.; Lee, S.; van der Zande, A.; Petrone, N.; Hammerberg, A.G.; Lee, C.; Crawford, B.; Oliver, W.; et al. High-Strength Chemical-Vapor–Deposited Graphene and Grain Boundaries. Science 2013, 340, 1073–1076. [Google Scholar] [CrossRef]
  49. Milaninia, K.M.; Baldo, M.A.; Reina, A.; Kong, J. All graphene electromechanical switch fabricated by chemical vapor deposition. Appl. Phys. Lett. 2009, 95, 183105. [Google Scholar] [CrossRef]
  50. Hage, F.S.; Radtke, G.; Kepaptsoglou, D.M.; Lazzeri, M.; Ramasse, Q.M. Single-atom vibrational spectroscopy in the scanning transmission electron microscope. Science 2020, 367, 1124–1127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  51. Garcia-Sanchez, D.; van der Zande, A.M.; Paulo, A.S.; Lassagne, B.; McEuen, P.L.; Bachtold, A. Imaging Mechanical Vibrations in Suspended Graphene Sheets. Nano Lett. 2008, 8, 1399–1403. [Google Scholar] [CrossRef] [Green Version]
  52. Chen, C.; Rosenblatt, S.; Bolotin, K.I.; Kalb, W.; Kim, P.; Kymissis, I.; Stormer, H.L.; Heinz, T.F.; Hone, J. Performance of monolayer graphene nanomechanical resonators with electrical readout. Nat. Nanotechnol. 2009, 4, 861–867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Oshidari, Y.; Hatakeyama, T.; Kometani, R.; Warisawa, S.; Ishihara, S. High Quality Factor Graphene Resonator Fabrication Using Resist Shrinkage-Induced Strain. Appl. Phys. Express 2012, 5, 117201. [Google Scholar] [CrossRef]
  54. Lee, S.; Chen, C.; Deshpande, V.V.; Lee, G.-H.; Lee, I.; Lekas, M.; Gondarenko, A.; Yu, Y.-J.; Shepard, K.L.; Kim, P.; et al. Electrically integrated SU-8 clamped graphene drum resonators for strain engineering. Appl. Phys. Lett. 2013, 102, 153101. [Google Scholar] [CrossRef] [Green Version]
  55. Atalaya, J.; Isacsson, A.; Kinaret, J.M. Continuum Elastic Modeling of Graphene Resonators. Nano Lett. 2008, 8, 4196–4200. [Google Scholar] [CrossRef] [Green Version]
  56. Scarpa, F.; Adhikari, S.; Phani, S. Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology 2009, 20, 065709. [Google Scholar] [CrossRef]
  57. Georgantzinos, S.; Giannopoulos, G.; Katsareas, D.; Kakavas, P.; Anifantis, N. Size-dependent non-linear mechanical properties of graphene nanoribbons. Comput. Mater. Sci. 2011, 50, 2057–2062. [Google Scholar] [CrossRef]
  58. Rouhi, S.; Ansari, R. Atomistic finite element model for axial buckling and vibration analysis of single-layered graphene sheets. Phys. E Low-Dimens. Syst. Nanostruct. 2011, 44, 764–772. [Google Scholar] [CrossRef]
  59. Sakhaee-Pour, A.; Ahmadian, M.; Vafai, A. Applications of single-layered graphene sheets as mass sensors and atomistic dust detectors. Solid State Commun. 2008, 145, 168–172. [Google Scholar] [CrossRef]
  60. Lee, H.-L.; Hsu, J.-C.; Lin, S.-Y.; Chang, W.-J. Sensitivity analysis of single-layer graphene resonators using atomic finite element method. J. Appl. Phys. 2013, 114, 123506. [Google Scholar] [CrossRef]
  61. Wu, Y.; Hui, Y.; Guo, D. Modeling of graphene-based sensor for super sensitivity application in bio-molecular detection. In Proceedings of the 10th IEEE International Conference on Anti-Counterfeiting, Security, and Identification (ASID), Xiamen, China, 23–25 September 2016. [Google Scholar]
  62. Shen, Z.-B.; Tang, H.-L.; Li, D.-K.; Tang, G.-J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
  63. Murmu, T.; Pradhan, S.C. Vibration analysis of nano-single-layered graphene sheets embedded in elastic medium based on nonlocal elasticity theory. J. Appl. Phys. 2009, 105, 064319. [Google Scholar] [CrossRef]
  64. Arash, B.; Wang, Q. Vibration of Single- and Double-Layered Graphene Sheets. J. Nanotechnol. Eng. Med. 2011, 2, 011012. [Google Scholar] [CrossRef]
  65. Chang, W.-J.; Lee, H.-L. Mass detection using a double-layer circular graphene-based nanomechanical resonator. J. Appl. Phys. 2014, 116, 034303. [Google Scholar] [CrossRef]
  66. Jiang, R.W.; Shen, B.Z.; Tang, G.J. Vibration analysis of a single-layered graphene sheet-based mass sensor using the Galerkin strip distributed transfer function method. Acta Mech. 2016, 227, 2899–2910. [Google Scholar] [CrossRef]
  67. Shen, Z.B.; Jiang, R.W.; Zhang, L.; Tang, G.J. Nonlocal Galerkin Strip Transfer Function Method for Vibration of Double-Layered Graphene Mass Sensor. J. Solid Mech. 2018, 31, 14. [Google Scholar] [CrossRef]
  68. Kwon, O.K.; Lee, J.H.; Park, J.; Kim, K.-S.; Kang, J.W. Molecular dynamics simulation study on graphene-nanoribbon-resonators tuned by adjusting axial strain. Curr. Appl. Phys. 2013, 13, 360–365. [Google Scholar] [CrossRef]
  69. Kwon, O.; Lee, K.; Hwang, G.Y.; Kang, H.J. Molecular dynamics modeling and simulations to understand gate-tunable graphene-nanoribbon-resonator. Phys. E Low-Dimens. Syst. Nanostruct. 2012, 45, 194–200. [Google Scholar] [CrossRef]
  70. Kang, J.W.; Kim, H.-W.; Kim, K.-S.; Lee, J.H. Molecular dynamics modeling and simulation of a graphene-based nanoelectromechanical resonator. Curr. Appl. Phys. 2013, 13, 789–794. [Google Scholar] [CrossRef]
  71. Kim, S.Y.; Cho, S.-Y.; Kang, J.W.; Kwon, O.K. Molecular dynamics simulation study on mechanical responses of nanoindented monolayer-graphene-nanoribbon. Phys. E Low-Dimens. Syst. Nanostruct. 2013, 54, 118–124. [Google Scholar] [CrossRef]
  72. Jiang, S.; Shi, S.; Wang, X. Nanomechanics and vibration analysis of graphene sheets via a 2D plate model. J. Phys. D Appl. Phys. 2013, 47, 45104. [Google Scholar] [CrossRef]
  73. Gong, X.; Jiang, S.; Wang, X.; Sheng, L.; Wang, S. Finite element analysis of graphene resonator tuned by pressure difference. In Proceedings of the International Conference on Electronic Packaging Technology, Chengdu, China, 12–15 August 2014. [Google Scholar]
  74. Zhang, C. Study on Resonance Characteristics of Single-Layer Graphene Resonator. Master’s Thesis, Beihang University, Beijing, China, 2016. [Google Scholar]
  75. Xing, W.-W.; Zhang, C.-X.; Fan, S.-C. Progress in graphene resonance properties. J. Inorg. Mater. 2016, 7, 673–680. [Google Scholar]
  76. Park, S.K.; Gao, X.L. Bernoulli-Euler beam model based on a modified couple stress theory. J. Micromech. Microeng. 2006, 16, 2355. [Google Scholar] [CrossRef]
  77. Sun, C.T.; Zhang, H. Size-dependent elastic moduli of platelike nanomaterials. J. Appl. Phys. 2003, 93, 1212–1218. [Google Scholar] [CrossRef]
  78. Robinson, J.T.; Zalalutdinov, M.; Baldwin, J.W.; Snow, E.S.; Wei, Z.; Sheehan, P.; Houston, B.H. Wafer-scale Reduced Graphene Oxide Films for Nanomechanical Devices. Nano Lett. 2008, 8, 3441–3445. [Google Scholar] [CrossRef]
  79. Suk, J.W.; Kitt, A.; Magnuson, C.W.; Hao, Y.; Ahmed, S.; An, J.; Swan, A.K.; Goldberg, B.B.; Ruoff, R.S. Transfer of CVD-Grown Monolayer Graphene onto Arbitrary Substrates. ACS Nano 2011, 5, 6916–6924. [Google Scholar] [CrossRef]
  80. Ying, F.; Chen, K. Dry transfer of chemical-vapor-deposition-grown graphene onto liquid-sensitive surfaces for tunnel junction applications. Nanotechnology 2015, 26, 035302. [Google Scholar]
  81. Van der Zande, A.M.; Barton, R.A.; Alden, J.S.; Ruiz-Vargas, C.S.; Whitney, W.S.; Pham, P.H.Q.; Park, J.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Large-Scale Arrays of Single-Layer Graphene Resonators. Nano Lett. 2010, 10, 4869–4873. [Google Scholar] [CrossRef]
  82. Li, X.; Cai, W.; An, J.; Kim, S.; Nah, J.; Yang, D.; Piner, R.; Velamakanni, A.; Jung, I.; Tutuc, E.; et al. Large-Area Synthesis of High-Quality and Uniform Graphene Films on Copper Foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef] [Green Version]
  83. Gao, M.; Pan, Y.; Huang, L.; Hu, H.; Zhang, L.Z.; Guo, H.M.; Du, S.; Gao, H.-J. Epitaxial growth and structural property of graphene on Pt (111). Appl. Phys. Lett. 2011, 98, 033101. [Google Scholar] [CrossRef]
  84. Pan, Y.; Zhang, H.; Shi, D.; Sun, J.; Du, S.; Liu, F.; Gao, H.J. Highly Ordered, Millimeter-Scale, Continuous, Single-Crystalline Graphene Monolayer Formed on Ru (0001); John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
  85. Tombros, N.; Veligura, A.; Junesch, J.; Berg, J.J.V.D.; Zomer, P.J.; Wojtaszek, M.; Marun, I.J.V.; Jonkman, H.T.; Van Wees, B.J. Large yield production of high mobility freely suspended graphene electronic devices on a polydimethylglutarimide based organic polymer. J. Appl. Phys. 2011, 109, 93702. [Google Scholar] [CrossRef] [Green Version]
  86. Kwon, O.K.; Kim, K.-S.; Park, J.; Kang, J.W. Molecular dynamics modeling and simulations of graphene-nanoribbon-resonator-based nanobalance as yoctogram resolution detector. Comput. Mater. Sci. 2013, 67, 329–333. [Google Scholar] [CrossRef]
  87. Fazelzadeh, S.A.; Ghavanloo, E. Nanoscale mass sensing based on vibration of single-layered graphene sheet in thermal environments. Acta Mech. Sin. 2014, 30, 84–91. [Google Scholar] [CrossRef]
  88. Karličić, D.; Kozić, P.; Adhikari, S.; Cajić, M.; Murmu, T.; Lazarević, M. Nonlocal mass-nanosensor model based on the damped vibration of single-layer graphene sheet influenced by in-plane magnetic field. Int. J. Mech. Sci. 2015, 96, 132–142. [Google Scholar] [CrossRef]
  89. Natsuki, T.; Shi, J.-X.; Ni, Q.-Q. Vibration analysis of nanomechanical mass sensor using double-layered graphene sheets resonators. J. Appl. Phys. 2013, 114, 094307. [Google Scholar] [CrossRef]
  90. Dai, M.D.; Kim, C.-W.; Eom, K. Nonlinear vibration behavior of graphene resonators and their applications in sensitive mass detection. Nanoscale Res. Lett. 2012, 7, 499. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  91. Xiao, X.; Li, S.-C.; Xing, C.; Xing, W.-W. Stress-Insensitive Resonant Graphene Mass Sensing via Frequency Ratio. Sensors 2019, 19, 3027. [Google Scholar] [CrossRef] [Green Version]
  92. Xiao, X.; Fan, S.-C.; Li, C. The Effect of Edge Mode on Mass Sensing for Strained Graphene Resonators. Micromachines 2021, 12, 189. [Google Scholar] [CrossRef]
  93. Patel, R.; Mathew, J.P.; Borah, A.; Deshmukh, M.M. Low tension graphene drums for electromechanical pressure sensing. 2D Mater. 2016, 3, 011003. [Google Scholar] [CrossRef]
  94. Wang, Q.; Hong, W.; Dong, L. Graphene “microdrums” on a freestanding perforated thin membrane for high sensitivity MEMS pressure sensors. Nanoscale 2016, 8, 7663–7671. [Google Scholar] [CrossRef]
  95. Yumei, S. Effect of Pressure Sensing on Resonant Graphene Membrane. Master’s Thesis, Beihang University, Beijing, China, 2017. [Google Scholar]
  96. Jiang, S.; Gong, X.; Guo, X.; Wang, X. Potential application of graphene nanomechanical resonator as pressure sensor. Solid State Commun. 2014, 193, 30–33. [Google Scholar] [CrossRef]
  97. Fan Shangchun, Z.J.; Liming, Z. Study on sensitive structure of graphene resonant pressure sensor. J. Zhengzhou Univ. 2019, 40, 6. [Google Scholar]
  98. Fan, S.; Weiwei, X. A Double Graphene Resonant Beam Pressure Sensor; Beihang University: Beijing, China, 2017. [Google Scholar]
  99. Bunch, J.S.; Dunn, M.L. Adhesion mechanics of graphene membranes. Solid State Commun. 2012, 152, 1359–1364. [Google Scholar] [CrossRef] [Green Version]
  100. Koenig, S.; Boddeti, N.; Dunn, M.; Bunch, J.S. Ultrastrong adhesion of graphene membranes. Nat. Nanotechnol. 2011, 6, 543–546. [Google Scholar] [CrossRef]
  101. Lu, Z.; Dunn, M.L. van der Waals adhesion of graphene membranes. J. Appl. Phys. 2010, 107, 2458. [Google Scholar] [CrossRef]
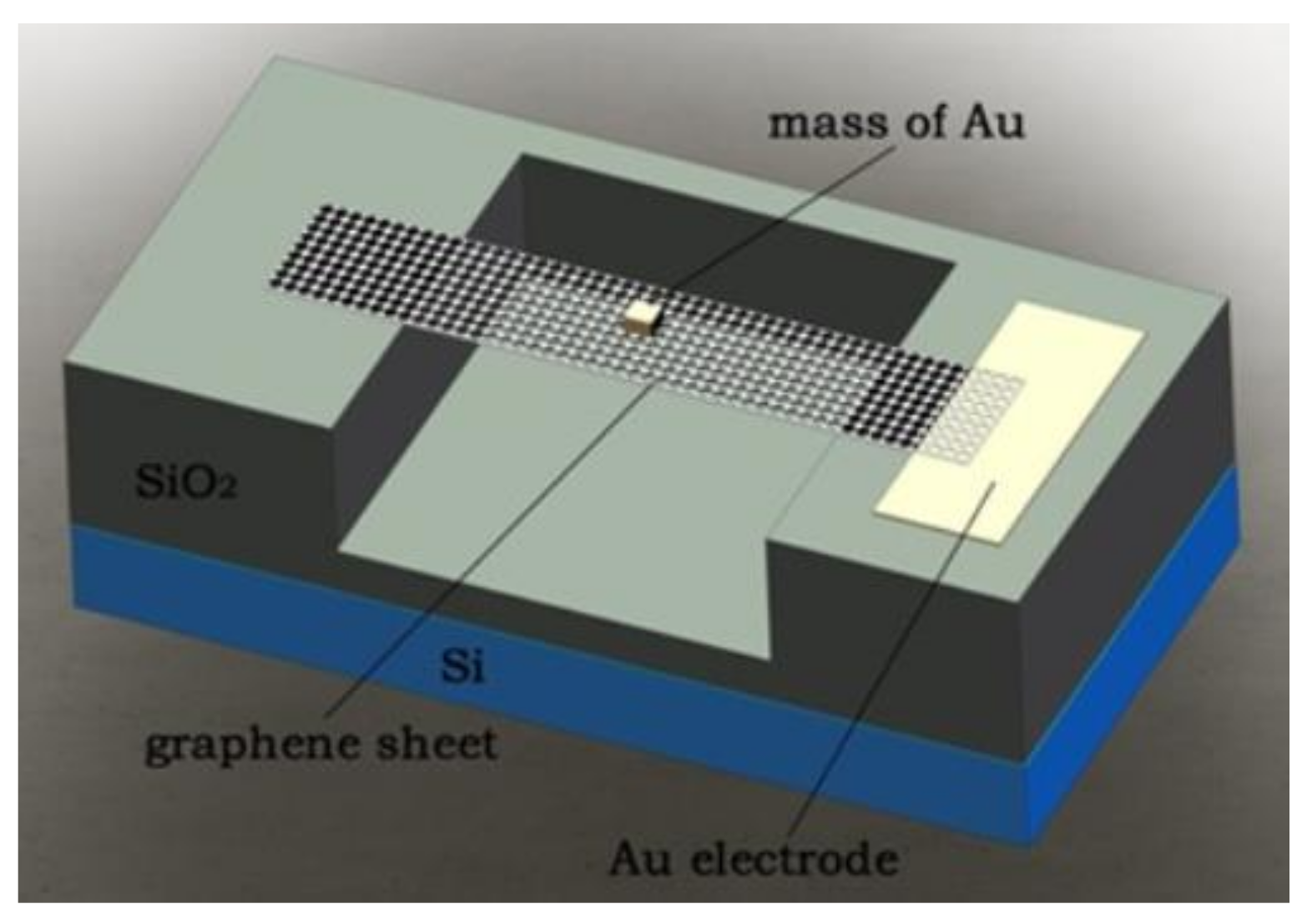
  102. Kang, J.W.; Lee, J.H.; Hwang, H.J.; Kim, K.S. Developing accelerometer based on graphene nanoribbon resonators. Phys. Lett. A 2012, 376, 3248–3255. [Google Scholar] [CrossRef]
  103. Kang, J.W.; Park, J.H.; Lee, G.Y.; Kim, K.S. Molecular Dynamics Simulation on Crossroad-Type Graphene-Resonator Accelerometer. J. Comput. Theor. Nanosci. 2015, 12, 4186–4190. [Google Scholar] [CrossRef]
  104. Hurst, A.M.; Lee, S.; Cha, W.; Hone, J. A graphene accelerometer. In Proceedings of the 28th IEEE International Conference on Micro Electro Mechanical Systems, Estorial, Portugal, 18–22 January 2015. [Google Scholar]
  105. Jie, W.; Hu, F.; Wang, X.; Qin, S. Acceleration sensing based on graphene resonator. In Proceedings of the International Conference on Photonics & Optical Engineering, Kaohsiung, Taiwan, 4–7 April 2017. [Google Scholar]
  106. Shi, F.-T.; Fan, S.-C.; Li, C.; Peng, X.-B. Modeling and Analysis of a Novel Ultrasensitive Differential Resonant Graphene Micro-Accelerometer with Wide Measurement Range. Sensors 2018, 18, 2266. [Google Scholar] [CrossRef] [Green Version]
  107. Matsui, K.; Inaba, A.; Oshidari, Y.; Takei, Y.; Takahashi, H.; Takahata, T.; Kometani, R.; Matsumoto, K.; Shimoyama, I. Mechanical properties of few layer graphene cantilever. In Proceedings of the IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 26–30 January 2014. [Google Scholar]
  108. Blees, M.K.; Barnard, A.W.; Rose, P.A.; Roberts, S.P.; McGill, K.L.; Huang, P.Y.; Ruyack, A.R.; Kevek, J.W.; Kobrin, B.; Muller, D.A.; et al. Graphene kirigami. Nature 2015, 524, 204–207. [Google Scholar] [CrossRef]
  109. Lu, Y.; Guo, Z.-S.; Fan, S.-C. An Ultrahigh-Sensitivity Graphene Resonant Gyroscope. Nanomaterials 2021, 11, 1890. [Google Scholar] [CrossRef]
Micromachines 13 00241 g001 550
Figure 1. Graphene two-dimensional honeycomb structure.
Figure 1. Graphene two-dimensional honeycomb structure.
Micromachines 13 00241 g001
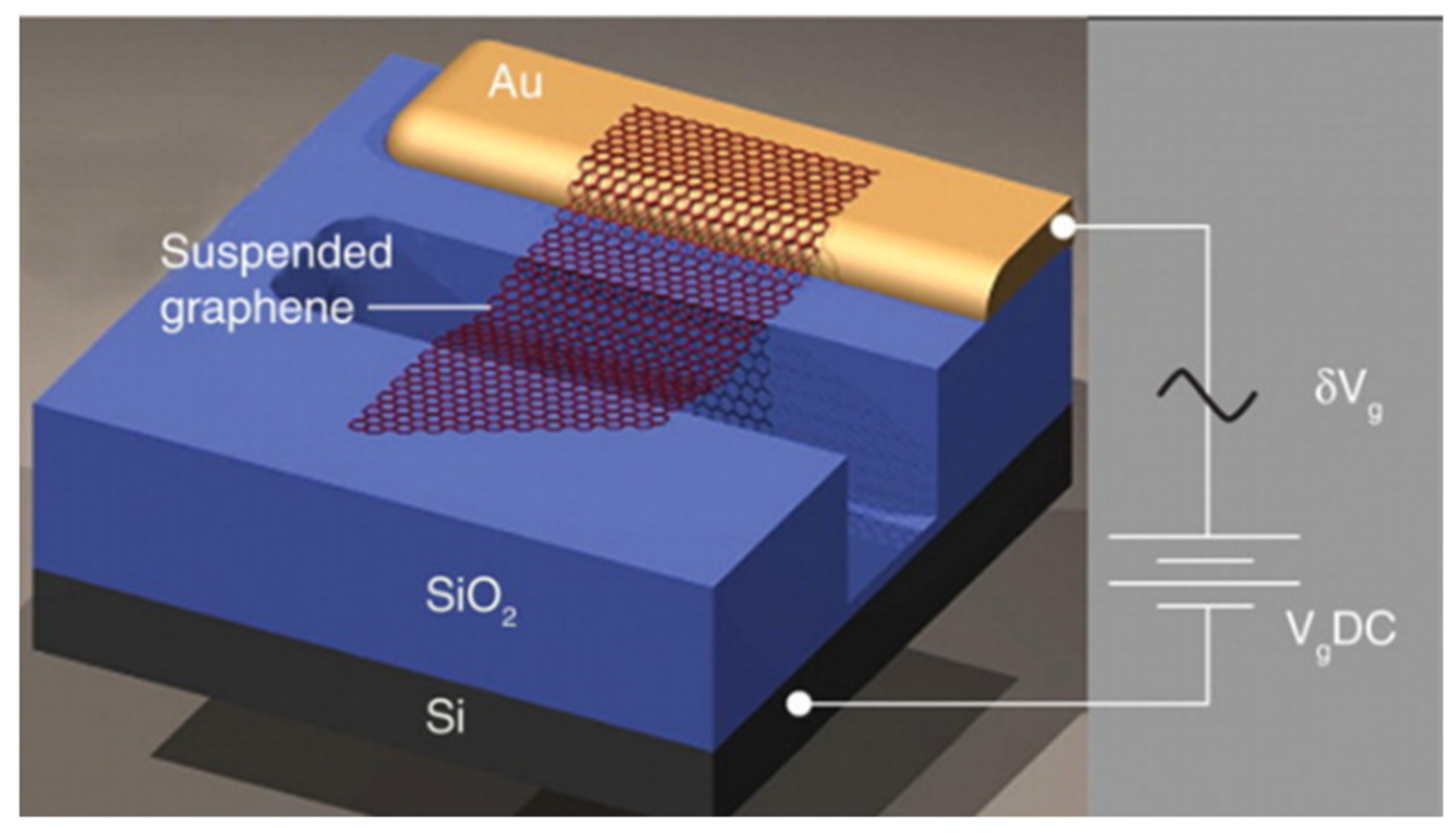
Micromachines 13 00241 g002 550
Figure 2. Prototype of graphene resonator [33].
Figure 2. Prototype of graphene resonator [33].
Micromachines 13 00241 g002
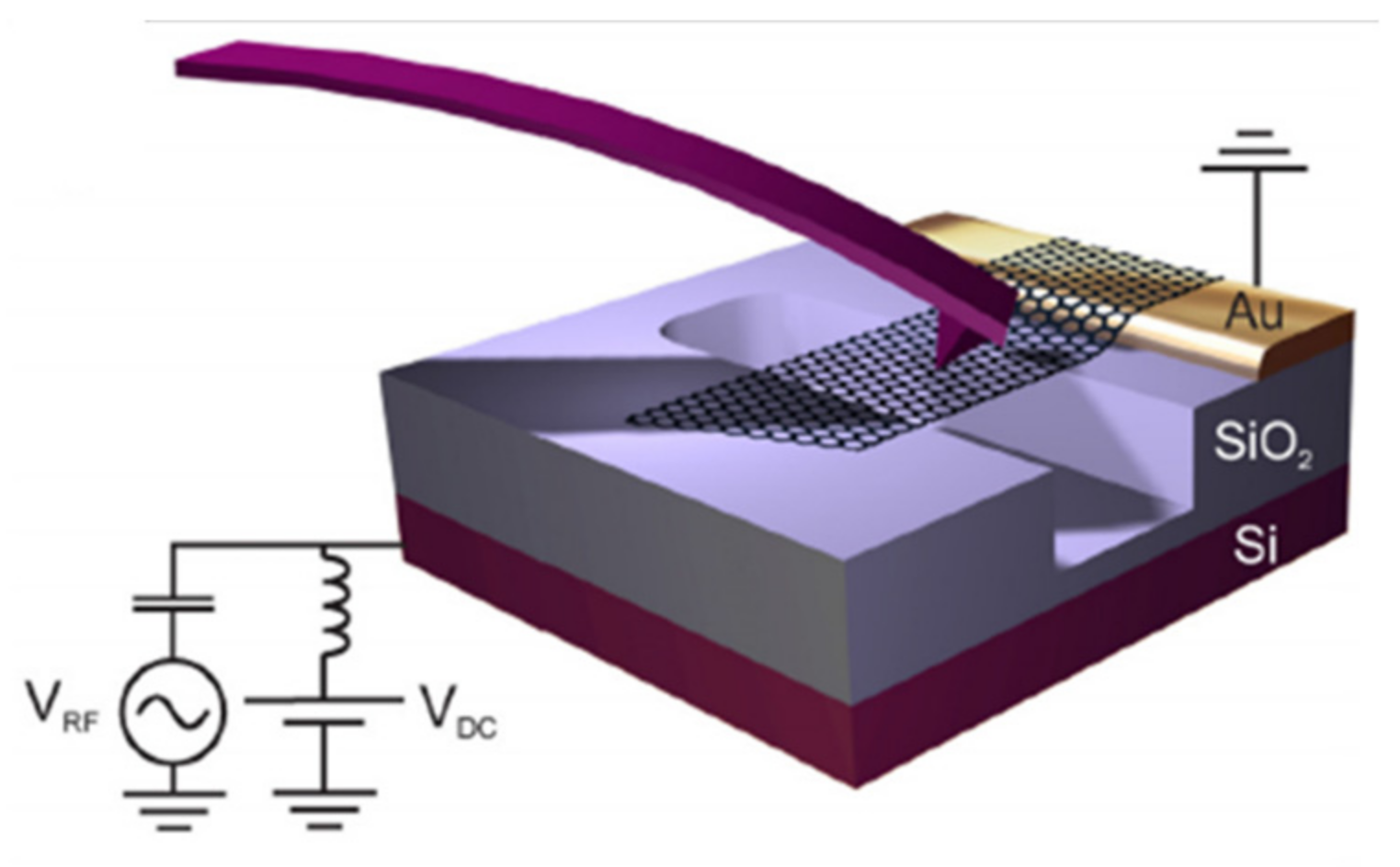
Micromachines 13 00241 g003 550
Figure 3. Schematic of the resonator together with the SFM cantilever [51].
Figure 3. Schematic of the resonator together with the SFM cantilever [51].
Micromachines 13 00241 g003
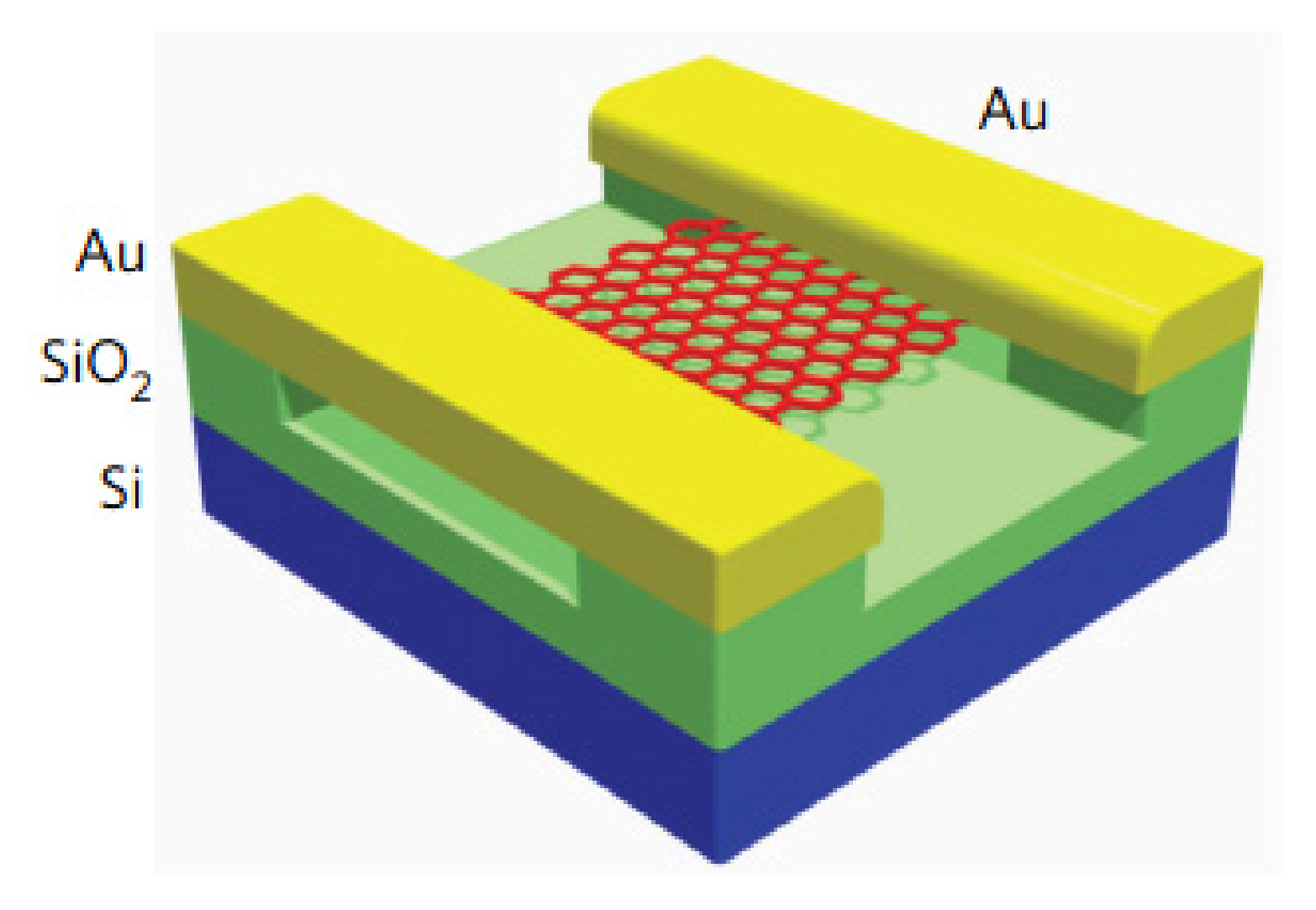
Micromachines 13 00241 g004 550
Figure 4. Schematic of single-layer graphene resonator model [52].
Figure 4. Schematic of single-layer graphene resonator model [52].
Micromachines 13 00241 g004
Micromachines 13 00241 g005 550
Figure 5. Graphene resonator with SU-8 resist substrate: (a) SEM image of graphene resonator after 500 °C annealing. (b) SEM image of broken graphene resonator after 600 °C annealing [53].
Figure 5. Graphene resonator with SU-8 resist substrate: (a) SEM image of graphene resonator after 500 °C annealing. (b) SEM image of broken graphene resonator after 600 °C annealing [53].
Micromachines 13 00241 g005
Micromachines 13 00241 g006 550
Figure 6. Graphene-nanoribbon-resonator [69].
Figure 6. Graphene-nanoribbon-resonator [69].
Micromachines 13 00241 g006
Micromachines 13 00241 g007 550
Figure 7. Transfer and drying of rGO(reduced graphene oxide) films in air on prepatterned substrates [78].
Figure 7. Transfer and drying of rGO(reduced graphene oxide) films in air on prepatterned substrates [78].
Micromachines 13 00241 g007
Micromachines 13 00241 g008 550
Figure 8. Double clamped graphene beam array [39].
Figure 8. Double clamped graphene beam array [39].
Micromachines 13 00241 g008
Micromachines 13 00241 g009 550
Figure 9. Suspended graphene sheet resonator array. (a) Angled scanning electron microscopy (SEM) image of Type A suspended graphene membranes over trenches in silicon oxide. (b) Angled SEM of an array of graphene membranes [81].
Figure 9. Suspended graphene sheet resonator array. (a) Angled scanning electron microscopy (SEM) image of Type A suspended graphene membranes over trenches in silicon oxide. (b) Angled SEM of an array of graphene membranes [81].
Micromachines 13 00241 g009
Micromachines 13 00241 g010 550
Figure 10. Schematic diagram of graphene resonator with additional mass [86].
Figure 10. Schematic diagram of graphene resonator with additional mass [86].
Micromachines 13 00241 g010
Micromachines 13 00241 g011 550
Figure 11. Comparison of frequency offset between double-layer and single-layer graphene sheets [89].
Figure 11. Comparison of frequency offset between double-layer and single-layer graphene sheets [89].
Micromachines 13 00241 g011
Micromachines 13 00241 g012 550
Figure 12. Drum-shaped graphene resonant pressure sensor [93].
Figure 12. Drum-shaped graphene resonant pressure sensor [93].
Micromachines 13 00241 g012
Micromachines 13 00241 g013 550
Figure 13. Fabry-Perot light cavity graphene resonant pressure sensor [95].
Figure 13. Fabry-Perot light cavity graphene resonant pressure sensor [95].
Micromachines 13 00241 g013
Micromachines 13 00241 g014 550
Figure 14. Double-clamped graphene beam resonant pressure sensor [96].
Figure 14. Double-clamped graphene beam resonant pressure sensor [96].
Micromachines 13 00241 g014
Micromachines 13 00241 g015 550
Figure 15. Single graphene beam resonant pressure sensor [97].
Figure 15. Single graphene beam resonant pressure sensor [97].
Micromachines 13 00241 g015
Micromachines 13 00241 g016 550
Figure 16. Schematic diagram of graphene nanoribbon acceleration sensor [102].
Figure 16. Schematic diagram of graphene nanoribbon acceleration sensor [102].
Micromachines 13 00241 g016
Micromachines 13 00241 g017 550
Figure 17. SEM image of an SU-8 resist graphene accelerometer [54].
Figure 17. SEM image of an SU-8 resist graphene accelerometer [54].
Micromachines 13 00241 g017
Micromachines 13 00241 g018 550
Figure 18. Model of graphene acceleration sensor [105].
Figure 18. Model of graphene acceleration sensor [105].
Micromachines 13 00241 g018
Table
Table 1. Structure comparison of graphene resonant pressure sensor.
Table 1. Structure comparison of graphene resonant pressure sensor.
Graphene ShapeSensitive MethodAnalysis MethodSensitivity AnalysisYear/Author
Drum ShapePressure Direct SensitiveExperimental Verification1Torr2016
Raj
[93]
Pressure Direct SensitiveExperimental Verification2.8 × 10−5 mbar−12016 Qiugu Wang
[94]
Pressure Direct SensitiveExperimental Verification0.298 kHz/kPa
(10~1000)kPa		2016 She
[95]
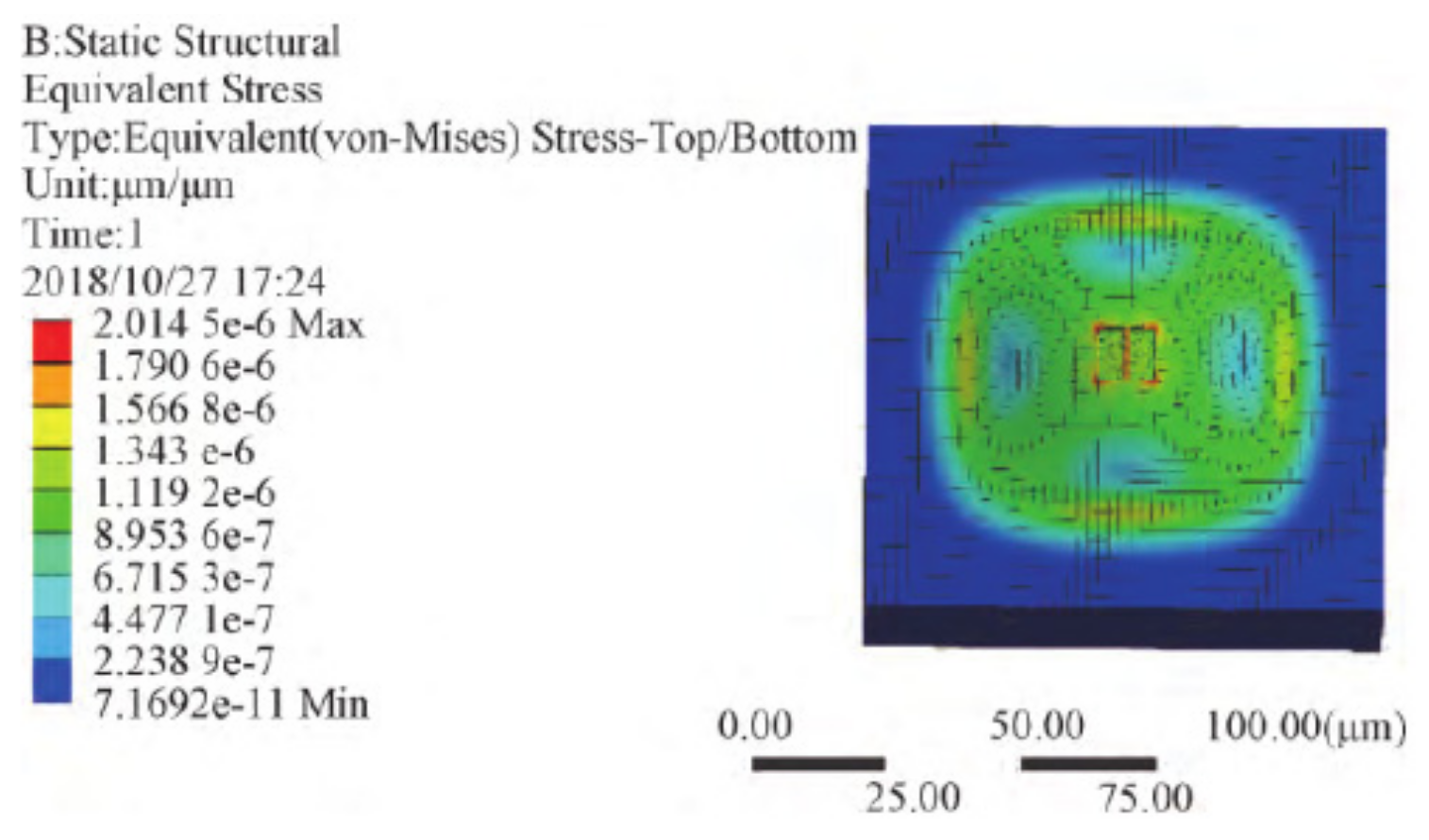
Beam
Shape		Secondary sensitiveFinite Element Simulation26.838 kHz/kPa
(0–1000)kPa		2014 Jiang
[96]
Secondary sensitiveFinite Element Simulation81.3 Hz/Pa (0–10) kPa2016
Fan
[97]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Fan, S.-C.; Lu, Y.; Zhao, P.-C.; Shi, F.-T.; Guo, Z.-S.; Xing, W.-W. Research Progress of Graphene Nano-Electromechanical Resonant Sensors—A Review. Micromachines 2022, 13, 241. https://doi.org/10.3390/mi13020241

AMA Style

Fan S-C, Lu Y, Zhao P-C, Shi F-T, Guo Z-S, Xing W-W. Research Progress of Graphene Nano-Electromechanical Resonant Sensors—A Review. Micromachines. 2022; 13(2):241. https://doi.org/10.3390/mi13020241

Chicago/Turabian Style

Fan, Shang-Chun, Yang Lu, Peng-Cheng Zhao, Fu-Tao Shi, Zhan-She Guo, and Wei-Wei Xing. 2022. "Research Progress of Graphene Nano-Electromechanical Resonant Sensors—A Review" Micromachines 13, no. 2: 241. https://doi.org/10.3390/mi13020241

APA Style

Fan, S. -C., Lu, Y., Zhao, P. -C., Shi, F. -T., Guo, Z. -S., & Xing, W. -W. (2022). Research Progress of Graphene Nano-Electromechanical Resonant Sensors—A Review. Micromachines, 13(2), 241. https://doi.org/10.3390/mi13020241

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop