Optical Coupling Efficiency of a Coupler with Double-Combined Collimating Lenses and Thermally Expanded Core Fibers
Abstract
:1. Introduction
2. Analysis of the Characteristics for Fiber Coupler
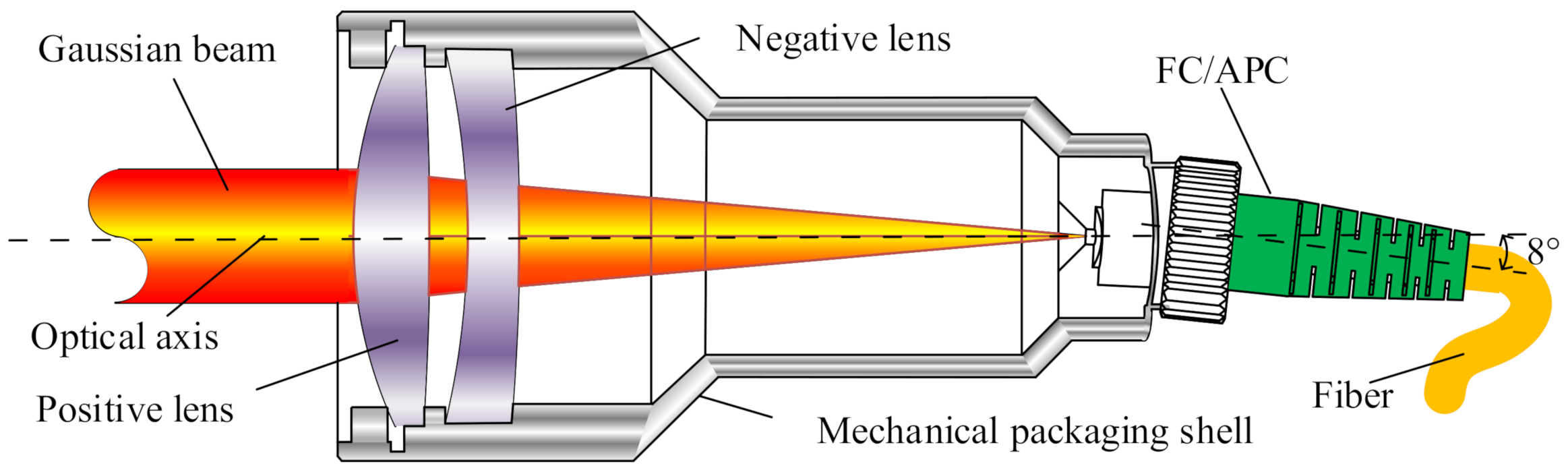
2.1. Structure Analysis
2.2. Characteristic Analysis of the TECF
2.3. Analysis of the Coupling Mechanism
2.4. Coupling Efficiency of the LBFC
3. Optimization Analysis for Simulation
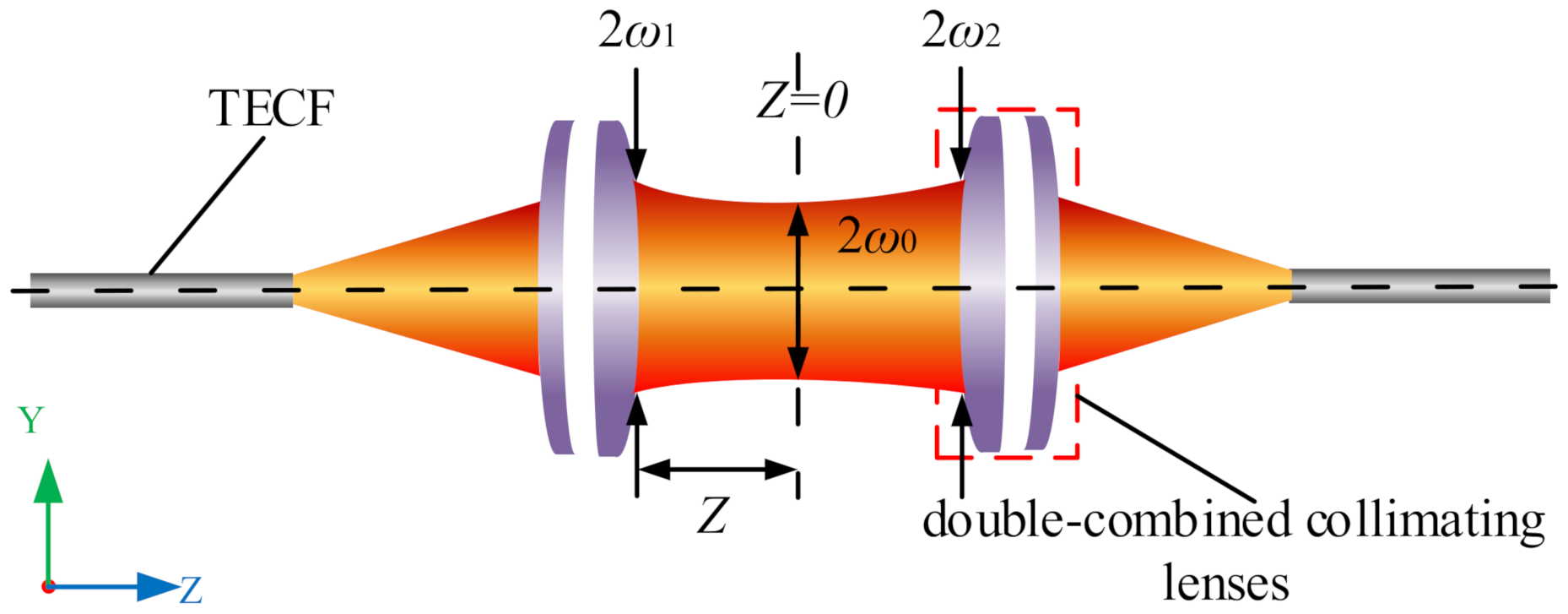
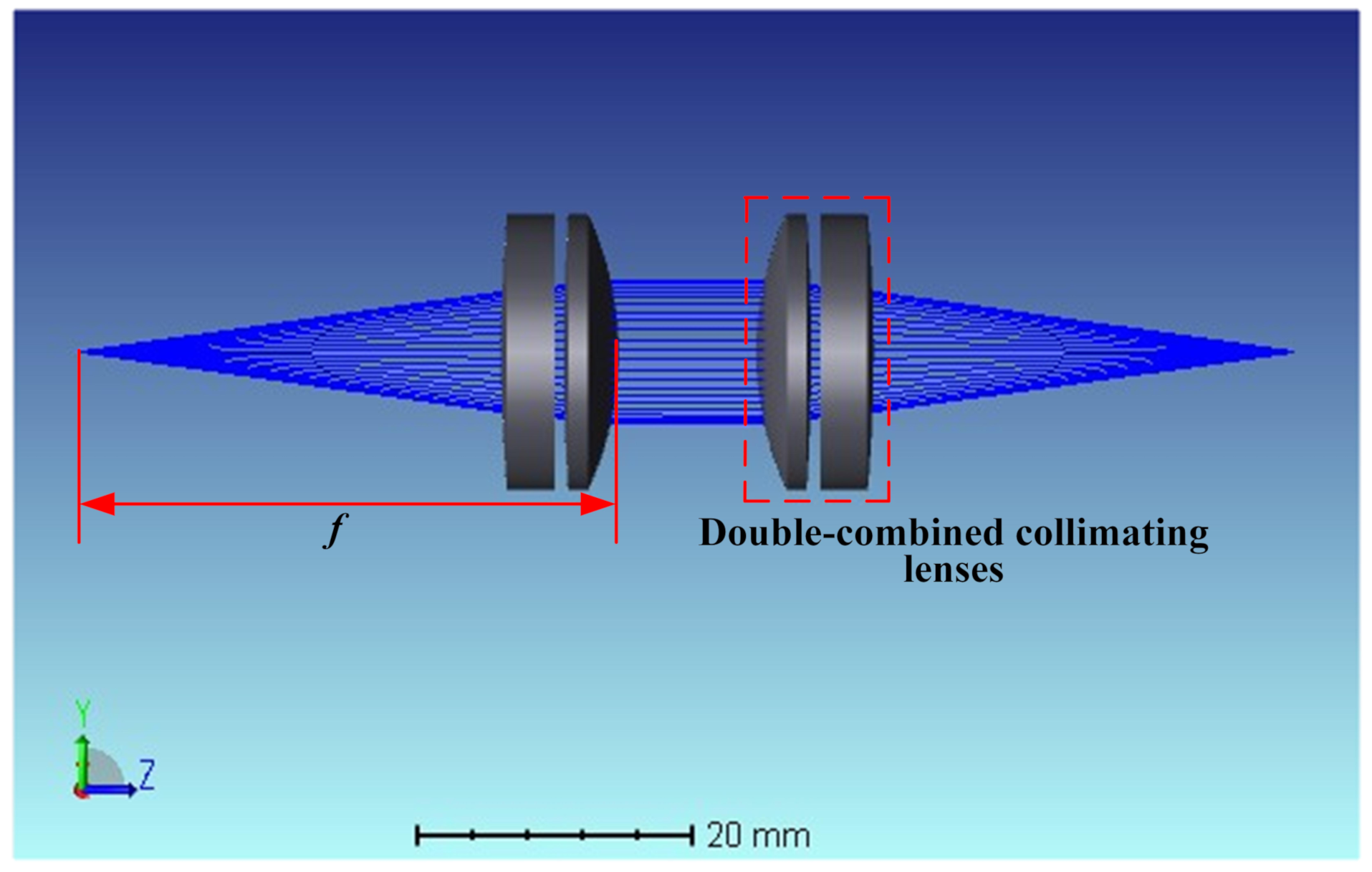
3.1. Modeling
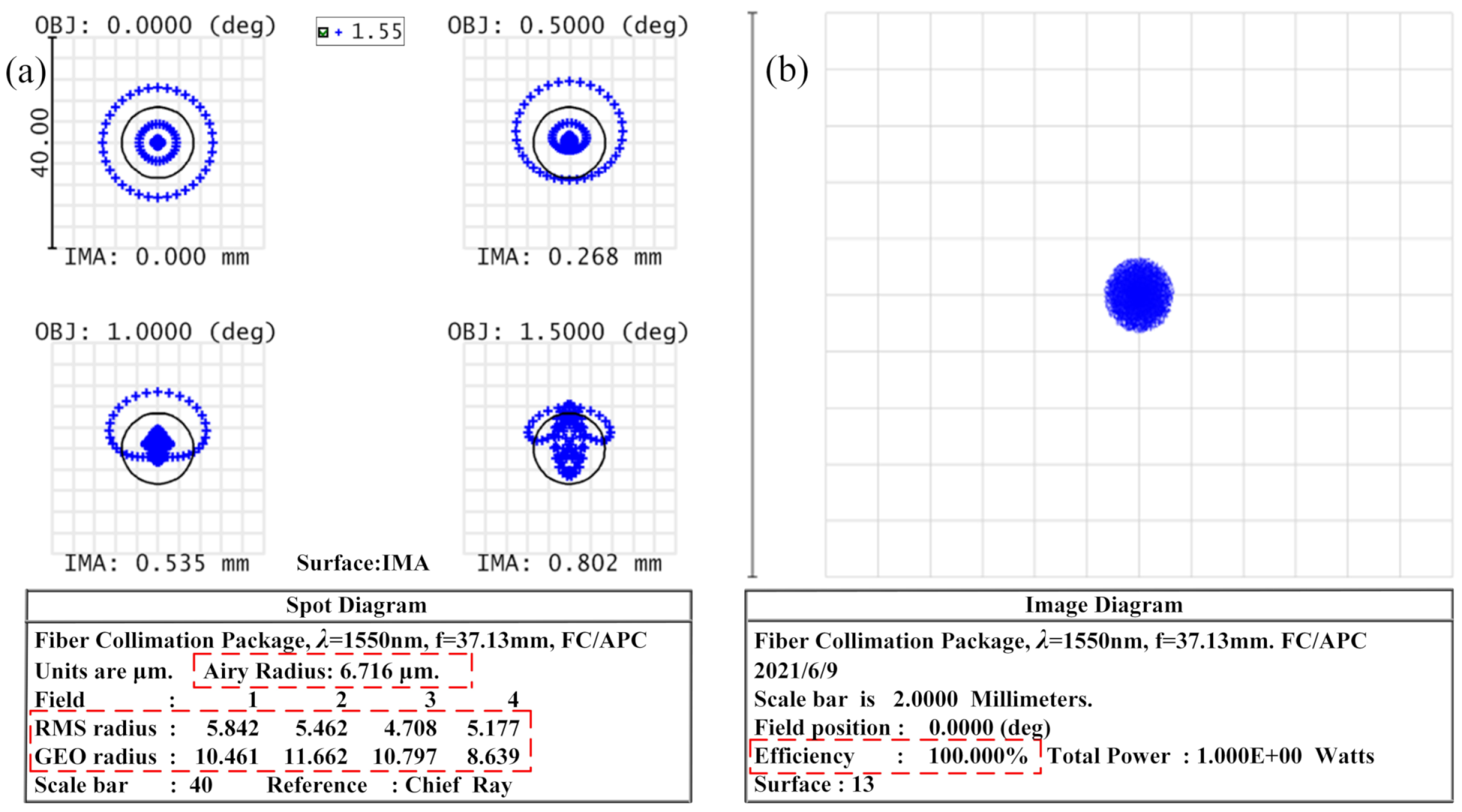
3.2. Analysis of Models
3.3. Coupling Analysis
4. Experimental Analysis
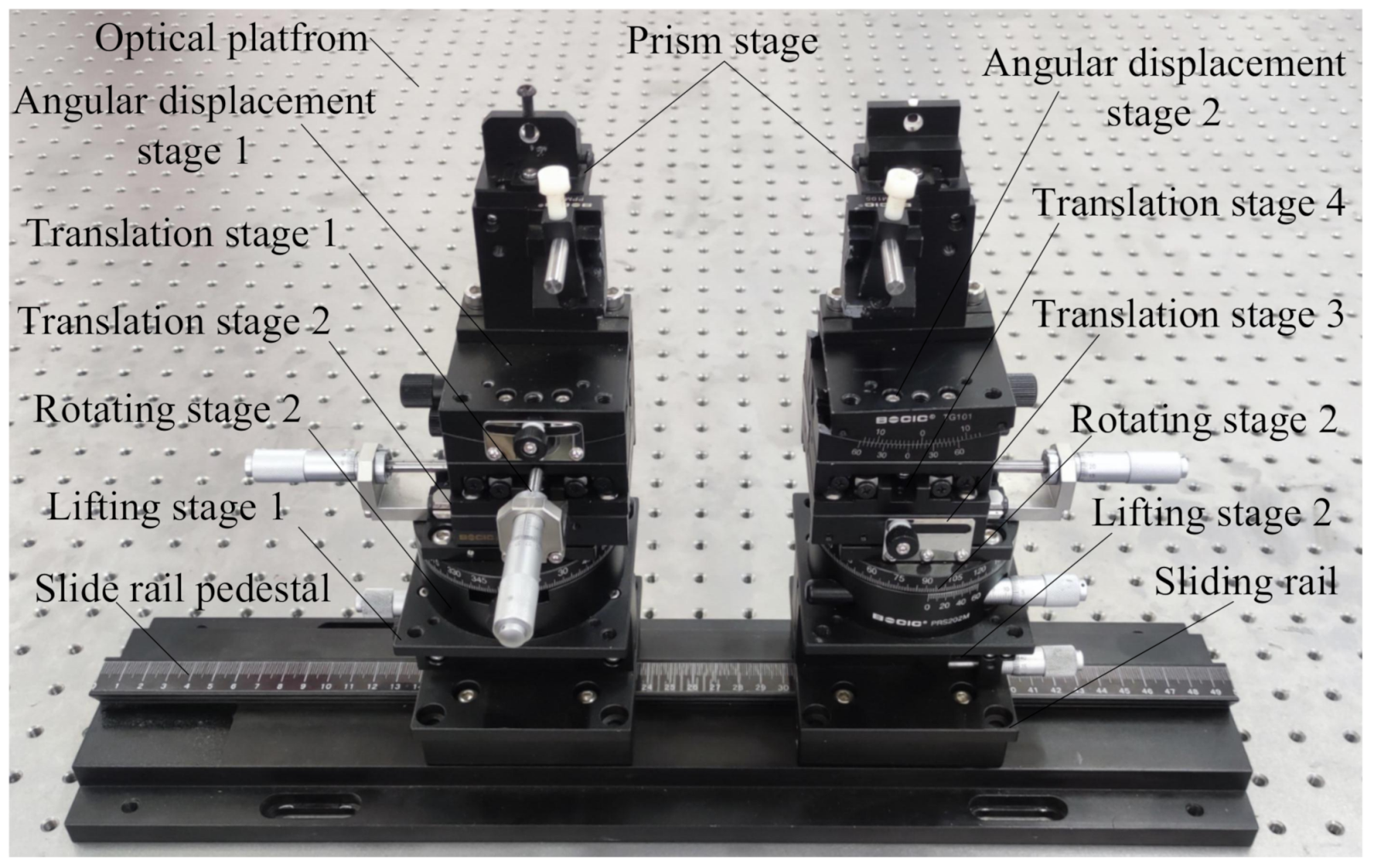
4.1. Experiment Build
4.2. The Influence of the MFD for Fiber on the Coupling Efficiency
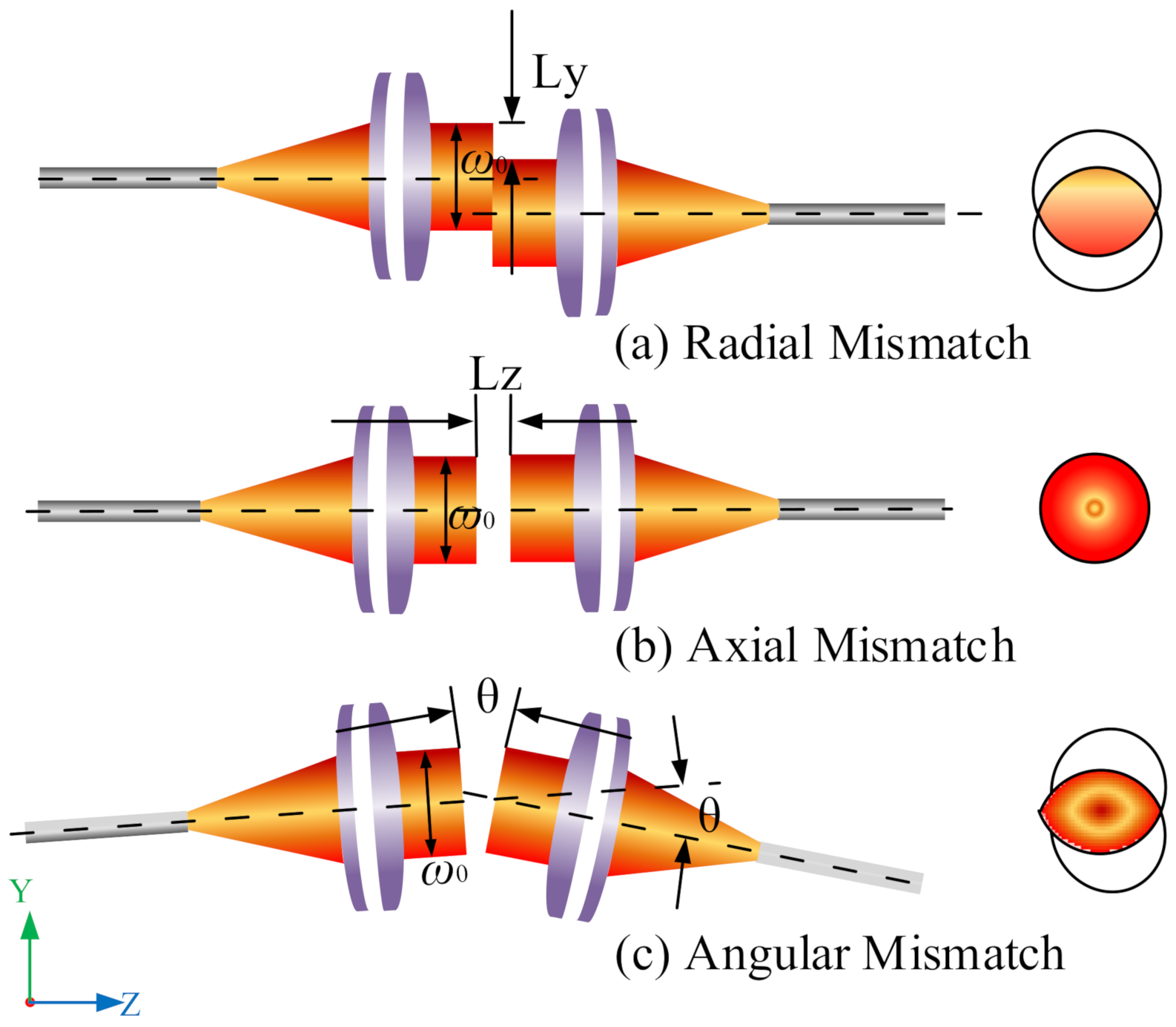
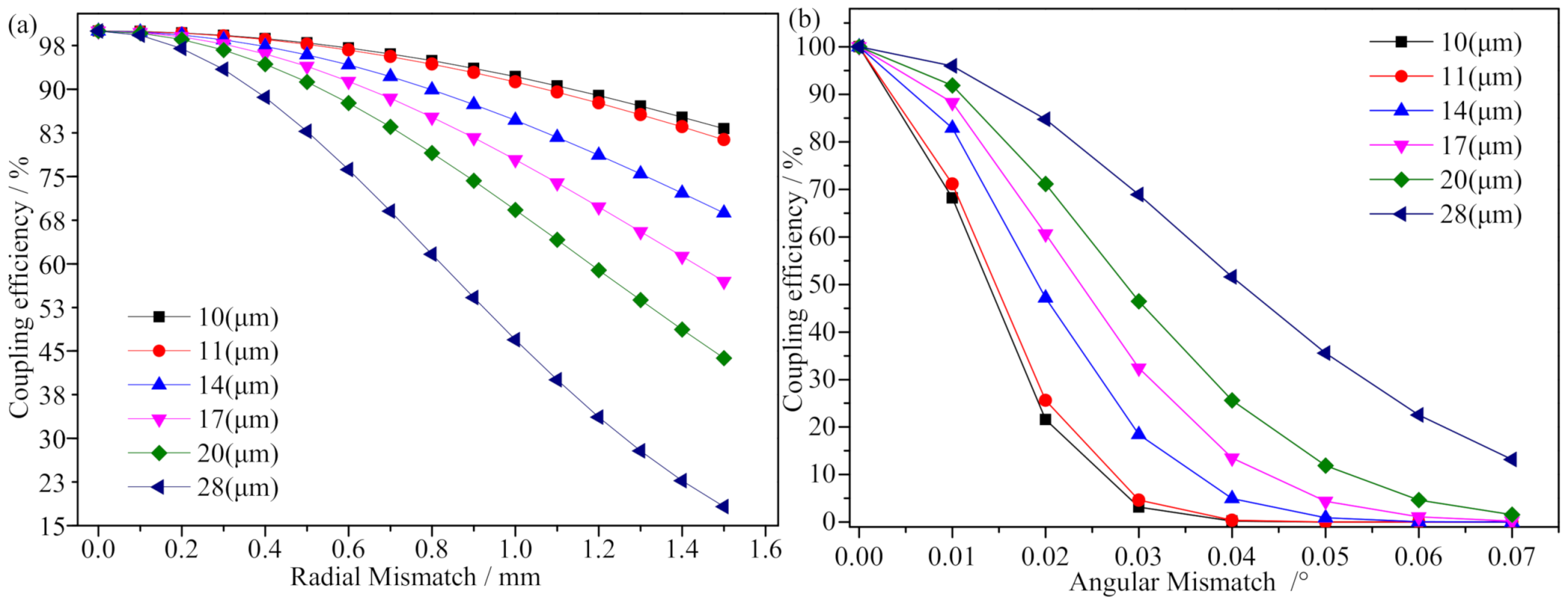
4.3. The Influence of the Mismatch on the Coupling Efficiency
5. Conclusions
- When the fiber coupler met the coupling requirements, the larger the MFD of the fiber, the higher the coupling efficiency. If there was a coupling mismatch between the fiber couplers, the angular mismatch had the most influence, followed by the radial mismatch, with the axial mismatch being the smallest. When the MFD of the fiber was 10 m, the coupling efficiency of the coupler was 57.41% through simulation, and 49.73% in the experiment. When the MFD was 28 m, the simulation coupling efficiency was 100%, while the experiment was 95.16%. As such, compared with an ordinary SMF, the coupling efficiency of the large-mode field TECF to the coupler was significantly improved.
- When all mismatches of the coupler were present, a 20 m fiber was chosen to couple the signal. The coupling efficiency could reach over 50.4% (loss within 3 dB), which met the signal transmission requirements of the FORJ for a single-mode large-beam TEC. The aforementioned conclusions can guide the design of such fiber optic rotary connector.
- The double-lens expands and collimates the beam, has a small divergence angle, a large working distance, and stable transmission performance. Moreover, this lens can better reduce the influence of aberration on the coupling efficiency.
- This work can provide some instructive technical support for the bi-directional transmission of fiber couplers, the online monitoring of signals with fiber grating sensing, and the research on the transmission performance of couplers under rotating conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dorsey, G.F. Fiber Optic Rotary Joints—A Review; IEEE: New York, NY, USA, 1981; pp. 37–41. [Google Scholar]
- Ji, Z.; Jia, D.; Xu, Q.; Zhang, H.; Zhang, H.; Zhang, D.; Zhang, Y. Design and implementation of a plastic fiber optical rotary joint using upside down taper lens. Opt. Commun. 2013, 292, 57–61. [Google Scholar] [CrossRef]
- Williams, R.J.; Krämer, R.G.; Nolte, S.; Withford, M.J. Femtosecond direct-writing of low-loss fiber Bragg gratings using a continuous core-scanning technique. Opt. Lett. 2013, 38, 1918–1920. [Google Scholar] [CrossRef] [PubMed]
- Cho, I.K.; Mun, J.I.; Han, Y.T.; Kim, S.M.; Yun, J.H. Fiber-Optic Rotary Joint and Optical Link for RF-Antenna Measurement. IEEE Photonics Technol. Lett. 2010, 22, 447–449. [Google Scholar] [CrossRef]
- Leigh, M.S.; Armstrong, J.J.; Paduch, A.; Walsh, J.H.; Hillman, D.R.; Eastwood, P.R.; Sampson, D.D. Anatomical Optical Coherence Tomography for Long-Term, Portable, Quantitative Endoscopy. IEEE Trans. Bio-Med Eng. 2008, 55, 1438. [Google Scholar] [CrossRef] [PubMed]
- Iida, F.; Aul, C. Design and Control of a Pendulum Driven Hopping Robot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002. [Google Scholar]
- Mi, L.; Yao, S.; Sun, C.; Sun, B.; Zhang, H. Development and military application of fiber optic rotary joint. Infrared Laser Eng. 2011, 40, 1138–1142. [Google Scholar]
- Jing, W.; Zhang, Y.; Zhou, G.; Jia, D.; Liu, B.; Tang, F. Design of single-channel optical rotary joint using bulk optical detector. Opt. Eng. 2003, 42, 3285–3289. [Google Scholar] [CrossRef]
- Fei, L.; Yi, L.; Rulong, H.; Yao, S.; Han, X. Design and Implementation of an Off-Axis Rotary Optical Fiber Transmission System. Chin. J. Lasers 2015, 42, 0905001. [Google Scholar]
- Kliros, G.S.; Divari, P.C. Coupling characteristics of laser diodes to high numerical aperture thermally expanded core fibers. J. Mater. Sci. Mater. Electron. 2009, 20, 59–62. [Google Scholar] [CrossRef]
- Blomqvist, M.; Pålsson, M.; Blomster, O.; Manneberg, G. Fundamental-mode fiber-to-fiber coupling at high-power. Proc. SPIE—Int. Soc. Opt. Eng. 2014, 7193, 71930F. [Google Scholar]
- Chen, H.; Qiu, Y.; Li, G.; Hao, Z.; Chen, Q. Improving fiber to waveguide coupling efficiency by use of a highly germanium-doped thermally expanded core fiber. Opt. Laser Technol. 2012, 44, 679–682. [Google Scholar] [CrossRef]
- Yan, Y.; Zheng, Y.; Duan, J.; Huang, Z. Influence of positioning errors of the laser collimator on the beam shape and coupling efficiency. Opt. Fiber Technol. 2020, 58, 102301. [Google Scholar] [CrossRef]
- Zhang, M.; Zhi, D.; Chang, Q.; Ma, P.; Si, L. Comprehensive investigation of combining efficiency with a misaligned coherent fiber-optics-array collimator. Laser Phys. 2019, 29, 115101. [Google Scholar] [CrossRef]
- Mashalchi, S.; Pahlavan, S.; Hejazi, M. A novel fluorescent cardiac imaging system for preclinical intraoperative angiography. BMC Med. Imaging 2021, 21, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Sakurada, N.; Ishii, Y.; Watanabe, K.; Kubota, Y. Visualization of molten pools and invisible laser beam profiles using an ultraviolet CCD camera. J. Vis. 2001, 4, 349–356. [Google Scholar] [CrossRef]
- Mallick, K.; Mandal, P.; Mandal, G.C.; Mukherjee, R.; Das, B.; Patra, A.S. Hybrid MMW-over fiber/OFDM-FSO transmission system based on doublet lens scheme and POLMUX technique. Opt. Fiber Technol. 2019, 52, 101942. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, R. Initial structure of dispersion objective for chromatic confocal sensor based on doublet lens. Opt. Lasers Eng. 2021, 139, 106424. [Google Scholar] [CrossRef]
- Shiraishi, K.; Aizawa, Y.; Kawakami, S. Beam expanding fiber using thermal diffusion of the dopant. J. Light. Technol. 1990, 8, 1151–1161. [Google Scholar] [CrossRef]
- Kihara, M.; Matsumoto, M. Characteristics of thermally expanded core fiber. J. Lightw. Technol. 1996, 14, 2209–2214. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, Z.; Chen, H.; Jie, L.; Jing, H. Mode field adaptation between single-mode fiber and large mode area fiber by thermally expanded core technique. Opt. Laser Technol. 2013, 47, 72–75. [Google Scholar] [CrossRef]
- Kliros, G.S.; Tsironikos, N. Variational analysis of propagation characteristics in thermally diffused expanded core fibers. Opt. Int. J. Light Electron Opt. 2005, 116, 365–374. [Google Scholar] [CrossRef]
- Mi, L.; Yao, S.; Sun, C.; Bo, S.; Zhang, H. A single-channel fiber optic rotary joint on the basis Of TEC fiber collimators. In Proceedings of the International Conference on Optical Communications & Networks, Nanjing, China, 24–27 October 2011. [Google Scholar]
- Liu, X.; Guo, J.; Li, G.; Chen, N.; Shi, K. Research on the influence of alignment error on coupling efficiency and beam quality for Gaussian beam to multimode fiber. Results Phys. 2019, 12, 1044–1049. [Google Scholar] [CrossRef]
- Nemoto, S.; Makimoto, T. Analysis of splice loss in single-mode fibres using a Gaussian field approximation. Opt. Quantum Electron. 1979, 11, 447–457. [Google Scholar] [CrossRef]
- Palais, J.C. Fiber coupling using graded-index rod lenses. Appl. Opt. 1980, 19, 2011–2018. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Li, Z.; Yang, Y.; Sun, G.; Qiang, W. The refractive index distribution of even polygonal selfoc lens. Opt. Laser Technol. 2011, 43, 674–678. [Google Scholar] [CrossRef]
- Fan, Y.; Luo, S.; Kang, H. A comparison of the Long Working Distance of the GRIN Lens- and C-Lens-Based OCT Probe. IEEE Access 2019, 7, 93212–93218. [Google Scholar] [CrossRef]
- Zhang, M.R.; He, Z.Q.; Hu, B.W.; Kong, D.P.; Li, Y.L. Reaserch on Loss of Fiber Optic Rotary Joint Based on Virtual Prototype. Acta Photonica Sin. 2014, 43, 137–142. [Google Scholar]
- Yuan, S.; Riza, N.A. General Formula for Coupling-Loss Characterization of Single-Mode Fiber Collimators by use of Gradient-Index Rod Lenses. Appl. Opt. 1999, 38, 3214–3222. [Google Scholar] [CrossRef]









| References | Method/Structure | Results |
|---|---|---|
| Jing et al. [8] | SMF G-lens | Relaxed the assembly accuracy requirement Achieved an insertion loss of 3 dB |
| Blomqvist et al. [11] | Single lens | Radial displacement of 3.7 μm reduces the coupling efficiency with 50% |
| George et al. [10] | TECF SMF | TECF has lower coupling losses Larger tolerances |
| Chen et al. [12] | TECF | The TECF mode field radius extension is more effective than the SMF |
| Mi et al. [7] | TECF G-lens | Less sensitive to angular tilt |
| Yan et al. [13] | FAC SAC | The positioning error of FAC had a greater effect on the coupling efficiency than SAC |
| Zhang et al. [14] | ZEMAX Coupler | Achieved the simulation of the fiber array coupler |
| Sara et al. [15] | ZEMAX Dual-lens | Dual-lenses reduce chromatic aberration and improve image resolution |
| Wavelength/nm | Focal Length/mm | Numerical Aperture | Length/mm | Width/mm |
|---|---|---|---|---|
| 1550 | 37 | 42 | 25 |
| nm | m | m | ||
|---|---|---|---|---|
| 1550 | 10 |
| − | − | |||
| − | − | |||
| 4 | ||||
| 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Zhao, Z.; Ye, X.; Luo, C.; Zhang, D.; Wang, S.; Xu, X. Optical Coupling Efficiency of a Coupler with Double-Combined Collimating Lenses and Thermally Expanded Core Fibers. Micromachines 2022, 13, 324. https://doi.org/10.3390/mi13020324
He Q, Zhao Z, Ye X, Luo C, Zhang D, Wang S, Xu X. Optical Coupling Efficiency of a Coupler with Double-Combined Collimating Lenses and Thermally Expanded Core Fibers. Micromachines. 2022; 13(2):324. https://doi.org/10.3390/mi13020324
Chicago/Turabian StyleHe, Qi, Zhengang Zhao, Xiaoda Ye, Chuan Luo, Dacheng Zhang, Sifei Wang, and Xiaoping Xu. 2022. "Optical Coupling Efficiency of a Coupler with Double-Combined Collimating Lenses and Thermally Expanded Core Fibers" Micromachines 13, no. 2: 324. https://doi.org/10.3390/mi13020324
APA StyleHe, Q., Zhao, Z., Ye, X., Luo, C., Zhang, D., Wang, S., & Xu, X. (2022). Optical Coupling Efficiency of a Coupler with Double-Combined Collimating Lenses and Thermally Expanded Core Fibers. Micromachines, 13(2), 324. https://doi.org/10.3390/mi13020324







