A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming
Abstract
:1. Introduction
2. Numerical Methods
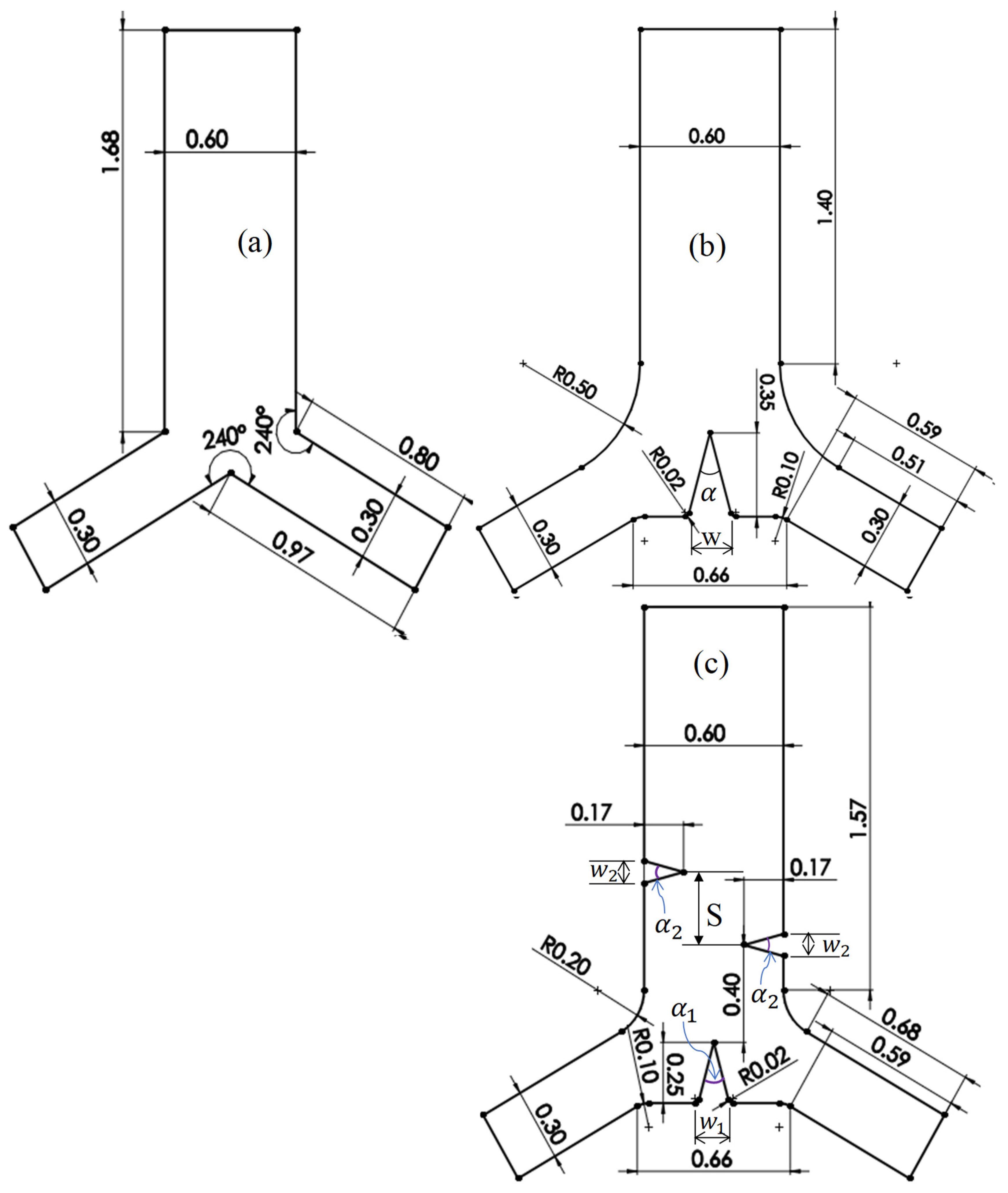
2.1. Microchannel Geometry and Numerical Scheme
2.2. Governing Equations and Boundary Conditions
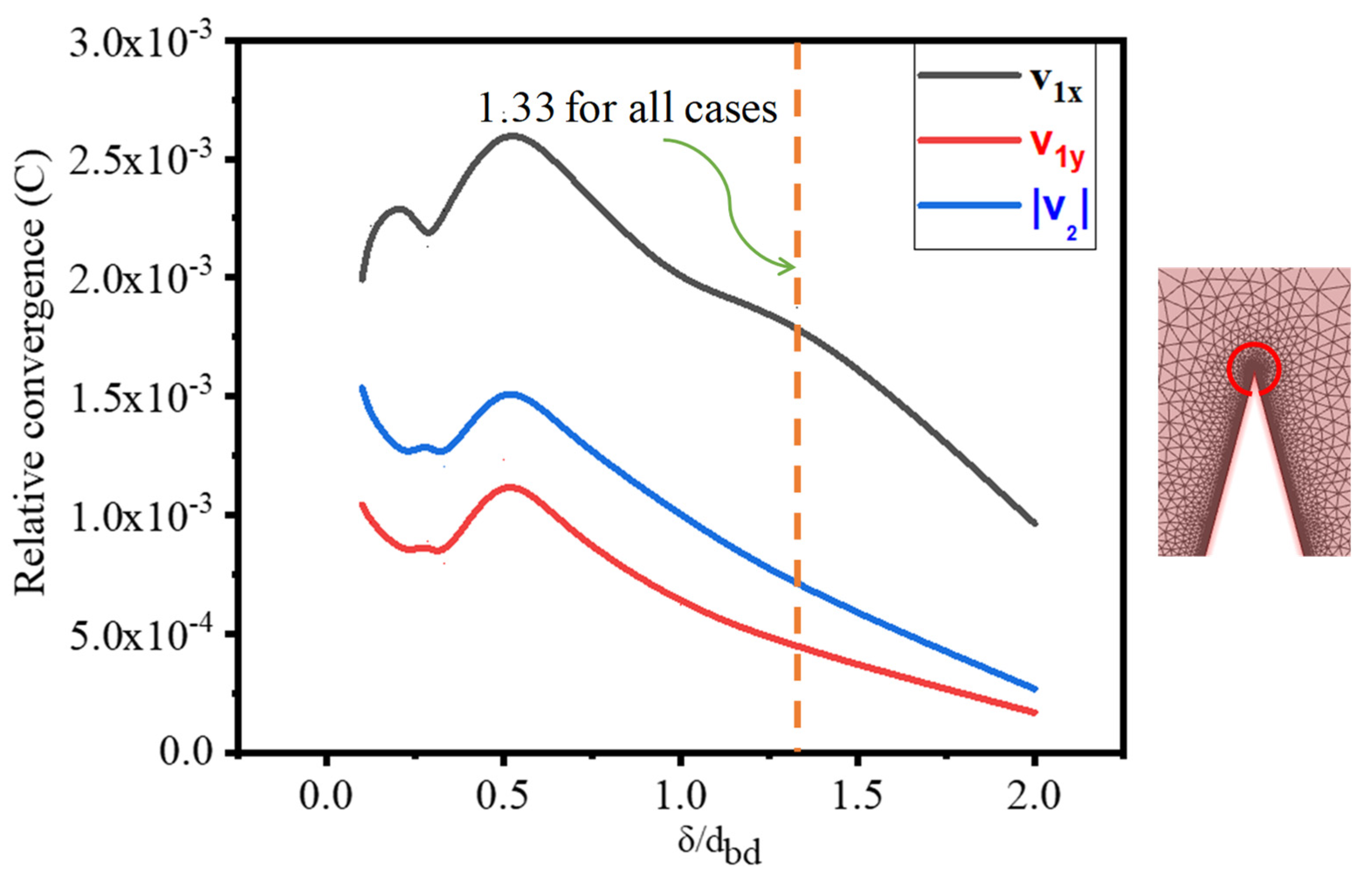
2.3. Mesh Independence Test
3. Results and Discussion
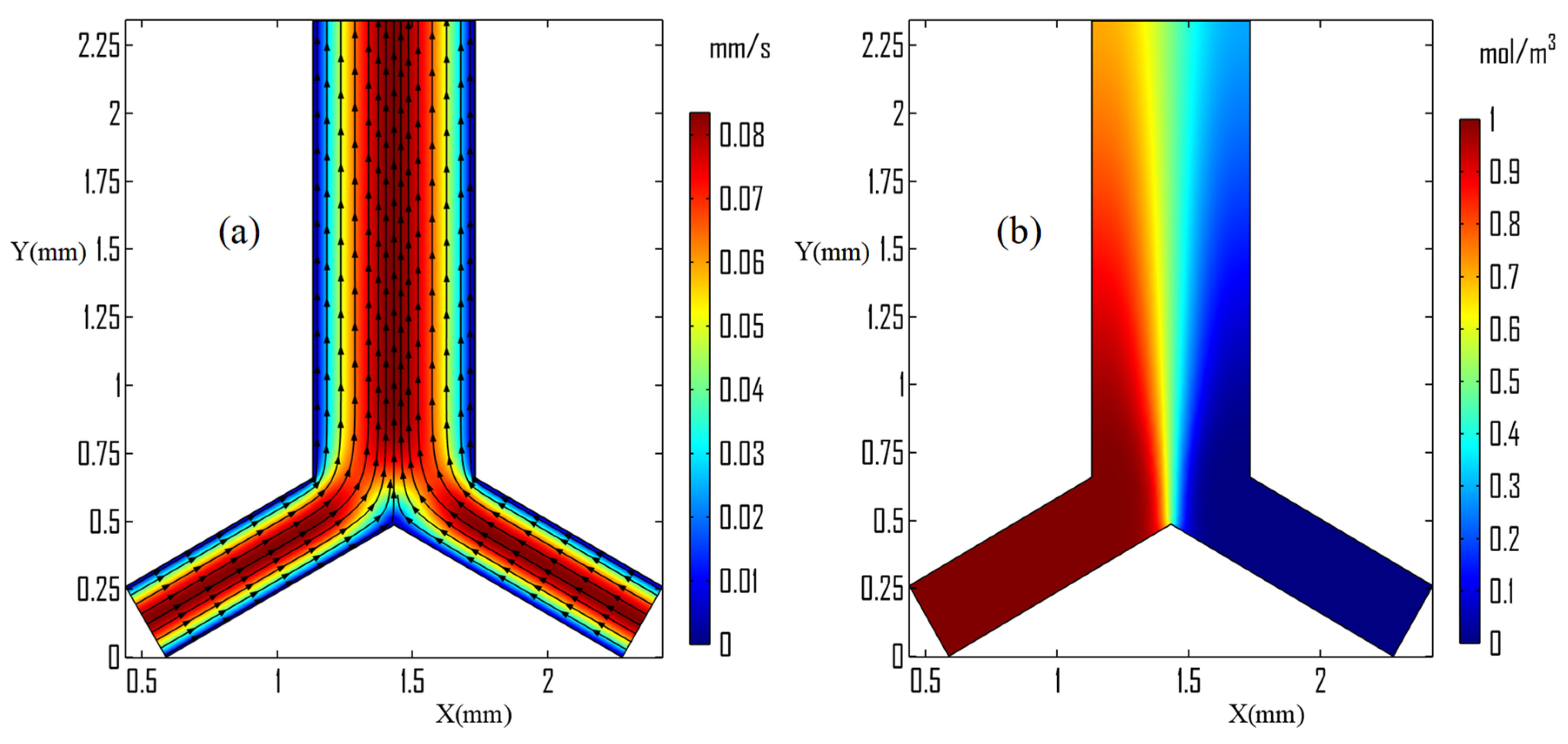
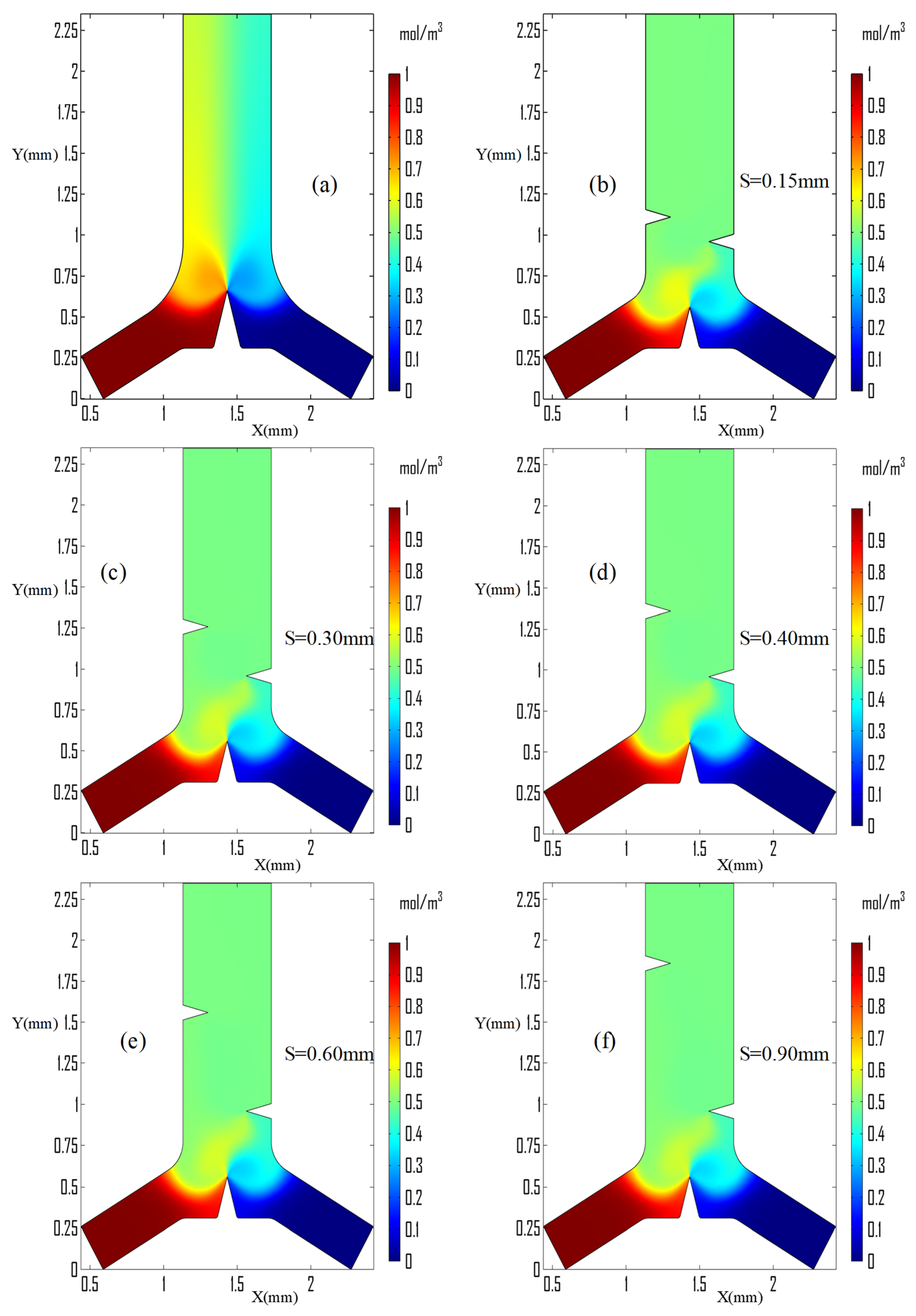
3.1. Normal Y-Junction Microchannel
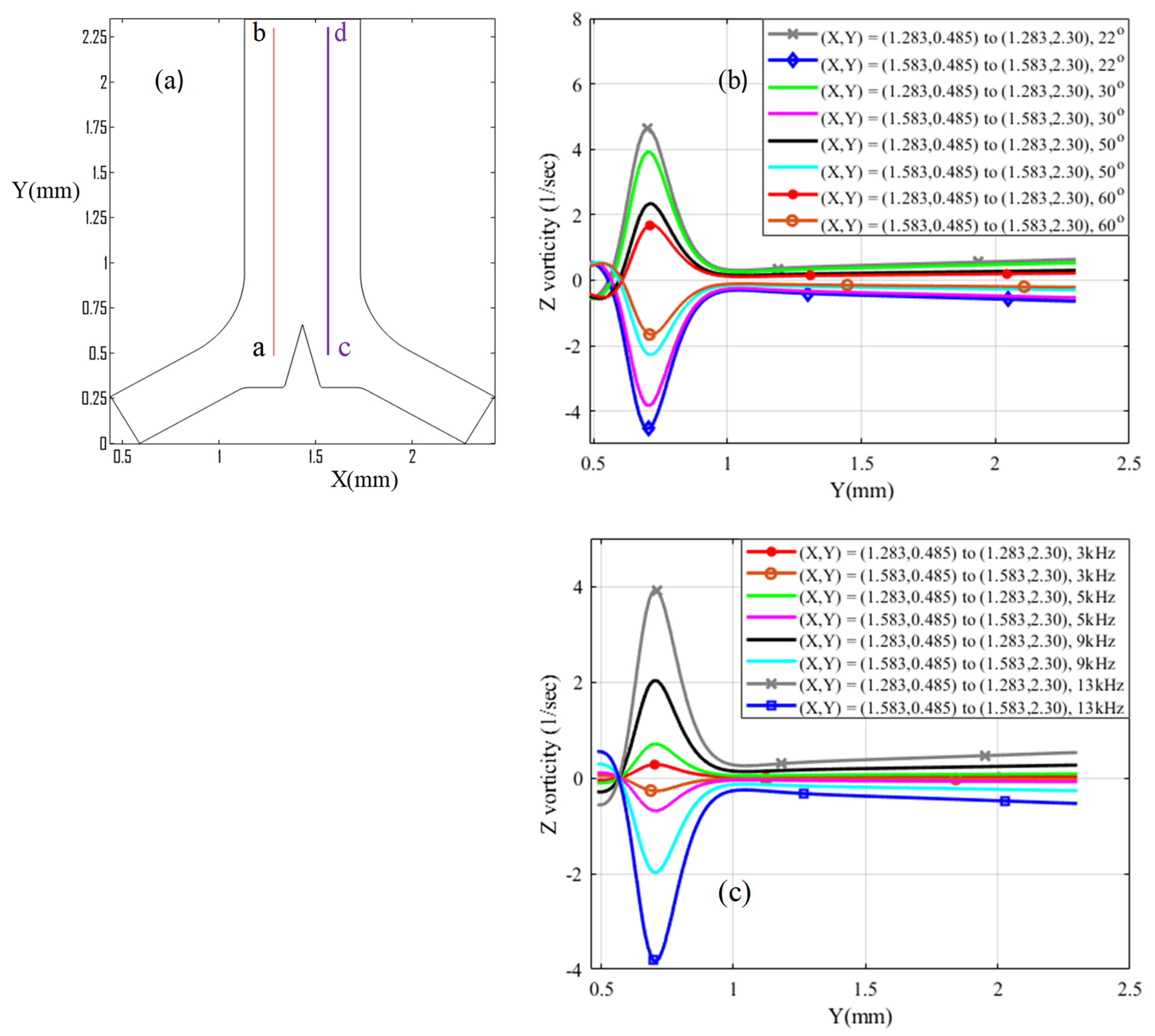
3.2. Acoustic Streaming Generation
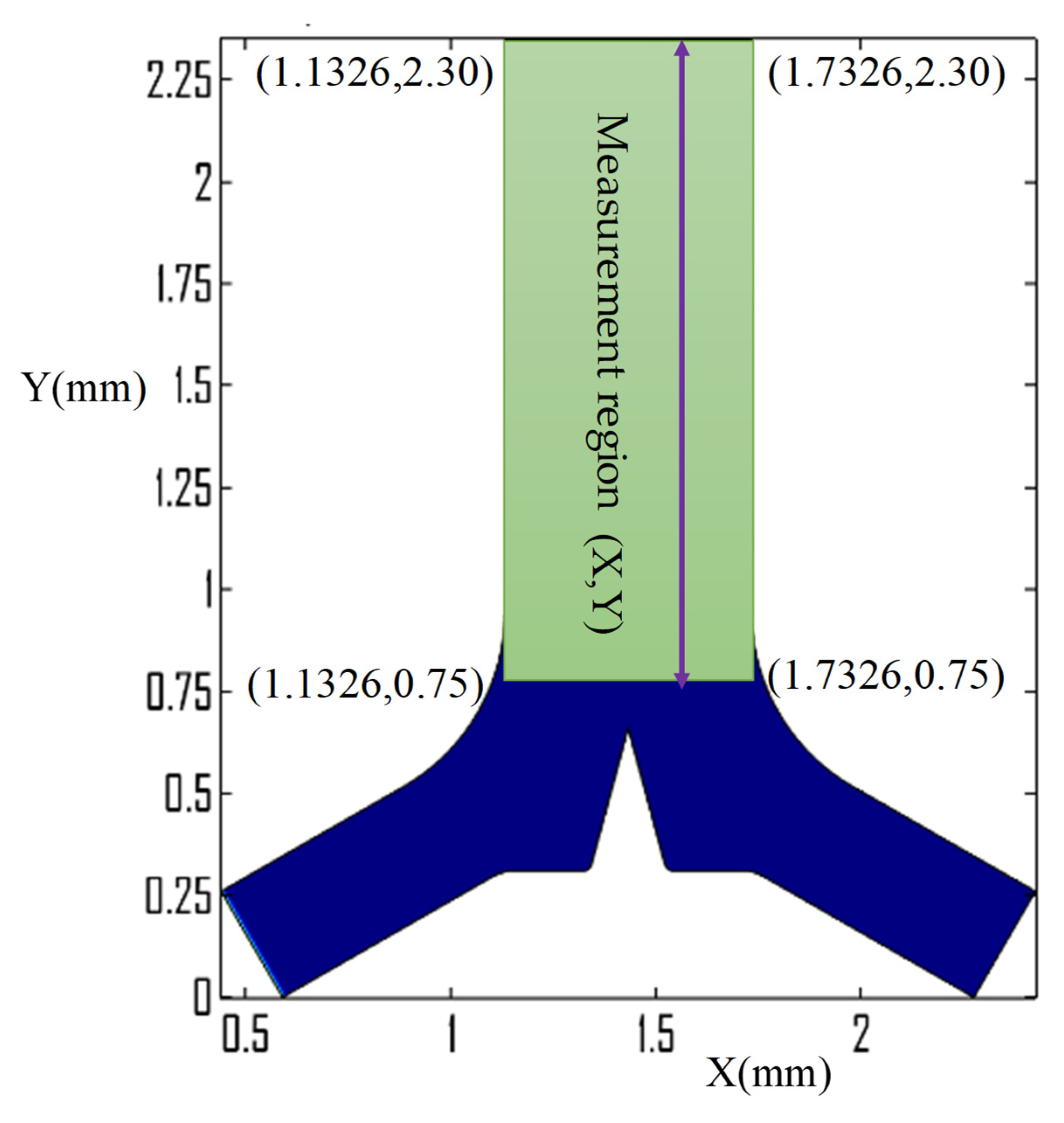
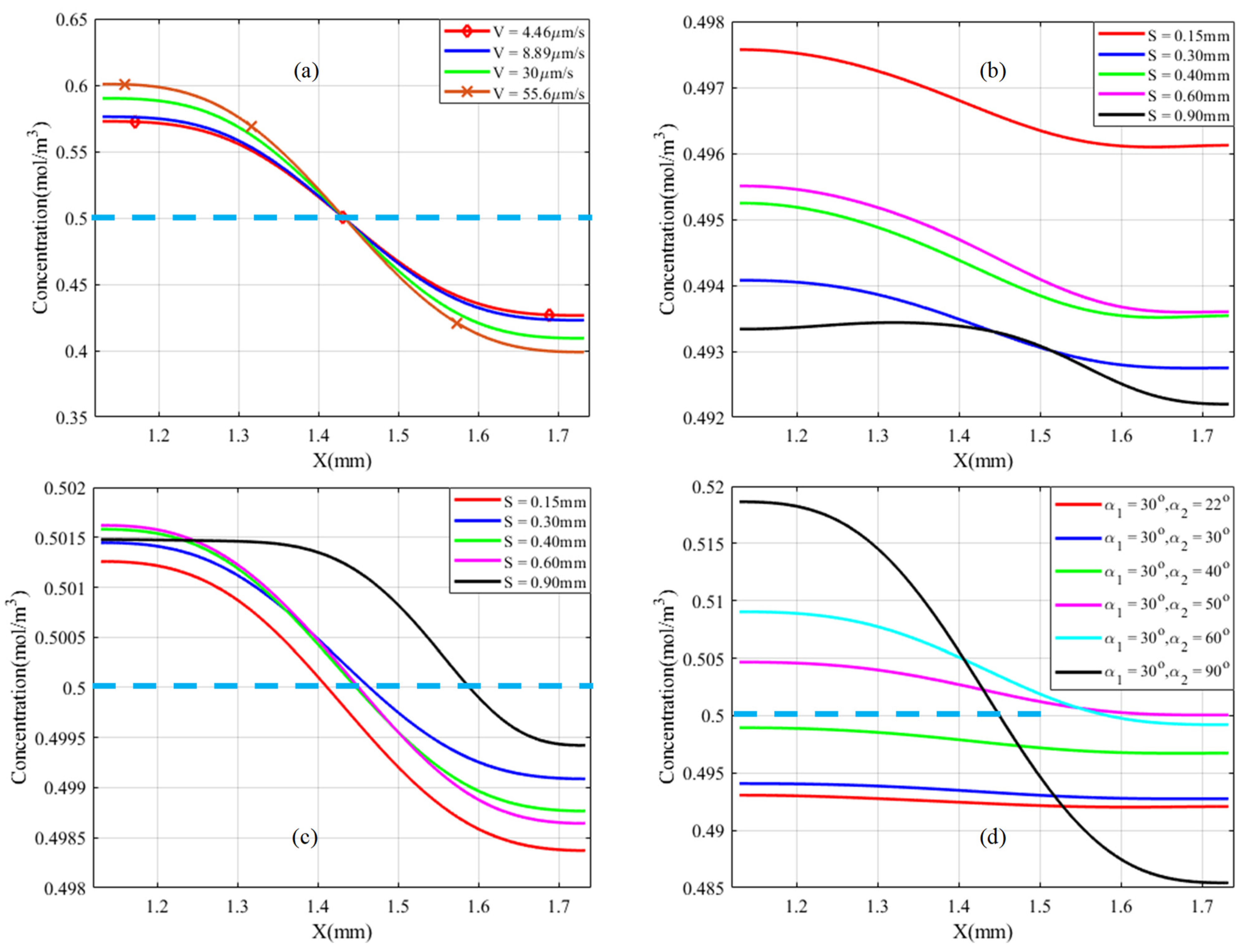
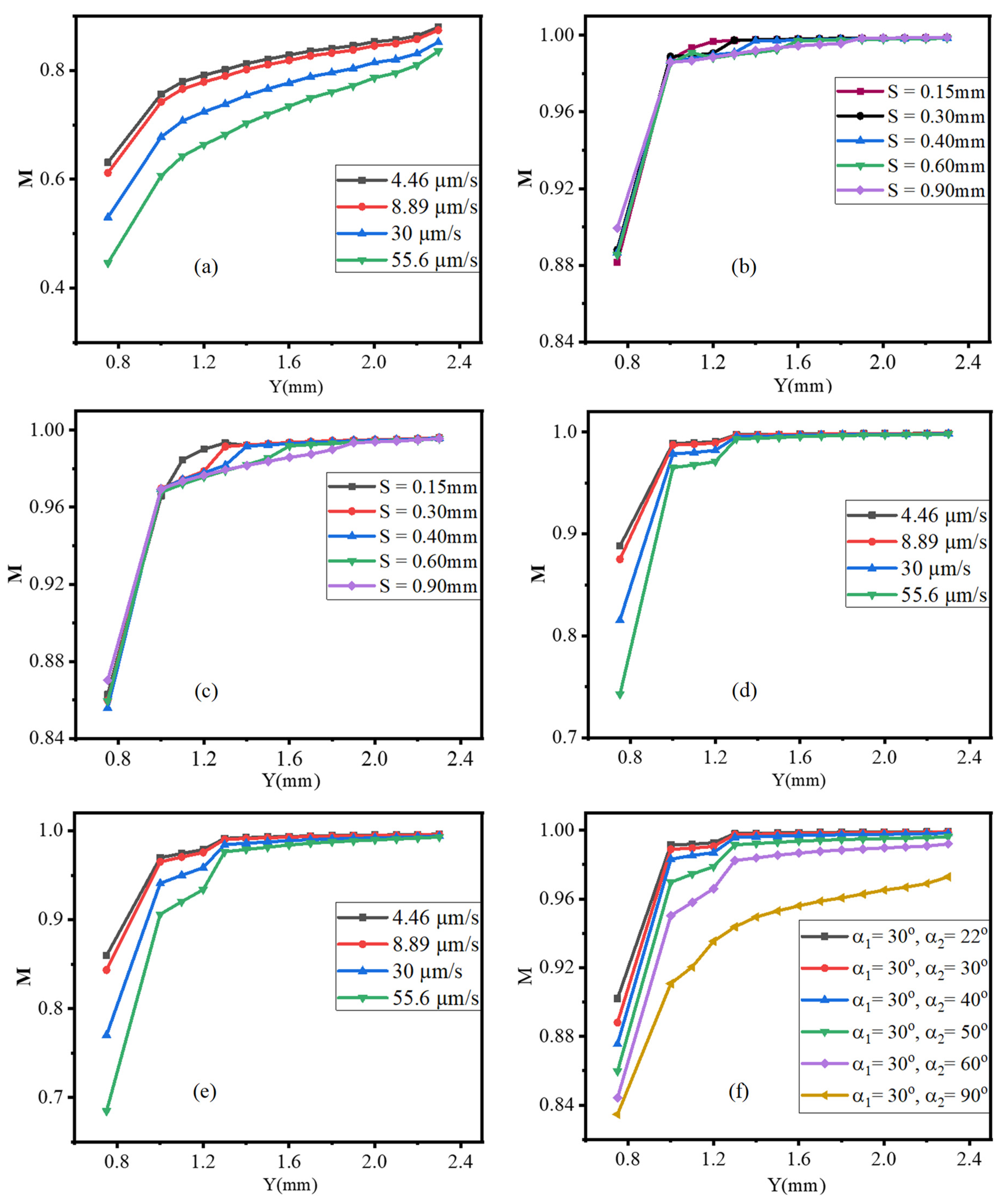
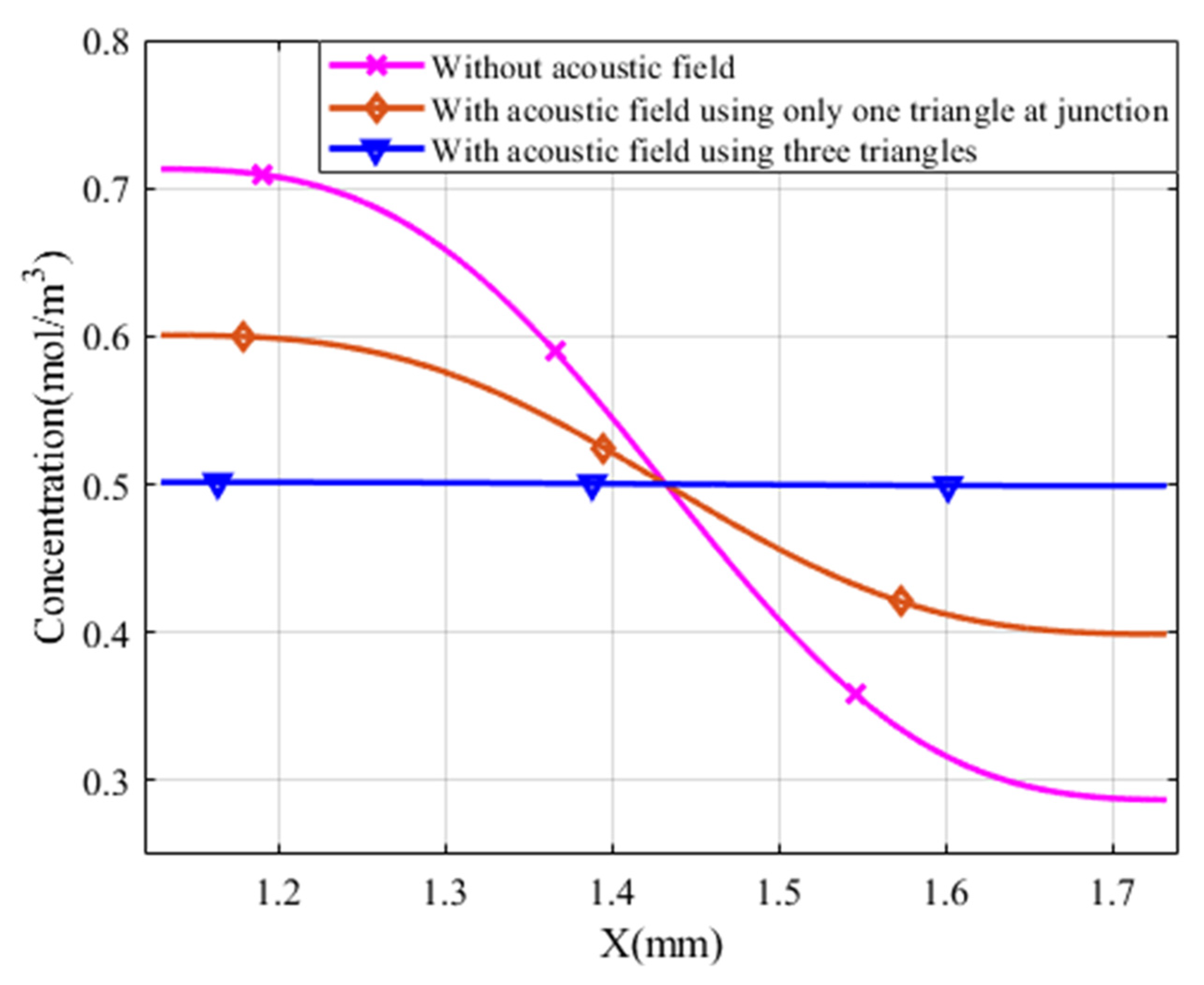
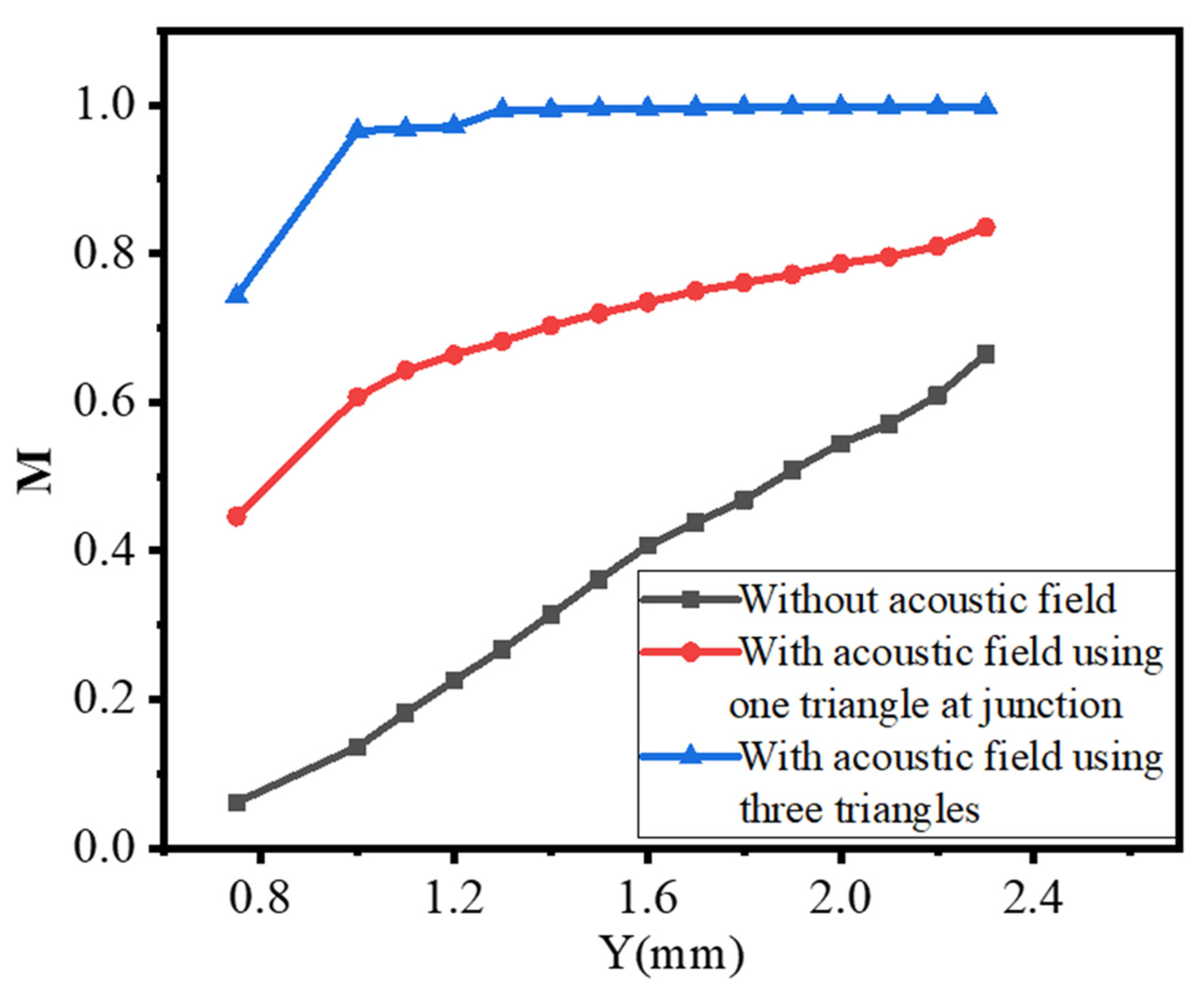
3.3. Mixing Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bayareh, M.; Ashani, M.N.; Usefian, A. Active and passive micromixers: A comprehensive review. Chem. Eng. Process. Process Intensif. 2020, 147, 107771. [Google Scholar] [CrossRef]
- Matsunaga, T.; Nishino, K. Swirl-inducing inlet for passive micromixers. RSC Adv. 2014, 4, 824–829. [Google Scholar] [CrossRef]
- Alam, A.; Afzal, A.; Kim, K.-Y. Mixing performance of a planar micromixer with circular obstructions in a curved microchannel. Chem. Eng. Res. Des. 2014, 92, 423–434. [Google Scholar] [CrossRef]
- Antognoli, M.; Stoecklein, D.; Galletti, C.; Brunazzi, E.; Di Carlo, D. Optimized design of obstacle sequences for microfluidic mixing in an inertial regime. Lab Chip 2021, 21, 3910–3923. [Google Scholar] [CrossRef]
- Luong, T.-D.; Phan, V.-N.; Nguyen, N.-T. High-throughput micromixers based on acoustic streaming induced by surface acoustic wave. Microfluid. Nanofluid. 2011, 10, 619–625. [Google Scholar] [CrossRef] [Green Version]
- Xia, Q.; Zhong, S. Liquid mixing enhanced by pulse width modulation in a Y-shaped jet configuration. Fluid Dyn. Res. 2013, 45, 025504. [Google Scholar] [CrossRef]
- Usefian, A.; Bayareh, M. Numerical and experimental study on mixing performance of a novel electro-osmotic micro-mixer. Meccanica 2019, 54, 1149–1162. [Google Scholar] [CrossRef]
- Hejazian, M.; Nguyen, N.-T. A Rapid Magnetofluidic Micromixer Using Diluted Ferrofluid. Micromachines 2017, 8, 37. [Google Scholar] [CrossRef] [Green Version]
- Ozcelik, A.; Aslan, Z. A practical microfluidic pump enabled by acoustofluidics and 3D printing. Microfluid. Nanofluidics 2021, 25, 10. [Google Scholar] [CrossRef]
- Hao, N.; Pei, Z.; Liu, P.; Bachman, H.; Naquin, T.D.; Zhang, P.; Zhang, J.; Shen, L.; Yang, S.; Yang, K.; et al. Acoustofluidics-Assisted Fluorescence-SERS Bimodal Biosensors. Small 2020, 16, 11. [Google Scholar] [CrossRef]
- Gelin, P.; Sukas, O.S.; Hellemans, K.; Maes, D.; De Malsche, W. Study on the mixing and migration behavior of micron-size particles in acoustofluidics. Chem. Eng. J. 2019, 369, 370–375. [Google Scholar] [CrossRef]
- Bach, J.S.; Bruus, H.J.P.R.L. Suppression of acoustic streaming in shape-optimized channels. Phys. Rev. Lett. 2020, 124, 214501. [Google Scholar] [CrossRef] [PubMed]
- Marmottant, P.; Raven, J.P.; Gardeniers, H.; Bomer, J.G.; Hilgenfeldt, S. Microfluidics with ultrasound-driven bubbles. J. Fluid Mech. 2006, 568, 109–118. [Google Scholar] [CrossRef]
- Lutz, B.R.; Chen, J.; Schwartz, D.T. Microscopic steady streaming eddies created around short cylinders in a channel: Flow visualization and Stokes layer scaling. Phys. Fluids 2005, 17, 023601. [Google Scholar] [CrossRef]
- Ovchinnikov, M.; Zhou, J.; Yalamanchili, S. Acoustic streaming of a sharp edge. J. Acoust. Soc. Am. 2014, 136, 22–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doinikov, A.A.; Gerlt, M.S.; Pavlic, A.; Dual, J. Acoustic streaming produced by sharp-edge structures in microfluidic devices. Microfluid. Nanofluid. 2020, 24, 13. [Google Scholar] [CrossRef]
- Liou, Y.-S.; Kang, X.-J.; Tien, W.-H. Particle aggregation and flow patterns induced by ultrasonic standing wave and acoustic streaming: An experimental study by PIV and PTV. Exp. Therm. Fluid Sci. 2019, 106, 78–86. [Google Scholar] [CrossRef]
- Nama, N.; Barnkob, R.; Mao, Z.; Kähler, C.J.; Costanzo, F.; Huang, T.J. Numerical study of acoustophoretic motion of particles in a PDMS microchannel driven by surface acoustic waves. Lab Chip 2015, 15, 2700–2709. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, X.; Royon, L.; Brunet, P. Unveiling of the mechanisms of acoustic streaming induced by sharp edges. Phys. Rev. E 2020, 102, 043110. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, X.; Brunet, P.; Costalonga, M.; Royon, L. Acoustic streaming near a sharp structure and its mixing performance characterization. Microfluid. Nanofluidics 2019, 23, 104. [Google Scholar] [CrossRef]
- Huang, P.H.; Xie, Y.; Ahmed, D.; Rufo, J.; Nama, N.; Chen, Y.; Chan, C.Y.; Huang, T.J. An acoustofluidic micromixer based on oscillating sidewall sharp-edges. Lab Chip 2013, 13, 3847–3852. [Google Scholar] [CrossRef] [PubMed]
- Legay, M.; Simony, B.; Boldo, P.; Gondrexon, N.; Le Person, S.; Bontemps, A. Improvement of heat transfer by means of ultrasound: Application to a double-tube heat exchanger. Ultrason. Sonochem. 2012, 19, 1194–1200. [Google Scholar] [CrossRef] [PubMed]
- Rasouli, M.R.; Tabrizian, M. An ultra-rapid acoustic micromixer for synthesis of organic nanoparticles. Lab Chip 2019, 19, 3316–3325. [Google Scholar] [CrossRef] [PubMed]
- Vuillermet, G.; Gires, P.-Y.; Casset, F.; Poulain, C. Chladni Patterns in a Liquid at Microscale. Phys. Rev. Lett. 2016, 116, 184501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nama, N.; Huang, P.-H.; Huang, T.J.; Costanzo, F. Investigation of micromixing by acoustically oscillated sharp-edges. Biomicrofluidics 2016, 10, 024124. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, A.; Ahmed, D.; Xie, Y.; Nama, N.; Qu, Z.; Nawaz, A.A.; Huang, T.J. An Acoustofluidic Micromixer via Bubble Inception and Cavitation from Microchannel Sidewalls. Anal. Chem. 2014, 86, 5083–5088. [Google Scholar] [CrossRef]
- Wang, S.S.; Jiao, Z.J.; Huang, X.Y.; Yang, C.; Nguyen, N.T. Acoustically induced bubbles in a microfluidic channel for mixing enhancement. Microfluid. Nanofluid. 2009, 6, 847–852. [Google Scholar] [CrossRef]
- Lee, S.H.; van Noort, D.; Lee, J.Y.; Zhang, B.-T.; Park, T.H. Effective mixing in a microfluidic chip using magnetic particles. Lab Chip 2009, 9, 479–482. [Google Scholar] [CrossRef]
- Lee, C. Optimum design of a y-channel micromixer for enhanced mixing according to the configuration of obstacles. Adv. Appl. Fluid Mech. 2016, 19, 1–22. [Google Scholar] [CrossRef]
- Wang, C.-T.; Hu, Y.-C. Mixing of Liquids Using Obstacles in Y-Type Microchannels. Tamkang J. Sci. Eng. 2010, 13, 385–394. [Google Scholar]
- Wu, Z.; Nguyen, N.-T.; Huang, X. Nonlinear diffusive mixing in microchannels: Theory and experiments. J. Micromech. Microeng. 2004, 14, 604–611. [Google Scholar] [CrossRef]
- Shah, I.; Kim, S.W.; Kim, K.; Doh, Y.H.; Choi, K.H. Experimental and numerical analysis of Y-shaped split and recombination micro-mixer with different mixing units. Chem. Eng. J. 2019, 358, 691–706. [Google Scholar] [CrossRef]
- Sahu, P.K.; Golia, A.; Sen, A.K. Investigations into mixing of fluids in microchannels with lateral obstructions. Microsyst. Technol. 2013, 19, 493–501. [Google Scholar] [CrossRef]
- Wang, L.; Ma, S.; Han, X. Micromixing enhancement in a novel passive mixer with symmetrical cylindrical grooves. Asia-Pac. J. Chem. Eng. 2015, 10, 201–209. [Google Scholar] [CrossRef]
- Hsieh, S.-S.; Lin, J.-W.; Chen, J.-H. Mixing efficiency of Y-type micromixers with different angles. Int. J. Heat Fluid Flow 2013, 44, 130–139. [Google Scholar] [CrossRef]
- COMSOL Multiphysics 5.6. Available online: www.comsol.com (accessed on 23 September 2021).
- CRCnetBASE Product. Handbook of Chemistry and Physics, 97th ed.; CRC Press: Boca Raton, FL, USA, 2016–2017. [Google Scholar]
- Bruus, H. Acoustofluidics 2: Perturbation theory and ultrasound resonance modes. Lab Chip 2012, 12, 20–28. [Google Scholar] [CrossRef]
- Friend, J.; Yeo, L.Y. Microscale acoustofluidics: Microfluidics driven via acoustics and ultrasonics. Rev. Mod. Phys. 2011, 83, 647–704. [Google Scholar] [CrossRef] [Green Version]
- Rafeie, M.; Welleweerd, M.; Hassanzadeh-Barforoushi, A.; Asadnia, M.; Olthuis, W.; Warkiani, M.E. An easily fabricated three-dimensional threaded lemniscate-shaped micromixer for a wide range of flow rates. Biomicrofluidics 2017, 11, 014108. [Google Scholar] [CrossRef] [Green Version]
- Muller, P.B.; Barnkob, R.; Jensen, M.J.H.; Bruus, H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab Chip 2012, 12, 4617–4627. [Google Scholar] [CrossRef] [Green Version]



| [37] | Value | Units |
|---|---|---|
| Viscous dynamics viscosity, µ | 890 | µPas |
| 4180 | J/kg·K | |
| 997 | kg/m3 | |
| 1497 | m/s | |
| 1/Pa | ||
| Specific heat capacity ratio, γ | 1.012 | |
| 0.61 | W/m·K | |
| 1/K | ||
| /s | ||
| 2.47 | mPas |
| Parameters | Values | Units |
|---|---|---|
| Inlets velocities | 4.46, 8.89, 30, 55.6 | µm/s |
| Oscillation frequency | 13 | kHz |
| Oscillation amplitude | 3–6 | µm |
| Vertex angles | ||
| Spacing gap S of the side walls triangles | 0.15, 0.30, 0.40, 0.60, 0.90 | mm |
| Diffusion coefficient (fluorescein sodium salt) | 10−9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Endaylalu, S.A.; Tien, W.-H. A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming. Micromachines 2022, 13, 338. https://doi.org/10.3390/mi13020338
Endaylalu SA, Tien W-H. A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming. Micromachines. 2022; 13(2):338. https://doi.org/10.3390/mi13020338
Chicago/Turabian StyleEndaylalu, Sintayehu Assefa, and Wei-Hsin Tien. 2022. "A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming" Micromachines 13, no. 2: 338. https://doi.org/10.3390/mi13020338
APA StyleEndaylalu, S. A., & Tien, W.-H. (2022). A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming. Micromachines, 13(2), 338. https://doi.org/10.3390/mi13020338






