Trampolining of Droplets on Hydrophobic Surfaces Using Electrowetting
Abstract
:1. Introduction
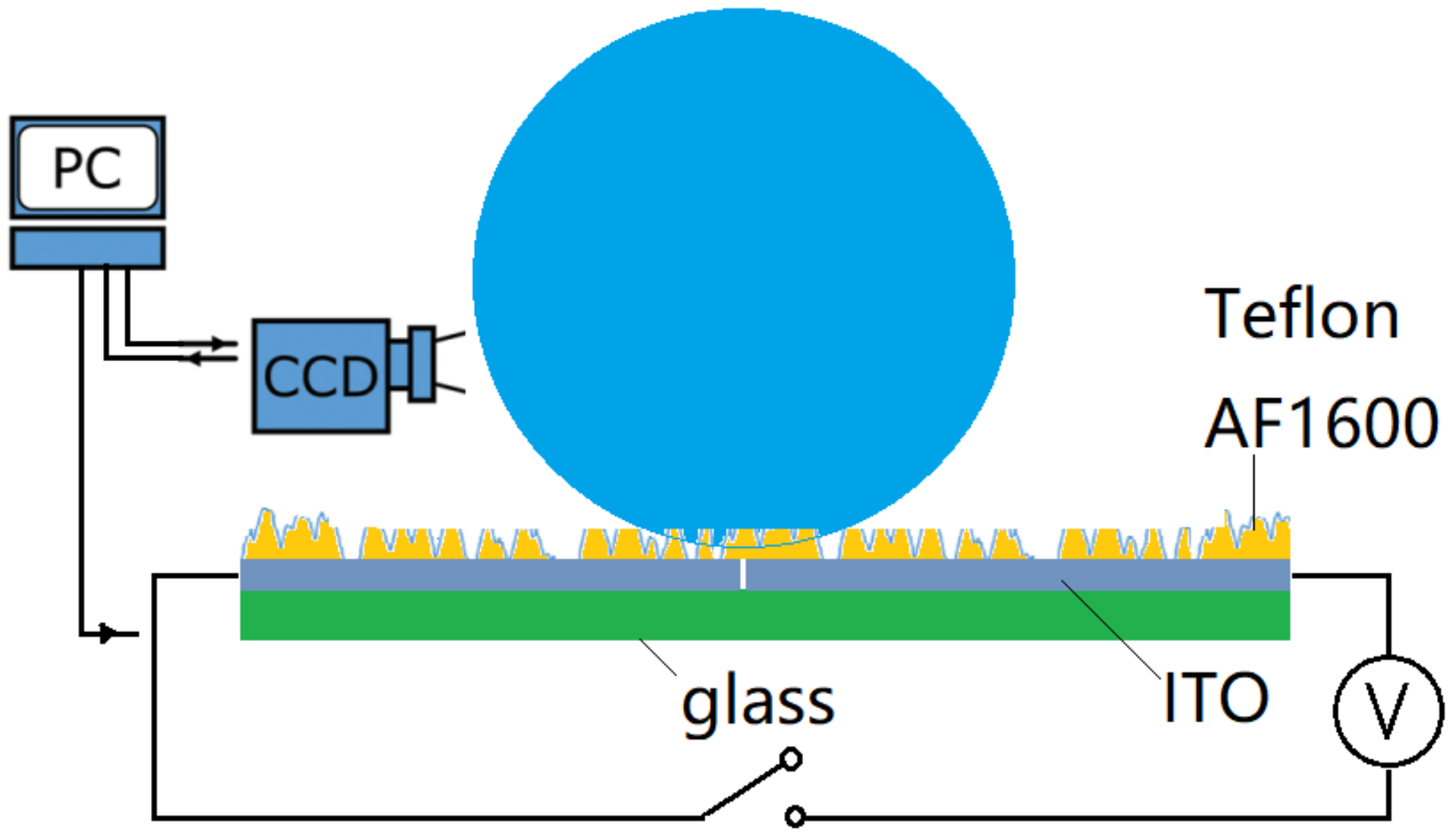
2. Experiments and Methods
3. Results and Discussion
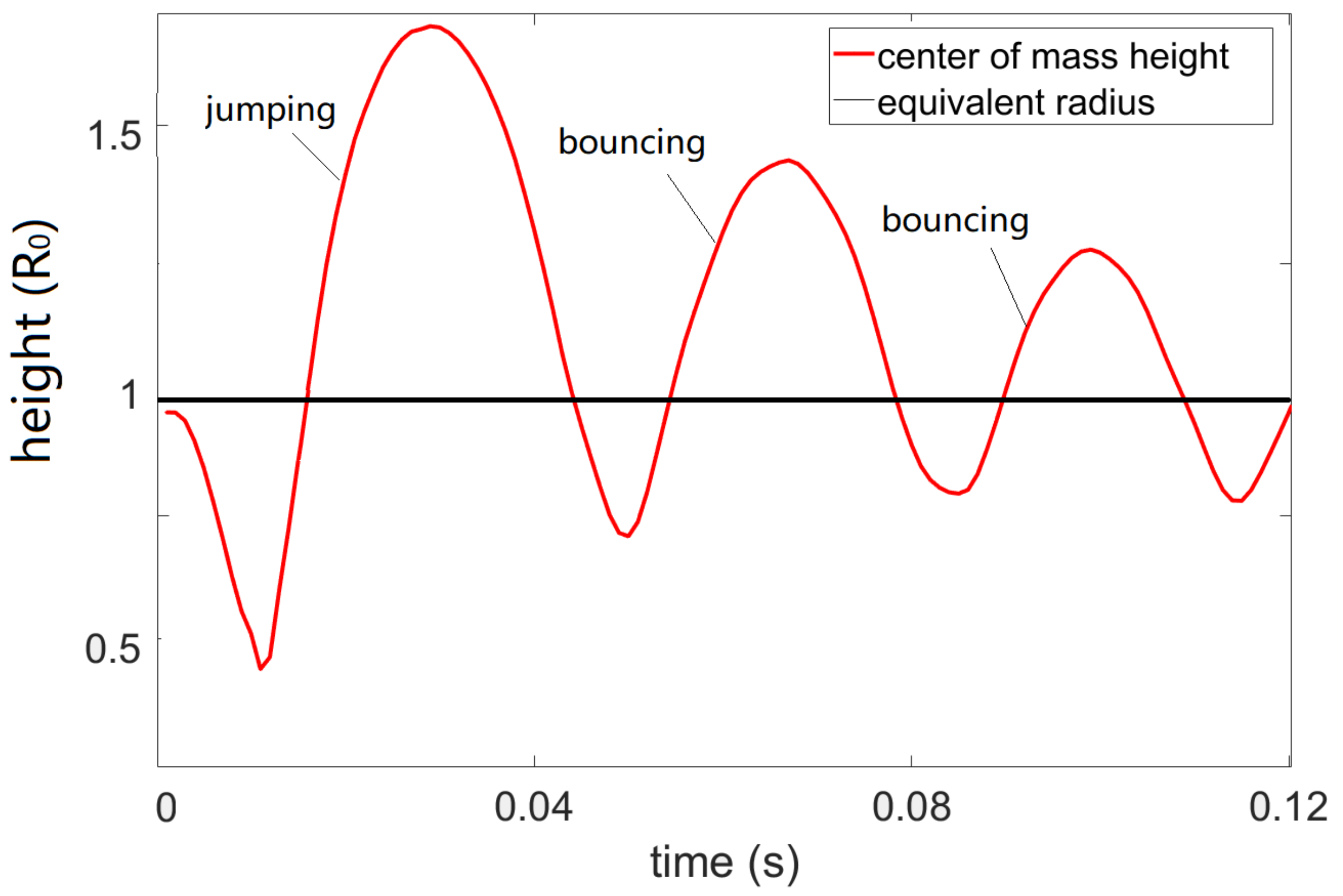
3.1. EW-Induced Droplet Jumping
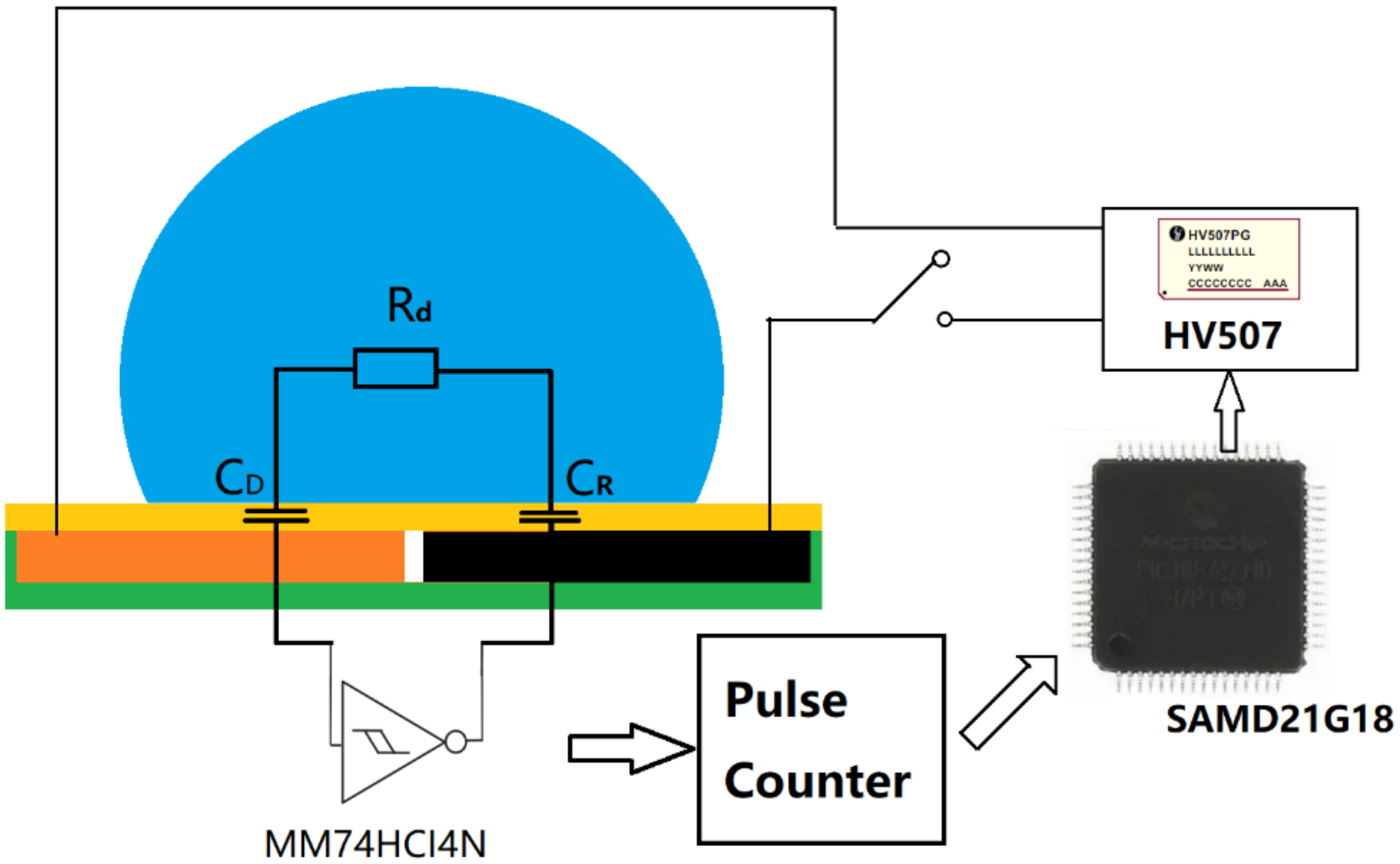
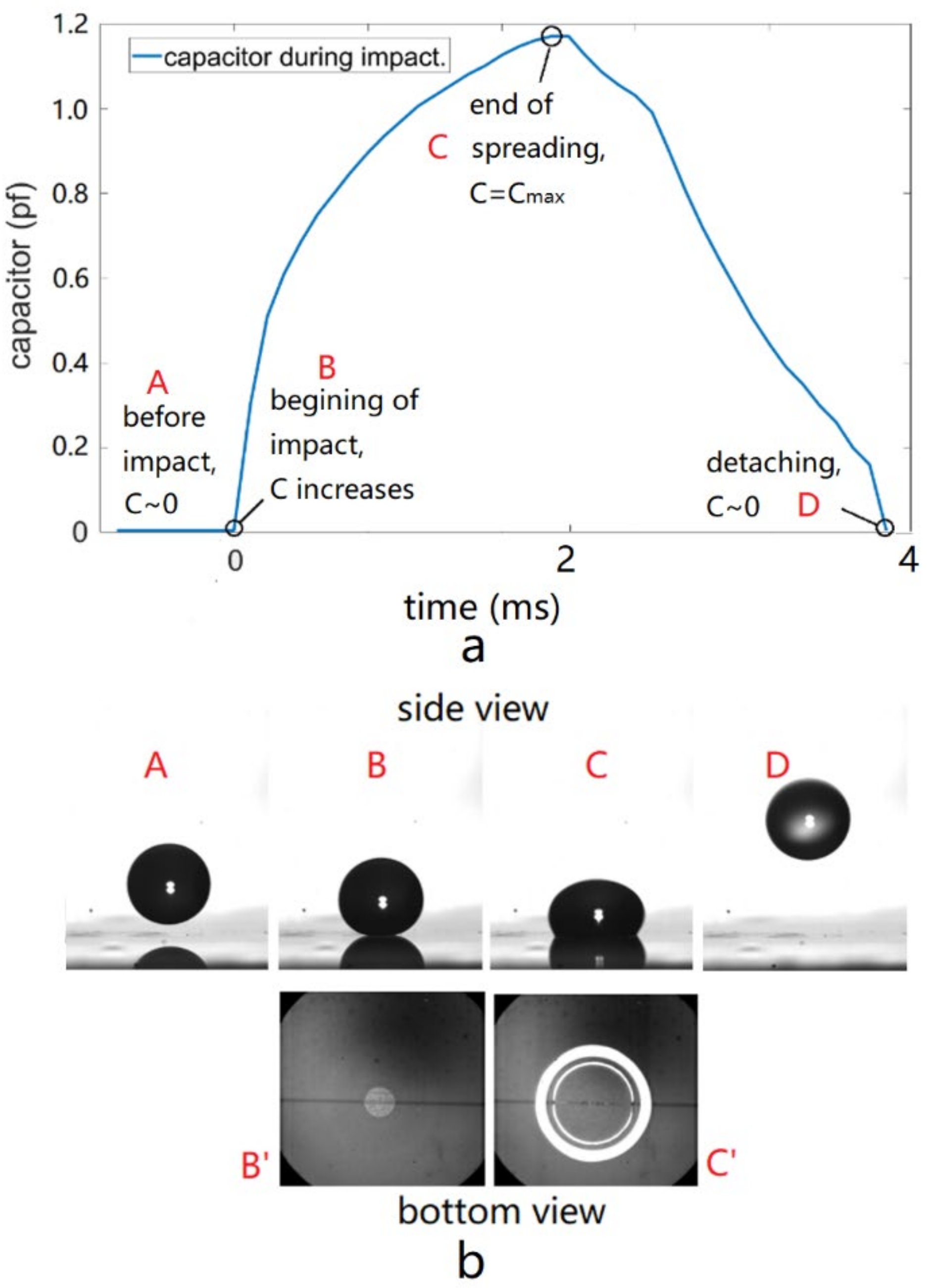
3.2. Droplet Monitoring Using Capacitor Sensor
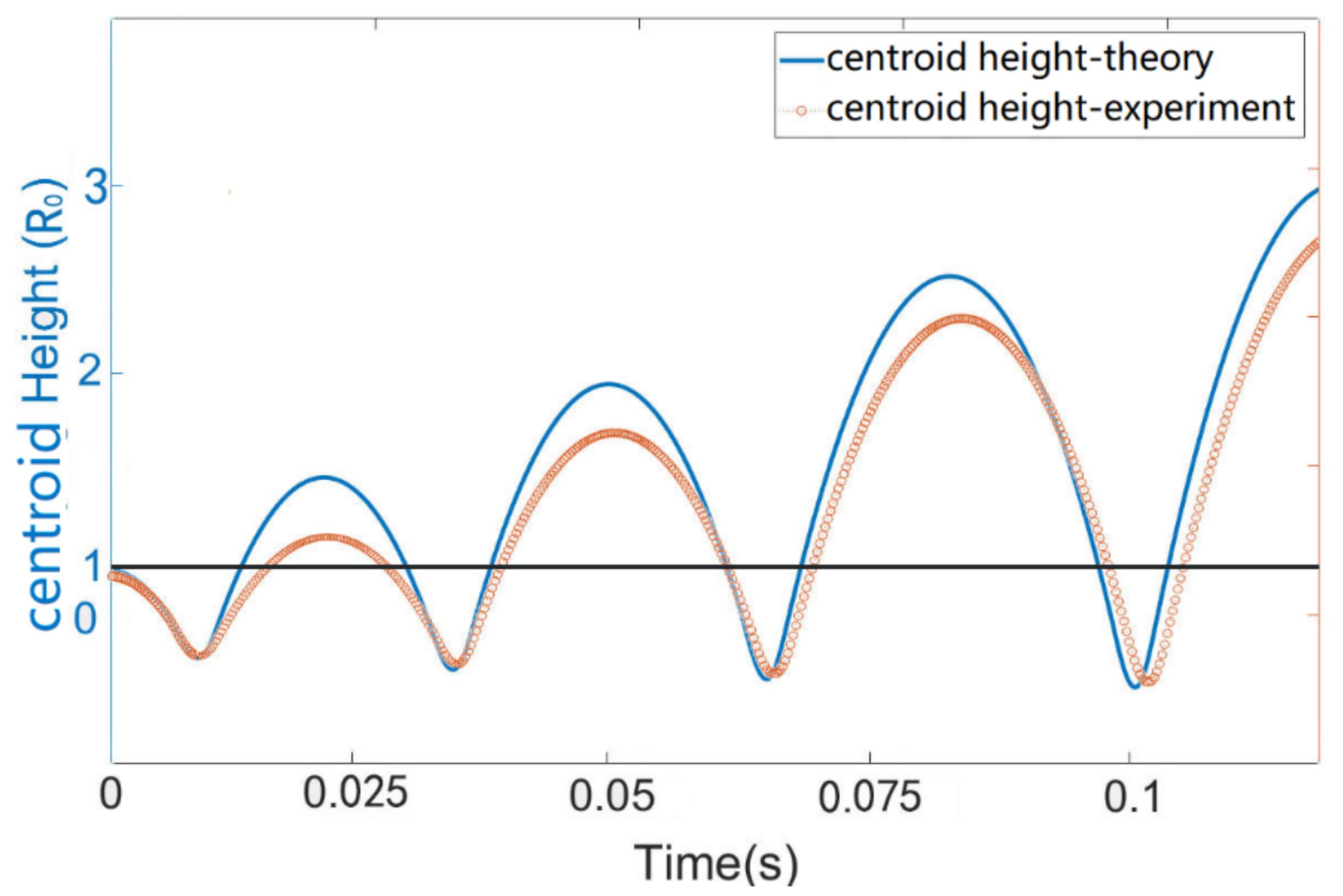
3.3. Modeling of EW-Driven Droplet Trampoline
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wisdom, K.M.; Watson, J.A.; Qu, X.; Liu, F.; Watson, G.S.; Chen, C.-H. Self-cleaning of superhydrophobic surfaces by self-propelled jumping condensate. Proc. Natl. Acad. Sci. USA 2013, 110, 7992. [Google Scholar] [CrossRef] [Green Version]
- Krupenkin, T.; Taylor, J.A. Reverse electrowetting as a new approach to high-power energy harvesting. Nat. Commun. 2011, 2, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schutzius, T.M.; Jung, S.; Maitra, T.; Graeber, G.; Köhme, M.; Poulikakos, D. Spontaneous droplet trampolining on rigid superhydrophobic surfaces. Nature 2015, 527, 82. [Google Scholar] [CrossRef] [PubMed]
- Boreyko, J.B.; Chen, C.-H. Self-propelled dropwise condensate on superhydrophobic surfaces. Phys. Rev. Lett. 2009, 103, 184501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bormashenko, E.; Pogreb, R.; Whyman, G.; Bormashenko, Y.; Erlich, M. Vibration-induced Cassie-Wenzel wetting transition on rough surfaces. Appl. Phys. Lett. 2007, 90, 201917. [Google Scholar] [CrossRef]
- Chen, R.; Jiao, L.; Zhu, X.; Liao, Q.; Ye, D.; Zhang, B.; Li, W.; Lei, Y.; Li, D. Cassie-to-Wenzel transition of droplet on the superhydrophobic surface caused by light induced evaporation. Appl. Therm. Eng. 2018, 144, 945. [Google Scholar] [CrossRef]
- Liu, G.; Fu, L.; Rode, A.V.; Craig, V.S. Water droplet motion control on superhydrophobic surfaces: Exploiting the Wenzel-to-Cassie transition. Langmuir 2011, 27, 2595. [Google Scholar] [CrossRef]
- Wang, Z.; Ende, D.V.D.; Pit, A.M.; Lagraauw, R.; Mugele, F. Jumping drops on hydrophobic surfaces, controlling energy transfer by timed electric actuation. Soft Matter 2017, 13, 4856–4863. [Google Scholar] [CrossRef]
- Sourais, A.G.; Papathanasiou, A.G. Modelling of Electrowetting-Induced Droplet Detachment and Jumping over Topographically Micro-Structured Surfaces. Micromachines 2021, 12, 592. [Google Scholar] [CrossRef]
- Mugele, F.; Baret, J.-C. Electrowetting: From basics to applications. J. Phys. Condens. Matter 2005, 17, R705. [Google Scholar] [CrossRef]
- Moon, H.; Cho, S.K.; Garrell, R.L.; Kim, C.-J.C. Low voltage electrowetting-on-dielectric. J. Appl. Phys. 2002, 92, 4080. [Google Scholar] [CrossRef]
- Pollack, M.G.; Fair, R.B.; Shenderov, A.D. Electrowetting-based actuation of liquid droplets for microfluidic applications. Appl. Phys. Lett. 2000, 77, 1725. [Google Scholar] [CrossRef] [Green Version]
- Berge, B.; Peseux, J. Variable focal lens controlled by an external voltage: An application of electrowetting. Eur. Phys. J. E 2000, 3, 159. [Google Scholar] [CrossRef]
- Hayes, R.A.; Feenstra, B.J. Video-speed electronic paper based on electrowetting. Nature 2003, 425, 383. [Google Scholar] [CrossRef]
- Cho, S.K.; Moon, H.; Kim, C.-J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. J. Microelectromech. Syst. 2003, 12, 70. [Google Scholar]
- Lee, S.J.; Lee, S.; Kang, K.H. Droplet jumping by electrowetting and its application to the three-dimensional digital microfluidics. Appl. Phys. Lett. 2012, 100, 10318. [Google Scholar]
- Raman, K.A.; Jaiman, R.K.; Lee, T.-S.; Low, H.-T. A numerical study on electrowetting-induced jumping and transport of droplet. Int. J. Heat Mass Transf. 2016, 99, 805–821. [Google Scholar] [CrossRef]
- Zhang, K.; Li, Z.; Chen, S. Analytical prediction of electrowetting-induced jumping motion for droplets on hydrophobic substrates. Phys. Fluids 2019, 31, 081703. [Google Scholar]
- Burkhart, C.T.; Maki, K.L.; Schertzer, M.J. Coplanar Electrowetting-Induced Droplet Detachment from Radially Symmetric Electrodes. Langmuir 2020, 36, 8129. [Google Scholar] [CrossRef]
- Hong, J.; Lee, S.J. Detaching droplets in immiscible fluids from a solid substrate with the help of electrowetting. Lab A Chip 2015, 15, 900. [Google Scholar] [CrossRef] [PubMed]
- Merdasi, A.; Moosavi, A.; Shafii, M. Electrowetting-induced droplet jumping over topographically structured surfaces. Mater. Res. Express 2019, 6, 086333. [Google Scholar] [CrossRef]
- Weng, N.; Wang, Q.; Gu, J.; Li, J.; Wang, C.; Yao, W. The dynamics of droplet detachment in reversed electrowetting (REW). Colloids Surf. A Physicochem. Eng. Asp. 2021, 616, 126303. [Google Scholar] [CrossRef]
- Xiao, K.; Wu, C.-X. Curvature effect of electrowetting-induced droplet detachment. J. Appl. Phys. 2021, 129, 234701. [Google Scholar] [CrossRef]
- Hong, J.; Kim, Y.K.; Won, D.J.; Kim, J.; Lee, S.J. Three-dimensional digital microfluidic manipulation of droplets in oil medium. Sci. Rep. 2015, 5, 10685. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Li, L.; Gu, J.; Zhang, C.; Lyu, J.; Yao, W. Manipulation of a Nonconductive Droplet in an Aqueous Fluid with AC Electric Fields: Droplet Dewetting, Oscillation, and Detachment. Langmuir 2021, 37, 12098. [Google Scholar] [CrossRef] [PubMed]
- Vo, Q.; Tran, T. Droplet ejection by electrowetting actuation. Appl. Phys. Lett. 2021, 118, 161603. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, S.; Kang, K.H. Jumping of a droplet on a superhydrophobic surface in AC electrowetting. J. Vis. 2011, 14, 259. [Google Scholar] [CrossRef]
- Vo, Q.; Tran, T. Critical conditions for jumping droplets. Phys. Rev. Lett. 2019, 123, 024502. [Google Scholar] [CrossRef]
- Lee, S.J.; Hong, J.; Kang, K.H.; Kang, I.S.; Lee, S.J. Electrowetting-induced droplet detachment from hydrophobic surfaces. Langmuir 2014, 30, 1805. [Google Scholar] [CrossRef]
- Cavalli, A.; Preston, D.J.; Tio, E.; Martin, D.W.; Miljkovic, N.; Wang, E.N.; Blanchette, F.; Bush, J.W. Electrically induced drop detachment and ejection. Phys. Fluids 2016, 28, 022101. [Google Scholar] [CrossRef] [Green Version]
- Islam, M.A.; Tong, A.Y. A numerical study on electrowetting-induced droplet detachment from hydrophobic surface. J. Heat Transf. 2018, 140, 052003. [Google Scholar] [CrossRef]
- Lapierre, F.; Coffinier, Y.; Boukherroub, R.; Thomy, V. Electro-(de)wetting on Superhydrophobic Surfaces. Langmuir 2013, 29, 13346. [Google Scholar] [CrossRef]
- Gong, J. All-electronic droplet generation on-chip with real-time feedback control for EWOD digital microfluidics. Lab A Chip 2008, 8, 898. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Z.; Darhuber, A.A.; Troian, S.M.; Wagner, S. Capacitive sensing of droplets for microfluidic devices based on thermocapillary actuation. Lab A Chip 2004, 4, 473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shih, S.C.; Fobel, R.; Kumar, P.; Wheeler, A.R. A feedback control system for high-fidelity digital microfluidics. Lab A Chip 2011, 11, 535. [Google Scholar] [CrossRef] [PubMed]
- Murran, M.A.; Najjaran, H. Capacitance-based droplet position estimator for digital microfluidic devices. Lab A Chip 2012, 12, 2053. [Google Scholar] [CrossRef]
- Bhattacharjee, B.; Najjaran, H. Droplet sensing by measuring the capacitance between coplanar electrodes in a digital microfluidic system. Lab A Chip 2012, 12, 4416. [Google Scholar] [CrossRef]
- Pham, J.T.; Paven, M.; Wooh, S.; Kajiya, T.; Butt, H.-J.; Vollmer, D. Spontaneous jumping, bouncing and trampolining of hydrogel drops on a heated plate. Nat. Commun. 2017, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Graeber, G.; Regulagadda, K.; Hodel, P.; Küttel, C.; Landolf, D.; Schutzius, T.M.; Poulikakos, D. Leidenfrost droplet trampolining. Nat. Commun. 2021, 12, 1. [Google Scholar] [CrossRef]
- Liu, M.; Du, H.; Cheng, Y.; Zheng, H.; Jin, Y.; To, S.; Wang, S.; Wang, Z. Explosive Pancake Bouncing on Hot Superhydrophilic Surfaces. ACS Appl. Mater. Interfaces 2021, 13, 24321–24328. [Google Scholar] [CrossRef]
- Gilet, T.; Bush, J.W. The fluid trampoline: Droplets bouncing on a soap film. J. Fluid Mech. 2009, 625, 167. [Google Scholar] [CrossRef]
- Ryu, J.; Kim, K.; Park, J.; Hwang, B.G.; Ko, Y.; Kim, H.; Han, J.; Seo, E.; Park, Y.; Lee, S.J. Nearly perfect durable superhydrophobic surfaces fabricated by a simple one-step plasma treatment. Sci. Rep. 2017, 7, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yi, U.C.; Kim, C.J. Characterization of electrowetting actuation on addressable single-side coplanar electrodes. J. Micromech. Microeng. 2006, 16, 2053. [Google Scholar] [CrossRef] [Green Version]
- Bostwick, J.; Steen, P. Capillary oscillations of a constrained liquid drop. Phys. Fluids 2009, 21, 032108. [Google Scholar] [CrossRef]
- Vejrazka, J.; Vobecka, L.; Tihon, J. Linear oscillations of a supported bubble or drop. Phys. Fluids 2013, 25, 062102. [Google Scholar] [CrossRef]
- Miller, C.; Scriven, L. The oscillations of a fluid droplet immersed in another fluid. J. Fluid Mech. 1968, 32, 417. [Google Scholar] [CrossRef]
- Boreyko, J.B.; Chen, C.H. Self-propelled jumping drops on superhydrophobic surfaces. Phys Fluids 2010, 22, 091110. [Google Scholar] [CrossRef] [Green Version]
- Enright, R.; Miljkovic, N.; Sprittles, J.; Nolan, K.; Mitchell, R.; Wang, E.N. How Coalescing Droplets Jump. Acs Nano 2014, 8, 10352. [Google Scholar] [CrossRef]
- Okumura, K.; Chevy, F.; Richard, D.; Quéré, D.; Clanet, C. Water spring: A model for bouncing drops. EPL (Europhys. Lett.) 2003, 62, 237. [Google Scholar] [CrossRef] [Green Version]
- Hong, J.; Kim, Y.K.; Kang, K.H.; Oh, J.M.; Kang, I.S. Effects of drop size and viscosity on spreading dynamics in DC electrowetting. Langmuir 2013, 29, 9118. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, X.; Wang, L.; Zhao, C.; Zhou, D.; Wei, J. Trampolining of Droplets on Hydrophobic Surfaces Using Electrowetting. Micromachines 2022, 13, 345. https://doi.org/10.3390/mi13030345
Wang Z, Liu X, Wang L, Zhao C, Zhou D, Wei J. Trampolining of Droplets on Hydrophobic Surfaces Using Electrowetting. Micromachines. 2022; 13(3):345. https://doi.org/10.3390/mi13030345
Chicago/Turabian StyleWang, Zhantao, Xiaojuan Liu, Li Wang, Cunlu Zhao, Danfeng Zhou, and Jiazheng Wei. 2022. "Trampolining of Droplets on Hydrophobic Surfaces Using Electrowetting" Micromachines 13, no. 3: 345. https://doi.org/10.3390/mi13030345





