Normalization of Blood Viscosity According to the Hematocrit and the Shear Rate
Abstract
:1. Introduction
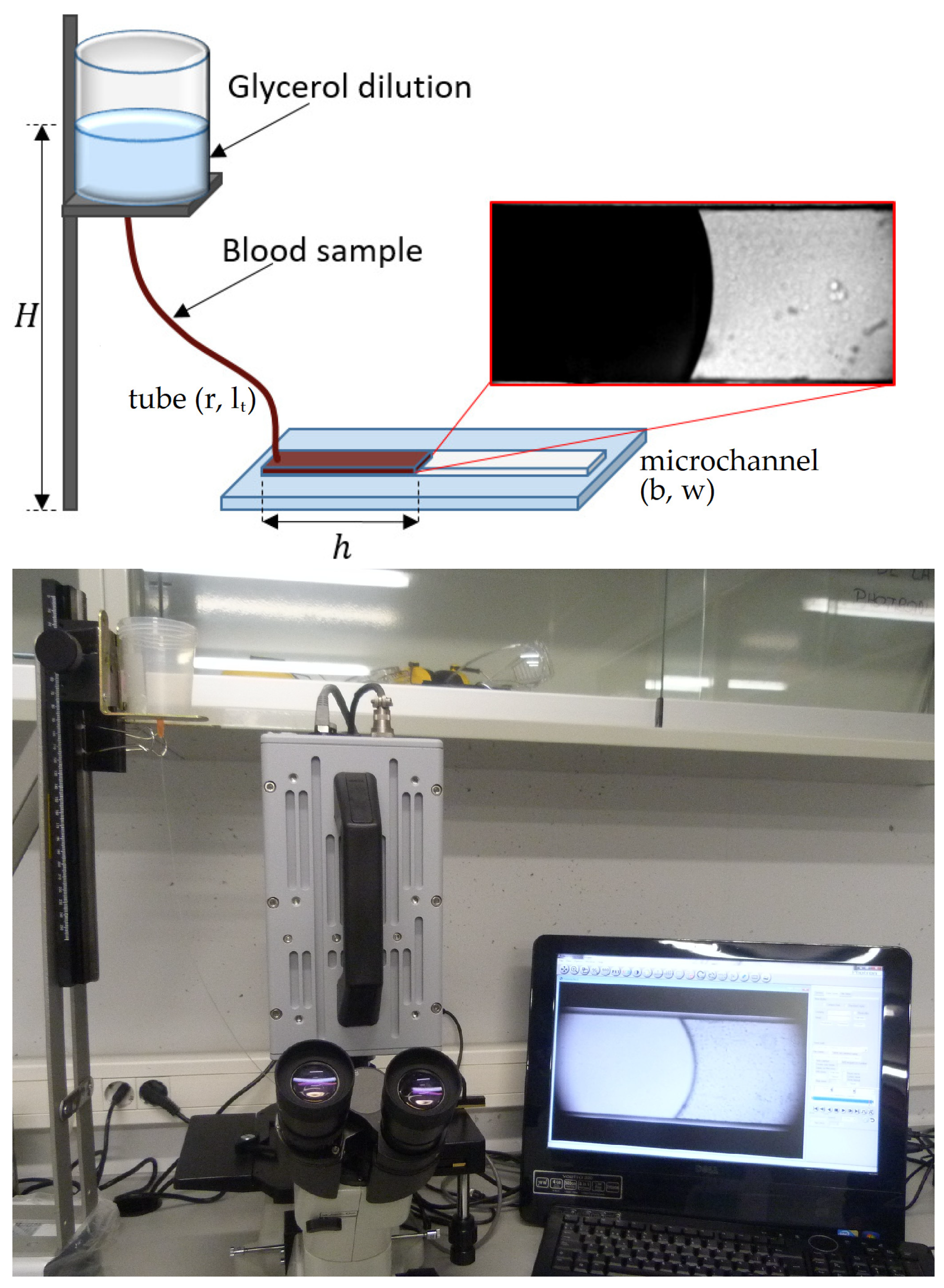
2. Materials and Methods
3. Theoretical Model
4. Results
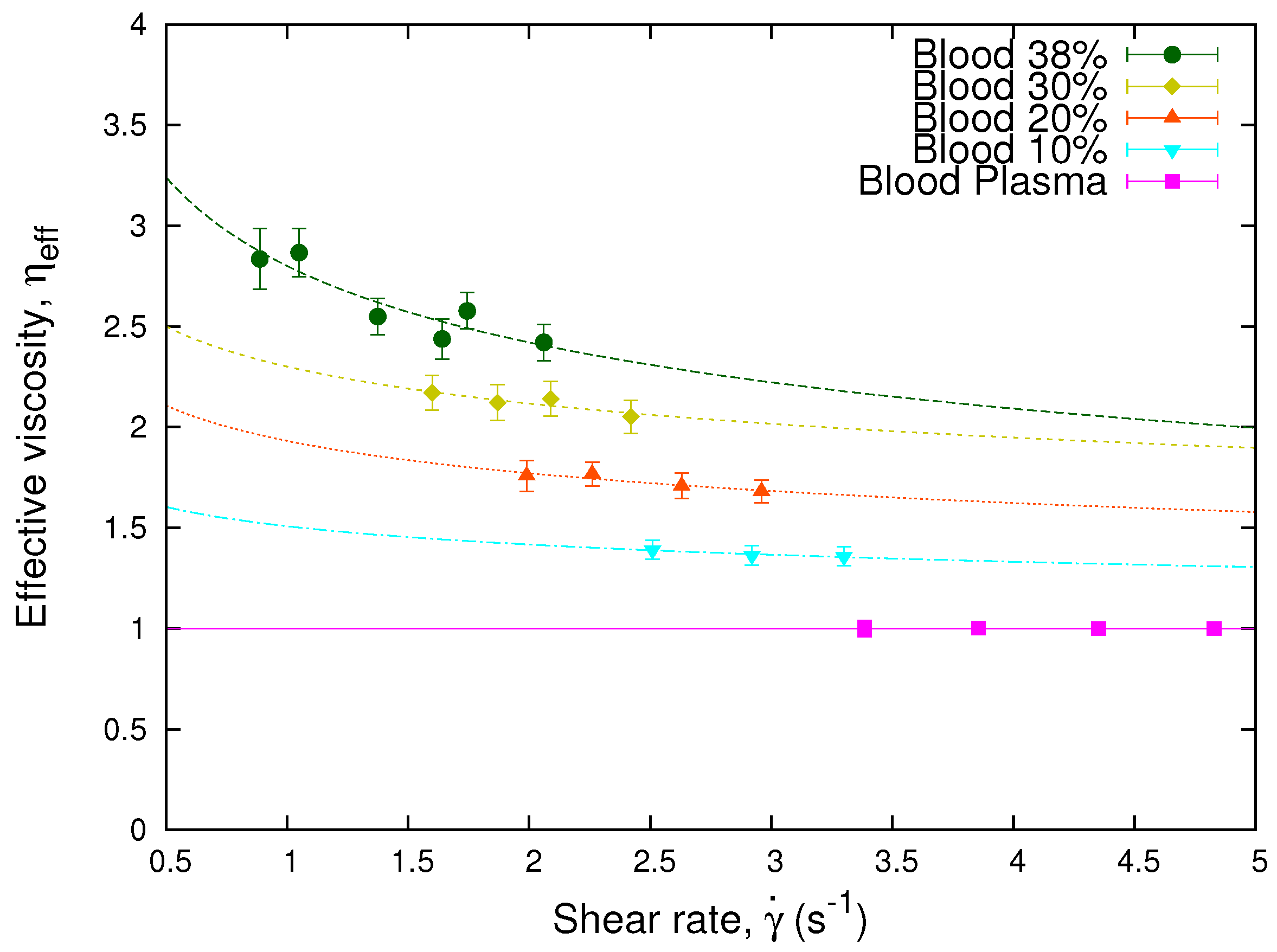
4.1. Effective Viscosity
4.2. Normalization of Blood Viscosity According to the Hematocrit
4.2.1. Effective Viscosity and Red Blood Cells Concentration of the Same Donor: A Linear Approach
4.2.2. Viscosity and Red Blood Cell Concentration for Different Donors
4.2.3. Non-Linear Scaling According to the Hematocrit
4.3. Normalization of Blood Viscosity for Different Donors According to the Shear Rate
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Q | Flow rate | or |
| Viscosity | Pa·s | |
| Density | ||
| Shear rate | s−1 | |
| Shear stress | Pa | |
| Pressure gradient | Pa/m | |
| Pressure drop | Pa | |
| Capillary pressure | Pa | |
| Hydrostatic pressure | Pa | |
| g | Acceleration of gravity | |
| H | Column height | m |
| h | Position | m |
| Mean velocity | or | |
| Velocity in the tube | ||
| Velocity in the channel | ||
| Channel length | m | |
| w | Channel width | m |
| b | Channel height, gap, or depth | μm |
| Tube length | m | |
| r | Tube radius | m |
| Blood plasma viscosity | Pa·s | |
| Effective viscosity | ||
| m | Consistency index | |
| n | Viscosity exponent | |
| Generalized consistency index | ||
| Normalized viscosity to hematocrit | ||
| Red blood cells concentration | ||
| Intrinsic viscosity | ||
| Maximum packing fraction | ||
| Characteristic number | ||
| Bending energy of a healthy RBC | J | |
| d | Mean diameter of a RBC | μm |
| Effective shear rate | s−1 | |
| Variation coefficient | ||
| Wall stress | Pa | |
| Wall shear rate | s−1 |
Appendix A. Comparison with Weissenberg–Rabinowitch–Mooney Correction
References
- Baskurt, O.K. Handbook of Hemorheology and Hemodynamics; IOS Press: Amsterdam, The Netherlands, 2007; Volume 69. [Google Scholar]
- Thurston, G.B.; Henderson, N.M. Effects of flow geometry on blood viscoelasticity. Biorheology 2006, 43, 729–746. [Google Scholar] [PubMed]
- Merrill, E.W. Rheology of blood. Physiol. Rev. 1969, 49, 863–888. [Google Scholar] [CrossRef] [PubMed]
- Cokelet, G.R.; Merrill, E.W.; Gilliland, E.R.; Shin, H.; Britten, A.; Wells, R.E., Jr. The rheology of human blood—Measurement near and at zero shear rate. Trans. Soc. Rheol. (1957–1977) 1963, 7, 303–317. [Google Scholar] [CrossRef]
- Chien, S. Shear dependence of effective cell volume as a determinant of blood viscosity. Science 1970, 168, 977–979. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Pan, W.; Caswell, B.; Gompper, G.; Karniadakis, G.E. Predicting human blood viscosity in silico. Proc. Natl. Acad. Sci. USA 2011, 108, 11772–11777. [Google Scholar] [CrossRef] [Green Version]
- Lanotte, L.; Mauer, J.; Mendez, S.; Fedosov, D.A.; Fromental, J.M.; Claveria, V.; Nicoud, F.; Gompper, G.; Abkarian, M. Red cells’ dynamic morphologies govern blood shear thinning under microcirculatory flow conditions. Proc. Natl. Acad. Sci. USA 2016, 113, 13289–13294. [Google Scholar] [CrossRef] [Green Version]
- Merrill, E.; Benis, A.; Gilliland, E.; Sherwood, T.; Salzman, E. Pressure-flow relations of human blood in hollow fibers at low flow rates. J. Appl. Physiol. 1965, 20, 954–967. [Google Scholar] [CrossRef]
- Viallat, A.; Abkarian, M. Red blood cell: From its mechanics to its motion in shear flow. Int. J. Lab. Hematol. 2014, 36, 237–243. [Google Scholar] [CrossRef]
- Chien, S.; Usami, S.; Taylor, H.M.; Lundberg, J.L.; Gregersen, M.I. Effects of hematocrit and plasma proteins on human blood rheology at low shear rates. J. Appl. Physiol. 1966, 21, 81–87. [Google Scholar] [CrossRef]
- Eckmann, D.M.; Bowers, S.; Stecker, M.; Cheung, A.T. Hematocrit, volume expander, temperature, and shear rate effects on blood viscosity. Anesth. Analg. 2000, 91, 539–545. [Google Scholar] [CrossRef]
- Abkarian, M.; Viallat, A. Vesicles and red blood cells in shear flow. Soft Matter 2008, 4, 653–657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohandas, N.; Gallagher, P.G. Red cell membrane: Past, present, and future. Blood J. Am. Soc. Hematol. 2008, 112, 3939–3948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- George, M.J.; Bynum, J.; Nair, P.; Cap, A.P.; Wade, C.E.; Cox, C.S., Jr.; Gill, B.S. Platelet biomechanics, platelet bioenergetics, and applications to clinical practice and translational research. Platelets 2018, 29, 431–439. [Google Scholar] [CrossRef] [PubMed]
- Trejo-Soto, C.; Costa-Miracle, E.; Rodriguez-Villarreal, I.; Cid, J.; Castro, M.; Alarcon, T.; Hernandez-Machado, A. Front microrheology of the non-Newtonian behaviour of blood: Scaling theory of erythrocyte aggregation by aging. Soft Matter 2017, 13, 3042–3047. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Liu, W.K. Rheology of red blood cell aggregation by computer simulation. J. Comput. Phys. 2006, 220, 139–154. [Google Scholar] [CrossRef]
- McWhirter, J.L.; Noguchi, H.; Gompper, G. Deformation and clustering of red blood cells in microcapillary flows. Soft Matter 2011, 7, 10967–10977. [Google Scholar] [CrossRef] [Green Version]
- Tomaiuolo, G.; Simeone, M.; Martinelli, V.; Rotoli, B.; Guido, S. Red blood cell deformation in microconfined flow. Soft Matter 2009, 5, 3736–3740. [Google Scholar] [CrossRef]
- Mauer, J.; Mendez, S.; Lanotte, L.; Nicoud, F.; Abkarian, M.; Gompper, G.; Fedosov, D.A. Flow-induced transitions of red blood cell shapes under shear. Phys. Rev. Lett. 2018, 121, 118103. [Google Scholar] [CrossRef] [Green Version]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering Flows in Small Devices: Microfluidics Toward a Lab-on-a-Chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef] [Green Version]
- Pipe, C.; McKinley, G.H. Microfluidic rheometry. Mech. Res. Commun. 2009, 36, 110–120. [Google Scholar] [CrossRef] [Green Version]
- Nghe, P.; Terriac, E.; Schneider, M.; Li, Z.; Cloitre, M.; Abecassis, B.; Tabeling, P. Microfluidics and complex fluids. Lab Chip 2011, 11, 788–794. [Google Scholar] [CrossRef] [PubMed]
- Gervais, L.; De Rooij, N.; Delamarche, E. Microfluidic chips for point-of-care immunodiagnostics. Adv. Mater. 2011, 23, H151–H176. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Wang, W.S.; Vanapalli, S.A. Microfluidic viscometers for shear rheology of complex fluids and biofluids. Biomicrofluidics 2016, 10, 043402. [Google Scholar] [CrossRef] [Green Version]
- Khnouf, R.; Karasneh, D.; Abdulhay, E.; Abdelhay, A.; Sheng, W.; Fan, Z.H. Microfluidics-based device for the measurement of blood viscosity and its modeling based on shear rate, temperature, and heparin concentration. Biomed. Microdevices 2019, 21, 80. [Google Scholar] [CrossRef]
- Kucukal, E.; Man, Y.; Hill, A.; Liu, S.; Bode, A.; An, R.; Kadambi, J.; Little, J.A.; Gurkan, U.A. Whole blood viscosity and red blood cell adhesion: Potential biomarkers for targeted and curative therapies in sickle cell disease. Am. J. Hematol. 2020, 95, 1246–1256. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, V.; Gonçalves, I.M.; Souza, A.; Souza, M.S.; Bento, D.; Ribeiro, J.E.; Lima, R.; Pinho, D. Manual and Automatic Image Analysis Segmentation Methods for Blood Flow Studies in Microchannels. Micromachines 2021, 12, 317. [Google Scholar] [CrossRef] [PubMed]
- Abkarian, M.; Faivre, M.; Horton, R.; Smistrup, K.; Best-Popescu, C.A.; Stone, H.A. Cellular-scale hydrodynamics. Biomed. Mater. 2008, 3, 034011. [Google Scholar] [CrossRef] [Green Version]
- Secomb, T.W. Mechanics and computational simulation of blood flow in microvessels. Med. Eng. Phys. 2011, 33, 800–804. [Google Scholar] [CrossRef] [Green Version]
- Tomaiuolo, G.; Guido, S. Start-up shape dynamics of red blood cells in microcapillary flow. Microvasc. Res. 2011, 82, 35–41. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Noguchi, H.; Gompper, G. Multiscale modeling of blood flow: From single cells to blood rheology. Biomech. Model. Mechanobiol. 2014, 13, 239–258. [Google Scholar] [CrossRef]
- Kim, S.; Kim, K.C.; Yeom, E. Microfluidic method for measuring viscosity using images from smartphone. Opt. Lasers Eng. 2018, 104, 237–243. [Google Scholar] [CrossRef]
- Jun Kang, Y.; Yeom, E.; Lee, S.J. A microfluidic device for simultaneous measurement of viscosity and flow rate of blood in a complex fluidic network. Biomicrofluidics 2013, 7, 054111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, Y.J.; Yoon, S.Y.; Lee, K.H.; Yang, S. A highly accurate and consistent microfluidic viscometer for continuous blood viscosity measurement. Artif. Organs 2010, 34, 944–949. [Google Scholar] [CrossRef] [PubMed]
- Yeom, E.; Park, J.H.; Kang, Y.J.; Lee, S.J. Microfluidics for simultaneous quantification of platelet adhesion and blood viscosity. Sci. Rep. 2016, 6, 24994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassan, U.; Reddy, B., Jr.; Damhorst, G.; Sonoiki, O.; Ghonge, T.; Yang, C.; Bashir, R. A microfluidic biochip for complete blood cell counts at the point-of-care. Technology 2015, 3, 201–213. [Google Scholar] [CrossRef] [Green Version]
- Kucukal, E.; Man, Y.; Gurkan, U.A.; Schmidt, B. Blood Flow Velocimetry in a Microchannel During Coagulation Using Particle Image Velocimetry and Wavelet-Based Optical Flow Velocimetry. J. Biomech. Eng. 2021, 143, 091004. [Google Scholar] [CrossRef]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181–189. [Google Scholar] [CrossRef]
- Tomaiuolo, G. Biomechanical properties of red blood cells in health and disease towards microfluidics. Biomicrofluidics 2014, 8, 051501. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Chaudhury, A.; Higgins, J.M.; Wood, D.K. Oxygen-dependent flow of sickle trait blood as an in vitro therapeutic benchmark for sickle cell disease treatments. Am. J. Hematol. 2018, 93, 1227–1235. [Google Scholar] [CrossRef] [Green Version]
- Picart, C.; Piau, J.M.; Galliard, H.; Carpentier, P. Human blood shear yield stress and its hematocrit dependence. J. Rheol. 1998, 42, 1–12. [Google Scholar] [CrossRef]
- Thurston, G.B. Viscoelasticity of human blood. Biophys. J. 1972, 12, 1205. [Google Scholar] [CrossRef] [Green Version]
- Guruprasad, P.; Mannino, R.G.; Caruso, C.; Zhang, H.; Josephson, C.D.; Roback, J.D.; Lam, W.A. Integrated automated particle tracking microfluidic enables high-throughput cell deformability cytometry for red cell disorders. Am. J. Hematol. 2019, 94, 189–199. [Google Scholar] [CrossRef] [Green Version]
- Man, Y.; Kucukal, E.; An, R.; Watson, Q.D.; Bosch, J.; Zimmerman, P.A.; Little, J.A.; Gurkan, U.A. Microfluidic assessment of red blood cell mediated microvascular occlusion. Lab Chip 2020, 20, 2086–2099. [Google Scholar] [CrossRef] [PubMed]
- Man, Y.; Maji, D.; An, R.; Ahuja, S.P.; Little, J.A.; Suster, M.A.; Mohseni, P.; Gurkan, U.A. Microfluidic electrical impedance assessment of red blood cell-mediated microvascular occlusion. Lab Chip 2021, 21, 1036–1048. [Google Scholar] [CrossRef] [PubMed]
- Man, Y.; Kucukal, E.; An, R.; Bode, A.; Little, J.A.; Gurkan, U.A. Standardized microfluidic assessment of red blood cell–mediated microcapillary occlusion: Association with clinical phenotype and hydroxyurea responsiveness in sickle cell disease. Microcirculation 2021, 28, e12662. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Galarneau, M.M.; Higgins, J.M.; Wood, D.K. A microfluidic platform to study the effects of vascular architecture and oxygen gradients on sickle blood flow. Microcirculation 2017, 24, e12357. [Google Scholar] [CrossRef] [PubMed]
- Islamzada, E.; Matthews, K.; Guo, Q.; Santoso, A.T.; Duffy, S.P.; Scott, M.D.; Ma, H. Deformability based sorting of stored red blood cells reveals donor-dependent aging curves. Lab Chip 2020, 20, 226–235. [Google Scholar] [CrossRef]
- Dondorp, A.M.; Kager, P.A.; Vreeken, J.; White, N.J. Abnormal blood flow and red blood cell deformability in severe malaria. Parasitol. Today 2000, 16, 228–232. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Feng, J.J. How malaria parasites reduce the deformability of infected red blood cells. Biophys. J. 2012, 103, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Sloop, G.D.; De Mast, Q.; Pop, G.; Weidman, J.J.; Cyr, J.A.S. The role of blood viscosity in infectious diseases. Cureus 2020, 12, e7090. [Google Scholar] [CrossRef] [Green Version]
- Chien, S.; Usami, S.; Bertles, J.F. Abnormal rheology of oxygenated blood in sickle cell anemia. J. Clin. Investig. 1970, 49, 623. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Connes, P.; Alexy, T.; Detterich, J.; Romana, M.; Hardy-Dessources, M.D.; Ballas, S.K. The role of blood rheology in sickle cell disease. Blood Rev. 2015, 30, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.I.; Mooney, M.P.; Cho, D.J. Hemorheological disorders in diabetes mellitus. J. Diabetes Sci. Technol. 2008, 2, 1130–1138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Luca, A.C.; Rusciano, G.; Ciancia, R.; Martinelli, V.; Pesce, G.; Rotoli, B.; Selvaggi, L.; Sasso, A. Spectroscopical and mechanical characterization of normal and thalassemic red blood cells by Raman tweezers. Opt. Express 2008, 16, 7943–7957. [Google Scholar] [CrossRef] [Green Version]
- Advani, R.; Sorenson, S.; Shinar, E.; Lande, W.; Rachmilewitz, E.; Schrier, S.L. Characterization and comparison of the red blood cell membrane damage in severe human alpha-and beta-thalassemia. Blood 1992, 79, 1058–1063. [Google Scholar] [CrossRef] [Green Version]
- Méndez-Mora, L.E.; Cabello-Fusarés, M.; Ferré-Torres, J.; Riera-Llobet, C.; Krishnevskaya, E.; Trejo-Soto, C.A.; Payán-Pernía, S.; Hernández-Rodríguez, I.; Morales-Indiano, C.; Alarcón, T.; et al. Blood Rheological Characterization of β-thalassemia Trait and Iron Deficiency Anemia Using Front Microrheometry. Front. Physiol. 2021, 12, 761411. [Google Scholar] [CrossRef] [PubMed]
- Trejo-Soto, C.; Costa-Miracle, E.; Rodriguez-Villarreal, I.; Cid, J.; Alarcón, T.; Hernández-Machado, A. Capillary Filling at the Microscale: Control of Fluid Front Using Geometry. PLoS ONE 2016, 11, e0153559. [Google Scholar] [CrossRef] [Green Version]
- Krieger, I.M.; Dougherty, T.J. A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 1959, 3, 137–152. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of concentrated disperse systems II. A model for non-newtonian shear viscosity in steady flows. Rheol. Acta 1978, 17, 632–642. [Google Scholar] [CrossRef]
- Morrison, F.A. Understanding Rheology; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Rosina, J.; Kvasnak, E.; Suta, D.; Kolarova, H.; Malek, J.; Krajci, L. Temperature dependence of blood surface tension. Physiol. Res. 2007, 56, S93. [Google Scholar] [CrossRef]
- Pries, A.R.; Neuhaus, D.; Gaehtgens, P. Blood viscosity in tube flow: Dependence on diameter and hematocrit. Am. J. Physiol.-Heart Circ. Physiol. 1992, 263, H1770–H1778. [Google Scholar] [CrossRef] [PubMed]
- Chien, S. Biophysical behavior of red cells in suspensions. Red Blood Cell 1975, 2, 1031–1133. [Google Scholar]
- Pal, R. Rheology of concentrated suspensions of deformable elastic particles such as human erythrocytes. J. Biomech. 2003, 36, 981–989. [Google Scholar] [CrossRef]
- Berli, C.L.; Quemada, D. Aggregation behavior of red blood cells in shear flow. A theoretical interpretation of simultaneous rheo-optical and viscometric measurements. Biorheology 2001, 38, 27–38. [Google Scholar]
- Lázaro, G.R.; Hernández-Machado, A.; Pagonabarraga, I. Rheology of red blood cells under flow in highly confined microchannels: I. effect of elasticity. Soft Matter 2014, 10, 7195–7206. [Google Scholar] [CrossRef] [PubMed]
- Lázaro, G.R.; Hernández-Machado, A.; Pagonabarraga, I. Collective behavior of red blood cells in confined channels. Eur. Phys. J. E 2019, 42, 46. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.A. Bending elastic modulus of red blood cell membrane derived from buckling instability in micropipet aspiration tests. Biophys. J. 1983, 43, 27–30. [Google Scholar] [CrossRef] [Green Version]
- Scheffer, L.; Bitler, A.; Ben-Jacob, E.; Korenstein, R. Atomic force pulling: Probing the local elasticity of the cell membrane. Eur. Biophys. J. 2001, 30, 83–90. [Google Scholar] [CrossRef]
- Betz, T.; Lenz, M.; Joanny, J.F.; Sykes, C. ATP-dependent mechanics of red blood cells. Proc. Natl. Acad. Sci. USA 2009, 106, 15320–15325. [Google Scholar] [CrossRef] [Green Version]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trejo-Soto, C.; Hernández-Machado, A. Normalization of Blood Viscosity According to the Hematocrit and the Shear Rate. Micromachines 2022, 13, 357. https://doi.org/10.3390/mi13030357
Trejo-Soto C, Hernández-Machado A. Normalization of Blood Viscosity According to the Hematocrit and the Shear Rate. Micromachines. 2022; 13(3):357. https://doi.org/10.3390/mi13030357
Chicago/Turabian StyleTrejo-Soto, Claudia, and Aurora Hernández-Machado. 2022. "Normalization of Blood Viscosity According to the Hematocrit and the Shear Rate" Micromachines 13, no. 3: 357. https://doi.org/10.3390/mi13030357
APA StyleTrejo-Soto, C., & Hernández-Machado, A. (2022). Normalization of Blood Viscosity According to the Hematocrit and the Shear Rate. Micromachines, 13(3), 357. https://doi.org/10.3390/mi13030357





