A Novel Self-Temperature Compensation Method for Mode-Localized Accelerometers
Abstract
:1. Introduction
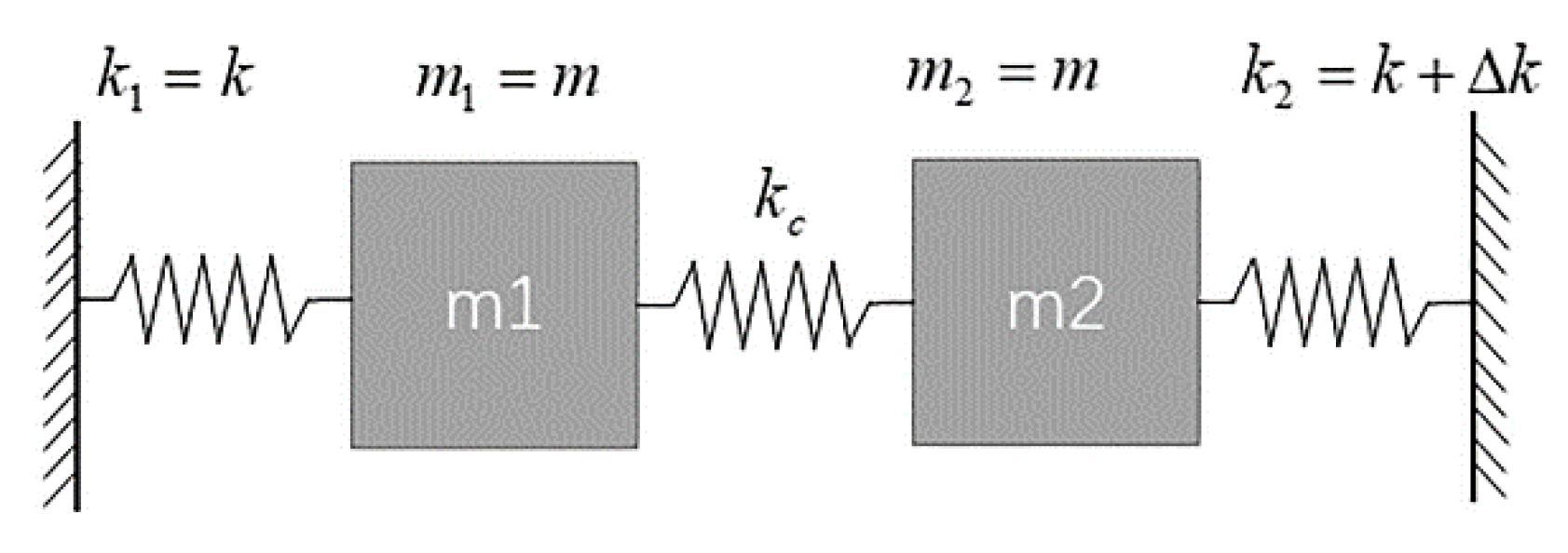
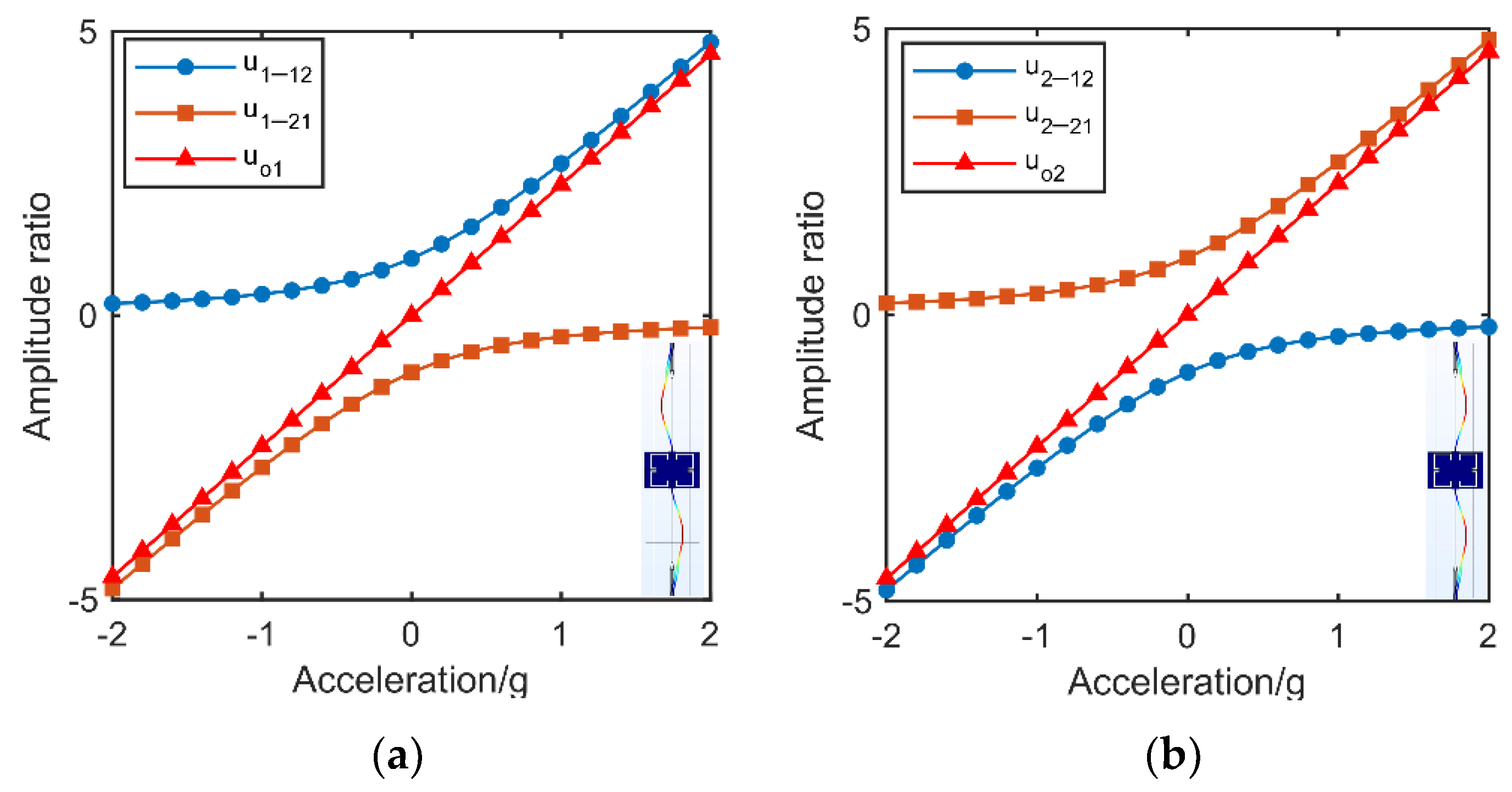
2. Two-DoF WCRs Accelerometer
3. Temperature Dependence Analysis of 2-DoF Accelerometer
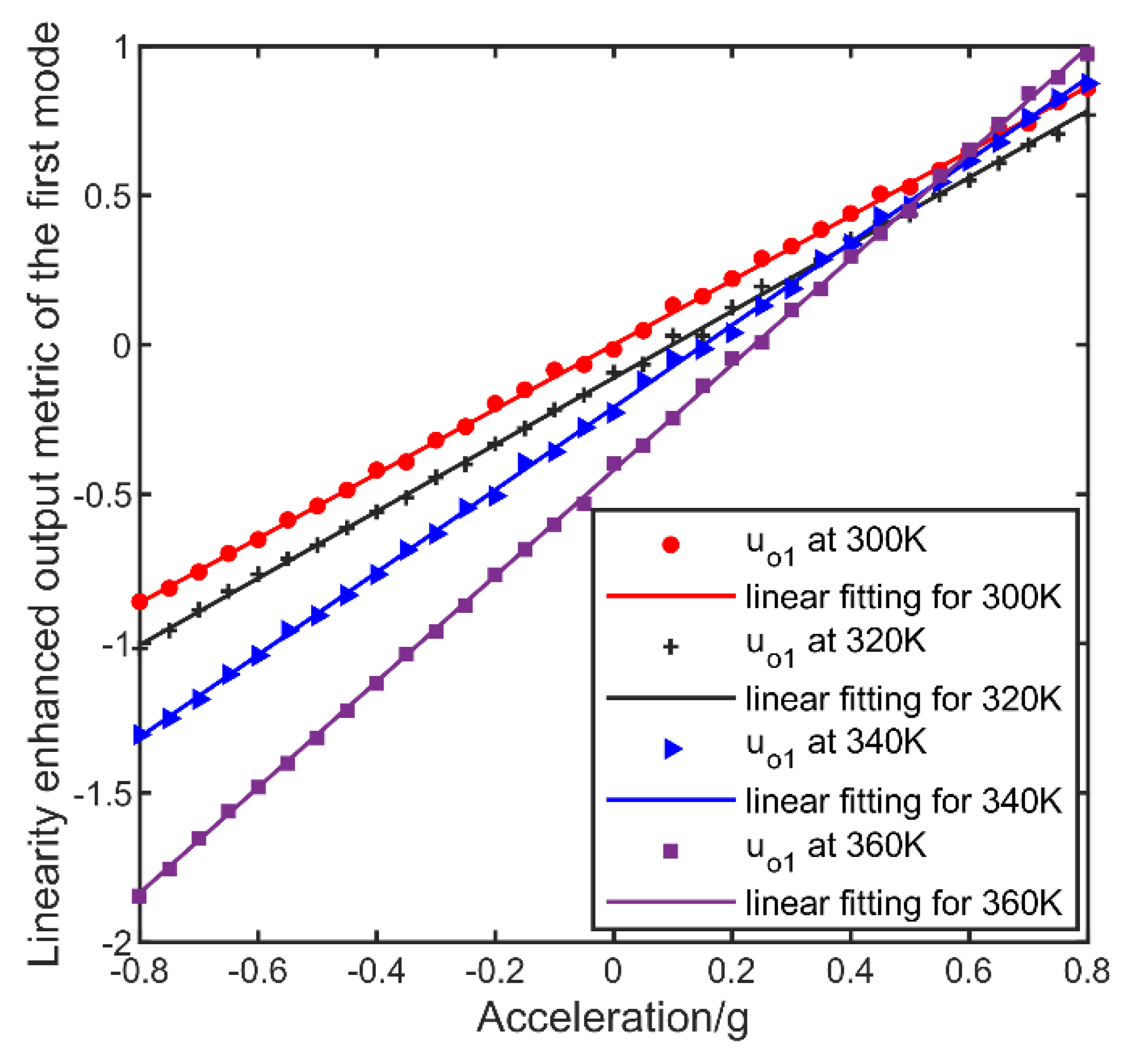
3.1. The Dependence of Linearity-Enhanced Output Metric on Temperature
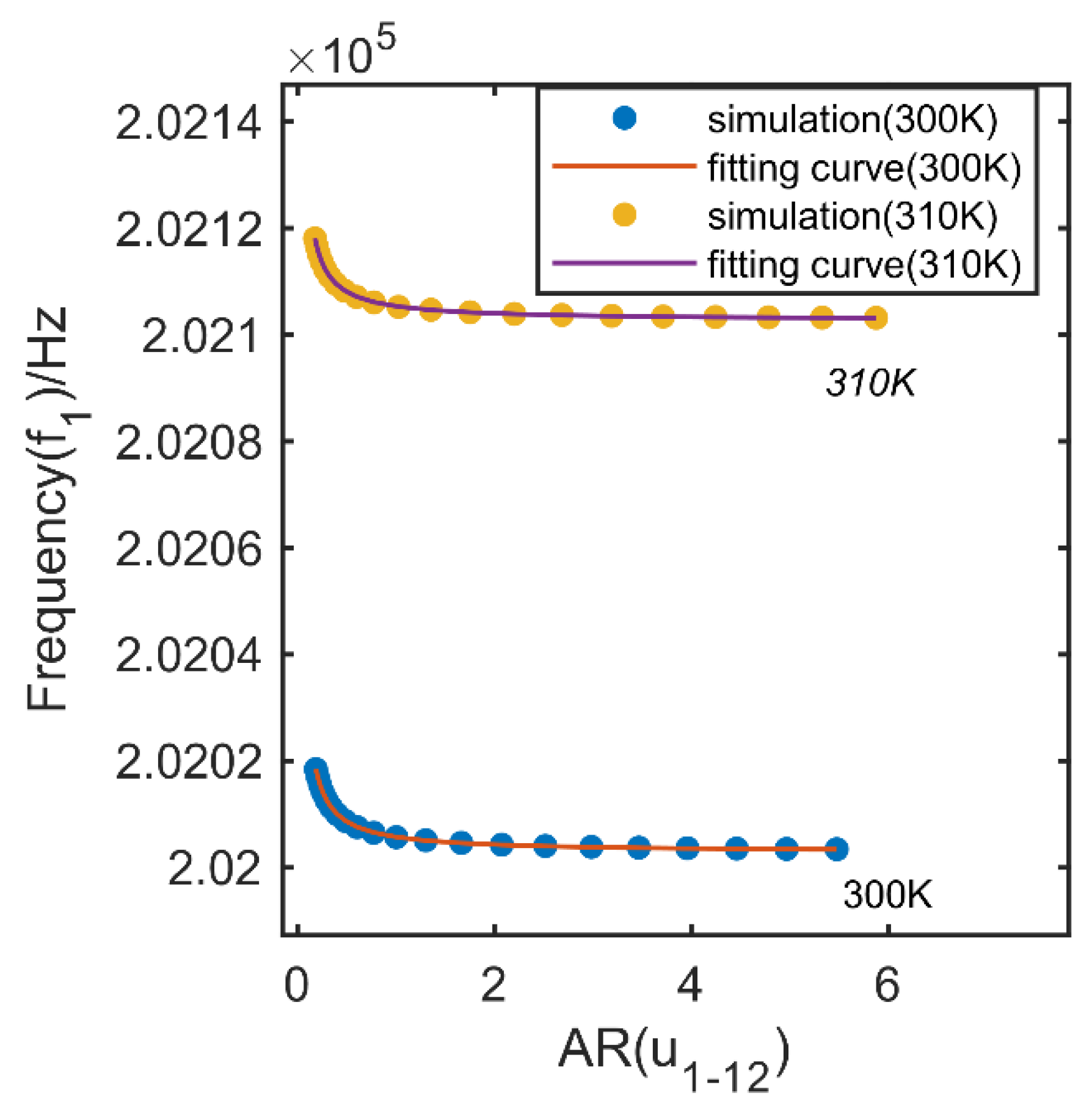
3.2. The Dependence of Frequency on Temperature
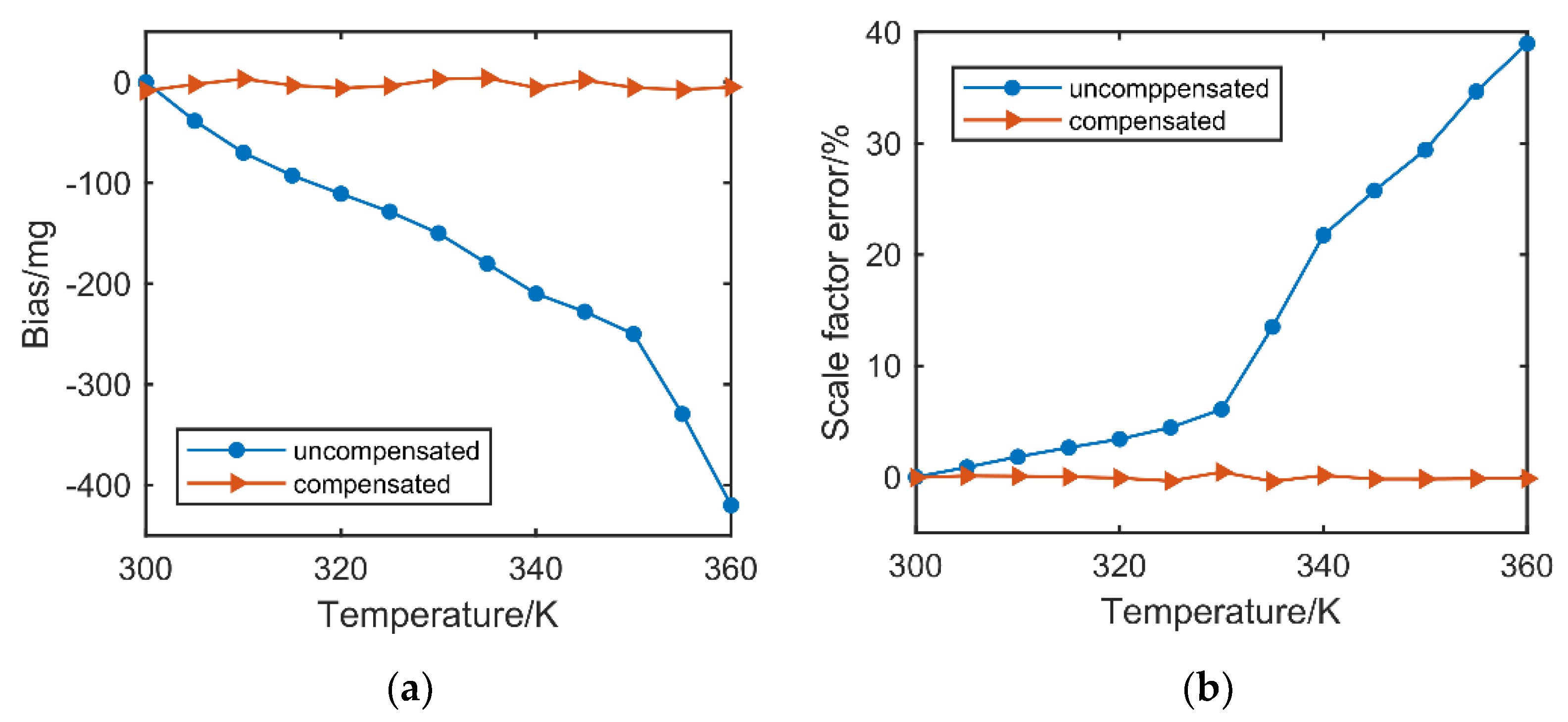
4. The Method of Temperature Compensation
5. Experiment
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weinberg, M.S.; Bernstein, J.; Borenstein, J.T.; Campbell, J.; Sohn, J.B. Micromachining inertial instruments. In Micromachining and Microfabrication Process Technology II; International Society for Optics and Photonics: Bellingham, WA, USA, 1996; Volume 2879, pp. 26–36. [Google Scholar]
- Judy, M.W. Evolution of integrated inertial mems technology. In Proceedings of the Solid-State Sensors Actuator and Microsystems Workshop, 6–10 June 2004, Hilton Head Island, SC, USA; 2004; pp. 27–32. [Google Scholar]
- Marek, J. MEMS for automotive and consumer electronics. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 7–11 February 2010. [Google Scholar]
- Comi, C.; Corigliano, A.; Langfelder, G.; Longoni, A.; Tocchio, A.; Simoni, B. A Resonant Microaccelerometer With High Sensitivity Operating in an Oscillating Circuit. J. Microelectromechanical Syst. 2010, 19, 1140–1152. [Google Scholar] [CrossRef]
- Seshia, A.A.; Palaniapan, M.; Roessig, T.A.; Howe, R.T.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromechanical Syst. 2003, 11, 784–793. [Google Scholar] [CrossRef] [Green Version]
- Omura, Y.; Nonomura, Y.; Tabata, O. New resonant accelerometer based on rigidity change. In Proceedings of the International Conference on Solid State Sensors & Actuators, Chicago, IL, USA, 19–19 June 1997. [Google Scholar]
- Kim, S.Y.; Go, J.S.; Cho, Y.H. Design, fabrication and static test of a resonant microaccelerometer. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 1997; Volume 18435, pp. 21–26. [Google Scholar]
- Spletzer, M.; Raman, A.; Sumali, H.; Sullivan, J.P. Highly sensitive mass detection and identification using vibration localization in coupled microcantilever arrays. Appl. Phys. Lett. 2008, 92, 122. [Google Scholar] [CrossRef] [Green Version]
- Manav, M.; Reynen, G.; Sharma, M.; Cretu, E.; Phani, A.S. Ultrasensitive resonant MEMS transducers with tunable coupling. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), 16–20 June 2013, Barcelona, Spain; pp. 996–999.
- Zhao, C.; Wood, G.S.; Xie, J.; Chang, H.; Pu, S.H.; Kraft, M. A Three Degree-of-Freedom Weakly Coupled Resonator Sensor With Enhanced Stiffness Sensitivity. J. Microelectromechanical Syst. 2016, 25, 38–51. [Google Scholar] [CrossRef]
- Zhao, C.; Wood, G.S.; Xie, J.; Chang, H.; Pu, S.H.; Kraft, M. A Comparative Study of Output Metrics for an MEMS Resonant Sensor Consisting of Three Weakly Coupled Resonators. J. Microelectromechanical Syst. 2016, 25, 626–636. [Google Scholar] [CrossRef]
- Kang, H.; Yang, J.; Chang, H. A Closed-Loop Accelerometer Based on Three Degree-of-Freedom Weakly Coupled Resonator With Self-Elimination of Feedthrough Signal. IEEE Sens. J. 2018, 18, 3960–3967. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B.; Yuan, W.; Kraft, M.; Chang, H. An Acceleration Sensing Method Based on the Mode Localization of Weakly Coupled Resonators. J. Microelectromechanical Syst. 2016, 25, 286–296. [Google Scholar] [CrossRef]
- Peng, B.; Hu, K.; Shao, L.; Yan, H.; Li, L.; Wei, X.; Zhang, W. A Sensitivity Tunable Accelerometer Based on Series-Parallel Electromechanically Coupled Resonators Using Mode Localization. J. Microelectromechanical Syst. 2020, 29, 3–13. [Google Scholar] [CrossRef]
- Zhang, H.; Zhong, J.; Yuan, W.; Yang, J.; Chang, H. Ambient pressure drift rejection of mode-localized resonant sensors. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 1095–1098. [Google Scholar]
- Thiruvenkatanathan, P.; Yan, J.; Seshia, A.A. Common mode rejection in electrically coupled MEMS resonators utilizing mode localization for sensor applications. In Proceedings of the 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time forum, Besancon, France, 20–24 April 2009; pp. 358–363. [Google Scholar]
- Zhong, J.; Yang, J.; Chang, H. The temperature drift suppression of mode-localized resonant sensors. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 467–470. [Google Scholar]
- Pandit, M.; Zhao, C.; Sobreviela, G.; Seshia, A.A. Immunity to Temperature Fluctuations in Weakly Coupled MEMS Resonators. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar]
- Pandit, M.; Zhao, C.; Sobreviela, G.; Seshia, A. Practical Limits to Common Mode Rejection in Mode Localized Weakly Coupled Resonators. IEEE Sens. J. 2020, 20, 6818–6825. [Google Scholar] [CrossRef]
- Xu, C.; Segovia-Fernandez, J.; Kim, H.J.; Piazza, G. Temperature-Stable Piezoelectric MEMS Resonators Using Integrated Ovens and Simple Resistive Feedback Circuits. J. Microelectromechanical Syst. 2017, 26, 187–195. [Google Scholar] [CrossRef]
- Liu, C.; Tabrizian, R.; Ayazi, F. A ± 0.3 ppm Oven-Controlled MEMS Oscillator Using Structural Resistance-Based Temperature Sensing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1492–1499. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Woo, J.K.; Lee, S.; Mitchell, J.; Challoner, A.D.; Najafi, K. A Micro Oven-Control System for Inertial Sensors. J. Microelectromechanical Syst. 2017, 26, 507–518. [Google Scholar] [CrossRef]
- Salvia, J.C.; Melamud, R.; Chandorkar, S.A.; Lord, S.F.; Kenny, T.W. Real-Time Temperature Compensation of MEMS Oscillators Using an Integrated Micro-Oven and a Phase-Locked Loop. J. Microelectromechanical Syst. 2010, 19, 192–201. [Google Scholar] [CrossRef]
- Ng, E.J.; Ahn, C.H.; Yang, Y.; Hong, V.A.; Chiang, C.; Ahadi, E.; Ward, M.W.; Kenny, T.W. Localized, degenerately doped epitaxial silicon for temperature compensation of resonant MEMS systems. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 2419–2422. [Google Scholar]
- Li, B.; Li, C.; Zhao, Y.; Han, C.; Zhang, Q. An integrated packaged resonant accelerometer with temperature compensation. Rev. Sci. Instrum. 2020, 91, 105004. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.; Graham, A.B.; Lee, B.J.; Ahn, C.H.; Kenny, T.W. Resonant pressure sensor with on-chip temperature and strain sensors for error correction. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 16–20 June 2013. [Google Scholar]
- Kang, H.; Ruan, B.; Hao, Y.; Chang, H. A Mode-Localized Resonant Accelerometer With Self-Temperature Drift Suppression. IEEE Sens. J. 2020, 20, 12154–12165. [Google Scholar] [CrossRef]
- Zotov, S.A.; Simon, B.R.; Trusov, A.A.; Shkel, A.M. High Quality Factor Resonant MEMS Accelerometer With Continuous Thermal Compensation. IEEE Sens. J. 2015, 15, 5045–5052. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Luo, Z.; Chen, D.; Chen, J. A Resonant Pressure Microsensor Capable of Self-Temperature Compensation. Sensors 2015, 15, 10048–10058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, X.; Yang, B.; Li, C.; Liang, Z. Enhancing Output Linearity of Weakly Coupled Resonators by Simple Algebraic Operations. Sens. Actuators A Phys. 2021, 325, 112696. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Device thickness | 40 μm |
| Length of CC resonant beam | 400 μm |
| Width of CC resonant beam | 7 μm |
| Gap of resonant beam | 2 μm |
| Quality of proof mass | 1.50 mg |
| Quality factor | 15,600 |
| Glass thickness | 50 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, P.; Xiong, X.; Wang, K.; Ma, L.; Wang, Z.; Liu, Y.; Zou, X. A Novel Self-Temperature Compensation Method for Mode-Localized Accelerometers. Micromachines 2022, 13, 437. https://doi.org/10.3390/mi13030437
Cai P, Xiong X, Wang K, Ma L, Wang Z, Liu Y, Zou X. A Novel Self-Temperature Compensation Method for Mode-Localized Accelerometers. Micromachines. 2022; 13(3):437. https://doi.org/10.3390/mi13030437
Chicago/Turabian StyleCai, Pengcheng, Xingyin Xiong, Kunfeng Wang, Liangbo Ma, Zheng Wang, Yunfei Liu, and Xudong Zou. 2022. "A Novel Self-Temperature Compensation Method for Mode-Localized Accelerometers" Micromachines 13, no. 3: 437. https://doi.org/10.3390/mi13030437
APA StyleCai, P., Xiong, X., Wang, K., Ma, L., Wang, Z., Liu, Y., & Zou, X. (2022). A Novel Self-Temperature Compensation Method for Mode-Localized Accelerometers. Micromachines, 13(3), 437. https://doi.org/10.3390/mi13030437






