Fine Texture Detection Based on a Solid–Liquid Composite Flexible Tactile Sensor Array
Abstract
:1. Introduction
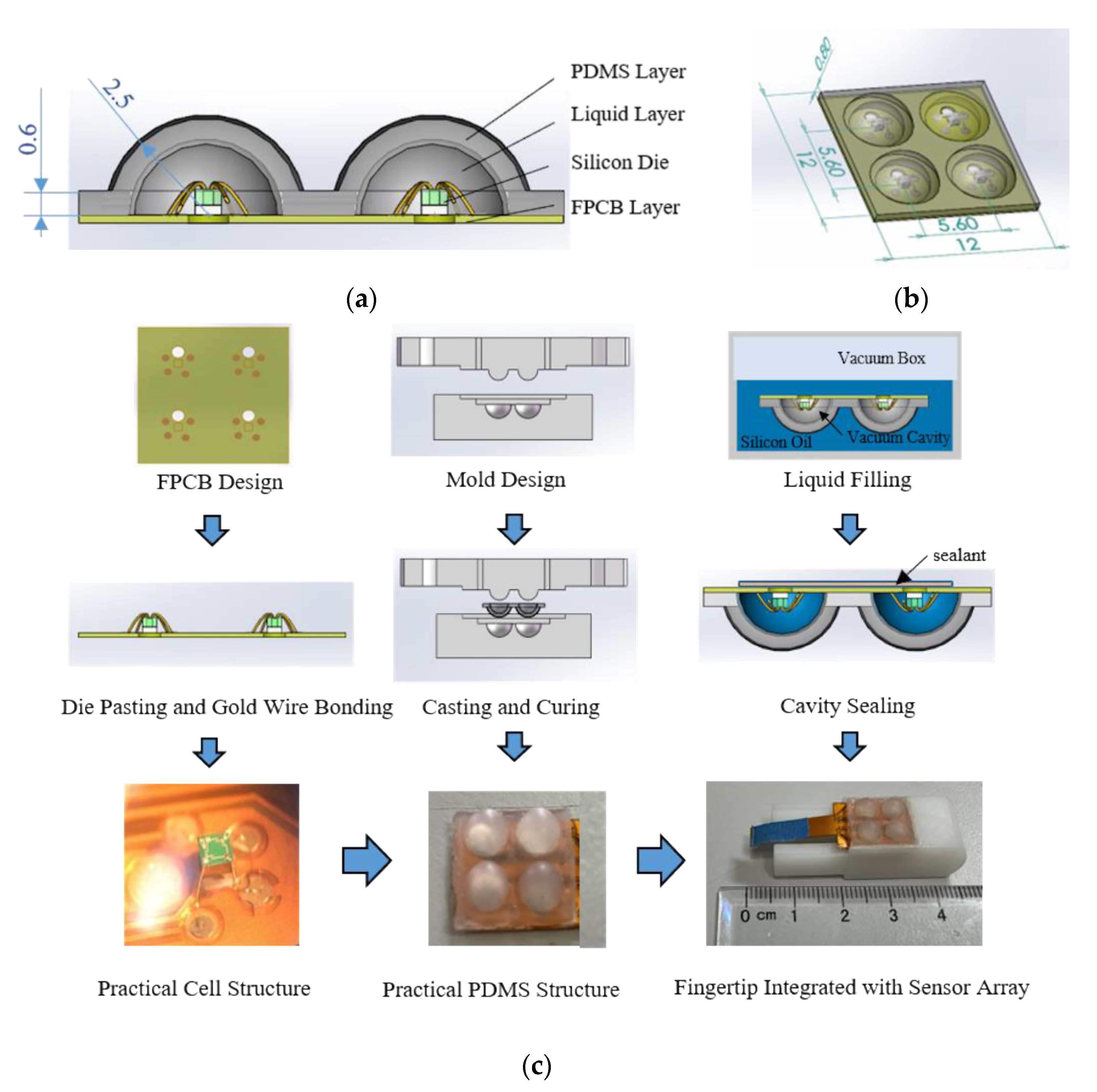
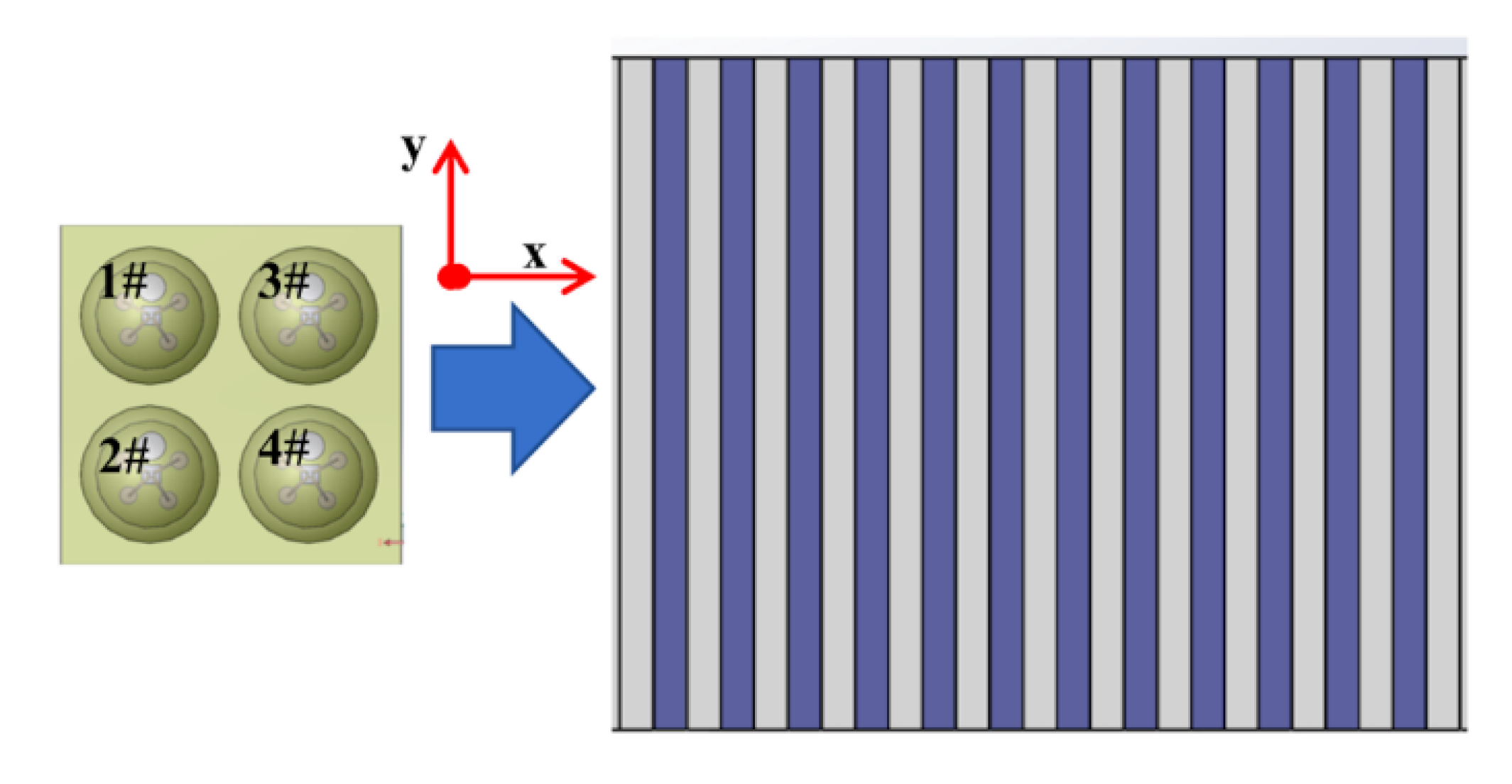
2. Tactile Senor Device
3. Methodology
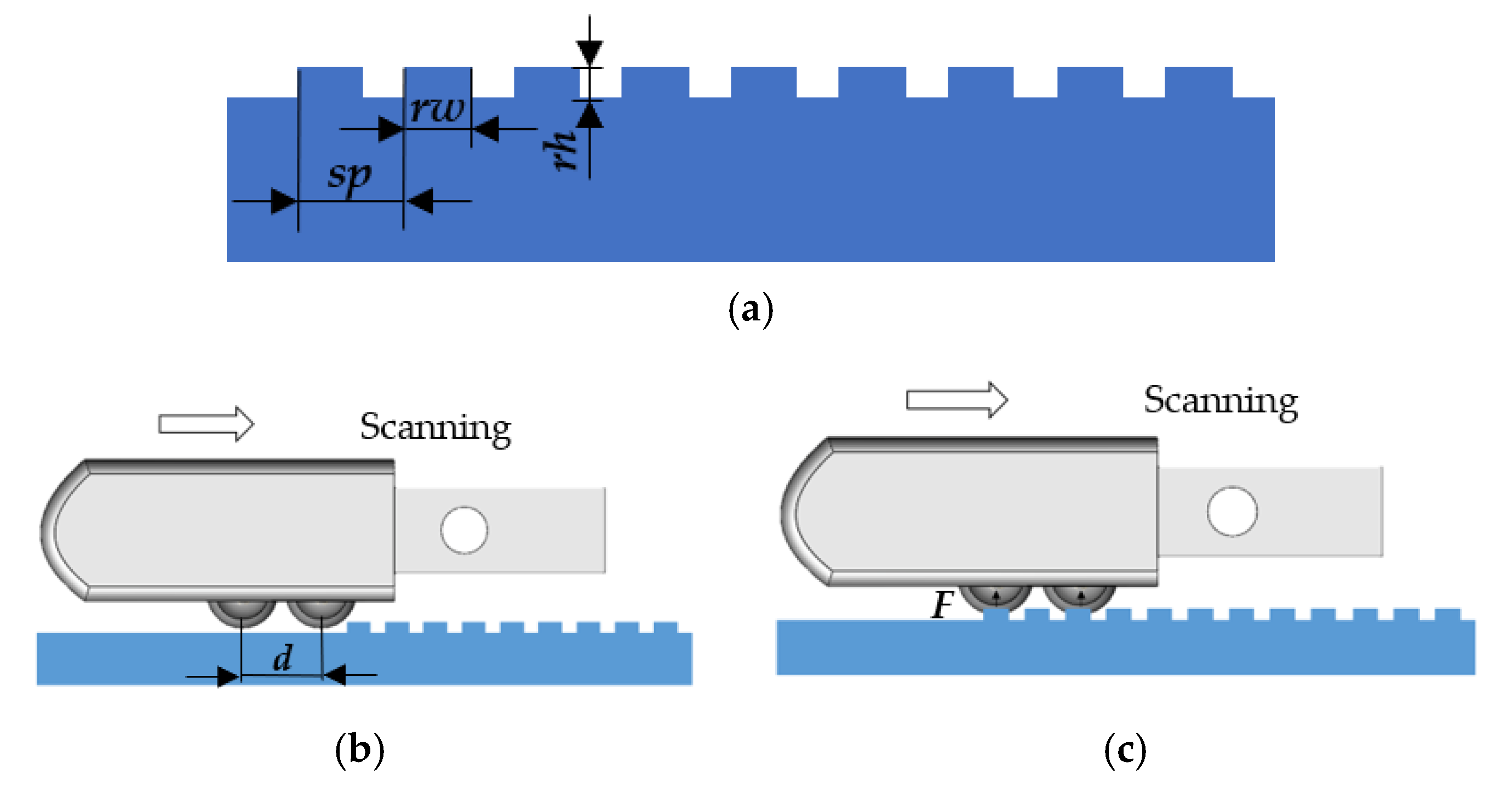
3.1. Texture Detection
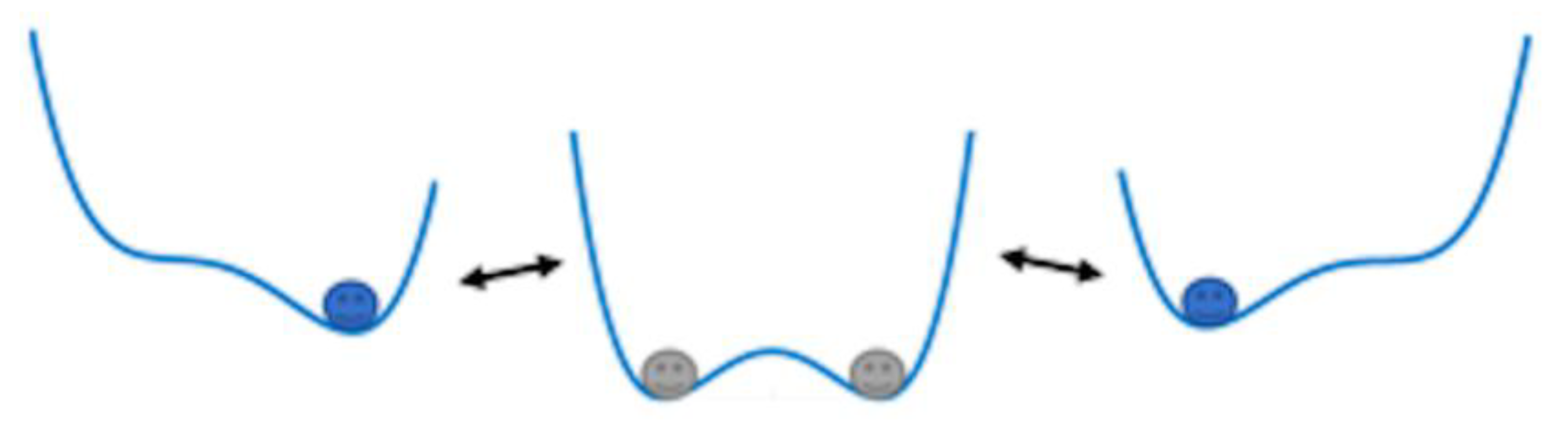
3.2. Stochastic Resonance Method
4. Experiment
4.1. Experiment Platform
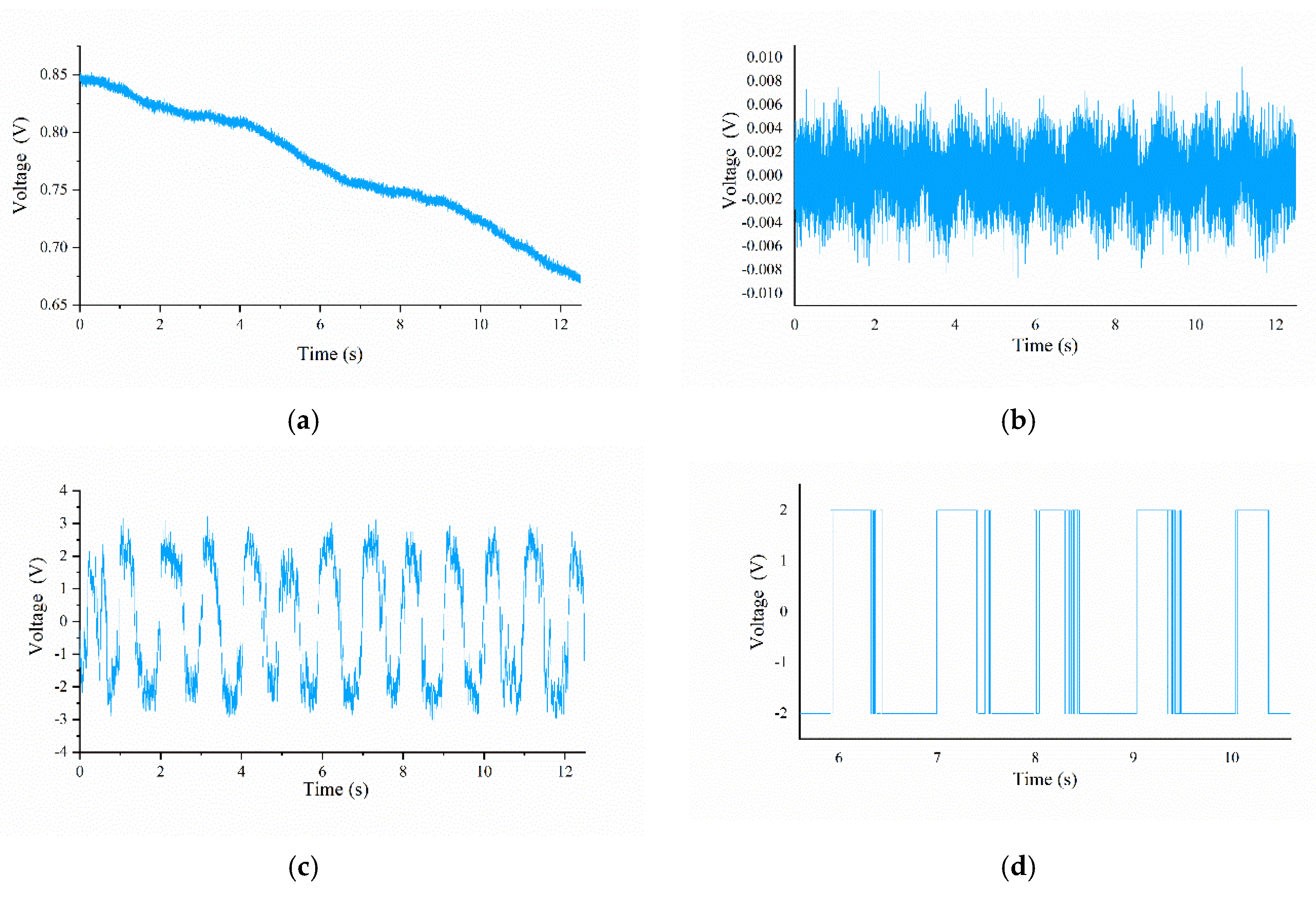
4.2. Experiment Detail
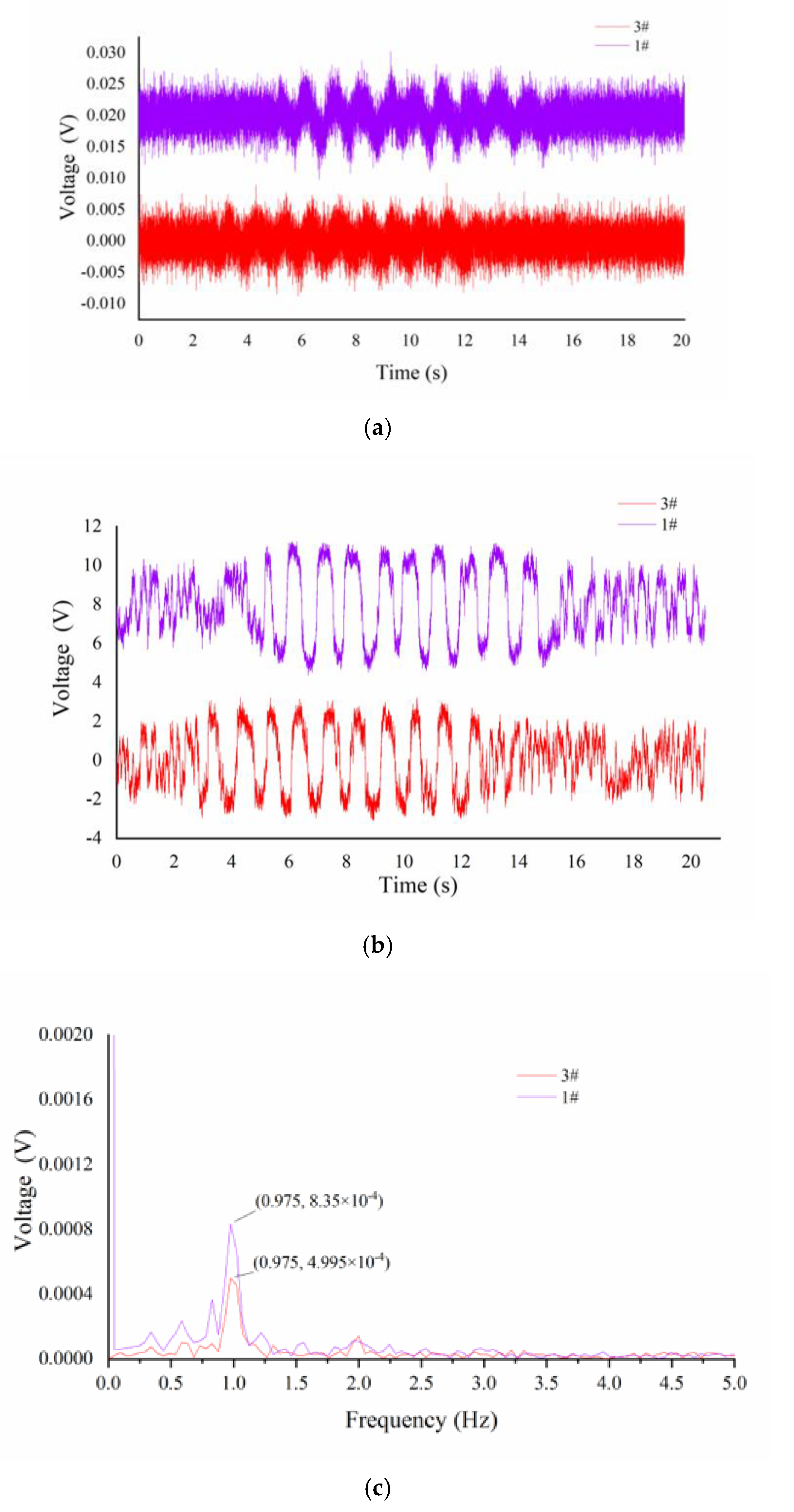
4.3. Experiment Result
5. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Truby, R.L.; Wehner, M.; Grosskopf, A.K. Soft Somatosensitive Actuators via Embedded 3D Printing. Adv. Mater. 2018, 30, 1706383. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogt, D.; Park, Y.-L.; Wood, R.J. A soft multi-axis force sensor. In Proceedings of the 2012 IEEE Sensors, Taipei, Taiwan, 28–31 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4. [Google Scholar]
- Low, J.H.; Lee, W.W.; Khin, P.M.; Thakor, N.V.; Kukreja, S.L.; Ren, H.L.; Yeow, C.H. Hybrid Tele-Manipulation System Using a Sensorized 3-D-Printed Soft Robotic Gripper and a Soft Fabric-Based Haptic Glove. IEEE Robot. Autom. Lett. 2017, 2, 880–887. [Google Scholar] [CrossRef]
- Balamurugan, D.; Nakagawa-Silva, A.; Nguyen, H. Texture Discrimination using a Soft Biomimetic Finger for Prosthetic Ap-plications. In Proceedings of the 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), Toronto, ON, Canada, 24–28 June 2019; pp. 380–385. [Google Scholar]
- Sankar, S.; Brown, A.; Balamurugan, D. Texture discrimination using a flexible tactile sensor array on a soft biomimetic finger. In Proceedings of the 2019 IEEE SENSORS, Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar]
- Bholat, O.S.; Haluck, R.S.; Kutz, R.H.; Gorman, P.J.; Krummel, T.M. Defining the Role of Haptic Feedback in Minimally Invasive Surgery. Stud. Health Technol. Inform. 1999, 62, 62–66. [Google Scholar] [PubMed]
- Ong, R.; Glisson, C.L.; Burgner-Kahrs, J.; Simpson, A.L.; Danilchenko, A.; Lathrop, R.A.; Herrell, S.D.; Webster, R.J.; Miga, M.I.; Galloway, R.L. A novel method for texture-mapping conoscopic surfaces for minimally invasive image-guided kidney surgery. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 1515–1526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdulhafez, A.; Chari, V. Reliable 2D Tracking using good texture and edge features for Robotic Vision. Control Eng. Appl. Inform. 2018, 20, 15–24. [Google Scholar]
- Asano, S.; Okamoto, S.; Matsuura, Y. Toward quality texture display: Vibrotactile stimuli to modify material roughness sensa-tions. Adv. Robot. 2014, 28, 1079–1089. [Google Scholar] [CrossRef]
- Oddo, C.M.; Beccai, L.; Felder, M.; Giovacchini, F.; Carrozza, M.C. Artificial Roughness Encoding with a Bio-inspired MEMS-based Tactile Sensor Array. Sensors 2009, 9, 3161–3183. [Google Scholar] [CrossRef] [Green Version]
- Oddo, C.M.; Controzzi, M.; Beccai, L.; Cipriani, C.; Carrozza, M.C. Roughness Encoding for Discrimination of Surfaces in Artificial Active-Touch. IEEE Trans. Robot. 2011, 27, 522–533. [Google Scholar] [CrossRef]
- Muhammad, H.; Recchiuto, C.; Oddo, C.; Beccai, L.; Anthony, C.; Adams, M.; Carrozza, M.; Ward, M. A capacitive tactile sensor array for surface texture discrimination. Microelectron. Eng. 2011, 88, 1811–1813. [Google Scholar] [CrossRef]
- Miyaoka, T. Tactile Information Processing Mechanisms of Fine Surface Texture Discrimination in Humans: A Study with Ridge Height Discrimination Tasks. In Proceedings of the International Ergonomics Association Triennial Congress of the IEA, Tampere, Finland, 29 June–4 July 1997. [Google Scholar]
- Miyaoka, T.; Mano, T.; Ohka, M. Mechanisms of fine-surface-texture discrimination in human tactile sensation. J. Acoust. Soc. Am. 1999, 105, 2485–2492. [Google Scholar] [CrossRef]
- Natsume, M.; Tanaka, Y.; Sano, A. Skin-Propagated Vibration for Roughness and Textures; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Takekawa, Y.; Hasegawa, T.; Tanaka, Y.; Minamizawa, K.; Sano, A. Tactile Display Based on Skin-Propagated Vibration. In Lecture Notes in Electrical Engineering; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 2017; Volume 432, pp. 121–123. [Google Scholar]
- Tanaka, Y.; Hasegawa, T.; Hashimoto, M.; Igarashi, T. Artificial Fingers Wearing Skin Vibration Sensor for Evaluating Tactile Sensations. In Proceedings of the 2019 IEEE World Haptics Conference (WHC), Tokyo, Japan, 9–12 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 377–382. [Google Scholar]
- Fishel, J.A.; Loeb, G.E. Sensing tactile microvibrations with the BioTac Comparison with human sensitivity. In Proceedings of the 2012 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1122–1127. [Google Scholar]
- Fishel, J.A.; Loeb, G.E. Bayesian Exploration for Intelligent Identification of Textures. Front. Neurorobotics 2012, 6, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rongala, U.B.; Mazzoni, A.; Oddo, C.M. Neuromorphic Artificial Touch for Categorization of Naturalistic Textures. IEEE Trans. Neural Netw. Learn. Syst. 2015, 28, 819–829. [Google Scholar] [CrossRef] [PubMed]
- Rongala, U.B.; Mazzoni, A.; Spanne, A.; Jörntell, H.; Oddo, C.M. Cuneate spiking neural network learning to classify naturalistic texture stimuli under varying sensing conditions. Neural Netw. 2019, 123, 273–287. [Google Scholar] [CrossRef] [PubMed]
- Sankar, S.; Balamurugan, D.; Brown, A. Texture Discrimination with a Soft Biomimetic Finger Using a Flexible Neuromor-phic Tactile Sensor Array That Provides Sensory Feedback. Soft Robot. 2021, 8, 577–587. [Google Scholar] [CrossRef] [PubMed]
- Gescheider, G.A. Psychophysics: The Fundamentals; Psychology Press: Hove, East Sussex, UK, 1997. [Google Scholar]
- Luca, G.; Peter, H.; Peter, J. Stochastic Resonance. Rev. Mod. Phys. Am. 1998, 70, 223. [Google Scholar]
- Beceren, K.; Ohka, M.; Jin, T.; Miyaoka, T.; Yussof, H. Optimization of Human Tactile Sensation Using Stochastic Resonance. Procedia Eng. 2012, 41, 792–797. [Google Scholar] [CrossRef] [Green Version]
- Beceren, K.; Ohka, M.; Jin, T.; Miyaoka, T.; Yussof, H. Human Tactile Stochastic Resonance Affected by Stimulus Direction. Int. J. Adv. Robot. Syst. 2013, 10, 178. [Google Scholar] [CrossRef]
- Kurita, Y.; Sueda, Y.; Ishikawa, T. Surgical Grasping Forceps with Enhanced Sensorimotor Capability via the Stochastic Res-onance Effect. IEEE/ASME Tran. Mechatron. 2016, 21, 2624–2634. [Google Scholar] [CrossRef]
- Vásárhelyi, G.; Ádám, M.; Vázsonyi, É.; Bársony, I.; Dücső, C. Effects of the elastic cover on tactile sensor arrays. Sens. Actuators A Phys. 2006, 132, 245–251. [Google Scholar] [CrossRef]
- Liu, W.; Gu, C.; Zeng, R.; Yu, P.; Fu, X. A Novel Inverse Solution of Contact Force Based on a Sparse Tactile Sensor Array. Sensors 2018, 18, 351. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Ping, Y.; Gu, C. Fingertip Piezoelectric Tactile Sensor Array for Roughness Encoding under Varying Scanning Velocity. IEEE Sens. J. 2017, 21, 6867–6879. [Google Scholar] [CrossRef]

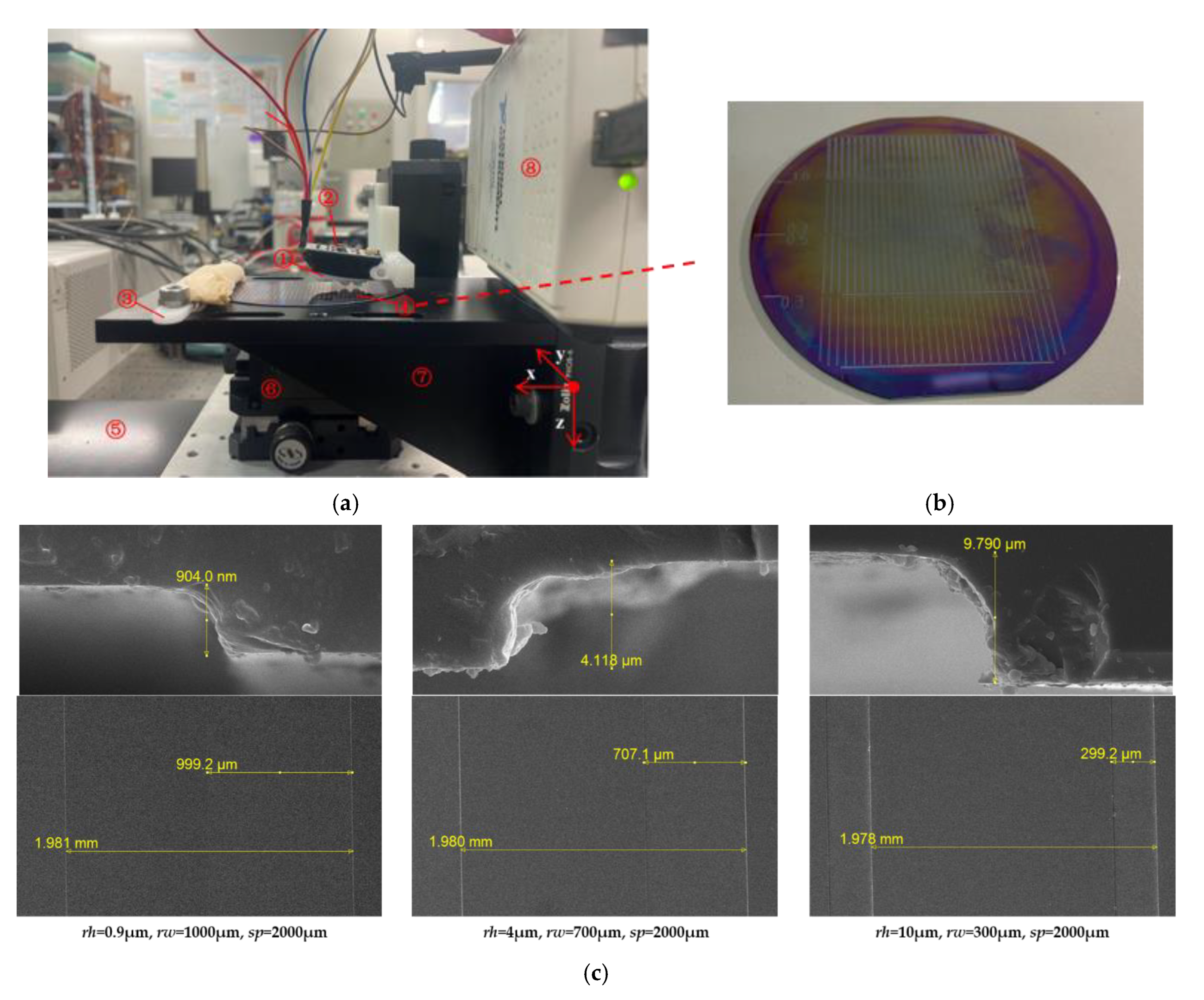

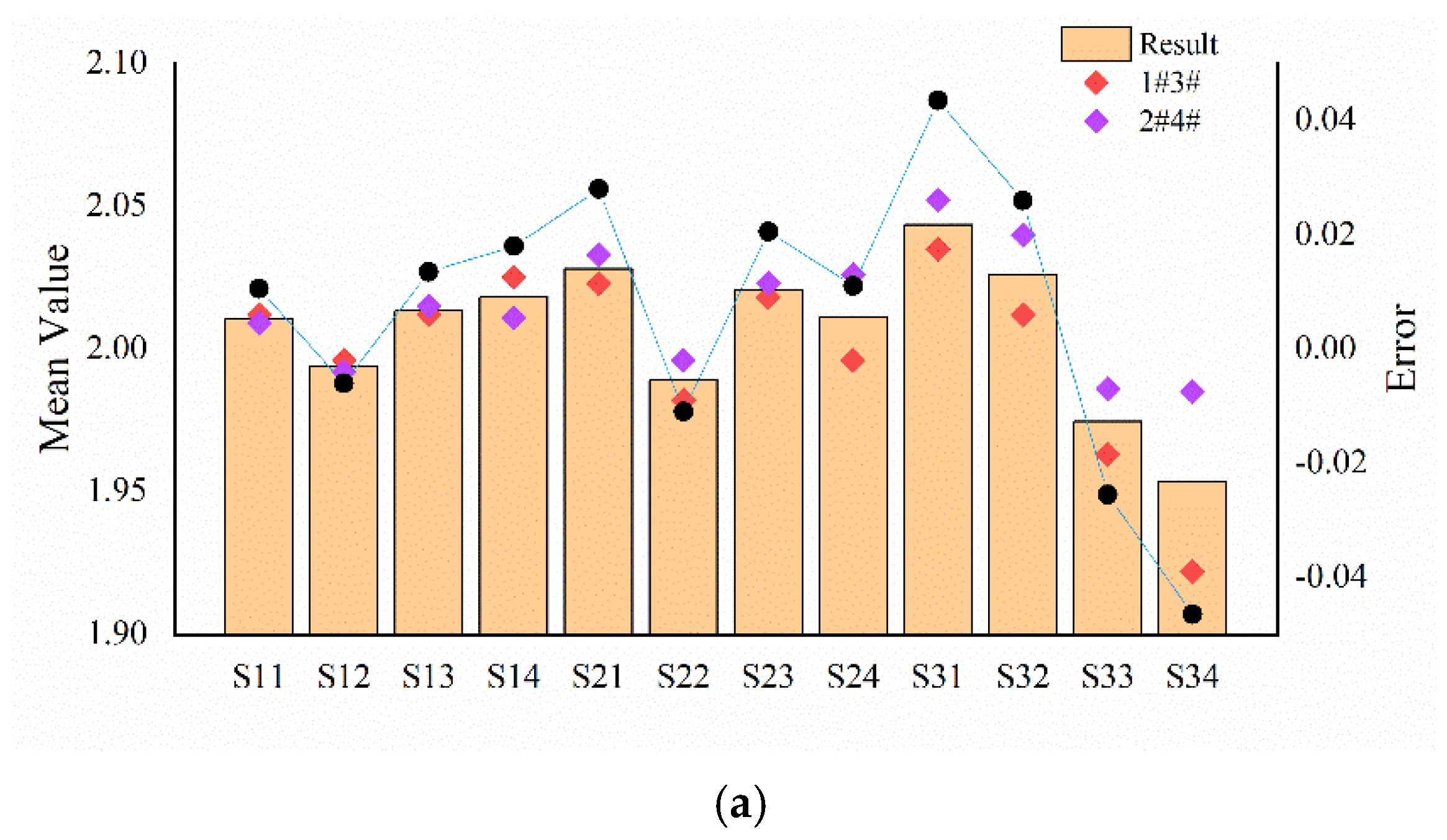
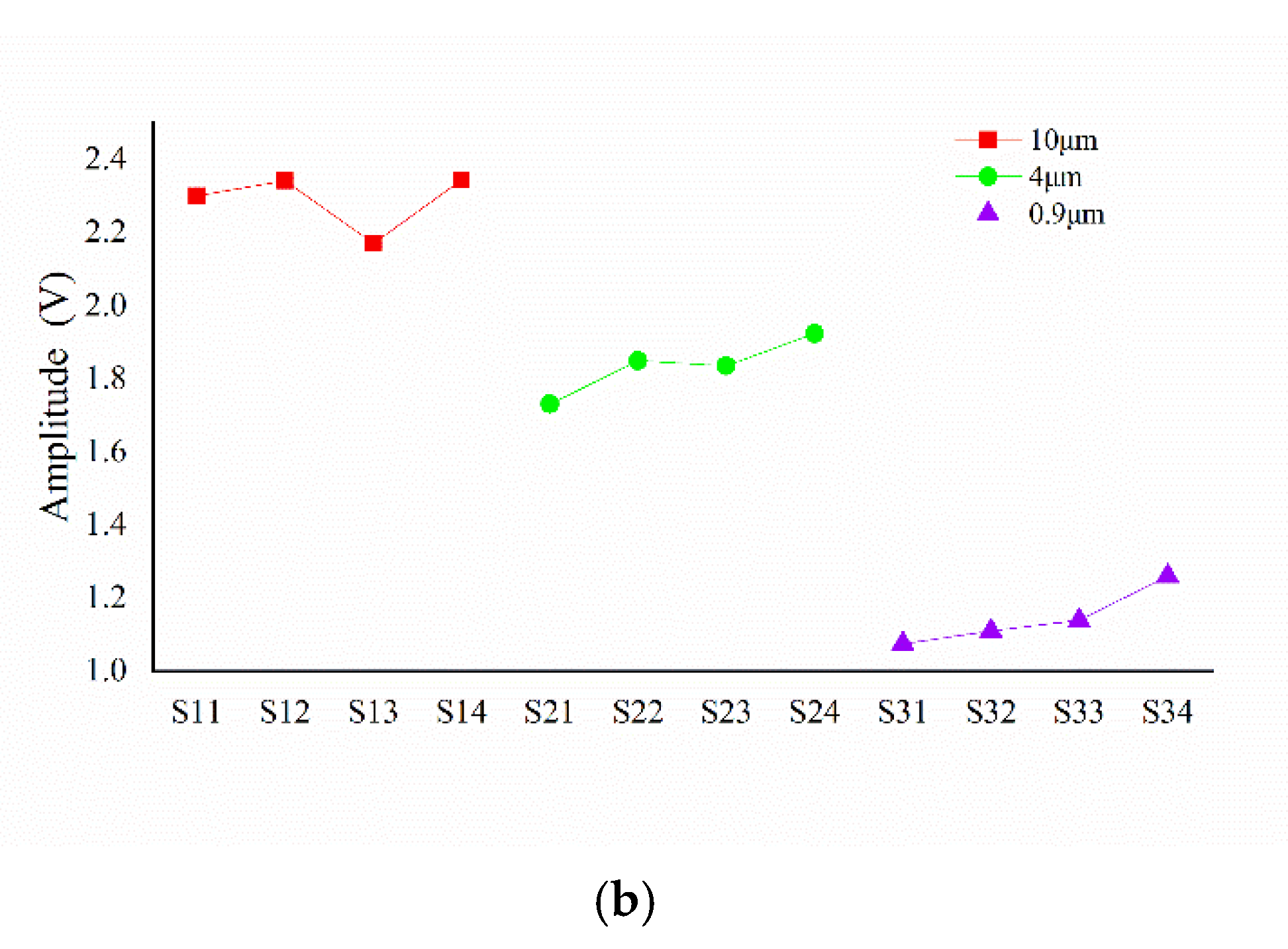
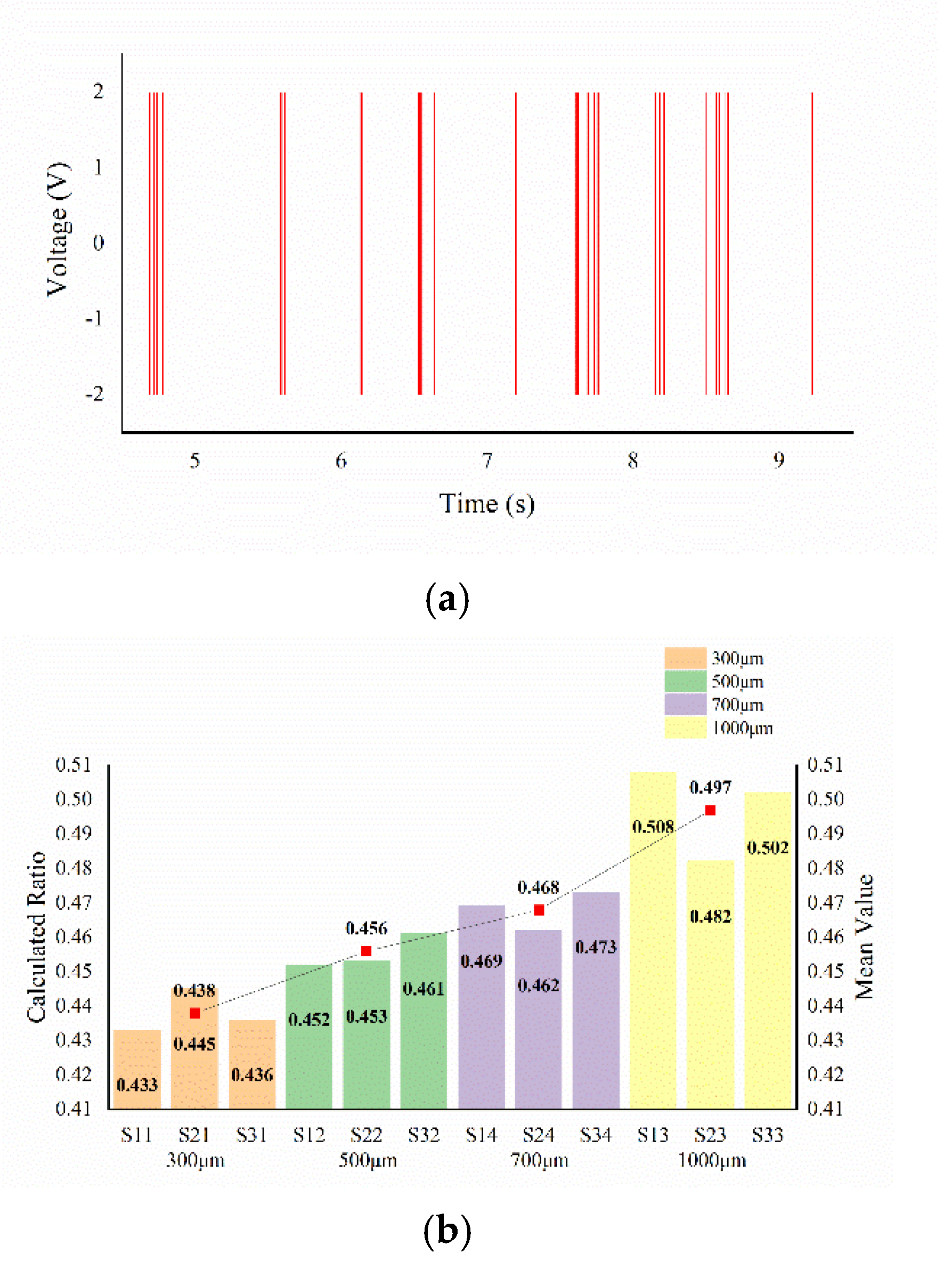
| NUMBER | RIDGE HEIGHT RH (μM) | RIDGE WIDTH RW (μM) | SPATIAL PERIOD SP (μM) |
|---|---|---|---|
| S11 | 10 | 300 | 2000 |
| S12 | 500 | ||
| S13 | 700 | ||
| S14 | 1000 | ||
| S21 | 4 | 300 | |
| S22 | 500 | ||
| S23 | 700 | ||
| S24 | 1000 | ||
| S31 | 0.9 | 300 | |
| S32 | 500 | ||
| S33 | 700 | ||
| S34 | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhang, G.; Zhan, B.; Hu, L.; Liu, T. Fine Texture Detection Based on a Solid–Liquid Composite Flexible Tactile Sensor Array. Micromachines 2022, 13, 440. https://doi.org/10.3390/mi13030440
Liu W, Zhang G, Zhan B, Hu L, Liu T. Fine Texture Detection Based on a Solid–Liquid Composite Flexible Tactile Sensor Array. Micromachines. 2022; 13(3):440. https://doi.org/10.3390/mi13030440
Chicago/Turabian StyleLiu, Weiting, Guoshi Zhang, Binpeng Zhan, Liang Hu, and Tao Liu. 2022. "Fine Texture Detection Based on a Solid–Liquid Composite Flexible Tactile Sensor Array" Micromachines 13, no. 3: 440. https://doi.org/10.3390/mi13030440
APA StyleLiu, W., Zhang, G., Zhan, B., Hu, L., & Liu, T. (2022). Fine Texture Detection Based on a Solid–Liquid Composite Flexible Tactile Sensor Array. Micromachines, 13(3), 440. https://doi.org/10.3390/mi13030440








