Simulation and Optimization of a Planar-Type Micro-Hotplate with Si3N4-SiO2 Transverse Composite Dielectric Layer and Annular Heater
Abstract
:1. Introduction
2. Analytical Models and Design Methods
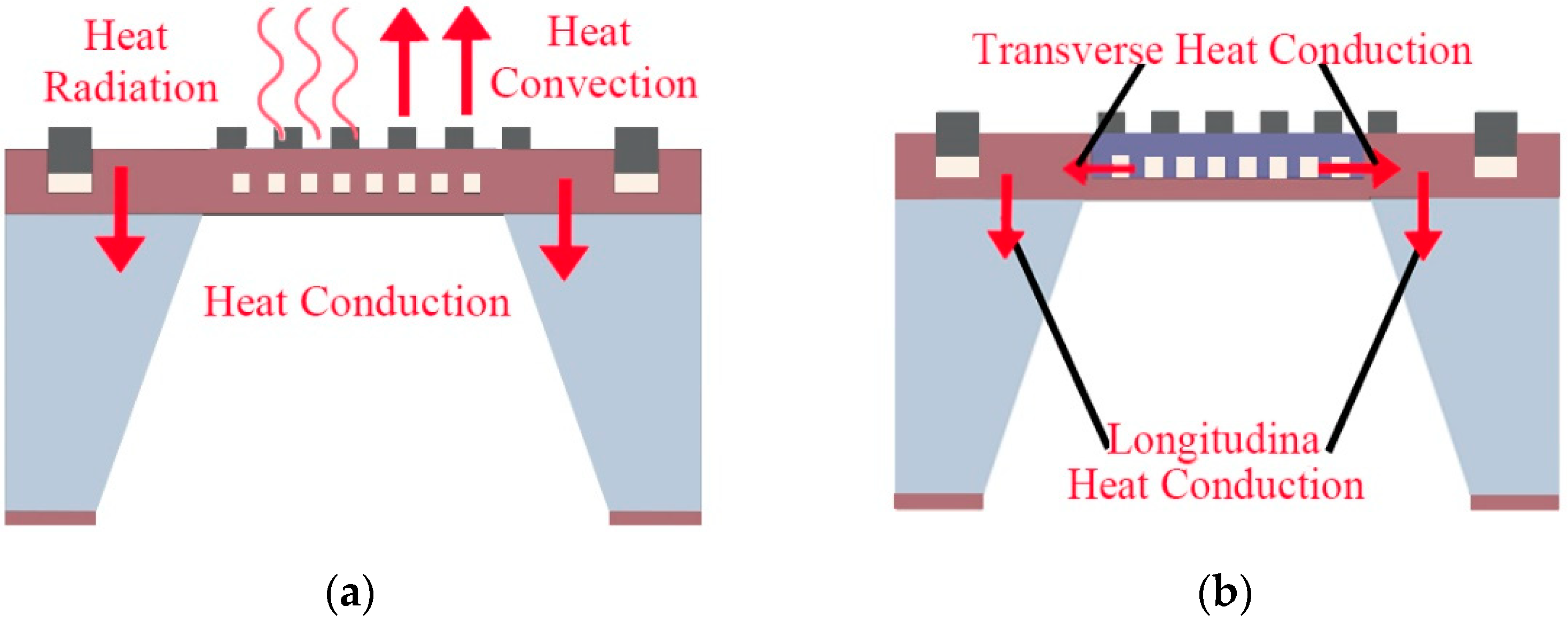
2.1. Heat Transfer Model of MHP
2.2. Thermal Deformation Computation
2.3. Presumption Verification
2.4. Structural Design of the New MHP
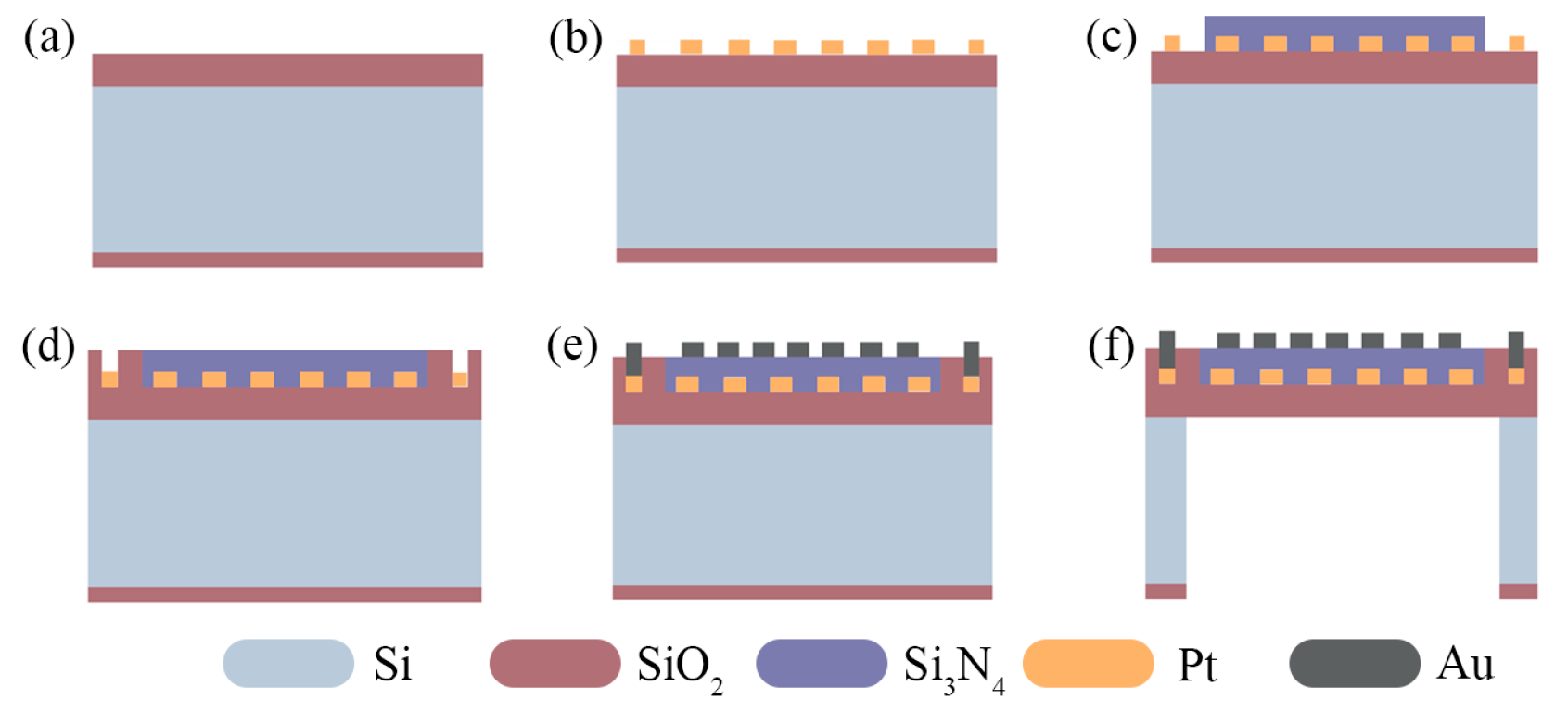
2.5. The Process Design
3. Simulation and Optimization
3.1. Validation of the MHP Model
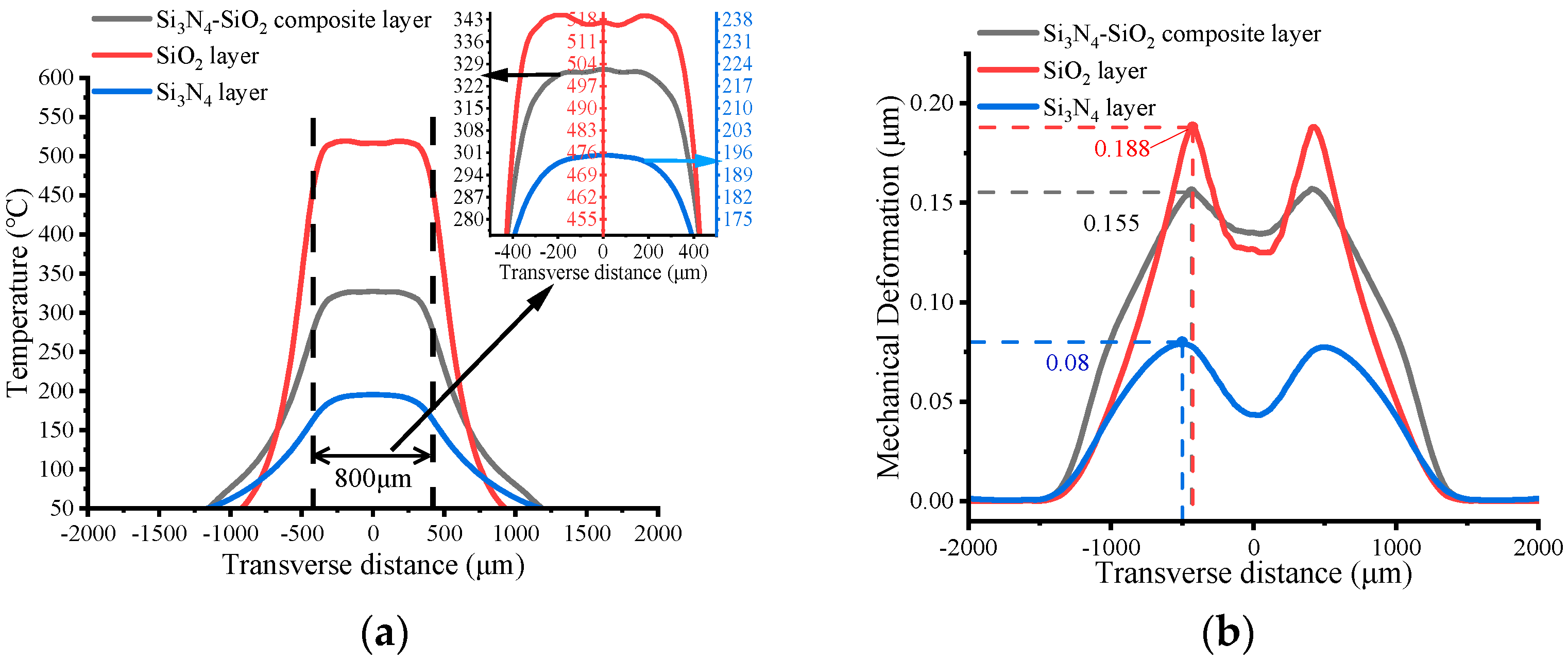
3.2. Dielectric Layer Analysis
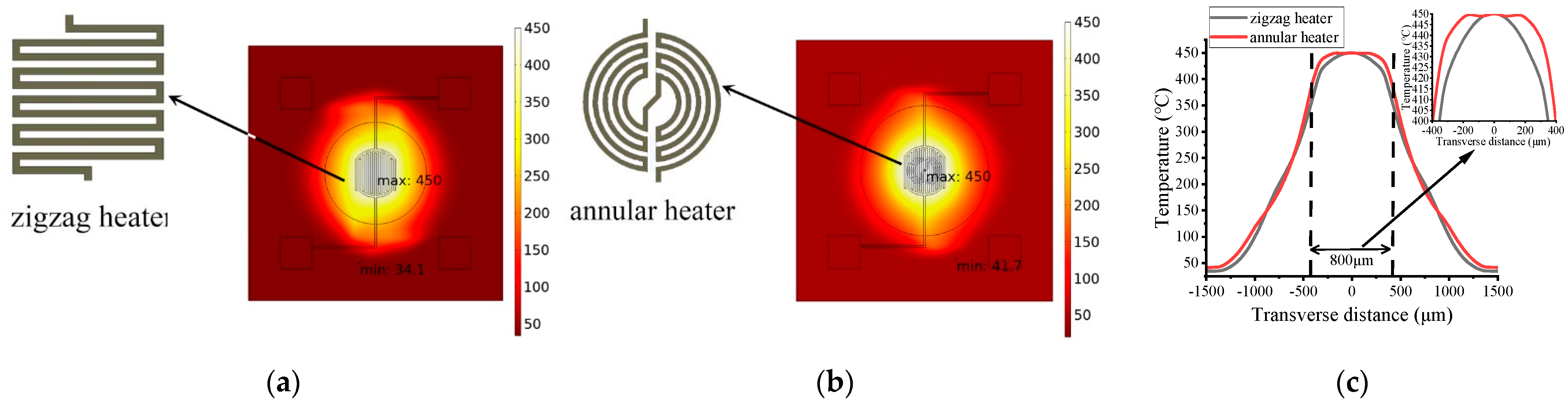
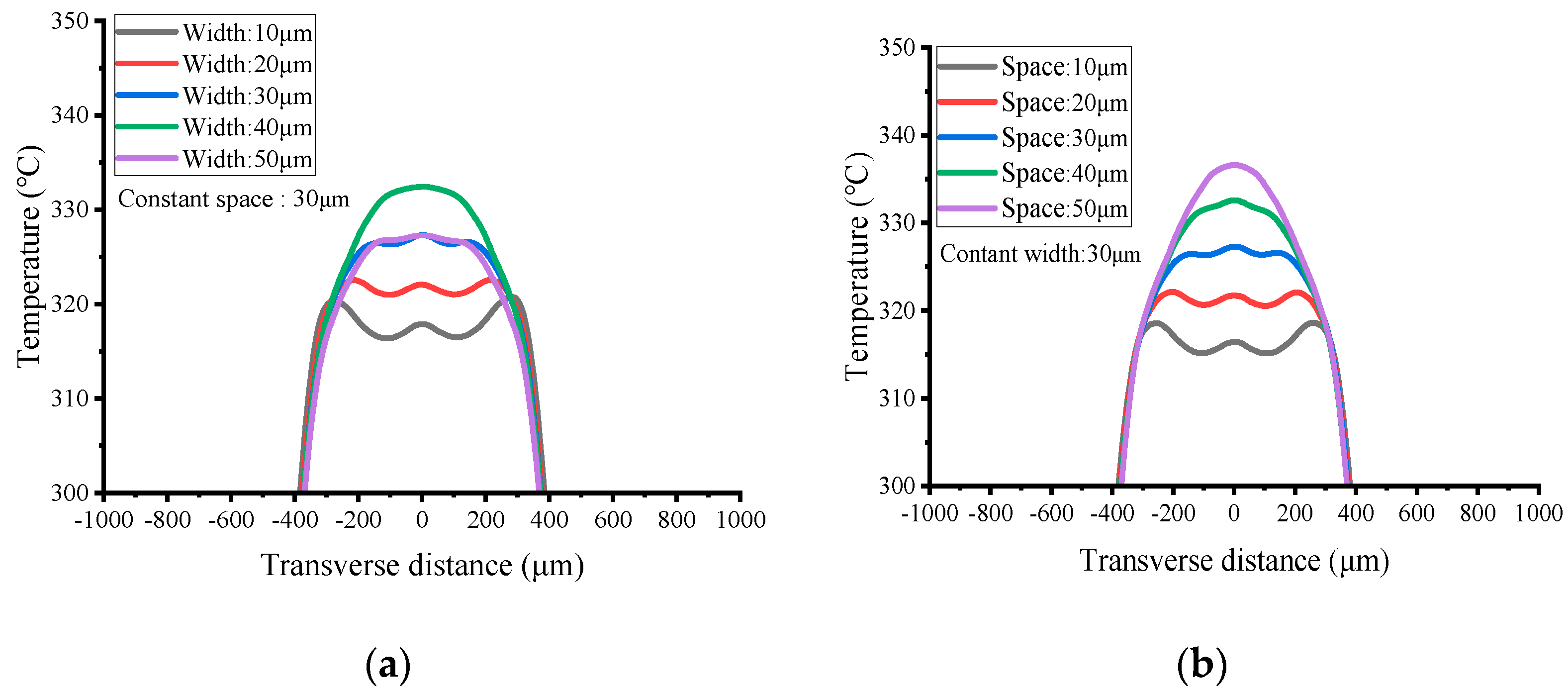
3.3. The Heater Design
3.4. Effect of Back-Side Etching Window Size
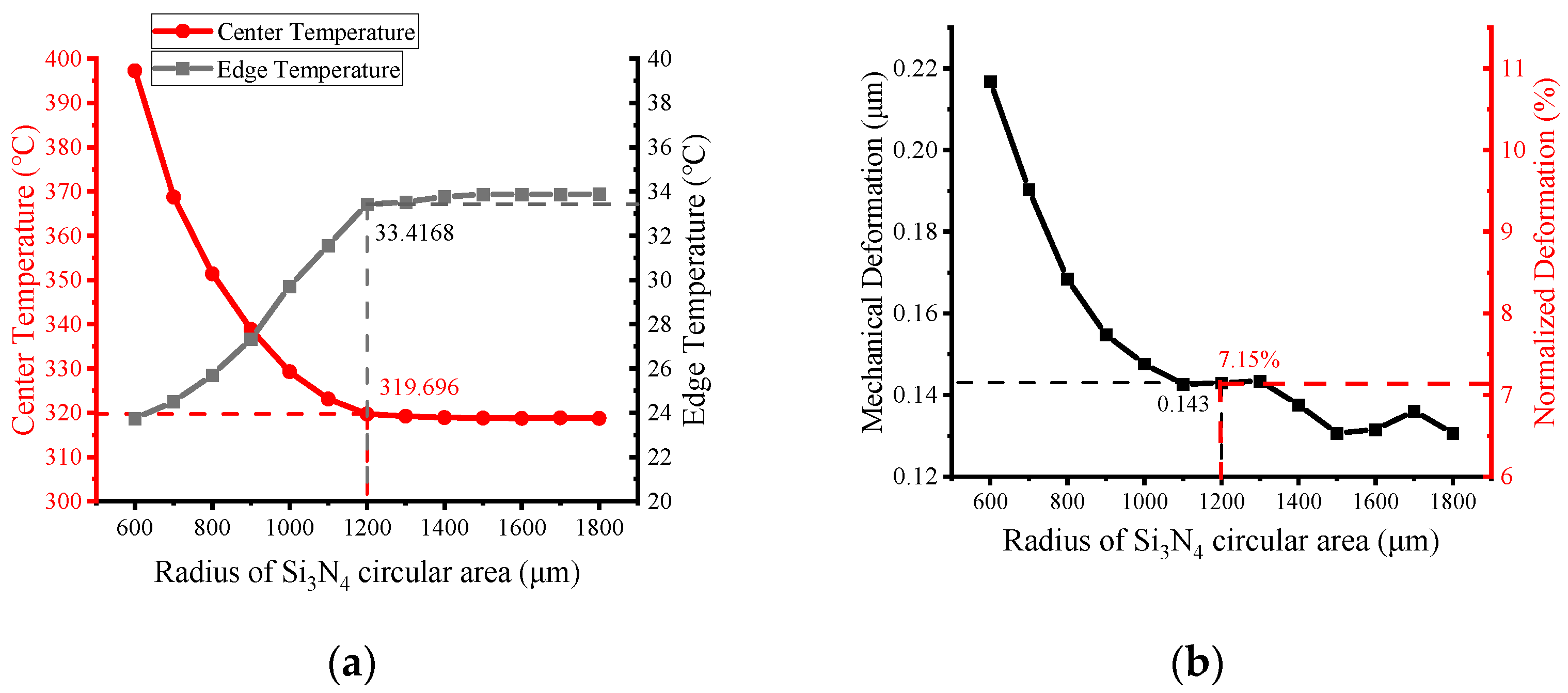
3.5. Effect of Si3N4 Circular Area in the Composite Layer
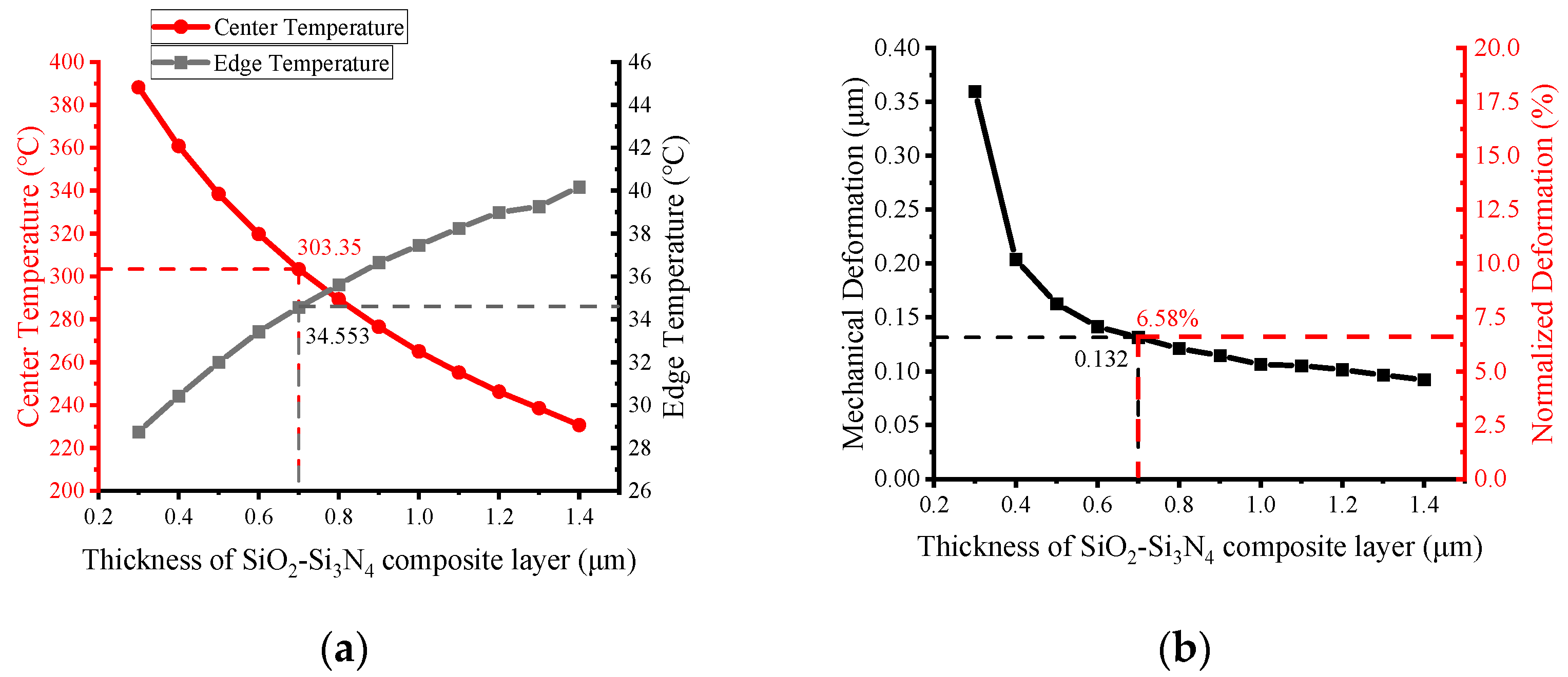
3.6. Effect of the Thickness of the Dielectric Layer
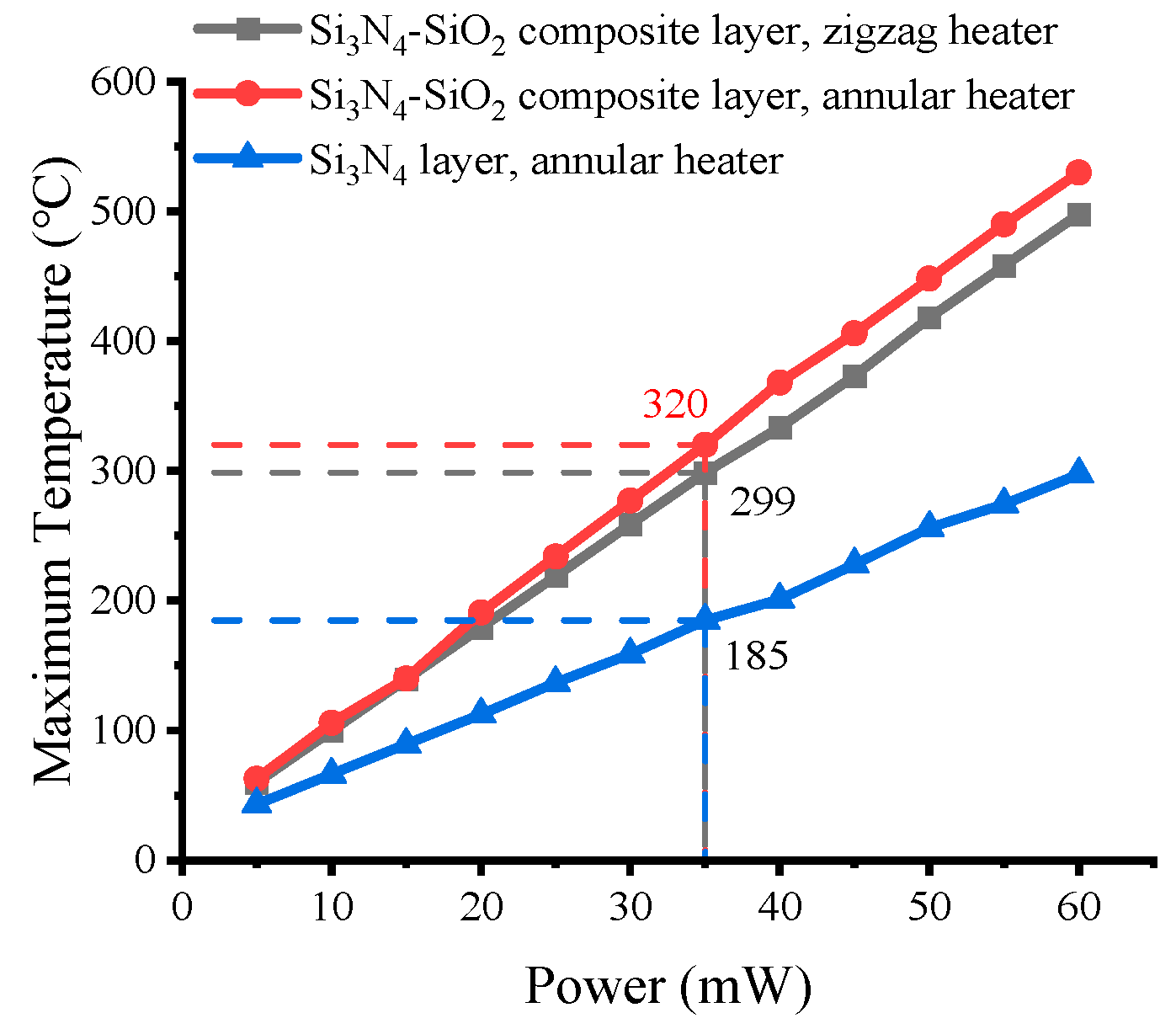
3.7. Power Optimization Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, H.; Yu, J.; Li, Z.; Yao, G.; Cao, R.; Li, X.; Zhu, H.; He, A.; Tang, Z. Microhotplate gas sensors incorporated with Al electrodes and 3D hierarchical structured PdO/PdO2-SnO2: Sb materials for sensitive VOC detection. Sens. Actuators B. 2021, 329, 128984. [Google Scholar] [CrossRef]
- Wang, J.; Yu, J. Multifunctional platform with CMOS-compatible tungsten microhotplate for pirani, temperature, and gas Sensor. Micromachines 2015, 6, 1597–1605. [Google Scholar] [CrossRef] [Green Version]
- Hwang, W.J.; Shin, K.S.; Roh, J.H.; Lee, D.S.; Choa, S.H. Development of micro-heaters with optimized temperature compensation design for gas sensors. Sensors 2011, 11, 2580–2591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spruit, R.G.; van Omme, J.T.; Ghatkesar, M.K.; Garza, H.H.P. A Review on development and optimization of microheaters for high-temperature in situ studies. J. Microelectromech. Syst. 2017, 26, 1165–1182. [Google Scholar] [CrossRef]
- Park, J.H.; Park, K.M.; Kim, T.W.; Shin, S.; Park, C.O.; Yoo, H.J. Three-electrode metal-oxide gas sensor system with CMOS interface IC. IEEE Sens. J. 2017, 17, 784–793. [Google Scholar] [CrossRef]
- Johnson, C.L.; Wise, K.D.; Schwank, J.W. A thin-film gas detector for semiconductor process gases. In Proceedings of the International Electron Devices Meeting, San Francisco, CA, USA, 11–14 December 1988; pp. 662–665. [Google Scholar]
- Prasad, M.; Dutta, P.S. Development of micro-hotplate and its reliability for gas sensing applications. Appl. Phys. A Mater. Sci. Process. 2018, 124, 788. [Google Scholar] [CrossRef]
- Chen, Y.; Li, M.; Yan, W.; Xin, Z.; Ng, K.; Cheng, X. Sensitive and low-power metal oxide gas sensors with a low-cost microelectromechanical heater. ACS Omega 2021, 6, 1216–1222. [Google Scholar] [CrossRef]
- Rajeswara Rao, L.L.; Singha, M.K.; Subramaniam, K.M.; Jampana, N.; Asokan, S. Molybdenum microheaters for MEMS-Based gas sensor applications: Fabrication, electro-thermo-mechanical and response characterization. IEEE Sens. J. 2017, 17, 22–29. [Google Scholar] [CrossRef]
- Lerond, T.; Yarekha, D.; Avramovic, V.; Mélin, T.; Arscott, S. Surface micromachining of chip-edge silicon microcantilevers using xenon difluoride etching of silicon-on-insulator. J. Micromech. Microeng. 2018, 31, 85001. [Google Scholar] [CrossRef]
- Askari Moghadam, R.; Saffari, H.; Koohsorkhi, J. Ni–P electroless on nonconductive substrates as metal deposition process for MEMS fabrication. Microsyst. Technol. 2021, 27, 79–86. [Google Scholar] [CrossRef]
- Girija, K.G.; Chakraborty, S.; Menaka, M. Low-cost surface micromachined microhotplates for chemiresistive gas sensors. Microsyst. Technol. 2018, 24, 3291–3297. [Google Scholar] [CrossRef]
- Christina, L.; Hannu, K.; Roy, K. Surface micromachining. Handbook of Silicon Based MEMS Materials and Technologies, 2nd ed.; Tilli, M., Motooka, T., Airaksinen, V., Eds.; Matthew Deans: Oxford, UK, 2015; pp. 525–539. ISBN 978-0-323-29965-7. [Google Scholar]
- Kataria, D.; Kumar, S.; Balguvhar, S.; Mukhiya, R.; Jain, A.; Kumar, S.S.; Sinha, S. Realization of MEMS-based silicon cantilever using bulk micromachining. In Proceedings of the 2017 International Conference on Recent Innovations in Signal processing and Embedded Systems (RISE), Bhopal, India, 27–29 October 2017; pp. 422–426. [Google Scholar]
- Rao, A.V.N.; Pal, P.; Pandey, A.K.; Menon, P.K.; Tanaka, H.; Sato, K. High speed silicon wet bulk micromachining of Si{111} in KOH based solution. In Proceedings of the 2020 Symposium on Design, Test, Integration & Packaging of MEMS and MOEMS (DTIP), Lyon, France, 15–26 June 2020; pp. 1–5. [Google Scholar]
- Cho, Y.C.; Elsayed, M.Y.; El-Gamal, M.N. Fabrication of micromachined hotplates by combining the PolyMUMPs technology with self-aligned post-processing steps. J. Micromech. Microeng. 2020, 30, 107001. [Google Scholar] [CrossRef]
- Sun, J.; Zhan, T.; Sokolovskij, R.; Liu, Z.; Sarro, P.M.; Zhang, G. Enhanced sensitivity Pt/AlGaN/GaN heterostructure NO2 sensor using a two-step gate recess technique. IEEE Sens. J. 2021, 21, 16475–16483. [Google Scholar] [CrossRef]
- Choi, K.-W.; Lee, J.-S.; Seo, M.-H.; Jo, M.-S.; Yoo, J.-Y.; Sim, G.S.; Yoon, J.-B. Batch-fabricated CO gas sensor in large-area (8-inch) with sub-10 mW power operation. Sens. Actuators B 2019, 289, 153–159. [Google Scholar] [CrossRef]
- Çakir, M.C.; Çaliskan, D.; Bütün, B.; Özbay, E. Planar indium tin oxide heater for improved thermal distribution for metal oxide micromachined gas sensors. Sensors 2018, 16, 1612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wojcik, B.U.; Vincent, T.A.; Gardner, J.W. H2S sensing properties of WO3 based gas sensor. Procedia Eng. 2016, 168, 255–268. [Google Scholar] [CrossRef]
- Ahmed, A.Y.; Baskaran, F.M.F.; Rabih, A.A.S.; Dennis, J.O.; Khir, M.H.M.; Elmaleeh, M.A.A. Design, modeling and simulation of microhotplate for application in gas detection. In Proceedings of the 2018 International Conference on Intelligent and Advanced System (ICIAS), Kuala Lumpur, Malaysia, 13–14 August 2018; pp. 1–5. [Google Scholar]
- Prášek, J.; Vančík, S.; Svatoš, V.; Klempa, J.; Gablech, I.; Pytlíček, Z.; Levek, V. MEMS microhotplates for chemical sensors. In Proceedings of the 2018 41st International Spring Seminar on Electronics Technology (ISSE), Zlatibor, Serbia, 16–20 May 2018; pp. 1–5. [Google Scholar]
- Lv, P.; Tang, Z.; Yu, J.; Zhang, F.; Wei, G.; Huang, Z.; Hu, Y. Study on a micro-gas sensor with SnO2–NiO sensitive film for indoor formaldehyde detection. Sens. Actuators B 2008, 132, 74–80. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Yao, J.; Ding, G. Impact resistance and static strength analysis of an extremely simplified micro hotplate with novel suspended film. Sens. Actuators B 2018, 280, 495–504. [Google Scholar] [CrossRef]
- Zhu, B.; Yin, C.; Zhang, Z.; Tao, C.; Dong, N. Design and fabrication of planar-type micro-hotplate with Si-island gas sensor. Adv. Mater. Res. 2012, 345, 23–28. [Google Scholar] [CrossRef]
- Lahlalia, A.; Neel, O.L.; Shankar, R.; Kam, S.Y.; Filipovic, L. Electro-thermal simulation & characterization of a microheater for SMO gas sensors. J. Microelectromech. Syst. 2018, 27, 529–537. [Google Scholar]
- Maccagnani, P.; Angelucci, R.; Pozzi, P.; Poggi, A.; Dori, L.; Cardinali, G.C.; Negrini, P. Thick oxidised porous silicon layer as a thermoinsulating membrane for high-temperature operating thin-and thick-film gas sensors. Sens. Actuators B 1998, 49, 22–29. [Google Scholar] [CrossRef]
- Prasad, M. Design, development and reliability testing of a low power bridge-type micromachined hotplate. Microelectron. Reliab. 2015, 55, 937–944. [Google Scholar] [CrossRef]
- Chowdhury, P.; Roy, S. TEM analysis of microheater using SiO2/Si3N4 composite membrane for long term gas sensing applications. In Proceedings of the 2017 1st International Conference on Electronics, Kolkata, India, 28–29 April 2017; pp. 1–6. [Google Scholar]
- Wu, Y.; Du, X.; Li, Y.; Tai, H.; Su, Y. Optimization of temperature uniformity of a serpentine thin film heater by a two-dimensional approach. Microsyst. Technol. 2019, 25, 69–82. [Google Scholar] [CrossRef]
- Creemer, J.F.; Briand, D.; Zandbergen, H.W.; Vlist, W.V.D.; Boer, C.R.D.; Rooij, N.F.; Sarro, P.M. Microhotplates with TiN heaters. Sens. Actuators A 2008, 148, 416–421. [Google Scholar] [CrossRef]
- Akasaka, S.; Boku, E.; Amamoto, Y.; Yuji, H.; Kanno, I. Ultrahigh temperature platinum microheater encapsulated by reduced-TiO2 barrier layer. Sens. Actuators A 2019, 296, 286–291. [Google Scholar] [CrossRef]
- Lahlalia, A.; Filipovic, L.; Selberherr, S. Modeling and simulation of novel semiconducting metal oxide gas sensors for wearable devices. IEEE Sens. J. 2018, 18, 1960–1970. [Google Scholar] [CrossRef]
- Afridi, M.Y.; Suehle, J.S.; Zaghloul, M.E.; Berning, D.W.; Hefner, A.R.; Cavicchi, R.E.; Semancik, S.; Montgomery, C.B.; Taylor, C.J. A monolithic CMOS microhotplate-based gas sensor system. IEEE Sens. J. 2002, 2, 644–655. [Google Scholar] [CrossRef]
- Mele, L.; Santagata, F.; Iervolino, E.; Mihailovic, M.; Rossi, T.; Tran, A.T.; Schellevis, H.; Creemer, J.F.; Sarro, P.M. A molybdenum MEMS microhotplate for high-temperature operation. Sens. Actuators A 2012, 188, 173–180. [Google Scholar] [CrossRef]
- Li, Y.; Yu, J.; Wu, H.; Tang, Z. Design and fabrication of a CMOS-compatible MHP gas sensor. AIP Adv. 2014, 4, 31339. [Google Scholar] [CrossRef]
- Briand, D.; Colin, S.; Courbat, J.; Raible, S.; Kappler, J.; Rooij, N.F.D. Integration of MOX gas sensors on polyimide hotplates. Sens. Actuators B 2008, 130, 430–435. [Google Scholar] [CrossRef] [Green Version]
- Shim, J.; Chung, G. Fabrication and characteristics of Pt/ZnO NO sensor integrated SiC micro heater. In Proceedings of the 2010 IEEE Sensors, Waikoloa, HI, USA, 1–4 November 2010; pp. 350–353. [Google Scholar]
- Carole, R.; Pierre, T.B.; Daniel, E. Realization and performance of thin SiO2/SiNx membrane for microheater applications. Sens. Actuators A 1998, 64, 241–245. [Google Scholar]
- Kwak, S.; Shim, Y.S.; Yoo, Y.K.; Lee, J.H.; Kim, I.; Kim, J.; Lee, K.H.; Lee, J.H. MEMS-based gas sensor using PdO-decorated TiO2 thin film for highly sensitive and selective H2 detection with low power consumption. Electron. Mater. Lett. 2018, 14, 305–313. [Google Scholar] [CrossRef]
- Tommasi, A.; Cocuzza, M.; Perrone, D.; Pirri, C.; Mosca, R.; Villani, M.; Delmonte, N.; Zappettini, A.; Calestani, D.; Marasso, S.L. Modeling, fabrication and testing of a customizable micromachined hotplate for sensor applications. Sensors 2016, 17, 62. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saxena, G.; Paily, R. Performance improvement of square microhotplate with insulation layer and heater geometry. Microsyst. Technol. 2015, 21, 2331–2338. [Google Scholar] [CrossRef]
- Ahmed, A.Y.; Dennis, J.O.; Saad, M.N.M.; Talah, W.A. Design and simulation of a high temperature MEMS micro-hotplate for application in trace gas detection. In Proceedings of the 2008 IEEE International Conference on Semiconductor Electronics, Johor Bahru, Malaysia, 25–27 November 2008; pp. 153–157. [Google Scholar]
- Shen, B.; Cao, S.W.; Yang, P.Q.; Liu, X.L. Study on thermal field coupling simulation of methane sensor based on ceramic micro-hot plate. IPO Conf. Ser. Mater. Sci. Eng. 2019, 490, 22007. [Google Scholar] [CrossRef]
- Sidek, O.; Ishak, M.Z.; Khalid, M.A.; Bakar, M.Z.A. Effect of heater geometry on the high temperature distribution on a MEMS micro-hotplate. In Proceedings of the 2011 3rd Asia Symposium on Quality Electronic Design (ASQED), Kuala Lumpur, Malaysia, 19–20 July 2011; pp. 100–104. [Google Scholar]
- Kulhari, L.; Khanna, P.K. Design, simulation and fabrication of LTCC-based microhotplate for gas sensor applications. Microsyst. Technol. 2018, 24, 2169–2175. [Google Scholar] [CrossRef]
- Saxena, G.; Paily, R. Analytical modeling of square microhotplate for gas sensing application. IEEE Sens. J. 2013, 13, 4851–4859. [Google Scholar] [CrossRef]
- Yu, J.; Tang, Z.; Chan, P.C.H.; Wei, G.; Wang, W.L.; Yan, G.Z. Thermal analysis of silicon micromachining based micro hotplates. Chin. J. Semicond. 2005, 26, 192–196. [Google Scholar]
- Yuan, Z.; Yang, F.; Meng, F.; Zuo, K.; Li, J. Research of low-power MEMS-based micro hotplates gas sensor: A Review. IEEE Sens. J. 2021, 21, 18368–18380. [Google Scholar] [CrossRef]
- Mo, Y.; Okawa, Y.; Inoue, K.; Natukawa, K. Low-voltage and low-power optimization of micro-heater and its on-chip drive circuitry for gas sensor array. Sens. Actuators A 2002, 100, 94–101. [Google Scholar] [CrossRef]
- Kozlov, A.G. Optimization of structure and power supply conditions of catalytic gas sensor. Sens. Actuators B 2002, 82, 24–33. [Google Scholar] [CrossRef]
- Saxena, G.; Singh, D.; Raaj, M. Thermal analysis of a microhotplate—An experimental study. J. Microelectromech. Syst. 2020, 29, 408–417. [Google Scholar] [CrossRef]
- Furmański, P.; Łapka, P. Micro-macro heat conduction model for the prediction of local, transient temperature in composite media. Int. J. Therm. Sci. 2020, 154, 106401. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, J.; Bai, S.; Guan, J.; Zhang, F.; Tang, Z. Size effect of heat transport in microscale gas gap. IEEE Trans. Ind. Electron. 2017, 64, 7387–7391. [Google Scholar] [CrossRef]
- Kim, K.J.; King, W.P. Thermal conduction between a heated microcantilever and a surrounding air environment. Appl. Therm. Eng. 2009, 29, 1631–1641. [Google Scholar] [CrossRef]
- Walden, P.; Kneer, J.; Knobelspies, S.; Kronast, W.; Mescheder, U.; Palzer, S. Micromachined hotplate platform for the investigation of Ink-Jet printed, functionalized metal oxide nanoparticles. J. Microelectromech. Syst. 2015, 24, 1384–1390. [Google Scholar] [CrossRef]
- Joy, S.; Antony, J.K. Design and simulation of a micro hotplate using COMSOL multiphysics for MEMS based gas sensor. In Proceedings of the 2015 Fifth International Conference on Advances in Computing and Communications (ICACC), Kochi, India, 2–4 September 2015; pp. 465–468. [Google Scholar]
- Linear Elasticity. Available online: https://en.wikipedia.org/wiki/Linear_elasticity#Displacement_formulation (accessed on 10 December 2021).
- Ali, S.Z.; Udrea, F.; Milne, W.I.; Gardner, J.W. Tungsten-based SOI microhotplates for smart gas Sensors. J. Microelectromech. Syst. 2008, 17, 1408–1417. [Google Scholar] [CrossRef]
- MEMS Software—For Micro-Electromechanical Systems. Available online: www.comsol.com/mems-module (accessed on 10 December 2021).
- Mehmood, Z.; Haneef, I.; Udrea, F. Material selection for micro-electro-mechanical-systems (MEMS) using Ashby’s approach. Mater. Des. 2018, 157, 412–430. [Google Scholar] [CrossRef]
- Udrea, F.; Gardner, J.W.; Setiadi, D.; Covington, J.A. Design and simulations of SOI CMOS micro-hotplate gas sensors. Sens. Actuators B 2001, 78, 180–190. [Google Scholar] [CrossRef]
- Simon, I.; Bârsan, N.; Bauer, M.; Weimar, U. Micromachined metal oxide gas sensors: Opportunities to improve sensor performance. Sens. Actuators B 2001, 73, 412–430. [Google Scholar] [CrossRef]
- Castagna, M.E.; Modica, R.; Cascino, S. A high stability and uniformity W micro hot plate. Sens. Actuators A 2018, 279, 617–623. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yin, C.B.; Tao, C.M.; Zhu, B.; Dong, N.N. Design and optimization of planar structure micro-hotplate. Procedia Eng. 2011, 12, 105–110. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Yuan, L.J.; Hua, Z.Q.; Zhen, D. Design and optimization of heating plate for metal oxide semiconductor gas sensor. Microsyst. Technol. 2019, 25, 3511–3519. [Google Scholar] [CrossRef]


| Year | Active Area | MHP Area | Power at 300 °C (mW) | Power/ Heater Area 1 | Already Fabricated? | Planar/ Suspended | Material of Heater | Material of Plate | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| 2002 | 10 | 30 | 3 | Yes | Suspended | Poly Si | SiO2 | [26] | |
| 2010 | 140.6 | 13.5 | 0.096 | Yes | Suspended | 3C-SiC | AlN/SiC | [27] | |
| 2012 | 108 | 1000 | 22.68 | 0.21 | Yes | Planar | Molybdenum | SiO2/SiN | [28] |
| 2014 | 10 | 19 | 1.9 | Yes | Suspended | W | SiO2 | [29] | |
| 2014 | 10 | 267.3 | 27.66 (367 °C) | 2.77 | No | Planar | Pt | SiO2/Si3N4 | [30] |
| 2016 | 846.4 | 100 | 0.118 | Yes | Planar | ITO | Si3N4 | [19] | |
| 2016 | 17.6 | 250 | 14 | 0.79 | Yes | Planar | W | SiO2 | [20] |
| 2018 | 250 | 4 | 0.016 | No | Suspended | Pt | Si3N4/SiC | [21] | |
| 2018 | 6.4 | 22.5 | 10 | 1.56 | Yes | Suspended | Pt | SiO2 | [22] |
| 2018 | 10 | 90 | 13 | 1.3 | Yes | Suspended | W | SiO2/Si3N4 | [23] |
| 2018 | 101.7 | 540 | 8 | 0.079 | No | Suspended | Pt | SiO2/Si3N4 | [31] |
| 2019 | 0.032 | 7 | 218.75 | Yes | Suspended | Pt | Si | [18] | |
| 2019 | 250 | 490 | 30 | 0.12 | Yes | Planar | Pt | SiN/SiO2 | [32] |
| Thiswork | 553.9 | 6154.4 | 35.2 | 0.064 | No | Planar | Pt | SiO2-Si3N4 |
| Type | Structure | Center Temperature (°C) | Maximum | |
|---|---|---|---|---|
| A |  | 800 × 800 | 158 | 0.052 |
| B |  | 800 × 800 | 174 | 0.223 |
| C |  | 800 × 800 | 199 | 0.228 |
| D |  | 800 × 800 | 275 | 0.098 |
| Material | Pt | Si | SiO2 | Si3N4 | Au |
|---|---|---|---|---|---|
| Thermal conductivity coefficient (W m−1 K−1) | 71.6 | 130 | 1.4 | 20 | 317 |
| Range of thermal conductivity coefficient found in literature (W m−1 K−1) | 70–72 | 130 | 1.2–1.4 | 9–30 | 317 |
| Electrical conductivity (S m−1) | 8.9 × 106 | 1 × 10−12 | 1 × 10−10 | 1 × 10−2 | 45.6 × 106 |
| Heat capacity (J Kg−1 K−1) | 133 | 703 | 730 | 700 | 129 |
| Density (Kg m−3) | 24,150 | 2329 | 2200 | 3100 | 19,300 |
| Thermal expansion coefficient (10−6 K−1) | 8.80 | 2.6 | 0.5 | 2.3 | 14.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, G.; Wang, P.; Li, M.; Lin, Z.; Nai, C. Simulation and Optimization of a Planar-Type Micro-Hotplate with Si3N4-SiO2 Transverse Composite Dielectric Layer and Annular Heater. Micromachines 2022, 13, 601. https://doi.org/10.3390/mi13040601
Wei G, Wang P, Li M, Lin Z, Nai C. Simulation and Optimization of a Planar-Type Micro-Hotplate with Si3N4-SiO2 Transverse Composite Dielectric Layer and Annular Heater. Micromachines. 2022; 13(4):601. https://doi.org/10.3390/mi13040601
Chicago/Turabian StyleWei, Guangfen, Pengfei Wang, Meihua Li, Zhonghai Lin, and Changxin Nai. 2022. "Simulation and Optimization of a Planar-Type Micro-Hotplate with Si3N4-SiO2 Transverse Composite Dielectric Layer and Annular Heater" Micromachines 13, no. 4: 601. https://doi.org/10.3390/mi13040601
APA StyleWei, G., Wang, P., Li, M., Lin, Z., & Nai, C. (2022). Simulation and Optimization of a Planar-Type Micro-Hotplate with Si3N4-SiO2 Transverse Composite Dielectric Layer and Annular Heater. Micromachines, 13(4), 601. https://doi.org/10.3390/mi13040601





