Study of the Pattern Preparation and Performance of the Resistance Grid of Thin-Film Strain Sensors
Abstract
:1. Introduction
2. Experimental Design
2.1. Thin-Film Resistance Grid Patterning Method Comparison Test Design
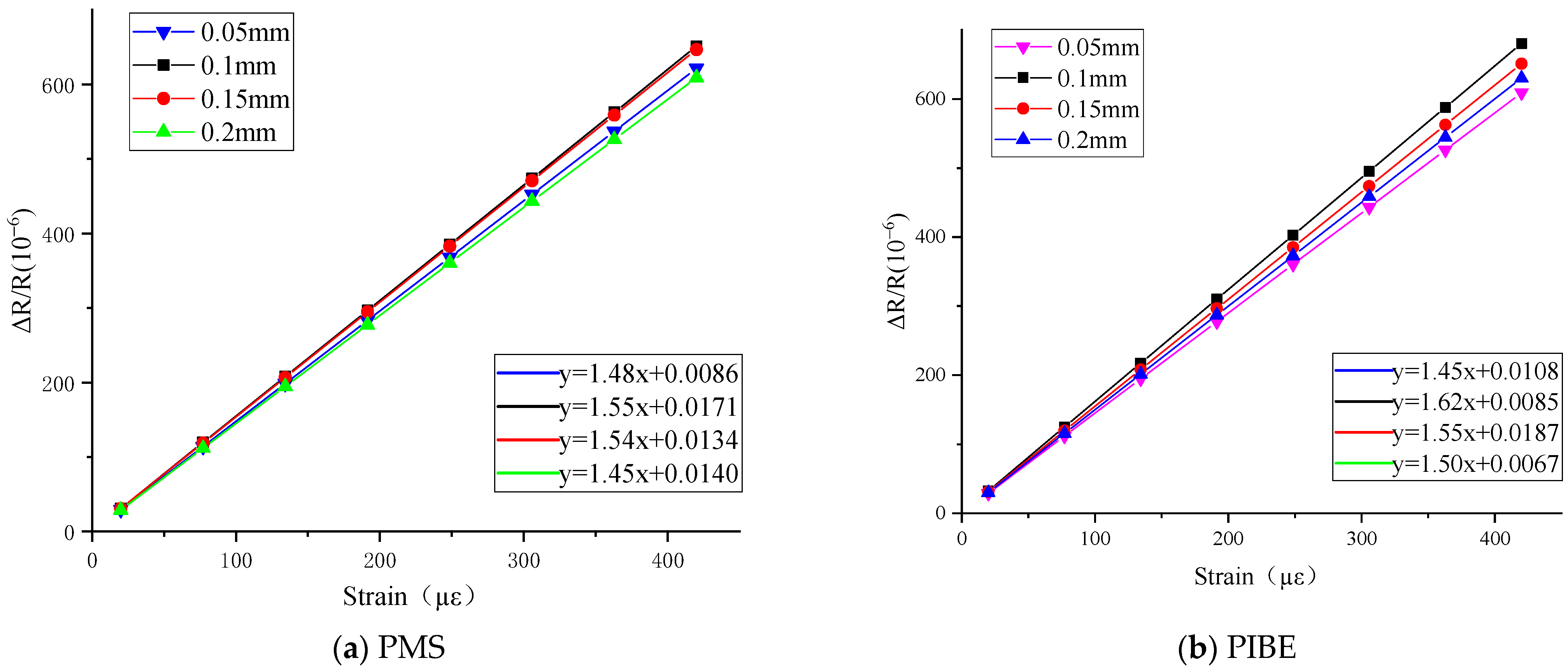
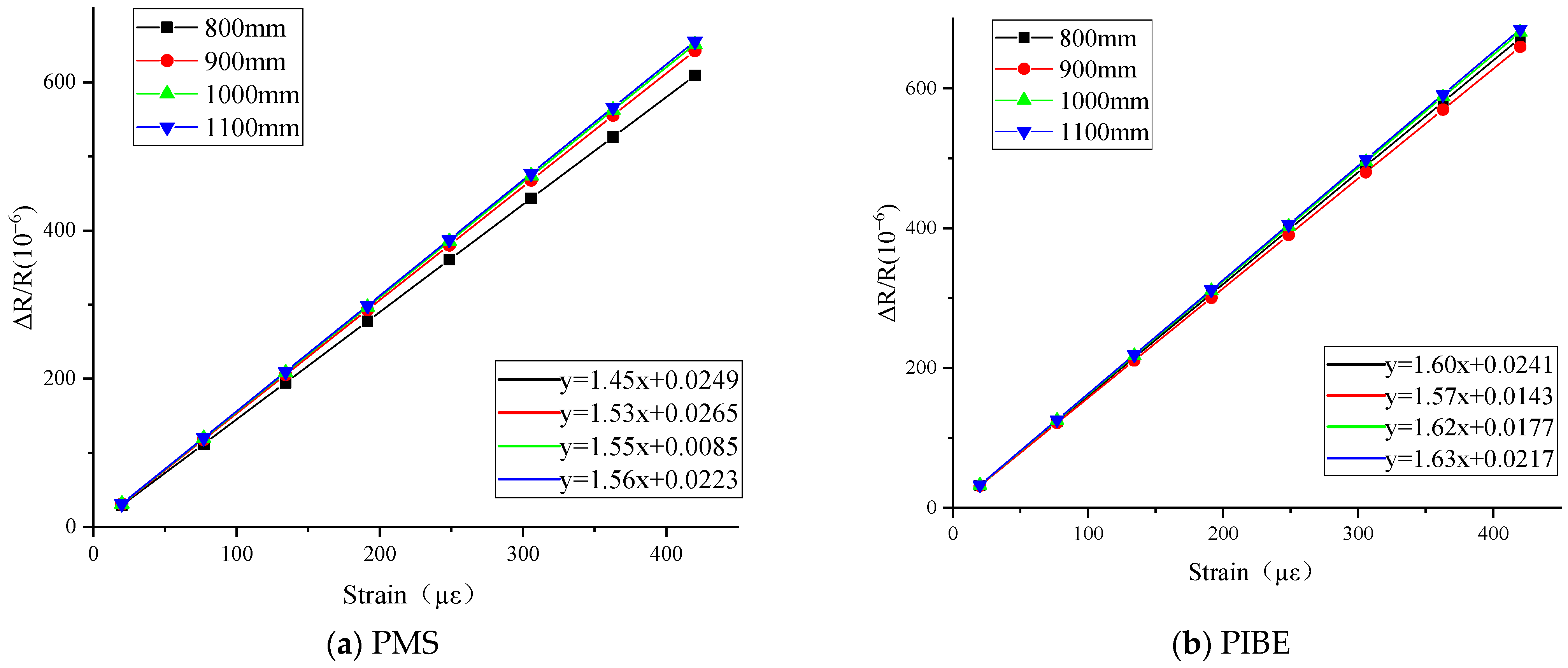
2.2. Resistance Value and Resistance Strain Coefficient with Different Geometric Dimensions of Thin-Film Strain Sensors Prepared by PMS and PIBE
2.3. Orthogonal Experiment on Process Parameters of PIBE
3. Results and Analysis
3.1. Resistance Strain Coefficient and Error Analysis of Resistance Grid
3.2. Comparative Analysis of Thin-Film Resistor Grid Preparation Methods
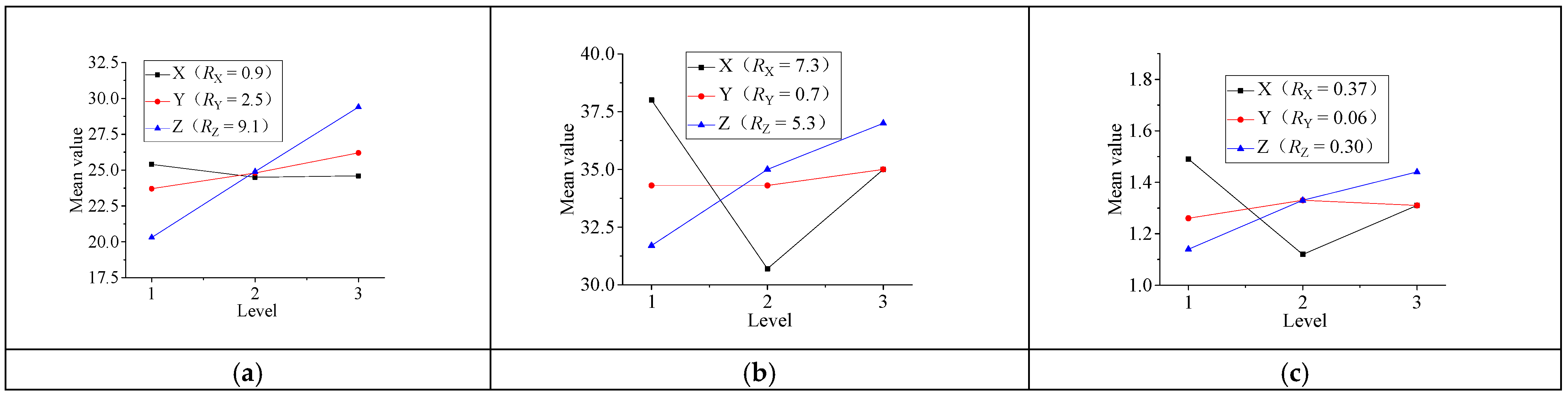
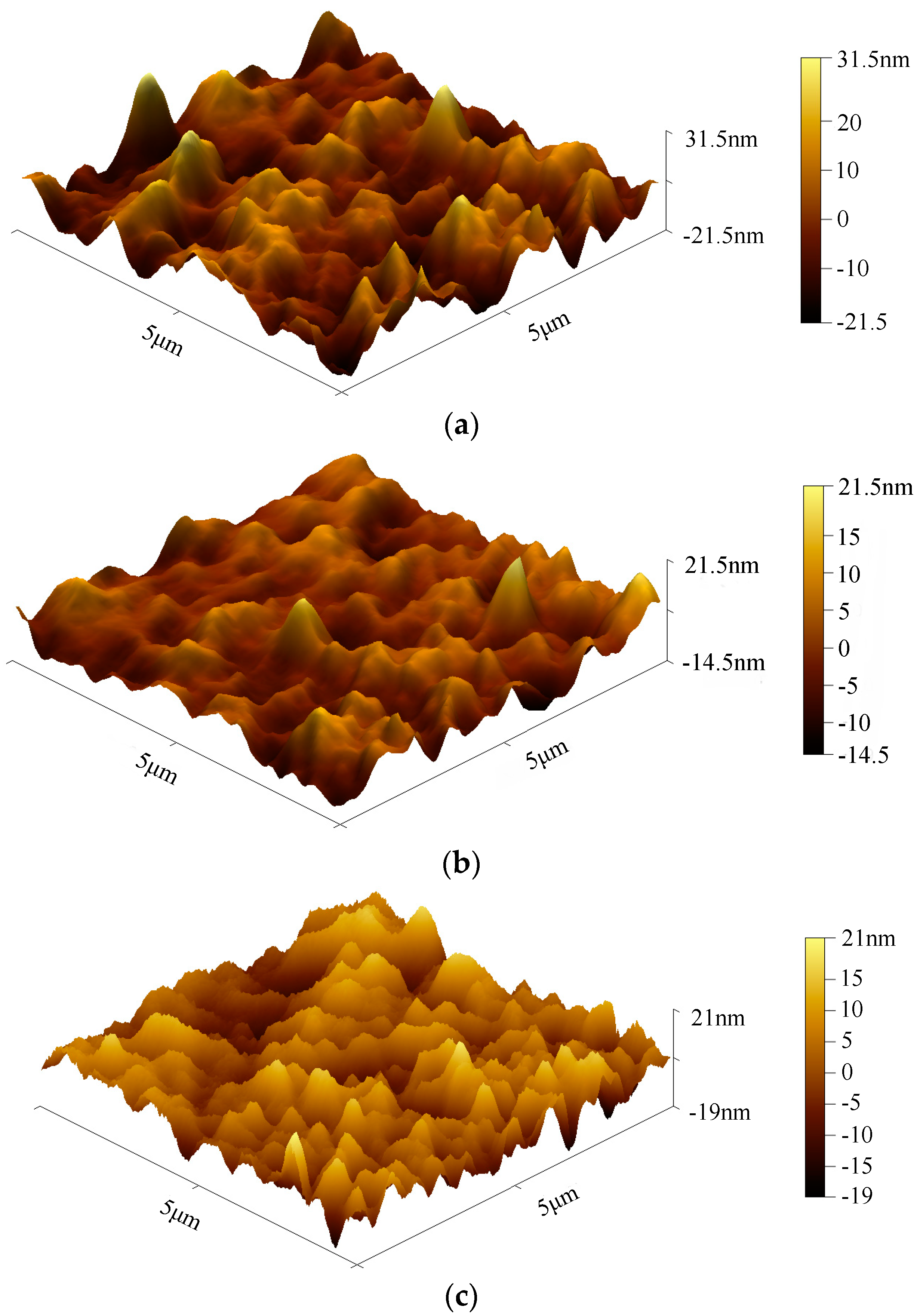
3.3. Effects of Etching Process Parameters on Etching Rate, Surface Quality, and Resistivity
3.4. Variance Analysis of Thin-Film Etching Process Parameters
3.5. Effect of Substrate Temperature on Ni Cr Alloy Film
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kuntoğlu, M.; Acar, O.; Gupta, M.K.; Sağlam, H.; Sarikaya, M.; Giasin, K.; Pimenov, D.Y. Parametric optimization for cutting forces and material removal rate in the turning of AISI 5140. Machines 2021, 9, 90. [Google Scholar] [CrossRef]
- Kuntoğlu, M.; Aslan, A.; Sağlam, H.; Pimenov, D.Y.; Giasin, K.; Mikolajczyk, T. Optimization and analysis of surface roughness, flank wear and 5 different sensorial data via tool condition monitoring system in turning of AISI 5140. Sensors 2020, 20, 4377. [Google Scholar] [CrossRef] [PubMed]
- Kiswanto, G.; Putri, S.K.; Fitriawan, M.R.; Hiltansyah, F.; Putra, R.G. Modeling, Simulation, and Analysis of Cutting Force in Micro End Milling Process of Mild Steel Using Mechanistic Model. In Proceedings of the 2021 7th International Conference on Mechatronics and Robotics Engineering (ICMRE), Budapest, Hungary, 3–5 February 2021. [Google Scholar]
- Yaldız, S.; Ünsaçar, F. Design, development and testing of a turning dynamometer for cutting force measurement. Mater. Des. 2006, 27, 839–846. [Google Scholar] [CrossRef]
- Castro, L.R.; Viéville, P.; Lipinski, P. Correction of dynamic effects on force measurements made with piezoelectric dynamomters. Int. J. Mach. Tools Manuf. 2006, 46, 1707–1715. [Google Scholar] [CrossRef]
- Yaldız, S.; Ünsaçar, F.; Sağlam, H.; Işık, H. Design, development and testing of a four-component milling dynamometer for the measurement of cutting force and torque. Mech. Syst. Signal Process. 2007, 21, 1499–1511. [Google Scholar] [CrossRef]
- Saglam, H.; Unuvar, A. Three-Component, Strain Gage Based Milling Dynamometer Design and Manufacturing. J. Integr. Des. Process Sci. 2001, 5, 95–109. [Google Scholar]
- Liu, H.; Zhao, H.; Li, S.; Hu, J.; Zheng, X.; Li, R.; Chen, Y.; Su, Y. Adhesion-Free Thin-Film-Like Curvature Sensors Integrated on Flexible and Wearable Electronics for Monitoring Bending of Joints and Various Body Gestures. Adv. Mater. Technol. 2019, 4, 1800327. [Google Scholar] [CrossRef] [Green Version]
- Lipomi, D.J.; Vosgueritchian, M.; Tee, B.C.; Hellstrom, S.L.; Lee, J.A.; Fox, C.H.; Bao, Z. Skin-like pressure and strain sensors based on transparent elastic films of carbon nanotubes. Nat. Nanotechnol. 2011, 6, 788. [Google Scholar] [CrossRef]
- Žlebič, Č.; Živanov, L.; Menićanin, A.; Blaž, N.; Damnjanović, M. Inkjet printed resistive strain gages on flexible substrates. Facta Univ. -Ser. Electron. Energ. 2016, 29, 89–100. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Y.; Yuan, Y.; Li, D. A novel microfluidic resistive pulse sensor with multiple voltage input channels and a side sensing gate for particle and cell detection. Anal. Chim. Acta 2019, 1052, 113–123. [Google Scholar] [CrossRef] [Green Version]
- Zymelka, D.; Yamashita, T.; Takamatsu, S.; Itoh, T.; Kobayashi, T. Thin-film flexible sensor for omnidirectional strain measurements. Sens. Actuators A Phys. 2017, 263, 391–397. [Google Scholar] [CrossRef]
- Petley, V.; Raman, K.T.; Kumar, S.; Jain, R.; Rao, G.M. Stress evolution mechanism of NiCr thin-films on titanium alloy. J. Alloys Compd. 2017, 695, 2253–2260. [Google Scholar] [CrossRef]
- Han, C.J.; Chiang, H.P.; Cheng, Y.C. Using Micro-Molding and Stamping to Fabricate Conductive Polydimethylsiloxane-Based Flexible High-Sensitivity Strain Gauges. Sensors 2018, 18, 618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.; Jiang, S.; Jiang, H.; Zhao, X.; Zhang, W. Development of PdCr Thin-Film Resistance Strain Gauge and Its High Temperature Strain Sensitivity Performance. J. Transduct. Technol. 2017, 30, 348–352. [Google Scholar]
- Yang, S.; Zhang, C.; Wang, H.; Ding, G. An in-situ prepared synchronous self-compensated film strain gage for high temperature. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; IEEE: New York, NY, USA, 2017; pp. 1021–1024. [Google Scholar]
- Desbiolles, B.X.E.; Bertsch, A.; Renaud, P. Ion beam etching redeposition for 3D multimaterial nanostructure manufacturing. Microsyst. Nanoeng. 2019, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Chkhalo, N.I.; Mikhailenko, M.S.; Mil’kov, A.V.; Pestov, A.E.; Polkovnikov, V.N.; Salashchenko, N.N.; Salashchenko, I.L.; Strulya, M.V.; Zorina, S.; Zuev, S.Y. Effect of ion beam etching on the surface roughness of bare and silicon covered beryllium films. Surf. Coat. Technol. 2017, 311, 351–356. [Google Scholar] [CrossRef]
- Srinivasan, N.; Rook, K.; Ip, V.; Lee, M.H.; Kohli, S.; Cerio, F.; Devasahayam, A.J. Ion Beam Etching of New Absorber Materials for Sub-5 nm Euv Masks. In Advanced Lithography; SPIE: Bellingham, WA, USA, 2019; Volume 20. [Google Scholar]
- Abdullaev, D.A.; Seregin, D.S.; Vorotilov, K.A.; Sigov, A.S. Ion beam etching of dense and porous PZT films. Ferroelectrics 2019, 544, 75–81. [Google Scholar] [CrossRef]
- Soyer, C.; Cattan, E.; Remiens, D.; Guilloux-Viry, M. Ion beam etching of lead–zirconate–titanate thin-films: Correlation between etching parameters and electrical properties evolution. J. Appl. Phys. 2002, 92, 1048–1055. [Google Scholar] [CrossRef]
- Soyer, C.; Cattan, E.; Remiens, D. Electrical damage induced by reactive ion-beam etching of lead-zirconate-titanate thin-films. J. Appl. Phys. 2005, 97, 114110. [Google Scholar] [CrossRef]
- Ou, S.L.; Wuu, D.S.; Fu, Y.C.; Liu, S.P.; Horng, R.H.; Liu, L.; Feng, Z.C. Growth and etching characteristics of gallium oxide thin-films by pulsed laser deposition. Mater. Chem. Phys. 2012, 133, 700–705. [Google Scholar] [CrossRef]
- Cheng, Y.; Wu, W.; Liu, L.; Zhang, Y.; He, Z.; Song, D. Fabrication, Performance, Characterization and Experimental Calibration of Embedded Thin-Film Sensor for Tool Cutting Force Measurement. Micromachines 2022, 13, 310. [Google Scholar] [CrossRef] [PubMed]
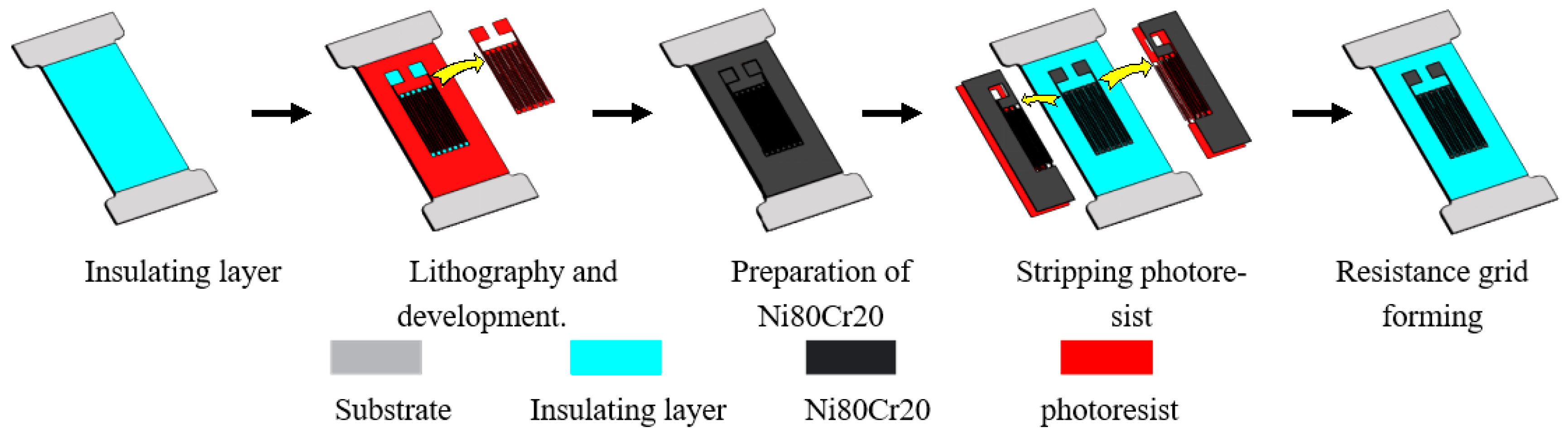
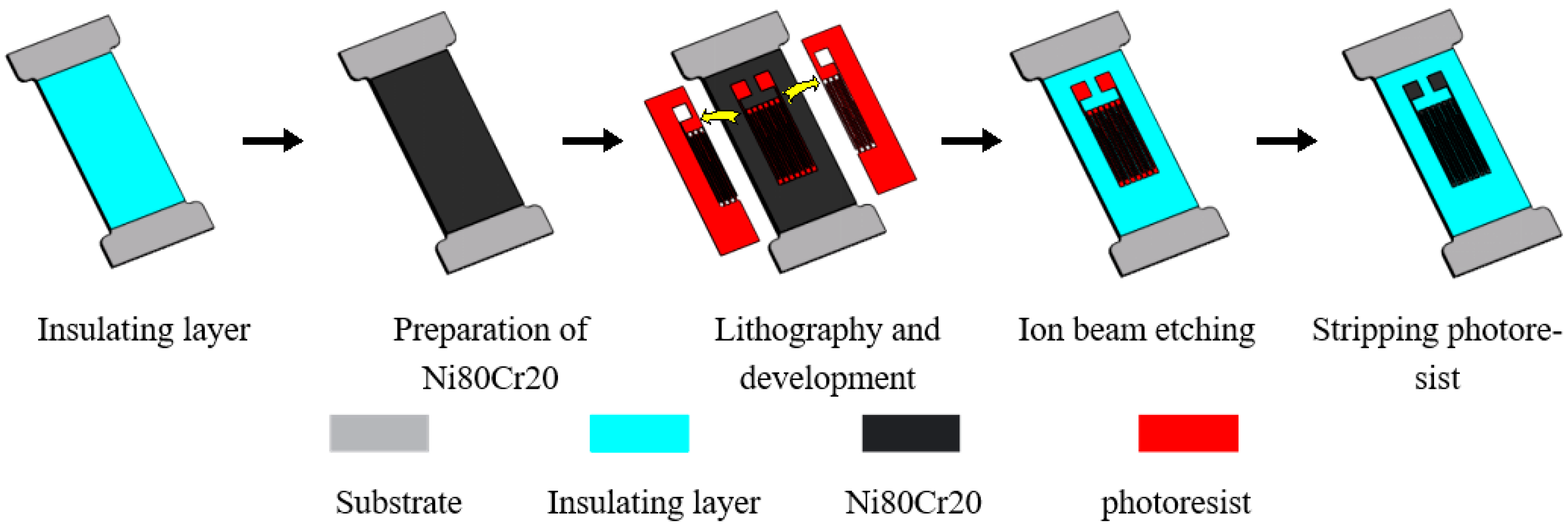




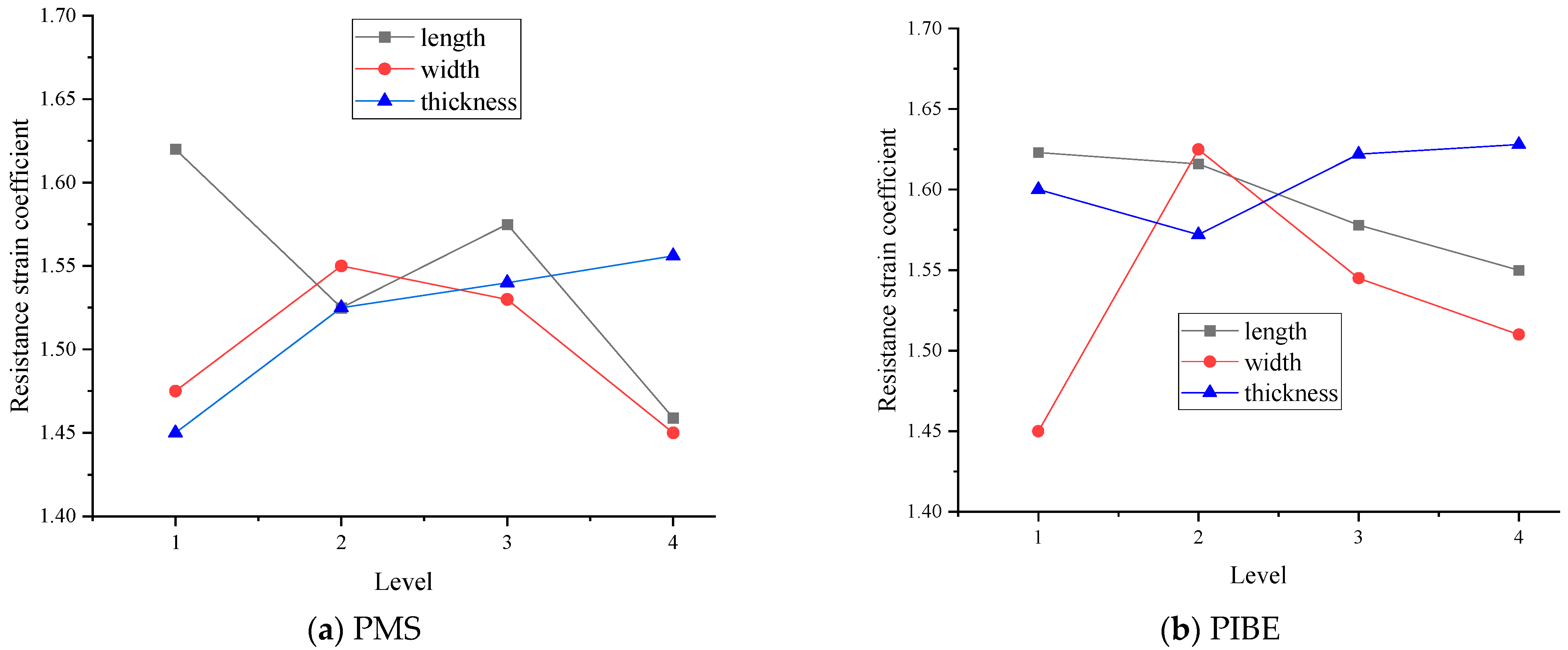



| Resistance Value/Ω | 3 mm | 4 mm | 5 mm | 6 mm | ||||
|---|---|---|---|---|---|---|---|---|
| PMS | PIBE | PMS | PIBE | PMS | PIBE | PMS | PIBE | |
| Total resistance | 5127 | 3692 | 5314 | 3728 | 5449 | 3812 | 5829 | 3841 |
| Single grid 1 | 183.5 | 128.3 | 268.1 | 178.2 | 306.1 | 220.4 | 410.2 | 291.3 |
| Single grid 2 | 189.2 | 139.2 | 253.3 | 169.5 | 319.4 | 236.1 | 428.2 | 281.7 |
| Single grid 3 | 188.6 | 131.8 | 258.6 | 171.6 | 311.8 | 223.8 | 430.6 | 279.6 |
| Single grid 4 | 181.4 | 119.4 | 259.4 | 195.6 | 315.4 | 229.5 | 415.7 | 270.4 |
| Single grid 5 | 190.2 | 134.1 | 264.9 | 180.2 | 309.9 | 236.7 | 420.5 | 280.3 |
| Single grid range | 8.8 | 19.8 | 14.8 | 26.1 | 13.3 | 16.3 | 20.4 | 20.9 |
| Average error multiple | 3.523 | 2.165 | 3.743 | 2.255 | 3.546 | 2.354 | 4.104 | 2.401 |
| Sample | Width of Longitudinal Grid | Resistance Value: 1200 Ω; Length of Longitudinal Grid; 6 mm; Thickness of Longitudinal Grid: 800 nm | |||
|---|---|---|---|---|---|
| Transverse Grid Area | Number of Longitudinal Grids | Single Grid Resistance (Ω) | Electrode Area | ||
| 1 | 0.05 mm | 0.3 mm × 0.3 mm | 7 | 165 | 2 mm × 2 mm |
| 2 | 0.1 mm | 0.4 mm × 0.4 mm | 14 | 82.5 | |
| 3 | 0.15 mm | 0.5 mm × 0.5 mm | 21 | 55 | |
| 4 | 0.2 mm | 0.6 mm × 0.6 mm | 29 | 41.25 | |
| Resistance Value/Ω | 0.05 mm | 0.1 mm | 0.15 mm | 0.2 mm | ||||
|---|---|---|---|---|---|---|---|---|
| PMS | PIBE | PMS | PIBE | PMS | PIBE | PMS | PIBE | |
| Total resistance | 7134 | 5645 | 5618 | 3606 | 5059 | 4696 | 4693 | 4501 |
| Single grid 1 | 1031.4 | 800.2 | 395.2 | 255.2 | 244.1 | 223.1 | 168.1 | 159.2 |
| Single grid 2 | 1024.6 | 803.1 | 406.1 | 258.1 | 236.4 | 228.4 | 173.4 | 157.4 |
| Single grid 3 | 1019.2 | 792.8 | 410.9 | 268.0 | 229.1 | 226.8 | 165.9 | 138.4 |
| Single grid 4 | 1014.4 | 811.6 | 401.1 | 266.7 | 250.6 | 219.1 | 159.8 | 168.1 |
| Single grid 5 | 1026.8 | 808.7 | 393.8 | 246.9 | 243.7 | 217.3 | 167.1 | 171.5 |
| Single grid range | 17 | 18.8 | 17.1 | 21.1 | 21.5 | 11.1 | 13.6 | 33.1 |
| Average error multiple | 5.202 | 3.868 | 3.866 | 2.139 | 3.378 | 3.053 | 3.045 | 2.853 |
| Sample | Thickness of Longitudinal Grid | Resistance Value: 1200 Ω; Length of Longitudinal Grid: 6 mm; Width of Longitudinal Grid: 0.1 mm; | |||
|---|---|---|---|---|---|
| Transverse Grid Area | Number of Longitudinal Grids | Single Grid Resistance (Ω) | Electrode Area | ||
| 1 | 800 nm | 0.4 mm × 0.4 mm | 14 | 82.5 | 2 mm × 2 mm |
| 2 | 900 nm | 16 | 73.3 | ||
| 3 | 1000 nm | 18 | 66 | ||
| 4 | 1100 nm | 20 | 59 | ||
| Resistance Value/Ω | 800 nm | 900 nm | 1000 nm | 1100 nm | ||||
|---|---|---|---|---|---|---|---|---|
| PMS | PIBE | PMS | PIBE | PMS | PIBE | PMS | PIBE | |
| Total resistance | 5726 | 3928 | 5618 | 3847 | 5464 | 3714 | 5328 | 3682 |
| Single grid 1 | 403.4 | 286.7 | 344.7 | 235.9 | 310.1 | 203.8 | 321.4 | 188.6 |
| Single grid 2 | 419.2 | 291.8 | 359.1 | 238.4 | 308.6 | 209.1 | 322.9 | 186.7 |
| Single grid 3 | 416.5 | 281.6 | 362.7 | 241.7 | 300.8 | 214.8 | 318.2 | 176.8 |
| Single grid 4 | 398.7 | 280.6 | 348.2 | 240.5 | 311.5 | 206.6 | 314.9 | 192.4 |
| Single grid 5 | 402.9 | 276.8 | 351.6 | 250.0 | 297.5 | 196.8 | 308.4 | 184.6 |
| Single grid range | 20.5 | 15 | 18 | 14.1 | 14 | 18 | 14.5 | 15.6 |
| Average error multiple | 3.947 | 2.436 | 3.819 | 2.292 | 3.632 | 2.125 | 4.376 | 2.149 |
| Level | X | Y | Z |
|---|---|---|---|
| Incident Angle (°) | Argon Flow (m3/s) | Substrate Negative Bias (V) | |
| 1 | 20 | 1 × 10−5 | 350 |
| 2 | 45 | 1.25 × 10−5 | 450 |
| 3 | 70 | 1.5 × 10−5 | 550 |
| NO. | Incident Angle (°) | Argon Flow (sccm) | Substrate Negative Bias (V) | Etching Rate v/(nm/min) | Roughness Ra/(nm) | Resistivity ρ (μΩ·m) | |
|---|---|---|---|---|---|---|---|
| NiCr | Photoresist AZ6140 | ||||||
| 1 | 20 | 6 | 350 | 19.8 | 18.2 | 35 | 1.21 |
| 2 | 20 | 7.5 | 450 | 25.0 | 23.4 | 38 | 1.57 |
| 3 | 20 | 9 | 550 | 31.5 | 27.8 | 41 | 1.68 |
| 4 | 45 | 6 | 450 | 23.6 | 22.6 | 31 | 1.10 |
| 5 | 45 | 7.5 | 550 | 29.1 | 26.3 | 33 | 1.19 |
| 6 | 45 | 9 | 350 | 20.9 | 18.1 | 28 | 1.06 |
| 7 | 70 | 6 | 550 | 27.6 | 26.6 | 37 | 1.46 |
| 8 | 70 | 7.5 | 350 | 20.2 | 17.4 | 32 | 1.16 |
| 9 | 70 | 9 | 450 | 26.1 | 24.2 | 36 | 1.32 |
| Resistance R (kΩ) | PIBE | PMS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sample 1 | Sample 2 | Sample 3 | Multiple of Average Error | Sample 1 | Sample 2 | Sample 3 | Multiple of Average Error | ||
| width d (mm) | 0.05 | 5.645 | 5.798 | 5.499 | 3.706 | 7.633 | 7.849 | 7.134 | 5.282 |
| 0.1 | 3.606 | 3.823 | 3.937 | 2.157 | 5.726 | 5.328 | 5.618 | 3.631 | |
| 0.15 | 4.696 | 4.821 | 4.810 | 2.979 | 4.898 | 5.274 | 5.059 | 3.231 | |
| 0.2 | 4.501 | 4.134 | 4.794 | 2.730 | 4.852 | 5.091 | 4.693 | 3.065 | |
| Film Etching Rate v/(nm/min) | Film Roughness Ra/(nm) | Resistivity ρ (μΩ·m) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | X | Y | Z | |
| K1 | 25.4 | 23.7 | 20.3 | 38.0 | 34.3 | 31.7 | 1.49 | 1.26 | 1.14 |
| K2 | 24.5 | 24.8 | 24.9 | 30.7 | 34.3 | 35.0 | 1.12 | 1.33 | 1.33 |
| K3 | 24.6 | 26.2 | 29.4 | 35.0 | 35.0 | 37.0 | 1.31 | 1.31 | 1.44 |
| Rj | 0.9 | 2.5 | 9.1 | 7.3 | 0.7 | 5.3 | 0.37 | 0.06 | 0.30 |
| Influence level Z > Y > X | Influence level X > Z > Y | Influence level X > Z > Y | |||||||
| Freedom | SS | MS | F | P | ||
|---|---|---|---|---|---|---|
| etching rate, v | regression | 3 | 134.55 | 44.85 | 191.67 | 0.000 |
| Residual Error | 5 | 1.17 | 0.234 | |||
| total | 8 | 135.72 | ||||
| Roughness, Ra | regression | 3 | 56.83 | 18.94 | 1.37 | 0.354 |
| Residual Error | 5 | 69.39 | 13.88 | |||
| total | 8 | 126.22 | ||||
| Resistivity, ρ | regression | 3 | 0.19408 | 0.06469 | 1.74 | 0.275 |
| Residual Error | 5 | 0.18634 | 0.03727 | |||
| total | 8 | 0.38042 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Wu, W.; Zhao, Y.; Han, Y.; Song, D. Study of the Pattern Preparation and Performance of the Resistance Grid of Thin-Film Strain Sensors. Micromachines 2022, 13, 892. https://doi.org/10.3390/mi13060892
Cheng Y, Wu W, Zhao Y, Han Y, Song D. Study of the Pattern Preparation and Performance of the Resistance Grid of Thin-Film Strain Sensors. Micromachines. 2022; 13(6):892. https://doi.org/10.3390/mi13060892
Chicago/Turabian StyleCheng, Yunping, Wenge Wu, Yongjuan Zhao, Yanwen Han, and Ding Song. 2022. "Study of the Pattern Preparation and Performance of the Resistance Grid of Thin-Film Strain Sensors" Micromachines 13, no. 6: 892. https://doi.org/10.3390/mi13060892
APA StyleCheng, Y., Wu, W., Zhao, Y., Han, Y., & Song, D. (2022). Study of the Pattern Preparation and Performance of the Resistance Grid of Thin-Film Strain Sensors. Micromachines, 13(6), 892. https://doi.org/10.3390/mi13060892





