Probabilistic Circuit Implementation Based on P-Bits Using the Intrinsic Random Property of RRAM and P-Bit Multiplexing Strategy
Abstract
:1. Introduction
2. Proposed P-Bit Design
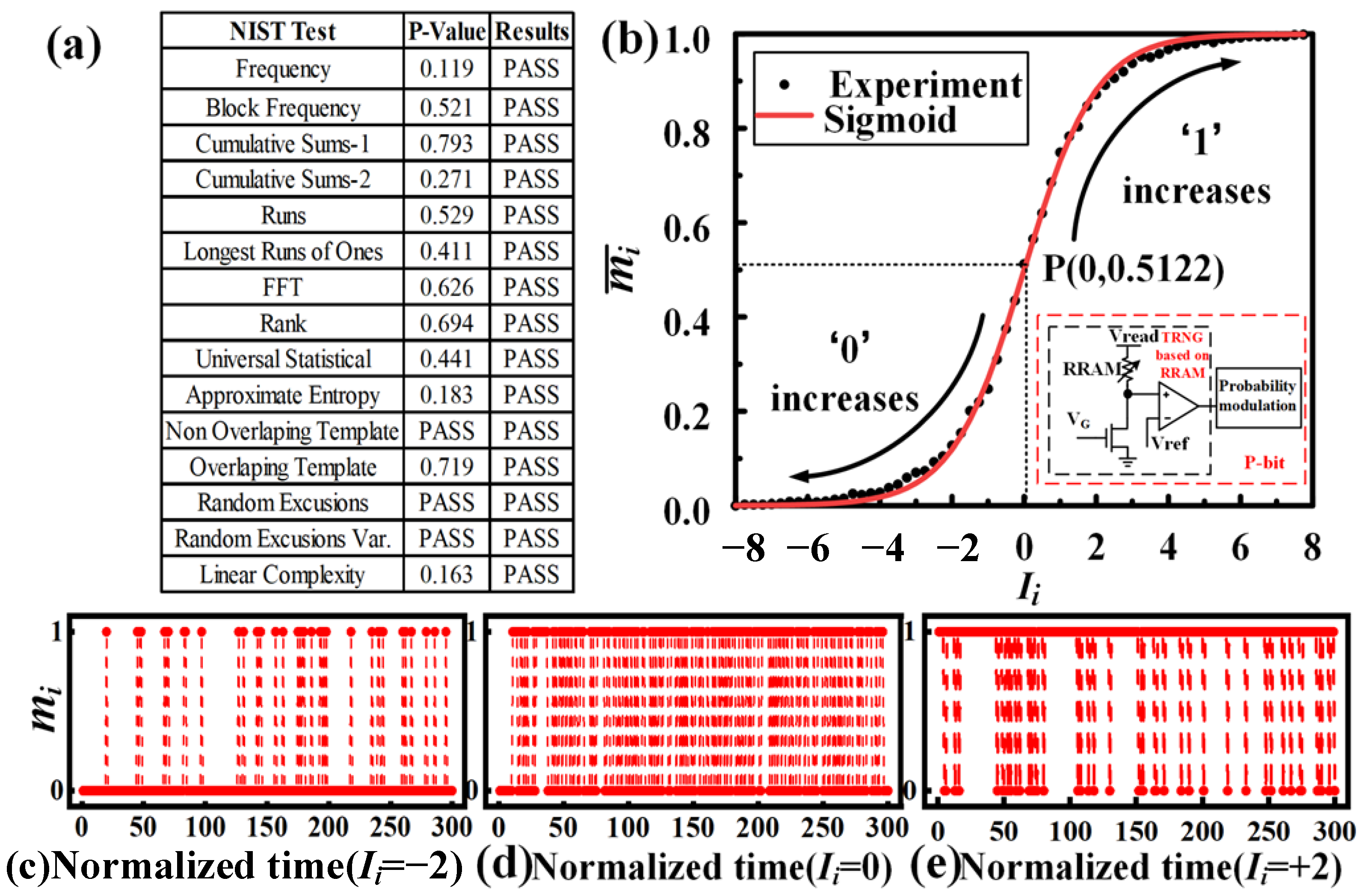
2.1. TRNG Based on RRAM
2.2. Sigmoid Function
2.3. Comparator
3. Weight-Logic Implementation
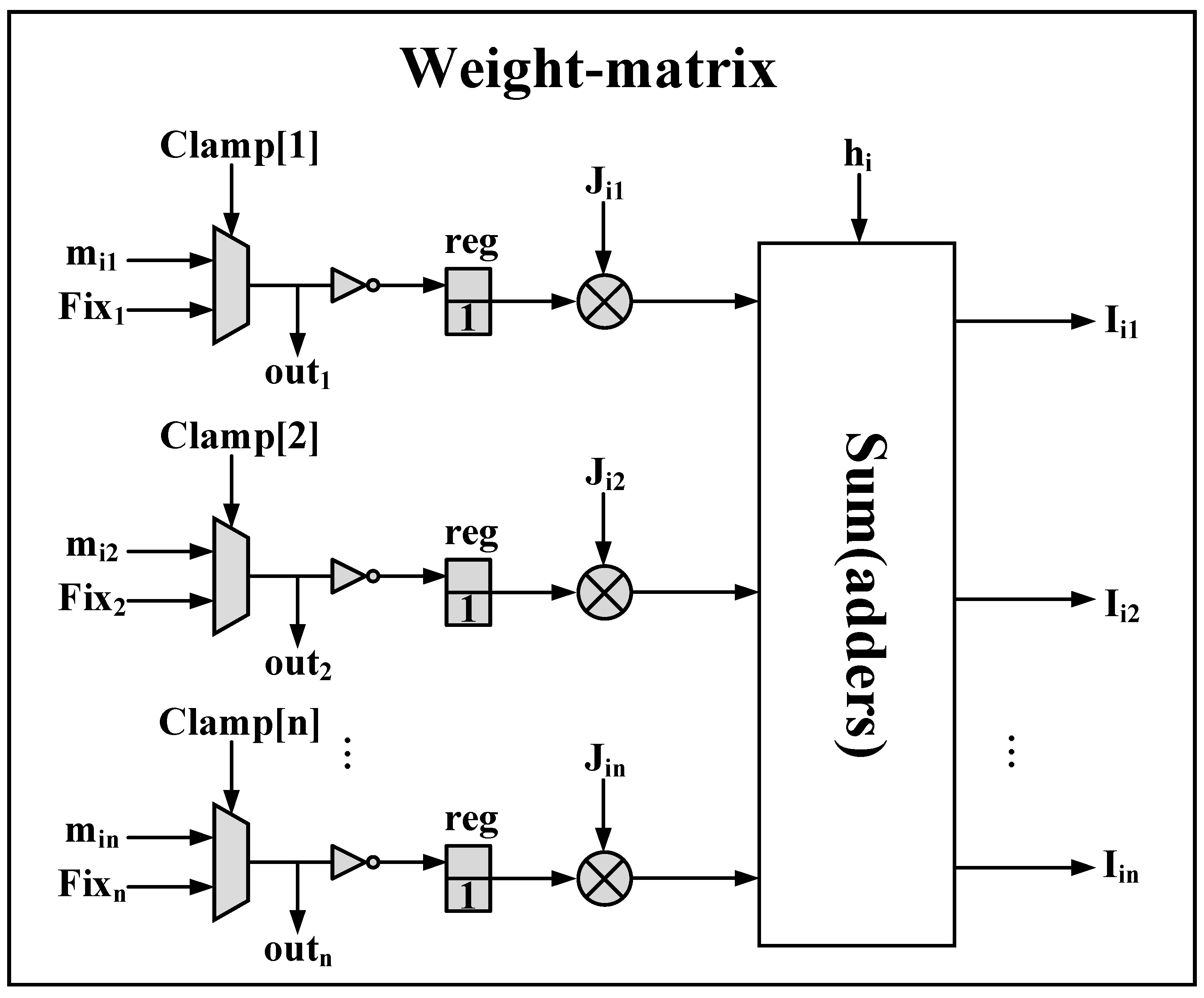
3.1. Weight-Matrix
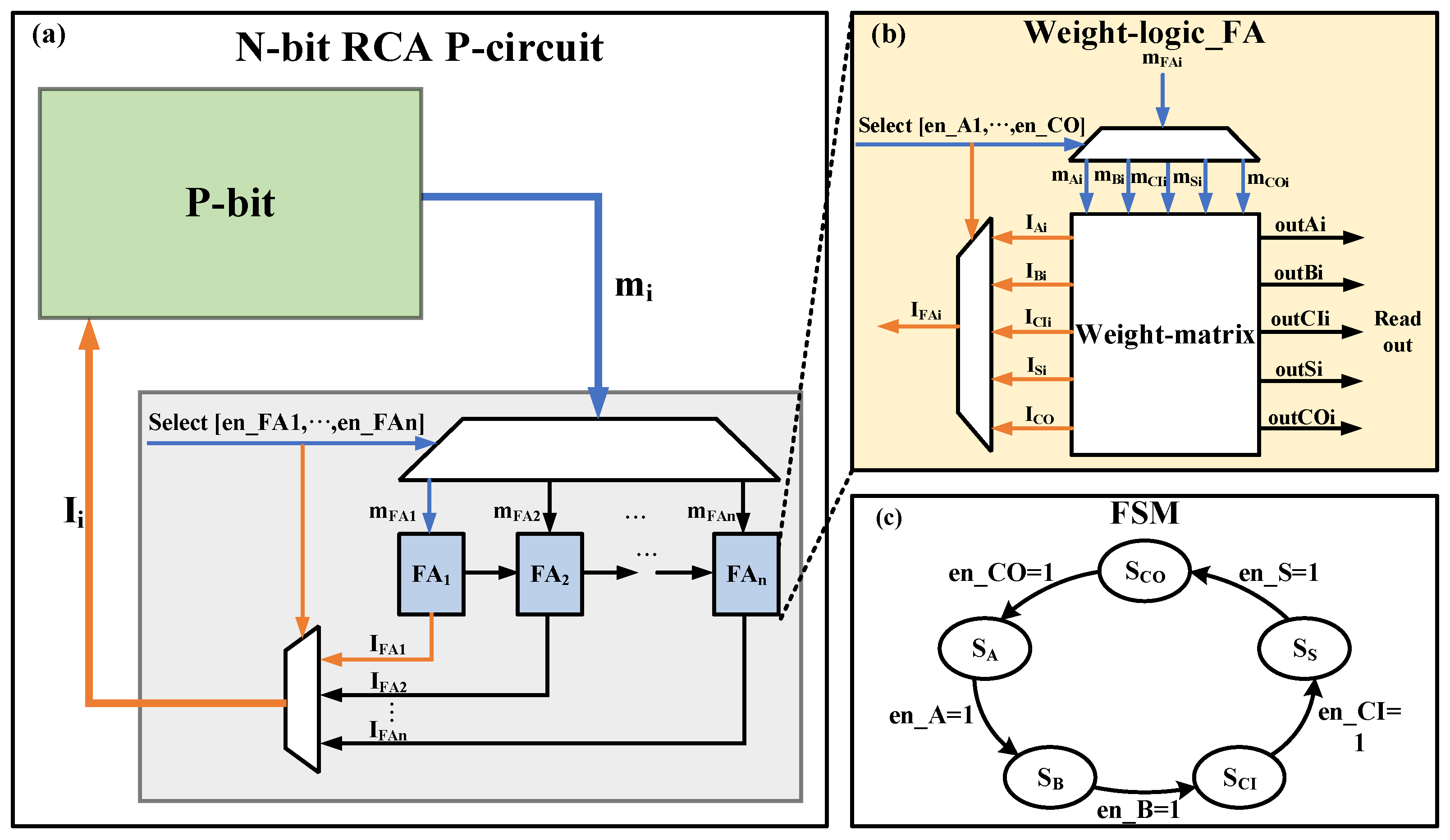
3.2. Multiplexing Strategy
4. Implementation Results
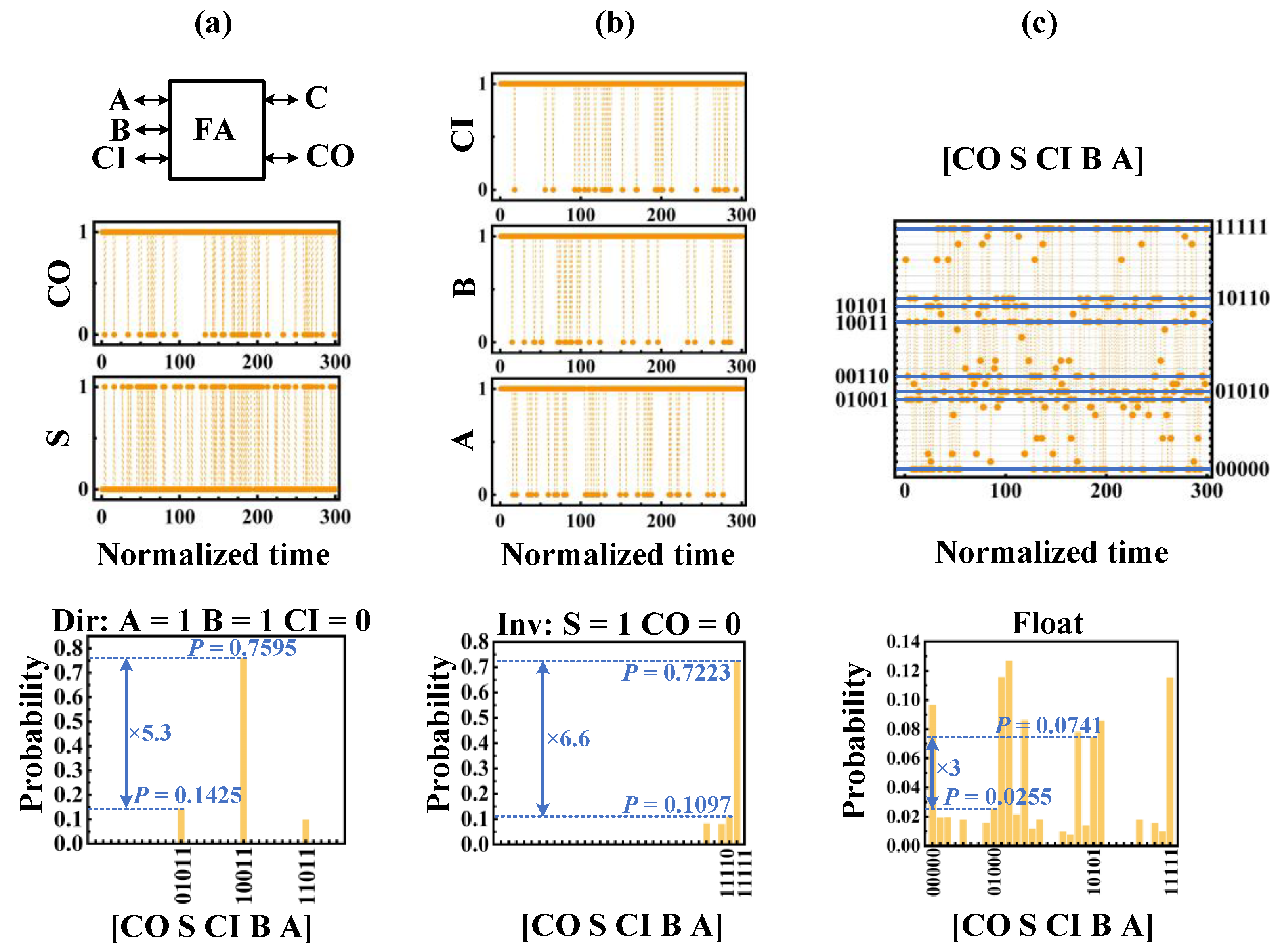
4.1. Invertible AND Gate and Full Adder (FA)
4.2. 16-Bit Ripple Carry Adders (RCA)
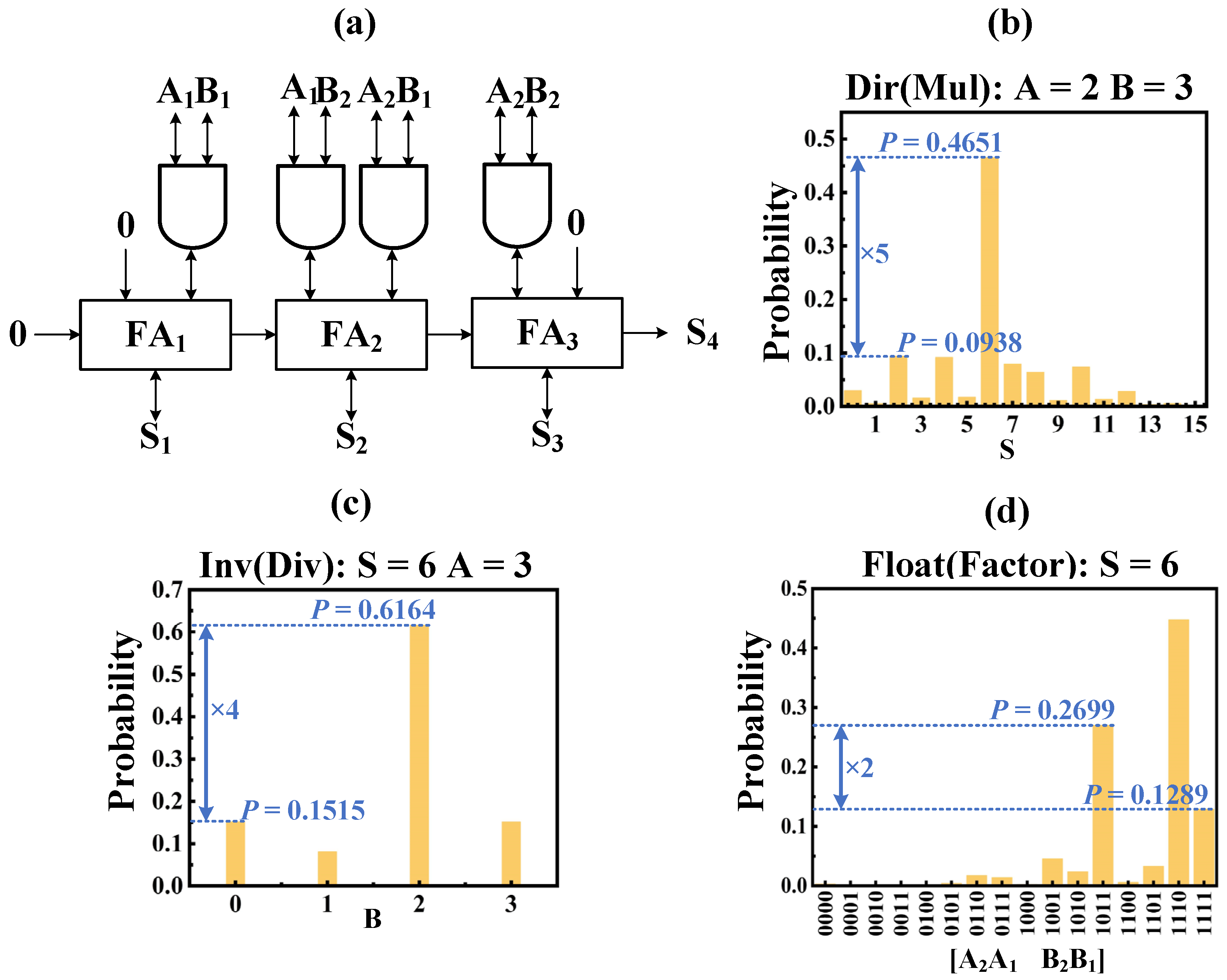
4.3. 4-Bit Multiplier
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sutton, B.; Camsari, K.Y.; Behin-Aein, B.; Datta, S. Intrinsic optimization using stochastic nanomagnets. Sci. Rep. 2017, 7, 44370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.; Zhang, Q.; Tang, J.; Gao, B.; Li, C.; Yao, P.; Liu, Z.; Zhu, J.; Lu, J.; Hu, X.S.; et al. Bayesian Neural Network Realization by Exploiting Inherent Stochastic Characteristics of Analog RRAM. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019. [Google Scholar]
- Pervaiz, A.Z.; Ghantasala, L.A.; Camsari, K.Y.; Datta, S. Hardware emulation of stochastic p-bits for invertible logic. Sci. Rep. 2017, 7, 10994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pervaiz, A.Z.; Sutton, B.M.; Ghantasala, L.A.; Camsari, K.Y. Weighted p-Bits for FPGA Implementation of Probabilistic Circuits. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1920–1926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smithson, S.C.; Onizawa, N.; Meyer, B.H.; Gross, W.J.; Hanyu, T. Efficient CMOS invertible logic using stochastic computing. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2263–2274. [Google Scholar] [CrossRef]
- Camsari, K.Y.; Salahuddin, S.; Datta, S. Implementing p-bits with embedded MTJ. IEEE Electron Device Lett. 2017, 38, 1767–1770. [Google Scholar] [CrossRef]
- Camsari, K.Y.; Faria, R.; Sutton, B.M.; Datta, S. Stochastic p-bits for invertible logic. Phys. Rev. 2017, 7, 031014. [Google Scholar] [CrossRef] [Green Version]
- Faria, R.; Camsari, K.Y.; Datta, S. Low-barrier nanomagnets as p-bits for spin logic. IEEE Magn. Lett. 2017, 8, 1–5. [Google Scholar] [CrossRef]
- Borders, W.A.; Pervaiz, A.Z.; Fukami, S.; Camsari, K.Y.; Ohno, H.; Datta, S. Integer factorization using stochastic magnetic tunnel junctions. Nature 2019, 573, 390–393. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Belkin, D.; Savel’ev, S.E.; Lin, S.; Wang, Z.; Li, Y.; Joshi, S.; Midya, R.; Li, C.; Rao, M.; et al. A novel true random number generator based on a stochastic diffusive memristor. Nat. Commun. 2017, 8, 882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rai, V.K.; Tripathy, S.; Mathew, J. Memristor based random number generator: Architectures and evaluation. Procedia Comput. Sci. 2018, 125, 576–583. [Google Scholar] [CrossRef]
- Stoller, S.; Campbell, K.A. Demonstration of three true random number generator circuits using memristor created entropy and commercial off-the-shelf components. Entropy 2021, 23, 371. [Google Scholar] [CrossRef] [PubMed]
- Taskiran, Z.G.C.; Taşkıran, M.; Kıllıoğlu, M.; Kahraman, N.; Sedef, H. A novel memristive true random number generator design. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 208–224. [Google Scholar] [CrossRef]
- Lv, H.; Xu, X.; Yuan, P.; Dong, D.; Gong, T.; Liu, J.; Yu, Z.; Huang, P.; Zhang, K.; Huo, C.; et al. BEOL based RRAM with one extra-mask for low cost, highly reliable embedded application in 28 nm node and beyond. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), Piscataway, NJ, USA, 2–6 December 2017. [Google Scholar]
- Veksler, D.; Bersuker, G.; Vandelli, L.; Padovani, A.; Larcher, L.; Muraviev, A.; Chakrabarti, B.; Vogel, E.; Gilmer, D.C.; Kirsch, P.D. Random telegraph noise (RTN) in scaled RRAM devices. In Proceedings of the 2013 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 14–18 April 2013. [Google Scholar]
- Gong, T.; Dong, D.; Luo, Q.; Xu, X.; Yang, J.; Yu, J.; Ding, Q.; Lv, H.; Liu, M. Quantitative Analysis on Resistance Fluctuation of Resistive Random Access Memory by Low Frequency Noise Measurement. IEEE Electron Device Lett. 2021, 42, 312–314. [Google Scholar] [CrossRef]
- Tommiska, M.T. Efficient digital implementation of the sigmoid function for reprogrammable logic. IEE Proc. Comput. Digit. Tech. 2003, 150, 403–411. [Google Scholar] [CrossRef] [Green Version]
- Biamonte, J.D. Nonperturbative k-body to two-body commuting conversion Hamiltonians and embedding problem instances into Ising spins. Phys. Rev. A 2008, 77, 052331. [Google Scholar] [CrossRef] [Green Version]




| Input Range | Input Value | Output Range | Output Value | Slope |
|---|---|---|---|---|
| [0, 1) | 0000xxxxxxxxxxxx | [0.5, 0.75) | 10xxxxxxxxxxxxxx | 0.25 |
| [1, 2) | 0001xxxxxxxxxxxx | [0.75, 0.875) | 110xxxxxxxxxxxxx | 0.125 |
| [2, 3) | 0010xxxxxxxxxxxx | [0.875, 0.9375) | 1110xxxxxxxxxxxx | 0.0625 |
| [3, 4) | 0011xxxxxxxxxxxx | [0.9375, 0.96875) | 11110xxxxxxxxxxx | 0.03125 |
| [4, 5) | 0100xxxxxxxxxxxx | [0.96875, 0.984375) | 111110xxxxxxxxxx | 0.015625 |
| [5, 6) | 0101xxxxxxxxxxxx | [0.984375, 0.9921875) | 1111110xxxxxxxxx | 0.0078125 |
| [6, 7) | 0110xxxxxxxxxxxx | [0.9921875, 0.99609375) | 11111110xxxxxxxx | 0.00390625 |
| [7, 8) | 0111xxxxxxxxxxxx | [0.99609375, 1) | 11111111xxxxxxxx | 0.001953125 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Hu, Q.; Wu, Q.; Liu, X.; Zhao, Y.; Zhang, D.; Han, Z.; Cheng, J.; Ding, Q.; Han, Y.; et al. Probabilistic Circuit Implementation Based on P-Bits Using the Intrinsic Random Property of RRAM and P-Bit Multiplexing Strategy. Micromachines 2022, 13, 924. https://doi.org/10.3390/mi13060924
Liu Y, Hu Q, Wu Q, Liu X, Zhao Y, Zhang D, Han Z, Cheng J, Ding Q, Han Y, et al. Probabilistic Circuit Implementation Based on P-Bits Using the Intrinsic Random Property of RRAM and P-Bit Multiplexing Strategy. Micromachines. 2022; 13(6):924. https://doi.org/10.3390/mi13060924
Chicago/Turabian StyleLiu, Yixuan, Qiao Hu, Qiqiao Wu, Xuanzhi Liu, Yulin Zhao, Donglin Zhang, Zhongze Han, Jinhui Cheng, Qingting Ding, Yongkang Han, and et al. 2022. "Probabilistic Circuit Implementation Based on P-Bits Using the Intrinsic Random Property of RRAM and P-Bit Multiplexing Strategy" Micromachines 13, no. 6: 924. https://doi.org/10.3390/mi13060924
APA StyleLiu, Y., Hu, Q., Wu, Q., Liu, X., Zhao, Y., Zhang, D., Han, Z., Cheng, J., Ding, Q., Han, Y., Peng, B., Jiang, H., Xue, X., Lv, H., & Yang, J. (2022). Probabilistic Circuit Implementation Based on P-Bits Using the Intrinsic Random Property of RRAM and P-Bit Multiplexing Strategy. Micromachines, 13(6), 924. https://doi.org/10.3390/mi13060924







