Micro-Milling Tool Wear Monitoring via Nonlinear Cutting Force Model
Abstract
:1. Introduction
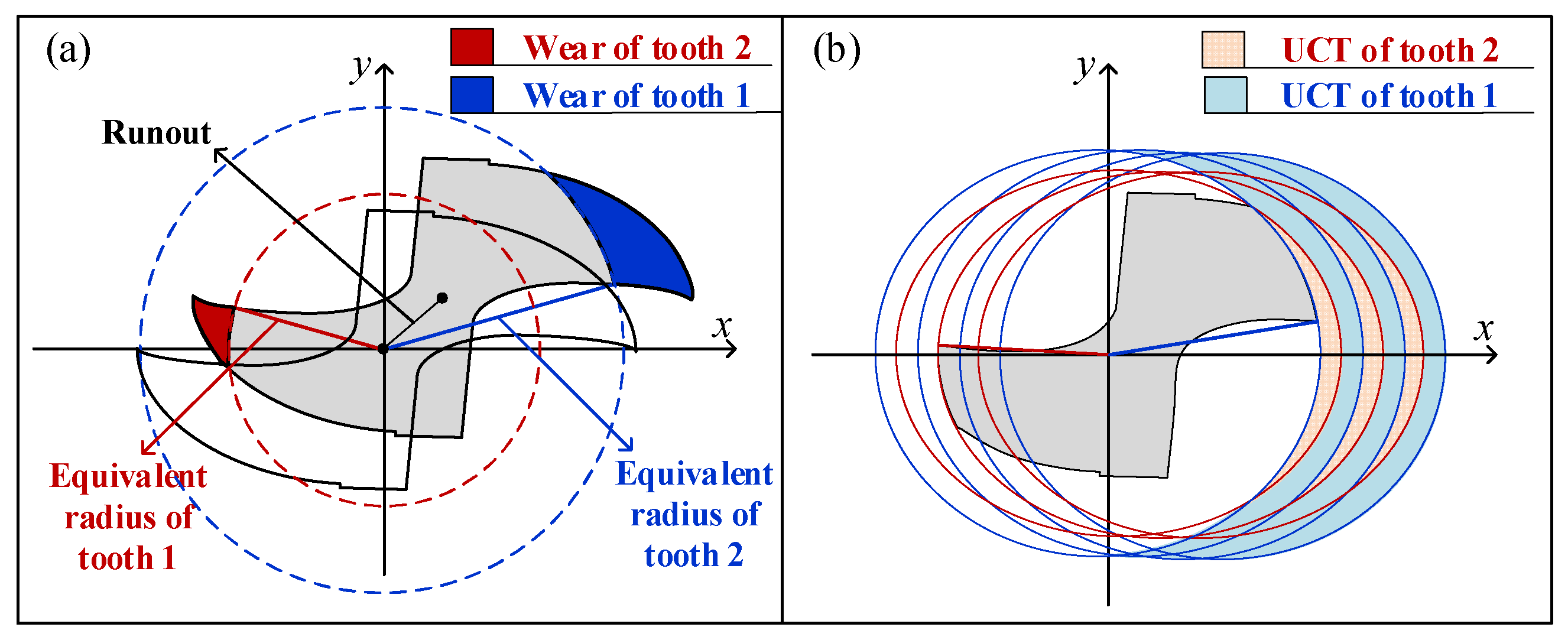
2. Nonlinear Cutting Force Model of Micro-Milling
3. Tool Wear Monitoring with Nonlinear Cutting Force Model
3.1. Off-Line Parameters Estimation

3.2. On-Line Tool Wear Monitoring
4. Experimental Validation
4.1. Experimental Setup
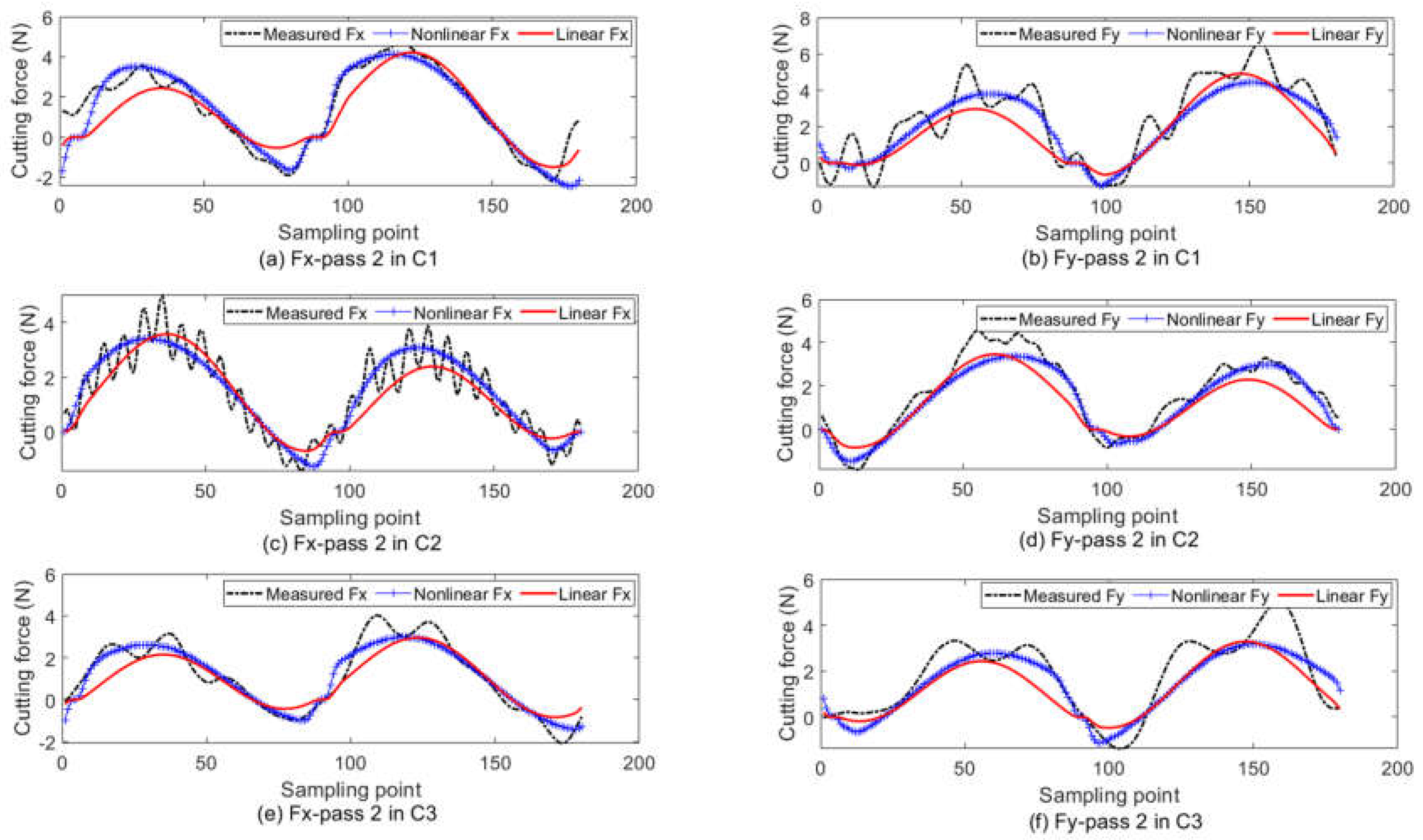
4.2. Results of Parameters Estimation and Cutting Force Prediction
4.3. Tool Wear Monitoring Results
5. Conclusions
- (1)
- The force prediction accuracy and tool wear monitoring accuracy of the nonlinear model improved compared with the linear model.
- (2)
- The flank wear width increases with the cutting time, and the effective cutting-edge radius does not have an obvious increasing trend due to the compensation effect of the flank wear on the cutting-edge wear.
- (3)
- The nonlinear effect increases as the feed per tooth decreases, and the monitoring accuracy of the linear model increases with the feed per tooth.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mian, A.J.; Driver, N.; Mativenga, P.T. Micromachining of coarse-grained multi-phase material. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2009, 223, 377–385. [Google Scholar] [CrossRef]
- Chen, N.; Li, H.N.; Wu, J.M.; Li, Z.J.; Li, L.; Liu, G.Y.; He, N. Advances in micro milling: From tool fabrication to process outcomes. Int. J. Mach. Tools Manuf. 2020, 160, 103670. [Google Scholar] [CrossRef]
- Alhadeff, L.L.; Marshall, M.B.; Curtis, D.T.; Slatter, T. Protocol for tool wear measurement in micro-milling. Wear 2019, 420, 54–67. [Google Scholar] [CrossRef]
- Malekian, M.; Park, S.S.; Jun, M.B.G. Tool wear monitoring of micro-milling operations. J. Mater. Process. Technol. 2009, 209, 4903–4914. [Google Scholar] [CrossRef]
- Kiswanto, G. Digital twin approach for tool wear monitoring of micro-milling. Procedia CIRP 2020, 93, 1532–1537. [Google Scholar]
- Xie, Y.; Lian, K.; Liu, Q.; Zhang, C.; Liu, H. Digital twin for cutting tool: Modeling, application and service strategy. J. Manuf. Syst. 2021, 58, 305–312. [Google Scholar] [CrossRef]
- Chen, N.; Wu, C.; Chen, M.; Li, L.; He, N. Research on the relationship between cutting force and machined surface quality in micro ball end-milling of potassium dihydrogen phosphate crystal. Micromachines 2018, 9, 574. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.Y.; Chen, J.H. Development of dual-axis MEMS accelerometers for machine tools vibration monitoring. Appl. Sci. 2016, 6, 201. [Google Scholar] [CrossRef] [Green Version]
- Wan, B.S.; Lu, M.C.; Chiou, S.J. Analysis of spindle AE signals and development of AE-based tool wear monitoring system in micro-milling. J. Manuf. Mater. Process. 2022, 6, 42. [Google Scholar] [CrossRef]
- Carrino, S.; Guerne, J.; Dreyer, J.; Ghorbel, H.; Schorderet, A.; Montavon, R. Machining quality prediction using acoustic sensors and machine learning. Proceedings 2020, 63, 31. [Google Scholar]
- Hsieh, W.H.; Lu, M.C.; Chiou, S.J. Application of backpropagation neural network for spindle vibration-based tool wear monitoring in micro-milling. Int. J. Adv. Manuf. Technol. 2012, 61, 53–61. [Google Scholar] [CrossRef]
- Guo, J.; Li, A.; Zhang, R. Tool condition monitoring in milling process using multifractal detrended fluctuation analysis and support vector machine. Int. J. Adv. Manuf. Technol. 2020, 110, 1445–1456. [Google Scholar] [CrossRef]
- Zhu, K.; Mei, T.; Ye, D. Online condition monitoring in micromilling: A force waveform shape analysis approach. IEEE Trans. Ind. Electron. 2015, 62, 3806–3813. [Google Scholar]
- Lu, X.; Wang, F.; Jia, Z.; Si, L.; Zhang, C.; Liang, S.Y. A modified analytical cutting force prediction model under the tool flank wear effect in micro-milling nickel-based superalloy. Int. J. Adv. Manuf. Technol. 2017, 91, 3709–3716. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, D.; Wu, B.; Luo, M. Milling force modeling of worn tool and tool flank wear recognition in end milling. IEEE ASME Trans. Mechatron. 2014, 20, 1024–1035. [Google Scholar] [CrossRef]
- Nouri, M.; Fussell, B.K.; Ziniti, B.L.; Linder, E. Real-time tool wear monitoring in milling using a cutting condition independent method. Int. J. Mach. Tools Manuf. 2015, 89, 1–13. [Google Scholar] [CrossRef]
- Pan, T.; Zhang, J.; Zhang, X.; Zhao, W.; Zhang, H.; Lu, B. Milling force coefficients-based tool wear monitoring for variable parameter milling. Int. J. Adv. Manuf. Technol. 2022, 120, 4565–4580. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, K.; Wang, G. Micro-milling tool wear monitoring under variable cutting parameters and runout using fast cutting force coefficient identification method. Int. J. Adv. Manuf. Technol. 2020, 111, 3175–3188. [Google Scholar] [CrossRef]
- Mian, A.J. Size Effect in Micromachining. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2011. [Google Scholar]
- Oliveira, F.B.; Rodrigues, A.R.; Coelho, R.T.; Souza, A.F. Size effect and minimum chip thickness in micromilling. Int. J. Mach. Tools Manuf. 2015, 89, 39–54. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Shi, Z.Y.; Wan, Y. Definition and determination of the minimum uncut chip thickness of micro cutting. Int. J. Adv. Manuf. Technol. 2013, 69, 1219–1232. [Google Scholar]
- Jing, X.; Lv, R.; Chen, Y.; Tian, Y.; Li, H. Modelling and experimental analysis of the effects of run out, minimum chip thickness and elastic recovery on the cutting force in micro-end-milling. Int. J. Mech. Sci. 2020, 176, 105540. [Google Scholar] [CrossRef]
- Chen, N.; Li, L.; Wu, J.; Qian, J.; He, N.; Reynaerts, D. Research on the ploughing force in micro milling of soft-brittle crystals. Int. J. Mech. Sci. 2019, 155, 315–322. [Google Scholar] [CrossRef]
- Zhou, L.; Deng, B.; Peng, F.; Yang, M.; Yan, R. Semi-analytic modelling of cutting forces in micro ball-end milling of NAK80 steel with wear-varying cutting edge and associated nonlinear process characteristics. Int. J. Mech. Sci. 2020, 169, 105343. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, K.; Wang, G.; Wang, C. Prediction of Nonlinear Micro-milling force with a novel minimum uncut chip thickness model. Micromachines 2021, 12, 1495. [Google Scholar] [CrossRef]
- Li, K.; Zhu, K.; Mei, T. A generic instantaneous undeformed chip thickness model for the cutting force modeling in micromilling. Int. J. Mach. Tools Manuf. 2016, 105, 23–31. [Google Scholar] [CrossRef]
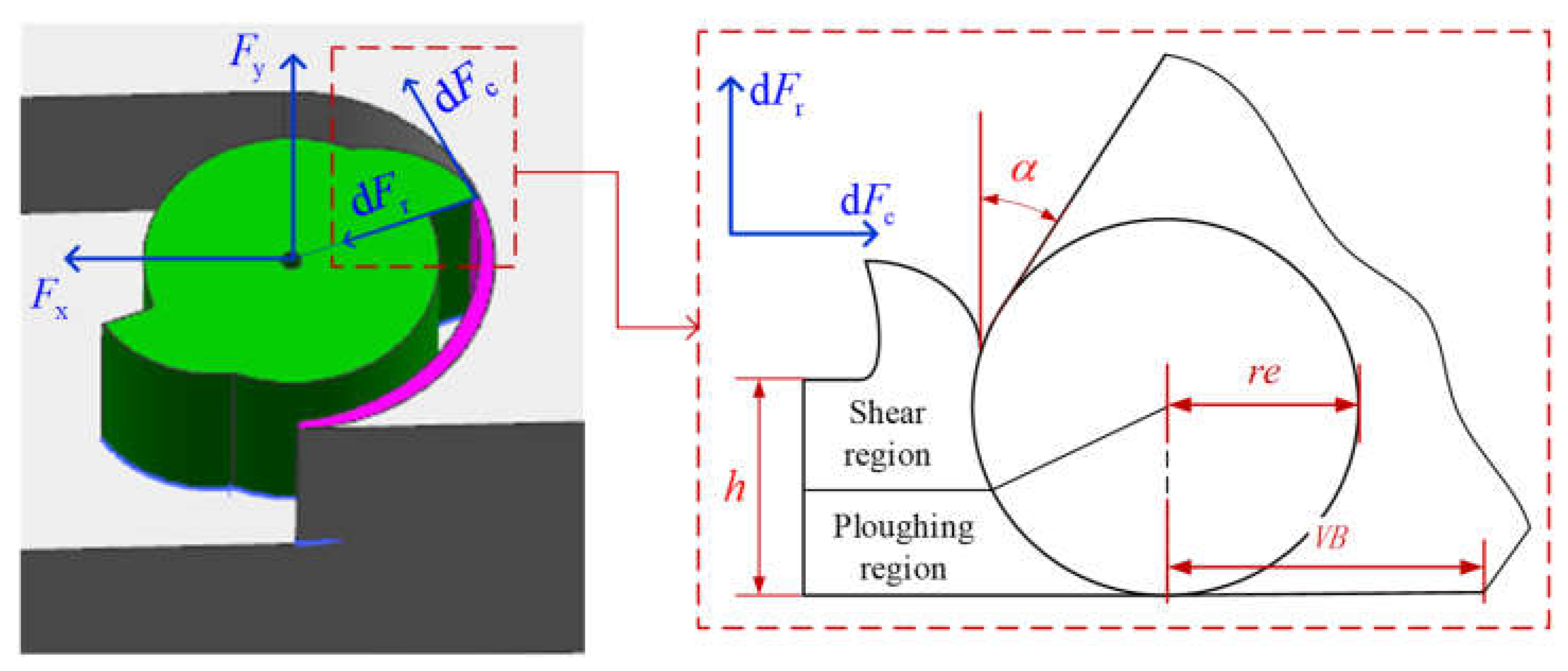


| Parameter | Description | Unit | |
|---|---|---|---|
| shear stress | GPa | ||
| βs | friction angle | deg | |
| σm | ploughing coefficient | GPa | |
| friction coefficient in ploughing region | GPa | ||
| σv | radial friction stress | GPa | |
| tangential friction stress | GPa | ||
| VB* | the width of the elastic contact region | μm | |
| Cutting Condition | Spindle Speed (rpm) | Cutting Speed (m/min) | Axial Cutting Depth (μm) | Feed Speed (mm/min) | Feed per Tooth (μm/Tooth) |
|---|---|---|---|---|---|
| C1 | 18,000 | 28.27 | 80 | 144 | 4 |
| C2 | 24,000 | 37.70 | 100 | 96 | 2 |
| C3 | 30,000 | 47.12 | 60 | 360 | 6 |
| Tooth Number | Tool Diameter | Rake Angle | Clearance Angle | Initial Flank Wear Width | Initial Cutting Edge Radius |
|---|---|---|---|---|---|
| 2 | 0.5 mm | 5° | 7° | 0 μm | 2 μm |
| Cutting Condition | Estimated with Fresh Tool | Estimated with Worn Tool | |||||
|---|---|---|---|---|---|---|---|
| βs | σm | σv | VB* | ||||
| C1 | 0.56 | 24.98 | 15.03 | 1.01 | 0.76 | 1.25 | 18.68 |
| C2 | 0.48 | 25.71 | 17.24 | 1.04 | 1.81 | 2.62 | 16.62 |
| C3 | 0.52 | 27.82 | 23.12 | 1.02 | 2.22 | 2.98 | 18.77 |
| Cutting Pass | Nonlinear Force Model | Linear Force Model |
|---|---|---|
| C1 | 7.85% | 12.25% |
| C2 | 6.11% | 8.94% |
| C3 | 9.68% | 12.96% |
| Cutting Pass | Pass 2 | Pass 3 | Pass 4 | Pass 5 | Pass 6 | Pass 7 | Pass 8 | Pass 9 | Pass 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | (μm) | −0.28 | −0.43 | 0.38 | −0.49 | −0.36 | 0.32 | 0.55 | 0.34 | 0.34 |
| (μm) | 3.65 | 4.18 | 4.00 | 4.22 | 3.72 | 4.48 | 4.28 | 4.73 | 5.62 | |
| (μm) | 15.26 | 16.54 | 23.43 | 23.83 | 26.37 | 25.03 | 31.35 | 28.09 | 36.32 | |
| VB(μm) | 11.92 | 15.00 | 20.00 | 22.50 | 24.50 | 27.00 | 29.00 | 33.50 | 35.00 | |
| C2 | (μm) | −0.22 | −0.32 | 0.24 | 0.31 | 0.47 | 0.41 | 0.00 | 0.28 | 0.49 |
| (μm) | 3.86 | 3.74 | 2.96 | 2.87 | 4.02 | 4.24 | 4.95 | 5.69 | 6.03 | |
| (μm) | 11.90 | 14.07 | 12.10 | 15.10 | 19.32 | 21.53 | 23.68 | 23.85 | 24.40 | |
| VB(μm) | 10.00 | 11.00 | 15.00 | 15.50 | 16.00 | 19.00 | 21.50 | 23.00 | 26.50 | |
| C3 | (μm) | −0.19 | −0.40 | 0.53 | 0.63 | 0.64 | 0.65 | −0.54 | −0.60 | −0.61 |
| (μm) | 3.73 | 4.23 | 4.41 | 3.78 | 4.65 | 4.22 | 4.87 | 4.85 | 4.46 | |
| (μm) | 1.51 | 11.27 | 9.78 | 11.79 | 18.90 | 20.93 | 22.78 | 22.11 | 26.74 | |
| VB(μm) | 4.50 | 9.00 | 12.50 | 15.00 | 16.00 | 17.00 | 22.50 | 26.50 | 28.00 | |
| Cutting Condition | Cutting Distance per Tooth |
|---|---|
| C1 | 29.45 m |
| C2 | 58.90 m |
| C3 | 19.64 m |
| Cutting Pass | Monitoring via Nonlinear Force Model | Monitoring via Linear Force Model |
|---|---|---|
| C1 | 2.51 μm | 4.30 μm |
| C2 | 2.14 μm | 4.45 μm |
| C4 | 2.66 μm | 3.86 μm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Wang, Q.; Wang, W. Micro-Milling Tool Wear Monitoring via Nonlinear Cutting Force Model. Micromachines 2022, 13, 943. https://doi.org/10.3390/mi13060943
Liu T, Wang Q, Wang W. Micro-Milling Tool Wear Monitoring via Nonlinear Cutting Force Model. Micromachines. 2022; 13(6):943. https://doi.org/10.3390/mi13060943
Chicago/Turabian StyleLiu, Tongshun, Qian Wang, and Weisu Wang. 2022. "Micro-Milling Tool Wear Monitoring via Nonlinear Cutting Force Model" Micromachines 13, no. 6: 943. https://doi.org/10.3390/mi13060943
APA StyleLiu, T., Wang, Q., & Wang, W. (2022). Micro-Milling Tool Wear Monitoring via Nonlinear Cutting Force Model. Micromachines, 13(6), 943. https://doi.org/10.3390/mi13060943





