Design and Experimental Research of 3-RRS Parallel Ankle Rehabilitation Robot
Abstract
:1. Introduction
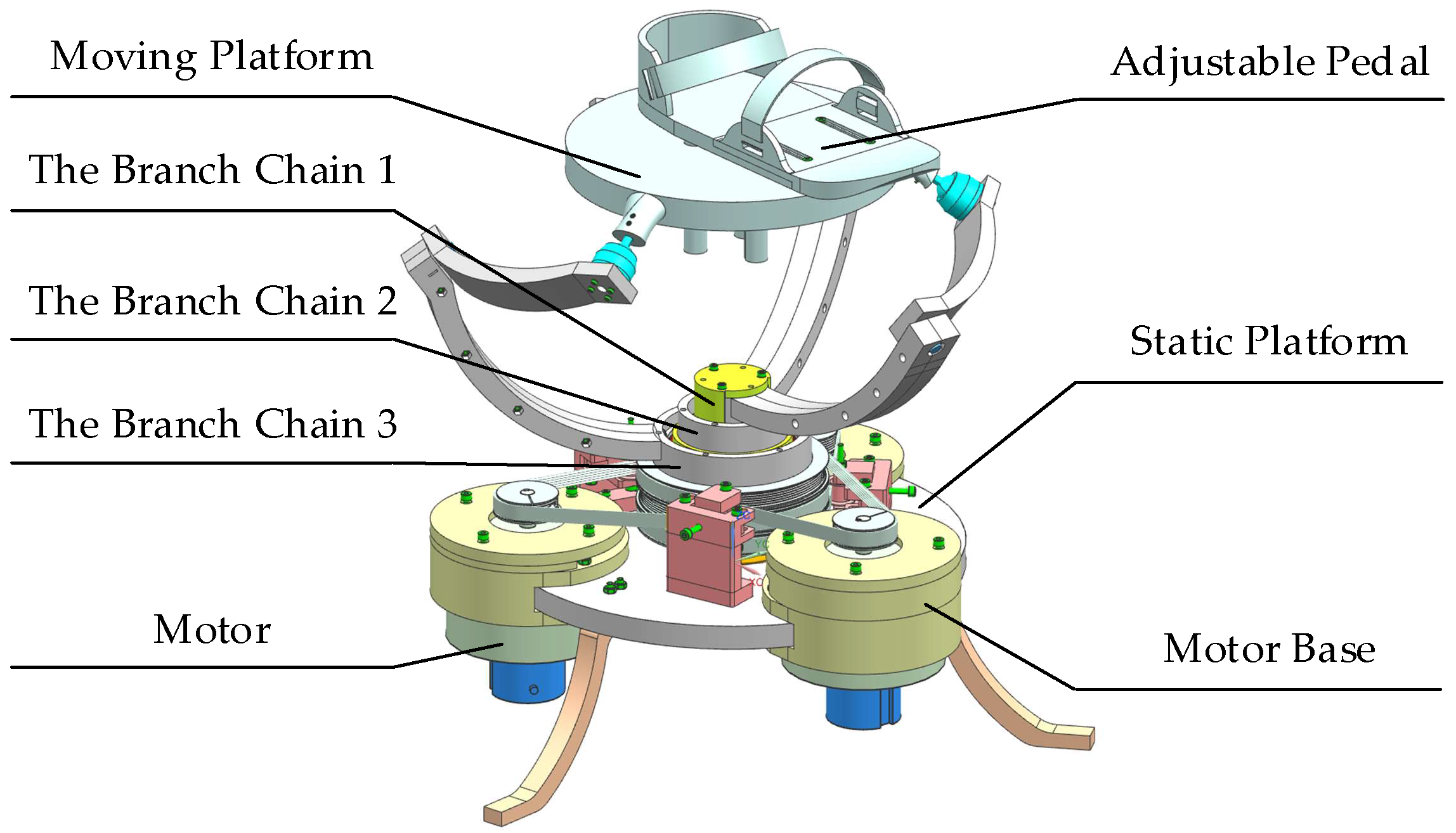
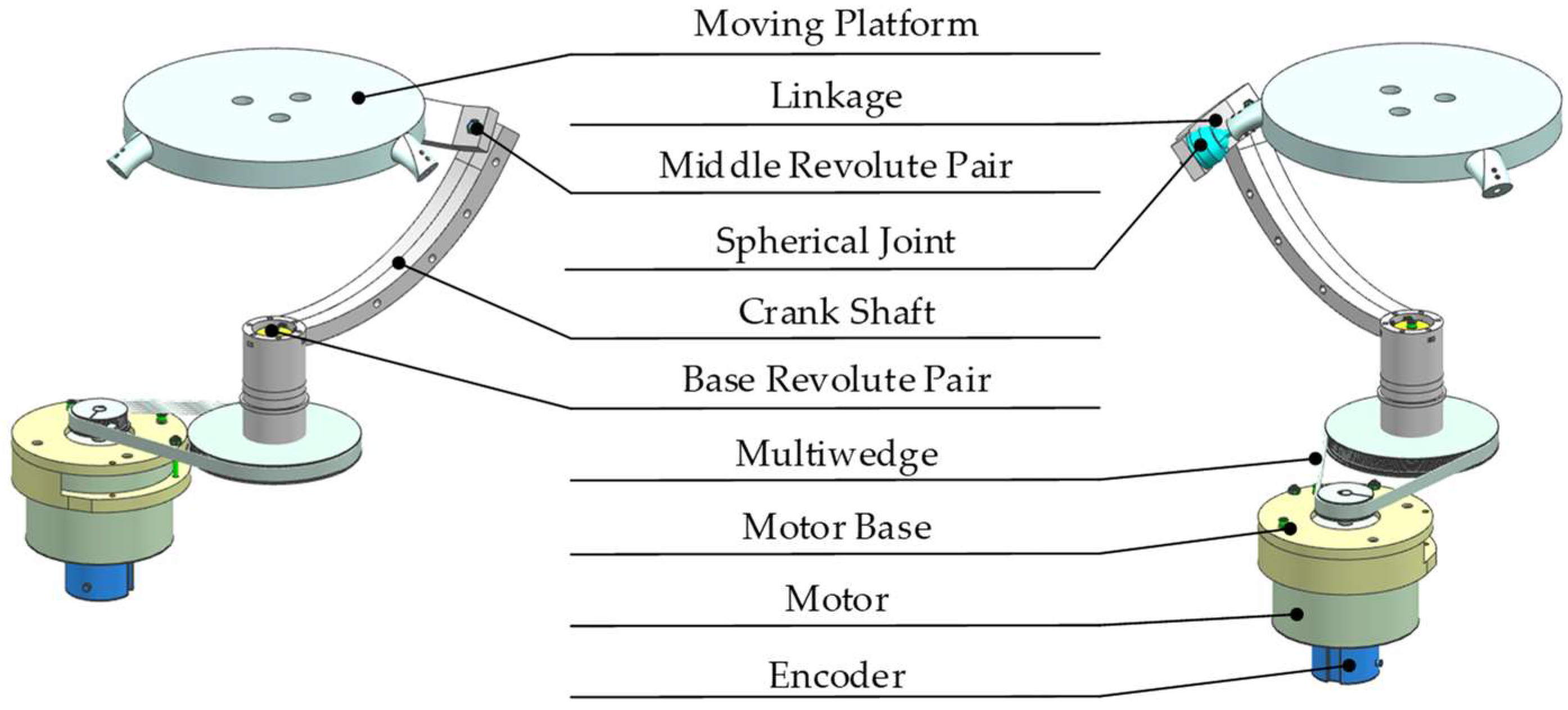
2. Mechanical Structure
2.1. Ankle Motion Mechanism
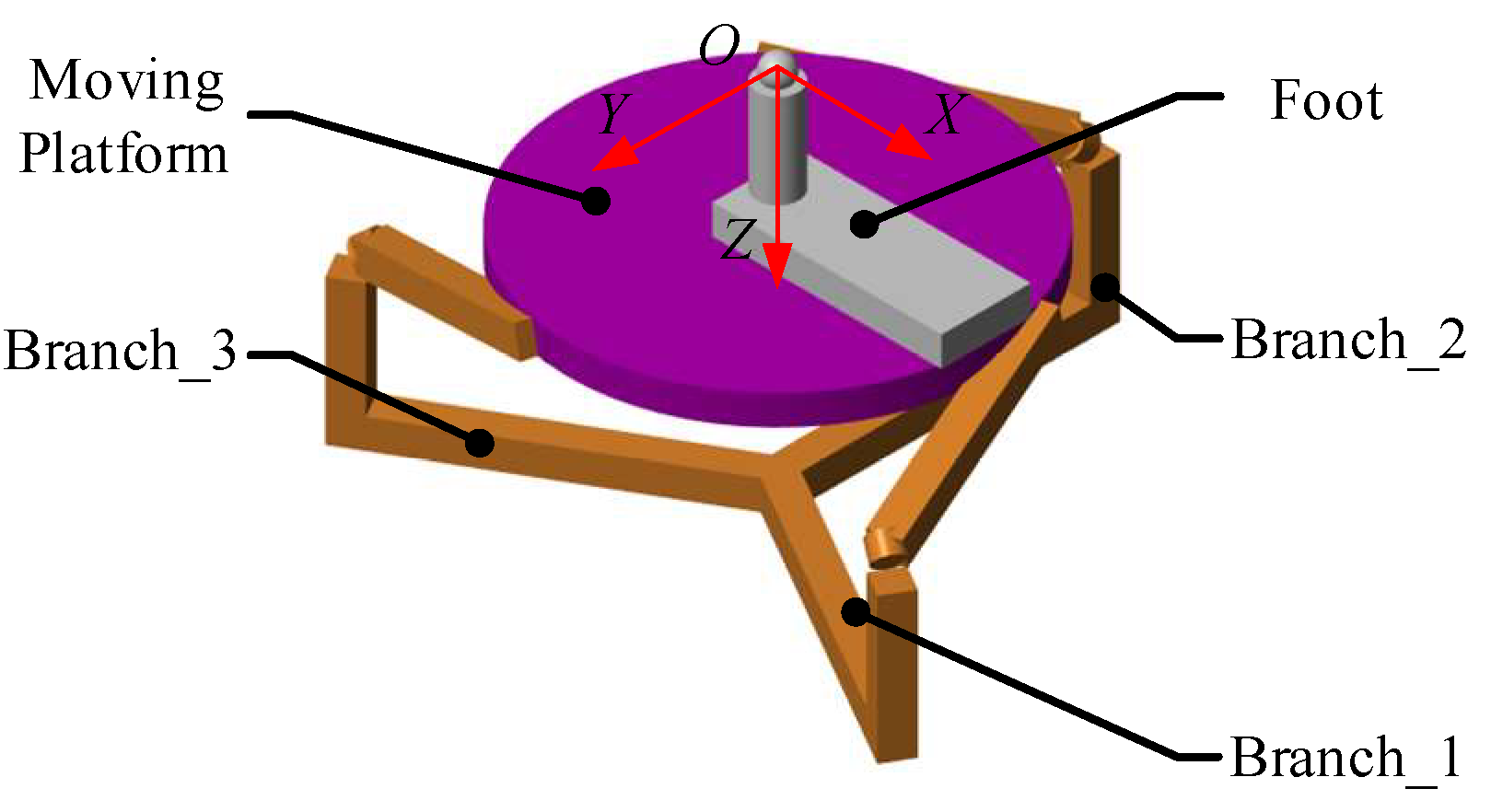
2.2. Mechanical Structure of the 3-RRS PARR
3. Robot Kinematics Analysis
3.1. Robot Kinematics Modeling
3.2. DOF Analysis of PARR
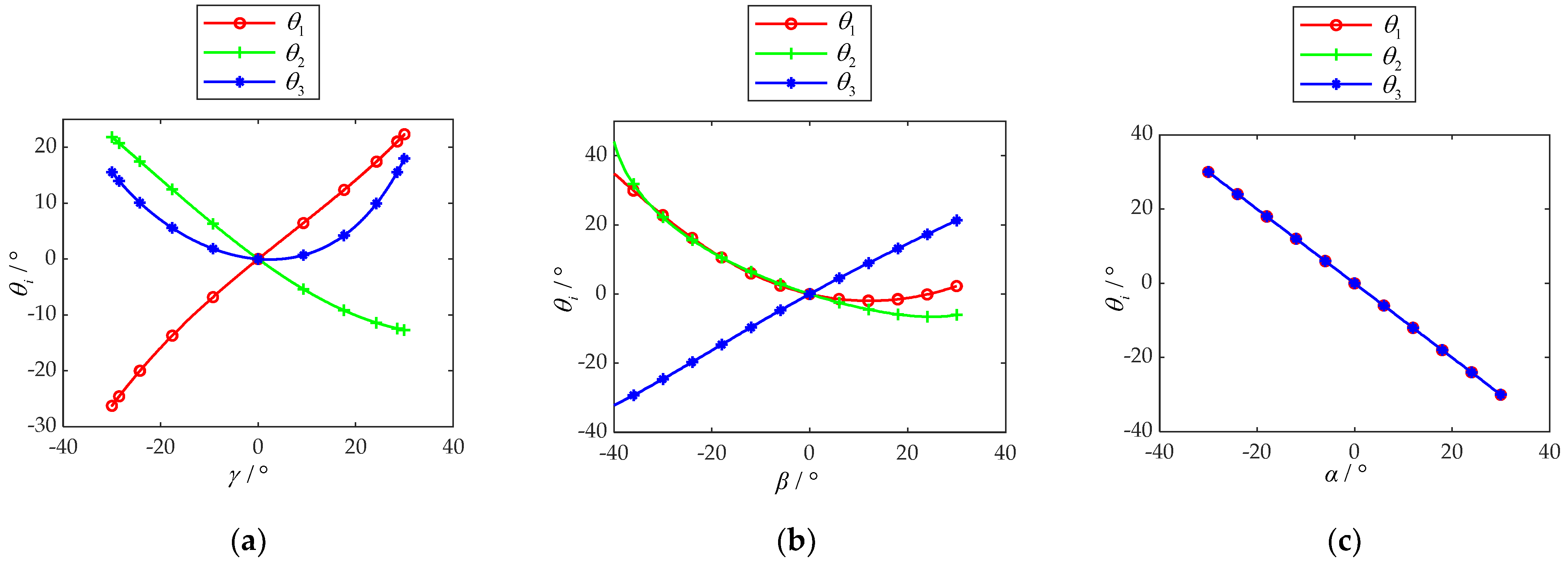
3.3. Inverse Kinematics Model
3.4. Forward Kinematics Model
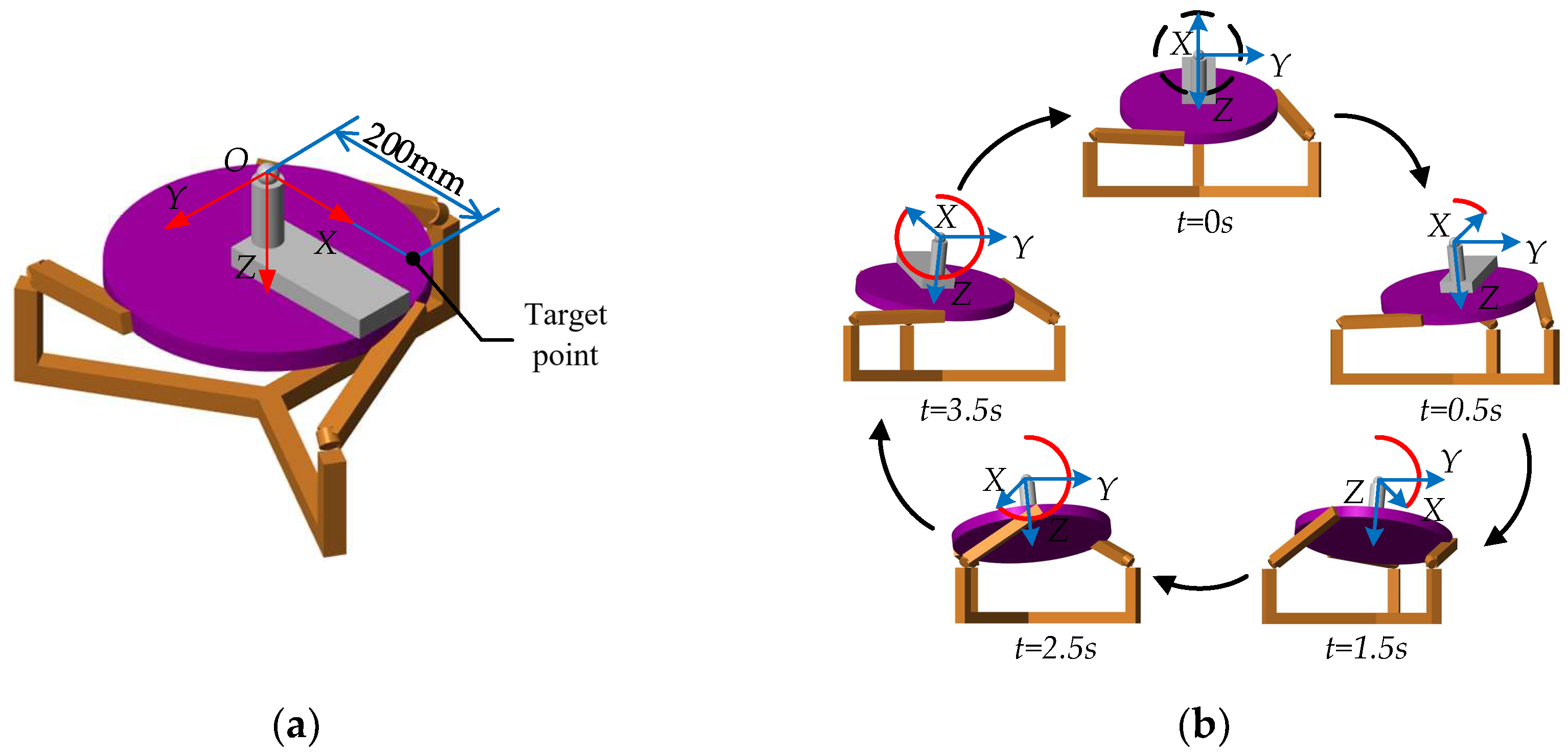
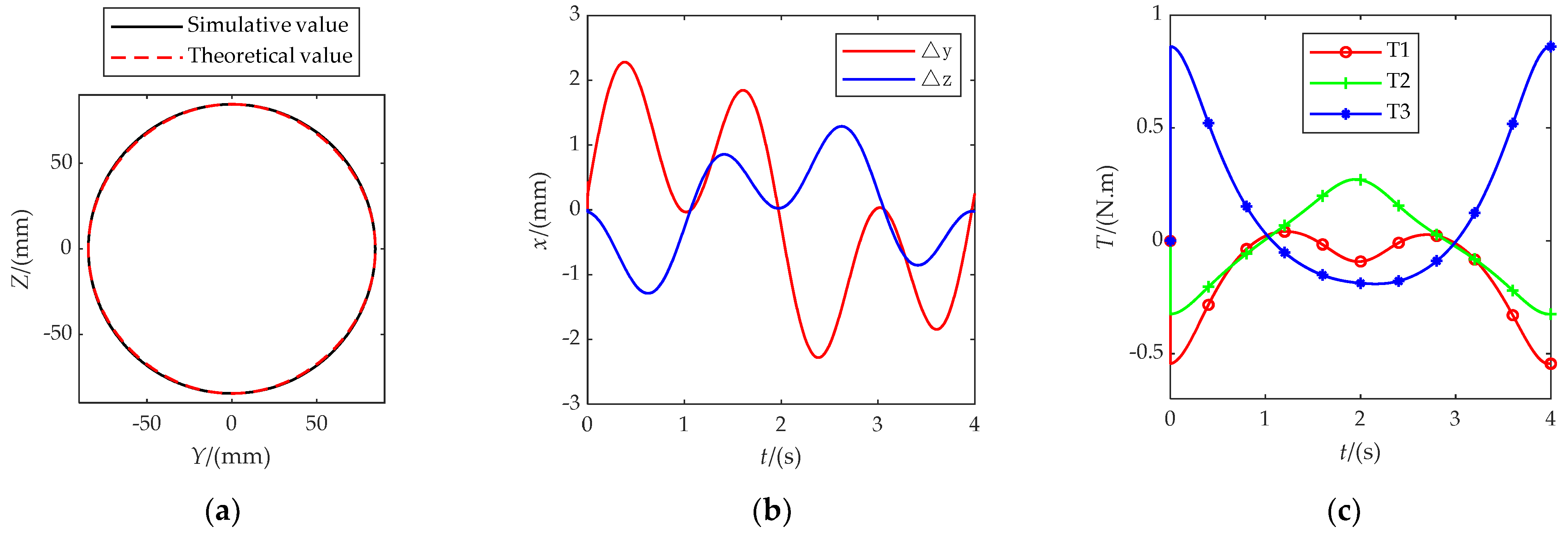
3.5. Numerical Example
4. Multibody Simulation Analysis
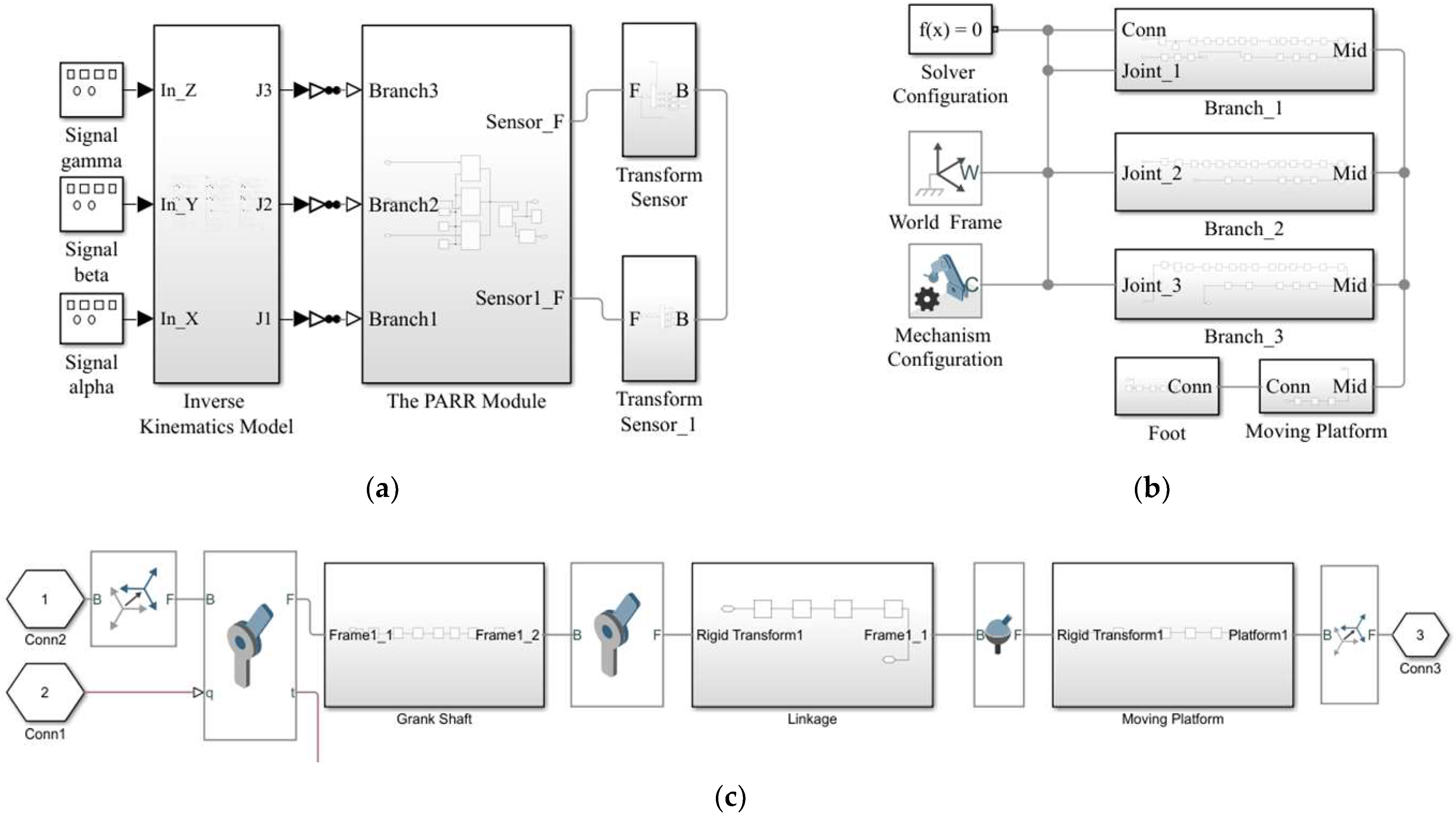
4.1. Simulation Model
4.2. Kinematics Simulation Analysis
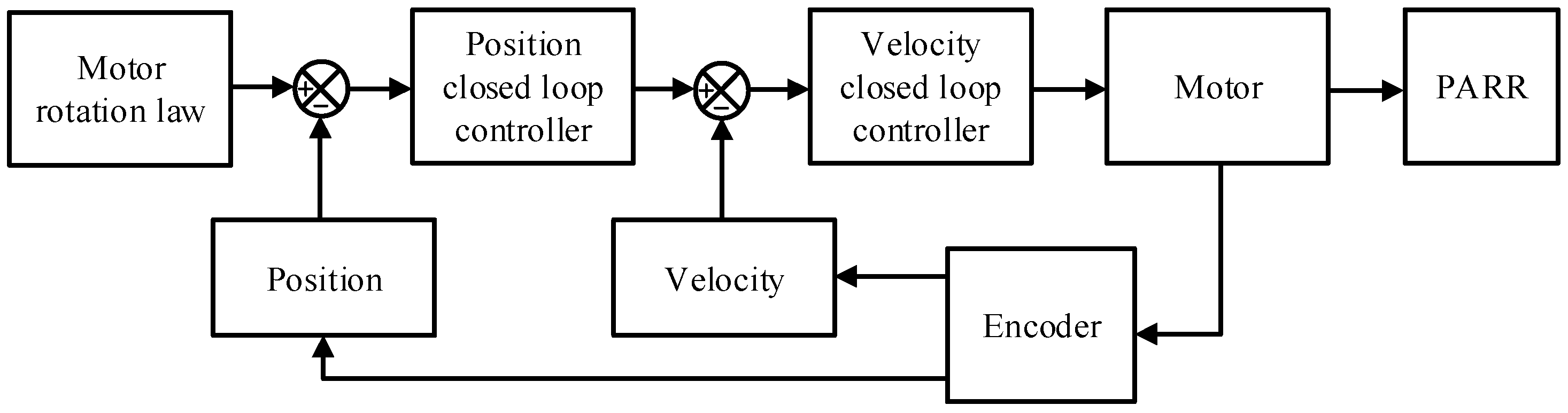
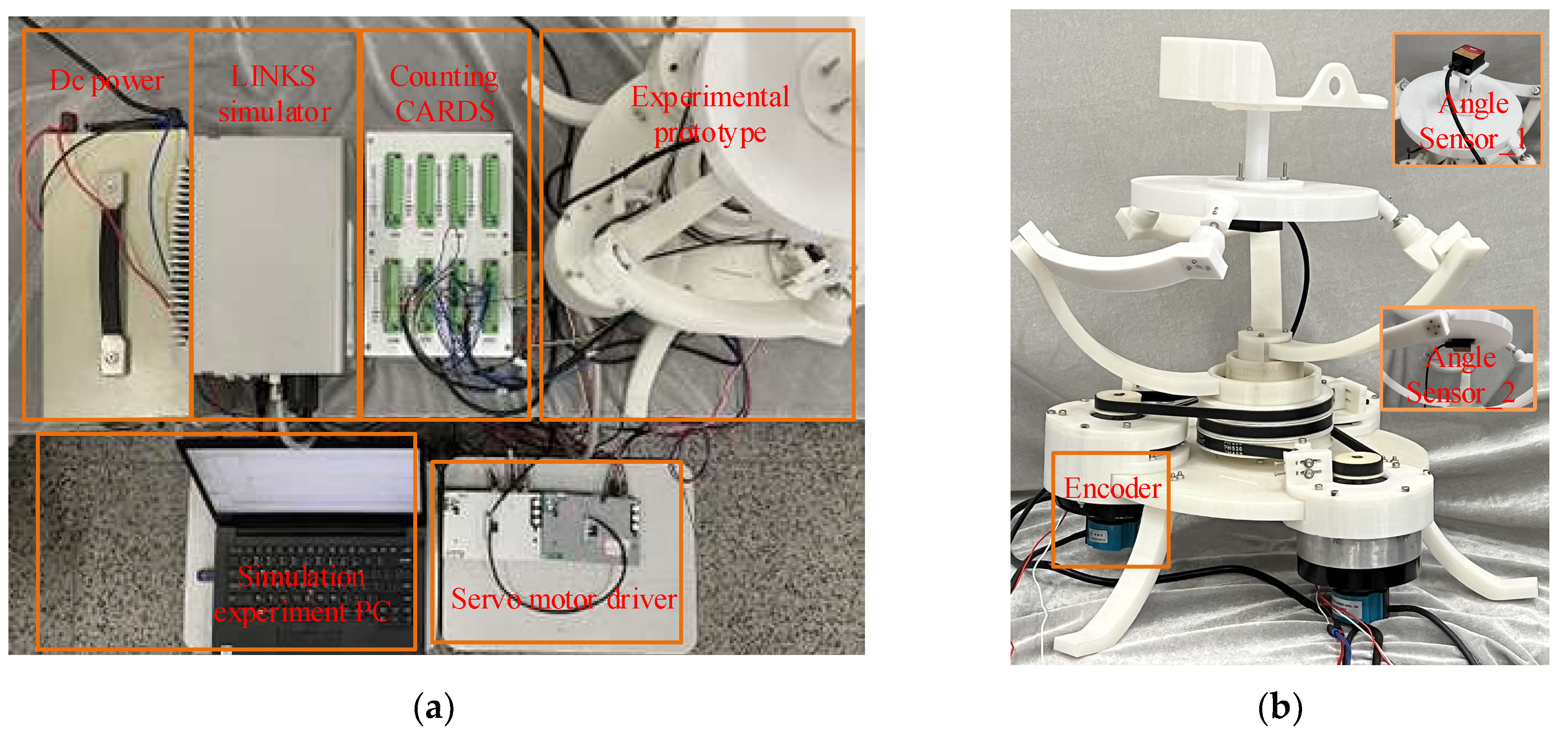
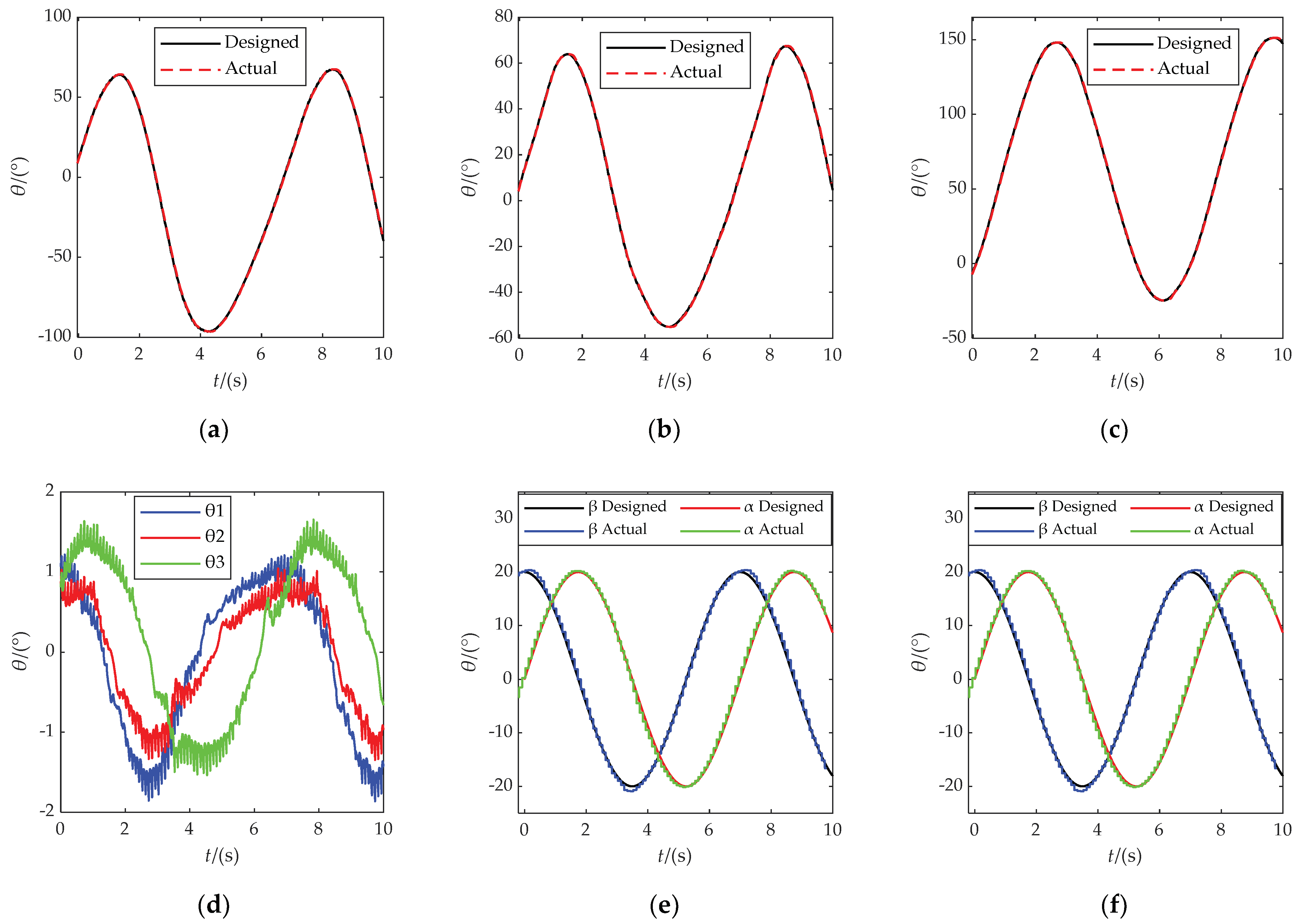
5. Prototype Experiment
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wells, B.; Allen, C.; Deyle, G.; Croy, T. Management of acute grade ii lateral ankle sprains with an emphasis on ligament protection: A descriptive case series. Int. J. Sports Phys. Ther. 2019, 14, 445–458. [Google Scholar] [CrossRef] [PubMed]
- Farzin, H.; Mohammad, H. Acute ankle sprain in athletes: Clinical aspects and algorithmic approach. World J. Orthop. 2020, 11, 534–558. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y. The Effects of Vibration Exercise after Modified Bröstrom Operation in Soccer Players with Ankle Instability. J. Int. Acad. Phys. Ther. Res. 2019, 10, 1791–1796. [Google Scholar] [CrossRef]
- Torp, D.M.; Thomas, A.C.; HubbardTurner, T.; Donovan, L. Biomechanical Response to External Biofeedback During Functional Tasks in Individuals with Chronic Ankle Instability. J. Athl. Train. 2020, 5, 263–271. [Google Scholar] [CrossRef]
- Shi, M.; Yang, C.; Zhang, D. A Novel Human-Machine Collaboration Model of an Ankle Joint Rehabilitation Robot Driven by EEG Signals. Math. Probl. Eng. 2021, 2021, 5564235. [Google Scholar] [CrossRef]
- Zheng, J.-J.; Shen, L.-Y.; Duan, L.-R.; Dong, X.; Qu, B.; Gao, W.; Wu, H. Investigatation of Rehabilitation Human Resources in Shanghai, China. Chin. J. Rehabil. Theory Pract. 2020, 26, 1471–1476. [Google Scholar]
- Li, H.; Xia, C.; Li, F.; Yin, J.; Wang, X.; Cheng, J.; Yang, B.; Dong, P.; Chen, E. Motion simulation of Bionic Auxiliary Device for Ankle Rehabilitation based on small driving moment function. J. Phys. Conf. Ser. 2021, 1802, 042086. [Google Scholar] [CrossRef]
- Li, J.; Zuo, S.; Zhang, L.; Dong, M.; Zhang, Z.; Tao, C.; Ji, R. Mechanical Design and Performance Analysis of a Novel Parallel Robot for Ankle Rehabilitation. J. Mech. Robot. 2020, 12, 051007. [Google Scholar] [CrossRef]
- Jiang, J.-G.; Min, Z.; Huang, Z.; Ma, X.; Chen, Y.; Yu, X. Research Status on Ankle Rehabilitation Robot. Recent Patents Mech. Eng. 2019, 12, 104–124. [Google Scholar] [CrossRef]
- Shi, B.; Chen, X.; Yue, Z.; Yin, S.; Weng, Q.; Zhang, X.; Wang, J.; Wen, W. Wearable Ankle Robots in Post-stroke Rehabilitation of Gait: A Systematic Review. Front. Neurorobotics 2019, 13, 63. [Google Scholar] [CrossRef] [Green Version]
- Forrester, L.W.; Roy, A.; Krywonis, A.; Kehs, G.; Krebs, H.I.; Macko, R.F. Modular Ankle Robotics Training in Early Subacute Stroke. Neurorehabilit. Neural Repair 2014, 28, 678–687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, Y.; Li, R.; Li, D.; Bai, S. An ankle rehabilitation robot based on 3-RRS spherical parallel mechanism. Adv. Mech. Eng. 2017, 9, 6–12. [Google Scholar] [CrossRef] [Green Version]
- Jamwal, P.; Hussain, S.; Xie, S.Q. Review on design and control aspects of ankle rehabilitation robots. Disabil. Rehabil. Assist. Technol. 2015, 10, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Miao, Q.; Zhang, M.; Wang, C.; Li, H. Towards Optimal Platform-Based Robot Design for Ankle Rehabilitation: The State of the Art and Future Prospects. J. Healthc. Eng. 2018, 2018, 1534247. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Perez, M.G.; Garcia-Murillo, M.A.; Cervantes-Sánchez, J.J. Robot-assisted ankle rehabilitation: A review. Disabil. Rehabil. Assist. Technol. 2020, 15, 394–408. [Google Scholar] [CrossRef] [PubMed]
- Wiggin, M.B.; Sawicki, G.S.; Collins, S.H. An Exoskeleton using Controlled Energy Storage and Release to Aid Ankle Propulsion. IEEE Int. Conf. Rehabil. Robot. 2011, 2011, 5975342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jamwal, P.K.; Hussain, S.; Mir-Nasiri, N.; Ghayesh, M.H.; Xie, S.Q. Tele-rehabilitation using In-house Wearable Ankle Rehabilitation Robot. Assist. Technol. 2018, 30, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Jamwal, P.K.; Hussain, S.; Ghayesh, M.H.; Rogozina, S.V. Adaptive Impedance Control of Parallel Ankle Rehabilitation Robot. J. Dyn. Syst. Meas. Control 2017, 139, 111006. [Google Scholar] [CrossRef]
- Park, Y.L.; Chen, B.R.; Pérez-Arancibia Néstor, O.; Young, D.; Stirling, L.; Wood, R.J.; Goldfield, E.C.; Nagpal, R. Design and Control of A Bio-inspired Soft Wearable Robotic Device for Ankle-foot Rehabilitation. Bioinspiration Biomim. 2014, 9, 016007. [Google Scholar] [CrossRef]
- Shorter, K.A.; Kogler Géza, F.; Loth, E.; Durfee, W.K.; Hsiao-Wecksler, E.T. A Portable Powered Ankle-foot Orthosis for Rehabilitation. J. Rehabil. Res. Dev. 2011, 48, 459–472. [Google Scholar] [CrossRef]
- Blaya, J.A.; Herr, H. Adaptive Control of A Variable-impedance Ankle-foot Orthosis to Assist Drop-foot Gait. IEEE Trans. Neural. Syst. Rehabil. Eng. 2004, 12, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Nurahmi, L.; Caro, S.; Solichin, M. A Novel Ankle Rehabilitation Device Based on a Reconfigurable 3-RPS Parallel Manipulator. Mech. Mach. Theory 2019, 134, 135–150. [Google Scholar] [CrossRef] [Green Version]
- Gordon, K.E.; Ferris, D.P. Learning to Walk with a Robotic Ankle Exoskeleton. J. Biomech. 2007, 40, 2636–2644. [Google Scholar] [CrossRef] [PubMed]
- Kao, P.C.; Lewis, C.L.; Ferris, D.P. Invariant Ankle Moment Patterns when Walking with and without A Robotic Ankle Exoskeleton. J. Biomech. 2010, 43, 203–209. [Google Scholar] [CrossRef] [Green Version]
- Yoon, J.; Ryu, J. A Novel Reconfigurable Ankle/Foot Rehabilitation Robot. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005. [Google Scholar]
- Zeng, X.; Zhu, G.; Zhang, M.; Xie, S.Q. Reviewing Clinical Effectiveness of Active Training Strategies of Platform-Based Ankle Rehabilitation Robots. J. Healthc. Eng. 2018, 2018, 2858294. [Google Scholar] [CrossRef] [Green Version]
- Gao, C.; Chen, Z.; Cheng, Y.; Li, J.K.; Huang, X.W.; Wei, L.Y.; He, F.; Luo, Z.P.; Zhang, H.T.; Yu, J. Comparative anatomy of the mouse and human ankle joint using Micro-CT: Utility of a mouse model to study human ankle sprains. Math. Biosci. Eng. 2019, 16, 2959–2972. [Google Scholar] [CrossRef]
- Zhao, X.; Tsujimoto, T.; Kim, B.; Katayama, K.; Tanaka, K. Association of Foot Structure with the Strength of Muscles that Move the Ankle and Physical Performance. J. Foot Ankle Surg. 2018, 57, 1143–1147. [Google Scholar] [CrossRef]
- David, H.-G.; José-María, B. A Randomized Controlled Trial Assessing the Evolution of the Weight-Bearing Ankle Dorsiflexion Range of Motion Over 6 Sessions of Talus Mobilizations in Older Adults. Phys. Ther. 2020, 100, 645–652. [Google Scholar] [CrossRef]
- Gomes, J.; Neto, T.; Vaz, J.R.; Schoenfeld, B.J.; Freitas, S.R. Is there a relationship between back squat depth, ankle flexibility, and Achilles tendon stiffness? Sports Biomech. 2020, 1–14. [Google Scholar] [CrossRef]
- Ye, W.; Li, Q. Type Synthesis of Lower Mobility Parallel Mechanisms: A Review. Chin. J. Mech. Eng. 2019, 32, 38. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Shan, Y.; Yu, J.; Ke, Y. Actuation Spaces Synthesis of Lower-Mobility Parallel Mechanisms Based on Spiral theory. Chin. J. Mech. Eng. 2021, 34, 28. [Google Scholar] [CrossRef]
- Li, Y.-B.; Li, T.-J.; Zhu, H.-F.; Yang, D.; Chen, Y.-J.; Zhang, W.-M.; Liu, J.-M.; Zhang, T. Comparative Analysis of the Kinematics Solution Based on the DH Method and Spiral theory. Math. Probl. Eng. 2021, 2021, 6694621. [Google Scholar] [CrossRef]
- Liao, Z.; Yao, L.; Lu, Z.; Zhang, J. Spiral theory based mathematical modeling and kinematic analysis of a novel ankle rehabilitation robot with a constrained 3-PSP mechanism topology. Int. J. Intell. Robot. Appl. 2018, 2, 351–360. [Google Scholar] [CrossRef]
- Javad, E.; Amir, S. On the position analysis of a new spherical parallel robot with orientation applications. Robot. Comput. Integr. Manuf. 2016, 37, 151–161. [Google Scholar] [CrossRef]
- Hou, Y.; Li, Z.; Wang, Y.; Zhang, W.; Zeng, D.; Zhou, Y. Mechanics unloading analysis and experimentation of a new type of parallel biomimetic shoulder complex. Chin. J. Mech. Eng. 2016, 29, 649–658. [Google Scholar] [CrossRef]
- Mazare, M.; Taghizadeh, M.; Najafi, M.R. Kinematic analysis and design of a 3-DOF translational parallel robot. Int. J. Autom. Comput. 2017, 14, 432–441. [Google Scholar] [CrossRef]

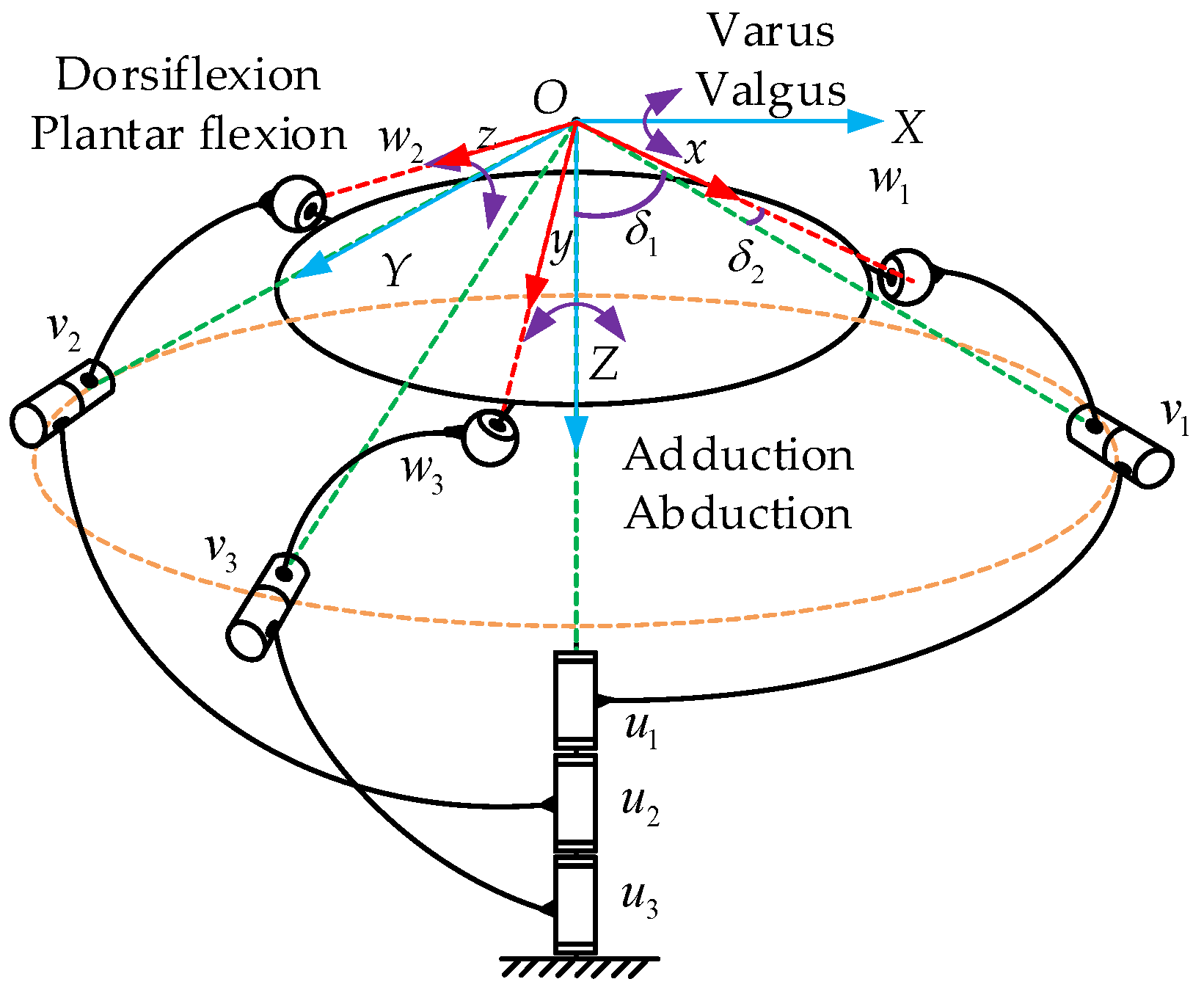


| Dorsiflexion: 0°–30° | Plantar flexion: 0°–40° |
| Adduction: 0°–30° | Abduction: 0°–20° |
| Varus: 0°–20° | Valgus: 0°–15° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Zhang, A.; Zhang, Q.; Zhang, B.; Wu, X.; Qin, T. Design and Experimental Research of 3-RRS Parallel Ankle Rehabilitation Robot. Micromachines 2022, 13, 950. https://doi.org/10.3390/mi13060950
Zou Y, Zhang A, Zhang Q, Zhang B, Wu X, Qin T. Design and Experimental Research of 3-RRS Parallel Ankle Rehabilitation Robot. Micromachines. 2022; 13(6):950. https://doi.org/10.3390/mi13060950
Chicago/Turabian StyleZou, Yupeng, Andong Zhang, Qiang Zhang, Baolong Zhang, Xiangshu Wu, and Tao Qin. 2022. "Design and Experimental Research of 3-RRS Parallel Ankle Rehabilitation Robot" Micromachines 13, no. 6: 950. https://doi.org/10.3390/mi13060950
APA StyleZou, Y., Zhang, A., Zhang, Q., Zhang, B., Wu, X., & Qin, T. (2022). Design and Experimental Research of 3-RRS Parallel Ankle Rehabilitation Robot. Micromachines, 13(6), 950. https://doi.org/10.3390/mi13060950








