WEDM-Generated Slot Width Variation Modeling
Abstract
1. Background
2. Materials and Methods
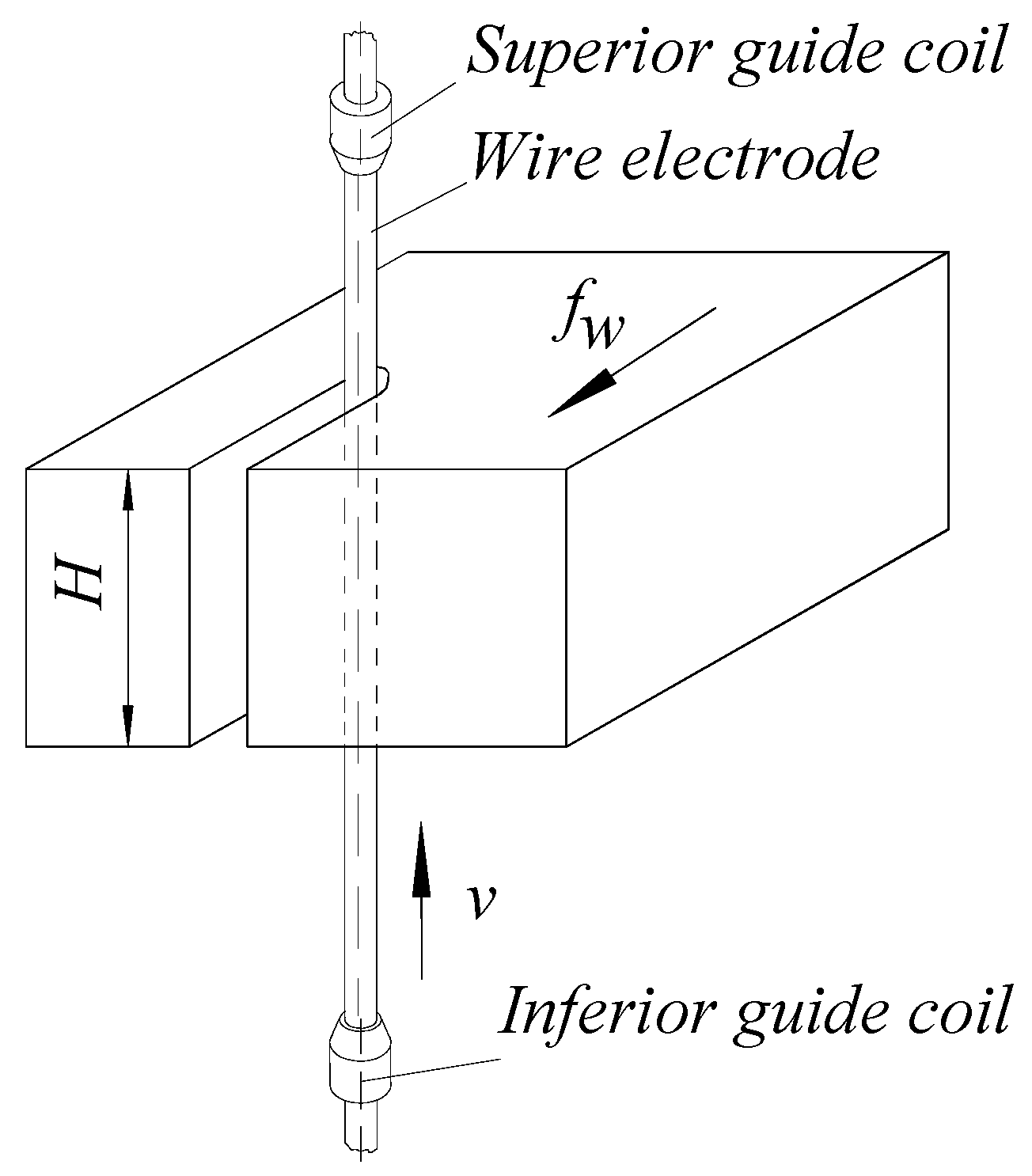
2.1. Theoretical Considerations
- (a)
- Characteristics of electric discharges (voltage, current, pulse shape, pulse-on time, pulse-off time, filling factor, etc.)
- (b)
- Some physical-mechanical properties that define the behavior of the test sample material under the action of electric discharges (density, melting temperature, vaporization temperatures, etc.)
- (c)
- The characteristics of the dielectric liquid (density, fluidity, etc.) and its way of circulation in the working gap
- (d)
- The test sample thickness
- (e)
- The tension force of the wire electrode
- (f)
- The speed of movement of the wire electrode along its axis.
2.2. Experimental Conditions
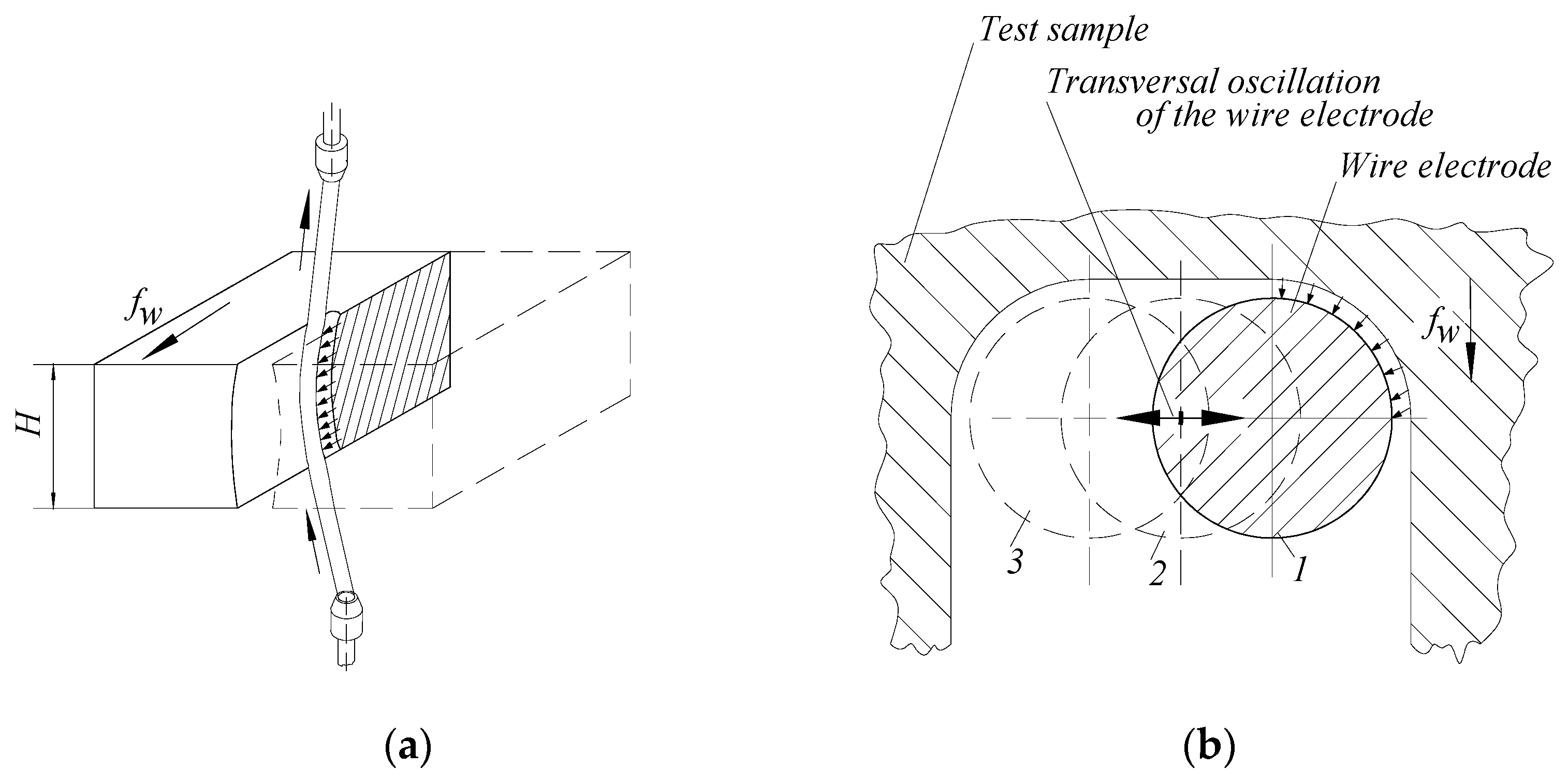
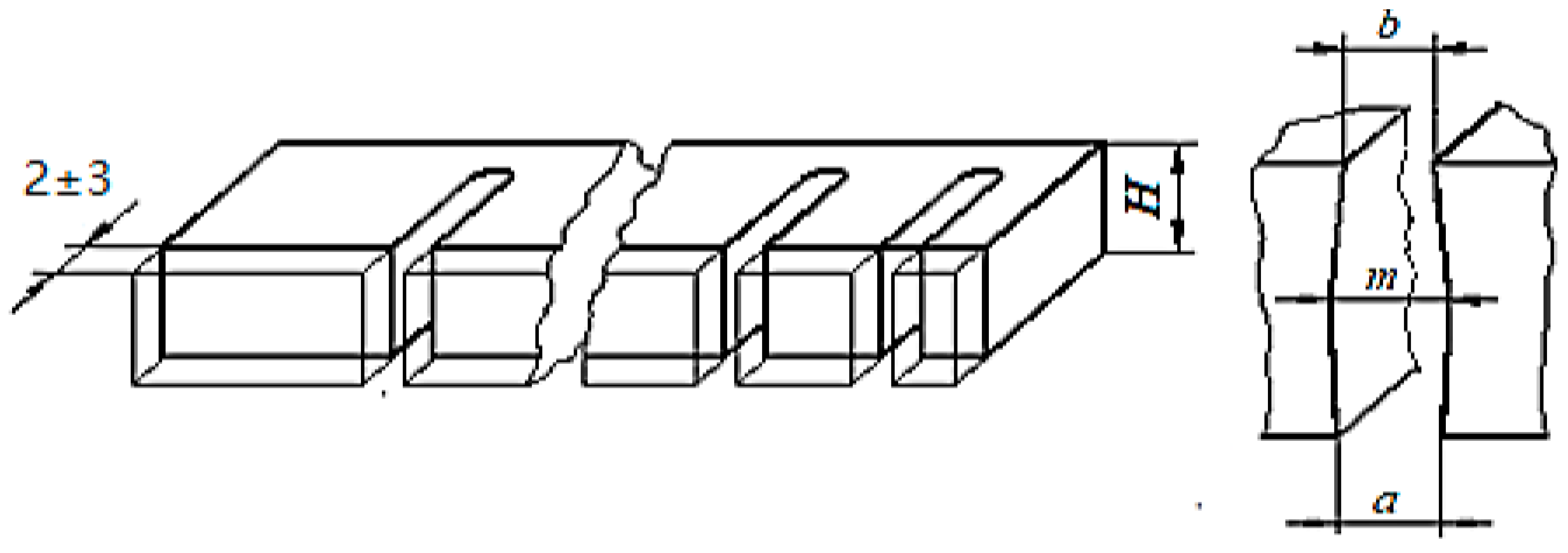
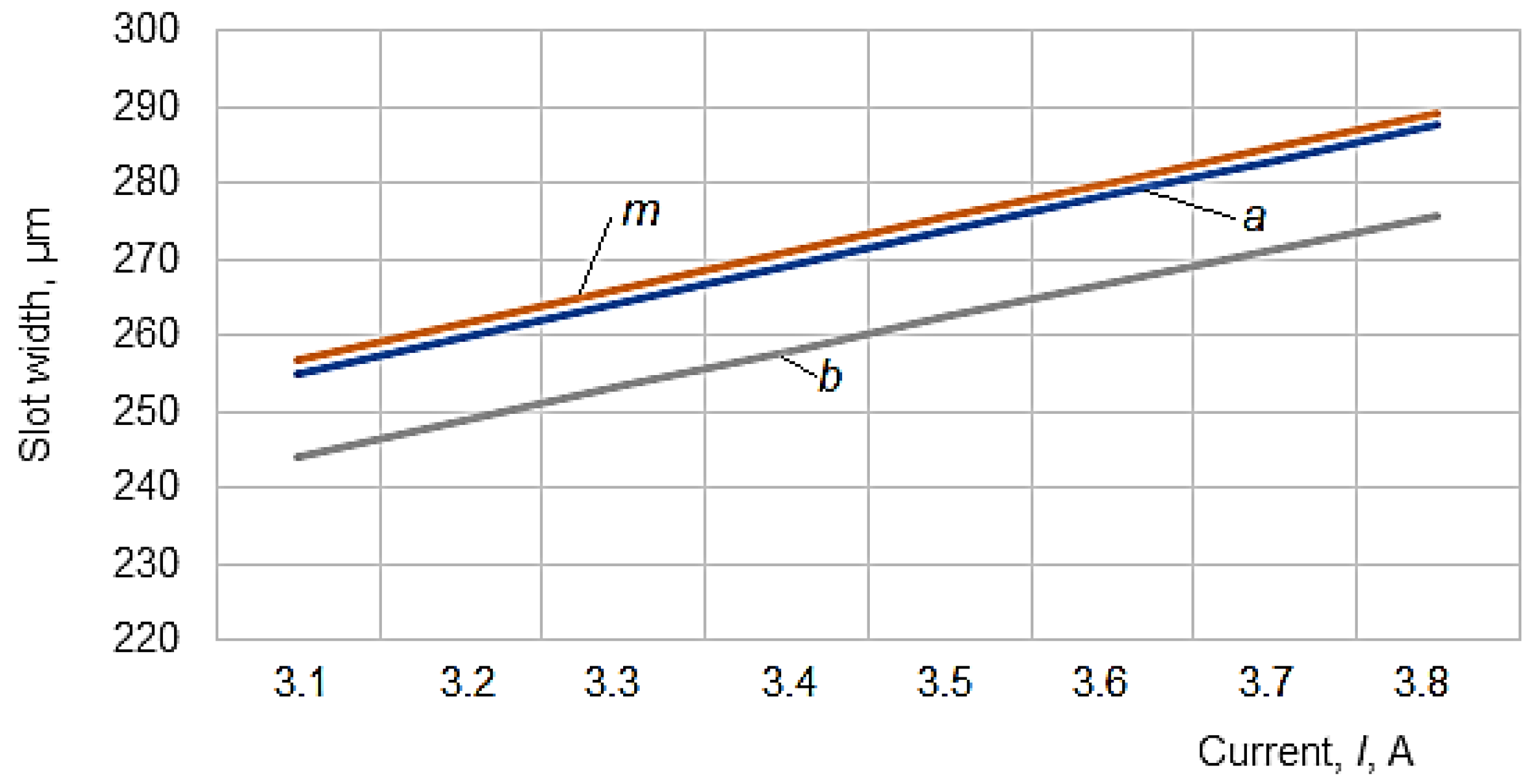
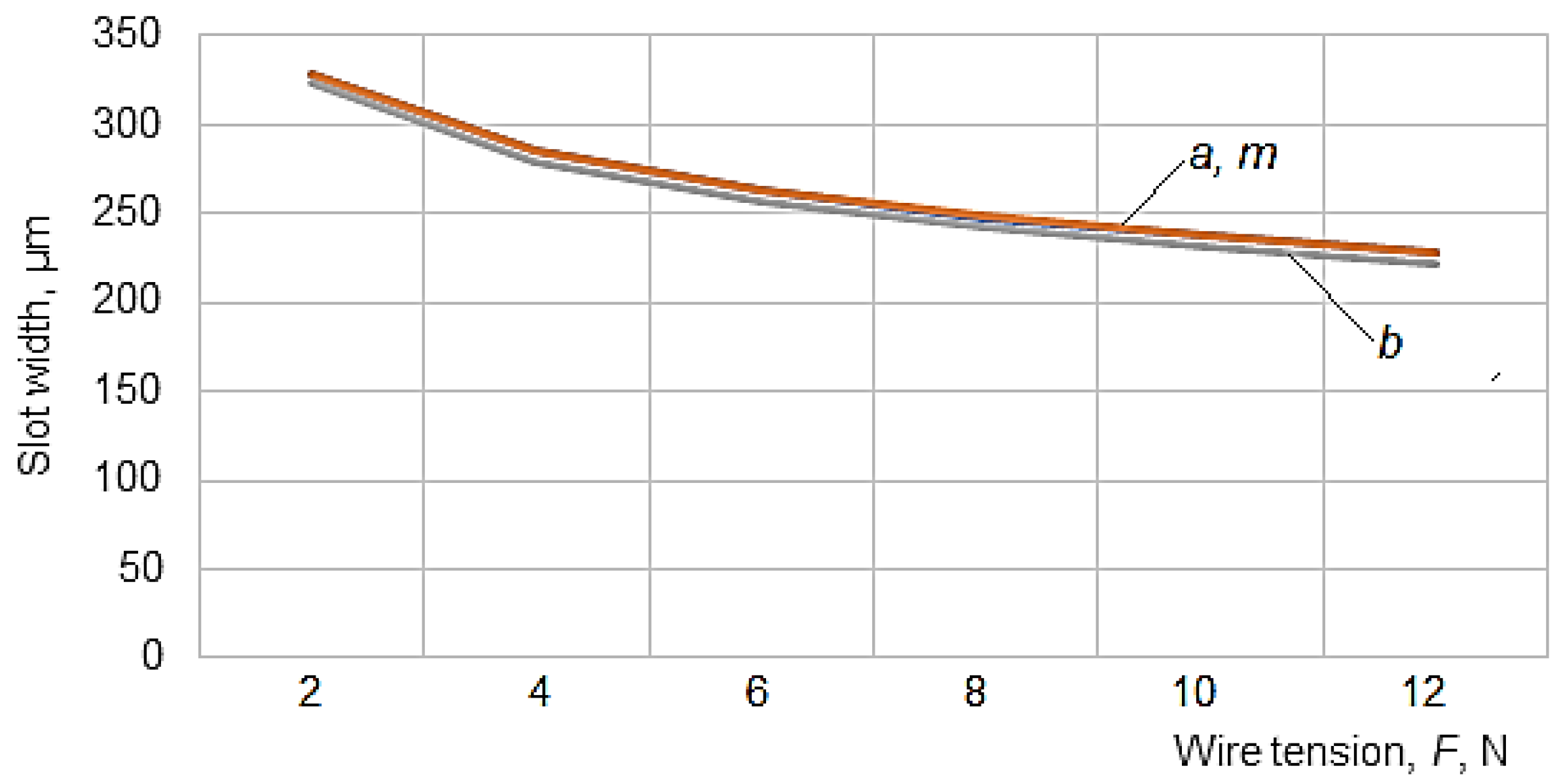
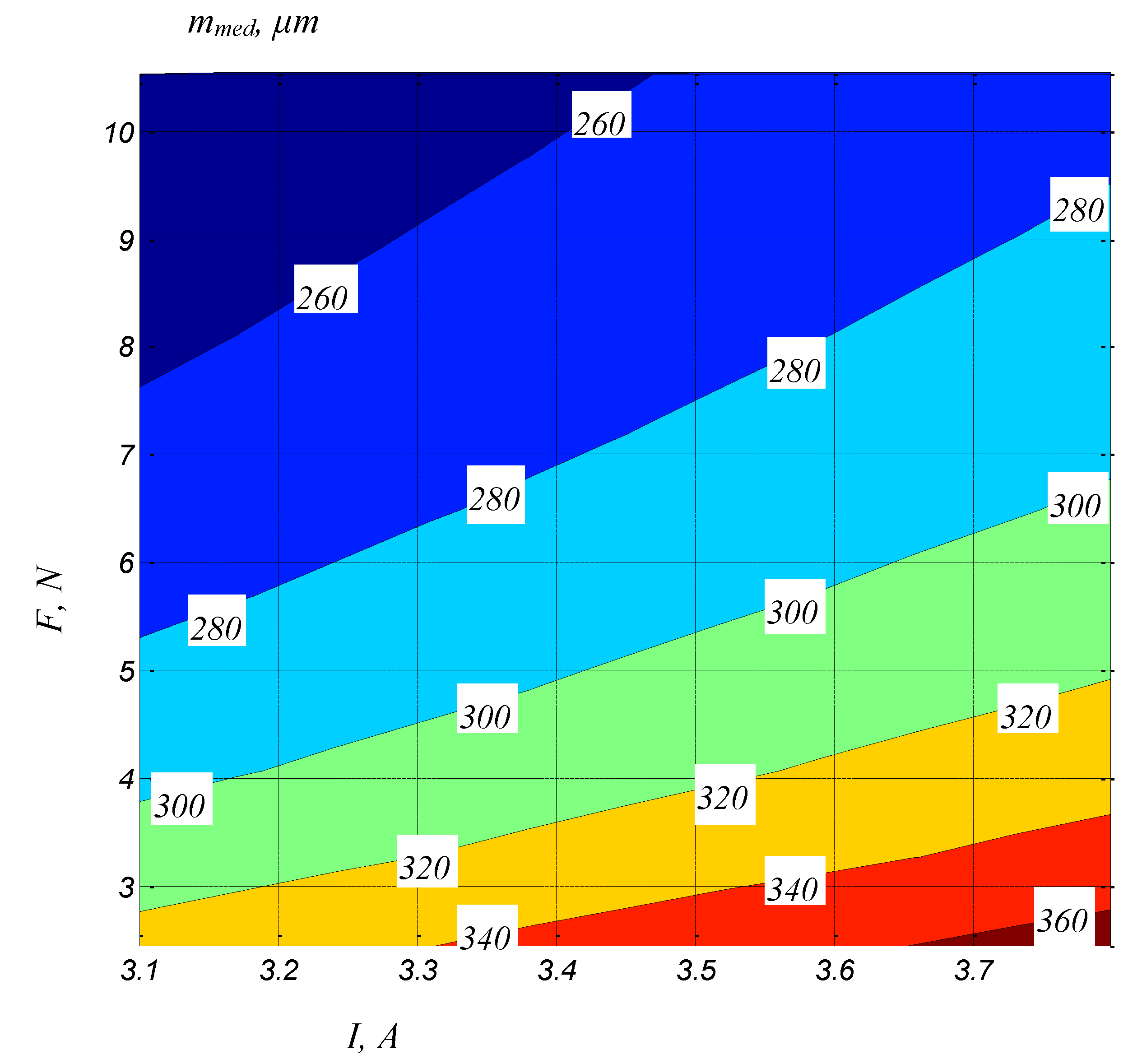
- a—the width of the slot in the lower part of the test sample, where the wire electrode enters the test sample
- b—the width of the slot in the upper area of the test sample, where the wire electrode comes out of the test sample
- m—the width of the slot corresponding approximately to the middle of the thickness H of the test sample.
- -
- test sample thickness H1 = 1 mm and H2 = 20 mm
- -
- pulse-on time Ton 1 = 2 µs and Ton 2 = 12 µs
- -
- pulse-off time Toff 1 = 7 µs and Toff 2 = 30 µs
- -
- average current intensity I1 = 3.1 A and I2 = 3.8 A
- -
- tension force F1 = 2.45 N and F2 = 10.54 N
- -
- wire movement speed along with its axis v1 = 500 mm/min and v2 = 2500 mm/min
- -
- average voltage U1 = 135 V and U2 = 160 V.
3. Results
4. Discussion
- -
- for which Gauss’s criterion has the value SG = 2354.82
- -
- for the slot width amed:for which the Gauss’s criterion has the value SG = 2337.5
- -
- for the slot width mmed:the Gauss’s criterion having the value SG = 2319.72
- -
- for the slot width bmed:
- -
- for which the Gauss’s criterion has the value SG = 2359.49
5. Conclusions
- The width of the slot generated by WEDM can be taken into account in the area of entry of the wire electrode into the test sample, in the area of exit of the wire electrode from the test sample, and respectively in the area corresponding to the middle of the thickness of the test sample.
- Distinct factors influence the slot width values in the three distinct areas mentioned. A factorial experiment was designed and materialized, with six independent variables at two levels of variation and one variable at four levels of variation; The seven independent variables considered were the thickness of the test sample, the pulse-on time, the pulse-off time, the average current, the wire electrode tension force, the wire traveling speed, and the average voltage.
- By mathematically processing the experimental results, empirical models of power type were established for the three widths of the slot. Empirical mathematical models highlight the variation of slot widths and the intensity of the influence exerted by the seven factors taken into account on the values of slot widths.
- The values of the exponents attached to the input factors in the WEDM process were examined, providing information on the intensity of the influence exerted by each of the input factors in the WEDM process on the width of the slot in the three areas.
- It was found that the strongest influence on the width of the slot is exerted by the average current, followed by the average voltage and the tension force of the wire. The other factors exert a low or negligible influence on the variation of the slot width generated by WEDM.
- In the future, there is the intention to perform experimental tests on test samples made of other materials, following the influence of the seven factors on other output parameters of the WEDM process, such as the roughness of the machined surface, the wear of the wire electrode, and the material removal rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, X. Modeling and Simulation of Crater Formation and Wire Vibration in Micro WEDM. Ph.D. Thesis, National University of Singapore, Singapore, 2013; p. 46. Available online: https://www.researchgate.net/publication/263365525_Modeling_and_Simulation_of_Crater_Formation_and_Wire_Vibration_in_Micro_WEDM (accessed on 7 June 2022).
- Puri, A.B.; Bhattacharyya, B. Modelling and analysis of the wire-tool vibration in wire-cut EDM. J. Mater. Process. Technol. 2003, 141, 295–301. [Google Scholar] [CrossRef]
- Slatineanu, L.; Dodun, O.; Coteață, M.; Nagîț, G.; Beșliu Bancescu, I.; Hrițuc, A. Wire electrical discharge machining—A review. Machines 2020, 8, 69. [Google Scholar] [CrossRef]
- Dodun, O.; Gonçalves-Coelho, A.; Slătineanu, L.; Nagîţ, G. Using wire electrical discharge machining for improved corner cutting accuracy of thin parts. Int. J. Adv. Manuf. Technol. 2009, 41, 858–864. [Google Scholar] [CrossRef]
- Dauw, D.F.; Sthioul, H.; Delpretti, R.; Tricarico, C. Wire analysis and control for precision EDM cutting. CIRP Ann. 1989, 38, 191–194. [Google Scholar] [CrossRef]
- Hsue, W.J.; Liao, Y.S.; Lu, S.S. Fundamental geometry analysis of wire electrical discharge machining in corner cutting. Int. J. Mach. Tools Manuf. 1999, 39, 651–667. [Google Scholar] [CrossRef]
- Mahapatra, S.S.; Patnaik, A. Optimization of wire electrical discharge machining (WEDM) process parameters using Taguchi method. Int. J. Adv. Manuf. Technol. 2007, 34, 911–925. [Google Scholar] [CrossRef]
- Sanchez, J.A.; Plaza, S.; Lopez De Lacalle, L.N.; Lamikiz, A. Computer simulation of wire-EDM taper-cutting. Int. J. Comput. Integr. 2006, 19, 727–735. [Google Scholar] [CrossRef]
- Sanchez, J.A.; Rodil, J.L.; Herrero, A.; Lopez de Lacalle, L.N.; Lamikiz, A. On the influence of cutting speed limitation on the accuracy of wire-EDM corner-cutting. J. Mater. Process. Technol. 2007, 182, 574–579. [Google Scholar] [CrossRef]
- Sanchez, J.A.; Plaza, S.; Ortega, N.; Marcos, M.; Albizuri, J. Experimental and numerical study of angular error in wire-EDM taper-cutting. Int. J. Mach. Tools Manuf. 2008, 48, 1420–1428. [Google Scholar] [CrossRef]
- Liang, J.F.; Tsai, C.F.; Lin, M.H.; Liao, Y.S. Measurement of Wire Deflection in Wire—Cut EDM Machining. In Proceedings of the 16th International Symposium on Electromachining, Shanghai, China, 19–23 April 2010; Shanghai Jiao Tong University Press: Shanghai, China; pp. 223–226. [Google Scholar]
- Feng, X.; Wong, Y.S.; Hong, G.S. Modeling of micro wire EDM process and wire vibration. In Proceedings of the 7th International Conference on Micromanufacturing, ICOMM 2012, Evanston, IL, USA, 12–14 March 2012; Available online: https://www.researchgate.net/profile/Xiaobing-Feng-6/publication/263365332_Modeling_of_micro_wire_EDM_process_and_wire_vibration/links/54295a0b0cf26120b7b5ef4f/Modeling-of-micro-wire-EDM-process-and-wire-vibration.pdf (accessed on 7 June 2022).
- Chen, Z.; Huang, Y.; Zhang, Z.; Li, H.; Ming, W.Y.; Zhang, G. An analysis and optimization of the geometrical inaccuracy in WEDM rough corner cutting. Int. J. Adv. Manuf. Technol. 2014, 74, 917–929. Available online: https://link.springer.com/article/10.1007/s00170-014-6002-5 (accessed on 7 June 2022). [CrossRef]
- Chen, Z.; Huang, Y.; Huang, H.; Zhang, Z.; Zhang, G. Three-dimensional characteristics analysis of the wire-tool vibration considering spatial temperature field and electromagnetic field in WEDM. Int. J. Mach. Tools Manuf. 2015, 92, 85–96. [Google Scholar] [CrossRef]
- Dongre, G.; Zaware, S.; Dabade, U.; Joshi, S.S. Multi-objective optimization for silicon wafer slicing using wire-EDM process. Mater. Sci. Semicond. Process. 2015, 39, 793–806. [Google Scholar] [CrossRef]
- Conde, A.; Sanchez, J.A.; Plaza, S.; Ramos, J.M. On the influence of wire-lag on the WEDM of low-radius free-form geometries. Procedia CIRP 2016, 42, 274–279. [Google Scholar] [CrossRef]
- Habib, S.; Okada, A. Study on the movement of wire electrode during fine wire electrical discharge machining process. J. Mater. Process. Technol. 2016, 227, 147–152. [Google Scholar] [CrossRef]
- Ablyaz, T.R.; Lesnikov, R.V. Influence of the wire EDM conditions on the cut width. Russ. Eng. Res. 2016, 36, 786–787. [Google Scholar] [CrossRef]
- Straka, L.; Corn, I.; Pitel’, J. Prediction of the geometrical accuracy of the machined surface of the tool steel EN X30WCrV9-3 after electrical discharge machining with CuZn37 wire electrode. Metals 2017, 7, 462. [Google Scholar] [CrossRef]
- Conde, A.; Sanchez, J.A.; Plaza, S.; Ostolaza, M.; de la Puerta, I.; Li, Z. Experimental measurement of wire-lag effect and its relation with signal classification on wire EDM. Procedia CIRP 2018, 68, 132–137. [Google Scholar] [CrossRef]
- Conde, A.; Arriandiaga, A.; Sanchez, J.A.; Portillo, E.; Plaza, S.; Cabanes, I. High-accuracy wire electrical discharge machining using artificial neural networks and optimization techniques. Robot. Comput.-Integr. Manuf. 2018, 49, 24–38. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Zhang, G.; Li, W. Modeling and reducing workpiece corner error due to wire deflection in WEDM rough corner-cutting. J. Manuf. Process. 2018, 36, 557–564. [Google Scholar] [CrossRef]
- Abyar, H.; Abdullah, A.; Akbarzadeh, A. Analyzing wire deflection errors of WEDM process on small arced corners. J. Manuf. Process. 2018, 36, 216–223. [Google Scholar] [CrossRef]
- Abyar, H.; Abdullah, A.; Akbarzadeh, A. Prediction algorithm for WEDM arced path errors based on spark variable gap and nonuniform spark distribution models. J. Manuf. Sci. Eng. 2019, 141, 011011. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, G. Study on magnetic field distribution and electro-magnetic deformation in wire electrical discharge machining sharp corner workpiece. Int. J. Adv. Manuf. Technol. 2018, 98, 1913–1923. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Zhang, G.; Li, W. Reduction of energy consumption and thermal deformation in WEDM by magnetic field assisted technology. Int. J. Precis. Eng. Manuf.-Gr. Technol. 2020, 7, 391–404. [Google Scholar] [CrossRef]
- Sabyrov, N.; Jahan, M.P.; Bilal, A.; Perveen, A. Ultrasonic vibration assisted electro-discharge machining (EDM)—An overview. Materials 2019, 12, 522. [Google Scholar] [CrossRef] [PubMed]
- Parthiban, M.; Prabhukarthi, A.; Anthuvan, N. Development of a mechanistic model for WEDM. Int. J. Mod. Stud. Mech. Eng. (IJMSME) 2019, 5, 1–9. [Google Scholar] [CrossRef]
- Yan, H.; Bakadiasa, K.D.; Chen, Z.; Yan, Z.; Zhou, H.; Han, F. Attainment of high corner accuracy for thin-walled sharp-corner part by WEDM based on magnetic field-assisted method and parameter optimization. Int. J. Adv. Manuf. Technol. 2020, 106, 4845–4857. [Google Scholar] [CrossRef]
- Rohilla, V.K.; Goyal, R.; Kumar, A.; Singla, Y.K.; Sharma, N. Surface integrity analysis of surfaces of nickel-based alloys machined with distilled water and aluminium powder-mixed dielectric fluid after WEDM. Int. J. Adv. Manuf. Technol. 2021, 116, 2467–2472. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.J.; Mani Prabu, S.S.; Palani, I.A.; Patel, V.K.; Parikh, D.M.; de Lacalle, L.N.L. Multi-response optimization of WEDM process parameters for machining of superelastic nitinol shape-memory alloy using a heat-transfer search algorithm. Materials 2019, 12, 1277. [Google Scholar] [CrossRef]
- Dodun, O. Contribution to the Optimization of the Wire Electrical Discharge Machining. Ph.D. Thesis, “Gheorghe Asachi” Technical University of Iași, Iași, Romania, 2000. (In Romanian). [Google Scholar]
- Dodun, O.; Slatineanu, L.; Gherman, L. Improving the WEDM process acting on the tool electrode. Procedia Technol. 2014, 12, 427–432. [Google Scholar] [CrossRef][Green Version]
- Nanu, A. Materials Technology; Didactic and Pedagogical Publishing House: Bucharest, Romania, 1983. (In Romanian) [Google Scholar]
- Zhang, M.; Zhang, Q.; Dou, L.; Liu, Q.; Zhu, G. Research on the impulse force in electrical discharge machining using a new measuring method. Int. J. Adv. Manuf. Technol. 2016, 82, 463–471. [Google Scholar] [CrossRef]
- Mohanty, C.P.; Sahu, J.; Mahapatra, S.S. Thermal-structural analysis of electrical discharge machining process. Procedia Eng. 2013, 51, 508–513. [Google Scholar] [CrossRef]
- Kumar, A.; Bagal, D.K.; Maity, K.P. Numerical modeling of wire electrical discharge machining of super alloy Inconel 718. Procedia Eng. 2014, 97, 1512–1523. [Google Scholar] [CrossRef][Green Version]
- Crețu, G. Fundamentals of Experimental Research. Laboratory Handbook; “Gheorghe Asachi” Technical University of Iași: Iași, Romania, 1992. (In Romanian) [Google Scholar]


| Input Factors | Output Parameters | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Experiment No. | H, mm | Ton, μs | Toff, μs | I, A | F, N | v, mm/min | U, V | Measured Values for b, μm | bmed, μm | Measured Values for m, μm | mmed, μm | Measured Values for a, μm | amed, µm |
| Column1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 1 | 2 | 7 | 3.1 | 2.45 | 500 | 135 | 281,282,287 | 283 | 281,282,287 | 283 | 281,282,287 | 283 |
| 2 | 1 | 2 | 7 | 3.8 | 10.54 | 2500 | 135 | 270,273,269 | 270 | 270,273,269 | 270 | 270,273,269 | 270 |
| 3 | 1 | 2 | 30 | 3.1 | 2.45 | 2500 | 135 | 265,261,271 | 265 | 265,261,271 | 265 | 265,261,271 | 265 |
| 4 | 1 | 2 | 30 | 3.8 | 10.54 | 500 | 135 | 287,281,283 | 283 | 287,281,283 | 283 | 287,281,283 | 283 |
| 5 | 1 | 12 | 7 | 3.8 | 2.45 | 2500 | 135 | 315,289,298 | 300 | 315,289,298 | 300 | 315,289,298 | 300 |
| 6 | 1 | 12 | 7 | 3.1 | 10.54 | 500 | 135 | 254,259,258 | 257 | 254,259,258 | 257 | 254,259,258 | 257 |
| 7 | 1 | 12 | 30 | 3.1 | 2.45 | 500 | 135 | 312,306,320 | 312 | 312,306,320 | 312 | 312,306,320 | 312 |
| 8 | 1 | 12 | 30 | 3.8 | 10.54 | 2500 | 135 | 268,273,269 | 270 | 268,273,269 | 270 | 268,273,269 | 270 |
| 9 | 20 | 2 | 7 | 3.1 | 2.45 | 2500 | 135 | 280,291,288 | 286 | 294,288,293 | 291 | 304,282,285 | 290 |
| 10 | 20 | 2 | 7 | 3.8 | 10.54 | 500 | 135 | 302,298,300 | 300 | 300,306,311 | 305 | 302,303,309 | 304 |
| 11 | 20 | 2 | 30 | 3.1 | 2.45 | 500 | 135 | 296,291,293 | 293 | 302,297,299 | 299 | 288,290,315 | 297 |
| 12 | 20 | 2 | 30 | 3.8 | 10.54 | 2500 | 135 | 250,255,252 | 252 | 259,254,261 | 258 | 254,249,267 | 256 |
| 13 | 20 | 12 | 7 | 3.8 | 2.45 | 500 | 135 | 381,395,375 | 383 | 393,387,389 | 389 | 388,380,396 | 388 |
| 14 | 20 | 12 | 7 | 3.1 | 10.54 | 2500 | 135 | 258,251,250 | 253 | 256,259,260 | 258 | 257,254,260 | 257 |
| 15 | 20 | 12 | 30 | 3.1 | 2.45 | 2500 | 135 | 356,351,351 | 352 | 353,359,363 | 358 | 357,356,358 | 357 |
| 16 | 20 | 12 | 30 | 3.8 | 10.54 | 500 | 135 | 230,234,242 | 235 | 245,238,239 | 240 | 236,248,235 | 239 |
| 17 | 20 | 2 | 7 | 3.1 | 2.45 | 500 | 160 | 300,301,307 | 302 | 310,315,314 | 313 | 311,304,312 | 309 |
| 18 | 20 | 2 | 7 | 3.8 | 10.54 | 2500 | 160 | 332,330,328 | 330 | 338,343,340 | 340 | 332,339,340 | 337 |
| 19 | 20 | 2 | 30 | 3.1 | 2.45 | 2500 | 160 | 301,306,305 | 304 | 315,311,316 | 314 | 305,315,310 | 310 |
| 20 | 20 | 2 | 30 | 3.8 | 10.54 | 500 | 160 | 278,272,272 | 274 | 282,284,286 | 284 | 284,273,286 | 281 |
| 21 | 20 | 12 | 7 | 3.8 | 2.45 | 2500 | 160 | 405,400,398 | 401 | 415,410,412 | 412 | 400,416,408 | 408 |
| 22 | 20 | 12 | 7 | 3.1 | 10.54 | 500 | 160 | 287,292,291 | 290 | 302,299,298 | 299 | 293,283,315 | 297 |
| 23 | 20 | 12 | 30 | 3.1 | 2.45 | 500 | 160 | 381,384,384 | 383 | 392,396,394 | 394 | 391,386,393 | 390 |
| 24 | 20 | 12 | 30 | 3.8 | 10.54 | 2500 | 160 | 269,267,267 | 267 | 279,278,276 | 277 | 271,278,273 | 274 |
| 25 | 40 | 2 | 7 | 3.1 | 2.45 | 2500 | 160 | 316,312,306 | 311 | 325,323,322 | 323 | 326,314,320 | 320 |
| 26 | 40 | 2 | 7 | 3.8 | 10.54 | 500 | 160 | 328,327,325 | 326 | 336,339,341 | 338 | 324,338,346 | 336 |
| 27 | 40 | 2 | 30 | 3.1 | 2.45 | 500 | 160 | 308,311,315 | 311 | 320,326,325 | 323 | 312,326,322 | 320 |
| 28 | 40 | 2 | 30 | 3.8 | 10.54 | 2500 | 160 | 239,242,242 | 241 | 256,252,252 | 253 | 249,253,248 | 250 |
| 29 | 40 | 12 | 7 | 3.8 | 2.45 | 500 | 160 | 431,428,427 | 428 | 441,442,443 | 442 | 427,440,447 | 438 |
| 30 | 40 | 12 | 7 | 3.1 | 10.54 | 2500 | 160 | 245,240,239 | 241 | 250,252,259 | 253 | 253,247,250 | 250 |
| 31 | 40 | 12 | 30 | 3.1 | 2.45 | 2500 | 160 | 411,409,407 | 409 | 423,422,418 | 421 | 423,414,417 | 418 |
| 32 | 40 | 12 | 30 | 3.8 | 10.54 | 500 | 160 | 236,232,231 | 233 | 246,243,244 | 244 | 239,247,240 | 242 |
| 33 | 40 | 2 | 7 | 3.1 | 2.45 | 500 | 190 | 310,308,306 | 308 | 329,326,325 | 326 | 326,316,318 | 320 |
| 34 | 40 | 2 | 7 | 3.8 | 10.54 | 2500 | 190 | 364,364,367 | 365 | 384,385,382 | 383 | 376,381,377 | 378 |
| 35 | 40 | 2 | 30 | 3.1 | 2.45 | 2500 | 190 | 339,340,337 | 338 | 356,354,360 | 356 | 356,342,352 | 350 |
| 36 | 40 | 2 | 30 | 3.8 | 10.54 | 500 | 190 | 335,339,337 | 337 | 352,355,357 | 354 | 359,342,349 | 350 |
| 37 | 40 | 12 | 7 | 3.8 | 2.45 | 2500 | 190 | 446,448,447 | 447 | 464,469,468 | 467 | 467,453,460 | 460 |
| 38 | 40 | 12 | 7 | 3.1 | 10.54 | 500 | 190 | 316,313,310 | 313 | 333,334,324 | 330 | 326,319,333 | 326 |
| 39 | 40 | 12 | 30 | 3.1 | 2.45 | 500 | 190 | 390,386,385 | 387 | 408,408,404 | 406 | 396,405,399 | 400 |
| 40 | 40 | 12 | 30 | 3.8 | 10.54 | 2500 | 190 | 263,266,267 | 265 | 281,283,285 | 283 | 274,268,289 | 277 |
| 41 | 60 | 2 | 7 | 3.1 | 2.45 | 2500 | 190 | 387,385,383 | 385 | 401,405,414 | 406 | 406,397,400 | 401 |
| 42 | 60 | 2 | 7 | 3.8 | 10.54 | 500 | 190 | 370,374,367 | 370 | 393,392,391 | 392 | 395,381,388 | 388 |
| 43 | 60 | 2 | 30 | 3.1 | 2.45 | 500 | 190 | 330,325,329 | 328 | 350,351,349 | 350 | 339,350,343 | 344 |
| 44 | 60 | 2 | 30 | 3.8 | 10.54 | 2500 | 190 | 234,230,226 | 230 | 256,252,249 | 252 | 249,240,252 | 247 |
| 45 | 60 | 12 | 7 | 3.8 | 2.45 | 500 | 190 | 474,471,470 | 471 | 492,496,497 | 495 | 487,492,488 | 489 |
| 46 | 60 | 12 | 7 | 3.1 | 10.54 | 2500 | 190 | 225,228,222 | 225 | 246,248,246 | 246 | 245,238,240 | 241 |
| 47 | 60 | 12 | 30 | 3.1 | 2.45 | 2500 | 190 | 460,464,466 | 463 | 486,485,483 | 484 | 485,476,479 | 480 |
| 48 | 60 | 12 | 30 | 3.8 | 10.54 | 500 | 190 | 233,229,226 | 229 | 251,248,250 | 249 | 249,240,249 | 246 |
| 49 | 60 | 2 | 7 | 3.1 | 2.45 | 500 | 215 | 320,325,318 | 321 | 349,352,349 | 350 | 343,338,339 | 340 |
| 50 | 60 | 2 | 7 | 3.8 | 10.54 | 2500 | 215 | 410,419,413 | 414 | 440,447,439 | 442 | 430,433,439 | 434 |
| 51 | 60 | 2 | 30 | 3.1 | 2.45 | 2500 | 215 | 370,373,373 | 372 | 406,399,395 | 400 | 394,387,389 | 390 |
| 52 | 60 | 2 | 30 | 3.8 | 10.54 | 500 | 215 | 380,373,381 | 378 | 400,397,417 | 404 | 396,399,399 | 398 |
| 53 | 60 | 12 | 7 | 3.8 | 2.45 | 2500 | 215 | 515,518,521 | 518 | 547,542,558 | 549 | 539,542,536 | 539 |
| 54 | 60 | 12 | 7 | 3.1 | 10.54 | 500 | 215 | 342,349,335 | 342 | 362,369,374 | 368 | 360,365,361 | 362 |
| 55 | 60 | 12 | 30 | 3.1 | 2.45 | 500 | 215 | 389,395,407 | 397 | 419,427,434 | 426 | 413,419,419 | 417 |
| 56 | 60 | 12 | 30 | 3.8 | 10.54 | 2500 | 215 | 263,269,254 | 262 | 293,288,286 | 289 | 284,277,279 | 280 |
| 57 | 80 | 2 | 7 | 3.1 | 2.45 | 2500 | 215 | 340,337,328 | 335 | 369,366,369 | 368 | 364,358,358 | 360 |
| 58 | 80 | 2 | 7 | 3.8 | 10.54 | 500 | 215 | 330,339,330 | 333 | 361,365,370 | 365 | 363,359,358 | 360 |
| 59 | 80 | 2 | 30 | 3.1 | 2.45 | 500 | 215 | 345,348,342 | 345 | 372,379,385 | 378 | 367,374,369 | 370 |
| 60 | 80 | 2 | 30 | 3.8 | 10.54 | 2500 | 215 | 226,220,226 | 224 | 259,258,255 | 257 | 252,248,250 | 250 |
| 61 | 80 | 12 | 7 | 3.8 | 2.45 | 500 | 215 | 508,516,509 | 511 | 543,547,550 | 546 | 536,541,537 | 538 |
| 62 | 80 | 12 | 7 | 3.1 | 10.54 | 2500 | 215 | 325,329,321 | 325 | 353,359,362 | 358 | 352,346,352 | 350 |
| 63 | 80 | 12 | 30 | 3.1 | 2.45 | 2500 | 215 | 510,518,520 | 516 | 546,549,551 | 548 | 544,539,543 | 542 |
| 64 | 80 | 12 | 30 | 3.8 | 10.54 | 500 | 215 | 228,221,223 | 224 | 251,257,256 | 254 | 253,247,250 | 250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dodun, O.; Slătineanu, L.; Nagîț, G.; Hrițuc, A.; Mihalache, A.M.; Beșliu-Băncescu, I. WEDM-Generated Slot Width Variation Modeling. Micromachines 2022, 13, 1231. https://doi.org/10.3390/mi13081231
Dodun O, Slătineanu L, Nagîț G, Hrițuc A, Mihalache AM, Beșliu-Băncescu I. WEDM-Generated Slot Width Variation Modeling. Micromachines. 2022; 13(8):1231. https://doi.org/10.3390/mi13081231
Chicago/Turabian StyleDodun, Oana, Laurențiu Slătineanu, Gheorghe Nagîț, Adelina Hrițuc, Andrei Marius Mihalache, and Irina Beșliu-Băncescu. 2022. "WEDM-Generated Slot Width Variation Modeling" Micromachines 13, no. 8: 1231. https://doi.org/10.3390/mi13081231
APA StyleDodun, O., Slătineanu, L., Nagîț, G., Hrițuc, A., Mihalache, A. M., & Beșliu-Băncescu, I. (2022). WEDM-Generated Slot Width Variation Modeling. Micromachines, 13(8), 1231. https://doi.org/10.3390/mi13081231







