Performance Analysis of a CSFH-Based Microgripper: Analytical Modeling and Simulation
Abstract
:1. Introduction
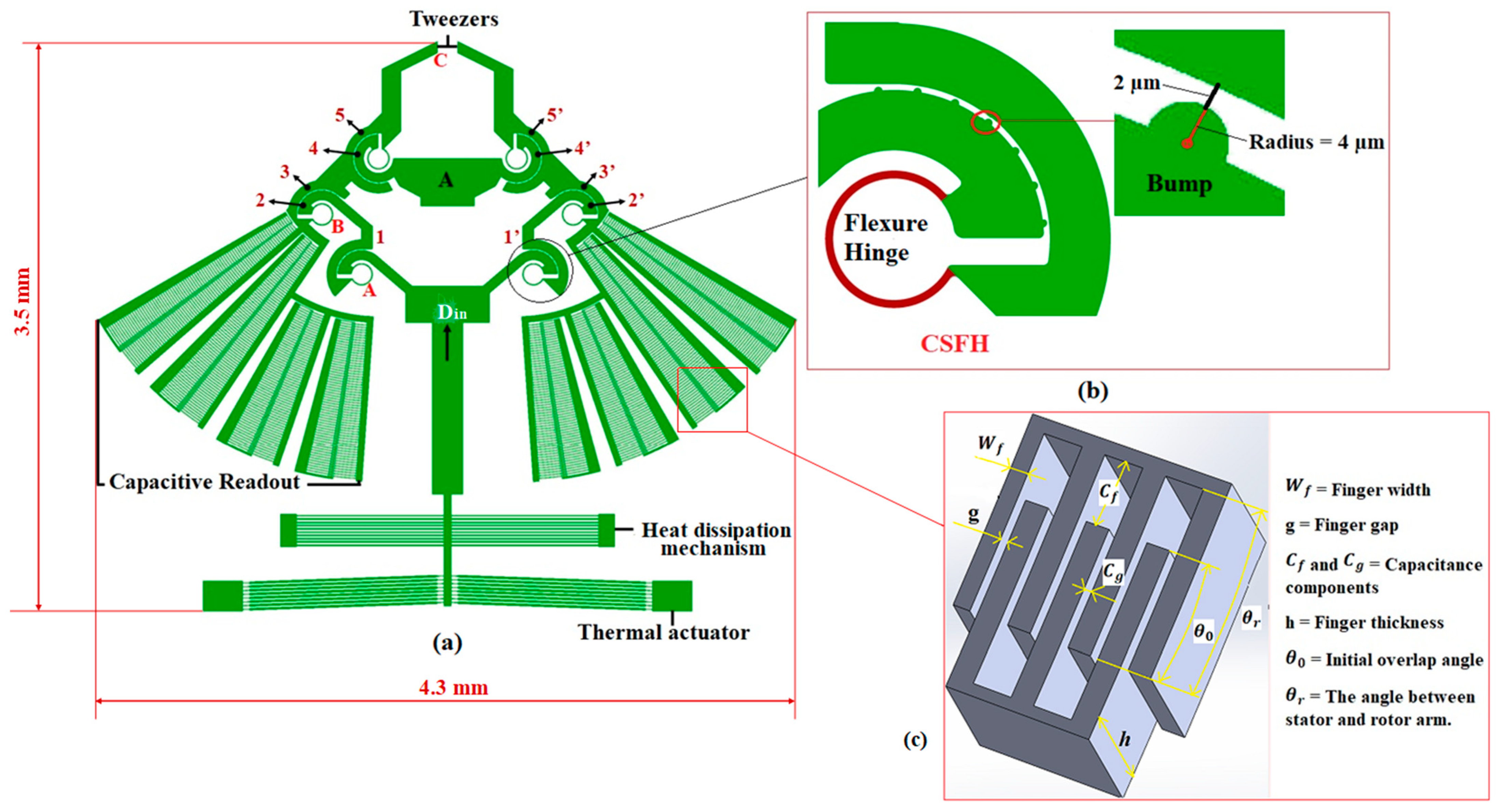
2. Overall Design of the Microgripper
2.1. Working Principle of the Microgripper
2.2. Modeling of the Microgripper
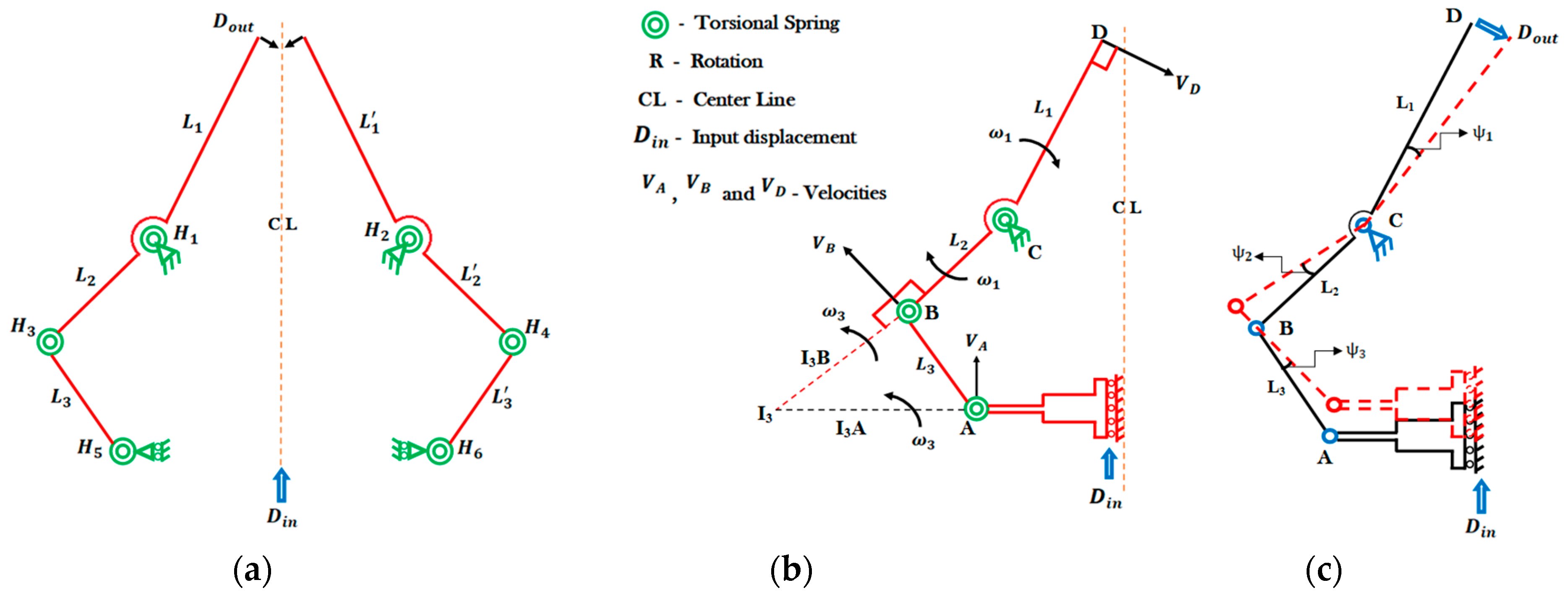
2.2.1. Kinematic Modeling
2.2.2. Input Stiffness of the Microgripper
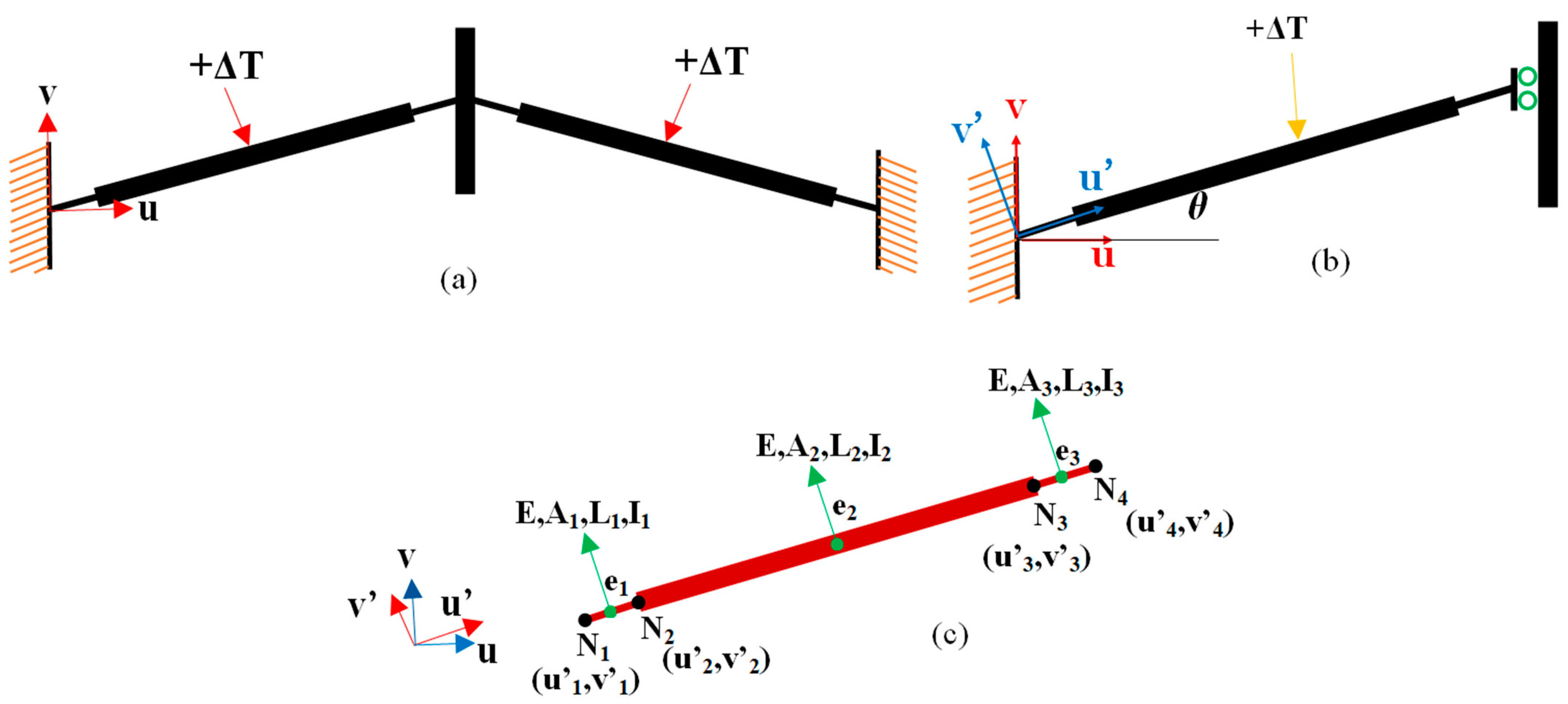
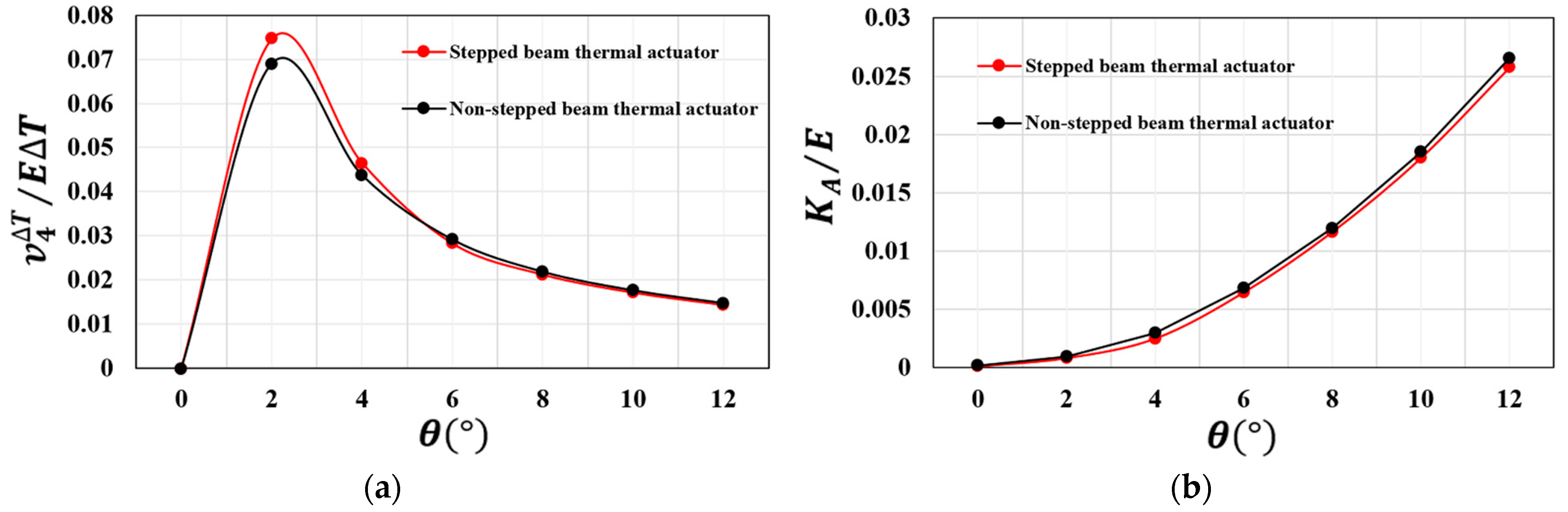
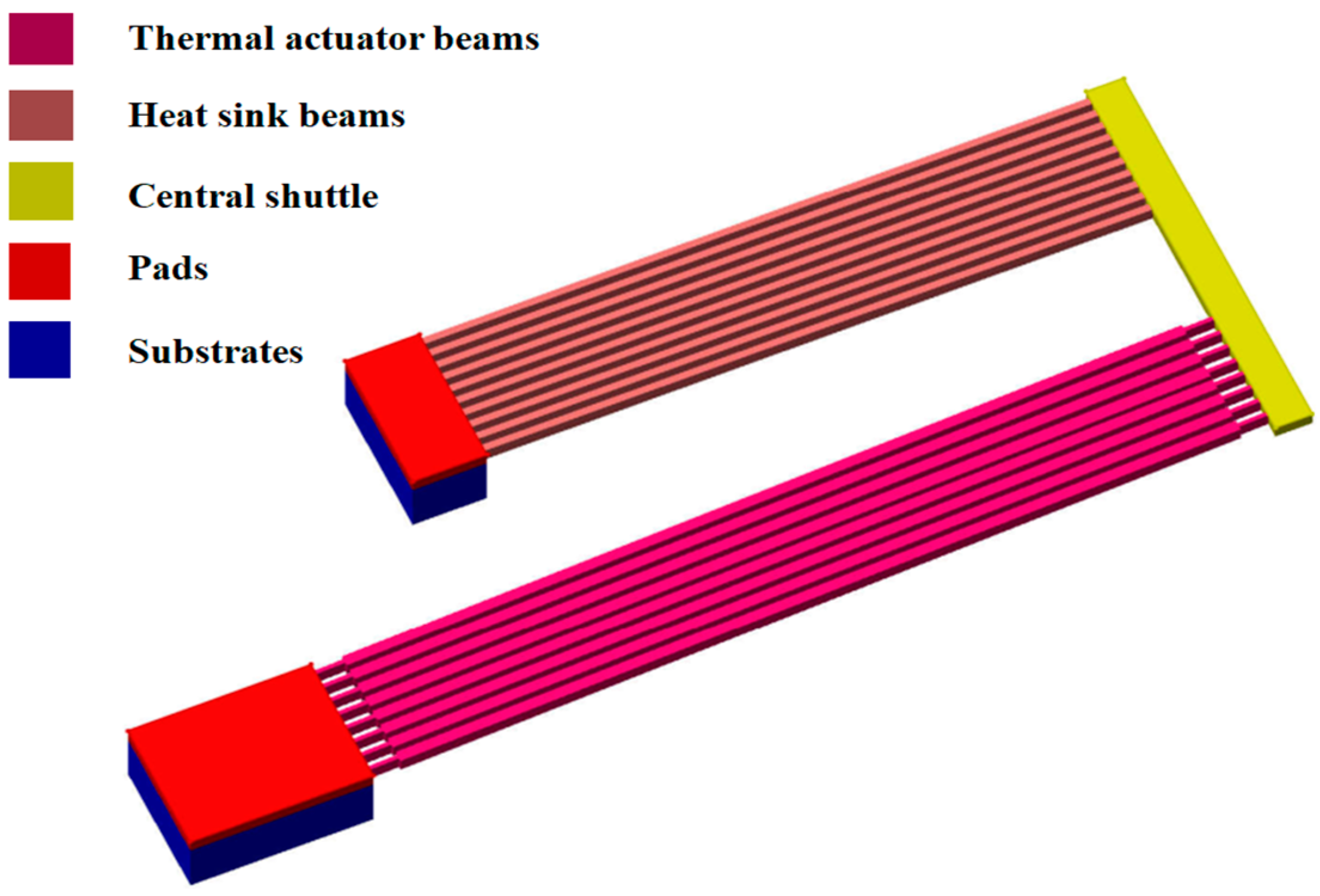
2.3. Analytical Modeling of V-Shaped Thermal Actuator and Heat Sink Beams
- Input displacement of ~39 µm to achieve the desired output displacement of each tweezer (52.5 µm).
- Ambient temperature (22 °C) at the tweezer region.
2.4. Comparison between the Performances of the Microgripper, the Electrothermal Actuator, and the Heat Dissipation Mechanism Obtained from the Analytical Modeling and Simulations
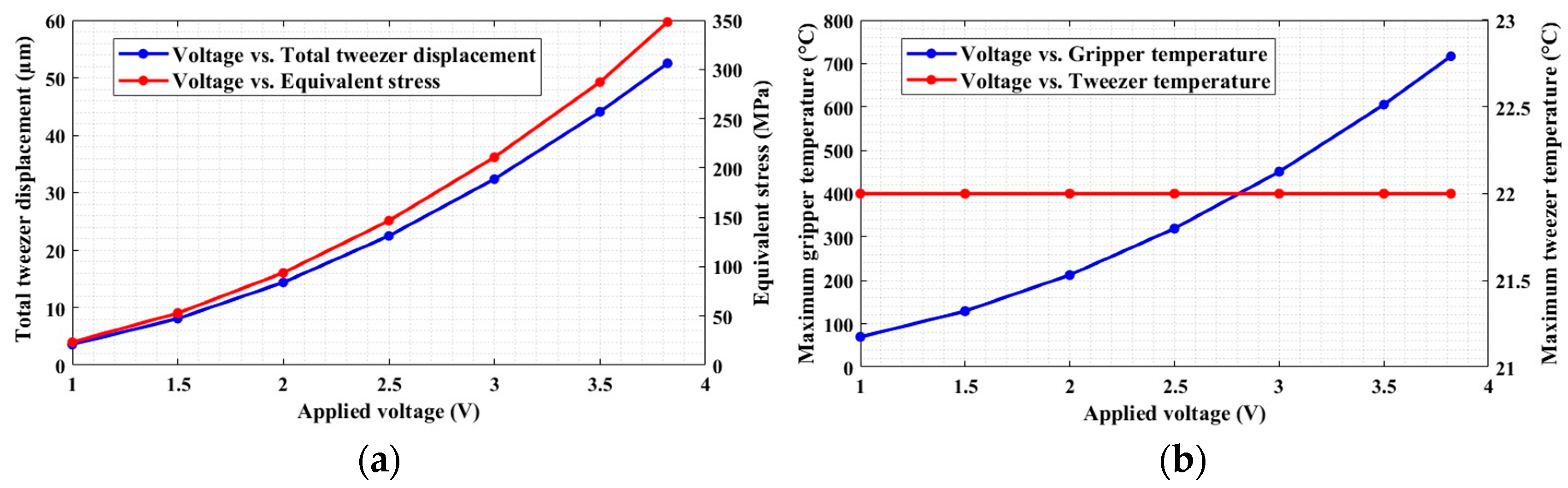
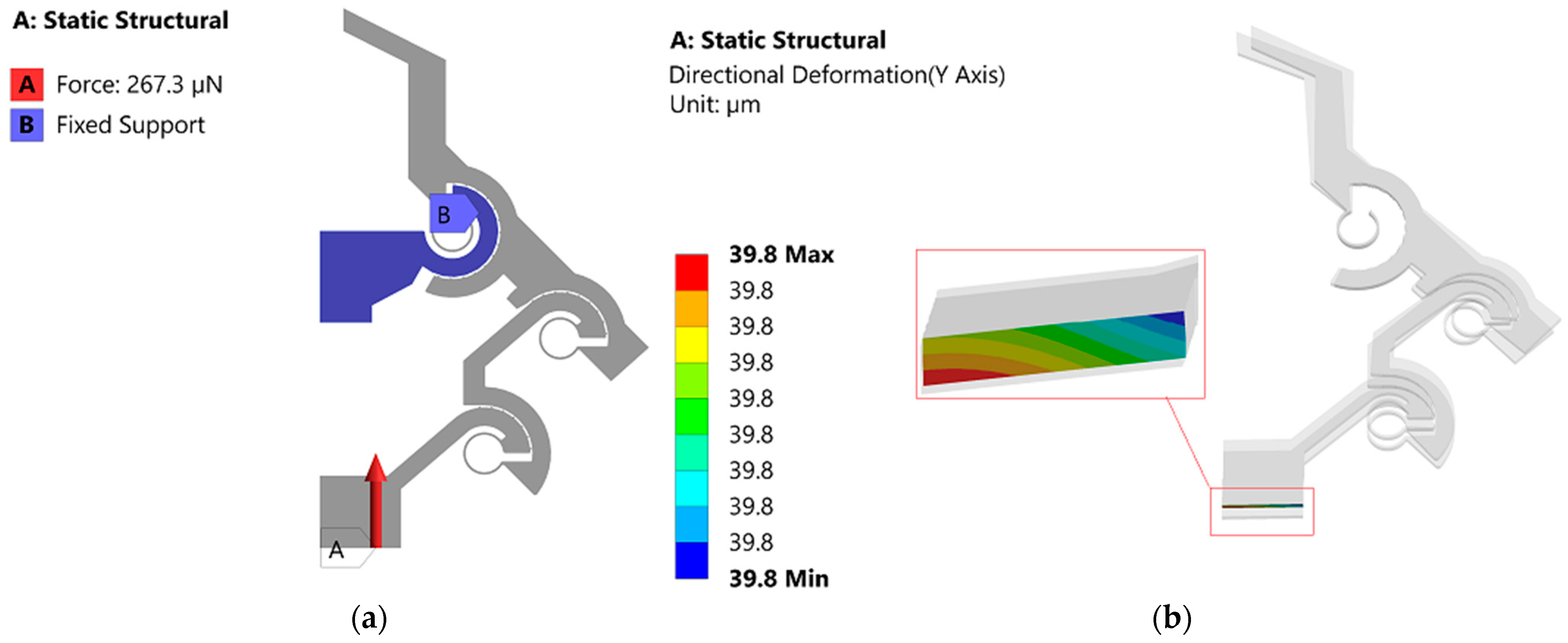
2.4.1. Microgripper’s Deformation and Stress
2.4.2. Microgripper Stiffness
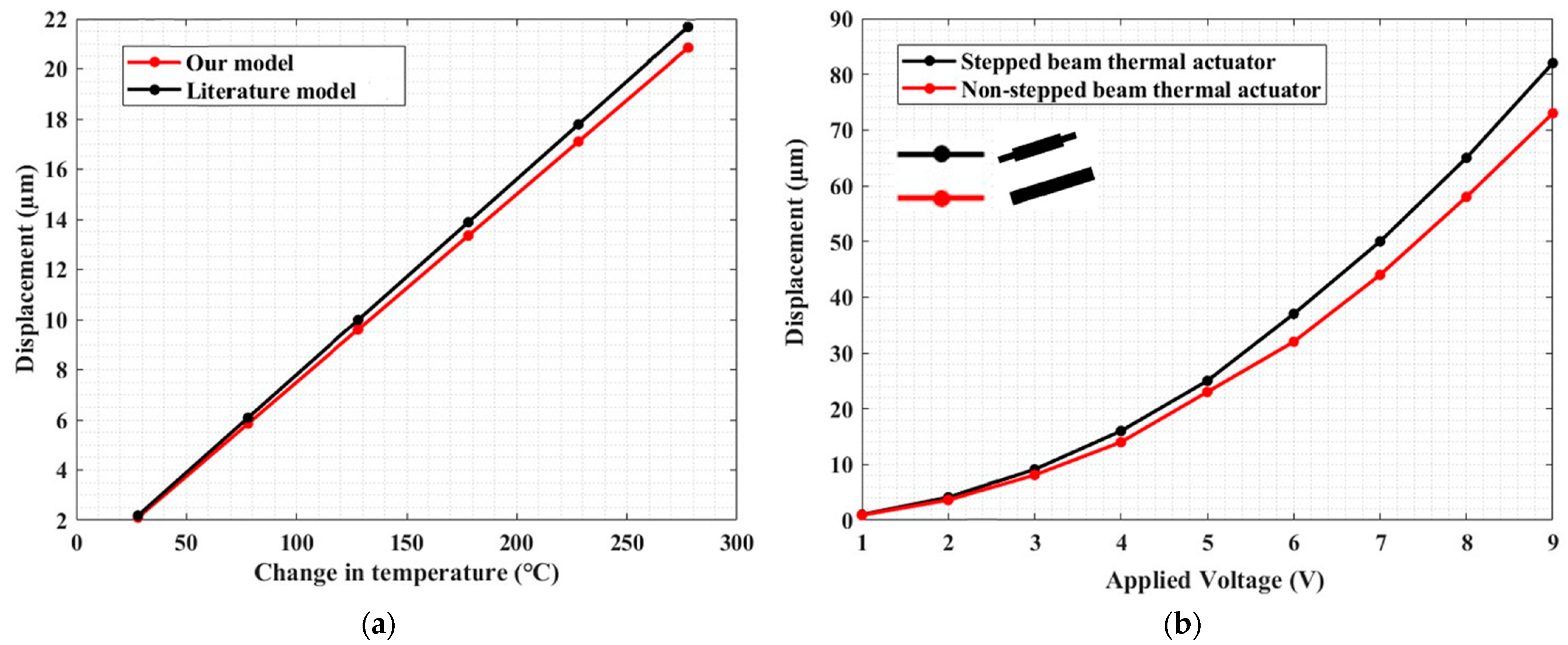
2.4.3. Electrothermal Actuator
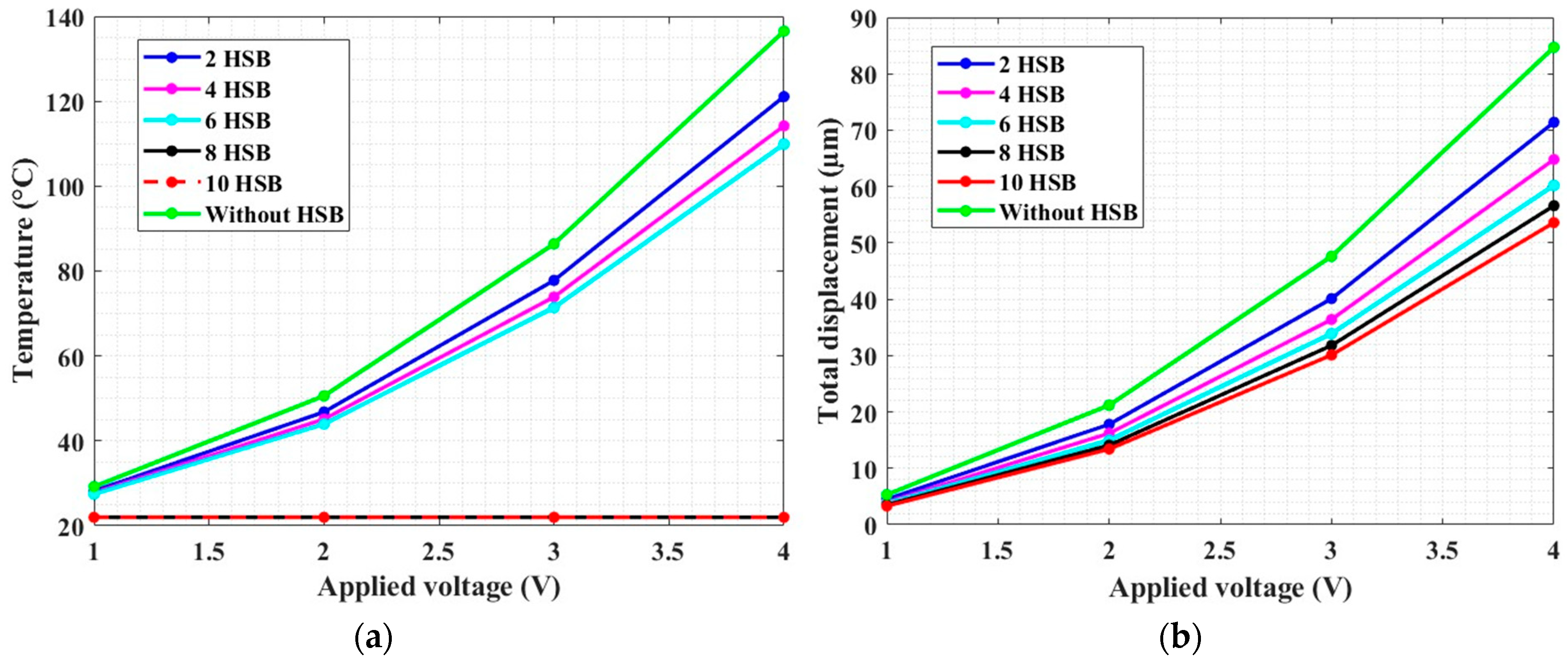
2.4.4. Thermomechanical Actuation and Heat Dissipation Mechanism
3. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
- 1.
- Computation of the elastic stiffness matrix in a local reference frame (), as shown in Figure 7.
- 2.
- Transformation of the local stiffness matrix to global stiffness matrix by means of a rotation matrix.
- 3.
- Assembly of the element matrices.
- 4.
- Boundary conditions.
- 5.
- Imposition of boundary conditions in the global matrix (A14) to find the displacement at node 4, and the global matrix is simplified as follows:
References
- Luo, T.; Fan, L.; Zhu, R.; Sun, D. Microfluidic single-cell manipulation and analysis: Methods and applications. Micromachines 2019, 10, 104. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Mechanical Structure. J. Mech. Des. 2017, 139, 060801. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Q. A review on actuation and sensing techniques for MEMS-based microgrippers. J. Micro-Bio Robot. 2017, 13, 1–14. [Google Scholar] [CrossRef]
- Xu, Q. Design, Fabrication, and Testing of an MEMS Microgripper with Dual-Axis Force Sensor. IEEE Sens. J. 2015, 15, 6017–6026. [Google Scholar] [CrossRef]
- Chronis, N.; Lee, L.P. Electrothermally activated SU-8 microgripper for single cell manipulation in solution. J. Microelectromech. Syst. 2005, 14, 857–863. [Google Scholar] [CrossRef]
- Hao, Y.; Cheng, S.; Tanaka, Y.; Hosokawa, Y.; Yalikun, Y.; Li, M. Mechanical properties of single cells: Measurement methods and applications. Biotechnol. Adv. 2020, 45, 107648. [Google Scholar] [CrossRef]
- Fu, Y.; Luo, J.; Flewitt, A.; Milne, W. Smart Microgrippers for BioMEMS Applications. In MEMS for Biomedical Applications; Shekhar, B., Abhay, V., Eds.; Woodhead: Cambridge, UK, 2012; pp. 291–336. [Google Scholar] [CrossRef]
- Lyu, Z.; Xu, Q. Recent design and development of piezoelectric-actuated compliant microgrippers: A review. Sens. Actuators A Phys. 2021, 331, 113002. [Google Scholar] [CrossRef]
- Dochshanov, A.; Verotti, M.; Belfiore, N.P. A Comprehensive Survey on Microgrippers Design: Operational Strategy. J. Mech. Des. 2017, 139, 070801. [Google Scholar] [CrossRef]
- Lin, F.Z.; Zai, F.Z.; Mu, Z.M.; Meng, J.L.; Qing, A.H. An efficient electro-thermo-mechanical model for the analysis of V-shaped thermal actuator connected with driven structures. Int. J. Numer. Model. Electron. Netw. Devices Fields 2020, 10, 1–14. [Google Scholar] [CrossRef]
- Pantano, M.; Bernal, R.; Pagnotta, L.; Espinosa, H.D. Multiphysics design and implementation of a microsystem for displacement-controlled tensile testing of nanomaterials. Meccanica 2015, 50, 549–560. [Google Scholar] [CrossRef]
- Kommanaboina, N.M.; Pantano, M.F.; Bagolini, A. Optimization of an amplification mechanism enabling large displacements in MEMS-based nanomaterial testing devices. Micro Nano Eng. 2022, 15, 100131. [Google Scholar] [CrossRef]
- Yallew, T.S.; Pantano, M.F.; Bagolini, A. Design and Finite Element Analysis of an Electrothermally Actuated Microgripper for Biomedical Applications. In Proceedings of the 2021 Symposium on Design, Test, Integration & Packaging of MEMS and MOEMS (DTIP), Paris, France, 25–27 August 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Potekhina, A.; Wang, C. Review of Electrothermal Actuators and Applications. Actuators 2019, 8, 69. [Google Scholar] [CrossRef]
- Iqbal, S.; Shakoor, R.I.; Gilani, H.N.; Abbas, H.; Malik, A.M. Performance Analysis of Microelectromechanical System Based Displacement Amplification Mechanism. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 507–528. [Google Scholar] [CrossRef]
- Pei, X.; Yu, J.; Zong, G.; Bi, S.; Su, H. The modeling of cartwheel flexural hinges. Mech. Mach. Theory 2009, 44, 1900–1909. [Google Scholar] [CrossRef]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. Compliance Synthesis of CSFH MEMS-Based Microgrippers. J. Mech. Des. 2017, 139, 022301. [Google Scholar] [CrossRef]
- Verotti, M.; Crescenzi, R.; Balucani, M.; Belfiore, N.P. MEMS-Based Conjugate Surfaces Flexure Hinge. J. Mech. Des. 2015, 137, 012301. [Google Scholar] [CrossRef]
- Zou, L.; Ge, C.; Wang, Z.J.; Cretu, E.; Li, X. Novel Tactile Sensor Technology and Smart Tactile Sensing Systems: A Review. Sensors 2017, 17, 2653. [Google Scholar] [CrossRef] [PubMed]
- Goldfarb, M.; Celanovic, N.; Engineering, M.; Station, B. A flexure-based gripper for small-scale manipulation. Robotica 1999, 17, 181–187. [Google Scholar] [CrossRef] [Green Version]
- Zubir, M.N.M.; Shirinzadeh, B. Development of a high precision flexure-based microgripper. Precis. Eng. 2009, 33, 362–370. [Google Scholar] [CrossRef]
- Bhagat, U.; Shirinzadeh, B.; Clark, L.; Chea, P.; Qin, Y.; Tian, Y.; Zhang, D. Design and analysis of a novel flexure-based 3-DOF mechanism. Mech. Mach. Theory 2013, 74, 173–187. [Google Scholar] [CrossRef]
- Xu, Q. A new compliant microgripper with integrated position and force sensing. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics: Mechatronics for Human Wellbeing, AIM 2013, Wollongong, NSW, Australia, 9–12 July 2013; pp. 591–596. [Google Scholar] [CrossRef]
- Sun, X.; Chen, W.; Tian, Y.; Fatikow, S.; Zhou, R.; Zhang, J.; Mikczinski, M. A novel flexure-based microgripper with double amplification mechanisms for micro/nano manipulation. Rev. Sci. Instrum. 2013, 84, 085002. [Google Scholar] [CrossRef] [PubMed]
- Khushboo, S.; Suhas, S.J. Design and development of compliant microgripper-based assembly station. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016; pp. 1–8. [Google Scholar]
- Zhang, W.-M.; Meng, G.; Chen, D. Stability, Nonlinearity and Reliability of Electrostatically Actuated MEMS Devices. Sensors 2007, 7, 760–796. [Google Scholar] [CrossRef]
- Sameoto, D.; Hubbard, T.; Kujath, M. Operation of electrothermal and electrostatic MUMPs microactuators underwater. J. Micromech. Microeng. 2004, 14, 1359–1366. [Google Scholar] [CrossRef]
- Abbas, M.Z.; Umar Masood, M.; Saleem, M.M.; Fahad Sheikh, M. Design of an Electrothermally Actuated SU-8 Based Microgripper for Biomedical Applications. In Proceedings of the 2018 3rd Asia-Pacific Conference on Intelligent Robot Systems, ACIRS 2018, Singapore, 21–23 July 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 97–102. [Google Scholar]
- Buzzin, A.; Cupo, S.; Giovine, E.; De Cesare, G.; Belfiore, N.P. Compliant Nano-Pliers as a Biomedical Tool at the Nanoscale: Design, Simulation and Fabrication. Micromachines 2020, 11, 1087. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, D.; Xu, D.; Zhang, Z. A kinematics modeling and stress analysis method for flexible micro-gripper. In Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation, ICMA 2012, Chengdu, China, 5–8 August 2012; pp. 825–830. [Google Scholar] [CrossRef]
- Sun, X.; Chen, W.; Fatikow, S.; Tian, Y.; Zhou, R.; Zhang, J.; Mikczinski, M. A novel piezo-driven microgripper with a large jaw displacement. Microsyst. Technol. 2014, 21, 931–942. [Google Scholar] [CrossRef]
- Lobontiu, N.; Garcia, E. Analytical model of displacement amplification and stiffness optimization for a class of flexure-based compliant mechanisms. Comput. Struct. 2003, 81, 2797–2810. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Tian, Y.; Zhao, X.; Zhang, H.; Cui, L.; Zhang, D.; Ferreira, P. A novel monolithic piezoelectric actuated flexure-mechanism based wire clamp for microelectronic device packaging. Rev. Sci. Instrum. 2015, 86, 045106. [Google Scholar] [CrossRef]
- Crescenzi, R.; Balucani, M.; Belfiore, N.P. Operational characterization of CSFH MEMS technology based hinges. J. Micromech. Microeng. 2018, 28, 055012. [Google Scholar] [CrossRef]
- Yang, Y.-L.; Wei, Y.-D.; Lou, J.-Q.; Tian, G.; Zhao, X.-W.; Fu, L. A new piezo-driven microgripper based on the double-rocker mechanism. Smart Mater. Struct. 2015, 24, 1–11. [Google Scholar] [CrossRef]
- Zhu, Y.; Corigliano, A.; Espinosa, H.D. A thermal actuator for nanoscale in situ microscopy testing: Design and characterization. J. Micromech. Microeng. 2006, 16, 242–253. [Google Scholar] [CrossRef]
- Steiner, H.; Keplinger, F.; Schalko, J.; Hortschitz, W.; Stifter, M. Highly Efficient Passive Thermal Micro-Actuator. J. Microelectromech. Syst. 2015, 24, 1981–1988. [Google Scholar] [CrossRef]
- Margarita, T.T.; Chablé, P.V.; Koshevaya, S.; Cabello-R, R.; Ocampo-D, A.; Vera-D, J.G. Design and simulation of a MEM pressure microgripper based on electrothermal microactuators. In Proceedings of the Thin Films for Solar and Energy Technology VIII, San Diego, CA, USA, 28 August–1 September 2016. [Google Scholar] [CrossRef]
- Norrie, D.H. A First Course in the Finite Element Method; Elsevier Inc.: Amsterdam, The Netherlands, 1987. [Google Scholar] [CrossRef]
- Tecpoyotl-Torres, M.; Vargas-Chable, P.; Robles-Casolco, S.; Cabello-Ruiz, R. Dynamic Analysis of a Microgripper and Its Components. Br. J. Appl. Sci. Technol. 2015, 9, 360–373. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, R.; Du, W.; Cheng, L.; Liang, G. Alkaline Phosphatase-Triggered Self-Assembly of Near-Infrared Nanoparticles for the Enhanced Photoacoustic Imaging of Tumors, 1st ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Pratt, S. Environmental Compensation on the AD7142: The Effects of Temperature and Humidity on Capacitance Sensors. 2005, pp. 1–8. Available online: https://www.analog.com/media/en/technical-documentation/application-notes/AN-829.pdf (accessed on 5 April 2022).



| Properties | Values | Properties | Values |
|---|---|---|---|
| Density | 2330 kg/m3 | Cross-Sectional Area of Beams ) | |
| Thermal expansion coefficient | Moment of inertia ) | ||
| Young’s modulus | 130.1 GPa | Length of stepped beam element–1 ) | 40 µm |
| Poisson’s ratio | 0.22 | Length of stepped beam element–2 ) | 1150 µm |
| Thermal conductivity | ) | Length of stepped beam element–3 ) | 40 µm |
| Resistivity | 0.005 Ω cm | Length of non-stepped beam ) | 1230 µm |
| Melting point | Width of main beams ) | 15 µm | |
| Reference temperature () | Width of short beams ) | 6 µm | |
| Inclined beam angle () | Thickness of beams () | 25 µm | |
| Thickness, width, and radius of flexure hinge, respectively | 25, 8, and 60 µm | Initial angle of flexure hinges () | |
| Total number of thermal actuator beams | 16 | Thickness, width, and length of heat sink beams, respectively | 25, 10, and 900 µm |
| Total number of heat sink beams | 20 |
| Geometrical Parameters | Values |
|---|---|
| Total Number of Beams | 16 |
| Pre-bending angle of beams | |
| Length of main beams | |
| Width of main beams | |
| Length of short beams | |
| Width of short beams | |
| Gap between beams | |
| Shuttle width |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yallew, T.S.; Belfiore, N.P.; Bagolini, A.; Pantano, M.F. Performance Analysis of a CSFH-Based Microgripper: Analytical Modeling and Simulation. Micromachines 2022, 13, 1391. https://doi.org/10.3390/mi13091391
Yallew TS, Belfiore NP, Bagolini A, Pantano MF. Performance Analysis of a CSFH-Based Microgripper: Analytical Modeling and Simulation. Micromachines. 2022; 13(9):1391. https://doi.org/10.3390/mi13091391
Chicago/Turabian StyleYallew, Teferi Sitotaw, Nicola Pio Belfiore, Alvise Bagolini, and Maria F. Pantano. 2022. "Performance Analysis of a CSFH-Based Microgripper: Analytical Modeling and Simulation" Micromachines 13, no. 9: 1391. https://doi.org/10.3390/mi13091391
APA StyleYallew, T. S., Belfiore, N. P., Bagolini, A., & Pantano, M. F. (2022). Performance Analysis of a CSFH-Based Microgripper: Analytical Modeling and Simulation. Micromachines, 13(9), 1391. https://doi.org/10.3390/mi13091391







