A Novel Manifold Dual-Microchannel Flow Field Structure with High-Performance Heat Dissipation
Abstract
:1. Introduction
2. Numerical Simulation of the MDMC Heat Sink
2.1. Geometrical Model of the MDMC Heat Sink
2.2. Governing Equations and Boundary Conditions
- The flow of the two flow fields do not interfere with each other, and there is no connected area inside, maintaining absolute independence.
- The flow in the two flow fields are single phase, laminar, and incompressible.
- Thermophysical properties are constant for both fluid and solid heat sink.
- Gravitational effects, viscous dissipation, and heat loss to the environment are ignored.
2.3. Heat Transfer Performance Evaluation Parameters Calculation
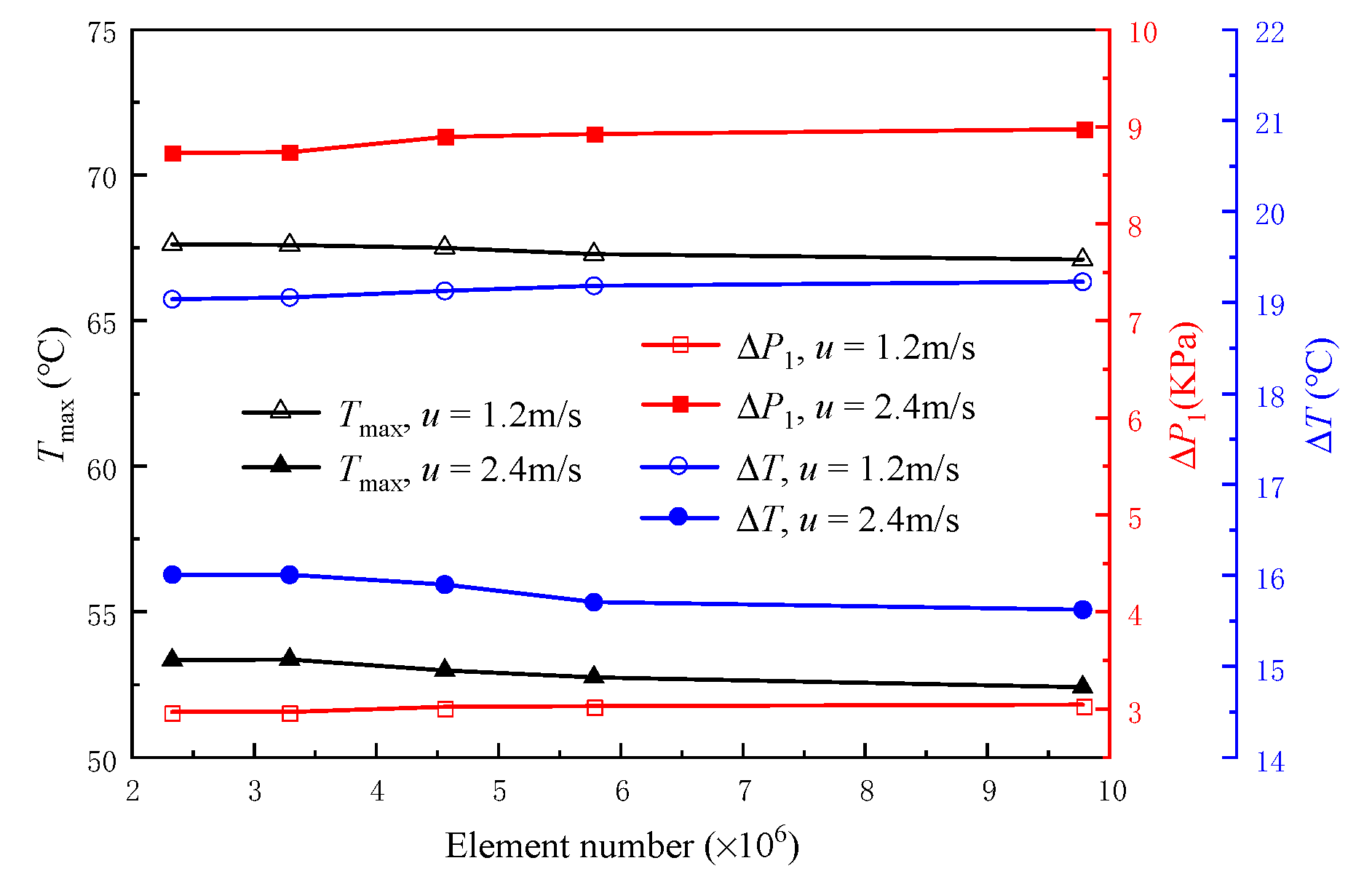
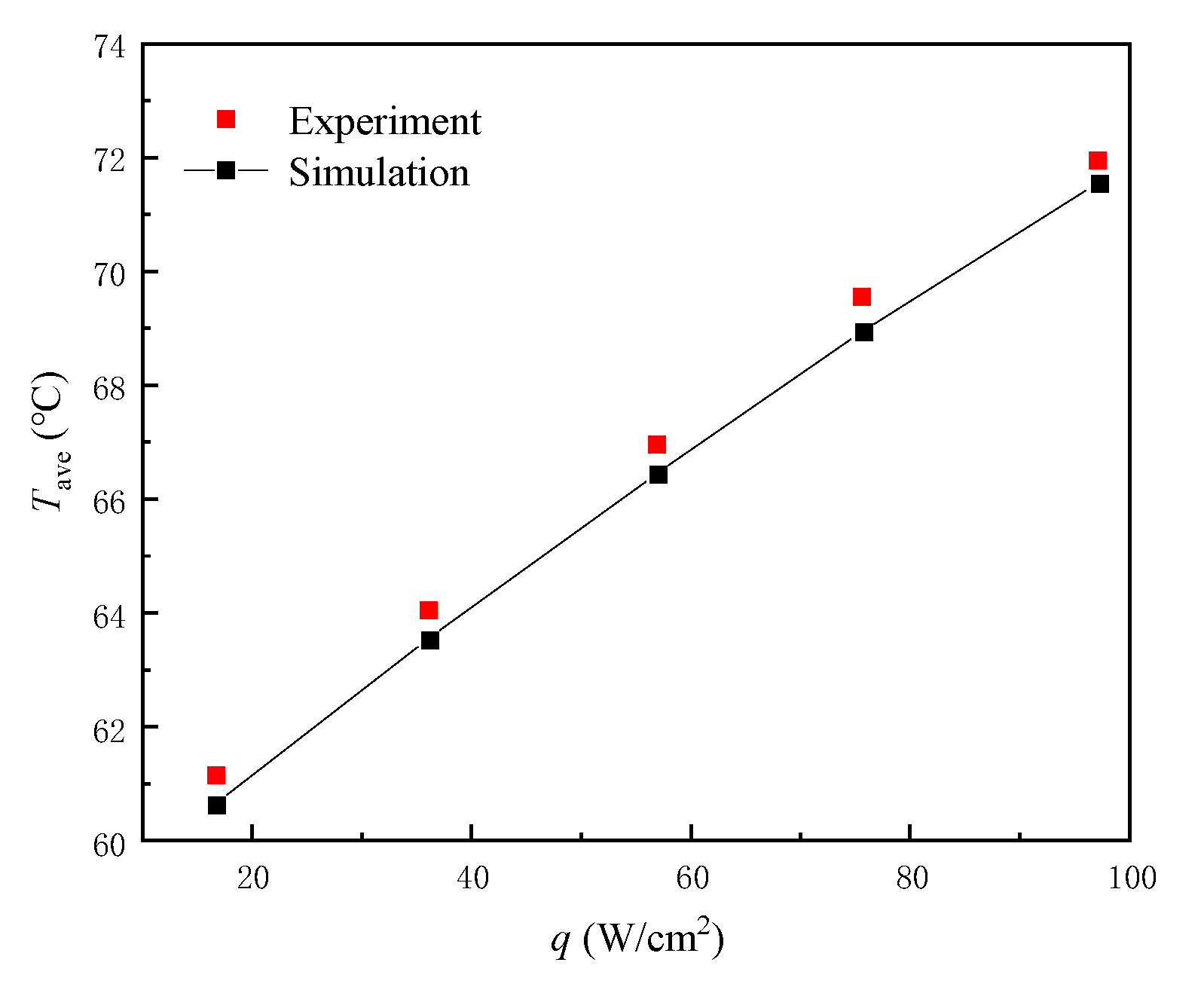
2.4. Mesh Independence and Simulation Verification
3. Simulation Results and Discussion of the MDMC Heat Sink
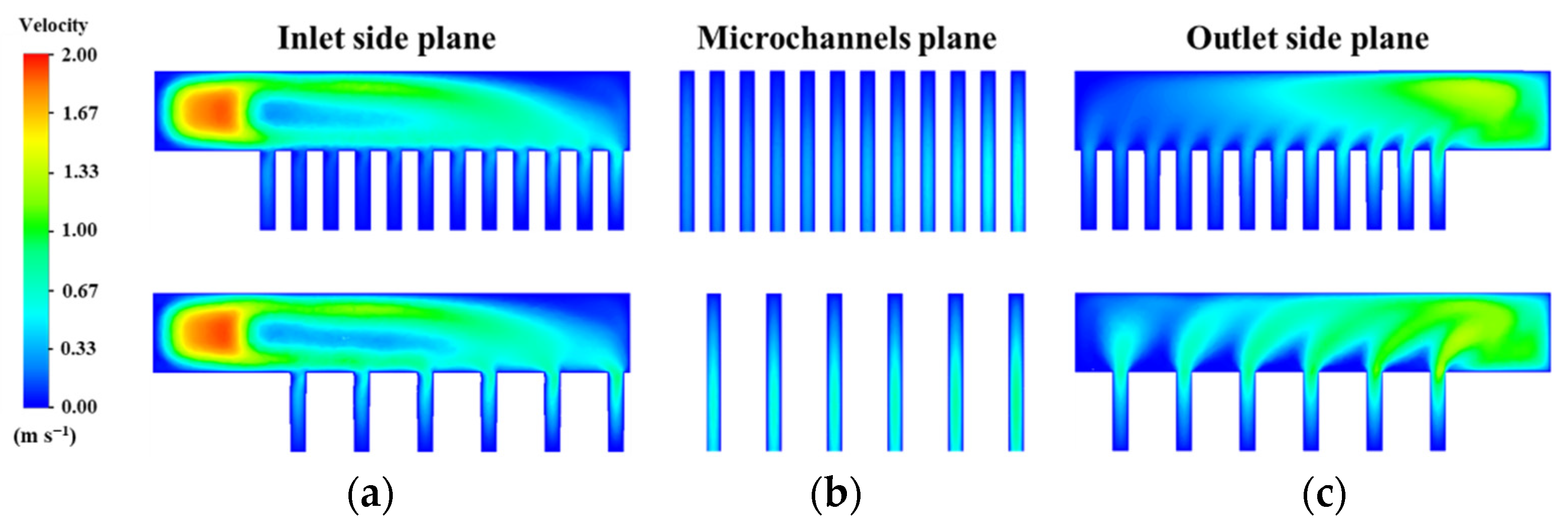
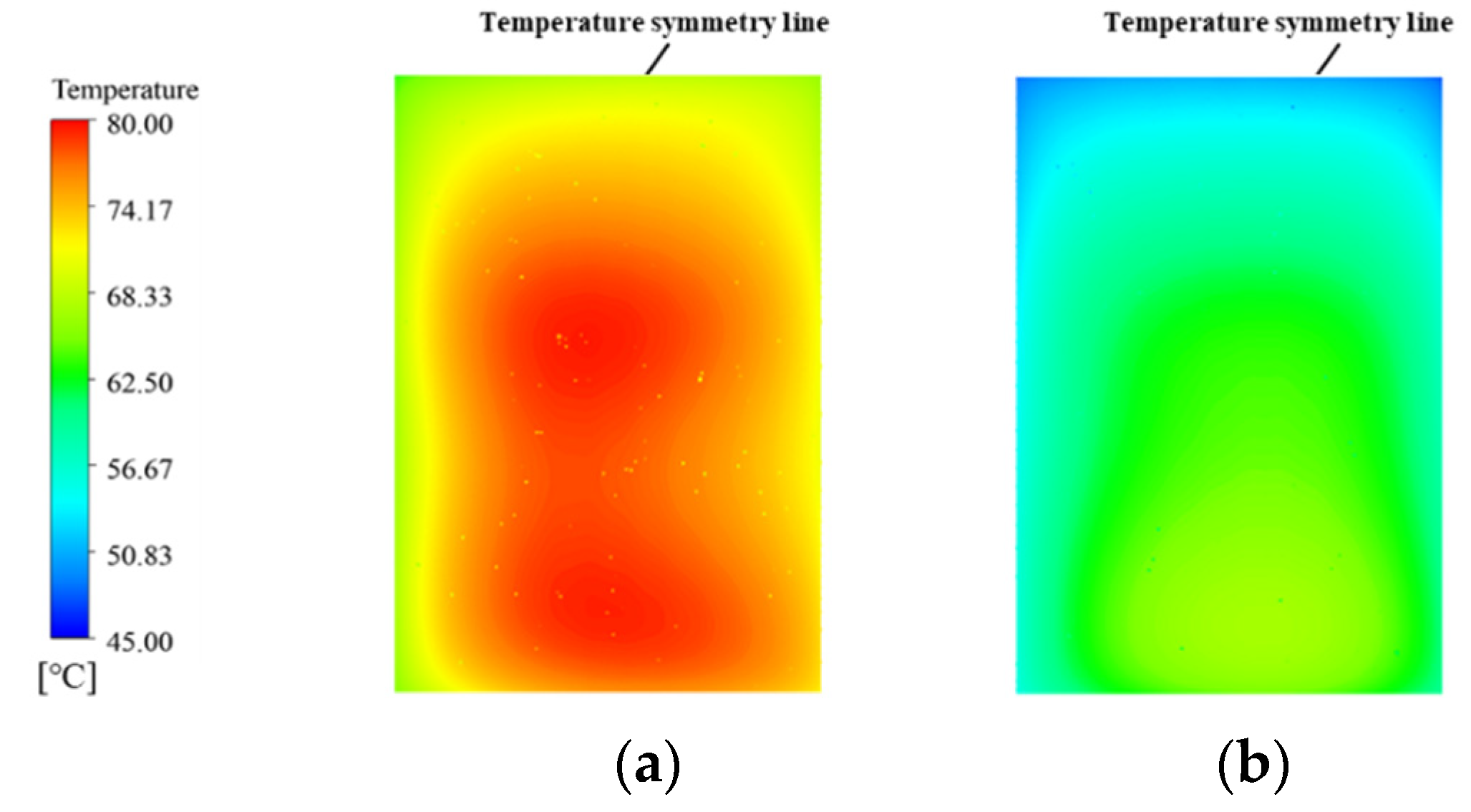
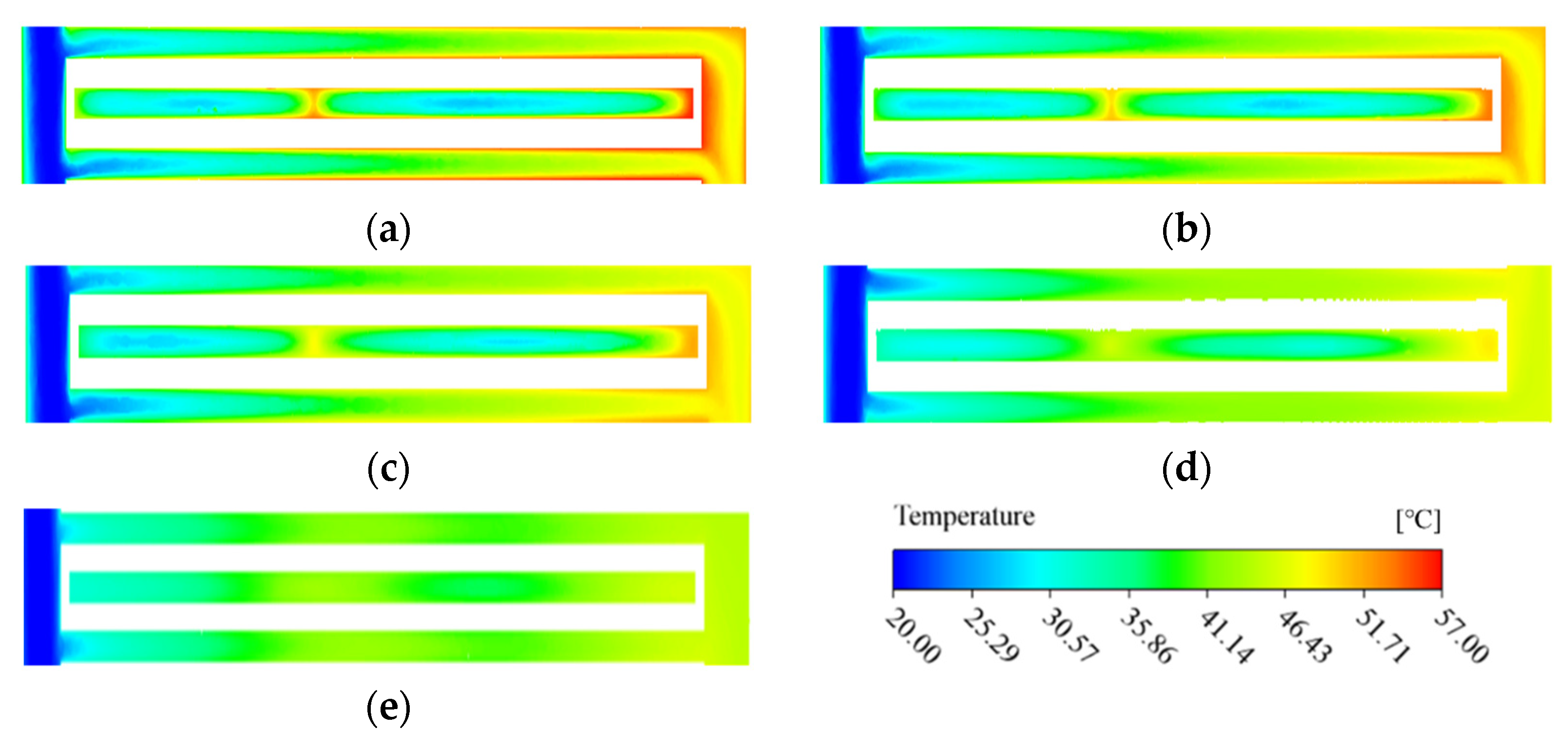
3.1. The Heat Transfer Performance Comparison of MMC and MDMC
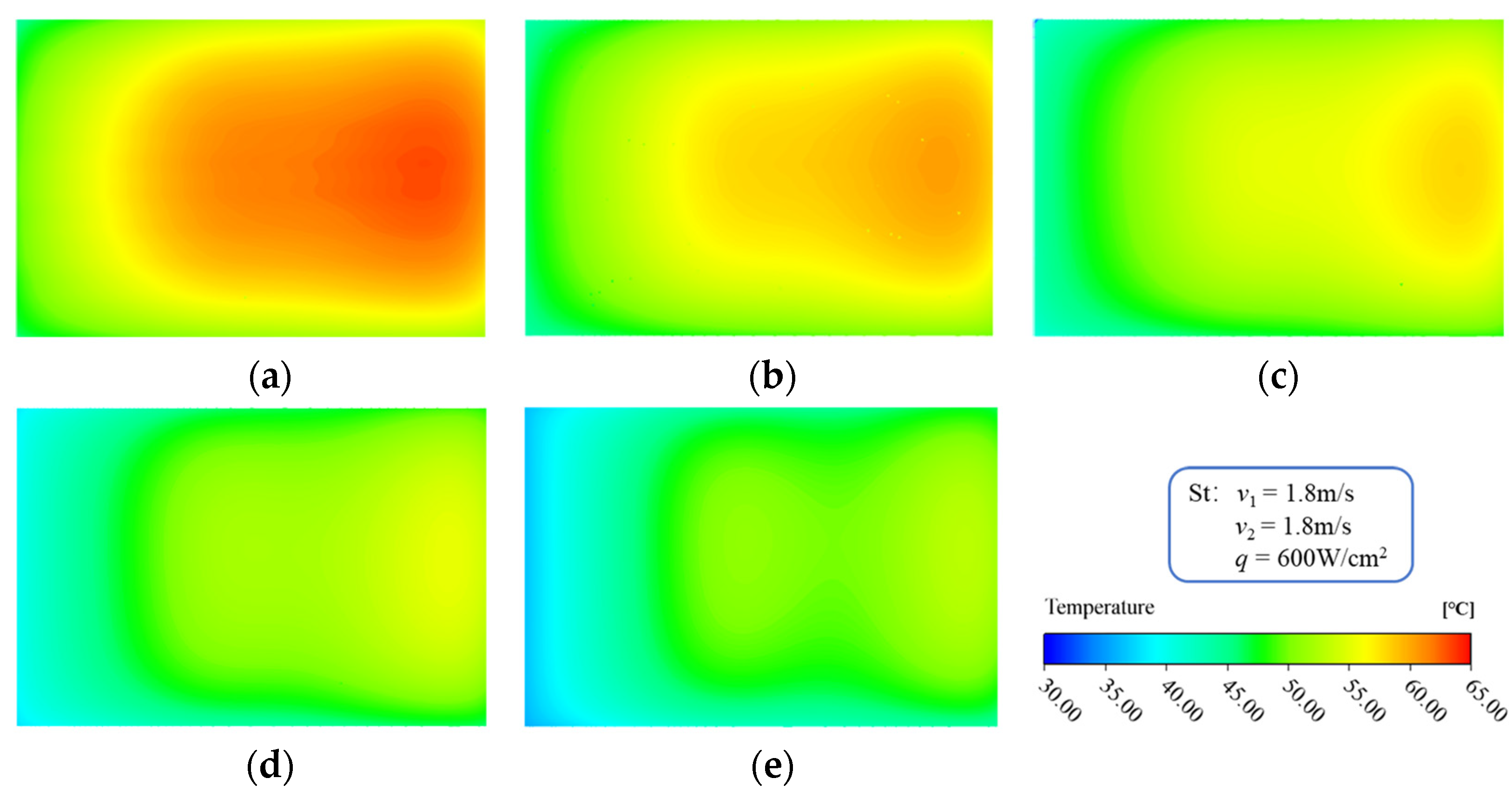
3.2. Influence of Inlet−2 Velocity on Heat Transfer Performance
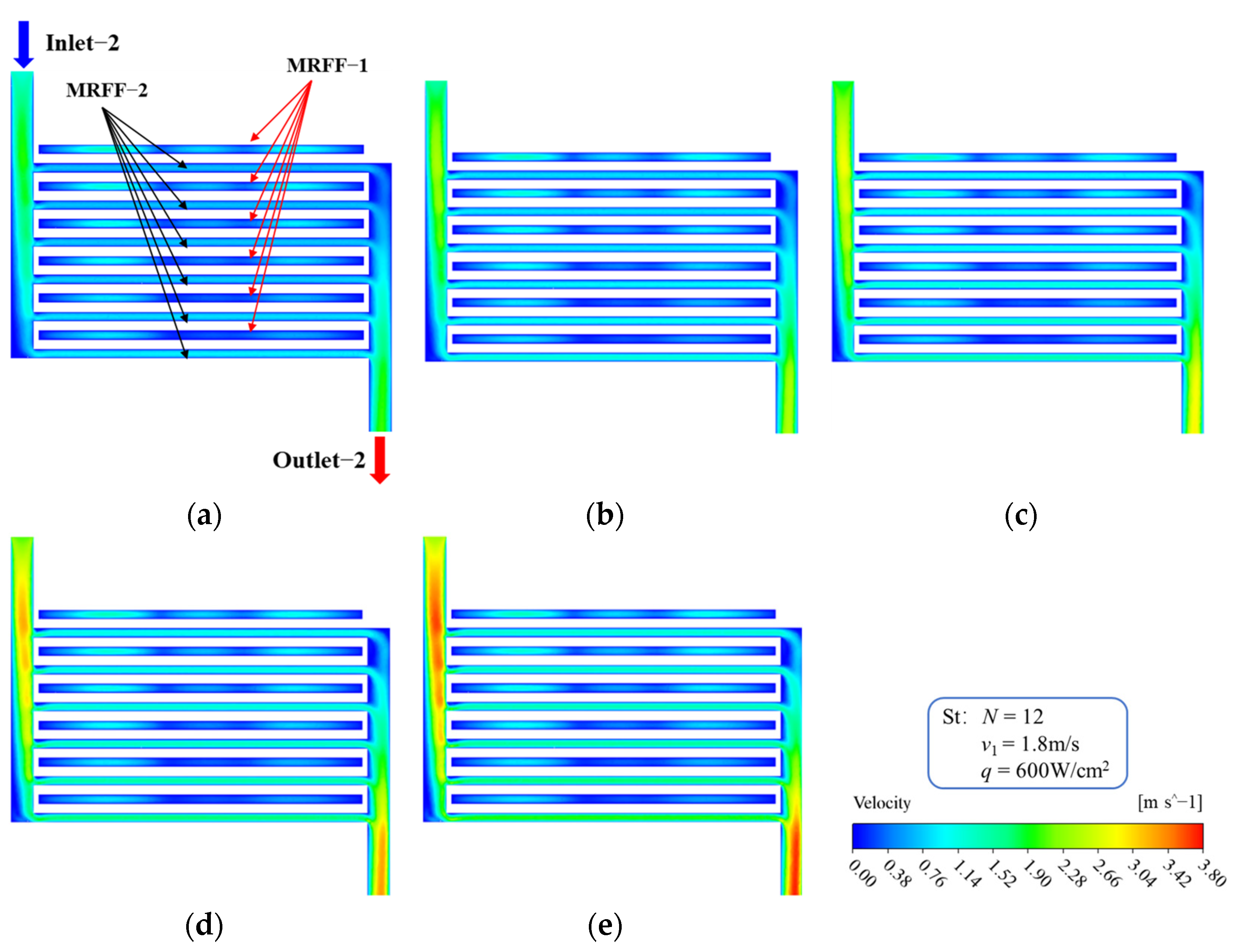
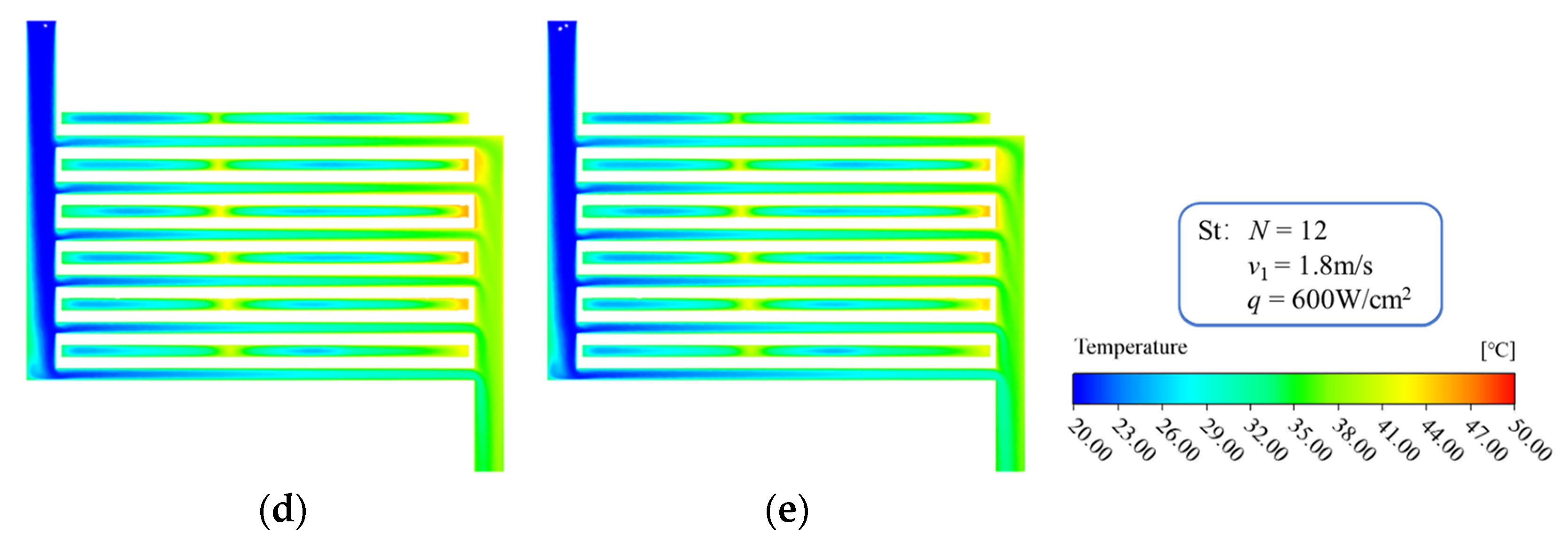
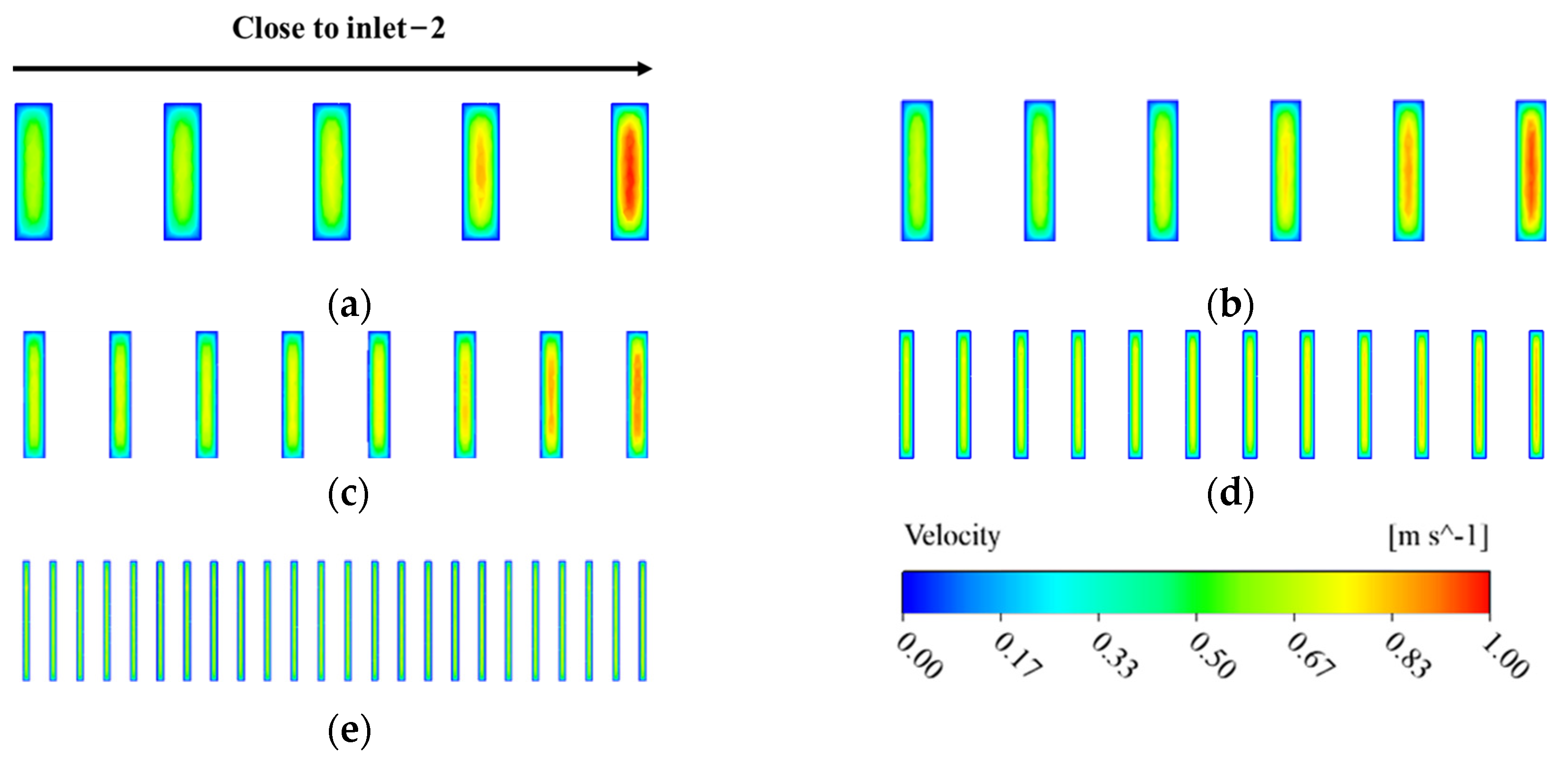
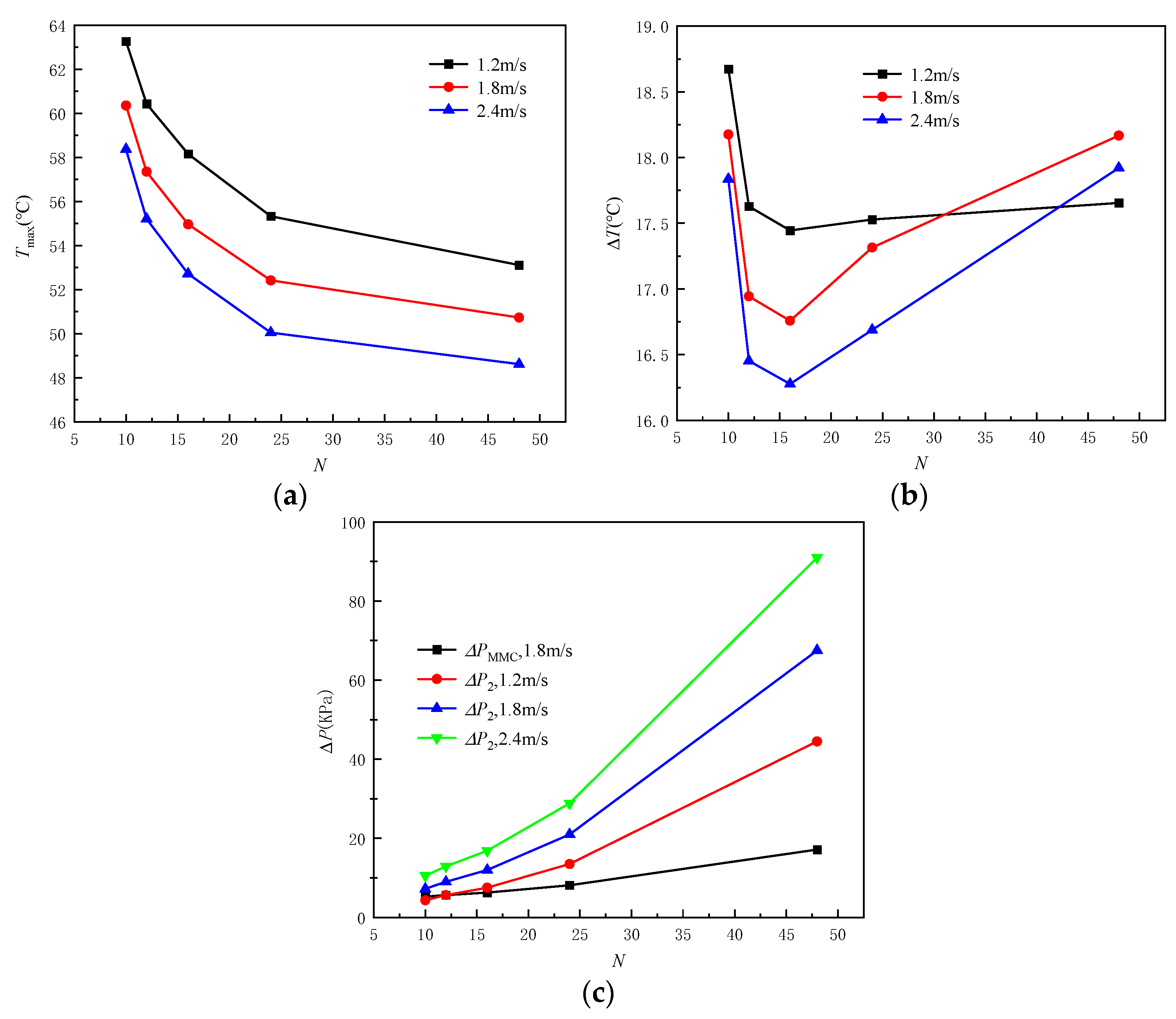
3.3. Influence of Microchannel Number on Heat Transfer Performance
4. Conclusions
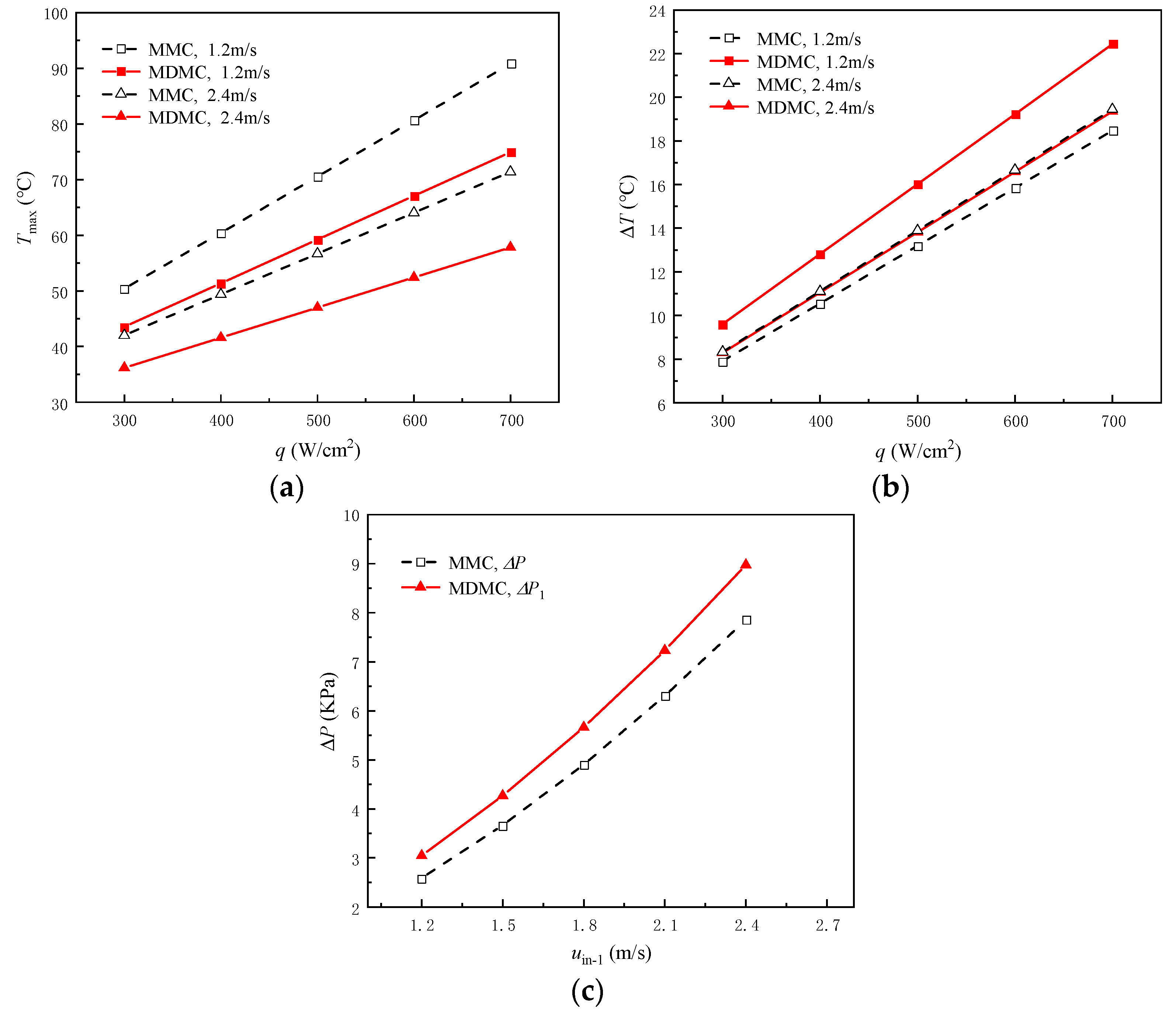
- The MDMC structure shows better heat transfer performance than the MMC structure at high flux density and large inlet−1 velocity due to the dual-microchannel flow field. With the heat flux increasing from 300 W/cm2 to 700 Wcm2, the Tmax decreases by 13.6% to 17.5% when inlet−1 velocity is 1.2 m/s, and by 13.8% to 19% when inlet−1 velocity is 2.4 m/s.
- The Tmax and ΔT decrease with increasing inlet−2 velocity. The Tmax decreases from 67.19 °C to 61.08 °C as inlet−2 velocity increases from 1.2 m/s to 2.4 m/s, and the decrease rate is 9.09%. Compared with the heat flux of 300 W/cm2, the decrease rate increased by 2.6%. The ΔT decrease rate is around 6.69% as inlet−2 velocity increases from 1.2 m/s to 2.4 m/s, which is independent of the heat flux density.
- The decrease rate of the Tmax is about 16% as microchannels number increases from 10 to 48, and the decrease rate is independent of the inlet−2 velocity. The best temperature uniformity is obtained when the number of microchannels is equal to 16. When the microchannels number increases from 10 to 16, the ΔT decreases, and the decrease rate is independent of the inlet−2 velocity. However, when the microchannels number exceeds 16, the ΔT curve has an inflection point and begins to rise gradually, and shows a faster rising rate at the larger inlet−2 velocity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| TMC | traditional microchannel |
| MMC | manifold microchannel |
| MDMC | manifold dual-microchannel |
| MRFF−1 | microchannel region of flow field−1 |
| MRFF−2 | microchannel region of flow field−2 |
| cp,f | specific heat capacity of the fluid (J/(kg⋅°C)) |
| h | height (μm) |
| k | thermal conductivity (W/(m⋅°C)) |
| l | length (μm) |
| N | microchannel number |
| P | Pressure (Pa) |
| q | heat flux of heating surface (W/cm2) |
| T | temperature (°C) |
| ΔT | temperature different (°C) |
| u | velocity (m/s) |
| w | width (μm) |
| Subscript | |
| 1 | flow field−1 |
| 2 | flow field−2 |
| c | microchannel |
| div | divider |
| f | fluid |
| in | inlet |
| max | maximum |
| min | minimum |
| out | outlet |
| s | solid |
| Green letters | |
| μ | dynamic viscosity (Pa s) |
| ρ | density (kg/m3) |
References
- Wang, Y.; Wang, C.S.; Lian, P.Y.; Xue, S.; Liu, J.; Gao, W.; Shi, Y.; Wang, Z.H.; Yu, K.P.; Peng, X.L.; et al. Effect of temperature on electromagnetic performance of active phased array antenna. Electronics 2020, 9, 1211. [Google Scholar] [CrossRef]
- Liu, S.Y.; Yan, Y.F.; Zhou, Y.J.; Han, B.Q.; Wang, B.B.; Zhang, D.X.; Xue, S.; Wang, Z.H.; Yu, K.P.; Shi, Y.; et al. Thermal induced interface mechanical response analysis of SMT lead-free solder joint and its adaptive optimization. Micromachines 2022, 13, 908. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chen, C.; Zhou, Y.; Yang, C.; Song, G.; Hou, F.; Jiao, B.; Liu, R. Evaluation and optimization of a cross-rib micro-channel heat sink. Micromachines 2022, 13, 132. [Google Scholar] [CrossRef] [PubMed]
- Peng, M.; Chen, L.; Ji, W.; Tao, W. Numerical study on flow and heat transfer in a multi-jet microchannel heat sink. Int. J. Heat Mass Transf. 2020, 157, 119982. [Google Scholar] [CrossRef]
- Tuckerman, D.B.; Pease, R. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.; Zhou, M.; Li, J.; Qi, J. Optimum thermal design of interrupted microchannel heat sink with rectangular ribs in the transverse microchambers. Appl. Therm. Eng. 2013, 51, 880–889. [Google Scholar] [CrossRef]
- Hong, F.; Ping, C. Three dimensional numerical analyses and optimization of offset strip-fin microchannel heat sinks. Int. Commun. Heat Mass Transf. 2009, 36, 651–656. [Google Scholar] [CrossRef]
- Li, W.; Ma, J.; Alam, T.; Yang, F.; Khan, J.; Li, C. Flow boiling of HFE-7100 in silicon microchannels integrated with multiple micro-nozzles and reentry micro-cavities. Int. J. Heat Mass Transf. 2018, 123, 354–366. [Google Scholar] [CrossRef]
- Yang, M.; Cao, B.Y. Numerical study on flow and heat transfer of a hybrid microchannel cooling scheme using manifold arrangement and secondary channels. Appl. Therm. Eng. 2019, 159, 113896. [Google Scholar] [CrossRef]
- Wang, C.S.; Wei, T.C.; Shen, P.Y.; Liou, T.M. Lattice Boltzmann study of flow pulsation on heat transfer augmentation in a louvered microchannel heat sink. Int. J. Heat Mass Transf. 2020, 148, 119139. [Google Scholar] [CrossRef]
- Li, S.N.; Zhang, H.N.; Li, X.B.; Li, Q.; Li, F.C.; Qian, S.; Joo, S.W. Numerical study on the heat transfer performance of non-Newtonian fluid flow in a manifold microchannel heat sink. Appl. Therm. Eng. 2017, 115, 1213–1225. [Google Scholar] [CrossRef]
- Pourfattah, F.; Arani, A.A.A.; Babaie, M.R.; Nguyen, H.M.; Asadi, A. On the thermal characteristics of a manifold microchannel heat sink subjected to nanofluid using two-phase flow simulation. Int. J. Heat Mass Transf. 2019, 143, 118518. [Google Scholar] [CrossRef]
- Narrein, K.; Sivasankaran, S.; Ganesan, P. Numerical investigation of two-phase laminar pulsating nanofluid flow in a helical microchannel. Numer. Heat Transf. Part A Appl. 2016, 69, 921–930. [Google Scholar] [CrossRef]
- Alam, T.; Li, W.; Chang, W.; Yang, F.; Khan, J.; Li, C. A comparative study of flow boiling HFE-7100 in silicon nanowire and plainwall microchannels. Int. J. Heat Mass Transf. 2018, 124, 829–840. [Google Scholar] [CrossRef]
- Jones, B.J.; Garimella, S.V. Surface Roughness Effects on Flow Boiling in Microchannels. J. Therm. Sci. Eng. Appl. 2009, 1, 041007. [Google Scholar] [CrossRef]
- Li, H.W.; Li, Y.J.; Huang, B.H.; Xu, T.T. Flow Characteristics of the entrance region with roughness effect within rectangular microchannels. Micromachines 2019, 11, 30. [Google Scholar] [CrossRef]
- Ansari, D.; Kim, K.Y. Performance analysis of double-Layer microchannel heat sinks under non-uniform heating conditions with random hotspots. Micromachines 2017, 8, 54. [Google Scholar] [CrossRef]
- Wang, G.D.; Cheng, P.; Wu, H.Y. Unstable and stable flow boiling in parallel microchannels and in a single microchannel. Int. J. Heat Mass Transf. 2016, 50, 4297–4310. [Google Scholar] [CrossRef]
- Bahiraei, M.; Monavari, A.; Naseri, M.; Moayedi, H. Irreversibility characteristics of a modified microchannel heat sink operated with nanofluid considering different shapes of nanoparticles. Int. J. Heat Mass Transf. 2020, 151, 119359. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.J.; Zhang, Y.N.; Li, B.X.; Sundén, B. Analysis of laminar flow and heat transfer in an interrupted microchannel heat sink with different shaped ribs. J. Therm. Anal. Calorim. 2020, 140, 1259–1266. [Google Scholar] [CrossRef] [Green Version]
- Joseph, J.; Rehman, D.; Delanaye, M.; Morini, G.L.; Nacereddine, R.; Korvink, J.G.; Brandner, J.J. Numerical and experimental study of microchannel performance on flow maldistribution. Micromachines 2020, 11, 323. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.H.; Chen, X.M.; Zhao, Q.; Lu, M.X.; Hu, D.H.; Li, Q. Flow thermohydraulic characterization of hierarchical-manifold microchannel heat sink with uniform flow distribution. Appl. Therm. Eng. 2021, 198, 117510. [Google Scholar] [CrossRef]
- Choi, C.; Kim, M. Flow pattern based correlations of two-phase pressure drop in rectangular microchannels. Int. J. Heat Fluid Flow 2011, 32, 1199–1207. [Google Scholar] [CrossRef]
- Huang, Y.Q.; Mei, P.; Lu, Y.J.; Huang, R.; Yu, X.L.; Chen, Z.L.; Roskilly, A.P. A novel approach for Lithium-ion battery thermal management with streamline shape mini channel cooling plates. Appl. Therm. Eng. 2019, 157, 113623. [Google Scholar] [CrossRef]
- Harpole, G.M.; Eninger, J.E. Micro-channel heat exchanger optimization. In Proceedings of the 7th IEEE SEMI-THERM Symposium, Phoenix, AZ, USA, 12–14 February 1991; pp. 59–63. [Google Scholar]
- Copeland, D.; Takahira, H.; Nakayama, W. Manifold microchannel heat sinks: Theory and experiments. In Advances in Electronic Packaging; ASME: New York, NY, USA, 1995; Volume 3, pp. 9–15. [Google Scholar]
- Andhare, R.S.; Shooshtari, A.; Dessiatoun, S.V.; Ohadi, M.M. Heat transfer and pressure drop characteristics of a flat plate manifold microchannel heat exchanger in counter flow configuration. Appl. Therm. Eng. 2016, 96, 178–189. [Google Scholar] [CrossRef]
- Pan, Y.H.; Zhao, R.; Fan, X.H.; Nian, Y.L.; Cheng, W.L. Study on the effect of varying channel aspect ratio on heat transfer performance of manifold microchannel heat sink. Int. J. Heat Mass Transf. 2020, 163, 120461. [Google Scholar] [CrossRef]
- Kim, Y.H.; Chun, W.C.; Kim, J.T.; Pak, B.C.; Baek, B.J. Forced air cooling by using manifold microchannel heat sinks. KSME Int. J. 1998, 12, 709–718. [Google Scholar] [CrossRef]
- Zajac, P. Comparison of cooling performance of manifold and straight microchannel heat sinks using CFD simulation. In Proceedings of the 2021 22nd International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Virtual Event, 19–22 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Escher, W.; Brunschwiler, T.; Michel, B.; Poulikakos, D. Experimental investigation of an ultrathin manifold microchannel heat sink for liquid-cooled chips. J. Heat Transf. 2010, 132, 081402. [Google Scholar] [CrossRef]
- Ryu, J.H.; Choi, D.H.; Kim, S.J. Three-dimensional numerical optimization of a manifold microchannel heat sink. Int. J. Heat Mass Transf. 2003, 46, 1553–1562. [Google Scholar] [CrossRef]
- Everhart, L.; Jankowski, N.; Geil, B.; Bayba, A.; Ibitayo, D.; McCluskey, P. Manifold microchannel cooler for direct backside liquid cooling of SiC power devices. In Proceedings of the ASME 2007 5th International Conference on Nanochannels, Microchannels, and Minichannels, Puebla, Mexico, 18–20 June 2007; pp. 285–292. [Google Scholar]
- Tang, W.; Sun, L.C.; Liu, H.T.; Xie, G.; Mo, Z.Y.; Tang, J.G. Improvement of flow distribution and heat transfer performance of a self-similarity heat sink with a modification to its structure. Appl. Therm. Eng. 2017, 121, 163–171. [Google Scholar] [CrossRef]
- Yang, M.; Li, M.T.; Hua, Y.C.; Wang, W.; Cao, B.Y. Experimental study on single-phase hybrid microchannel cooling using HFE-7100 for liquid-cooled chips. Int. J. Heat Mass Transf. 2020, 160, 120230. [Google Scholar] [CrossRef]
- Van Erp, R.; Soleimanzadeh, R.; Nela, L.; Kampitsis, G.; Matioli, E. Co-designing electronics with microfluidics for more sustainable cooling. Nature 2020, 585, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Mudawar, I. Assessment of high-heat-flux thermal management schemes. IEEE Trans. Compon. Packag. Technol. 2001, 24, 122–141. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Upadhye, H.R. Extending the heat flux limit with enhanced microchannels in direct single-phase cooling of computer chips. In Proceedings of the IEEE Semiconductor Thermal Measurement and Management Symposium, San Jose, CA, USA, 15–17 March 2005; pp. 8–15. [Google Scholar]
- Acrivos, A.; Babcock, B.D.; Pigford, R.L. Flow distributions in manifolds. Chem. Eng. Sci. 1959, 10, 112–124. [Google Scholar] [CrossRef]
- Kim, S.; Choi, E.; Cho, Y.I. The effect of header shapes on the flow distribution in a manifold for electronic packaging applications. Int. Commun. Heat Mass Transf. 1995, 22, 329–341. [Google Scholar] [CrossRef]
- Drummond, K.P.; Back, D.; Sinanis, M.D.; Janes, D.B.; Peroulis, D.; Weibel, J.A.; Garimella, S.V. Characterization of hierarchical manifold microchannel heat sink arrays under simultaneous background and hotspot heating conditions. Int. J. Heat Mass Transf. 2018, 126, 1289–1301. [Google Scholar] [CrossRef]
- Drummond, K.P.; Back, D.; Sinanis, M.D.; Janes, D.B.; Peroulis, D.; Weibel, J.A.; Garimella, S.V. A hierarchical manifold microchannel heat sink array for high-heat-flux two-phase cooling of electronics. Int. J. Heat Mass Transf. 2018, 117, 319–330. [Google Scholar] [CrossRef] [Green Version]
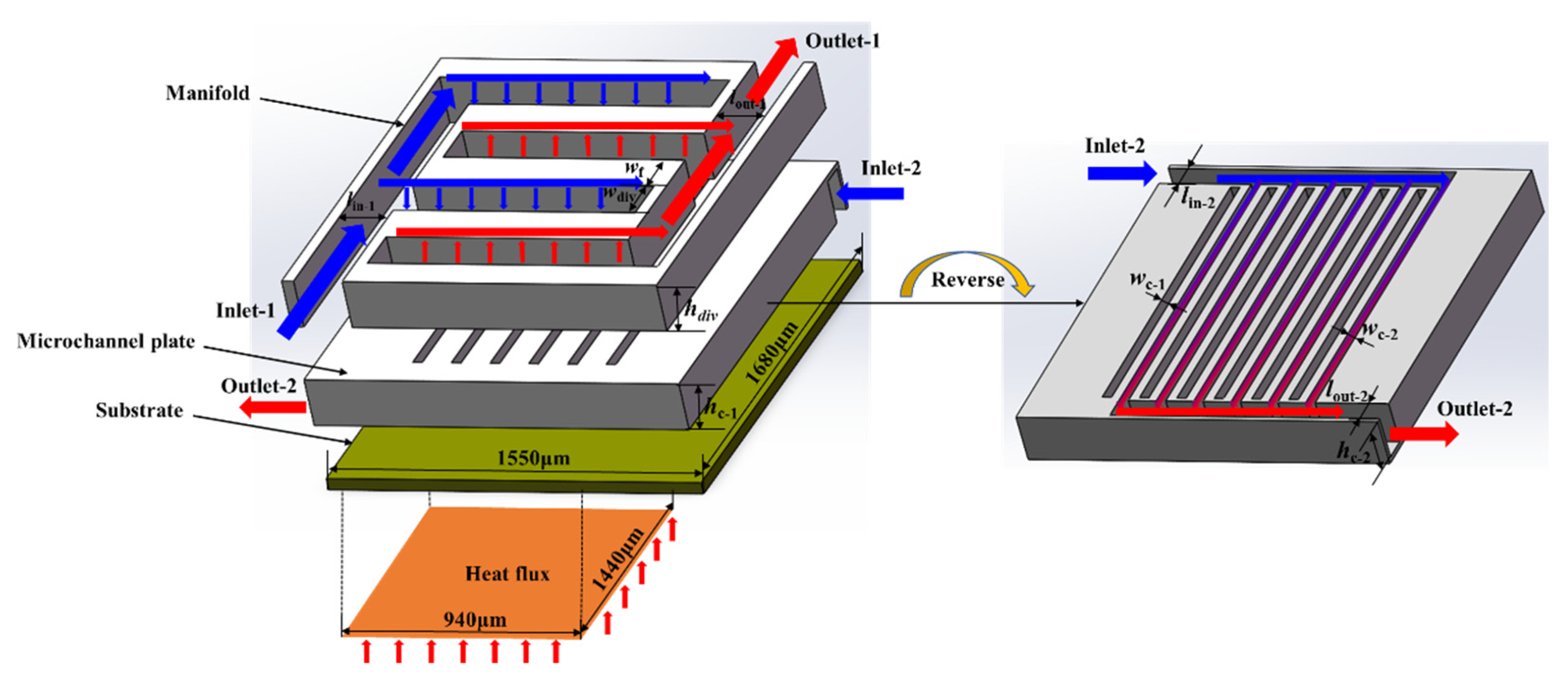





| Parameter | Variable | Dimension (μm) |
|---|---|---|
| Length of inlet−1 | lin−1 | 200 |
| Length of outlet−1 | lout−1 | 200 |
| Length of inlet−2 | lin−2 | 100 |
| Length of outlet−2 | lout−2 | 100 |
| Width of divider | wdiv | 200 |
| Height of divider | hdiv | 200 |
| Fin width | wf | 200 |
| Microchannel width of flow field−1 | wc−1 | 10, 20, 30, 40, 50 |
| Microchannel height of flow field−1 | hc−1 | 200 |
| Microchannel width of flow field−2 | wc−2 | 10, 20, 30, 40, 50 |
| Microchannel height of flow field−2 | hc−2 | 180 |
| Parameter | Variable | Dimension |
|---|---|---|
| Velocity of inlet−1 (m/s) | uin−1 | 1.2, 1.5, 1.8, 2.1, 2.4 |
| Pressure of outlet−1 (Pa) | Pout−1 | 0 |
| Velocity of inlet−2 (m/s) | uin−2 | 1.2, 1.5, 1.8, 2.1, 2.4 |
| Pressure of outlet−2 (Pa) | Pout−2 | 0 |
| Heat flux (W/cm2) | q | 300, 400, 500, 600, 700 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Lin, K.; Zhang, D.; Liu, S.; Han, B.; Wang, Z.; Yu, K.; Wu, W.; Ge, D.; Wang, C. A Novel Manifold Dual-Microchannel Flow Field Structure with High-Performance Heat Dissipation. Micromachines 2022, 13, 1420. https://doi.org/10.3390/mi13091420
Yang X, Lin K, Zhang D, Liu S, Han B, Wang Z, Yu K, Wu W, Ge D, Wang C. A Novel Manifold Dual-Microchannel Flow Field Structure with High-Performance Heat Dissipation. Micromachines. 2022; 13(9):1420. https://doi.org/10.3390/mi13091420
Chicago/Turabian StyleYang, Xing, Kabin Lin, Daxing Zhang, Shaoyi Liu, Baoqing Han, Zhihai Wang, Kunpeng Yu, Wenzhi Wu, Dongming Ge, and Congsi Wang. 2022. "A Novel Manifold Dual-Microchannel Flow Field Structure with High-Performance Heat Dissipation" Micromachines 13, no. 9: 1420. https://doi.org/10.3390/mi13091420
APA StyleYang, X., Lin, K., Zhang, D., Liu, S., Han, B., Wang, Z., Yu, K., Wu, W., Ge, D., & Wang, C. (2022). A Novel Manifold Dual-Microchannel Flow Field Structure with High-Performance Heat Dissipation. Micromachines, 13(9), 1420. https://doi.org/10.3390/mi13091420







