Diffusion-Slip Boundary Conditions for Isothermal Flows in Micro- and Nano-Channels
Abstract
:1. Introduction
2. Governing Equations and the New Models
2.1. Governing Equations
2.2. Slip boundary Conditions
2.3. Effects of Rarefaction
2.4. Analytical Solution
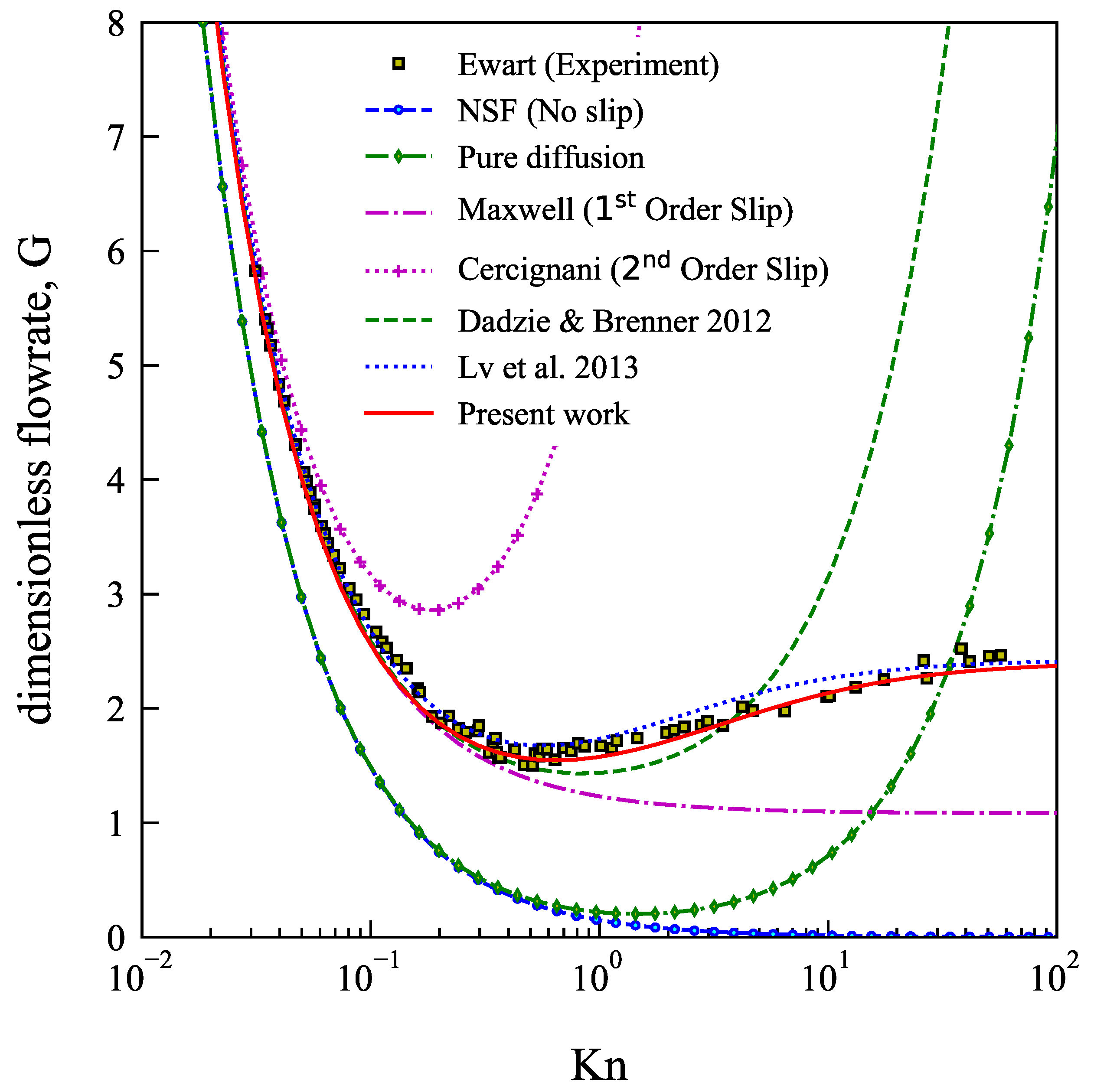
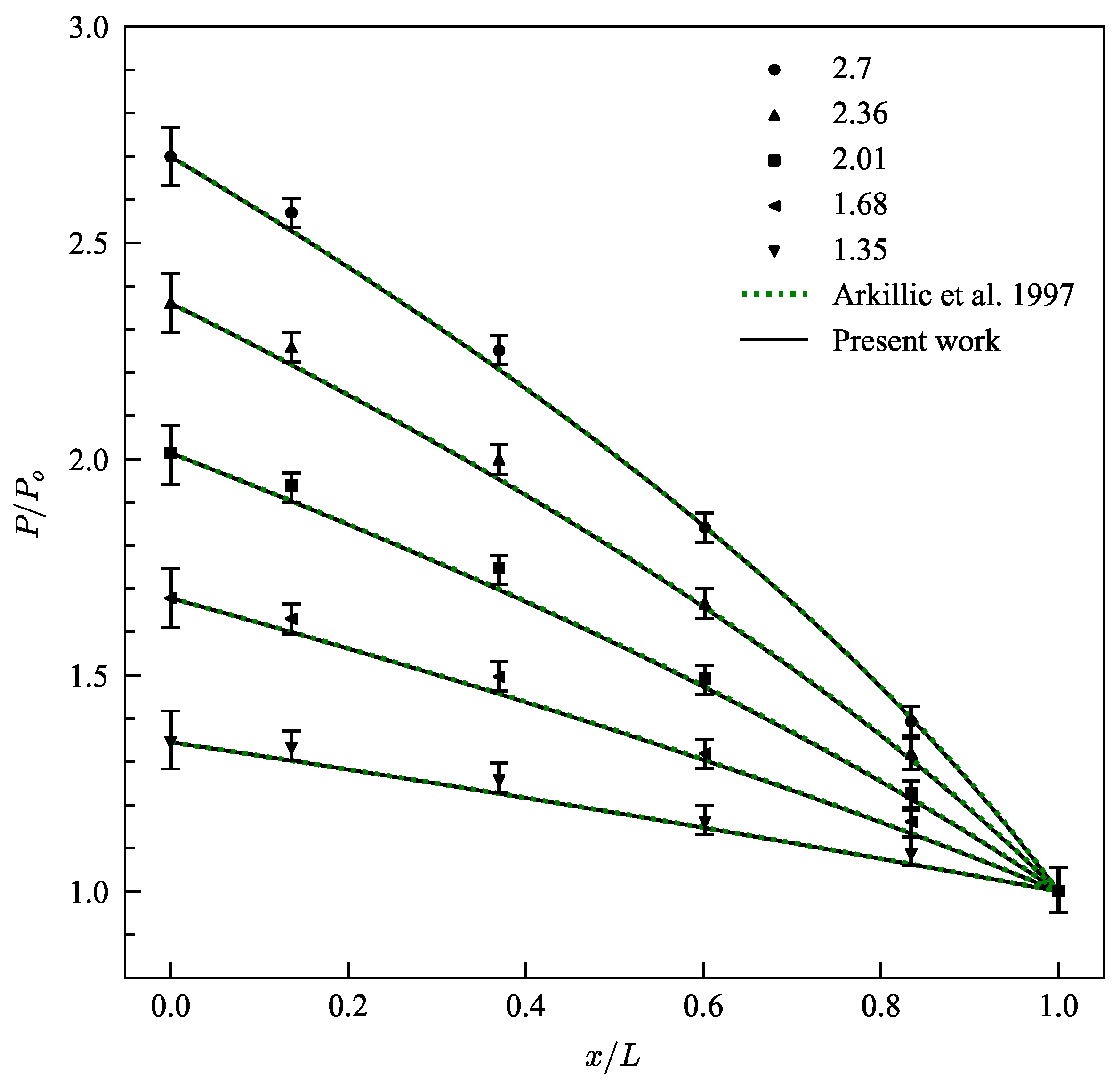
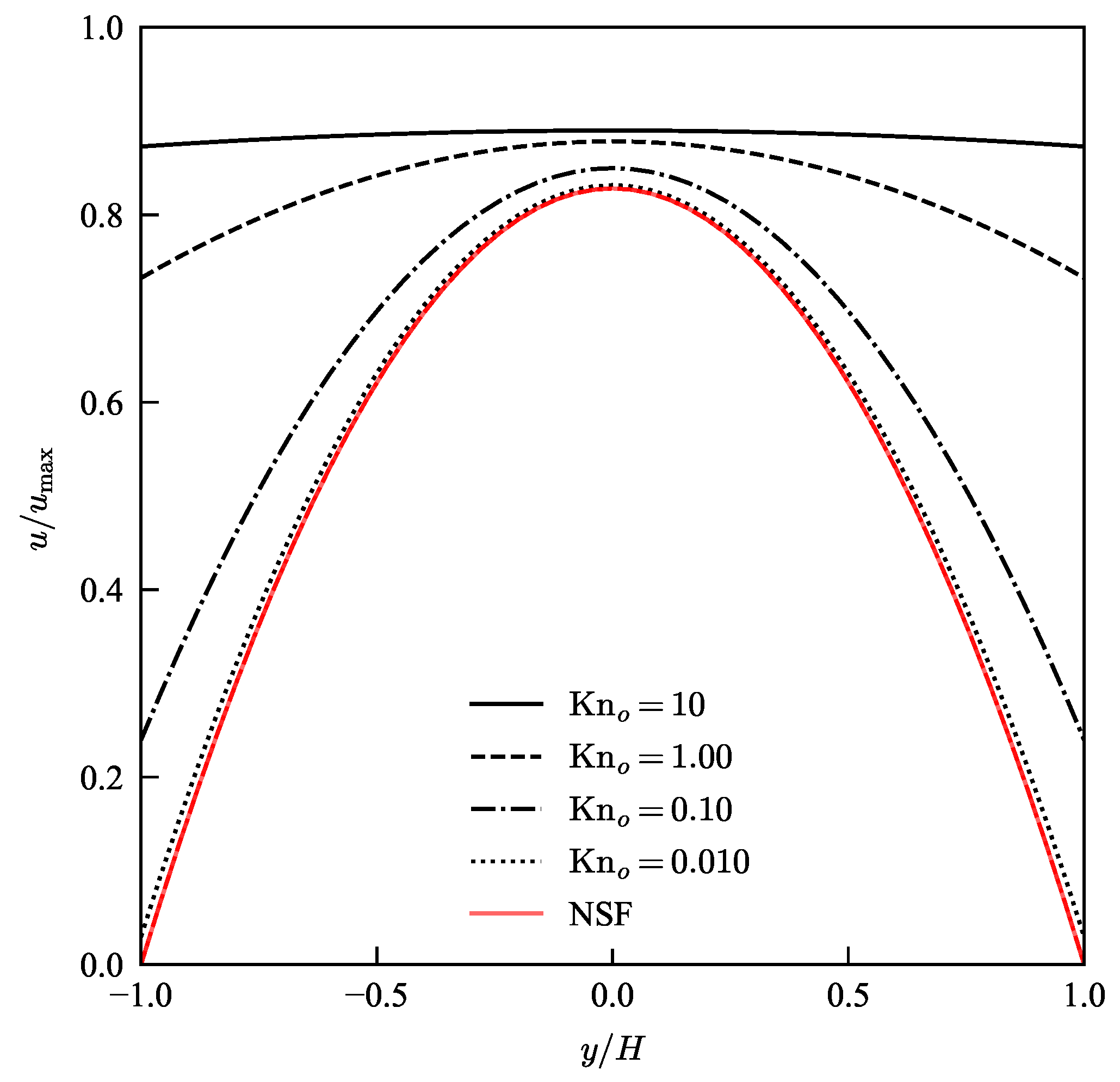
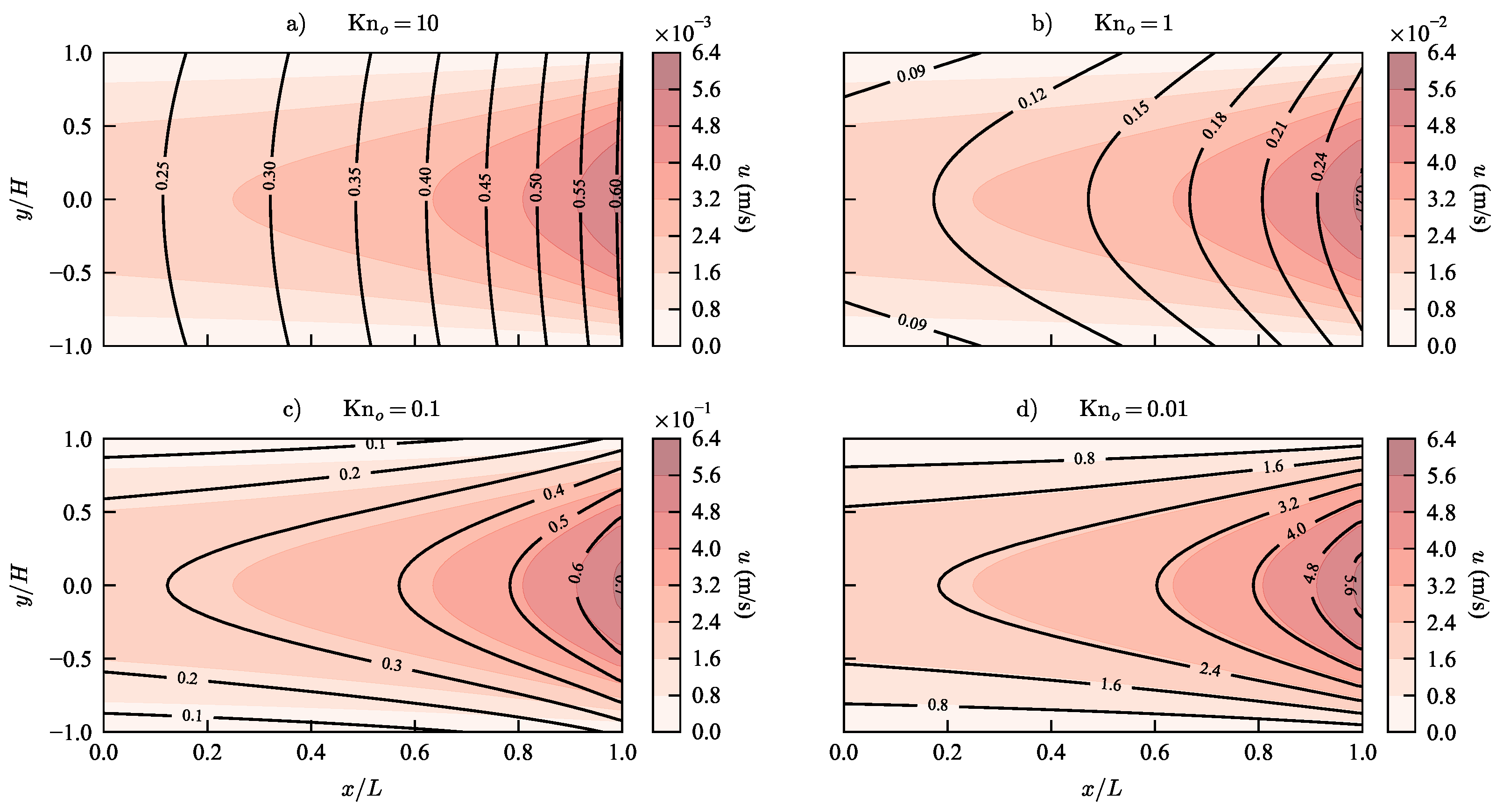
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Karniadakis, G.; Beskok, A.; Aluru, N. Microflows and Nanoflows: Fundamentals and Simulation; Springer: New York, NY, USA, 2006; Volume 29. [Google Scholar] [CrossRef]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices: Microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Gad-el Hak, M. The Fluid Mechanics of Microdevices—The Freeman Scholar Lecture. J. Fluids Eng. 1999, 121, 5–33. [Google Scholar] [CrossRef]
- Wei, T. All-in-one design integrates microfluidic cooling into electronic chips. Nature 2020, 585, 188–189. [Google Scholar] [CrossRef] [PubMed]
- Brenner, H. Beyond Navier–Stokes. Int. J. Eng. Sci. 2012, 54, 67–98. [Google Scholar] [CrossRef]
- Majumder, M.; Chopra, N.; Andrews, R.; Hinds, B.J. Enhanced flow in carbon nanotubes. Nature 2005, 438, 44. [Google Scholar] [CrossRef]
- Whitby, M.; Quirke, N. Fluid flow in carbon nanotubes and nanopipes. Nat. Nanotechnol. 2007, 2, 87. [Google Scholar] [CrossRef]
- Hemadri, V.; Varade, V.V.; Agrawal, A.; Bhandarkar, U. Investigation of rarefied gas flow in microchannels of non-uniform cross section. Phys. Fluids 2016, 28, 022007. [Google Scholar] [CrossRef]
- Knudsen, M. Die Gesetze der Molekularströmung und der inneren Reibungsströmung der Gase durch Röhren. Ann. Phys. 1909, 333, 75–130. [Google Scholar] [CrossRef] [Green Version]
- Arkilic, E.B.; Schmidt, M.A.; Breuer, K.S. Gaseous slip flow in long microchannels. J. Microelectromech. Syst. 1997, 6, 167–178. [Google Scholar] [CrossRef]
- Maurer, J.; Tabeling, P.; Joseph, P.; Willaime, H. Second-order slip laws in microchannels for helium and nitrogen. Phys. Fluids 2003, 15, 2613–2621. [Google Scholar] [CrossRef]
- Ewart, T.; Perrier, P.; Graur, I.A.; Méolans, J.G. Mass flow rate measurements in a microchannel, from hydrodynamic to near free molecular regimes. J. Fluid Mech. 2007, 584, 337–356. [Google Scholar] [CrossRef]
- Cheng, J.T.; Giordano, N. Fluid flow through nanometer-scale channels. Phys. Rev. E 2002, 65, 031206. [Google Scholar] [CrossRef]
- Kavokine, N.; Bocquet, M.L.; Bocquet, L. Fluctuation-induced quantum friction in nanoscale water flows. Nature 2022, 602, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Oxford Engineering Science Series; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Chakraborty, S.; Durst, F. Derivations of extended Navier–Stokes equations from upscaled molecular transport considerations for compressible ideal gas flows: Towards extended constitutive forms. Phys. Fluids 2007, 19, 088104. [Google Scholar] [CrossRef]
- Dongari, N.; Agrawal, A.; Agrawal, A. Analytical solution of gaseous slip flow in long microchannels. Int. J. Heat Mass Transf. 2007, 50, 3411–3421. [Google Scholar] [CrossRef]
- Brenner, H. Bi-velocity hydrodynamics. Physica A 2009, 388, 3391–3398. [Google Scholar] [CrossRef]
- Reddy, M.H.L.; Dadzie, S.K.; Ocone, R.; Borg, M.K.; Reese, J.M. Recasting Navier–Stokes equations. J. Phys. Commun. 2019, 3, 105009. [Google Scholar] [CrossRef]
- Stamatiou, A.; Dadzie, S.K.; Reddy, M.L. Investigating enhanced mass flow rates in pressure-driven liquid flows in nanotubes. J. Phys. Commun. 2019, 3, 125012. [Google Scholar] [CrossRef]
- Maxwell, J.C. VII. On stresses in rarified gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. 1879, 170, 231–256. [Google Scholar] [CrossRef]
- Duan, Z. Second-order gaseous slip flow models in long circular and noncircular microchannels and nanochannels. Microfluid Nanofluid 2012, 12, 805–820. [Google Scholar] [CrossRef]
- Hemadri, V.; Agrawal, A.; Bhandarkar, U. Determination of tangential momentum accommodation coefficient and slip coefficients for rarefied gas flow in a microchannel. Sādhanā 2018, 43, 1–7. [Google Scholar] [CrossRef]
- Adachi, T.; Sambasivam, R.; Durst, F.; Filimonov, D. Analytical treatments of micro-channel and micro-capillary flows. In Proceedings of the 3rd Micro and Nano Flows Conference, Thessaloniki, Greece, 22–24 August 2011; Brunel University: Thessaloniki, Greece, 2011; pp. 22–24. [Google Scholar]
- Veltzke, T.; Thöming, J. An analytically predictive model for moderately rarefied gas flow. J. Fluid Mech. 2012, 698, 406–422. [Google Scholar] [CrossRef]
- Dongari, N.; Durst, F.; Chakraborty, S. Predicting microscale gas flows and rarefaction effects through extended Navier–Stokes–Fourier equations from phoretic transport considerations. Microfluid Nanofluid 2010, 9, 831–846. [Google Scholar] [CrossRef]
- Brenner, H. Navier–Stokes revisited. Phys. Fluids 2005, 349, 60–132. [Google Scholar] [CrossRef]
- Brenner, H. Diffuse volume transport in fluids. Physica A 2010, 389, 4026–4045. [Google Scholar] [CrossRef]
- Dadzie, S.K.; Brenner, H. Predicting enhanced mass flow rates in gas microchannels using nonkinetic models. Phys. Rev. E 2012, 86, 036318. [Google Scholar] [CrossRef]
- Lockerby, D.A.; Reese, J.M.; Emerson, D.R.; Barber, R.W. Velocity boundary condition at solid walls in rarefied gas calculations. Phys. Rev. E 2004, 70, 017303. [Google Scholar] [CrossRef]
- Jaishankar, A.; McKinley, G.H. An analytical solution to the extended Navier–Stokes equations using the Lambert W function. AIChE J. 2014, 60, 1413–1423. [Google Scholar] [CrossRef]
- Reddy, L.M.H.; Dadzie, S.K. Effects of molecular diffusivity on shock-wave structures in monatomic gases. Phys. Rev. E 2021, 104, 035111. [Google Scholar] [CrossRef]
- Stops, D. The mean free path of gas molecules in the transition regime. J. Phys. D 1970, 3, 685. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. Report: A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophys. Eng. 1999, 3, 43–77. [Google Scholar] [CrossRef]
- Lockerby, D.A.; Reese, J.M.; Gallis, M.A. Capturing the Knudsen layer in continuum-fluid models of non-equilibrium gas flows. AIAA J. 2005, 43, 1391–1393. [Google Scholar] [CrossRef]
- Lv, Q.; Liu, X.; Wang, E.; Wang, S. Analytical solution to predicting gaseous mass flow rates of microchannels in a wide range of Knudsen numbers. Phys. Rev. E 2013, 88, 013007. [Google Scholar] [CrossRef]
- Michalis, V.K.; Kalarakis, A.N.; Skouras, E.D.; Burganos, V.N. Rarefaction effects on gas viscosity in the Knudsen transition regime. Microfluid Nanofluid 2010, 9, 847–853. [Google Scholar] [CrossRef]
- Cercignani, C. Mathematical Methods in Kinetic Theory; Springer: New York, NY, USA, 1969. [Google Scholar] [CrossRef]
- Sreekanth, A.K. Slip flow through long circular tubes. In Proceedings of the Sixth International Symposium on Rarefied Gas Dynamics, Cambridge, MA, USA, 22–26 July 1969; Academic Press: New York, NY, USA, 1969; pp. 667–680. [Google Scholar]
- Pong, K.C.; Ho, C.M.; Liu, J.; Tai, Y.C. Non-linear pressure distribution in uniform microchannels. Am. Soc. Mech. Eng. 1994, 197, 51. [Google Scholar]
- Dadzie, S.K.; Dongari, N. Transition regime analytical solution to gas mass flow rate in a rectangular micro channel. AIP Conf. Proc. 2012, 1501, 720–726. [Google Scholar] [CrossRef]
- Christou, C.; Dadzie, S.K. On the numerical simulation of rarefied gas flows in micro-channels. J. Phys. Commun. 2018, 2, 035002. [Google Scholar] [CrossRef]
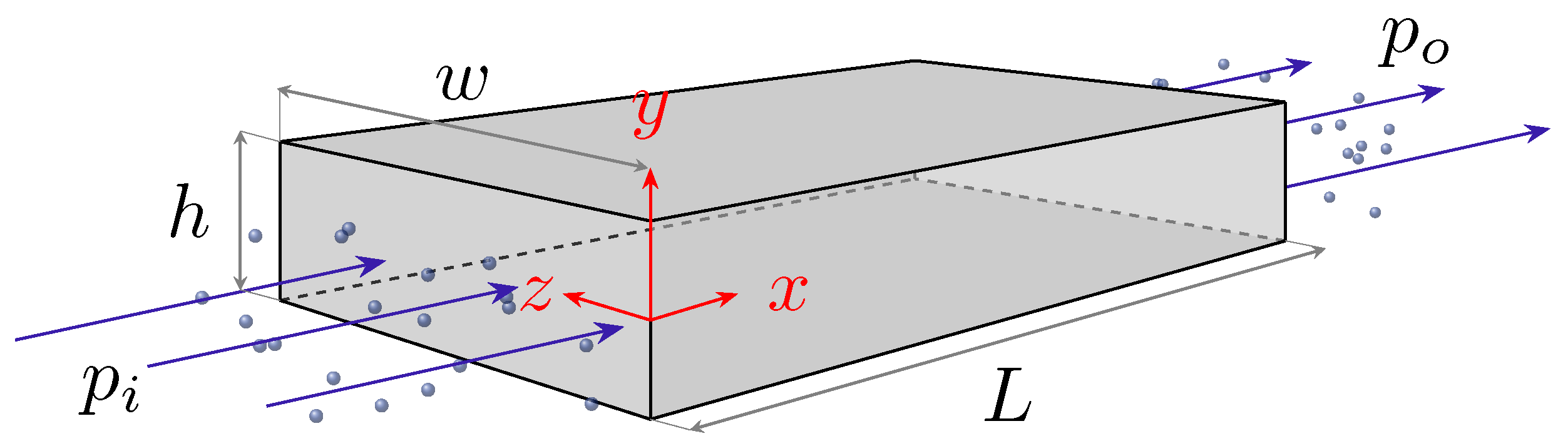

| Experimental Parameters | Value |
|---|---|
| Gas used | Helium |
| Length, L | 9.39 ± 0.1 mm |
| Height, h | 9.38 ± 0.2 m |
| Width, w | 492 ± 1 m |
| Avg. Temperature, T | 296 K |
| Viscosity, | Pa s |
| Gas Constant, | 2078.5 J/(kg K) |
| Inlet Pressure range | 60.4–109,825 Pa |
| Outlet Pressure range | 12.2–22,633 Pa |
| Average Kn range | 0.027–50.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomy, A.M.; Dadzie, S.K. Diffusion-Slip Boundary Conditions for Isothermal Flows in Micro- and Nano-Channels. Micromachines 2022, 13, 1425. https://doi.org/10.3390/mi13091425
Tomy AM, Dadzie SK. Diffusion-Slip Boundary Conditions for Isothermal Flows in Micro- and Nano-Channels. Micromachines. 2022; 13(9):1425. https://doi.org/10.3390/mi13091425
Chicago/Turabian StyleTomy, Alwin Michael, and S. Kokou Dadzie. 2022. "Diffusion-Slip Boundary Conditions for Isothermal Flows in Micro- and Nano-Channels" Micromachines 13, no. 9: 1425. https://doi.org/10.3390/mi13091425
APA StyleTomy, A. M., & Dadzie, S. K. (2022). Diffusion-Slip Boundary Conditions for Isothermal Flows in Micro- and Nano-Channels. Micromachines, 13(9), 1425. https://doi.org/10.3390/mi13091425








